A smeared crack modeling framework accommodating multi-directional fracture at finite strains

Abstract

A generic smeared crack modeling framework predicated on the deformation gradient decomposition (DGD) approach is proposed for use in dynamic fracture problems at finite strains, accommodating failure along multiple mutually orthogonal fracture planes embedded within an independently defined bulk material model. Within this constitutive framework, the traction equilibrium conditions imposed at each failure surface are used to determine the associated crack displacements stored as internal state variables. In general, the enforcement of interfacial equilibrium entails the implicit solution of a non-linear system of equations within the constitutive update procedure. However, if inertial effects arising due to the relative motion of the fractured material are incorporated within the model, the traction equilibrium conditions are shown to give rise to corresponding dynamic equations of motion governing the time-evolution of the crack opening displacements. For dynamic problems, an explicit time-integration procedure is devised to efficiently update the material state, subject to a set of internal frictionless contact constraints to prevent material inversion. The efficacy of the proposed modeling framework is investigated through several benchmark dynamic fracture problems run within the explicit finite element code DYNA3D.

1 Introduction

The numerical modeling of fracture in the finite element method (FEM) poses several significant challenges which have spawned a plethora of competing methodologies. Because the underlying continuum theory does not admit strong discontinuities in the trial solution space for the displacement field, various enhancements to the classical theory have been developed, the majority of which may be lumped into two primary categories: models which represent cracks in a discrete sense, and models which employ a diffused representation of fracture through material damage and softening.

Notable modeling approaches belonging to the former category include: the extended finite element method (X-FEM) (Moës and Belytschko 2002), and cohesive zone models (CZM) inserted at inter-element boundaries (Xu and Needleman 1994; Camacho and Ortiz 1996; Ortiz and Pandolfi 1999) or embedded within locally enriched finite element domains (E-FEM) (da Costa et al. 2009; Armero and Linder 2008; Kim and Armero 2017). The aforementioned strategies offer several advantages: they handle crack tracking through the resolution of discrete crack paths, and achieve good accuracy at coarser levels of discretization.

In contrast, diffused crack modeling approaches encompass: continuum damage mechanics (CDM) (Ambroziak and Kłosowski 2007), strong discontinuity approaches (SDA) (Oliver et al. 1999; Armero and Linder 2009), phase-field methods (PFM) (Francfort and Marigo 1998; Borden et al. 2012; Hofacker and Miehe 2013), and smeared crack models (SCM) (Rashid 1968). Despite advances in various discrete crack modeling methods, compelling justifications for the continued use and development of diffused crack modeling techniques still exist: because they operate primarily at the level of the constitutive model, they are generally more computationally efficient, more easily implemented within existing commercial finite element frameworks, and readily compatible with different discretization methods and element formulations.

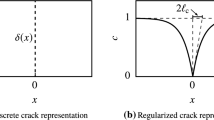
SCM and CDM are regarded as closely related methodologies, in the sense that fracture and material separation are approximated by a degradation of the constitutive response in a determined failure direction (Armero and Oller 2000). CDM typically presumes that material damage manifests in the form of distributed micro-crack networks. To correctly represent such phenomena while maintaining a consistent dissipation of energy, the ensuing damage field must be regularized to avoid spurious mesh-dependent localization within a zone of vanishingly small size (Ambroziak and Kłosowski 2007). In contrast, SCM seeks to represent individual cracks at the continuum scale which manifest as strong discontinuities in the regularized displacement field.

A key disadvantage of SCM concerns the phenomenon of stress locking (Rots et al. 1985; Rots 1988), wherein the constrained orientations of the damage planes within the continuum leads to the development of non-physical stresses in the elements surrounding the crack path. Stress locking may be viewed as a deficiency in the local kinematics used to represent the displacement discontinuity. Degrading the material in an isotropic fashion partially overcomes this issue, but results in a nonphysical degradation of the transverse strength of the material, and may lead to an incorrect prediction of the crack path biased by the mesh design (Cervera and Chiumenti 2006).

Recent modeling efforts for meta-materials and composites have further motivated the development of SCM approaches to account for anisotropy and complex material behavior that can be coupled more directly to the fracture phenomenology. For example, in materials such as fiber reinforced composites, pervasive failure at the micro-scale is more appropriately represented in a diffused sense, while larger cracks are more amenable to a discrete representation. In such cases, it is potentially advantageous to allow a transition between discrete and smeared representations of cracks (Lu et al. 2019), facilitated by a statement of energetic equivalence between damage and fracture dissipation mechanisms (Mazars and Pijaudier-Cabot 1996).

Notably, the recently proposed deformation gradient decomposition (DGD) approach of Leone (2015) enables generic coupling of an embedded CZM to an underlying bulk constitutive model within a modular SCM framework. The approach postulates an additive decomposition of the deformation gradient due to a discontinuous displacement enrichment, closely resembling the kinematic enhancements employed by SDA/E-FEM. In contrast to such enhancements which are typically introduced and solved for at the element level, the displacement jumps are instead solved for within the constitutive modeling framework, such that traction continuity across the cracked continuum interface is effectively enforced in a point-wise sense. The chosen deformation gradient-based decomposition was also demonstrated to overcome issues of stress locking under large shearing deformations which otherwise manifest nonphysical stresses in conventional strain-based SCM approaches with fixed crack directions. The modularity of the DGD approach offers several distinct advantages for the modeling of failure in complicated materials at finite strains and was successfully applied to emulate kink-band propagation within fiber reinforced composites (Bergan and Leone 2016). However, the use of an embedded extrinsic CZM in this setting introduces many of the numerical problems inherent to such models, such as traction locking and time-discontinuity of the constitutive stress during the instantaneous transition to separation (Papoulia et al. 2003). Moreover, inertial effects during crack opening are presently neglected within this framework.

The presently proposed SCM framework may be viewed as an extension of the DGD approach to accommodate multiple (up to 3) intersecting cracks, as well as localized inertial effects due to crack opening. As in the original DGD approach, the treatment of discontinuities is addressed within the constitutive framework, involving a coupled internal solution procedure for the opening displacements which locally enforce traction equilibrium across each cracked interface, subject to a set of additional frictionless contact constraints. In the general case, the resulting inequality-constrained non-linear system of equations must be solved implicitly in an iterative fashion (e.g., using a Newton-Raphson procedure within an overarching active set strategy). However, if inertial effects are considered relevant and are incorporated within the modeling framework, the traction equilibrium conditions give rise to decoupled equations of motion governing the time-evolution of each crack, each of which may be efficiently updated using an explicit time integrator.

The primary advantages of the proposed methodology are that: it is computationally efficient; it remains suitable at finite strains; it accommodates the development of multiple orthogonal cracks, and thus partially alleviates the effects of stress locking; it accounts for inertial effects which are potentially relevant in the modeling of dynamic fracture propagation; and it permits the incorporation of complicated constitutive models within a modular framework.

The remainder of this paper is organized as follows: Sect. 2 provides an overview of the chosen kinematic idealization for a homogenized continuum with multiple discrete cracks; Sect. 3 presents the generic constitutive modeling framework motivated by thermodynamic arguments and Sect. 3.3 proposes an efficient update procedure for the explicit time-evolution of dynamic crack models incorporating inertial effects; Sect. 4 provides a specific example of a model incorporating plasticity and brittle fracture formulated within the proposed framework, followed by a numerical evaluation of the resulting model on a number of benchmark test problems in Sect. 5 and Sect. 6 concludes with a discussion of the obtained results, limitations of the modeling framework, and intended future work.

2 RVE idealization, kinematics, and inertia of embedded cracks

In continuum damage mechanics (CDM), the representation of a damaged region of material consists of envisioning a representative volume element (RVE) whose macroscopic deformation state is characterized by the continuum deformation gradient ${\mathbf {F}}$. Generically, the continuum RVE may be regarded as consisting of two distinct phases: the solid (or bulk) phase, and the void (or crack) phase. In the reference configuration of the material, the crack phase is presumed to occupy a set of zero measure, such that the initial mass density of the RVE is equal to that of the solid phase.

The majority of CDM approaches regard the precise arrangement and orientation of cracks within the RVE as microscopic details which are represented in a distributed, or homogenized sense via one or more damage parameters which serve to degrade the macroscopic properties of the material. In contrast, the present SCM idealization considers the explicit representation of a finite number of discrete cracks in the form of strong discontinuities. Each such crack is regarded as distinct and planar, passing through the centroid of the undeformed RVE, and fully separating the solid material into two halves of equal volume.

Consequently, the arrangement of the solid constituent is such that the bulk material deforms homogeneously (almost everywhere) according to the bulk deformation gradient ${\mathbf {F}}^b$, which depends implicitly upon the orientations and opening displacements of each crack in the material. The relative opening displacements of each such crack are regarded within the present framework as internal state variables belonging to the macroscopic constitutive model.

When represented in this fashion, the RVE-scale fractures are dissociated from—and agnostic of—the discretization at the continuum scale, thereby circumventing the difficulties inherent to discrete fracture modeling approaches which rely upon element- or nodal-enrichments to the displacement field or splitting of discrete fractures along inter-element interfaces.

2.1 Geometric idealization of the RVE domain

Within the proposed modeling framework, a representative volume $\varOmega \subset {\mathbb {R}}^3$ is presumed to have finite extent, encompassing a material neighborhood with its centroid at $\bar{{\mathbf {X}}} = \frac{1}{| \varOmega |} \int _{\varOmega } {\mathbf {X}} \, d\varOmega$. The uncracked geometry of the bulk material is idealized as an ellipsoidal region with possibly unequal axes. This stands in contrast with the work of Leone (2015), wherein the RVE domain is idealized as a rectangular cuboid.

The geometric characteristics (orientation and dimensions) of the ellipsoidal RVE associated with a given material point are informed by the chosen discretization method (e.g., the isoparametric element Jacobian), or approximated with a minimum knowledge of the material point’s volume.

The metric tensor ${\mathbf {G}}$ characterizing the ellipsoidal geometry of the RVE domain can be expressed in terms of the ellipsoid’s principal axes ${\mathbf {g}}_i$ and corresponding diameters $d_i$:

$$\begin{aligned} {\mathbf {G}} = \sum _{i=1}^3 \left( \frac{d_i}{2} \right) ^2 {\mathbf {g}}_i \otimes {\mathbf {g}}_i . \end{aligned}$$

(1)

The volume of the ellipsoid is computed as

$$\begin{aligned} | \varOmega | = \frac{4}{3} \pi \sqrt{\det ({\mathbf {G}})}. \end{aligned}$$

(2)

Within $\varOmega$, the bulk material is idealized as being intersected by a total number of $N_{\text {cracks}}$ fracture planes passing through the centroid of the RVE. For each crack index $c \in \left\{ 1, \ldots , N_{\text {cracks}} \right\}$, let $\varGamma _c$ denote the discrete fracture surface with corresponding unit normal ${\mathbf {N}}_c$ defined in the reference configuration of the material (refer to Fig. 1). The surface area of the ellipse formed by the intersection of $\varGamma _c$ with $\varOmega$ is given by

$$\begin{aligned} | \varGamma _c | = \pi \frac{\sqrt{\det ({\mathbf {G}})}}{\left| \left| {\mathbf {N}}_c \right| \right| _{{\mathbf {G}}}} , \end{aligned}$$

(3)

where $\left| \left| {\mathbf {N}}_c \right| \right| _{{\mathbf {G}}} \equiv \sqrt{\langle {\mathbf {N}}_c, {\mathbf {N}}_c \rangle _{{\mathbf {G}}}}$ is the induced norm of the inner product $\langle {\mathbf {N}}_c, {\mathbf {N}}_c \rangle _{{\mathbf {G}}} \equiv {\mathbf {N}}_c \cdot {\mathbf {G}} \cdot {\mathbf {N}}_c$.

For a given crack plane $\varGamma _c$, its associated characteristic RVE fracture length scale is defined as $\ell _c \equiv \frac{| \varOmega |}{| \varGamma _c |}$, which may be expressed in terms of the induced norm:

$$\begin{aligned} \ell _c = \frac{4}{3} \left| \left| {\mathbf {N}}_c \right| \right| _{{\mathbf {G}}} . \end{aligned}$$

(4)

2.2 Kinematics of a homogenized continuum with multiple discrete cracks

Let the macroscopic deformation of the continuum RVE be denoted ${\mathbf {F}} = \nabla \bar{{\mathbf {x}}}$, arising from the continuous deformation field $\bar{{\mathbf {x}}} = \chi ({\mathbf {X}},t)$ supplied by the chosen discretization method (i.e. the interpolated finite element displacement field).

Fig. 1

Depiction of a representative volume $\varOmega$ with embedded discontinuities in its reference (left), damaged/intermediate (bottom), and deformed (right) configurations

Within $\varOmega$, the inhomogeneous motion of the cracked solid material is characterized by the following discontinuous deformation field:

$$\begin{aligned} {\mathbf {x}} = {\mathbf {x}}^b + \sum _{c=1}^{N_{\text {cracks}}} \frac{1}{2} {\mathscr {H}} ({\mathbf {N}}_c) \, {\mathbf {u}}_c , \end{aligned}$$

(5)

where ${\mathbf {x}}^b$ is the homogeneous part of the bulk material motion, ${\mathbf {u}}_c \in {\mathbb {R}}^3$ are the (assumed constant) relative opening displacement vectors for each crack, and ${\mathscr {H}} ({\mathbf {N}}_c)$ denotes the discontinuous Heaviside step function:

$$\begin{aligned} {\mathscr {H}} ({\mathbf {N}}_c) = \left\{ \begin{array}{cc} -1 &{} \quad \forall \, ({\mathbf {X}} - \bar{{\mathbf {X}}}) \cdot {\mathbf {N}}_c < 0 \\ +1 &{} \quad \forall \, ({\mathbf {X}} - \bar{{\mathbf {X}}}) \cdot {\mathbf {N}}_c \ge 0 \end{array} \right. . \end{aligned}$$

(6)

The macroscopic deformation gradient ${\mathbf {F}}$ may be regarded as a homogenization of $\nabla {\mathbf {x}}$ over $\varOmega$, i.e.

$$\begin{aligned} {\mathbf {F}} = \frac{1}{| \varOmega |} \int _{\varOmega } \nabla {\mathbf {x}} \, d\varOmega . \end{aligned}$$

(7)

From (5) and (7) it follows that ${\mathbf {F}}$ may be expressed in the form of an additive decomposition:

$$\begin{aligned} {\mathbf {F}} = {\mathbf {F}}^b + \sum _{c=1}^{N_{\text {cracks}}} \frac{{\mathbf {u}}_c}{\ell _c} \otimes {\mathbf {N}}_c, \end{aligned}$$

(8)

where

$$\begin{aligned} {\mathbf {F}}^b \equiv \frac{1}{| \varOmega |} \int _{\varOmega } \nabla {\mathbf {x}}^b \, d\varOmega , \end{aligned}$$

(9)

denotes the (assumed homogenous) deformation gradient in the bulk material, and each crack displacement vector ${\mathbf {u}}_c$ is effectively homogenized over its associated characteristic RVE fracture length scale $\ell _c$.

For notational convenience, the following matrices with variable dimension are defined:

$$\begin{aligned}&{\mathbf {U}} \equiv \left[ \begin{array}{ccc} {\mathbf {u}}_1&\ldots&{\mathbf {u}}_{N_{\text {cracks}}} \end{array} \right] , \end{aligned}$$

(10)

$$\begin{aligned}&\varvec{\ell } \equiv \left[ \begin{array}{ccc} \ell _1 &{} \hdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \hdots &{} \ell _{N_{\text {cracks}}} \end{array} \right] , \end{aligned}$$

(11)

$$\begin{aligned}&{\mathbf {Q}} \equiv \left[ \begin{array}{ccc} {\mathbf {N}}_1&\ldots&{\mathbf {N}}_{N_{\text {cracks}}} \end{array} \right] ^T, \end{aligned}$$

(12)

where ${\mathbf {U}}$ is a $3 \times N_{\text {cracks}}$ matrix whose columns contain the individual crack displacement vectors, $\varvec{\ell }$ is an $N_{\text {cracks}} \times N_{\text {cracks}}$ matrix whose diagonal entries are the characteristic length scales associated with each crack, and ${\mathbf {Q}}$ is a $N_{\text {cracks}} \times 3$ matrix whose rows contain the crack normal vectors. The additive decomposition from (8) is succinctly expressed in terms of the above matrices as:

$$\begin{aligned} {\mathbf {F}} = {\mathbf {F}}^b + {\mathbf {U}} \varvec{\ell }^{-1} {\mathbf {Q}} , \end{aligned}$$

(13)

implicitly accounting for a variable number of cracks.

Alternatively, ${\mathbf {F}}$ may be multiplicatively decomposed into a sequence of deformation processes due to homogenized damage (represented via ${\mathbf {F}}^d$) and bulk material deformation (via ${\mathbf {F}}^b$), in analog to the decomposition proposed by Lee (1969) in the setting of finite deformation elasto-plasticity:

$$\begin{aligned} {\mathbf {F}} = {\mathbf {F}}^b {\mathbf {F}}^d, \qquad {\mathbf {F}}^d \equiv {\mathbf {1}} + \tilde{{\mathbf {U}}} \varvec{\ell }^{-1} {\mathbf {Q}}, \end{aligned}$$

(14)

where $\tilde{{\mathbf {U}}} = {{\mathbf {F}}^b}^{-1} {\mathbf {U}}$, such that the columns of $\tilde{{\mathbf {U}}}$ constitute the “co-rotational” opening displacements $\tilde{{\mathbf {u}}}_c$ for each crack, i.e.

$$\begin{aligned} \tilde{{\mathbf {U}}} \equiv \left[ \begin{array}{ccc} \tilde{{\mathbf {u}}}_1&\ldots&\tilde{{\mathbf {u}}}_{N_{\text {cracks}}} \end{array} \right] . \end{aligned}$$

(15)

Figure 1 depicts the configurational arrangement of the fractured bulk material following each deformation process.

Note that two cracks with normals ${\mathbf {N}}_1$ and ${\mathbf {N}}_2$ defined orthogonal to one another in the reference configuration will not necessarily remain orthogonal in the deformed configuration of the RVE. While this aspect of the model may affect the resulting fracture behavior of the material, its impact is expected to be relatively minor in cases where the bulk material undergoes only modest distortional deformations.

2.2.1 Unique determination of kinematic state variables

In the proposed modeling framework, $\tilde{{\mathbf {U}}}$ and ${\mathbf {Q}}$ are retained as internal kinematic state variables. For a known damaged state of the material expressed via $\tilde{{\mathbf {U}}}$ (and ${\mathbf {Q}}$), the damage deformation gradient ${\mathbf {F}}^d$ may be directly determined from (14). Conversely, if ${\mathbf {F}}^d$ is known, $\tilde{{\mathbf {U}}}$ is required to be uniquely determined by an appropriately defined inverse relationship. This requirement ultimately facilitates the developments in Sect. 3.2, entailing the specification of independent traction-separation laws associated with each embedded crack.

Denote by ${\mathbf {Q}}^\dagger$ the matrix pseudo-inverse of ${\mathbf {Q}}$. If all crack orientations are distinct and $N_{\text {cracks}} \le 3$, then ${\mathbf {Q}} {\mathbf {Q}}^\dagger = {\mathbf {1}}_{N_\text {cracks} \times N_{\text {cracks}}}$. Under the aforementioned conditions, the individual crack displacements are uniquely determined via

$$\begin{aligned} \tilde{{\mathbf {U}}} = \left( {\mathbf {F}}^d - {\mathbf {1}} \right) {\mathbf {Q}}^\dagger \varvec{\ell }. \end{aligned}$$

(16)

Provided ${\mathbf {Q}} {\mathbf {Q}}^T$ is non-singular (when all crack orientations are sufficiently distinct), the pseudo-inverse may be computed via

$$\begin{aligned} {\mathbf {Q}}^\dagger = {\mathbf {Q}}^T \left( {\mathbf {Q}} {\mathbf {Q}}^T \right) ^{-1} . \end{aligned}$$

(17)

If $N_{\text {cracks}} = 3$, ${\mathbf {Q}}^\dagger$ reduces to the direct inverse ${\mathbf {Q}}^{-1}$, and in the special case where all crack normals are mutually orthogonal (encompassing the case when $N_{\text {cracks}} = 1$), the pseudo-inverse of ${\mathbf {Q}}$ is simply its transpose ${\mathbf {Q}}^T$.

2.2.2 Frictionless contact constraints

To properly account for the conditions of crack closure, internal contact constraints must be enforced such that the material does not invert under compressive loading. To accommodate these conditions, a set of inequality gap constraint equations enforcing frictionless contact under the conditions of crack closure are associated with each relative opening displacement vector such that

$$\begin{aligned} g_c = \frac{1}{\ell _c} \tilde{{\mathbf {u}}}_c \cdot \text {cof} ({\mathbf {F}}^d_{c-1}) \cdot {\mathbf {N}}_c \ge 0 \quad \forall c = 1, \ldots , N_{\text {cracks}}, \end{aligned}$$

(18)

where the opening of each crack is presumed to occur in sequence, and the damage deformation gradient ${\mathbf {F}}^d_c$ immediately following the opening of crack c assumes the following recursive form:

$$\begin{aligned} {\mathbf {F}}^d_c = {\mathbf {F}}^d_{c-1} + \frac{1}{\ell _c} \tilde{{\mathbf {u}}}_c \otimes {\mathbf {N}}_c, \qquad {\mathbf {F}}^d_0 = {\mathbf {1}}. \end{aligned}$$

(19)

By the matrix determinant lemma, it may be shown that

$$\begin{aligned} g_c = \det ({\mathbf {F}}^d_c) - \det ({\mathbf {F}}^d_{c-1}) \ge 0, \end{aligned}$$

(20)

thereby enforcing that the incremental change in volume following the sequential opening of each crack must be non-negative.

The chosen representation of the kinematic inequality constraints expressed in (18) gives rise to associated KKT multipliers $p_c \ge 0 \, \forall c$ which physically correspond to the contact pressure across each interface. The resulting KKT conditions are thus

$$\begin{aligned} g_c \ge 0, \quad p_c \ge 0, \quad p_c \, g_c = 0 \quad \forall c = 1, \ldots , N_{\text {cracks}}. \end{aligned}$$

(21)

2.3 Internal kinetic energy associated with the damage deformation process

Consider the material motion ${\mathbf {x}}^d = \chi ^d ({\mathbf {X}}) \, \forall {\mathbf {X}} \in \varOmega$ associated with the damage deformation process:

$$\begin{aligned} {\mathbf {x}}^d = {\mathbf {X}} + \sum _{c=1}^{N_{\text {cracks}}} \frac{1}{2} {\mathscr {H}} ({\mathbf {N}}_c) \, \tilde{{\mathbf {u}}}_c , \end{aligned}$$

(22)

whose homogenized deformation gradient yields:

$$\begin{aligned} {\mathbf {F}}^d = \frac{1}{| \varOmega |} \int _{\varOmega } \nabla {\mathbf {x}}^d \, dV . \end{aligned}$$

(23)

This motion characterizes the irrotational, rigid separation of the bulk material across all of its embedded fracture planes, inducing no homogenous deformation in the solid phase.

For elasto-dynamics problems, the corresponding velocity field

$$\begin{aligned} \dot{{\mathbf {x}}}^d = \sum _{c=1}^{N_{\text {cracks}}} \frac{1}{2} {\mathscr {H}} ({\mathbf {N}}_c) \, \dot{\tilde{{\mathbf {u}}}}_c , \end{aligned}$$

(24)

has zero mean value over $\varOmega$, and is therefore decoupled from the homogenized motion $\dot{\bar{{\mathbf {x}}}} = \dot{{\mathbf {x}}}^b$. Consequently, the relative separation of the damaged material generates no kinetic energy via ${\bar{T}} \equiv \frac{1}{2} \rho \, \dot{\bar{{\mathbf {x}}}} \cdot \dot{\bar{{\mathbf {x}}}}$ which would otherwise give rise to inertial body forces at the scale of the original continuum (i.e. finite element) problem.

Nonetheless, the relative crack opening velocities $\dot{\tilde{{\mathbf {u}}}}_c$ may become arbitrarily large, and contribute to a form of kinetic energy via $\frac{1}{2} \rho \, \dot{{\mathbf {x}}}^d \cdot \dot{{\mathbf {x}}}^d$ measurable at sub-RVE length scales, whose homogenization over $\varOmega$ is denoted:

$$\begin{aligned} T^d \equiv \frac{1}{|\varOmega |} \int _{\varOmega } \frac{1}{2} \rho \, \dot{{\mathbf {x}}}^d \cdot \dot{{\mathbf {x}}}^d \, dV . \end{aligned}$$

(25)

Henceforth, $T^d$ is referred to as the “internal kinetic energy density,” and is assumed to be exclusively associated with the damage deformation process.

The vast majority of continuum damage models generally assume $T^d = 0$, but this overlooks the potential importance of localized inertial effects in dynamically driven fracture processes and imposes discretization size limits. Moreover, the consideration of internal kinetic energy within the proposed modeling framework aids in regularizing the constitutive relations governing damage evolution—a feature which will be exploited in Sect. 3.3 to devise a stable and efficient material update procedure.

Assuming that the bulk material density $\rho$ remains spatially constant over $\varOmega$, the homogenized internal kinetic energy reduces to:

$$\begin{aligned} T^d = \frac{\rho }{8} \sum _{a,b=1}^{N_{\text {cracks}}} (\dot{\tilde{{\mathbf {u}}}}_a \cdot \dot{\tilde{{\mathbf {u}}}}_b) \frac{1}{|\varOmega |} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV. \end{aligned}$$

(26)

As demonstrated in Appendix 1, the homogenized integral products $\frac{1}{|\varOmega |} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV$ can be reasonably well-approximated by the following inner product:

$$\begin{aligned} \frac{1}{|\varOmega |} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV \approx \frac{16}{9} \left\langle \frac{{\mathbf {N}}_a}{\ell _a}, \frac{{\mathbf {N}}_b}{\ell _b} \right\rangle _{{\mathbf {G}}} , \end{aligned}$$

(27)

and the internal kinetic energy density may therefore be expressed in terms of previously defined tensorial quantities:

$$\begin{aligned} T^d (\dot{{\mathbf {F}}}^d) = \frac{2 \rho }{9} \, \text {tr} \left( \dot{{\mathbf {F}}}^d {\mathbf {G}} ( \dot{{\mathbf {F}}}^d )^T \right) , \end{aligned}$$

(28)

where the time-rate of ${\mathbf {F}}^d$ is equivalently expressed as

$$\begin{aligned} \dot{{\mathbf {F}}}^d = \dot{\tilde{{\mathbf {U}}}} \varvec{\ell }^{-1} {\mathbf {Q}}. \end{aligned}$$

(29)

For the special case where the crack orientations ${\mathbf {N}}_c$ are aligned with the principal axes of ${\mathbf {G}}$, a relatively simple and convenient form for $T^d$ arises which yields the following partition into separable kinetic energy contributions from each crack:

$$\begin{aligned} T^d (\dot{{\mathbf {F}}}^d) = \sum _{c=1}^{N_{\text {cracks}}} T^c (\dot{\tilde{{\mathbf {u}}}}^c), \qquad T^c (\dot{\tilde{{\mathbf {u}}}}^c) = \frac{1}{2} \frac{m^c}{(\ell ^c)^2} \dot{\tilde{{\mathbf {u}}}}^c \cdot \dot{\tilde{{\mathbf {u}}}}^c, \end{aligned}$$

(30)

where $m^c = \rho \left( \frac{\ell ^c}{2} \right) ^2 \, \forall c$, and it follows that

$$\begin{aligned} \frac{d}{dt} \frac{\partial T^d}{\partial \dot{{\mathbf {F}}}^d} = \sum _{c=1}^{N_{\text {cracks}}} m^c \frac{\ddot{\tilde{{\mathbf {u}}}}^c}{\ell ^c} \otimes {\mathbf {N}}^c. \end{aligned}$$

(31)

3 Generalized constitutive framework

The preceding section focused exclusively on the kinematics of the idealized RVE domain. Up to this point, no specification has been made regarding the constitutive behaviors associated with the bulk material phase or the embedded cohesive cracks. In what follows, a modular constitutive modeling framework is established in which the decomposed deformation measures ${\mathbf {F}}^b$ and ${\mathbf {F}}^d$ are ascribed to independently defined constitutive responses associated with the bulk and void phases, respectively. We begin by postulating a statement of the total potential energy collectively stored by the material which exploits the chosen kinematic decomposition, giving rise to distinct bulk and damage free energies. The development at this stage is entirely generic and makes no specification of the chosen idealizations for either the bulk or cohesive constitutive behaviors. Particular examples of the implemented framework are considered later on in Sect. 4.

3.1 Derivation of constitutive relations

Suppose that the free energy per unit initial RVE volume attributable to the bulk material is expressed as $\psi ^b ({\mathbf {F}}^b)$, while the free energy per unit surface area associated with each cracked interface in the material is expressed as $\varPsi _c ({\mathbf {F}}^d) \, \forall c = 1,\ldots ,N_{\text {cracks}}$.

The total (homogenized) free energy per unit RVE volume ${\bar{\psi }}$ is related to the free energy in the combined media (including internal kinetic energy) via

$$\begin{aligned} \int _{\varOmega } {\bar{\psi }} \, dV = \int _{\varOmega } \psi ^b \, dV + \sum _{c=1}^{N_{\text {cracks}}} \int _{\varGamma _c} \varPsi _c \, dA + \int _{\varOmega } T^d \, dV. \end{aligned}$$

(32)

Assuming homogeneity of all quantities within their respective domains of integration:

$$\begin{aligned} {\bar{\psi }} = \psi ^b + \psi ^d + T^d, \end{aligned}$$

(33)

where

$$\begin{aligned} \psi ^d ({\mathbf {F}}^d) \equiv \sum _{c=1}^{N_{\text {cracks}}} \frac{\varPsi _c}{\ell _c} \end{aligned}$$

(34)

denotes the total homogenized damage strain energy per unit volume.

From the Clausius-Duhem inequality (under isothermal conditions, and subject to the internal contact constraints), the total dissipation in the material is given by

$$\begin{aligned} {\mathcal {D}} = \varvec{\tau } : {\mathbf {L}} - \dot{{\bar{\psi }}} \ge 0, \end{aligned}$$

(35)

balancing the rate of change in the stored free energy ${\bar{\psi }}$ with the rate of external work. The macroscopic Kirchhoff stress $\varvec{\tau }$ is work-conjugated with the homogenized velocity gradient ${\mathbf {L}}$, these being the measures of deformation and stress supplied/required by the numerical discretization (i.e. finite element) method.

Given the chosen multiplicative decomposition of the deformation gradient in equation (14), the total velocity gradient ${\mathbf {L}} = \dot{{\mathbf {F}}} {\mathbf {F}}^{-1}$ is additively decomposed as

$$\begin{aligned} {\mathbf {L}} = {\mathbf {L}}^b + {\mathbf {F}}^b {\mathbf {L}}^d {{\mathbf {F}}^b}^{-1} , \end{aligned}$$

(36)

where

$$\begin{aligned} {\mathbf {L}}^b \equiv \dot{{\mathbf {F}}}^b {{\mathbf {F}}^b}^{-1} , \qquad {\mathbf {L}}^d \equiv \dot{{\mathbf {F}}}^d {{\mathbf {F}}^d}^{-1} . \end{aligned}$$

(37)

It follows that

$$\begin{aligned}&{\mathcal {D}} = \left( \varvec{\tau } - \frac{\partial \psi ^b}{\partial {\mathbf {F}}^b} {{\mathbf {F}}^b}^T \right) : {\mathbf {L}}^b \nonumber \\&\quad + \left( {{\mathbf {F}}^b}^{T} \varvec{\tau } {{\mathbf {F}}^b}^{-T} - \left[ \frac{\partial \psi ^d}{\partial {\mathbf {F}}^d} + \frac{d}{dt} \frac{\partial T^d}{\partial \dot{{\mathbf {F}}}^d} \right] {{\mathbf {F}}^d}^T \right) : {\mathbf {L}}^d .\nonumber \\ \end{aligned}$$

(38)

For arbitrary, independent rates of deformation ${\mathbf {L}}^b$ and ${\mathbf {L}}^d$, the procedure of Coleman and Noll (Lubliner 1972, 1973) is used to infer the expression for the macroscopic Kirchhoff stress:

$$\begin{aligned} \varvec{\tau } = \frac{\partial \psi ^b}{\partial {\mathbf {F}}^b} {{\mathbf {F}}^b}^T, \end{aligned}$$

(39)

and the conditions governing dynamic traction equilibrium across all embedded cohesive interfaces:

$$\begin{aligned} \frac{\partial \psi ^d}{\partial {\mathbf {F}}^d} + \frac{d}{dt} \frac{\partial T^d}{\partial \dot{{\mathbf {F}}}^d} = {{\mathbf {F}}^b}^{T} {\mathbf {P}}, \end{aligned}$$

(40)

where ${\mathbf {P}} = \varvec{\tau } {\mathbf {F}}^{-T}$ is the macroscopic first Piola-Kirchhoff stress tensor.

The expression provided by equation (40) contains an inertial term $\frac{d}{dt} \frac{\partial T^d}{\partial \dot{{\mathbf {F}}}^d}$ associated with the relative opening motion of all embedded cracks. If the internal kinetic energy $T^d$ assumes the general form given by equation (30), the inertial term appears as:

$$\begin{aligned} \frac{d}{dt} \frac{\partial T^d}{\partial \dot{{\mathbf {F}}}^d} = \frac{4\rho }{9} \, \ddot{{\mathbf {F}}}^d {\mathbf {G}} . \end{aligned}$$

(41)

Alternatively, if inertial effects are considered negligible ($T^d \approx 0$), then the traction equilibrium conditions under quasi-static conditions are recovered:

$$\begin{aligned} \frac{\partial \psi ^d}{\partial {\mathbf {F}}^d} = {{\mathbf {F}}^b}^{T} {\mathbf {P}}. \end{aligned}$$

(42)

If $\psi ^b ({\mathbf {F}}^b,{\mathbf {q}}^b)$ and $\psi ^d ({\mathbf {F}}^d,{\mathbf {q}}^d)$ additionally depend upon independent sets of internal variables ${\mathbf {q}}^b$ and ${\mathbf {q}}^d$, then the dissipation function ultimately appears as:

$$\begin{aligned} {\mathcal {D}} = - \frac{\partial \psi ^b}{\partial {\mathbf {q}}^b} \cdot \dot{{\mathbf {q}}}^b - \frac{\partial \psi ^d}{\partial {\mathbf {q}}^d} \cdot \dot{{\mathbf {q}}}^d \ge 0. \end{aligned}$$

(43)

For example, these additional dissipation terms are relevant to the formulation of plasticity in the bulk phase (where ${\mathbf {q}}^b$ corresponds to the plastic strain), or damage in the cohesive interfaces (where ${\mathbf {q}}^d$ comprise one or more cohesive damage parameters).

Crucially, the chosen ordering of the bulk and damage deformation processes ensures that the macroscopic Kirchhoff stress $\varvec{\tau }$ is directly equal to the Kirchhoff stress in the bulk material $\varvec{\tau }^b \equiv \frac{\partial \psi ^b}{\partial {\mathbf {F}}^b} {{\mathbf {F}}^b}^T$. Moreover, the macroscopic Cauchy stress $\varvec{\sigma }$ is obtained by a simple scaling of the (effective) Cauchy stress in the bulk material $\varvec{\sigma }^b$:

$$\begin{aligned} \varvec{\sigma } = \frac{1}{J^d} \varvec{\sigma }^b, \end{aligned}$$

(44)

where $J^d \equiv \det ({\mathbf {F}}^d) \ge 1$ guarantees a reduction in the effective stress due to crack expansion.

In spite of the scaled reduction of the effective stress by $1/J^d$, the bulk material is still capable of sustaining stresses transverse to the failure directions. This is evidenced more clearly by examining the net differential force $\text {d} {\mathbf {f}} = \varvec{\sigma } \cdot \text {cof} ({\mathbf {F}}) \cdot {\mathbf {N}} \text {d}A$ acting upon an internal surface with initial normal ${\mathbf {N}}$ and differential area $\text {d}A$. Consider the case where a single crack exists such that ${\mathbf {F}}^d = {\mathbf {1}} + \ell _1^{-1} \tilde{{\mathbf {u}}}_1 \otimes {\mathbf {N}}_1$ and $\text {cof} ({\mathbf {F}}^d) = J^d {\mathbf {1}} - \ell _1^{-1} \tilde{{\mathbf {u}}}_1 \otimes {\mathbf {N}}_1$. For all transverse directions ${\mathbf {N}}$ perpendicular to the crack direction ${\mathbf {N}}_1$, the differential force is seen to be $\text {d} {\mathbf {f}} = \varvec{\sigma }^b \cdot \text {cof} ({\mathbf {F}}^b) \cdot {\mathbf {N}} \text {d}A$, such that transverse forces are altogether sustained by the material. This stands in contrast with other SCM approaches which induce an isotropic degradation of the material stiffness, rendering such methods incapable of supporting transverse loads.

3.2 Specialization for potential-based cohesive traction-separations laws

Let each cohesive potential $\varPsi _c (\tilde{{\mathbf {u}}}_c)$ depend upon its corresponding co-rotational opening displacement $\tilde{{\mathbf {u}}}_c$. The associated cohesive traction vector $\tilde{{\mathbf {t}}}_c \equiv \frac{\partial \varPsi _c}{\partial \tilde{{\mathbf {u}}}_c}$ across a given cracked interface in the damaged (intermediate) configuration of the RVE is presumed to be derived from a generic potential-based cohesive traction-displacement model, as suggested by Ortiz and Pandolfi (1999).

Accordingly, one may show:

$$\begin{aligned} \frac{\partial \psi ^d}{\partial {\mathbf {F}}^d} = \tilde{{\mathbf {T}}}^d {{\mathbf {Q}}^\dagger }^T, \end{aligned}$$

(45)

where the columns of the $3 \times N_{\text {cracks}}$ matrix $\tilde{{\mathbf {T}}}^d \equiv \frac{\partial \psi ^d}{\partial \tilde{{\mathbf {U}}}}$ consist of the individual cohesive traction vectors associated with each crack, namely:

$$\begin{aligned} \tilde{{\mathbf {T}}}^d = \left[ \begin{array}{ccc} \tilde{{\mathbf {t}}}_1&\ldots&\tilde{{\mathbf {t}}}_{N_{\text {cracks}}} \end{array} \right] . \end{aligned}$$

(46)

The dynamic traction equilibrium relations expressed by equation (40) may be rearranged with the aid of equations (29), (41), and (45) to provide an expression for the acceleration of all co-rotational crack displacements:

$$\begin{aligned} \ddot{\tilde{{\mathbf {U}}}} = \frac{9}{4} \frac{1}{\rho } \left[ {{\mathbf {F}}^b}^{T} {\mathbf {P}} - \tilde{{\mathbf {T}}}^d {{\mathbf {Q}}^\dagger }^T \right] {\mathbf {G}}^{-1} {\mathbf {Q}}^\dagger \varvec{\ell }. \end{aligned}$$

(47)

For the special case where all ${\mathbf {N}}_c$ are mutually orthogonal and aligned with the principal directions of the characteristic length tensor ${\mathbf {G}}$, the separable equations of motion for each crack are obtained:

$$\begin{aligned} \frac{\rho \, \ell _c}{4} \ddot{\tilde{{\mathbf {u}}}}_c + \tilde{{\mathbf {t}}}_c = {{\mathbf {F}}^b}^{T} {\mathbf {P}} \cdot {\mathbf {N}}_c \quad \forall c = 1,\ldots ,N_{\text {cracks}} . \end{aligned}$$

(48)

Henceforth, it is assumed for the sake of simplicity that the conditions of mutual crack orthogonality are satisfied, such that equation (48) remains valid.

3.2.1 Failure initiation criterion

Let $\tilde{{\mathbf {t}}}^* = {{\mathbf {F}}^b}^{T} {\mathbf {P}} \cdot {\mathbf {N}}^*$ denote the traction acting upon a candidate crack plane with normal ${\mathbf {N}}^*$ that is orthogonal to all other existing cracks (i.e. ${\mathbf {N}}^* \cdot {\mathbf {N}}_c = 0 \, \forall c$). A new crack is presumed to form when the normal component of the candidate traction $\sigma ^* = \tilde{{\mathbf {t}}}^* \cdot {\mathbf {N}}^*$ exceeds the critical stress at rupture initiation $\sigma _f$ (a model parameter). This assumes mode I fracture initiation associated with brittle material behavior, as will be explored in the remainder of this work.

Among all candidate crack normal directions, the one which maximizes the expression for the normal traction $\sigma ^*$ is obtained via maximization of the following Rayleigh quotient:

$$\begin{aligned} {\mathbf {N}}_{N_{\text {cracks}}+1} = \arg \max _{{\mathbf {N}}^* \in {\mathbb {R}}^3} \frac{{\mathbf {N}}^* \cdot ({\mathbf {Q}}_\perp {{\mathbf {F}}^b}^{T} {\mathbf {P}} {\mathbf {Q}}_\perp ) \cdot {\mathbf {N}}^*}{{\mathbf {N}}^* \cdot {\mathbf {N}}^*} , \end{aligned}$$

(49)

where the sub-space projection operator ${\mathbf {Q}}_\perp$ is defined:

$$\begin{aligned} {\mathbf {Q}}_\perp \equiv {\mathbf {1}} - \sum _{c=1}^{N_{\text {cracks}}} {\mathbf {N}}_c \otimes {\mathbf {N}}_c . \end{aligned}$$

(50)

The solution to the above is equivalent to the canonical maximum principal stress failure criterion, such that new crack normal directions will coincide with the direction of maximum principal stress in the following projected (and symmetrized) tensor: ${\mathbf {Q}}_\perp \text {sym} ({{\mathbf {F}}^b}^{T} {\mathbf {P}}) {\mathbf {Q}}_\perp$.

3.3 Explicit constitutive update procedure

Consider a discretization in time t. A modular procedure is sought for the purpose of efficiently updating the macroscopic state of the material from time $t_n$ to $t_{n+1}$. Several alternatives are possible: if inertial effects are considered negligible, the quasi-static traction equilibrium conditions given by equation (42) may be solved at the constitutive level for the updated crack opening displacements; otherwise, if inertial effects during crack opening are included by the model, the equilibrium conditions arising from equation (40) must be solved. When solved implicitly for the updated opening displacements, either approach will necessitate an iterative Newton-Raphson procedure to enforce traction equilibrium, subject to the inequality gap constraint equations (18). This may result in an untenable computational overhead within the constitutive update procedure.

Alternatively, a fully explicit algorithm applied to the dynamic equations supplied by (40) offers a more efficient solution strategy, albeit at the expense of conditional stability in the constitutive update. If the time steps taken during the finite element analysis are already sufficiently small (such as for applications in explicit dynamics), the stability requirements of the constitutive update become less onerous and do not necessitate further or severe reductions in the existing time step size. The remainder of this section outlines the resulting explicit update procedure implemented and explored in this work.

First, the crack opening equations of motion given by equation (48) are solved directly for the crack accelerations $\ddot{\tilde{{\mathbf {u}}}}_c |_{t_{n}}$ at time $t_n$. These in turn may be used to update the independent crack opening displacements in time via an explicit Newmark algorithm:

$$\begin{aligned}&\dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n+1/2}} = \dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n-1/2}} + \ddot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n}} \, \varDelta t_{n}, \end{aligned}$$

(51)

$$\begin{aligned}&\tilde{{\mathbf {u}}}_{c} |_{t_{n+1}} = \tilde{{\mathbf {u}}}_{c} |_{t_{n}} + \dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n+1/2}} \, \varDelta t_{n+1/2}, \end{aligned}$$

(52)

where $\varDelta t_{n+1/2} \equiv t_{n+1} - t_{n}$ and $\varDelta t_{n} \equiv t_{n+1/2} - t_{n-1/2}$ with $t_{n+1/2} \equiv \frac{1}{2} (t_{n+1} - t_{n})$.

Next, the internal contact constraints are enforced using a two-step predictor-corrector approach. During the predictor step, the unconstrained crack displacements are integrated from time $t_n$ to $t_{n+1}$ according to the Newmark time-integration scheme previously described, and assuming that the contact pressures $p_c |_{t_n} = 0 \, \forall c$ remain inactive. During the subsequent corrector step, the internal contact gap constraints from equation (18) are explicitly enforced (in sequence) by retractions along the return directions ${\mathbf {n}}_c = \text {cof} ({\mathbf {F}}^d_{c-1}) \cdot {\mathbf {N}}_c$:

$$\begin{aligned}&{\hat{u}}_c = \frac{\tilde{{\mathbf {u}}}_c |_{t_{n+1}} \cdot {\mathbf {n}}_c}{{\mathbf {n}}_c \cdot {\mathbf {n}}_c} , \end{aligned}$$

(53)

$$\begin{aligned}&\dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n+1/2}} \leftarrow \dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n+1/2}} - \frac{{\hat{u}}_c}{\varDelta t_{n+1/2}} \, {\mathbf {n}}_c , \end{aligned}$$

(54)

$$\begin{aligned}&\tilde{{\mathbf {u}}}_{c} |_{t_{n+1}} \leftarrow \tilde{{\mathbf {u}}}_{c} |_{t_{n+1}} - {\hat{u}}_c \, {\mathbf {n}}_c . \end{aligned}$$

(55)

These modifications are only carried out if the normalized displacement gap ${\hat{u}}_c < 0$ is negative, signaling violation of the gap constraint.

Once the crack opening displacements have been determined, the end-step kinematic state of the material is fully specified, and the constituent bulk and cohesive models may be independently updated in a modular fashion. Finally, the failure initiation criterion from equation (49) is checked to see if a new crack should be instantiated.

The resulting explicit constitutive update procedure outlined below helps to illustrate the modularity of the established framework, in that any preferred choices for the bulk or cohesive material behavior can be used interchangeably.

• 1.) Solve for the crack accelerations $\ddot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n}}$ using equation (48).

• 2.) Given the stored history variables for $\tilde{{\mathbf {u}}}_{c} |_{t_{n}}$, $\dot{\tilde{{\mathbf {u}}}}_{c} |_{t_{n-1/2}}$, integrate the trial mid-step crack velocity and end-step crack displacement using equations (51) and (52), respectively.

• 3.) Loop over all cracks in sequence, and compute the displacement gap ${\hat{u}}_c$ from equation (53). If ${\hat{u}}_c<0$:

  • 3a.) Correct the mid-step crack velocity and end-step crack displacement via equations (51) and (52), respectively.

• 4.) Given ${\mathbf {F}} |_{t_{n+1}}$ and the updated end-step displacements $\tilde{{\mathbf {u}}}_{c} |_{t_{n+1}}$, compute ${\mathbf {F}}^d |_{t_{n+1}}$ and ${\mathbf {F}}^b |_{t_{n+1}}$ from equation (14).

• 5.) Update the stress in the bulk phase using ${\mathbf {F}}^b |_{t_{n+1}}$.

• 6.) Check for failure using equation (49), and conditionally insert and initialize a new cohesive interface.

• 7.) Update the stress in each cohesive interface using $\tilde{{\mathbf {u}}}_{c} |_{t_{n+1}}$.

The ensuing algorithm is conditionally stable, and is subject to the following restrictions on the choice of stable time step:

$$\begin{aligned} \varDelta t_{n+1/2} < \sqrt{\frac{\rho }{\lambda _{c,\max }}} \quad \forall c = 1, \ldots , N_{\text {cracks}}. \end{aligned}$$

(56)

where $\lambda _{c,\max }$ denotes the largest eigenvalue of the acoustic stiffness tensor $\frac{\partial ^2 {\bar{\psi }}}{\partial \tilde{{\mathbf {u}}}_c \otimes \partial \tilde{{\mathbf {u}}}_c}$. For isotropic materials, $\lambda _{c,\max }$ may be reasonably approximated as $\lambda _{c,\max } \approx M^b + E_c$, where $M^b = \kappa ^b + \frac{4}{3} \mu ^b$ is the P-wave modulus of the bulk material, and $E_c$ denotes the secant stiffness of the embedded cohesive model.

If the initial secant stiffness $E_c$ of the chosen cohesive model is large relative to $M^b$, then a severe restriction is imposed upon the resulting stable time step needed to update the embedded crack opening displacements. To circumvent this limitation, a modified CZ model is proposed in Sect. 4.2, wherein the effective initial cohesive stiffness $E_c$ is proportional to $M^b$. If the proposed explicit update framework is employed within a globally explicit dynamic finite element procedure, then the ensuing constraint imposed upon the stable time step size by equation (56) will be comparable to that of the time step used by the globally explicit time-stepping scheme. As such, the material may be updated in a manner which does not incur a significant computational overhead due to the potential need for sub-incrementation. Instead, the material may be stably updated using the selected global time step size.

In particular: for the modified CZ model proposed in Sect. 4.2, it was observed that the stable time step size required by the constitutive update procedure was roughly twice as small as the global time step, owing to the fact that $\lambda _{c,\max } \approx 2 M^b$ at the onset of failure. To ensure stability of the update procedure, two alternative remedies are proposed: the global time step may be reduced to satisfy the local stability requirements of the explicit constitutive update procedure; or the relative mass density used to compute the crack accelerations in equation (48) may be artificially increased, tantamount to a local form of selective mass augmentation. Henceforth, the latter strategy is employed. Increasing the density of the material by a corresponding factor of 2 was sufficient to resolve concerns related to local stability in the constitutive update procedure, without adversely impacting the physical behavior of the model.

4 Example constitutive formulation

Herein, a specific example of a material model formulated within the framework described in Sect. 3 is provided. The choice of bulk and cohesive constitutive models are described in the following sections.

4.1 Hyperelastic bulk material model formulation

A simple hyperelastic model consistent with a compressible Neo-Hookean solid is chosen from (Pence and Gou 2015). The elastic free energy $\psi ^b$ in the bulk phase assumes the following form:

$$\begin{aligned} \psi ^b ({\mathbf {F}}^b) = \frac{\kappa }{2} \left[ \frac{{J^b}^2 - 1}{2} - \log J^b \right] + \frac{\mu }{2} \left[ \text {tr} (\bar{{\mathbf {b}}}^b) - 3 \right] , \end{aligned}$$

(57)

where $J^b \equiv \det ({\mathbf {F}}^b)$, and $\bar{{\mathbf {b}}}^e \equiv {J^b}^{-\frac{2}{3}} {\mathbf {F}}^b {{\mathbf {F}}^b}^T$. The parameters $\kappa$ and $\mu$ denote the (undamaged) elastic bulk and shear moduli of the material, respectively.

From Eq. (39), the resulting macroscopic Kirchhoff stress (equivalent to the Kirchhoff stress in the bulk material) arises as:

$$\begin{aligned} \varvec{\tau } = \varvec{\tau }^b = \frac{\kappa }{2} \left[ {J^b}^2 - 1 \right] {\mathbf {1}} + \mu \left[ \bar{{\mathbf {b}}}^b - \frac{1}{3} \text {tr} (\bar{{\mathbf {b}}}^b) \right] . \end{aligned}$$

(58)

Thus, the Cauchy stress is computed via $\varvec{\sigma } = J^{-1} \varvec{\tau }^b$ with $J \equiv \det ({\mathbf {F}})$.

In spite of the relative simplicity of the chosen hyperelastic model, more complicated hyperelastic formulations accommodating plasticity or visco-elastic behavior (Simo and Hughes 2000) are readily compatible within the proposed modeling framework. The inherent modularity of the bulk constitutive component facilitates the use of preexisting material model implementations possessing a virtually arbitrary degree of behavioral complexity. This feature of the framework will be explored in future work relevant to the modeling of materials which exhibit a large degree of compressive ductility, but relatively brittle fracture behavior under tensile loading (e.g., pressed metal powder composites).

4.2 Embedded cohesive traction-separation model

To represent the degradation of stiffness and the dissipation of energy due to the formation of discrete cracks, an appropriate traction-separation law must be chosen to represent the cohesive failure of the embedded interfaces. As suggested by Leone (2015) for the DGD approach, virtually any cohesive model may be employed for this purpose, but numerical considerations impose practical limitations on this choice.

Most cohesive zone models proposed in the literature (refer to Park and Paulino (2011) for a representative survey) may be categorized into two groups: intrinsic (initially elastic) and extrinsic (initially rigid) models. Intrinsic models must assume the location and orientation of cracks within the problem domain a priori (e.g., across weak material interfaces whose failure is anticipated, such as in a laminated composite). By comparison, extrinsic models may be inserted into the domain and initialized dynamically during the analysis upon failure initiation.

If the presence or orientation of fractures is not known a priori, extrinsic cohesive zones models are preferred. However, because extrinsic CZ models possess an initially infinite cohesive stiffness to guarantee continuity of the stress during the transition to failure, they are susceptible to issues of poor numerical stability and ill-conditioning. Specifically, the large initial stiffness of extrinsic CZ models imposes a severe restriction on the allowable stable time step size for the explicit constitutive update scheme proposed in Sect. 3.3. This can be avoided by imposing a finite value of initial stiffness upon failure initiation, albeit at the expense of introducing a discontinuous stress-strain response at the onset of failure—an issue discussed at length by Papoulia et al. (2003).

To circumvent this shortcoming in the context of the presently proposed model framework, a supplementary dissipation mechanism is introduced within an extrinsic CZM to aid in transitioning from an initially rigid state to a damaged elastic state while preserving stress continuity at the onset of failure. A novel energy dissipation mechanism is proposed which remains active only during the initial stages of failure evolution, after which the model transitions to a traditional traction-separation model akin to the one described by Ortiz and Pandolfi (1999).

Henceforth, all subscripts denoting the crack index c are omitted, and the subsequent developments are assumed to pertain to a single cohesive interface. Consider the postulated expression of the stored energy $\varPsi (\tilde{{\mathbf {u}}})$ per unit of fracture surface area:

$$\begin{aligned} \varPsi (\tilde{{\mathbf {u}}}) \equiv \phi \sigma _f {\tilde{u}}_n + \frac{1}{2} (1 - D) \frac{E}{\ell } {\bar{u}}^2 . \end{aligned}$$

(59)

In the above, the effective opening displacement ${\bar{u}}$ is defined as

$$\begin{aligned} {\bar{u}} \equiv \sqrt{{\tilde{u}}_n^2 + \beta ^2 {\tilde{u}}_s^2}, \end{aligned}$$

(60)

where ${\tilde{u}}_n \equiv \tilde{{\mathbf {u}}} \cdot {\mathbf {N}}$ and ${\tilde{u}}_s \equiv \sqrt{\tilde{{\mathbf {u}}} \cdot \tilde{{\mathbf {u}}} - {\tilde{u}}_n^2}$ denote the normal and transverse opening displacements, respectively. The model parameter $\beta$ denotes the ratio of the normal and in-plane characteristic fracture length scales, $\phi , D \in [ 0, 1 ]$ are internal damage parameters, E is the initial (undamaged) elastic modulus of the surrounding bulk material (a finite value), and $\sigma _f$ is the normal failure stress at rupture. The primary novelty in the above expression regards the addition of the term $\phi \sigma _f {\tilde{u}}_n$ which encodes the initial traction at rupture, assuming a normal failure mode. As noted by Papoulia et al. (2003), this augmentation guarantees time continuity of the ensuing tractions at the onset of failure but avoids the issue of traction locking by requiring that the encoded initial traction acts strictly in the normal direction.

The resulting expression for the cohesive traction vector $\tilde{{\mathbf {t}}} \equiv \frac{\partial \varPsi }{\partial \tilde{{\mathbf {u}}}}$ is derived as

$$\begin{aligned} \tilde{{\mathbf {t}}} = \phi \sigma _f {\mathbf {N}} + (1-D) \frac{E}{\ell } \left\{ (1-\beta ^2) {\tilde{u}}_n {\mathbf {N}} + \beta ^2 \tilde{{\mathbf {u}}} \right\} . \end{aligned}$$

(61)

At the onset of failure, it is assumed that $\phi = 1$, $D = 0$, and $\tilde{{\mathbf {u}}} = {\mathbf {0}}$ such that the initial traction is $\tilde{{\mathbf {t}}} = \sigma _f {\mathbf {N}}$.

Immediately following the onset of failure, only the failure parameter $\phi$ is allowed to degrade while the damage parameter D is held fixed, i.e., ${\dot{\phi }} \le 0$ and ${\dot{D}} = 0$. Failure is allowed to progress until such time as $\phi = 0$, signaling the transition to conventional cohesive damage evolution via D such that ${\dot{D}} \ge 0$ and necessarily ${\dot{\phi }} = 0$. In either case, satisfaction of the effective traction-based failure constraint is imposed:

$$\begin{aligned} f_d = {\bar{t}} - {\bar{t}}_f ({\bar{u}}) \le 0, \end{aligned}$$

(62)

where the effective failure stress ${\bar{t}}_f$ is defined by a simple exponential softening model:

$$\begin{aligned} {\bar{t}}_f ({\bar{u}}) = \sigma _{f} e^{- \frac{\sigma _{f}}{{\mathcal {G}}_c} {\bar{u}}}, \end{aligned}$$

(63)

where ${\mathcal {G}}_c$ denotes the total fracture energy per unit surface area (in the undeformed configuration), and the effective traction ${\bar{t}}$ is evaluated via

$$\begin{aligned} {\bar{t}} = \sqrt{{\tilde{t}}_n^2 + \beta ^{-2} {\tilde{t}}_s^2}, \end{aligned}$$

(64)

where ${\tilde{t}}_n \equiv \tilde{{\mathbf {t}}} \cdot {\mathbf {N}}$ and ${\tilde{t}}_s \equiv \sqrt{\tilde{{\mathbf {t}}} \cdot \tilde{{\mathbf {t}}} - {\tilde{t}}_n^2}$ denote the normal and transverse cohesive traction components, respectively.

When $\phi > 0$, a direct solution for the diminished value of $\phi$ is obtained via:

$$\begin{aligned} \phi = \frac{E}{\ell \sigma _f} \left[ - {\tilde{u}}_n + \sqrt{\left( \frac{{\bar{t}}_d ({\bar{u}})}{E} \ell \right) ^2 - \beta ^2 {\tilde{u}}_s^2} \, \right] . \end{aligned}$$

(65)

If the discriminant in the above expression becomes negative, or if the resulting value of $\phi$ is negative, then no feasible solution for $\phi > 0$ exists. In such cases, $\phi$ is set equal to zero, and the damage parameter D is evolved to enforce $f_d \le 0$, as is done in traditional cohesive damage formulations; if ${\dot{D}} > 0$:

$$\begin{aligned} D = 1 - \frac{{\bar{t}}_f ({\bar{u}})}{E {\bar{u}}} \ell . \end{aligned}$$

(66)

Otherwise, if a solution for $\phi > 0$ exists such that ${\dot{\phi }} \le 0$, this new value is used to update $\phi$ while maintaining $D = 0$.

The intuitive behavior of the model immediately after failure initiation may be characterized by a bi-linear response in the elastic range, followed by softening along the failure envelope, as depicted in Fig. 2.

Fig. 2

The resulting RVE stress vs. strain curve using the proposed embedded cohesive zone model, with unloading/reloading paths at different levels of degradation indicated via dashed lines

It should be noted that the outlined cohesive zone modeling approach merely aims to stabilize the explicit update procedure, rather than to introduce a secondary dissipation mechanism which attempts to reproduce experimental observations. At the moment, a justification of the model as reproducing certain physical behaviors under crack growth would constitute a post-rationalization. Further investigation would be required to assess the validity of the model in this regard.

Nonetheless, the behavior of the proposed model under monotonic loading remains identical to the purely damage-based model, and rapidly reduces to the aforementioned model following the onset of failure. For these reasons, it suffices to assert that the proposed modifications yield only minor differences from the original damage-based extrinsic traction-separation model, and it therefore may be irrelevant to critique the physical validity of the alternative dissipation mechanism.

5 Model demonstration and evaluation

The proposed modeling framework was implemented within the DYNA3D finite element code (Zywicz et al. 2021), and a variety of simulations were explored to simultaneously verify the model’s numerical implementation, validate its usage in several benchmark dynamic fracture problems, and demonstrate the model’s ability to accommodate multi-directional failure. Attention is restricted to problems involving brittle material behavior that may be adequately characterized by the constitutive idealization presented in Sect. 4.

5.1 Single-element verification problem

To demonstrate the dynamic behavior of the model with the inclusion of internal kinetic energy, a simple one-dimensional verification problem consisting of a single element subjected to uni-axial extension is considered.

Fig. 3

Uni-axial extension problem setup

The problem setup comprises a single hexahedral element with side length h, as depicted in Fig. 3. The element is fully constrained and subjected to a constant uni-axial (engineering) strain rate ${\dot{\varepsilon }} > 0$. The resulting uni-axial stress-strain behavior of the model is compared in a range of tests spanning a series of decreasing values for the assigned mass density $\rho$, strain rate ${\dot{\varepsilon }}$, and element size h. The corresponding parameterizations for each study are summarized in Table 1.

Table 1 Variable parameterizations for the uni-axial verification problem

The dimensionless values for the Young’s modulus $E = 10.0$, Poisson’s ratio $\nu = 0.0$, initial failure stress $\sigma _f = 0.1$, fracture surface energy ${\mathcal {G}}_c = 0.003$, and fracture length scale ratio $\beta = 1.0$ are consistent between all variations of the uni-axial extension test.

The results obtained for each parametric series are presented separately in Fig. 4. In each such study, decreasing values of $\rho$, ${\dot{\varepsilon }}$, or h are examined. The anticipated outcome of each series is convergence to quasi-static behavior—i.e. the stress-strain response that one would expect to obtain in the limit of vanishing internal kinetic energy. The corresponding rates of energetic convergence in each variable may be surmised from equation (28), where it is readily observed that $T^d = O(\rho \, {\dot{\varepsilon }}^2 \, h^2)$ for the uni-axial extension problem.

Fig. 4

Stress-strain results for the uni-axial extension problem employing the parameterizations presented in Table 1

Table 2 Comparison of variable parameterizations and their resulting energetic ratios $\upsilon$ (from equation 67) for the uni-axial verification problem

The relative significance of inertial effects in the local stress-strain response of a given element with dimension h will henceforth be characterized by the dimensionless energetic ratio $\upsilon$:

$$\begin{aligned} \upsilon \equiv \frac{{\tilde{T}}^d (\rho , {\dot{\varepsilon }}, h)}{{\mathcal {G}}_c / h}, \end{aligned}$$

(67)

where ${\mathcal {G}}_c / h$ measures the regularized cohesive energy density per unit RVE volume, and ${\tilde{T}}^d \approx \rho \, {\dot{\varepsilon }}^2 \, h^2$ provides an estimate of the internal kinetic energy density based upon the external rate of loading ${\dot{\varepsilon }}$. For values of $\upsilon \ll 1$, inertial effects are deemed negligible in comparison with the cohesive behavior of the material during rupture. For values of $\upsilon$ approaching or exceeding a ratio of 1, the inclusion of internal kinetic energy becomes potentially relevant to account for the local dynamics of crack opening.

For all three parametric series, energetic convergence toward quasi-static behavior is evidenced by the attenuated amplitude of the oscillatory post-failure stress response with decreasing values of $\rho$, ${\dot{\varepsilon }}$, h. In each series, decreasing a given parameter value by the indicated factor (4 for $\rho$, 2 for ${\dot{\varepsilon }}$ and h) results in an anticipated reduction of the transient stress wave amplitude by a factor of 2, and an increase in wave frequency by this same factor. Table 2 further illustrates how the energetic ratio $\upsilon$ characterizes the relative influence of internal kinetic energy on the ensuing stress-strain response, with values of $\upsilon \ll 1$ converging toward locally quasi-static behavior within a single element.

To ensure the consistent dissipation of fracture surface energy, diminishing the element size h additionally results in a commensurately greater amount of energy per unit volume that must be locally dissipated within the homogenized material RVE. The relative increase in regularized fracture energy per unit volume with decreasing h is reflected in Fig. 4c, wherein the steady state post-failure softening slope is progressively flattened for diminishing values of h.

Concerning the post-failure behavior of the model: it is evident that the measured uni-axial stress within the RVE may exceed the failure stress by an amount proportional to the transient stress wave amplitude. This “dynamic over-stress” phenomenon manifests within a single element due to the inclusion of internal kinetic energy, combined with the chosen idealization of localized cohesive failure as occurring across a singular embedded interface. While this effect is apparently non-physical, it is nonetheless consistent with the behavior of conventional CZ modeling approaches for dynamic fracture, wherein the elements adjacent to a cohesive interface may experience dynamic stresses that exceed the failure stress.

As a supplementary observation: auxiliary sources of energy dissipation within the bulk material phase (e.g., due to plasticity or viscous effects) will attenuate the transient portion of the post-failure stress response without artificially retarding the steady state crack opening rate.

5.2 Dynamic crack growth rate validation test

The dynamic fracture experiments of Ravi-Chandar and Knauss (1984) examined the rate of crack growth in Homalite 100 sheets placed under time-varying loading conditions. These experiments were simulated by Chin et al. (2018) in an effort to reproduce comparable rates of crack growth using a CZM approach. To this end, a similarly motivated validation test for the proposed modeling approach is investigated under variable mesh refinement, with the intent of justifying the use of internal kinetic energy for dynamic fracture problems.

The test considers the specimen geometry depicted in Fig. 5 under approximately plane stress conditions with a plate of thickness of 4.8 mm, consistent with the test setup described by Ravi-Chandar and Knauss (1982). The crack faces are subjected to an externally applied traction ${\bar{\sigma }}(t)$ with loading history shown in Fig. 6. Beginning at $t = 0.0$ µs the traction is linearly increased to 10.0 MPa over the first 25.0 µs of dynamic loading. The traction is then held constant until the simulation is terminated at $t = 150.0$ µs. This loading history is consistent with the larger load case investigated by Chin et al. (2018), and falls within the higher range of loading rates considered by Ravi-Chandar and Knauss (1984), wherein the rate of crack growth is expected to remain constant.

Fig. 5

Testing arrangement for the experiment of Ravi-Chandar and Knauss (1984)

Fig. 6

Loading history for the applied crack face traction ${\bar{\sigma }}(t)$ as a function of time t

Elastic material properties for Homalite 100 are taken from Ravi-Chandar and Knauss (1982), namely: $E = 4.55$ GPa, $\rho =1230.0$ kg/m$^3$, $\nu = 0.31$. Although the results presented by Ravi-Chandar and Knauss (1984) demonstrate an apparent rate-dependent fracture toughness for Homalite, a rate-invariant set of cohesive parameters are chosen consistent with those used by Chin et al. (2018): $\sigma _f = 30$ MPa, and ${\mathcal {G}}_c = 75$ J/m$^2$ ($\beta = 1.0$). Comparable cohesive parameters have been used by Yu (2001) to investigate the dynamic fracture behavior of Homalite 100, yielding qualitative consistency with experimental data.

Contemplating the results obtained in Sect. 5.1, the transient effects due to the presence of internal kinetic energy are expected to be diminished at sufficiently refined mesh resolutions. A valid question concerns the extent to which this mesh-dependent behavior artificially affects the simulated rate of crack growth over a range of different mesh refinement levels. To investigate this question further, the specimen geometry is discretized uniformly with hexahedral finite elements of approximately equal dimension h, and the simulated results are compared across a sequence of nested mesh refinements with $h = 6.25$ mm, $h = 3.125$ mm, $h = 1.5625$ mm, $h = 0.78125$ mm, $h = 0.520833$ mm, and $h = 0.390625$ mm.

Fig. 7

Simulated crack growth rates under varying mesh refinement; representative experimental results from Ravi-Chandar and Knauss (1984)

Table 3 Simulated crack growth rates and initiation times across a range of mesh refinement levels

The results of the numerical study are presented in Fig. 7 and Table 3, wherein it is observed that the simulated rates of crack growth are roughly constant over the duration of the test across all mesh refinement levels. Experimental data obtained at a similar loading rate is provided for the sake of comparison, however it is noted that the precise rate of loading for this experiment is not provided by Ravi-Chandar and Knauss (1984). It therefore suffices to make only qualitative comparisons with the experimental results.

Differences in the estimated average rate of crack growth (determined by a linear fit of the data shown in Fig. 7) are observed at variable levels of mesh refinement. Faster rates of crack growth are obtained at finer discretizations, ultimately converging toward an average crack growth rate approaching 650 m/s.

According to Rice et al. (1968), the fracture process zone size R for the chosen material parameterization is estimated as $R = 0.6594$ mm. Consequently, mesh-size dependent behavior is anticipated (and observed) for levels of mesh refinement with $h > R$. This is further evidenced by the fact that at mesh resolutions coarser than $h = 0.78125$ mm, damage actively evolves in only a single element encompassing the process zone. At finer resolutions, damage actively evolves within a band of elements spanning the dimension of the process zone. Specifically: at $h = 0.78125$ mm, damage evolves within a zone spanning 1-2 elements, whereas at $h = 0.390625$ mm the process zone spans roughly 3 elements. As evidenced by the results shown in Table 3, sufficient refinement of the process zone is required to achieve convergence in the simulated results.

To investigate the effect that the inclusion of internal kinetic energy $T^d$ had on the simulated rate of crack growth at coarser levels of refinement, $T^d$ was artificially decreased in a separate study to emulate the limiting condition $T^d \rightarrow 0$; an additional scaling factor was applied to the mass density $\rho$ utilized in the expression for $T^d$, whereas the original (unscaled) mass density was used to assemble the (diagonalized) finite element mass matrix. As shown in Fig. 4a, sufficient reduction of the applied scaling factor recovers the limiting case $T^d \rightarrow 0$ as $\rho \rightarrow 0$. Following this investigation, it was observed that the omission of internal kinetic energy had little to no impact on the resulting crack growth behavior across all levels of mesh refinement.

Indeed, for the chosen material parameters, element size $h = 6.25$ mm, and approximate opening strain rate ${\dot{\varepsilon }} = 70$ s$^{-1}$, the energetic ratio from equation (67) was estimated as $\upsilon = 0.02$. For the problem under consideration, it therefore suffices to conclude that the inclusion of internal kinetic energy does not appreciably impact the resulting dynamic fracture characteristics of the model at levels of mesh refinement sufficient to resolve the process zone size. The apparent differences with respect to mesh refinement are evidently the consequence of inadequate resolution of the effective process zone size in the material.

Crack initiation is also observed to occur at progressively earlier times under mesh refinement, converging toward an initiation time of 20 $\mu$s. This converged value is consistent with the experimental results of Ravi-Chandar and Knauss (1984). Differences in the initiation time at different mesh refinement levels can be partially attributed to the sharp variation in the near-tip stress fields which are only sufficiently well-resolved in a highly refined mesh. For coarse meshes, the stresses in the elements surrounding the crack tip are less concentrated than the stresses at the crack tip, as determined by the theory of linear elastic fracture mechanics. The use of a maximum principal stress-based failure initiation criterion consequently results in the delayed onset and progression of cracking at coarse mesh scales. Nonetheless, this artifact of the numerical discretization does not significantly impact the ensuing rate of crack growth.

5.3 Kalthoff–Winkler experiment

The experiment of Kalthoff and Winkler (1987) is a common benchmark problem for various numerical fracture modeling approaches, serving primarily as a means of demonstrating the mesh bias (or lack thereof) of a particular model.

The test consists of a 9 mm thick notched 18Ni1900 maraging steel plate with geometry shown in Fig. 8, and the chosen material properties: $\rho = 8000.0$ kg/m$^3$, $E = 190.0$ GPa, $\nu = 0.3$, $\sigma _f = 2000.0$ MPa, ${\mathcal {G}}_c = 2.2 \times 10^4$ J/m$^2$ ($\beta = 1.0$). The cylindrical impactor is modeled as a rigid body with a total mass of roughly 1.57 kg, a radius of 25.0 cm, and an initial velocity of 32.0 m/s. Following impact, fracture is expected to initiate at the base of the vertical notches in the specimen, emanating at an angle of roughly $70^\circ$ away from the vertical plane.

Fig. 8

Testing arrangement for the experiment of Kalthoff and Winkler (1987)

The simulated results using a uniform hexahedral mesh with an average element size of $h = 0.357$ mm are shown in Fig. 9. The color plots depict the extent of embedded cohesive damage D in the specimen via a scalar parameter ranging from 0 to 1, where 0 represents a fully undamaged material state and 1 corresponds to a fully damaged state. Brittle cracking is observed at a somewhat shallower angle than the anticipated experimental result of $70^\circ$ on account of the model’s inherent mesh bias. Though not shown here, the orientation of cracking is observed to occur at angles approaching $90^\circ$ – in alignment with the edges of the mesh. The influence of mesh orientation on crack path trajectory is a well-known issue with local damage models which has been discussed in other works, with various remedies proposed; for example, Cervera and Chiumenti (2006) provide a detailed explanation of this phenomenon and propose a remedy in the form of a crack tracking algorithm. Nonetheless, the results obtained using the current approach are encouraging in sufficiently refined meshes, demonstrating lesser mesh bias with decreasing element size.

Fig. 9

Simulated results for the Kalthoff–Winkler experiment at 90 µs after impact

5.4 Dynamic Brazilian test

Yu et al. (2004) conducted numerical simulations using CZM of dynamic Brazilian tests on ceramic specimens and compared the results against experimental data collected by Rodriguez et al. (1994) and Gálvez et al. (1997).

Ruiz et al. (2000) pursued a similar investigation of the CZM approach to simulate dynamic Brazilian tests on granite specimens. Their investigations sought to demonstrate the apparent rate-dependent failure strength of brittle materials at variable rates of loading. Their findings indicate that this behavior is naturally obtained by CZM and does not require the use of a rate-dependent traction-separation law.

The numerical investigations conducted herein seek to confirm a similar rate-dependent behavior which naturally arises from a rate-independent embedded cohesive model. Additionally, the dynamic Brazilian test demonstrates the behavior of the proposed model in the presence of pervasive failure and fragmentation and highlights the importance of allowing for multiple intersecting cracks at a given material point.

A similar test setup as described in Yu et al. (2004) and depicted in Fig. 10 is utilized, employing a 2-dimensional plane strain representation of the sample. A sample diameter of $D = 8.0$ mm and thickness $W=1/3$ mm were used, and the chosen material properties were consistent with the parameterization of A98 alumina (98% $\text {Al}_2\text {O}_3$) estimated by Yu et al. (2004), i.e. $\rho = 3877.0$ kg/m$^3$, $E = 366.0$ GPa, $\nu = 0.3$, $\sigma _f = 179.0$ MPa, ${\mathcal {G}}_c = 98.0$ J/m$^2$ ($\beta = 1.0$). The material is assumed to exhibit predominantly brittle behavior, with little or no plasticity. The bearing strips are assigned purely elastic properties with the same material parameters used for the A98 alumina specimen. Frictionless contact constraints are imposed between the specimen and the bearing strips.

The motion of the incident and transmitter bars are modeled approximately as rigid boundary conditions imposed upon the bearing strips. The incident bar is assigned a constant applied velocity of $v=12.0$ m/s for the duration of the analysis, whereas the transmitter bar is held fixed.

Fig. 10

Experimental setup for the dynamic Brazilian test

The simulated results were obtained using a regular hexahedral mesh with an average element diameter of $h = 0.1$ mm, which is comparable to the degree of mesh resolution utilized by Yu et al. (2004).

The results at different analysis times are depicted in Fig. 11. As in the previous example, the color plots depict the extent of embedded cohesive damage $D \in [0,1]$. Elements which exceed a critical crack strain value of 100% are deleted from the analysis, thereby indicating the formation of distinct fragments. The resulting patterns of fracture closely emulate the experimental results observed by Gálvez et al. (1997), as well as the simulated results obtained by Yu et al. (2004). A single medial fracture is present at the peak load, followed by the development of several parallel cracks along the central column of the specimen, and pervasive cracking under the bearing strips.

Fig. 11

Depiction of cohesive damage at different analysis times for the dynamic Brazilian test

Following the stated methodology employed by Yu et al. (2004), the transmitted load P (measured as the net contact force acting between the sample and the bearing strip affixed to the transmitter bar) was used to estimate the tensile stress across the specimen’s medial plane via

$$\begin{aligned} \sigma = \frac{2P}{\pi W D}, \end{aligned}$$

(68)

whose time-rate of increase was further used to estimate the strain rate in the sample prior to failure:

$$\begin{aligned} {\dot{\epsilon }} = \frac{1}{E} \frac{\partial \sigma }{\partial t}. \end{aligned}$$

(69)

From the above estimates, the variable tensile strength of the sample under different loading rates was compared against the experimental results of Gálvez et al. (1997), and the simulated results of Yu et al. (2004). The results are summarized in Table 4, demonstrating notable similarities between the proposed method and the simulated results obtained by Yu et al. (2004).

Table 4 Estimated tensile strength of A98 specimen at variable strain rates, compared against the experimental results of Gálvez et al. (1997), and the simulated results of Yu et al. (2004)

Additionally, a comparison was made between different analyses which allowed for either a single crack or multiple intersecting cracks to develop (up to three) at each material point. The results depicted in Fig. 12 demonstrate the role that the allowance of multiple cracks plays in the simulated results. The pattern of damage observed in the model with multiple permitted cracks exhibits behavior similar to the failure patterns noted by Zhou et al. (2014) for granite specimens: a relatively narrow crushed strap of material develops due to parallel center cracks, accompanied by crushed zones of material near the supports.

Fig. 12

Comparison of single vs. multiple cracks permitted at each material point

In contrast, the pattern of damage observed when the model is constrained to allow only a single crack per material point exhibits diffuse levels of damage along a wider medial band through the specimen. The diffused extent of damage in this case appears to be the result of stress locking (Rots et al. 1985; Rots 1988), and is an apparent consequence of the chosen (effectively uni-directional) failure model permitting only a single crack. Common remediation strategies involve an isotropic degradation of the material stiffness under progressive failure, allowing the orientation of cracks to rotate, or accommodating multiple discrete cracks (Rots and Blaauwendraad 1989). The multiple crack approach adopted in this work aids in conditionally degrading the transverse stiffness of the fractured material, particularly in regions of the mesh which exhibit pervasive failure, ultimately yielding more physical results less prone to stress locking.

6 Conclusion

The smeared crack modeling framework proposed in this work offers several improvements over the related DGD approach of Leone (2015), notably: the internal traction equilibrium conditions and macroscopic stress state of the model are established via rigorous thermodynamic arguments, and multiple mutually orthogonal cracks at a single material point are permitted, which proves essential in mitigating the effects of stress locking.

To facilitate the efficient use of the proposed model in explicit dynamic simulations for dynamic fracture problems, a dynamic regularization of the equations of motion governing cohesive crack opening was introduced, resulting in an explicit constitutive update procedure. Unlike other artificial forms of (viscous) regularization, the proposed dynamic regularization scheme is motivated on physical grounds. The results presented in Sect. 5.1 demonstrate that the influence of local crack inertia diminishes under mesh refinement, but may become potentially significant if the internal kinetic energy density is large compared to the cohesive fracture energy of the material (e.g., at coarser discretization levels, larger length scales, or sufficiently high strain rates). For the problems considered in Sects. 5.2 and 5.4, the inclusion of crack opening inertial effects did not appreciably impact the dynamic fracture characteristics of the material for these problems. While the driving intent behind the inclusion of internal kinetic energy in the present work was to facilitate a more efficient constitutive update procedure, future investigations will seek to examine situations in which these inertial effects become relevant to the dynamics of crack growth.

As with conventional CZMs, sufficient resolution of the fracture process zone is required to obtain mesh-independent results. However, even with sufficient refinement, the proposed model exhibits similar issues of mesh bias seen in other SCM formulations predicated on a local form of damage evolution. Potential remediation strategies include: supplementary non-local regularization procedures, use of less biased meshes, crack tracking algorithms, or enhanced local kinematics to better represent crack opening. Continuing work aims to further investigate and resolve these deficiencies.

A simplified evaluation of integral products of Heaviside functions

Recall From Eq. (26) the expression for the total internal kinetic energy of the cracked continuum idealization, restated below:

$$\begin{aligned} T^d = \frac{\rho }{8} \sum _{a,b=1}^{N_{\text {cracks}}} (\dot{\tilde{{\mathbf {u}}}}_a \cdot \dot{\tilde{{\mathbf {u}}}}_b) \frac{1}{|\varOmega |} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV. \end{aligned}$$

(70)

The primary difficulty in evaluating the above concerns the computation of the integrals $\int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV$ containing products of Heaviside functions. Herein, the aforementioned integral products are evaluated approximately by assuming an idealized geometric distribution of material within the RVE domain $\varOmega$.

In particular, consider the case where $\varOmega$ is approximated as an ellipsoidal domain obtained through an affine mapping ${\mathbf {J}}$ from a reference sphere with unit volume. Let the volume of the ellipsoidal domain correspond to $| \varOmega | = \det ({\mathbf {J}})$. The directed area $d {\mathbf {a}}_c = {\mathbf {n}}_c \, da$ of any medial crack plane passing through the reference sphere with circular area $da = \root 3 \of {\frac{9 \pi }{16}}$ and unit normal ${\mathbf {n}}_c$ is transformed via Nanson’s relation into the directed area $d {\mathbf {A}}_c = {\mathbf {N}}_c \, dA_c$ of a corresponding medial crack plane passing though the ellipsoidal domain with area $dA_c = | \varGamma _c |$ and normal ${\mathbf {N}}_c$, i.e.

$$\begin{aligned} d {\mathbf {A}}_c = \text {cof} ({\mathbf {J}}) \cdot d {\mathbf {a}}_c . \end{aligned}$$

(71)

Referring to Fig. 13, the volume of an ellipsoidal wedge (denoted $|W_{12}|$) formed by the intersection of $\varOmega$ with two half spaces ${\mathbf {X}} \cdot {\mathbf {N}}_1 \ge 0$ and ${\mathbf {X}} \cdot {\mathbf {N}}_2 \ge 0$ may be computed as the transformed volume of the corresponding spherical wedge defined in the reference sphere, such that

$$\begin{aligned} |W_{12}| = \frac{\pi - \cos ^{-1} ({\mathbf {n}}_1 \cdot {\mathbf {n}}_2)}{2 \pi } \, |\varOmega |, \end{aligned}$$

(72)

A reasonable approximation to the above over the complete range of values for the inner product ${\mathbf {n}}_1 \cdot {\mathbf {n}}_2 \in \left[ -1,+1\right]$ is given by

$$\begin{aligned} |W_{12}| \approx \frac{1 + {\mathbf {n}}_1 \cdot {\mathbf {n}}_2}{4} \, |\varOmega |. \end{aligned}$$

(73)

Fig. 13

Two-dimensional depiction of the ellipsoidal idealization for $\varOmega$ with principal semi-diameters $r_i$; the ellipsoidal wedge $W_{12}$ is defined by the two unit normals ${\mathbf {N}}_1$ and ${\mathbf {N}}_2$, such that a corresponding spherical wedge may be defined between ${\mathbf {n}}_1$ and ${\mathbf {n}}_2$ in the reference sphere

Given the chosen idealization for the RVE domain, the Heaviside integral products may be directly evaluated via

$$\begin{aligned} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV = 4 |W_{ab}| - |\varOmega |. \end{aligned}$$

(74)

Exploiting the approximation given by equation (73), the above reduces to a bilinear product expressed in terms of the metric tensor ${\mathbf {G}}$ defined in Sect. 2.1:

$$\begin{aligned} \int _{\varOmega } {\mathscr {H}} ({\mathbf {N}}_a) {\mathscr {H}} ({\mathbf {N}}_b) \, dV \approx \frac{16}{9} \frac{{\mathbf {N}}_a}{\ell _a} \cdot {\mathbf {G}} \cdot \frac{{\mathbf {N}}_b}{\ell _b} \, |\varOmega |. \end{aligned}$$

(75)