Fracture mechanics approach to stress singularity in adhesive joints

Abstract

Adhesives offer significant advantages when joining materials since they do not create discontinuities in the material, unlike bolting or riveting. Another interest of adhesive joints is the possibility of joining different materials and the lower weight. The analysis of the stress singularity in adhesive joints can provide a better understanding of joint behaviour, and it is mesh independent. The ISSF is based on a fracture mechanics concept, the Stress Intensity Factor (SIF). However, generally, the SIF is only applicable to cracks in a single material, while the ISSF is applicable to multi-material corners and does not require a crack. This work aims to study the stress singularity of aluminium adhesive joints bonded with a brittle adhesive with four different overlap lengths (L_O) by determining the singularity’s exponents and its intensity. A method for joint strength prediction using the ISSF is also proposed. Additionally, the interface corner’s stress is studied, with the different singularity components presented separately to assess their influence on the overall stress. These predictions are also compared with the experimental strength to verify this strength prediction criterion’s accuracy when applied to brittle adhesives. In conclusion, the ISSF criterion provides accurate results and can be utilised for further studies in this area.

1 Introduction

Optimal structural design is intrinsically associated with multi-component structures since it is possible to optimise the specific strength and stiffness by combining different materials, each one tailored for its function within the structure (Jairaja and Naik 2019), and also to expedite fabrication and reduce the associated costs in structures with complex shapes, which can benefit from division in simpler shapes joined together (Jeevi et al. 2019). Depending on the application and design restrictions, varying joining techniques can be applied. A significant body of knowledge exists in the literature, including a comparison between joining technologies for selected purposes (Garrido et al. 2018). The most relevant joining methods for industrial applications are riveting, bolting, welding, brazing, and adhesive bonding. Although adhesive joints are used historically, their structural use was only widely developed in the first half of the twentieth century by the aeronautical field. With the advancements in the adhesives’ formulations, resulting in ever-increasing adhesive and joint performance, and design tools, consisting of simulation packages and suitable criteria for strength prediction, adhesive bonding is now essential in structural applications including aerospace, aeronautical, automotive, sports, civil engineering structures and electronics (Gui et al. 2018). This option became possible due to a set of characteristics (over conventional techniques) such as the unnecessity of drilling or damaging the parent materials to be joined, saving weight, improving stresses across the bonding regions, and ease of joining different materials. Possible limitations are the typical impossibility to disassemble after joining, required curing time, lack of confidence in the design, especially for fatigue and long-term analyses, and large scatter in experimental testing (Du et al. 2004).

Since the use of adhesive joints has been increasing in several industries in recent times (Konstantakopoulou et al. 2016), it is important to use design tools that accurately model and predict the behaviour of adhesive joints to reduce the amount of experimental tests needed, which are, usually, costlier and take more time than numerical simulations. In the early stages of adhesive joint analysis, analytical methods were used to determine the stress distributions at the adhesive layer, namely the Volkersen (1938) model, the Goland and Reissner (1944) model or the Hart-Smith (1973) model. However, these models have severe limitations since, for some, the formulation is difficult, while for others, the formulation is simple, but many assumptions are made, rendering the resulting stress distribution less accurate. These limitations mean that in recent years most literature focuses on numerical methods to analyse adhesive joints, although examples of analytical models developed in recent times can still be found, like the work by Carbas et al. (2014) for graded adhesive joints. A literature review by Ramalho et al. (2020) found that the most commonly used method to predict the strength of adhesive joints is Cohesive Zone Models (CZM), used together with the Finite Element Method (FEM) (Blackman et al. 2003). CZM generally provide accurate strength predictions, as long as the cohesive law shape/formulation and the respective parameters are appropriate. A simple triangular law can be used for brittle adhesives, but ductile adhesives generally require more complex laws, such as the trapezoidal law or an exponential law (Carvalho and Campilho 2017). Campilho et al. (2013) evaluated the CZM accuracy of adhesive layers modelled with different law shapes in predicting the strength of composite single-lap joints (SLJ) under different geometries. The obtained results showed that triangular CZM models are most suitable for brittle adhesives, while ductile adhesives can be accurately dealt with trapezoidal CZM laws that capture the high-stress levels after damage onset. Despite this fact, the relative errors of these two law shapes were always under 10%, reinforcing that CZM, which is based on an area concept for crack propagation, i.e., mainly depending on the fracture energies, which gives satisfactory results even with less adequate models. Even though the strength predictions with CZM are accurate, these models have a significant drawback in that they require extensive experimental testing because the cohesive law parameters change with the adhesive thickness (t_A) and other geometric parameters affecting the damage zone in the adhesive in the advent of crack propagation. The t_A effect in CZM modelling with a triangular law was addressed by Xu and Wei (2013) by simulating SLJ with different t_A, particularly showing that smaller t_A increases the joint strength. Additionally, the proposed CZM yielded accurate strength predictions for the brittle adhesive, although the ductile adhesive joint performance with the smallest t_A is underestimated. Demiral and Kadioglu (2018) also showed the t_A influence on strength by CZM, namely SLJ strength reduction by increasing t_A, although this effect was much smaller than that of the overlap length (L_O), whose increase highly benefited the joint strength. Therefore, authors have also experimented with other methods to predict joint strength, such as the eXtended FEM (XFEM) (Stein et al. 2017), sometimes also combined with CZM (Stuparu et al. 2016), or even the common FEM using failure criteria based on continuum mechanics (Sánchez-Arce et al. 2021), fracture mechanics (Jiang et al. 2021) or damage mechanics (Sugiman and Ahmad 2017). Some authors have also used the previous criteria with meshless methods (Ramalho et al. 2019) or meshless methods combined with CZM (Tsai et al. 2014) to predict joint strength.

Fracture mechanics, in particular, can assess stress or strain singularities due to material discontinuities (Da Silva and Campilho 2012), which in bonded joints are usually related to the sharp corners at the overlap edges at the interface between an adherend and the adhesive layer. Conventionally, fracture mechanics can rely on stress intensity factors (Parks 1974; Matos et al. 1989) or energetic approaches (Lazzarin and Zambardi 2001), depending on the materials’ fracture toughness. In the last option, the most widespread techniques are the J-integral (Rice 1968) and the Virtual Crack Closure Technique (VCCT) (Rybicki and Kanninen 1977). More recently, Finite Fracture Mechanics (FFM) was proposed by Leguillon (2002), consisting of a coupled stress-energy criterion for crack initiation and accounting for published work on adhesive joints (Hell et al. 2014). FFM does not require an initial crack and, for crack initiation, both a stress and an energetic criterion should be fulfilled. However, it is essentially applicable to brittle adhesives. In adhesive joints, as previously discussed, there exists a stress singularity at the adhesive/adherend interface corners, whose magnitude is usually called Intensity of Singular Stress Fields (ISSF) or Generalised Stress Intensity Factor (GSIF). The first published works trying to characterise this singularity date back to the mid-twentieth century (Williams 1959; Bogy 1968).

This singularity analysis has been performed in many different types of adhesive joints, including scarf joints (Wu et al. 2014), butt joints (Afendi et al. 2013), Double Lap Joints (DLJ) (Mintzas and Nowell 2012) and SLJ (Rastegar et al. 2018). Zhang et al. (2015) proposed a new method to calculate the ISSF in bonded butt joints under tension and bending, due to the known difficulties in using the FEM because of the existing singularity. The new method only considers stresses of the first elements at the end of the interface between the adhesive and adherend materials. Different combinations of materials and values of tA were analysed and positively validated against experiments from previous works. It was also found that the ISSF was dependent on the joint materials and that the ISSF increased with tA until tA reached the joint width. Interactions between the singular stress fields at the two adhesive/adherend interfaces were also found, although this issue was remitted to future works. In the work of Li et al. (2018), SLJ and DLJ bonded joints were used to investigate the adhesive strength by evaluating and minimising the ISSF at the interface end. It was shown that the ISSF diminishes by increasing the adherends’ thickness (t_P) and that the minimum ISSF is achieved for a sufficiently high adherend thickness. Due to the DLJ having twice the bonding area and suppressing peel stresses and transverse deflection, the equivalent strength condition between identical material SLJ and DLJ was evaluated by the ISSF, leading to an equal strength between a SLJ with an adherend thickness of 7 mm and a DLJ with 1.5 mm. Galvez et al. (2019) applied the ISSF concept to analyse mixed adhesive joints, i.e., with two adhesives in the bond line (with different stiffness and mechanical properties), to achieve strength optimisation. Four adhesive combinations were tested, including the two with single use of each of the adhesives. The proposed approach was based on the reciprocal work contour integral method (RWCIM), and it involved estimating the ISSF for the reference models (joints with the single adhesive), which were then applied for the unknown solution (mixed-adhesive joints). A clear improvement was found for one of the mixed-adhesive joint configurations, with a 36% reduction in the ISSF, when compared to the single-adhesive solutions.

The present work aims at studying the singularity in SLJ, with different L_O, bonded with a brittle adhesive and proposing a method to determine joint strength using the ISSF. The ISSF analysis and the strength predictions are performed using the FEM. This analysis is done to a material combination that was never previously studied using the ISSF. The stress around the interface corner is also studied, with the different singularity components presented separately to assess their influence on the overall stress. Additionally, a comparison between the stress obtained with the ISSF formula and the stress extracted from the FEM for the different L_O is compared to validate the formulation used to obtain the ISSF. The mesh independence of this approach is also assessed by studying two different mesh refinement levels. Finally, these predictions are also compared with the experimental strength to verify this strength prediction criterion’s accuracy when applied to brittle adhesives.

2 Experimental work

2.1 Joint geometry

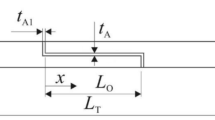
In this work, SLJ made of aluminium adherends bonded with the adhesive Araldite® AV138 were studied. The geometry and boundary conditions of the numerical model are shown in Fig. 1. The SLJ was fixed at the left boundary, and a displacement (δ) was imposed at the right boundary. Four different L_O were tested, from 12.5 to 50 mm in increments of 12.5 mm. The other relevant geometrical properties are the adherend thickness t_P = 3 mm, the adhesive thickness t_A = 0.2 mm, the total joint length L_T = 180 mm and the joint width B = 25 mm.

Fig. 1

Geometry and boundary conditions of the SLJ (dimensions in mm)

2.2 Materials

The SLJ were fabricated from Al6082-T651 aluminium alloy adherends. The adherend material is commonly used for structural appliances since it has good strength and ductility. Full characterisation of this aluminium is presented in previous works (Campilho et al. 2011a,b), consisting of tensile bulk testing and subsequent data analysis of the load–displacement (P–δ) curves. The collected data is presented in Table 1 (E is Young’s modulus, ν the Poisson coefficient, σ_y the tensile yield stress, σ_f the tensile strength and ε_f the tensile failure strain).

Table 1 Mechanical properties of the aluminium adherends (Campilho et al. 2011a,b)

Application of the ISSF to bonded joints was assessed by SLJ bonded with the Araldite® AV138, a strong but brittle epoxy adhesive. This adhesive has a tensile strength of approximately 40 MPa, which is significant for modern adhesives, but its brittleness highly limits the associated bonded joints’ performance, especially for high L_O. For short L_O, in which stresses in the bond line tend to be more uniform due to smaller shear-lag and rotation effects, this adhesive still manages to compete with ductile adhesives, but it quickly fails to work for high L_O, in which stress gradients become significant. These findings were reported in reference (Campilho et al. 2011a). This adhesive was evaluated by different testing architectures to acquire the required data to input into the models. The tensile mechanical properties (E, σ_y, σ_f and ε_f) were acquired from tensile tests to bulk specimens, considering the French standard NF T 76–142 indications for the geometry and fabrication process. The mechanical shear properties (shear modulus—G, shear yield stress—τ_y, shear strength—τ_f and shear failure strain—γ_f) were obtained from Thick Adherend Shear Tests (TAST). For this test, the 11003-2:1999 ISO standard was followed regarding the fabrication and testing procedures. Thus, all specimens were cured in a rigid mould to ensure the proper adherends’ longitudinal alignment, and DIN C45E steel adherends were used to minimise adherend-induced deformations affecting the obtained results. Table 2 collects all data for the adhesive. It should be mentioned that Hooke’s law relationship for isotropic materials (between E and G), and also the expected s_y/t_y relationship by Tresca or von Mises criteria, are not met in the obtained data due to different restraint conditions (unrestrained adhesive in the bulk tests vs. restrained adhesive in the TAST tests).

Table 2 Mechanical properties of the adhesive (De Sousa et al. 2017)

2.3 Fabrication and testing

For the joint fabrication, it was initially necessary to prepare the bonding surfaces. This process consisted of the adherends sandblasting with corundum sand followed by cleaning the surface with acetone until no traces of contaminants exist that can prevent a good bond. After the surface preparation, it was necessary to prepare the joints for bonding. With this purpose, the adherends should be aligned in a bonding jig and, to assure the designated t_A for the joints, calibrated nylon wires with 0.2 mm diameter were attached to the adherends at the overlap ends to stop the adherends’ from entering contact when pressed and acquire t_A = 0.2 mm. The adherends were then bonded together by applying adhesive to one of the elements and subsequent position the other adherend correctly. Then, pressure was applied with grips to reach the required thickness and cast out the excess adhesive, which was later removed after its cure. Due to the low pressure applied to the joints (minimum to expel the excess adhesive and promote the adherend/wire/adherend contact), it was assumed that the associated wires’ deformation was negligible, and that t_A would be accurately achieved by this process. Moreover, the t_A accuracy was checked after adhesive curing by direct measurements. The removal of the excess adhesive is done after its cure to achieve the joint’s theoretical layout without adhesive flaws at the joint boundaries. For testing, the joints were placed between the Universal Testing Machine (UTM) clamps using L_T = 180 mm for all L_O. All the joints were experimentally tested using a UTM Shimadzu AG-X 100 with a 100 kN load cell. The tests were performed with a constant speed of 1 mm/min. The average failure load from each set was considered as the experimental maximum load (P_m).

3 Numerical work

3.1 ISSF technique

The SIF is mainly used to characterise the stress fields of sharp cracks. However, the ISSF also allows the evaluation of multi-material corners with the most diverse geometries. Figure 2 presents an example of these corners for the geometry used in this work, i.e., SLJ. The stress near the interface corner can be described, in polar coordinates (r,θ), such as those presented in Fig. 3, using the interface singularity as:

$$ {\upsigma }_{ij} = \mathop \sum \nolimits_{n = 1}^{\infty } H_{n} r^{{{\uplambda }_{n} - 1}} f_{ij} \left( {\lambda_{n} ,\theta } \right). $$

(1)

Fig. 2

Example of multi-material corners in SLJ that the ISSF can evaluate

Fig. 3

Polar coordinates system

Additionally, the displacement in the same region, using the same coordinate system, can be described as:

$$ u_{j} = \mathop \sum \nolimits_{n = 1}^{\infty } H_{n} r^{{{\uplambda }_{n} }} g_{j} \left( {\lambda_{n} ,\theta } \right), $$

(2)

where n is the number of exponents (λ), which varies with the geometry of the interface corner, and H_n is a scalar value representing the ISSF. The exponents are determined by finding the solution for the following equation (Qian and Akisanya 1999):

$$ 0 = e^{2} + b^{2} - \left( {\lambda c} \right)^{2} - \left( {\lambda d} \right)^{2} , $$

(3)

where the equations to determine the parameters e, b, c and d can be found in Appendix 1. In these equations, θ₁ and θ₂ are the angles of the material interface corner, and α and β are the Dundurs parameters (Dundurs 1969), defined as follows:

$$ \alpha = \frac{{G_{1} \left( {\kappa_{2} + 1} \right) - G_{2} \left( {\kappa_{1} + 1} \right)}}{{G_{1} \left( {\kappa_{2} + 1} \right) + G_{2} \left( {\kappa_{1} + 1} \right)}} $$

(4)

$$ \beta = \frac{{G_{1} \left( {\kappa_{2} - 1} \right) - G_{2} \left( {\kappa_{1} - 1} \right)}}{{G_{1} \left( {\kappa_{2} + 1} \right) + G_{2} \left( {\kappa_{1} + 1} \right)}} $$

(5)

where κ_m = 3 − 4ν_m in plane strain cases and G_m is the shear modulus of material m. The subscripts 1 and 2 in κ and μ represent the two materials. Having determined λ using Eq. (3), it is then possible to calculate the f_ij(λ_n, θ) and g_j(λ_n, θ) by solving the following system of equations:

$$ \left\{ {\begin{array}{*{20}c} {g_{rr}^{m} } & {g_{\theta }^{m} } & {f_{rr}^{m} } & {f_{\theta \theta }^{m} } & {f_{\theta }^{m} } \\ \end{array} } \right\}^{T} = {\varvec{N}}_{{\varvec{m}}} {\varvec{X}}_{{\varvec{m}}} {\varvec{Y}}, $$

(6)

where m indicates the material and the matrices N_m and X_m, and vector Y, are defined as (Qian and Akisanya 1999):

$$ N_{m} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\left( {\kappa _{m} - \lambda } \right)\cos \left( {\left[ {\lambda - 1} \right]\theta } \right)}}{{2G_{m} }}} \\ {\frac{{\left( {\kappa _{m} + \lambda } \right)\sin \left( {\left[ {\lambda - 1} \right]\theta } \right)}}{{2G_{m} }}} \\ { - \left( {\lambda ^{2} - 3\lambda } \right)\cos \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ {\left( {\lambda ^{2} + \lambda } \right)\cos \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ \end{array} } \\ {\left( {\lambda ^{2} - \lambda } \right)\sin \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\left( { - \kappa _{m} + \lambda } \right)\sin \left( {\left[ {\lambda - 1} \right]\theta } \right)}}{{2G_{m} }}} \\ {\frac{{\left( {\kappa _{m} + \lambda } \right)\cos \left( {\left[ {\lambda - 1} \right]\theta } \right)}}{{2G_{m} }}} \\ \end{array} } \\ {\left( {\lambda ^{2} - 3\lambda } \right)\sin \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ { - \left( {\lambda ^{2} + \lambda } \right)\sin \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ {\left( {\lambda ^{2} - \lambda } \right)\cos \left( {\left[ {\lambda - 1} \right]\theta } \right)} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - \frac{{\cos \left( {\left[ {\lambda + 1} \right]\theta } \right)}}{{2G_{m} }}} \\ {\frac{{\sin \left( {\left[ {\lambda + 1} \right]\theta } \right)}}{{2G_{m} }}} \\ \end{array} } \\ { - \lambda \cos \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ {\lambda \cos \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ {\lambda \sin \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\sin \left( {\left[ {\lambda + 1} \right]\theta } \right)}}{{2G_{m} }}} \\ {\frac{{\cos \left( {\left[ {\lambda + 1} \right]\theta } \right)}}{{2G_{m} }}} \\ \end{array} } \\ {\lambda \sin \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ { - \lambda \sin \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ {\lambda \cos \left( {\left[ {\lambda + 1} \right]\theta } \right)} \\ \end{array} } \\ \end{array} } \right] $$

(7)

$$ {\varvec{X}}_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ {\chi_{31} } & {\chi_{32} } \\ {\chi_{41} } & {\chi_{42} } \\ \end{array} } \right];\, {\varvec{X}}_{2} = \left[ {\begin{array}{*{20}c} {\chi_{51} } & {\chi_{52} } \\ {\chi_{61} } & {\chi_{62} } \\ {\chi_{71} } & {\chi_{72} } \\ {\chi_{81} } & {\chi_{82} } \\ \end{array} } \right];\, {\varvec{Y}} = \left\{ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \end{array} } \right\}, $$

(8)

being the components of X_m and Y given by the equations in Appendix 2 (Qian and Akisanya 1999). There are several ways to determine the H_n using numerical methods. A popular method is performing an integration over a line, or area, encircling the interface corner as Qian and Akisanya (1999) did. Alternately, the H_n values can also be determined by extrapolating to the corner the H_n from values near the corner (Klusák et al. 2009). This was the method used in this work. For a n number of λ, a n number of points at different angles (θ) is needed to determine the H_n values at a fixed radius (r), by solving the following system of equations for the H vector:

$$ \left[ {\begin{array}{*{20}c} {r^{{\lambda_{1} - 1}} f_{\theta \theta } \left( {\lambda_{1} ,\theta_{n + 1} } \right)} & \cdots & {r^{{\lambda_{n} - 1}} f_{\theta \theta } \left( {\lambda_{n} ,\theta_{n + 1} } \right)} \\ \vdots & \ddots & \vdots \\ {r^{{\lambda_{1} - 1}} f_{\theta \theta } \left( {\lambda_{1} ,\theta_{n + n} } \right)} & \cdots & {r^{{\lambda_{n} - 1}} f_{\theta \theta } \left( {\lambda_{n} ,\theta_{n + n} } \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {H_{1} } \\ \vdots \\ {H_{n} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\sigma_{\theta \theta } \left( {r,\theta_{n + 1} } \right)} \\ \vdots \\ {\sigma_{\theta \theta } \left( {r,\theta_{n + n} } \right)} \\ \end{array} } \right\}. $$

(9)

The solution of Eq. 9 is obtained for several different r, and it is then extrapolated to r = 0 mm, from an r interval where it is stable, to obtain H at the interface corner.

3.2 Modelling conditions

A FEM analysis was performed to validate the ISSF criterion. For that, a MATLAB based tool was used, where the finite element discretisation was created, and the natural and essential boundary conditions were imposed. A script was added to this tool with the previously described ISSF formulation. The SLJ was modelled accordingly to Fig. 1. The left boundary was considered fixed (U_x = U_y = U_z = 0), while δ was imposed in the right boundary. The simulations were executed considering plane strain, linear elastic material behaviour and small deformations. For these simulations, four-node quadrilateral elements were chosen to describe the whole model. Two different refinements near the interface corner were applied to discretise the interface corner in order to evaluate the mesh’s influence on the results of the ISSF analysis. These discretizations near the corner were the same for all the studied L_O. The more refined mesh had approximately double the number of nodes when compared with the baseline mesh in this region. The radial region of the two discretizations used in the ISSF analysis is presented in Fig. 4a and b, with Fig. 4c showing the dimensions and the number of nodes in the region near the corner that was discretized in the same manner for all L_O. After these simulations were solved, the P_m values were determined through the ISSF criterion and then compared to the experimental data. An analysis of the stress in the mid-thickness line of the adhesive was also performed. To do this, a new set of discretizations for each L_O was needed. An example of this discretization at the left end of the overlap for the joint with L_O = 25 mm is shown in Fig. 4d. For the other L_O, the discretizations are similar. This discretization has 14 elements along the adherend thickness and six elements along the adhesive thickness. These simulations were performed under the same assumptions as the ISSF simulations, namely plane strain, linear elastic material behaviour and small deformations.

Fig. 4

Baseline (a) and refined (b) discretisation near the interface corner, dimensions and the number of nodes in the region near the corner (c) and discretization for the stress analysis (d)

4 Results

4.1 Experimental data and analysis

Every single one of the SLJ tested presented cohesive failure in the adhesive layer. On top of that, none of the adherends displayed plastic deformation, as it can be proved by the load–displacement curves from Fig. 5, considering the sample cases of L_O = 12.5 (a) and 50 mm (b). All curves show a small loss of linearity between 3 and 4 kN, but this issue was experimentally identified as a minor gripping problem in the testing machine. In all cases, failure takes place without visible plasticization. This, allied to the experimental data’s low variation, proves that the specimens were correctly prepared. Figure 6 presents the average P_m sustained by the joints for each L_O tested. From the observation of this graph, it is perceptible that the joint strength increases with each increment of L_O. This fact is in line with previous works where different adhesive types were tested, including the one used in this analysis (De Sousa et al. 2017). However, although the curve is nearly linear, P_m is not proportional to L_O, in the sense that the P_m/L_O ratio markedly diminishes for higher L_O, thus emphasizing the joints’ performance reduction. This behaviour is due to the adhesive’s brittleness, which does not accommodate the increasing peak stresses with L_O and fails prematurely, and contrasts with that of ductile adhesives, which usually manage to produce proportional P_m–L_O curves up to some extent (Nunes et al. 2016).

Fig. 5

Load–displacement curves for the SLJ bonded with the Araldite® AV138: L_O = 12.5 (a) and 50 mm (b)

Fig. 6

Average P_m sustained by the joints for each L_O tested

4.2 Stress analysis in the adhesive layer mid-thickness

The stress distributions along the adhesive layer are also crucial in this analysis. Figure 7 shows the peel (σ_yy) (a) and shear (τ_xy) (b) stresses along the adhesive layer mid-thickness, marked in red in the diagram of Fig. 7a. The adhesive length was normalised by L_O to allow an easier comparison. The mesh used to obtain these stresses had to be different from the radial mesh because this mesh cannot provide a steady set of nodes along the mid-thickness of the adhesive. Thus, a structured mesh was considered for this analysis only (Fig. 4d), while the other conditions remain equal. In this work, significant σ_yy stresses were observed at the overlap ends, mainly due to the joint rotation during the experimental tests. In fact, this is a common problem found in SLJ, and it arises since the overall joint deformation is ruled by the stiffer adherends, while the compliant adhesive is forced to follow the adherends separation at the overlap edges due to their opposed curvature. Owing to the same effect, compressive stresses are found towards the centre of the overlap (Fernandes et al. 2015). The singularity effect should also be considered, but it was numerically found that this effect was negligible since stresses were taken at the adhesive mid-thickness. Analysing the stress variation with L_O, it was concluded that incrementing this parameter led to higher σ_yy peak stresses. As a result, P_m averaged to the bonded area reduces by increasing L_O. τ_xy stresses are also present in this joint type. The characteristic distribution consists of a small load towards the centre of the overlap, while in the ends, τ_xy stresses increase. This distribution is related to each adherend’s varying longitudinal strains along the overlap (Jiang and Qiao 2015). Similarly to σ_yy stresses, τ_xy peak stresses increase with L_O. This fact is again related to the higher longitudinal strains of the adherends for bigger L_O (Campilho et al. 2011a). Based on this analysis, higher L_O should affect the joint strength, especially for this type of adhesive.

Fig. 7

σ_yy (a) and τ_xy (b) stresses along the adhesive layer

4.3 ISSF calculation

The SLJ geometry presents anti-symmetry, shown in Fig. 8, allowing the ISSF calculation for only one interface corner. The ISSF calculation was performed using the extrapolation method described in Sect. 3.1. The procedure started with the determination of the eigenvalues (λ_n) following Eq. (3). Considering the combination of materials and geometry of the joints tested, as presented in Fig. 8, with θ₁ = π/2 rad and θ₂ = π rad, two different exponents were found: λ₁ = 0.6539 and λ₂ = 0.9984. Therefore, according to Eq. (9), two different angles are needed to perform the extrapolation, equal to the number of exponents. The angles chosen were: θ₃ = π/4 rad and θ₄ = − 3π/4 rad, because this way the determination of H₁ and H₂ is based on nodes in the two materials, being one in the ascending part of the σ_θθ curve (θ₄) and the other in the descending part of the σ_θθ curve (θ₃).

Fig. 8

Anti-symmetry of the SLJ and corner geometry

Considering L_O = 37.5 mm as an example, the values of H₁ and H₂ were extrapolated to r = 0 mm from the values in the interval 0.01 < r < 0.02 mm, which are close enough to the corner tip to be influenced by other singularities. This extrapolation was performed when the reaction forces equalled the experimental failure at the joint end where δ was imposed. The process is the same for the other L_O. Figure 9 presents the H₁ extrapolations with the baseline discretization (a) and the refined discretization (b) for the L_O = 37.5 mm case. This figure only presents the first singularity (H₁) component since it is the most important. However, the same extrapolation can be used to obtain the second singularity (H₂) component. The comparison between the discretisations in Fig. 9 reveals that this calculation is discretisation independent. The graphs also show the H₁ extrapolations for the other L_O. These were performed at an imposed δ where H₁ would be the same as the H₁ of L_O = 37.5 mm at failure displacement. The comparison between the different L_O shows a more pronounced slope in the extrapolation for larger L_O.

Fig. 9

H₁ extrapolation for the L_O = 37.5 mm SLJ using the FEM with the baseline discretisation (a) and the refined discretisation (b)

Figure 10 compares the stresses obtained from the numerical simulations and the ones predicted by the analytical formula. The numerical stresses were obtained at r = 0.02 mm from the interface corner and when H₁ was the same for all L_O. In Fig. 10, it can be observed that the analytical stress is very similar to the numerical stress, thus proving that the analytical functions obtained with Eq. (6) fit well the numerical stresses for the three different components and showing that the stress singularity dominates this region. The comparison of the numerical results shows that the stress components are almost the same for all L_O, which would be expected in a case where H₁ was the same for all L_O.

Fig. 10

Stress components using the FEM with the refined discretisation compared to the analytical stress

4.4 Strength prediction

In order to predict the joint strength, it is necessary to determine the critical ISSF (H_c). However, there is no standardized purely experimental test that allows this determination. The widespread methods to obtain this parameter are usually based on integrals and their implementation is often considerably intricate. Therefore, a combination of numerical simulations and experimental data was used. This type of hybrid experimental/numerical approach to determine failure criteria has been used previously for other criteria, such as the CLS criterion (Ramalho et al. 2021), but also to determine H_c (Akhavan-Safar et al. 2017). The method proposed here consists of experimentally testing a SLJ of a given L_O and determining its P_m. Afterwards, a numerical simulation of the same joint is to be performed using the previously determined P_m as the imposed load. Then, the extracted singularity (H_n) components (n = 1 or n = 2) were used as the critical ISSF for both singularities (H_nc), which make possible the P_m prediction for different L_O. Since H₁ component is the most significant one, this method was used to obtain the H_1c estimates for each experimentally tested L_O.

Figure 11 shows that the H_1c values predicted using the two different discretisations present differences below 1%. It also shows that the H_1c estimated using L_O = 37.5 mm and L_O = 50 mm are similar, but for smaller L_O, the H_1c estimates are lower. This occurs because even an adhesive as brittle as this has a small amount of plasticity in longer L_O, which means that some energy would have to be spent in plasticizing the adhesive before a crack would form. Furthermore, in longer L_O, the crack can propagate stably for a few moments, but for shorter L_O, the joints fail as soon as there is a crack. Finally, P_m was predicted using each one of those H_1c. For example, using the H_1c obtained with the experiments and numerical simulations of L_O = 12.5 mm, P_m was numerically predicted for the other L_O (25, 37.5 and 50 mm). The same procedure was done for the H_1c obtained with the other L_O. Figure 12 presents the strength predictions only for the refined mesh since the results are similar to those obtained with the baseline mesh. On the other hand, it is observable that, as L_O increases, the curve slopes also increase. This fact is contrary to the experimental results where, for larger L_O, increasing L_O diminishes the returns in strength. However, this slope increase is minimal, and it is not a significant issue in the L_O range tested. For the largest L_O, the predicted strength increase is in line with what was verified experimentally, i.e., approximately a 1 kN strength increase between L_O = 37.5 mm and L_O = 50 mm. For the two shortest L_O, the predicted strength increases when L_O increases are smaller than those found experimentally, i.e., the strength prediction increase between L_O = 12.5 mm and L_O = 25 mm is smaller than 1 kN, while the experimental strength increase was over 1 kN.

Fig. 11

Comparison of the predicted H_1c values for the different L_O and discretisations

Fig. 12

Strength predictions using the FEM with the refined discretisation

By analysing the strength predictions for the L_O = 12.5 mm, it is perceptible that the nearest prediction (beyond its own H_1c curve) is the curve of H_1c determined with L_O = 25 mm. However, the joint strength is overpredicted, and the percentual deviation between this prediction and the experimental data is 9.75%, which can be considered high. The other two predictions are also higher than the experimental value, being the L_O = 37.5 mm case the furthest away with a percentual deviation of 17.33%. For L_O = 25 mm, similar behaviour is observed for the two highest L_O. Nonetheless, for the L_O = 12.5 mm prediction case, the joint strength is underpredicted with a percentual deviation of 8.92%. For the largest L_O, it is clear that the predictions are identical, with a percentual deviation of 0.84% when a L_O = 50 mm was used to predict the strength of the L_O = 37.5 mm joint and the same percentual deviation on the contrary case. For both these cases, the worst-case scenario is predicting the strength with a L_O = 12.5 mm, where percentual deviations over 16% were found.

5 Conclusions

The present work focused on the ISSF criterion, comparing the numerical analysis performed through FEM with experimental data. This work’s geometry and material combination lead to the existence of two components that characterise the stress singularity at the adhesive/adherend interface corner, being the first singularity the most significant one. The extrapolation method used to determine H₁ showed independence from the discretisation. This is a major advantage when compared to the stress, which is affected by the stress singularity in the corner, meaning that finer discretisations lead to higher stress levels in this region. The method proposed to determine H_1c showed some variance depending on which L_O is used, except when comparing the H_1c obtained with L_O = 37.5 mm with the one obtained with L_O = 50 mm, which were similar. The strength predictions were lower than the experiments when the H_1c determined with a smaller L_O was used to predict a larger L_O’s joint strength. However, joint strength was over predicted when an L_O smaller than the L_O with which H_1c was determined was used. The only exceptions to this rule are the two largest L_O, because the H_1c predicted with those two L_O are similar, meaning that the strength predictions for L_O = 37.5 mm using the H_1c determined with L_O = 50 mm, and vice-versa, are identical to the experimental P_m. Since it is better to have conservative P_m predictions due to safety reasons, it would be advisable to only predict P_m of joints with L_O larger than the L_O used to determine H_1c. The results found in this work revealed to be very promising, with very accurate results achieved, considering the simplicity of the method applied to determine H_1c. Although the method’s validity was only checked for a specific adhesive system, this technique can be further studied in the field of adhesive joints and applied to different systems/joint types, provided that further validation is accomplished.

Appendices

Appendix 1

$$ \begin{gathered} e = \left( {\alpha - \beta } \right)\left( {\cos \left[ {2\lambda \theta_{1} } \right] - \cos \left[ {2\lambda \theta_{1} - 2\lambda \theta_{2} } \right] + \lambda^{2} \left[ {\cos \left( {2\theta_{1} } \right) - \cos \left( {2\theta_{1} + 2\theta_{2} } \right) - 1 + \cos \left( {2\theta_{2} } \right)} \right]} \right) \\ + \left( {1 + \alpha } \right)\left( {1 - \cos \left[ {2\lambda \theta_{1} } \right]} \right) - \left( {1 - \beta } \right)\left( {1 - \cos \left[ {2\lambda \theta_{2} } \right]} \right) \\ \end{gathered} $$

(10)

$$ \begin{gathered} b = \left( {\alpha - \beta } \right)\left( {\sin \left[ {2\lambda \theta_{1} } \right] - \sin \left[ {2\lambda \theta_{1} - 2\lambda \theta_{2} } \right] - \lambda^{2} \left[ {\sin \left( {2\theta_{1} } \right) - \sin \left( {2\theta_{1} + 2\theta_{2} } \right) + \sin \left( {2\theta_{2} } \right)} \right]} \right) \\ - \left( {1 + \alpha } \right)\sin \left( {2\lambda \theta_{1} } \right) - \left( {1 - \beta } \right)\sin \left( {2\lambda \theta_{2} } \right) \\ \end{gathered} $$

(11)

$$ \begin{gathered} c = \left( {\alpha - \beta } \right)\left( {\cos \left[ {2\lambda \theta_{1} } \right] - \cos \left[ {2\lambda \theta_{1} + 2\theta_{2} } \right] + \cos \left[ {2\lambda \theta_{2} } \right] - \cos \left( {2\lambda \theta_{2} - 2\theta_{1} } \right) - 1 + \cos \left( {2\theta_{1} } \right)} \right) \\ + \left( {1 + \alpha } \right)\left( {1 - \cos \left[ {2\theta_{1} } \right]} \right) - \left( {1 - \beta } \right)\left( {1 - \cos \left[ {2\theta_{2} } \right]} \right) \\ \end{gathered} $$

(12)

$$ \begin{gathered} d = \left( {\alpha - \beta } \right)\left( {\sin \left[ {2\theta_{1} } \right] + \sin \left[ {2\lambda \theta_{2} - 2\theta_{1} } \right] - \sin \left[ {2\lambda \theta_{1} } \right] + \sin \left( {2\lambda \theta_{1} + 2\theta_{2} } \right) - \sin \left( {2\theta_{2} } \right)} \right) \\ - \left( {1 + \alpha } \right)\sin \left( {2\theta_{1} } \right) - \left( {1 - \beta } \right)\sin \left( {2\theta_{2} } \right) \\ \end{gathered} $$

(13)

Appendix 2

$$ \chi_{31} = - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right) $$

(14)

$$ \chi_{32} = \sin \left( {2\lambda \theta_{1} } \right) - \lambda \sin \left( {2\theta_{1} } \right) $$

(15)

$$ \chi_{41} = \sin \left( {2\lambda \theta_{1} } \right) + \lambda \sin \left( {2\theta_{1} } \right) $$

(16)

$$ \chi_{42} = \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right) $$

(17)

$$ \chi_{51} = \frac{{1 - \beta + \left( {\alpha - \beta } \right)\left( {\lambda - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right)}}{1 + \alpha } $$

(18)

$$ \chi_{52} = \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left( {2\lambda \theta_{1} } \right) - \lambda \sin \left( {2\theta_{1} } \right)} \right)}}{1 + \alpha } $$

(19)

$$ \chi_{61} = - \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left( {2\lambda \theta_{1} } \right) + \lambda \sin \left( {2\theta_{1} } \right)} \right)}}{1 + \alpha } $$

(20)

$$ \chi_{62} = \frac{{1 - \beta - \left( {\alpha - \beta } \right)\left( {\lambda + \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right)}}{1 + \alpha } $$

(21)

$$ \begin{gathered} \chi_{71} = \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left[ {2\lambda \theta_{1} } \right] + \lambda \sin \left[ {2\theta_{1} } \right]} \right)\left( {\sin \left[ {2\lambda \theta_{2} } \right] - \lambda \sin \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ - \frac{{\left( {1 - \beta + \left[ {\alpha - \beta } \right]\left[ {\lambda - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]} \right)\left( {\cos \left[ {2\lambda \theta_{2} } \right] + \lambda \cos \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ \end{gathered} $$

(22)

$$ \begin{gathered} \chi_{72} = - \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left[ {2\lambda \theta_{1} } \right] - \lambda \sin \left[ {2\theta_{1} } \right]} \right)\left( {\cos \left[ {2\lambda \theta_{2} } \right] + \lambda \cos \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ - \frac{{\left( {1 - \beta - \left[ {\alpha - \beta } \right]\left[ {\lambda + \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]} \right)\left( {\sin \left[ {2\lambda \theta_{2} } \right] - \lambda \sin \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ \end{gathered} $$

(23)

$$ \begin{gathered} \chi_{81} = - \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left[ {2\lambda \theta_{1} } \right] + \lambda \sin \left[ {2\theta_{1} } \right]} \right)\left( {\cos \left[ {2\lambda \theta_{2} } \right] - \lambda \cos \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ - \frac{{\left( {1 - \beta + \left[ {\alpha - \beta } \right]\left[ {\lambda - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]} \right)\left( {\sin \left[ {2\lambda \theta_{2} } \right] + \lambda \sin \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ \end{gathered} $$

(24)

$$ \begin{gathered} \chi_{82} = - \frac{{\left( {\alpha - \beta } \right)\left( {\sin \left[ {2\lambda \theta_{1} } \right] - \lambda \sin \left[ {2\theta_{1} } \right]} \right)\left( {\sin \left[ {2\lambda \theta_{2} } \right] + \lambda \sin \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ - \frac{{\left( {1 - \beta - \left[ {\alpha - \beta } \right]\left[ {\lambda + \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]} \right)\left( {\cos \left[ {2\lambda \theta_{2} } \right] - \lambda \cos \left[ {2\theta_{2} } \right]} \right)}}{1 + \alpha } \\ \end{gathered} $$

(25)

$$ y_{1} = \frac{c - e}{{\lambda \left( {\left[ {\lambda + 1 - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]\left[ {c - e} \right] + b + d} \right)}} $$

(26)

$$ y_{2} = \frac{b + d}{{\lambda \left( {\left[ {\lambda + 1 - \cos \left( {2\lambda \theta_{1} } \right) - \lambda \cos \left( {2\theta_{1} } \right)} \right]\left[ {c - e} \right] + b + d} \right)}} $$

(27)