Atomistic modeling of the fracture toughness of silicon and silicon-silicon interfaces

Abstract

Fracture modeling at the atomic scale is currently an intense area of research because the crack propagation process depends strongly on the description of interatomic interactions. Here we present first the mode-I plane strain quasi-static fracture toughness of single crystal silicon, along four orientations, as obtained using molecular statics simulations with nine empirical potentials. The “best” potential is determined by comparing the fracture toughness and trapping range of the simulations with available experimental data and with results calculated using first-principles molecular dynamics. The choice is buttressed by its ability to predict the effective toughness and propagation direction of a crack subjected to mode-II loading. The best performing potential is then used to investigate the fracture toughness and the role of bond trapping for a crack along the boundary of two silicon crystals belonging to two different tilt families.

1 Introduction

The fracture toughness of brittle materials, which is a measure of resistance to crack extension, is an important material property dictated by the atomic interactions in the immediate vicinity of the crack front, see e.g. Bitzek et al. (2015). Therefore, atomic level modeling of this property and of the deformation processes that determine its magnitude has become a significant research topic. The most accurate ab initio computational methods for simulating crack propagation quickly become computationally prohibitive with increasing system size, and therefore, most often less accurate but more efficient empirical interatomic potentials are used for molecular dynamics (MD) simulations that require accounting for relatively large material volumes. However, empirical potentials are designed and fitted to the material properties involved with specific phenomena (cohesive energy, lattice constant, elastic constants and basic point defect properties for example) and therefore their ability to accurately capture the material properties related to other phenomena is questionable. Choosing and using an empirical potential to simulate fracture is particularly challenging, as evidenced by the large number of MD studies on crack growth in silicon (Si), a quintessential brittle material that cleaves at temperatures below the brittle-ductile transition ($\sim$814 K), e.g. as demonstrated by Samuels and Roberts (1989). Representative experimental studies of the fracture toughness and the fracture energy of the Si single crystal (SC), which could be used to assess the validity of MD predictions, include works by Samuels and Roberts (1989), Tsai and Mecholsky (1991) and George and Michot (1993). The data suggests that atomistic modeling of quasi-static, see e.g. Gumbsch and Cannon (2000), Perez and Gumbsch (2000), Bailey and Sethna (2003), and dynamic, e.g. Bernstein and Hess (2003), Buehler et al. (2006) and Sen et al. (2010), crack propagation in Si continues to represent a very challenging task for the interatomic potentials not specifically designed for characterizing the behavior of cracks.

Table 1 Properties of a diamond cubic Si SC predicted by the nine interatomic potentials, as well as experimentally measured

The aim of this work is twofold; first is to test the most widely used empirical interatomic potentials for Si on their ability to predict the experimentally measured direction-dependent values of the mode-I quasi-static plane strain fracture toughness of the SC, and second to apply the best performing potential to investigate the fracture behavior of cracks along selected grain boundaries (GBs) that separate two SCs.

The paper has the following structure. In Sect. 2 the chosen empirical potentials are described with emphasis on the purposes for which they were designed. This is followed by the boundary conditions, the simulation procedure and the computation parameters that quantify the applied loading on a semi-infinite crack and determine its response. Section 3 presents the simulation results for the fracture behavior and toughness of a SC for four crack orientations as predicted by all nine potentials. The best performing potential is determined as the one whose predictions not only are closest to available experimental measurements and first-principles MD simulations, but also by its ability to predict the effective toughness and crack extension direction of a mode-II crack that is consistent with the maximum hoop stress criterion dictated by Linear Elastic Fracture Mechanics (LEFM). The selected potential is then used to simulate crack extension along two families of symmetric tilt GBs. Insights gained from the simulations are summarized in Sect. 4.

2 Methodology

2.1 Empirical potentials

Empirical interatomic potentials are constructed using simplified closed-form mathematical expressions that attempt to describe how the mechanical properties and energetics of a material are dictated by the complex interactions between its nuclei and electrons. This approach involves fitting the numerous parameters that appear in the mathematical representation of a given potential to accurately model specific phenomena. This tailoring poses the question of whether the potential is robust, i.e. for what class of problems for which it was not specifically designed for can it be applied with confidence? A thorough review of available (although developed quite long time ago) potentials for Si is presented in Balamane et al. (1992); in this section we briefly review the nine widely used and some more recent potentials we chose to study its fracture toughness.

The simulations considered in this paper rely on the fact that at room temperature Si is practically elastic. This allows the use of a crack modeling approach similar to those used for a cracked elastic continuum. Si possesses cubic symmetry, so the elastic stiffness tensor $\mathbf{C}$ that relates the stress tensor ${{\varvec{\sigma }}}$ to the strain tensor ${{\varvec{\varepsilon }}}$ according to ${{\varvec{\sigma }}}=\mathbf{C}{{\varvec{\varepsilon }}}$, has only three independent elements. Using the Voigt notation these elastic constants are written as $C_{11}$, $C_{12}$, and $C_{44}$. Table 1 presents some basic properties of the Si diamond cubic SC for the considered nine potentials. Specifically, the table contains the lattice constant $a_{0}$, binding energy $E_{0}$, elastic constants $C_{ij}$, and the anisotropy coefficient A, defined as $A=2C_{44}/(C_{11}-C_{12})$. Representative values of surface energies along the cleavage planes $\gamma _{\mathrm{(plane)}}$ are also provided because these values reflect the fracture energies that are used in the simulations to establish the initial crack loading.

A few words about the selected potentials. The first potential is an improved many-body bond-order potential constructed by Tersoff (1988) (usually referred to as T3) to model covalently bonded Si systems by fitting to ab initio results for several Si structures. It captures well the elastic properties of Si and the energetics of point defects, but misses some features of surface reconstructions and greatly overestimates the melting temperature. The second MOD potential proposed by Kumagai et al. (2007) is an improved version of T3 that relies on a modified angular-dependent term to reproduce values of the elastic constants and the melting temperature more accurately.

The third potential developed by Justo et al. (1998) is the environment-dependent interatomic potential (EDIP) for Si, which is approximated by two- and three-body interaction terms with theoretically motivated functional forms and fitted to ab initio data for different bulk phases and defects. The EDIP provides better descriptions of the local structures such as point defects and dislocation cores, as well as disordered structures and phase transitions.

The fourth potential introduced by Stillinger and Weber (1985) (SW), which consists of two- and three-body terms, was constructed to model solid and liquid forms of Si by fitting to the experimentally obtained properties. Because of unsatisfactory predictions of fracture behavior, ad hoc modification of the SW potential was proposed and tested in Holland and Marder (1998b, 1998a). Modified SW (mSW), the fifth considered potential, is obtained by increasing by the factor of two the parameter $\lambda$, which governs the stiffness of angle-dependent forces. This modification provides the desired brittle fracture response at the expense of noticeable changes in elastic constants (see Table 1) and a significant (roughly two times) increase in the melting temperature. Consequently, there are still opportunities for further enhancements of SW-like potentials for Si.

The modified embedded-atom method (MEAM) potential, denoted by number six in Table 1, was devised by Baskes (1992) for a variety of materials including Si. It is constructed by modifying a well established EAM potential that was developed for metals, which consists of pair potential interaction and an embedding energy term that is a function of distance-dependent atomic electron density. The MEAM potential is obtained by introducing angular terms in the electron density function that allow it to account for bond directionality in covalent solids such as Si. The seventh potential MEAM1 developed by Lenosky et al. (2000) is constructed by using the MEAM functional form. But instead of restricting the potential functions to closed-form expressions, they are represented by cubic splines fitted to a larger database of first principles and experimental results for Si. MEAM1 provides accurate description of elastic properties and defect energetics, especially for dislocation reconstruction and interstitial complexes. Using the same fitting procedure as for MEAM1, but changing the database to incorporate various Si interstitial structures, the MEAM potential MEAM2, eighth here, was developed by Du et al. (2011). MEAM2 was specifically designed to achieve more accurate predictions of tetra-interstitial defects in Si than other potentials which cannot characterize them sufficiently well. Finally, the ninth potentials labeled as MEAM3 refers to the spline-based MEAM potential with an additional generalized SW energy term that was originally developed for bcc transition metals by Nicklas (2013) and then applied to Si.

2.2 Boundary conditions

The elastic analysis of a finite-sized cracked continuum requires the solution of a boundary value problem, and the results are applicable to the considered geometry and loading. However, asymptotic solutions of the elasticity problem have shown that in the vicinity of a crack front the functional form of the stress, strain and displacement fields are universal and dominated by the so-called stress intensity factors. Closed-form expressions of the functional forms, which are typically expressed using polar coordinates, involve a power-law singularity with respect to the distance of a material point from the crack front, and trigonometric functions with respect to its angular position. Solutions are available for cracks in isotropic and anisotropic materials, and for cracks along the perfectly bonded interfaces between isotropic and/or anisotropic materials. The stress intensity factors, which depend on the details of the specimen geometry and applied loading, represent the relative levels of crack surface opening and crack surface sliding displacements, and the magnitudes of the singular stress and strain fields they produce in the immediate vicinity of the crack front. The importance of the asymptotic solution lies in the fact that as long as the nonlinear material response that develops to eliminate the unphysical stress singularity is limited to a sufficiently small region near the crack front (small-scale-yielding conditions), then the stress intensity factors alone dictate whether a crack remains stationary or extends. This is the basis of LEFM, a fracture theory that assumes a crack will extend when the combination of the stress intensity factors reaches a critical value that is proportional to what is referred to as the fracture toughness. A summary of the elastic fields produced by the cracks considered in this paper is provided in “Appendices A and B”.

The universal nature of the asymptotic fields near the crack front also eliminate the need to model finite geometry specimens and specific loadings when studying the near-crack front region. The dominance of the asymptotic solution allows a boundary layer analysis involving only the near-front region, to which the specifics of the loading and specimen geometry are transmitted by prescribing to its boundary the displacement field from this elastic solution and the associated stress intensity factors. The boundary layer analysis thus greatly reduces the simulation volume size, and allows the results to be applied to finite geometry configurations whose near-crack front regions are dominated by their own (known) stress intensity factors.

Fig. 1

a Schematics of the simulation setup. Here PBCs are applied only along the z-axis. b Imposed displacements, predicted by elasticity and given in Eq. (B.6), for the Si SC $(111)[11\bar{2}]$ crack system at $r=100\,\AA$ loaded with $K_{\mathrm{I}}=0.61$ MPa$\sqrt{\text {m}}$ for SW potential. Here the solid lines represent the elasticity solution for anisotropic Si SC, while the dashed lines show the solution for isotropic material, keeping $C_{11}$ and $C_{12}$ and assuming that $C_{44}=(C_{11}-C_{12})/2$

In the spirit of the continuum analyses, Fig. 1a shows the schematic of the boundary layer that will be simulated using molecular statics calculations. The cylindrical region of radius R is in general comprised of upper and lower portions representing two Si grains, and it contains an initial tilt GB crack whose front is placed at the center. For the general case $\mathbf{C}^{(1)}$ and $\mathbf{C}^{(2)}$ represent the elastic stiffness tensors of the distinct grains shown by different colors and obtained by $\theta _{1}$ and $\theta _{2}$ rotations about the z-axis. The coordinate system is chosen such that the crack propagation direction, crack plane normal, and crack front direction are oriented along the x, y, and z axes, respectively. Periodic boundary conditions (PBCs), mimicking plane strain conditions, are imposed along the crack front direction using the minimal periodic unit cell size. An atomically sharp crack is constructed by displacing the atoms according to the asymptotic plane strain solution for mode-I loading of a crack in an anisotropic material. A similar approach was used for an anisotropic material containing a SC crack by Perez and Gumbsch (2000) (to study cleavage in silicon using ab initio calculations); Möller and Bitzek (2014a) (to investigate fracture in $\alpha$-iron with available interatomic potentials) and for an interface crack between two anisotropic crystals, i.e. GB crack, by Möller and Bitzek (2014b) (to model brittle fracture behavior in tungsten using interatomic potentials).

2.2.1 Asymptotic solution for anisotropic crystals and bicrystals

The elastic fields near the front of a crack in an anisotropic plate subjected to plane strain conditions predicts the standard inverse square root stress singularity and can be found in Sih et al. (1965). However, the stress field produced near the front of an interfacial crack in generally anisotropic elastic solids behaves as $r^{-1/2+i\epsilon }$, where $\epsilon$ represents the oscillatory index whose magnitude depends on the level of elastic mismatch, see e.g. Suo (1990); Gao et al. (1992). In addition, the oscillatory nature of the singularity couples the loading phases, so that a pure mode-I and mode-II stress intensity factors cannot be defined. In other words, all loading types produce both crack surface opening and crack surface sliding displacements. The oscillatory response implies interpenetration of the upper and lower crack surfaces within a very small region near the front of a crack within a finite-sized structure. This physically unrealistic result has been discussed for decades in the literature. In this paper the oscillatory index is not an issue because attention is limited to cracks in Si SC and GBs for which the oscillatory index is null.

The complications associated with the oscillatory index are removed by considering the class of interfaces satisfying the non-oscillatory condition ($\epsilon =0$) identified for anisotropic materials in Qu and Bassani (1989). For this case matrix $\mathbf{W}$, defined in Eq. (B.4), that depends solely on the elastic properties of two anisotropic solids, must be equal to zero. In addition, it was shown that a tilt GB having the crack front along the tilt axis also satisfies the non-oscillatory condition when in-plane and anti-plane deformations are decoupled. This condition requires the high symmetry orientation of the tilt axis, as shown in Qu and Bassani (1989). In this work we study the class of tilt GB interfaces that satisfy the non-oscillatory condition ($\mathbf{W=0}$). We use the asymptotic linear elastic solution based on the Stroh formalism for the displacement and stress fields of the interface crack derived by Bassani and Qu (1989) and given in Eqs. (B.5) and (B.6) of “Appendix B”.

Alternatively, since the non-oscillatory condition implies that the crack-tip solutions in both materials are independent of each other, the linear elastic solution for a crack in one anisotropic media given in Sih et al. (1965) with corresponding elastic properties for each region can be used. In particular, for the interfacial crack in a bicrystal schematically shown in Fig. 1a, i.e. GB crack, regions 1 and 2 correspond to two grains which possess different crystallographic orientations. Due to cubic anisotropy of Si, grains in general have different stiffness matrices $\mathbf{C}^{(1)}$ and $\mathbf{C}^{(2)}$, as denoted in Fig. 1a. These matrices are obtained by applying the rotation transformations defined by the grains’ orientations to the original fourth order stiffness tensor $\mathbf{C}^{(0)}$ according to the procedure described in “Appendix A”. $\mathbf{C}^{(0)}$ shown in matrix form in Eq. (A.1), that satisfy cubic symmetry, is constructed for each potential using the elastic constants data presented in Table 1.

For the initial comparison of the performance of the potentials the applied loading is limited to a mode-I stress intensity factor denoted by $K_{\mathrm{I}}$. Mode-II loading is applied only for the “short list” of potentials from which the best potential is chosen. According to the Griffith energy criterion of brittle fracture, the critical stress intensity factor, or equivalently the fracture toughness $K_{\mathrm{I}c}$, can be calculated in terms of the critical energy release rate $G_{c}$ and the effective elastic modulus $E^{\prime }$ dictated by the orientations as follows

$$\begin{aligned} K_{\mathrm{I}G}=\sqrt{G_{c} E^{\prime }}. \end{aligned}$$

(1)

In our case, in agreement with the more general form for the energy release rate given in Eq. (B.8) in “Appendix B”, $E^{\prime }=4/D_{22}$, where $D_{22}$ is the 22 component of matrix $\mathbf{D}$ defined in Eq. (B.4). $G_{c}$ corresponds to the energy of the traction-free surfaces created by crack extension, and in case of crack propagating along an arbitrary tilt GB it writes as

$$\begin{aligned} G_{c}=\gamma _1+\gamma _2-\gamma _{GB}, \end{aligned}$$

(2)

where $\gamma _1$ and $\gamma _2$ are the surface energies of grains 1 and 2, $\gamma _{GB}$ is the GB interface energy.

It is recognized that Griffith’s energy criterion developed for crack propagation in continuous media does not account for the discrete nature of crack propagation at the atomic level, where extension is the result of the breaking of individual bonds along the crack front, a phenomenon defined as lattice (or bond) trapping, see e.g. Thomson et al. (1971) and Gumbsch and Cannon (2000). It implies that a crack remains stable until the upper trapping limit $K_{\mathrm{I}}^{+}$, which is higher than the theoretical value $K_{\mathrm{I}G}$, is reached, i.e. $K_{\mathrm{I}c}=K_{\mathrm{I}}^{+}$ and $K_{\mathrm{I}}^{+}>K_{\mathrm{I}G}$. Similarly, $K_{\mathrm{I}}^{-}$ defines the lower trapping limit, below which a crack starts to heal. The trapping range is usually defined as $\varDelta K_{\mathrm{I}}=K_{\mathrm{I}}^{+}/K_{\mathrm{I}}^{-}-1$.

2.3 Simulation setup and computation parameters

In this section we focus on modeling of the fracture behavior in Si under mode-I quasi-static loading. A crack with its front centered at the middle of the cylinder is achieved by specifying a critical value of $K_{\mathrm{I}}$ consistent with the fracture energies listed in Table 1 and letting the system approach the minimum energy state. Specifically, the atoms located in the outer annulus of thickness d, depicted in Fig. 1a by the gray area, are kept fixed during the energy minimization procedure, while the atoms in the inner core are allowed to relax. The molecular statics calculations are performed using LAMMPS developed by Plimpton (1995) and its fire energy minimization algorithm introduced by Bitzek et al. (2006). The stress intensity factor is then iteratively increased (decreased) and optimized through the energy minimization up to the point where the initial crack extends (heals). This procedure, as discussed subsequently, determines the lattice trapping range.

Regarding the notation used throughout the paper, a crack system in SC is represented as (cleavage plane)[crack front]. Similarly, an arbitrary tilt GB crack is defined as (cleavage plane)$_{1}\theta _{1}$(cleavage plane)$_{2}\theta _{2}$[crack front], but in case of a symmetric GB this notation reduces to (cleavage plane)$\theta _{m}$[crack front], where $\theta _{1}$ and $\theta _{2}$ are the tilt angles and $\theta _{m}=\theta _{1}+\theta _{2}$ is the total misalignment angle, see Fig. 1a.

Aiming to compute the upper and lower lattice trapping limits, we perform the following calculations. First, the simulation domain is constructed by applying the displacement field given by the linear elastic solution in Eq. (B.6) and produced by a critical loading that makes $K_{\mathrm{I}}=K_{\mathrm{I}G}$ to the relaxed crack-free structure in accordance with the schematics shown in Fig. 1a. To illustrate the boundary conditions, Fig. 1b shows the imposed displacements as functions of polar angle $\theta$ at fixed radial distance r for the Si SC $(111)[11\bar{2}]$ crack system that was relaxed with SW potential. The effect of anisotropy for the chosen orientation can be seen by comparing the actual anisotropic and isotropic, which is obtained by keeping $C_{11}$ and $C_{12}$ elastic constants, see Table 1, and assuming that $C_{44}=(C_{11}-C_{12})/2$, i.e. $A=1$.

Next, keeping atoms fixed within the outermost tube of thickness $d=2a_0$, where $a_0$ is the lattice constant given in Table 1 for all potentials (i.e. $d\approx 11\,\AA$), the atomic positions are optimized by minimizing the potential energy with the fire algorithm proposed by Bitzek et al. (2006). Although the original crack-free structure is optimized before applying the displacement field, for the GB crack the fixed atoms along the surfaces that define the inserted crack do not occupy their optimal positions. In other words, these atoms are fixed as if they see GB environment, but instead located at the free surface. To avoid this issue, the fixed boundary conditions are set iteratively for the initial structure, namely, first, the cylinder of larger radius $R+2d$ is constructed, crack is inserted and relaxed keeping atoms in $r\in [R+d,R+2d]$ fixed; next, the outermost region, defined as $r\in [R,R+2d]$, is deleted and the structure is optimized again keeping atoms in $r\in [R-d,R]$ fixed. Afterwards, this initial system is loaded/unloaded incrementally with $\pm \delta K_{\mathrm{I}}$ to determine both $K_{\mathrm{I}}^{+}$ and $K_{\mathrm{I}}^{-}$ lattice trapping limits. An increment of 0.1 MPa$\sqrt{\text {m}}$ is used initially for $\delta K_{\mathrm{I}}$, but the increment is reduced to 0.01 near the trapping limits within $\pm 0.1$ range to achieve targeted accuracy. In addition, since in some cases no abrupt bond breaking is observed upon loading (e.g. for the MEAM potential), 3.3 Å bond length (also used in Perez and Gumbsch (2000)) is taken as the threshold value to determine if the crack has extended or healed, as defined by bond breaking or bond healing.

Fig. 2

Plots of the upper $K_{\mathrm{I}}^{+}$ and lower $K_{\mathrm{I}}^{-}$ trapping limits together with the theoretical fracture toughness $K_{\mathrm{I}G}$ as functions of a force norm tolerance $f_{tol}$ with fixed radius $R=100$ Å and b simulation domain size represented by radius R with fixed $f_{tol}=10^{-4}$ eV/Å for the Si SC $(111)[11\bar{2}]$ crack system. Results for three different interatomic potentials are presented together, where superscripts refer to the fracture behavior, i.e. b brittle, d ductile, sd some ductility

Fig. 3

a Atomic representation (visualized with OVITO software developed by Stukowski (2010)) of the simulated Si SC $(111)[11\bar{2}]$ crack system loaded with $K_{\mathrm{I}G}=0.61$ MPa$\sqrt{\text {m}}$, where color refers to the magnitude of the virial stress component $\sigma _{yy}$ given by LAMMPS for SW potential. b Contour plot of the inverse distance weighted averaged atomistic results shown in a and c elasticity predictions for $\sigma _{yy}$ stress component, Eq. (B.5)

In order to select the simulation parameters that represent the fracture process near the crack front, simulations were performed to calculate the lower and upper bond trapping limits as functions of force norm tolerance, $f_{tol}$ and cylinder size R. As can be seen in Fig. 2a, the trapping limits values for the structure of radius $R=100$ Å converge rapidly with the force norm tolerance variation for all potentials, i.e. starting from $10^{-2}$ eV/Å. The effect of size is more pronounced, especially for the potentials predicting a more ductile fracture behavior (blunting of the crack front), although the deviation even for the smallest structure is relatively modest. Based on these findings, tolerance of $f_{tol}=10^{-4}$ eV/Å and radius of $R=100$ Å are chosen and used in all subsequent calculations.

3 Results and discussion

3.1 Single crystal

Consider the propagation of a crack along different orientations of a SC. We first compare the stress field of the molecular model with the asymptotic formulas provided by the theory of elasticity. It was reported in Sinclair and Lawn (1972) that in spite of the inherent nonlinearity associated with the interatomic interactions on which potentials are based, for very brittle materials such as Si there is remarkably good agreement between the stress (the atomistic model stress is defined as the virial stress), strain and displacement fields of molecular models and elastic continuum models within the region that extends from a few interatomic spacing from the crack front to a larger distance that is much smaller than other characteristic dimensions. Note that the question of validity of elasticity near the front of a crack in brittle solids was addresses in Singh et al. (2014), where a comparison of the predictions of a finite deformation continuum theory with zero temperature atomistic results of SW potential demonstrated that elasticity is valid even for relatively large strains at distances from the crack front larger than 1 nm.

Fig. 4

Comparison between the LAMMPS (symbols) and elasticity, Eq. (B.5), (solid lines) predictions by SW potential for all non-zero stress components of the Si SC $(111)[11\bar{2}]$ crack system loaded with $K_{\mathrm{I}G}=0.61$ MPa$\sqrt{\text {m}}$. a, b Present results for the radial distance dependence of the stress components at fixed polar angles $\theta =0$ and $\pi /4$, respectively. c, d show plots of the stresses as functions of polar angle at fixed radius $r=5$ and 50 Å, correspondingly

The contour plots in Fig. 3b, c show that the virial $\sigma _{yy}$ stress component (labeled by LAMMPS) and the asymptotic elastic solution (labeled by LEFM) are in excellent agreement for SW potential at the very crack front and along the fixed boundary atoms. To render the comparison more clear, Fig. 4 presents line plots for all non-zero components of stress as functions of radial distance and polar angle. It is observed that it takes but a few Å, from the crack front to recover the inverse square root stress singularity that is consistent with the asymptotic elastic solution. Figure 4d also shows excellent agreement of the angular variation of stresses at the distance $r=50$ Å; but note that even at $r = 5$ Å, as shown in Fig. 4c, the qualitative comparison is excellent and that the quantitative deviations are less than 20%.

Comparisons between atomistic and continuum predictions of the stress component $\sigma _{yy}$ for all potentials are shown in Fig. 5. The only potentials that do not match the elastic solution for stress to a high degree are MEAM2 and MEAM. The ability of MEAM2 to predict with high accuracy the elastic stress field in the vicinity of crack fronts is questionable, considering the approximately 20% difference that persists over the entire simulation domain of radius $R=100$ Å. Whether the discrepancy is caused by a large fracture process zone that prevents the development of a K-dominated region, or by significant nonlinear relations between stress and strain of the potential, can be determined through Fig. 6. These plots present the displacements, strains and stresses at a distance $r=50$ Å from the crack tip predicted by the MEAM2 potential for the same system analyzed in Fig. 5. It is observed in Fig. 6 that the displacements and strains produced by the atomistic model match to a very high degree those of the linear elastic solution (the deviations are <1 and 2%, respectively). However, the deviation in stress as discussed previously is as high as 20%. The agreements between the strains and displacements produced by the continuum solution and the atomistic model suggest the presence of a well-developed K-field. Thus it is concluded that the discrepancy is a result of the highly nonlinear relations between displacements (or strains) and forces (or stresses) associated with MEAM2. Fig. 7a,b confirms this result by showing a noticeable level of nonlinearity in the stress strain curves of the MEAM and MEAM2 potentials. As expected the SW potential is quite linear. For MEAM2, the Si SC is significantly softer in compression and slightly stiffer in tension. This explains why the elasticity solution underestimates $\sigma _{yy}$ and $\sigma _{xx}$.

Fig. 5

Comparison between the LAMMPS (dashed lines) and elasticity, Eq. (B.5), (solid lines) predictions for $\sigma _{yy}$ stress component of the Si SC $(111)[11\bar{2}]$ crack system of radius $R=100$ Å  loaded with $K_{\mathrm{I}G}$ listed in Table 2 for all considered potentials.s Here each plot is labeled according to the used potential, see Table 1. The shown crack opening displacement is computed from Eq. (B.7)

Fig. 6

Comparison between the LAMMPS (symbols) and elasticity, Eq. (B.5), (solid lines) predictions by MEAM2 potential for the Si SC $(111)[11\bar{2}]$ crack system loaded with $K_{\mathrm{I}G}=0.52$ MPa$\sqrt{\text {m}}$ for a displacements, b strains and c stresses as functions of polar angles at fixed radius $r=50$ Å

Fig. 7

a Stress–strain curve predicted by SW, MEAM, and MEAM2 potentials (left to right). b Deviation of stress response (effectively elastic constants) with respect to linear elastic regime ($|\varepsilon |<0.001$), i.e. measure of nonlinearity of the potentials as function of applied strain. c Comparison of $\varepsilon _{yy}$ strain component for the Si SC $(111)[11\bar{2}]$ crack system of radius $R = 100$ Å, loaded with $K_{\mathrm{I}G}$ listed in Table 2 for the considered three potentials labeled above

It appears that all of the considered potentials have unique nonlinear elastic behavior; this because none of them was fit to specific nonlinear response. According to recent experimental work by Zhang et al. (2016), defect-scarce Si SC nanowires demonstrate ultrahigh elasticity, being fully elastically loaded above 10% elastic strain (approaching the theoretical elastic limit of silicon, which is $\sim$17%, as found from DFT calculations by Roundy and Cohen (2001)) with full recovery during unloading with linear stress-versus-strain curve throughout the whole deformation. This suggests that an ideal interatomic potential for Si should display linear elastic response for up to 10% tensile deformation, which is not always the case with the available potentials.

Table 2 Fracture behavior predictions by our atomistic calculations in Si SC

For completeness, the contour plots of $\varepsilon _{yy}$ strain component presented in Fig. 7c demonstrate the overall strain range achieved in our simulation domain. Ahead of the crack front tensile strain $\varepsilon _{yy}$ reached $\approx$20% at the crack tip and falls down to $\approx$3% near the boundary at distance of 100 Å. A good agreement with linear elastic solution for $\varepsilon _{yy}$ is observed within the whole simulation domain even for potentials that predict high deviations in stresses that arise from elastic nonlinearity of the potential and should be addressed with care. The comparisons above suggest that interatomic potentials do quite a good job in predicting the strain fields in the vicinity of a crack front with linear elastic solution developing just within a few Å from the tip. But next it will be shown that predicting the loads at which a crack extends is a different story.

Fig. 8

Graphs of the upper $K_{\mathrm{I}}^{+}$ and lower $K_{\mathrm{I}}^{-}$ trapping limits together with the initial value of the stress intensity factor $K_{\mathrm{I}G}$ predicted by the considered potentials in Si SC for a (110) and b (111) cleavage planes with different propagation directions. This is a visualization of data given in Table 2

Due to discreteness of the atomic structure, the crack remains stable within the loading range $K_{\mathrm{I}}^{-}<K_{\mathrm{I}}<K_{\mathrm{I}}^{+}$, where $K_{\mathrm{I}}^{+}>K_{\mathrm{I}G}$. Note that this so-called lattice or bond trapping phenomenon was demonstrated by modeling by Thomson et al. (1971) and atomistic calculations by Gumbsch and Cannon (2000), Perez and Gumbsch (2000) and Zhu et al. (2006). The magnitude of lattice trapping depends on bond strength and bond directionality (the effect is higher for ionic and covalently bonded materials than for metals), density of the cleavage plane (it is larger for less dense cleavage planes) and temperature (trapping can be overcome by thermal fluctuations). For these reasons Si should experience significant levels of trapping. It is difficult to determine the magnitude of trapping experimentally, since only the upper limit is measurable. But it is recognized that the experimental values of $K_{\mathrm{I}}^{+}$ are at least two times larger than the calculated $K_{\mathrm{I}G}$, as discussed in Gumbsch and Cannon (2000). Lattice trapping is also responsible for the experimentally observed propagation anisotropy in Si, see e.g. Tsai and Mecholsky (1991), Perez and Gumbsch (2000) and Zhu et al. (2006).

Fig. 9

Series of the optimized atomic structures of the Si SC $(111)[11\bar{2}]$ crack system for loading with the stress intensity factors listed in Table 2 for a T3 and b mSW potentials exhibiting ductile and brittle response, correspondingly. The images are obtained with OVITO software developed by Stukowski (2010), where color reflects the magnitude of the potential energy U measured per atom

Our calculated results of the trapping limits for (111) and (110) planes, which are the principal cleavage planes in Si SC, are presented in Table 2 and illustrated in Fig. 8. The energy release rate is also listed in the table. Fracture toughness $K_{\mathrm{I}G}$ predicted by the continuum model given in Eq. (1) varies slightly among the potentials because of the difference in elastic constants and surface energies, see Table 1. As expected, $K_{\mathrm{I}G}$ lies within the lattice trapping range computed for the discrete system of atoms. The deviation between $K_{\mathrm{I}}^{+}$ and $K_{\mathrm{I}G}$ is not the result of only the discrete nature of the crack extension, but also because not all assumptions and approximations used to derive $K_{\mathrm{I}G}$ are fulfilled by some of the potentials. For instance; (1) some potentials lead to ductile instead of ideally brittle behavior, see Fig. 9 showing the examples of ductile and brittle response predictions by the T3 and mSW potentials, respectively. Crack front blunting, e.g. shown in Fig. 9a for Si SC $(111)[11\bar{2}]$ crack system for the T3 potential, is observed for the potentials with $K_{\mathrm{I}}^{+}$ values labeled by “d” in Table 2; (2) the fractured surface reconstructs during extension (as it happens for the (111) cleavage plane using MEAM potential), something that is not considered in the estimation of $K_{\mathrm{I}G}$; (3) the crack front turns (as indicated for $K_{\mathrm{I}}^{+}$ values labeled by “t” in Table 2), while $K_{\mathrm{I}G}$ is computed assuming planar propagation.

It is instructive to compare our results with those reported for ideally brittle Si by Gumbsch and Cannon (2000), Perez and Gumbsch (2000), Bailey and Sethna (2003) and Zhu et al. (2006). A comparative study of EDIP, mSW, MEAM, for modeling of fracture in notched SC Si was performed by Bailey and Sethna (2003). They also considered the (110)[001] crack system without a notch and reported results similar to ours for fracture toughness and behavior. Our study further considers other atomistic aspects that might be important, such as discontinuous versus continuous bond breaking. From our calculations all potentials, except MEAM, exhibit discontinuous bond breaking at the crack front for all considered crack systems. However, in ab initio study of fracture in Si by Perez and Gumbsch (2000) bonds broke discontinuously in the $(110)[1\bar{1}0]$ crack system and continuously for (110)[001] and $(111)[01\bar{1}]$ orientations.

Regarding the quantitative comparison for the fracture toughness, experimentally measured values are $K_{\mathrm{I}c}=1.15\pm 0.08$ MPa$\sqrt{\text {m}}$ for the (110) cleavage plane according to Fitzgerald et al. (2002) and $K_{\mathrm{I}c}=1.05$ and 1.19 MPa$\sqrt{\text {m}}$ for $(110)[1\bar{1}0]$ and (110)[001] crack systems, respectively, as reported by Tsai and Mecholsky (1991). It was also found that the (110) fracture plane displays noticeable propagation anisotropy, an effect that is significantly smaller for extension of cracks of the (111) plane type. Table 2 shows that potential MEAM2 gives the closest values of $K_{\mathrm{I}}^{+}$ for both propagation directions on the (110) cleavage plane as compared with Tsai and Mecholsky (1991). Obviously our two-dimensional models at zero temperature cannot capture some of the features of crack extension including the crack advancement through finite temperature-activated kink formation observed in three-dimensional computational studies by Zhu et al. (2006) and Kermode et al. (2015).

Although some potentials predict values close to the experimental measurements, see Fig. 8, quite large variations in the upper trapping limit $K_{\mathrm{I}}^{+}$ (or equivalently, fracture toughness) is observed. $K_{\mathrm{I}G}$ and $K_{\mathrm{I}}^{-}$, on the other hand differ less. Fracture toughness alone should not be used to decide whether a potential characterizes fracture sufficiently well. Figure 8 also shows that the deformation in the immediate vicinity of the crack front, demonstrated for two opposite cases in Fig. 9, has significant influence on the trapping range; it is noticeably larger for cracks that blunt. But a certain amount of variation in trapping range is observed among potentials. For example, the trapping range $\varDelta K_{\mathrm{I}}$ varies significantly among the considered potentials, e.g. from 0.09 for MEAM to 13.7 for T3 potential model of the $(111)[11\bar{2}]$ crack system. Such large variation in trapping and behavior along the crack front manifests high sensitivity to the potential form and its parameters. It is appropriate to compare our results for trapping ranges presented in Table 2 with ab initio values reported by Perez and Gumbsch (2000), which are $\varDelta K_{\mathrm{I}}=0.6$, 0.3, and 0.3 for $(110)[1\bar{1}0]$, (110)[001] and $(111)[1\bar{1}0]$ crack systems, respectively. Only mSW and MEAM predict values for $\varDelta K_{\mathrm{I}}$ in the same range and have the same trends. Other potentials noticeably overestimate the trapping range, presumably due to ductile response along the crack front. However, it should be mentioned that the screening cutoff procedure for bond-order potentials recently developed by Pastewka et al. (2013), such as T3 and MOD, modifies their ability to model crack propagation. Specifically, the screened T3 potential predicts values for critical stress intensity factors similar to ab initio results reported by Perez and Gumbsch (2000). The results suggest, with no surprise, that not all interatomic potentials are capable of predicting sufficiently well the fracture behavior of Si, because it is known to behave in a brittle manner and expected to have a moderate trapping range.

Additional results that are available to assess the performances of the studied potentials include the value of 6.0 J/m$^2$ obtained by hybrid classical/quantum mechanical molecular dynamics simulations at the lowest strain rate (0.1%ps$^{-1}$) as reported in Kermode et al. (2008) for the critical energy release rate in $(111)[1\bar{1}0]$ mode-I crack system. This upper bound value compares well with the prediction of mSW potential, $G^{+}=5.77$ J/m$^2$. All the other potentials except MEAM considerably overestimate this quantity, see Table 2. The same paper reports $G^{-}=2.1$ J/m$^2$, below which the crack closes. In our case the mSW potential predicts $G^{-}=1.21$ J/m$^2$, while all other potentials, except MEAM, noticeably underestimate this quantity. Consequently, mSW predicts reasonable values for the critical energy release, including the lattice trapping range.

Fig. 10

a Schematics of the polar coordinate representation of stresses. Plot of the stresses as functions of polar angle $\theta$ at radial distance of $r=50\,\AA$ from the crack tip under mode-I loading with $K_{\mathrm{I}G}=0.75$ MPa$\sqrt{\text {m}}$ for b a sharp crack and d notched crack; c notched crack under mode-II loading with $K^{\text {eff}}_{\mathrm{II}}=0.63$ MPa$\sqrt{\text {m}}$, as predicted by the simulations (symbols) and the continuum model (solid lines) with mSW potential. Vertical solid black lines depict the angle at which tensile stress $\sigma _{\theta \theta }$ is maximum, i.e. crack propagation angle $\theta _0$

Fig. 11

Plots of the $\sigma _{\theta \theta }$ stress component (hoop stress) of the Si SC $(111)[1\bar{1}0]$ crack system of radius $R=100\,\AA$ under a mode-I and b mode-II loading. (left) Comparison between the LAMMPS (dashed lines) and elasticity (solid lines) predictions for mSW potential. (middle, right) Atomic representation (visualized with OVITO software developed by Stukowski (2010)) of the simulated Si SC system. Here $K_{\mathrm{I}G}=0.75$, $K_{\mathrm{I}}^{+}=1.56$, $K_{\mathrm{I}}^{+}+\delta K_{\mathrm{I}}=1.57$; $K^{\text {eff}}_{\mathrm{II}}=0.63$, $K_{\mathrm{II}}^{+}=1.13$, $K_{\mathrm{II}}^{+}+\delta K_{\mathrm{II}}=1.14$, all are given in MPa$\sqrt{\text {m}}$

Then, which is the “best” interatomic potential for fracture of a Si SC? First, it is clear that only mSW and MEAM predict brittle fracture for the considered crack systems and yield reasonable values for fracture toughness and (perhaps more importantly) lattice trapping range, see Table 2. But the MEAM predicts a somewhat small trapping range and significant nonlinear relationships between stress and strain with increasing strain. mSW potential does capture the brittle fracture behavior of cracks in Si in most aspects, but it does so at the price of an unjustified modification of the SW potential that changes the elastic constants and the melting temperature, as demonstrated by Holland and Marder (1998b). Based on this assessment it is proposed that a robust potential does not yet exist, but if the goal is to provide qualitative predictions, i.e. trends associated with crack propagation in Si at 0 K temperature, then the mSW potential may be the best choice.

3.1.1 Additional validation of mSW potential

To verify the robustness of the potential in capturing the brittle response of a cracked Si SC, we next consider mode-II loading. No experimental results nor computational results are available for comparison. However, the results of our simulations could be compared with one of the so-called local symmetry criteria of LEFM, which dictates that a crack under mixed-mode loading will propagate along a direction perpendicular to the maximum hoop stress, see Erdogan and Sih (1963). Once this direction is determined, then the effective mode-II toughness could be defined as the critical value of the applied mode-II stress intensity factor that renders the tangential (or hoop) stress equal to the critical tensile (hoop) stress of a mode-I crack. Mathematically the maximum hoop stress is written in terms of the mode-I fracture toughness as $\sigma _{\theta \theta }|_{\mathrm{max}}=K_{\mathrm{I}c}/\sqrt{2\pi r}$.

Creating an atomically sharp mode-II crack by simply applying the corresponding displacement field is not possible because the proximity of fracture surface atoms prevents the formation of free surfaces. Instead, the crack is modeled as a finite-thickness notch created by removing a strip of atoms with one unit cell size in the y direction for a $x<0$ region. Consider the polar components of stress, i.e. the radial $\sigma _{rr}$, the tangential $\sigma _{\theta \theta }$ (hoop), and the shear $\sigma _{r\theta }$. It is observed in Fig. 10 that for mode-I loading the stress components associated with the elasticity solution are in agreement with those of the atomistic model for both the sharp crack and notch configurations, and that the stress fields of a sharp crack are well-approximated by those produced by the notch. Agreement between the mode-II asymptotic field (of a sharp crack) and the field produced by the atomistically-simulated notch are also shown in this figure. Note that despite the slight discrepancy in the radial stress between the notch and the sharp crack, the hoop stress distributions of the sharp and blunted configurations are indistinguishable.

The variation of the hoop stress $\sigma _{\theta \theta }$ throughout the whole simulation domain is shown in Fig. 11 for both the mode-I and mode-II loaded notches. The atomic configurations just before and after propagation shown in Fig. 11(middle, right) demonstrate brittle crack extension for both loading conditions. The simulations of this geometry and loading using the other potentials were performed but are not presented here. Suffice it to say that brittle extension was not always the case. SW potential, for example, for mode-II loading produced severe deformation in the vicinity of the notch-front for the case of the $(111)[1\bar{1}0]$ system; and a dislocation was emitted in the $(111)[11\bar{2}]$ system. Note that for the case of isotropy the analytic expression for the critical angle is given as $\theta _0=-\arccos {(1/3)}\approx -70.5^{\circ }$. However, the crack extension direction in the discrete atomistic system is highly influenced by the orientations of the surfaces with lower energies. As shown in Fig. 11b(right) the mode-II loaded crack in $(111)[1\bar{1}0]$ SC turns at approximately $-70^{\circ }$ in the simulations due to the presence along this direction of a $(11\bar{1})$ low energy plane. This is in excellent agreement with LEFM. In the $(111)[11\bar{2}]$ oriented SC, the mode-II crack turns at $-90^{\circ }$, along a $(1\bar{1}0)$ low energy plane.

As mentioned previously, for a given material system the maximum hoop stress criterion of LEFM can also provide the ratio between the critical mode-II stress intensity factor and the mode-I fracture toughness $K_{\mathrm{I}c}$. Defining the effective critical stress intensity for mode-II fracture as $K^{\text {eff}}_{\mathrm{II}}$, then for an isotropic material $K^{\text {eff}}_{\mathrm{II}}/K_{\mathrm{I}G}=\sqrt{3}/2\approx 0.87$. For the anisotropic material the ratio is computed numerically, e.g. for mSW potential the result is $K^{\text {eff}}_{\mathrm{II}}/K_{\mathrm{I}G}=0.84$ which is 2.6% lower. Note that the atomistic calculations provide a noticeably larger value of $K_{\mathrm{I}}^{+}=1.56$ for the notched structure as compared to the sharp crack value of $K_{\mathrm{I}}^{+}=1.09$ (for which $K_{\mathrm{I}G}=0.75$), while $K_{\mathrm{II}}^{+}=1.13$ for the notched structure with $K^{\text {eff}}_{\mathrm{II}}=0.63$ (all K values are in MPa$\sqrt{\text {m}}$). This yields the 14% lower ratio $K_{\mathrm{II}}^{+}/K_{\mathrm{I}}^{+}=0.72$. The small discrepancy between these ratios can be attributed to the effects of the notched crack geometry and bond trapping. Overall, mSW potential appears to be robust in terms of brittle response under mixed-mode loading.

Fig. 12

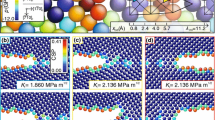
Optimized by mSW potential $\langle 1\bar{1}0\rangle$ projections of the atomic structures of $[1\bar{1}0]$ symmetric tilt GB crack systems under $K_{\mathrm{I}G}$ loading given in Table 3. Here color represents the potential energy U measured per atom

Table 3 Fracture toughness predictions by mSW potential for symmetric tilt GB cracks and corresponding SC systems in Si

3.2 Grain boundary

We now use mSW potential to investigate fracture along grain boundary (GB) defects, which are known to influence and in some cases dominate the mechanical and electronic properties of crystalline solids. GBs are usually identified by the relative orientation between the rotation axis and the normal to the boundary plane. The extreme cases correspond to a tilt GB for which the two directions are perpendicular to each other, and the twist GB for which they are parallel. Atomistic calculations show that twist GBs in Si are generally energetically less favorable than tilt GBs because they involve larger bond distortion and more coordination defects, see e.g. Kohyama and Yamamoto (1994). This explains why the majority of experimentally observed GBs in polycrystalline Si are of the symmetric tilt type and are consistent with the predicted GB energies, as reported by Ratanaphan et al. (2014). Here we focus on some of the most common tilt GBs observed in Si; those misoriented around $[1\bar{1}0]$ and [001] directions with the well known most stable structures identified by various atomistic techniques, reported e.g. in Kohyama (2002).

Consider first the (nn1) family of symmetric tilt GBs for n ranging from 1 to 5, formed by rotating initially $(110)[1\bar{1}0]$ oriented grains with specific angles $\theta _1=\theta _2=\theta _m/2$, see Fig. 1, where the total misalignment angle $\theta _m$ is dictated by the final orientations of the grains. This choice includes the primary coherent twin $\varSigma$3(111)70.53$^{\circ }[1\bar{1}0]$, the secondary twin $\varSigma$9(221)38.94$^{\circ }[1\bar{1}0]$, as well as lower angle GBs $\varSigma 19 (331)26.53^{\circ }[1\bar{1}0]$, $\varSigma 33 (441)20.05^{\circ }[1\bar{1}0]$, and $\varSigma 51 (551)16.10^{\circ }[1\bar{1}0]$. Figure 12 shows the atomic structures of the near-front region for systems containing a crack along these GBs, with structures corresponding to the optimized GB configurations reported by Kohyama et al. (1986), under $K_{\mathrm{I}G}$ loading given in Table 3. The fracture toughness and bond trapping range for crack extension and healing along the GB are calculated as before by incrementally loading and unloading the system depicted in Fig. 12.

The energy penalty of the primary twin $\varSigma 3$, shown in Fig. 12a is nearly zero, because its GB structure corresponds to a hexagonal diamond stacking sequence which does not distort the atomic arrangement. It is for this reason that it represents the largest fraction (30% by number) among all GBs in polycrystalline Si reported by Ratanaphan et al. (2014), and results in nearly identical fracture toughness as the $(111)[1\bar{1}0]$ SC system, see Table 3.

The $\varSigma 9$ GB is formed at the intersection of the two $\varSigma 3$ twin boundaries having different crystallographic directions, such as (111) and $(11\bar{1})$, see DiVincenzo et al. (1986). It is therefore the secondary twin boundary as a natural consequence of the high fraction of $\varSigma 3$. Two reconstruction models have been proposed for $\varSigma 9$; the lower energy “glide-plane” formed by $1/4[11\bar{4}]$ glide and labeled $\varSigma 9g$, and the higher energy “mirror-plane” (which has a mirror symmetry with respect to (221) plane) and denoted by $\varSigma 9m$. Figure 12b, c show the structures of the two models, respectively, where the color map represents the potential energy per atom. In these discrete systems the fracture toughness depends on the position of the crack front, the position dependence being a function of the variation in bond strength. For example, in the case of the $\varSigma 9g$ GB the periodic unit contains four different bonds, depicted as $b_1$-$b_4$ in Fig. 12b, although $b_1$ and $b_3$ (similarly, $b_2$ and $b_4$) are energetically identical. Extension of the crack front position produces a $K_{\mathrm{I}}^{+}$ of 1.06 MPa$\sqrt{\text {m}}$ for $b_1$ and $K_{\mathrm{I}}^{+}$ of 0.83 for $b_2$. Evidently, the critical stress intensity factor reflects the bond strength; bonds with lower potential energies lead to higher toughness. Therefore, all further calculations are performed for crack fronts positioned at the “strongest” bond within the GB. Note that when $K_{\mathrm{I}}^{+}$ is reached the crack extends across not only the “strongest” bond, but also the weaker bonds. For example, in case of the $\varSigma 9g$ GB two consecutive bonds ($b_1$ and $b_2$) break simultaneously at $K_{\mathrm{I}}>1.06$ MPa$\sqrt{\text {m}}$ (even though for the crack front positioned at the weaker bond $b_2$ only one bond breaks when $K_{\mathrm{I}}^{+}=0.83$ MPa$\sqrt{\text {m}}$ is reached). For the $\varSigma 9m$ GB, which has a larger variation in bond strength, four consecutive bonds (the whole GB periodic unit) break simultaneously when $K_{\mathrm{I}}$ exceeds 1.18 MPa$\sqrt{\text {m}}$.

Fig. 13

Graphs of the upper $K_{\mathrm{I}}^{+}$ and lower $K_{\mathrm{I}}^{-}$ trapping limits together with the initial value of the stress intensity factor $K_{\mathrm{I}G}$ predicted by mSW potentials in Si for cracks along selected GBs formed by symmetric tilt of a $(110)[1\bar{1}0]$ and b (110)[001] initially oriented grains. GB crack results correspond to open circles, while SC data are shown by plus sign symbols. This is a visualization of data given in Table 3

Fig. 14

Optimized by mSW potential $\langle 001\rangle$ projections of the atomistic structures of [001] symmetric tilt GB crack systems under $K_{\mathrm{I}G}$ loading given in Table 3. Here color represents the potential energy U measured per atom

The lower angle (nn1) GBs with $n\ge 3$ have a symmetric structure and are composed of a linear array of $\mathbf{b}=1/2\langle 110\rangle$ edge dislocations with fivefold-sevenfold ring core structure. Larger n, which implies smaller misalignment angle $\theta _m$ between the grains, corresponds to larger separation distance between the dislocation cores, as can be seen in Fig. 12d–f. Figure 13a shows the fracture toughness of the $(110)[1\bar{1}0]$ tilt family of GBs. These lower angle boundaries exhibit larger bond trapping in comparison with the corresponding SC and the $\varSigma 9$ and $\varSigma 3$ systems. $\varSigma 9m$ exhibits a similar trend, but is not as much different than the SC. The more stable $\varSigma 9g$ is found to have slightly lower $K_{\mathrm{I}}^{+}$ than SC. From the continuum model viewpoint the fracture toughness of GBs, because they have a positive energy penalty, should always be lower than SC [in accordance with the lower energy release rate $G_c$ given in Eq. (2)]. However, in agreement with other atomistic calculations, e.g. Möller and Bitzek (2014b), our results show that this is not always the case, since the atomic arrangement near the crack front significantly affects the bond strength, and hence, toughness. In summary, among the considered $(110)[1\bar{1}0]$ symmetric tilts, only the $\varSigma 9g$ GB has lower $K_{\mathrm{I}}^{+}$ than the corresponding SC; the primary twin $\varSigma 3$ has the same toughness as the SC; and the other GBs are tougher than ther respective SC.

Fig. 15

Comparison between the LAMMPS (top) and elasticity, Eq. (B.5), (bottom) predictions by mSW potential for the $\sigma _{yy}$ stress component of a $\varSigma 9g (221)38.94^{\circ }[1\bar{1}0]$, b $\varSigma 5 (120)36.87^{\circ }[001]$ and c $\varSigma 5 (130)Z53.13^{\circ }[001]$ GB crack systems of radius $R={100\,\AA }$ loaded with $K_{\mathrm{I}G}$ listed in Table 3

Next, we study the two most energetically stable, according to Kohyama (1987), and experimentally detected, e.g. by Ratanaphan et al. (2014), (110)[001] symmetric tilt GBs, which are the $\varSigma 5 (120)36.87^{\circ }[001]$ and $\varSigma$5(130)53.13$^{\circ }[001]$. Figure 14 presents the atomic structures of cracks running along the GB together with the corresponding SC system all loaded with $K_{\mathrm{I}G}$ reported in Table 3. The GB configurations agree with those published in Kohyama (1987). $\varSigma 5 (120)36.87^{\circ }[001]$, shown in Fig. 14a, has a symmetric structure and makes up the largest fraction of [001] tilt GBs observed in polycrystalline Si. $\varSigma 5 (130)53.13^{\circ }[001]$ in turn has two configurations, namely, higher energy symmetric $\varSigma 5S$ and lower energy zig-zag $\varSigma 5Z$ structures, shown in Fig. 14b, c, respectively. It should be noted that the free surface introduced by insertion of the crack reconstructs in case of $\varSigma 5Z$, as can be seen in Fig. 14c while comparing with the SC system in Fig. 14d. Regarding the fracture toughness values, all $\varSigma 5$ GBs appear to have slightly lower $K_{\mathrm{I}}^{+}$ than the corresponding SC and even all of the considered $(110)[1\bar{1}0]$ tilt GBs, see Fig. 13 or Table 3. Note that mSW potential predicts brittle fracture behavior for all presented here results for Si structures, including various SC orientations and GBs.

As was done for the SC, consider next how the GB affects the elastic response of a crystal to mode-I loading. Figure 15 shows the $\sigma _{yy}$ virial stress component averaged over neighboring atoms, and the asymptotic elastic solution for three different GBs that are weaker than the corresponding SC. It is observed that GBs introduce noticeable, but localized, distortions in the elastic response of the structures, and therefore, do not affect the overall stress field which can be well approximated by the elastic solution. The interface essentially is a defect not unlike the crack front, which produces fields that “perturb” the elastic solution in its immediate vicinity.

4 Summary

In this paper we revisited the question of how capable the widely used interatomic potentials are in characterizing the extension of cracks in Si and Si/Si grain boundaries subjected to quasi-static mode-I loading. Seven of the nine considered potentials produce stress, strain and displacement fields in the near crack-front region in accordance with the corresponding asymptotic elastic solution. Only the MEAM and MEAM2 potentials display noticeable levels of elastic nonlinearity, and hence, produce stress fields that deviate considerably throughout the simulation domain. The fracture toughness and bond trapping effect determined through our simulations in Si SC along its principal cleavage planes, i.e. (111) and (110), and different propagation directions, showed that seven of nine potentials predict ductile (manifested by crack tip blunting) instead of the desired brittle behavior, and overestimate the bond trapping range. Only for mSW and MEAM does the crack extend by cleavage in both mode-I and mode-II loadings. It is concluded that only mSW potential is able to capture the brittle fracture behavior and properly model the elastic response of Si material simultaneously, although it is still far from an ideal potential because of its unrealistic elastic constants and high melting temperature.

mSW potential was then used to study cracks placed along the most commonly observed tilt GBs in Si that belong to the class of interfaces having a non-oscillatory elastic solution. Focusing on $(110)[1\bar{1}0]$ and (110)[001] symmetric tilt GB systems, we showed that the fracture toughness for GBs can be larger than that of the corresponding SCs. This result, which is due to the fact that the fracture process involved discrete bond rupture within the local atomic arrangement, contradicts the classical continuum description of fracture. Thus the atomistic calculations confirmed the substantial role of bond trapping in cracks propagating along the GB in Si.

Appendices

Appendix A: Elasticity matrices

The elastic stiffness tensor of a (010)[001] oriented Si SC, that has cubic symmetry, can be expressed in matrix form using the Voigt notation as

$$\begin{aligned} \mathbf{C}^{(0)}= \left[ \begin{array}{cccccc} C_{11} &{} C_{12} &{} C_{12} &{} 0 &{} 0 &{} 0\\ C_{12} &{} C_{11} &{} C_{12} &{} 0 &{} 0 &{} 0\\ C_{12} &{} C_{12} &{} C_{11} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} C_{44} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} C_{44} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} C_{44}\end{array} \right] , \end{aligned}$$

(A.1)

where $C_{11}$, $C_{12}$, and $C_{44}$ are the only three independent elastic constants, listed in Table 1 for different interatomic potentials. Next, the forth order stiffness tensor for an arbitrary crystal orientation $(\mathbf{n}_2)[\mathbf{n}_3]$, labeled in accordance with the crack system notation and defined by the rotation matrix ${{\varvec{\varOmega }}}$, can be obtained in the following way.

$$\begin{aligned} C_{ijkl}=\varOmega _{ip}\varOmega _{jq}\varOmega _{kr}\varOmega _{st}C^{(0)}_{ijkl}, \end{aligned}$$

(A.2)

where Einstein summation rule is used. The matrix ${{\varvec{\varOmega }}}$, that rotates the initial (010)[001] crystal system around axis $\mathbf{m}$ by angle $\theta _0$ so that it orients the crystal as $(\mathbf{n}_2)[\mathbf{n}_3]$ (i.e. it has $\mathbf{n}_2$ crystallographic orientation along y axis and $\mathbf{n}_3$ along z axis), writes as

$$\begin{aligned} \varOmega _{ij}=\cos \theta _0\delta _{ij}+\sin \theta _0 \epsilon _{ikj}m_k+(1-\cos \theta _0)m_im_j, \end{aligned}$$

(A.3)

where $\delta$ is the Kronecker delta and $\epsilon$ is the Levi-Civita symbol.

For a SC system we define the stiffness tensor $\mathbf{C}$ obtained by applying rotational transformation ${{\varvec{\varOmega }}}^{\mathbf{m}}_{\theta _0}$ shown in Eq. (A.3), where axis $\mathbf{m}$ and angle $\theta _0$ are dictated by the considered crystal orientation, to the initial $\mathbf{C}^{(0)}$ given in Eq. (A.1). For the tilt boundaries we also find the stiffnesses $\mathbf{C}^{(1)}$ and $\mathbf{C}^{(2)}$ obtained by additional rotation about z axis by angles $\theta _1$ and $\theta _2$ of a SC with stiffness $\mathbf{C}={{\varvec{\varOmega }}}^{\mathbf{m}}_{\theta _0}\mathbf{C}^{(0)}$; this transformation is denoted by ${{\varvec{\varOmega }}}^{z}_{\theta _{\beta }}$ where $\beta =1$ and 2 correspond to the solutions for $\theta \in (0,\pi )$ and $\theta \in (-\pi ,0)$ regions, respectively, see Fig. 1. Equivalently, $\mathbf{C}^{(\beta )}$ can be computed by applying the total rotation operation being a product of two as ${{\varvec{\varOmega }}}^{(\beta )}={{\varvec{\varOmega }}}^{z}_{\theta _{\beta }}{{\varvec{\varOmega }}}^{\mathbf{m}}_{\theta _0}$ to $\mathbf{C}^{(0)}$ according to Eq. (A.2). For example, a (110)[001] SC system has $\mathbf{m}=(0,0,1)^{{\mathsf {T}}}$, $\theta _0=\pi /4$; $(110)[1\bar{1}0]$ has $\mathbf{m}=(-0.357,-0.863,0.357)^{\mathsf{T}}$, $\theta _0=1.718$; $(111)[1\bar{1}0]$ has $\mathbf{m}=(-0.642,-0.762,0.085)^{\mathsf{T}}$, $\theta _0=1.578$; $(111)[11\bar{2}]$ has $\mathbf{m}=(-0.367,-0.887,-0.282)^{\mathsf{T}}$, $\theta _0=2.909$.

Appendix B: Linear elastic solution for a bimaterial interface crack

This section briefly reviews the linear elastic solution obtained by Qu and Bassani (1989) and Bassani and Qu (1989) and includes the key expression needed to implement the used boundary conditions. In a rectangular coordinate system $x_i$ ($i=1,2,3$; $x_1$, $x_2$, $x_3$ correspond x, y, z coordinate system used in the paper), the infinitesimal strain tensor, defined as $\varepsilon _{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$, where comma refers to the partial derivative, $\mathbf{u}$ is the displacement, is related to the Cauchy stress tensor as $\sigma _{ij}=C_{ijkl}\varepsilon _{kl}$. Then the equilibrium equation writes as

$$\begin{aligned} C_{ijkl}u_{k,lj} =0. \end{aligned}$$

(B.1)

In case of the two-dimensional plain strain problem considered here $\varepsilon _{i3}=0$, $u_i=u_i(x_1,x_2)$. It allows to search for a solution in the form of $u_i=a_i f(z)$, where f is an arbitrary function of complex variable $z=x_1+px_2$. Substituting it into Eq. (B.1) leads to the following eigenvalue problem

$$\begin{aligned}{}[\mathbf{Q}+p(\mathbf{R}+\mathbf{R}^{\mathsf{T}})+p^2\mathbf{T}]\mathbf{a}=0, \end{aligned}$$

(B.2)

that yield six roots for p and corresponding eigenvectors a. Here are $\mathbf{Q}$, $\mathbf{R}$, $\mathbf{T}$ are the elasticity matrices defined as $Q_{ik}=C_{i1k1}$, $R_{ik}=C_{i1k2}$, $T_{ik}=C_{i2k2}$. Since $\mathbf{C}$ is positive definite, there are three pairs of complex conjugate roots, so that ${\text {Im}}(p_{\alpha })>0$, $p_{\alpha +3}=\bar{p}_{\alpha }$ (overbar denotes the complex conjugate) for $\alpha =1,2,3$. Next, additional matrices are introduced as $\mathbf{P}={\text {diag}}[p_1,p_2,p_3]=\langle p_{\alpha } \rangle$, $\mathbf{A}=[\mathbf{a}_1,\mathbf{a}_2,\mathbf{a}_3]$, $\mathbf{B}=\mathbf{R}^{\mathsf{T}}\mathbf{A}+\mathbf{T}\mathbf{A}\mathbf{P}$.

Moving to the interface crack problem, we first identify the matrices introduced above for a SC of a given orientation with stiffness $\mathbf{C}$ before tilt is applied, i.e. for perfect structure without the interface. Then, the properties of the system with a tilt boundary are computed as

$$\begin{aligned}&\mathbf{A}_{\beta }={{\varvec{\varOmega }}}^{x_3}_{\theta _{\beta }} \mathbf{A},\, \mathbf{B}_{\beta }={{\varvec{\varOmega }}}^{x_3}_{\theta _{\beta }} \mathbf{B},\, \mathbf{P}_{\beta }=\langle p^{(\beta )}_{\alpha } \rangle , \nonumber \\&\text {where} \qquad p_{\alpha }^{(\beta )}=\dfrac{p_{\alpha } \cos \theta _{\beta }+\sin \theta _{\beta }}{-p_{\alpha }\sin \theta _{\beta }+\cos \theta _{\beta }}, \end{aligned}$$

(B.3)

$\beta =1$ and 2 correspond to the solutions for materials having different tilt angles, i.e. for $y>0$ and $y<0$ regions, respectively. Solving for the asymptotic stress and displacement fields produced at the interface crack tip, Bassani and Qu (1989) introduced matrices $\mathbf{W}$ and $\mathbf{D}$ as

$$\begin{aligned} \mathbf{W}= & {} -{\text {Re}}(\mathbf{A}_1\mathbf{B}_1^{-1}-\bar{\mathbf{A}}_2\bar{\mathbf{B}}_2^{-1}),\nonumber \\ \mathbf{D}= & {} -{\text {Im}}(\mathbf{A}_1\mathbf{B}_1^{-1}-\bar{\mathbf{A}}_2\bar{\mathbf{B}}_2^{-1}), \end{aligned}$$

(B.4)

which reflect continuity of displacements and tractions across the bimaterial interface. Qu and Bassani (1989) also proved that if $\mathbf{W}=\mathbf{0}$ the crack tip fields are not oscillatory, i.e. solution for the stress field has the standard inverse square root singularity.

For the particular case of uniform tractions applied along the crack faces, that can be represented by the stress intensity vector $\mathbf{k} = (K_{\mathrm{II}},K_{\mathrm{I}},K_{\mathrm{III}})^{\mathsf{T}}$, for bimaterial satisfying $\mathbf{W}=\mathbf{0}$ the linear elastic solution for the stress being function of radial distance r and polar angle $\theta$ derived by Bassani and Qu (1989) takes the following form

$$\begin{aligned}&(\sigma _{12},\sigma _{22},\sigma _{32})^{\mathsf{T}}=\dfrac{{\varvec{\theta }}^{(\beta )}(\theta )\mathbf{k}}{\sqrt{2\pi r}}, \qquad \nonumber \\&(\sigma _{11},\sigma _{21},\sigma _{31})^{\mathsf{T}}=-\dfrac{\tilde{\varvec{\theta }}^{(\beta )}(\theta )\mathbf{k}}{\sqrt{2\pi r}}, \qquad \nonumber \\&{\varvec{\theta }}^{(1)}(\theta )\!=\!{\text {Re}}(\bar{\mathbf{B}}_1\bar{{{\varvec{\Lambda }}}}_1\bar{\mathbf{B}}_1^{-1}), \, \tilde{\varvec{\theta }}^{(1)}(\theta )\!=\!{\text {Re}}(\bar{\mathbf{B}}_1\bar{{{\varvec{\Lambda }}}}_1\bar{\mathbf{P}}_1\bar{\mathbf{B}}_1^{-1}),\nonumber \\&{\varvec{\theta }}^{(2)}(\theta )\!=\!{\text {Re}}({\mathbf{B}}_2{{\varvec{\Lambda }}}_2{\mathbf{B}}_2^{-1}), \, \tilde{\varvec{\theta }}^{(2)}(\theta )\!=\!{\text {Re}}({\mathbf{B}}_2{{\varvec{\Lambda }}}_2\mathbf{P}_2{\mathbf{B}}_2^{-1}),\nonumber \\&{{\varvec{\Lambda }}}_{\beta }=\langle {(\cos \theta +{p}_{\alpha }^{(\beta )}\sin \theta )^{-1/2}}\rangle . \end{aligned}$$

(B.5)

The asymptotic behavior of the displacements can be deduced from the full finite crack solution given in Eqs. (3.14a,b) in Bassani and Qu (1989) and it writes as

$$\begin{aligned}&{} \mathbf{u}(r,\theta )=\sqrt{\dfrac{2r}{\pi }}{\varvec{\theta }_\mathbf{u}}^{(\beta )}(\theta )\mathbf{k},\nonumber \\&{\varvec{\theta }_\mathbf{u}}^{(1)}(\theta )={\text {Re}}(\bar{\mathbf{A}}_1\langle {(\cos \theta +\bar{p}_{\alpha }^{(1)}\sin \theta )^{1/2}}\rangle \bar{\mathbf{B}}_1^{-1}),\nonumber \\&{\varvec{\theta }_\mathbf{u}}^{(2)}(\theta )={\text {Re}}({\mathbf{A}}_2\langle {(\cos \theta +p_{\alpha }^{(2)}\sin \theta )^{1/2}}\rangle {\mathbf{B}}_2^{-1}). \end{aligned}$$

(B.6)

The crack opening displacement can be calculated as

$$\begin{aligned} {{\varvec{\varDelta }}}(x_1)=\sqrt{2x_1/\pi }\mathbf{D}\mathbf{k} \, \text { for } \, x_1<0. \end{aligned}$$

(B.7)

Besides, according to Wu (1990), the energy release rate becomes

$$\begin{aligned} G_{c}=\dfrac{1}{4}{} \mathbf{k}^{\mathsf{T}}\mathbf{D}\mathbf{k}. \end{aligned}$$

(B.8)

Although this approach may seem complicated and unnecessary for the problems considered here, since the solution for a uniformly loaded interface crack of $\mathbf{W}=\mathbf{0}$ bimaterial is identical to the linear elastic solution for one anisotropic media obtained by Sih et al. (1965) with corresponding elastic properties for each region, it provides a more rigorous framework and allows to justify the solution type (oscillatory versus non-oscillatory) by computing the matrix $\mathbf{W}$.