Keywords

1 Introduction

With recent developments in miniaturization of electronics devices such as nano and micro-electromechanical systems (NEMS/MEMS), issues usually addressed at the macroscale, i.e. fatigue and fracture, have been brought into a completely new “scale” [1, 2]. At the same time, developments in nanotechnology give nowadays a completely new way at which the fatigue and fracture can be studied with a remarkable potential impact in several fields of engineering [3,4,5,6,7,8,9,10]. At such small scales, where discrete nature of atoms can’t be ignored, the continuum concepts largely used at the macroscale become questionable [11,12,13].

While methods based on energy have shown good potential to be extended from continuum to discrete system [12, 14,15,16,17,18], it is still debated whether the concept of “stress” should be applied to a system made of atoms [19, 20]. Stress is, indeed, a continuum concept, originated from the study of strength and failure of solid, and commonly defined as the quantity that represents the internal forces on a defined plane of a continuous material. Thus, questions arise on the definition of “atomic stress”. When investigating fracture at the atomic scale, the virial stress tensor is commonly employed to derive mechanical stresses acting on atoms [20,21,22]. Setting aside the debate on the validity of the virial stress as a representation of mechanical stress at atomic scale, in the present work the focus is on the applicability of classic continuum concepts in the presence of defects, such as the stress intensity factor (SIF). By reviewing recent molecular statistics (MS) analyses on single-edged cracked samples loaded under mode I [23], and representative of ideal brittle fracture, it is demonstrated that the virial stress shows the trend of inverse square root singularity and that computation of the SIF according to Irwin’s concept is possible. Furthermore, the breakdown of continuum linear elastic fracture mechanics, recently defined by means of energy concepts [11,12,13], is here quantified by using merely the stress fields.

It is concluded that the SIF from atomic stress may be useful in characterizing fracture at atomic scale, provided that the virial stress is accepted as representative of atomic mechanical stress. On the other hand, energy concepts should be anyway preferred for future developments, since they can provide a direct equivalence between continuum, discrete systems and among different scales.

2 Review of Recent Molecular Statistics Simulations on Cracked Samples

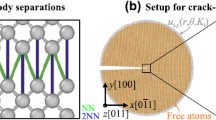
Recently, fracture tests by means of MS simulations were conducted by using open-source code LAMMPS [24]. While details can be found in [23], important aspects are presented hereafter. The modified Stillinger-Weber (SW) interatomic potential [25] was employed. The SW potential is representative of ideal brittle fracture, and often used when studying single crystal silicon. The focus was on single-edge cracked sample, loaded under mode I. Figure 1 depicts an example of the samples and orientation.

Fig. 1.
figure 1

Cracked samples employed in the molecular statistics analyses and orientation [23]. The thickness of the simulation cell is indicated as t.

Full size image

Several specimens where considered, scaling their size until few nanometers: the width of the sample W varied from 198 nm to 9.8 nm, while the crack length a was kept equal to W/3. The mechanical properties were given by the following material constants: C11 = 201 GPa, C12 = 51.4 GPa and C44 = 90.5 GPa. Along the direction [111], an ideal material strength σIS of 35 GPa at critical strain εC = 0.3 was obtained. A stepwise increment of strain ε is applied at the upper and lower layers of atoms according to Fig. 1, and the strain is increased until final fracture. At fracture, the critical displacement dC (maximum displacement before failure) is obtained. The mechanical stress is obtained dividing the virial stress (stress × volume quantity) by the per-atom volume at εC = 0.3, i.e. 24.44 Å3. This value is, indeed, a more reliable estimation of the atomic volume in regions that are highly deformed, such as close to the crack tip at failure conditions. Analyses were conducted at 0 K and fully included the lattice trapping.

3 Results and Discussion

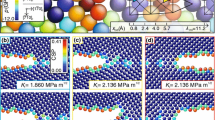
The crack tip stress fields of some selected considered geometries are presented in Fig. 2a for the sake of clarity. The values of the atoms at the crack tip are plotted at r = 0.1 Å for convenience, since as well known the log-log scale does not allow the value of 0. The depicted stress is the mechanical atomic stress, i.e. virial stress divided by the per-atom volume as explained in the previous section.

Fig. 2.
figure 2

(a) Near crack-tip atomic stress distribution for selected geometries; atomistic stress is derived from virial stress/per-atom volume. The stress values of the atoms at the crack tip are plotted for r = 0.1 Å rather than 0 Å in order to summarize in a single log-log scale graph both stress distribution and crack-tip values. (b) Critical stress intensity factors versus the variation of the specimen width W.

Full size image

The figure shows two very important results:

  • The MS analyses do not predict the infinite stress at the crack-tip but rather a finite value, i.e. the ideal material strength σIS, regardless of the specimen size. This indicates that the fracture, in the case of ideal brittle materials, is ultimately governed by atoms at crack tip.

  • Even if the stress singularity is missing, near the crack tip region the stress still varies with 1/r0.5 as expected from continuum LEFM. Figure 2a depicts only selected geometries for the sake of clarity, but same results are obtained for all the considered samples.

The results allow the quantification of the SIF at failure KIf (i.e. at critical displacement dC), according to the classic Irwin’s definition [26, 27]:

$$ K_{\text{If}} = \sigma_{\text{V}} \sqrt {2\pi r} \,, $$
(1)

where σV is the atomistic mechanical stress, perpendicular to the crack plane; r is the distance from the crack-tip along the crack plane. The results are presented in Fig. 2b and compared with other experimental and numerical works by other authors [16, 17, 28]. KIf ≈ 0.97 MPa·m0.5 is constant for all the geometries, and it agrees well with the fracture toughness of single crystal silicon, including bulk samples [29].

Finally, the comparison with continuum-based linear elastic solutions conducted in [23] is summarized in Fig. 3. The stress intensity factors at failure are normalized vs the KIf of the largest sample W = 198.41 nm, and plotted versus the length of the singular stress field ΛK normalized by the fracture process zone RFPZ. ΛK is the distance from the crack-tip at which the stress deviates more than 5% from the expected 1/r0.5, while the RFPZ is a constant value taken from the literature [12, 13]. When continuum and atomistic simulations are overlapped, the continuum-based formulation breaks down when the ratio between ΛK and RFPZ is approximately 4-5, in agreement with [12, 13]. The atomistic simulations, instead, show a clearly scale-independence, confirming that ideal brittle fracture is ultimately governed by atomic bond breaking [7, 17].

Fig. 3.
figure 3

Normalized SIF at failure versus the ratio of singular stress field length ΛK and fracture process zone length RFPZ. Numerical values are reported in [23].

Full size image

Concluding, the concept of SIF is still surprisingly valid if the atoms are modeled, and static crack and ideal brittle material containing no other defects are considered. This result also agrees well with conclusions made by other authors [30]. Provided that the virial stress is affectively accepted as representative of atomic stress, crack tip region stress field of molecular system may be described by continuum-based SIF concept.