Predicting failure of the Second Sandia Fracture Challenge geometry with a real-world, time constrained, over-the-counter methodology

Abstract

An over-the-counter methodology to predict fracture initiation and propagation in the challenge specimen of the Second Sandia Fracture Challenge is detailed herein. This pragmatic approach mimics that of an engineer subjected to real-world time constraints and unquantified uncertainty. First, during the blind prediction phase of the challenge, flow and failure locus curves were calibrated for Ti–6Al–4V with provided tensile and shear test data for slow (0.0254 mm/s) and fast (25.4 mm/s) loading rates. Thereafter, these models were applied to a 3D finite-element mesh of the non-standardized challenge geometry with nominal dimensions to predict, among other items, crack path and specimen response. After the blind predictions were submitted to Sandia National Labs, they were improved upon by addressing anisotropic yielding, damage initiation under shear dominance, and boundary condition selection.

1 Introduction

Modeling crack initiation and propagation in an alloy can be done with myriad computational techniques. For example, within the finite element method alone, cohesive zones, porous metal plasticity (i.e. GTN), and geometrically explicit crack growth can all be employed to model failure. Given all of these methods, it would seem that predicting crack growth is a fairly trivial task; however, this is not always the case. One sobering example is the First Sandia Fracture Challenge (SFC1).

SFC1 (Boyce et al. 2014) was conceived by Sandia National Laboratories to probe the scientific community’s ability to model crack growth in a non-standardized geometry made from a well-documented structural stainless steel. The geometry resembled a compact-tension specimen with three holes positioned beyond the notch (creating a multiaxial stress state for the crack to traverse). Several participants predicted the incorrect crack path, and while manufacturing discrepancies indiscernible to the naked eye contributed to these incorrect predictions, it was apparent that the modeling community as a whole lacked what SFC1 was probing for—a method to model accurately the evolution of a crack amidst a significant degree of mode-mixity.

The Second Sandia Fracture Challenge (SFC2) was announced in May 2014, approximately two years after SFC1 was announced. The geometry and material, though different from those in SFC1, presented similar challenges to the new set of participants. Again, Sandia asked teams to model crack growth in a novel geometry which was configured specifically to produce multiaxial stress states that would obfuscate damage evolution. In this paper, one team’s efforts to predict crack growth in the SFC2 challenge geometry are detailed. This team, dubbed “Team C” in the SFC2 lead article (Boyce et al. 2016), employed off-the-shelf tools and engineering judgment under considerable time constraints to predict failure in the specimen. Mimicking a full work week, approximately twenty man-hours were used to establish the blind predictions and an additional twenty were used to improve upon these predictions. While no new methods were developed, this pragmatic approach is representative of how engineers operate in industry wherein time and budget restrictions oftentimes trump more comprehensive, detailed investigations. Herein, this methodology is described, employed to establish blind predictions, and improved upon to arrive at more accurate predictions of failure history. In Sect. 2, the blind predictions are established by calibrating flow and failure locus curves with provided tensile and shear test data. In Sect. 3, the blind predictions are compared against experimental data. Finally, in Sect. 4, they are improved by readdressing items such as anisotropic yielding, damage initiation under shear dominance, and boundary condition selection.

2 Establishing blind predictions

2.1 Overview

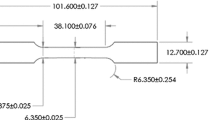
The organizers of SFC2 asked participants to model fracture in the specimen shown in Fig. 1c, which will subsequently be referred to as the “challenge specimen”. It was loaded at two loading rates: 0.0254 and 25.4 mm/s. Sandia’s quantities of interest (QOIs) included peak loads and corresponding notch openings (COD1 and COD2 labeled in Fig. 1), crack path, and expected load versus COD profiles for each loading rate. While all relevant details pertaining to SFC2 are included herein, the reader is encouraged to refer to the SFC2 lead article (Boyce et al. 2016) for an exhaustive account of challenge regulations, experimental setups and results, and modeling approaches.

Fig. 1

SFC2 tensile specimen (a). SFC2 shear specimen (b). SFC2 challenge specimen (c). Given dimensions are nominal and in millimeters. Dimensions between specimens not to scale. Nominal thickness of all three specimens is 3.124 mm

The methods detailed herein to predict fracture initiation and propagation in the challenge specimen are fairly commonplace. Abaqus/Explicit (Simulia 2011) was used to drive the simulations on a consumer-grade Intel processor. The tensile and shear calibration specimens and challenge specimen were modeled with their nominal (as-drafted) dimensions, Fig. 1. The continuum, the well-known titanium alloy Ti–6Al–4V, was modeled as linear elastic isotropic with the von Mises yield criterion. The two calibration specimens were used to tune the hardening rule, a tabular function of plastic strain. Damage was initiated when a material point reached a critical equivalent plastic strain, the magnitude of which was dictated by a function of stress triaxiality. Damage was modeled by way of an abrupt exponential degradation of element stiffness.

2.2 Material models

2.2.1 Elastic response

The tensile test results presented in the SFC2 lead article displayed negligible elastic anisotropy. Consequently, a linear elastic isotropic material model was adopted to model the elastic response in all three specimens. The Young’s modulus, E, and Poisson’s ratio, $\nu$, were taken to be 114 GPa and 0.34, respectively. It is noteworthy that any relevant thermal effects (i.e. dependence of E on temperature) were neglected during the study.

2.2.2 Hardening laws

For both the slow (0.0254 mm/s) and fast (25.4 mm/s) loading rates, yielding in shear started at approximately a 12 % lower von-Mises stress than in tension. This is an indication of anisotropic yielding; however, during the blind prediction phase of the challenge, it was not entirely clear how to accommodate this anisotropy in the plastic response. The flow curves calibrated from the tensile and shear tests for both loading rates are given in Fig. 2. The curves were derived iteratively—for each curve, the tabular data was incrementally adjusted until a reasonable fit was established with the corresponding test. All four flow curves consisted of 21 data points; linear interpolation was used between the entries. A simple power law was used for the extrapolation of the flow curves out to large strains:

$$\begin{aligned} \sigma =A\cdot \epsilon ^{n} \end{aligned}$$

(1)

where, for example, A = 1261 MPa and n = 0.09 for the shear flow curve under the slow loading rate.

Fig. 2

Calibrated flow curves

The anisotropic Drucker–Prager yield criterion was initially considered, but due to lack of time for calibration, it was eventually passed over for a simpler approach. Preliminary elastic–plastic analyses of the challenge specimen revealed that when assigned to the entire mesh, both the tensile and shear flow curves consistently favored the A–C–F failure path. Note that rigid body pins with friction were used for these analyses (to be discussed in greater detail in Sect. 2.3.1). Assuming material isotropy, the failure path certainly seemed insensitive to flow curve selection, but anisotropy simply could not be neglected. Although the A–C–F failure path was consistently favored, the authors expected the B–D–E–A path due to the combined shear and tensile loading ahead of the notch B. This was in contrast to the portion of the specimen beyond the notch A whose loading was primarily tensile. Because the shear tests had a lower ultimate strength than their tensile counterparts, it was assumed that the shear-dominance ahead of B would favor crack growth.

To establish upper bound and best (“expected”) predictions for Sandia, the flow curves from the tensile tests (with their higher yield stresses) were exercised, favoring the A–C–F path. To establish lower bound predictions, the challenge specimen was split into two regions. The flow curve from the shear test was assigned to the shear-stress controlled region (beyond the lower notch including the B–D–E–A path), and the flow curve from the tensile test was assigned to the axial-stress controlled region (beyond the upper notch including the A–C–F path), respectively, Fig. 3a. This favored the B–D–E–A path. The fact that the best (“expected”) prediction clashed with the authors’ own expected crack path deserves an explanation. During the prediction phase, no simulation save for the aforementioned lower-bound prediction (which, by virtue of hindsight, was admittedly too invasive) and an analysis with physically unrepresentative boundary conditions (to be discussed in Sect. 2.3.1) indicated B–D–E–A. Consequently, A–C–F was reported to Sandia to be the “expected” crack path while the authors anticipated either result from the tests.

Fig. 3

a Flow curve assignment to establish lower bound predictions: red demarcates shear-stress controlled region and gray demarcates axial-stress controlled region. b Stress triaxiality at predicted time of initiation (A–C–F) for slow loading rate

It is noteworthy that during the prediction phase, neither damage nucleation/propagation laws nor boundary conditions had been considered in great detail; as discussed later in this paper, these would prove decisive in favoring the experimentally-consistent failure path.

2.2.3 Damage initiation and propagation laws

A failure locus curve (FLC) was leveraged to model damage in the titanium alloy, effectively decoupling damage from plasticity. The FLC, an empirically derived exponential limit curve, takes root in the micro-void-based empirical criteria given by McClintock (1968), Rice and Tracey (1969), Hancock and Mackenzie (1976), and Atkins (1997). The FLC can be a function of strain rate, stress triaxiality, thickness, temperature, and normalized third deviatoric invariant (aka the Lode angle parameter), to name a few; however, due to lack of experimental data and time, the FLC calibrated for this study was simply a relationship between equivalent plastic strain at damage initiation and stress triaxiality, $\bar{{\epsilon }}_f^{pl} \left( \eta \right)$. When the equivalent plastic strain at a material point equaled $\bar{{\epsilon }}_f^{pl} \left( \eta \right)$, the material point began to evolve damage. Dubbed “estimated” hereafter, the FLC was calibrated using the slow tensile and shear test data. The stress triaxiality levels in the challenge specimen were predicted to be in the range between 0.2 and 0.6 (Fig. 3b), but the tensile and shear tests only provided data at stress triaxiality values 0.8 and 0.0, respectively, at time and location of predicted initial failure. Consequently, the remainder of the locus had to be estimated using recommendations from Ohata and Toyoda (2004), Fig. 4. Informed by the shear test results wherein samples subjected to the faster loading rate failed at lower strains, this locus was decreased by 20 % to give a FLC for the fast loading rate. After the blind prediction phase, a second FLC given by Giglio et al. (2013) for room-temperature Ti–6Al–4V under quasi-static loading was considered, Fig. 4. This particular FLC was calibrated by considering several test specimens which, collectively, interrogated a considerable range of stress triaxialities. Dubbed “Giglio” hereafter, it was reduced by 20 % also to give a locus appropriate for the fast loading rate.

Fig. 4

Failure locus curves. Note that each faint dashed-dotted line represents the evolution of strain as a function of stress triaxiality at the presumed location of failure

The FLC addresses how damage initiates in the discretization. Damage evolves according to an entirely different criterion. Due to lack of experimental data, damage was assumed to evolve based on a critical fracture energy, $G_f$, criterion with exponential softening:

$$\begin{aligned} d=1-\exp \left( {-\int _0^{\bar{{u}}^{pl}} \frac{\bar{{\sigma }}_y \dot{\bar{{u}}}^{pl}}{G_{f} }} \right) \end{aligned}$$

(2)

where $\dot{\bar{{u}}}^{pl}$ is the rate of change of the effective plastic displacement, $\bar{{u}}^{pl}$, $\bar{{\sigma }}_y$ is the effective yield stress, and d the damage variable wherein d = 1 represents complete failure. The critical fracture energy was assigned to be 10 N/mm based on the authors’ experience; however, the specimen’s response was, on the whole, insensitive to this value. In this scheme, cracks are not modeled as geometrically explicit features. Rather, once an element’s stiffness has degraded beyond acceptable limits, it is removed from the discretization. With subsequent element deletions, new free surface is introduced and a faceted “crack” or “discontinuity” forms.

2.3 Modeling details

2.3.1 Geometry and boundary conditions

The nominal dimensions of the tensile, shear, and challenge specimen were considered during the prediction phase. It is noteworthy that during SFC1, some of the dimensions of the challenge specimens were beyond drawing tolerances. This did not seem to be the case for SFC2—as-machined dimensions of the challenge specimens were reported during the prediction phase, and no dimension was beyond drawing tolerances. Given more time, a sensitivity analysis could have been conducted on the as-machined specimens to ensure that the nominal dimensions were indeed representative, but because no specimen was beyond design tolerances, this study was not a high priority.

With regards to boundary conditions, the shear specimen required special consideration simply because the shear test was novel and nontrivial. To model the fixture’s action on the specimen, all contact nodes on the specimen were tied to a rigid body. It is noted that during the experiments, the shear specimens slipped in the grips. Although this could have been modeled explicitly, Sandia’s provided first-order correction was employed to remove the contribution of this compliance from the experimental data, thereby allowing a one-to-one comparison between numerical and experimental results. The challenge specimen, in turn, showed significant sensitivity to how its pins were modeled. Pack et al. (2014) explored this issue in considerable detail during SFC1 and determined that boundary condition selection had no influence on the crack path and minimal influence on the specimen’s response. This did not seem to be the case for the SFC2 challenge specimen. Recall from Sect. 2.2.2 that the A–C–F failure path was favored when the entire discretization was assigned the same flow curve and the pins were modeled as rigid bodies with friction. Replacing the rigid pins with kinematic coupling constraints resulted in the same path; however, frictionless rigid body pins favored the B–D–E–A failure path. While failure along B–D–E–A was expected based on good engineering judgment, frictionless rigid body pins were deemed unrepresentative of how the specimens were loaded in the laboratory.

Ultimately, rigid body pins with friction (with a coefficient of friction of 0.10 based on the authors’ experience) were employed for the final predictions because (1) they were deemed more representative of the loading configuration than frictionless pins and (2) it was recognized that an inability to accommodate anisotropic yielding accurately was likely favoring the A–C–F path. For example, it could have been that all three types of boundary conditions favored the same crack path assuming anisotropic yielding had been accommodated more adeptly. The effect of a more comprehensive treatment of anisotropic yielding is discussed in Sect. 4.

2.3.2 Mesh refinement

The influence of the mesh size on the fracture behavior is expected as the FLC model belongs to the group of local damage models. The mesh size effect becomes more pronounced for lower material strain hardening and higher stress triaxiality levels. Furthermore, it is known that changes in element aspect ratio can lead to different fracture modes (Besson et al. 2001). Here, based on experience of team members with the FLC model, the same mesh size of 0.2 mm was chosen for tensile, shear, and notched regions of SFC specimens. To study the effect of mesh size on the load-displacement curve and fracture behavior of the challenge specimen, two element sizes were investigated: 0.1 mm and 0.5 mm. No significant difference in load-displacement response, crack initiation, and path was observed when using the finer mesh over the reference mesh (0.2 mm). However, the coarser mesh resulted in delayed crack initiation with a 10–15 % increase in displacements for both loading rates. Up to the point of fracture onset, similar load-displacement curves and the same crack paths were indicated for all three meshes. The element employed was a linear hexahedron with reduced integration (C3D8R).

2.3.3 Computational considerations

Abaqus/Explicit was the finite element solver for this investigation. All simulations were run on a consumer-grade 3.4 GHz Intel processor. Typically, an analysis of the 350k DOF challenge specimen model on four cores took approximately 24 h (wall clock) to complete. Mass scaling was leveraged to achieve reasonable step sizes. It was accomplished by increasing the density by three orders of magnitude. Additionally, only half of the specimen was modeled by virtue of symmetry along the half-thickness plane. Finally, simulations of the specimens subjected to the fast loading rate were done quasi-statically; the effect of the faster rate over the slower was reflected in separate flow and failure locus curves.

3 Blind predictions

Blind predictions were submitted to Sandia National Labs in early November 2014. The predictions are summarized briefly below:

• The expected failure path for both loading rates was A–C–F.

• It was assumed that the B–D–E–A failure path would be favored based on good engineering judgment. However, hampered by an inability to accommodate anisotropic yielding accurately, A–C–F was submitted to Sandia as the “expected” failure path.

• Teams were given the option to bound their expected predictions. The upper bound predictions were reported to be the same as expected. The lower bound, in turn, reflected the B–D–E–A failure path and a 1.5-times larger COD at failure.

Shortly after the predictions were submitted, Sandia disseminated the results of the nineteen laboratory tests to the participants. Ten of the eleven challenge specimens subjected to the slow loading rate failed as B–D–E–A while all eight subjected to the fast loading rate failed as B–D–E–A. The load versus COD profiles from both the experiments and simulations are given in Fig. 5. Comparing the expected blind predictions to the experimental results, the predicted maximum load and COD1 (see Fig. 1) at failure were off by approximately 15 %. The lower bound-predictions, being more representative of eighteen of nineteen tests, captured maximum load within an error band of 5 %, but the predicted COD1 at failure was approximately 2-times higher than observed. Moreover, for both sets of predictions, the predictions were too stiff during loading, an indication that the boundary conditions perhaps needed to be amended.

Fig. 5

Load versus COD profiles from experimental data and blind predictions for slow (a) and fast (b) loading rates

4 Improving blind predictions

4.1 Sources of discrepancy

There were three significant sources of uncertainty that compromised the blind predictions: anisotropic yielding, damage initiation, and boundary conditions. With the benefit of hindsight and additional time to conduct more comprehensive sensitivity studies, these epistemic uncertainties were quantified and reduced. This process is discussed herein.

As made evident by the relatively large discrepancy between the expected and lower-bound predictions in Fig. 5, the issue of anisotropy was the most critical. It was clear that an inability to accommodate plastic anisotropy favored the A–C–F path; however, based on the outcomes of the experiments, the interplay between tensile and shear-dominance throughout the specimen had to be considered to model accurately failure history, the effect of which is discussed in Sect. 4.2.

With regards to damage initiation, the lower-bound prediction with its experimentally-consistent B–D–E–A failure path demonstrated that the estimated failure locus curves for both loading rates were insufficient as damage initiated far too late in the analysis (approximately 2-times COD1 that observed in experiments). In Sect. 4.3, the effect of adopting a failure locus that is more appropriate in shear-dominant regimes (i.e. the B–D–E–A failure path) is demonstrated.

Finally, with regards to boundary conditions, the predictions did not account for some compliance as the response was too stiff during early loading. Apart from decreasing the Young’s modulus of the specimen (which would be unphysical), the only means to correct the response during early loading was to reassess boundary condition assignment, Sect. 4.4.

4.2 Anisotropic yielding: crack path

Anisotropic yielding was not accommodated accurately during the prediction phase. This issue was addressed shortly after submission of the blind predictions to Sandia. The lower-bound predictions, wherein the challenge specimen was split manually into tensile and shear-dominant regimes and assigned flow curves accordingly, achieved the desired B–D–E–A failure path. Here, this discrimination of tensile and shear-dominant stress states is done in a more automated fashion. Comparing the tensile and shear tests, the shear specimens yielded at a stress that was approximately 12 % lower than their tensile counterparts. To induce yielding due to shear earlier in the challenge specimens, the tensile flow curve was leveraged in conjunction with the “*POTENTIAL” option in Abaqus/Explicit. This option exercises Hill’s (1948) well known extension of the von Mises yield criterion. The aforementioned 12 % reduction was achieved by setting the R12 parameter (corresponding to in-plane shear) to 0.88. The effect of this modification, which was applied to the models corresponding to the expected predictions, is shown in Fig. 6 with curves labeled “R12 mod”. The experimentally-consistent B–D–E–A crack path was predicted; however, as in the lower-bound predictions, the COD1 was over-predicted for both loading rates. While this over-prediction is addressed in Sect. 4.3, these results confirm that the incorrect A–C–F prediction was the product of inaccurately accommodating anisotropic yielding, and not necessarily boundary condition selection.

Fig. 6

Load versus COD profiles from experimental data, blind predictions, and post-prediction modifications for slow (a) and fast (b) loading rates. Note that “R12 mod” refers to R12 = 0.88 and the estimated FLC (Sect. 4.2). “Giglio FLC”, in turn, inherits the R12 modification in addition to the Giglio FLC (Sect. 4.3). The oscillations are a product of mass scaling

4.3 Onset of damage

The estimated FLC was calibrated with the tensile and shear test data; however, as discussed in Sect. 2.2.3, the portions of the locus between stress triaxiality values 0 and 0.8 had to be estimated as neither test was relevant in this range. This produced a FLC that accommodated an inordinate amount of plastic deformation in the shear-dominant regime (i.e. the B–D–E–A failure path) before failure. Consequently, the Giglio FLC was adopted as it gave more realistic failure strains for low stress triaxialities. The effect of this modification is shown in Fig. 6 with curves labeled “Giglio FLC”. Note that these curves also reflect the R12-related modification discussed in the previous section. The Giglio-FLC-induced failure is well within the experimental scatter for both loading rates, confirming that the failure strains of the estimated FLC were approximately 2-times higher than they should have been in the shear-dominant regime.

Of course, this switch to a different failure locus curve begs the question whether or not the new FLC reproduces the response of the calibration specimen tests. Regarding the shear specimen specifically, compatibility is maintained. During the prediction phase, by virtue of hindsight, the shear specimen was over-constrained. This induced an inordinate amount of plastic strain in the critical element, thereby inflating the estimated FLC in the shear domain. After the predictions were submitted to Sandia, a more accurate treatment was given to these boundary conditions; multipoint constraints and springs elements were employed. This prompted an alteration to the existing shear flow curves whereby higher strain hardening was enforced for large strains. With this new flow curve and “Giglio FLC”, the response of the shear specimen was recovered.

4.4 Boundary conditions: stiffness mismatch during early loading

The corrections applied above have yet to address the stiffness mismatch during early loading, presumably the product of improper boundary condition selection. Rigid body pins with friction were deemed the most representative of the loading configuration during the prediction phase; however, the resulting response was too stiff. It is likely that during the tests, the loading pins rotated in the loading holes, and thus rigid body pins with a lower coefficient of friction would seem to better facilitate this rotation. Frictionless rigid body pins were reconsidered with the aforementioned R12 and FLC corrections for the slow loading rate, but the response was nearly indistinguishable from those with nonzero coefficients of friction, Fig. 7.

Fig. 7

Load versus COD profiles from experimental data and post-prediction modifications for slow (a) and fast (b) loading rates. Note that the curves labeled “Rigid Pins” and “Non-Rigid Pins” reflect the modifications from Sects. 4.2 and 4.3 while the latter incorporates the boundary condition modification discussed in Sect. 4.4

Team I of the SFC2 achieved conformity with the response of the specimens during early loading by employing kinematic boundary conditions on the top and bottom halves of the top and bottom loading holes, respectively (Boyce et al. 2016). The effect of replacing rigid body pins with these kinematic boundary conditions is demonstrated in Fig. 7. Labeled “Non-Rigid Pins”, the curves conform more closely to those of the experiments during early loading for both rates. The explicit analyses with relatively large step sizes produced some noise resulting in deviations from the experiments. This was purely a numerical artifact as an implicit analysis of the same model for the slow loading rate (see curve labeled “Non-Rigid Pins (imp)”) achieved a smoother, more conformal response during early loading.

5 Conclusions

During the blind prediction phase of the Second Sandia Fracture Challenge, three factors precluded Team C from obtaining accurate predictions of failure for both rates: anisotropic yielding, damage initiation under shear dominance, and boundary condition selection. During the prediction phase, it was unclear which of the three was most dominant, and therefore the blind predictions were made in the midst of a non-negligible amount of epistemic uncertainty. To quantify this uncertainty, the blind predictions were improved in a systematic fashion. The following can be concluded from this effort:

• The challenge specimen failed along a shear-dominant crack path. Regardless of boundary condition selection, when the specimen was partitioned into tensile and shear-dominant regimes (or the yield surface scaled accordingly), the predicted crack path was the experimentally-consistent B–D–E–A.

• The estimated failure locus curve from the tensile and shear test data was inaccurate in shear-dominant stress states; it gave inordinately high failure strains for low stress triaxiality values. Once a more appropriate failure locus curve was employed (one that gave lower failure strains for low stress triaxialities), failure occurred well within the experimental scatter.

• Stiffness mismatch during early loading was the result of improper boundary condition selection. The prescribed rigid body pins with friction induced too stiff a response. Kinematic boundary conditions assigned to the top and bottom halves of the top and bottom loading holes, respectively, produced a more physically representative response during early loading.

The procedures employed herein are fairly commonplace and representative of what an engineer in industry might leverage to solve such a problem. Oftentimes, engineers are forced to compromise accuracy for expediency in the presence of unquantified uncertainties. Herein, with the benefit of hindsight, the epistemic uncertainties encountered during the blind prediction phase were addressed, thereby strengthening the framework. Of course, these fairly simple methods should not be leveraged indiscriminately to model fracture; however, as shown herein, when coupled with an adequate understanding of the underlying stress state, they can be employed to establish accurate predictions of fracture-related phenomena.