Uncertain partial differential equation with application to heat conduction

Abstract

This paper first presents a tool of uncertain partial differential equation, which is a type of partial differential equations driven by Liu processes. As an application of uncertain partial differential equation, uncertain heat equation whose noise of heat source is described by Liu process is investigated. Moreover, the analytic solution of uncertain heat equation is derived and the inverse uncertainty distribution of solution is explored. This paper also presents a paradox of stochastic heat equation.

1 Introduction

Partial differential equation plays an important role in mathematics. As an old subject of partial differential equation, heat equation describes the variation of temperature in a given region over time. The study of heat equation was pioneered by Fourier (1878) in his famous book The Analysis Theory of Heat. This work makes heat equation hold an exciting and special position in the theory of partial differential equation.

However, heat source is often affected by the interference of noise in practice. For this reason, Walsh (1986) initiated stochastic heat equation driven by Wiener process. Following that, stochastic heat equation was studied by many researchers such as Chow (1989), Peter (1992), and Peszat and Zabczyk (1997). But, is it reasonable to describe real heat conduction process via stochastic heat equation? Section 8 will show that it is unreasonable for stochastic heat equation to model real heat conduction. This fact motives us to present an uncertain heat equation driven by Liu process.

Liu process was designed by Liu (2009) as a counterpart of Wiener process to deal with white noise. It is a Lipschitz continuous uncertain process with stationary and independent normal increments. Uncertain differential equation, a type of differential equations driven by Liu processes, was first studied in 2008 by Liu (2008). After that, Chen and Liu (2010) proved the existence and uniqueness theorem for the solution of an uncertain differential equation under linear growth condition and Lipschitz continuous condition. More importantly, Yao and Chen (2013) proved that the solution of an uncertain differential equation can be represented by a spectrum of ordinary differential equations. Nowadays, uncertain differential equation has been widely applied in many fields such as uncertain finance (Liu 2013), uncertain optimal control (Zhu 2010), and uncertain differential game (Yang and Gao 2013, 2015).

This paper will present the tool of uncertain partial differential equation driven by Liu process and investigate uncertain heat equation. For an uncertain heat equation, the solution and inverse uncertainty distribution of solution will be derived. The rest of the paper is arranged as follows. Section 2 reviews some basic concepts and theorems in uncertainty theory. Section 3 defines uncertain partial differential equation. Section 4 derives the Cauchy problem for the uncertain heat equation. Section 5 obtains the analytic solution of Cauchy problem for the uncertain heat equation. Section 6 presents the inverse uncertainty distribution of solution of Cauchy problem for the uncertain heat equation. Section 7 introduces some special uncertain partial differential equations. Section 8 introduces a paradox of stochastic heat equation that shows it is unreasonable for the real heat conduction to follow any stochastic heat equation. At last, a brief summary is given in Sect. 9.

2 Uncertainty theory

Uncertainty theory is a new mathematics theory based on normality, duality, subadditivity and product axioms. It was established by Liu (2007) and perfected by Liu (2009) to model human belief degree. In this section, we introduce some fundamental concepts and properties in uncertainty theory including uncertain variable, uncertain process and uncertain field.

Definition 1

(Liu 2007) Let be a $\sigma$-algebra on a nonempty set ${\varGamma }$. A set function is called an uncertain measure if it satisfies the following axioms:

• Axiom 1. (Normality Axiom) for the universal set ${\varGamma }$;

• Axiom 2. (Duality Axiom) for any event ${\varLambda }$;

• Axiom 3. (Subadditivity Axiom) For every countable sequence of events ${\varLambda }_1,{\varLambda }_2,\ldots ,$ we have

  

Besides, in order to provide the operational law, Liu (2009) defined the product uncertain measure on the product $\sigma$-algebre as follows.

Axiom 4. (Product Axiom) Let be uncertainty spaces for $k=1, 2, \ldots .$ The product uncertain measure is an uncertain measure satisfying

where ${\varLambda }_k$ are arbitrarily chosen events from for $k=1, 2, \ldots$, respectively.

An uncertain variable $\xi$ is a measurable function from an uncertainty space to the set of real numbers. In order to describe uncertain variable in practice, uncertainty distribution ${\varPhi }:\mathfrak {R}\rightarrow [0,1]$ of an uncertain variable $\xi$ is defined as . An uncertainty distribution ${\varPhi }(x)$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0<{\varPhi }(x)<1$, and

$$\begin{aligned} \lim _{x\rightarrow -\infty }{\varPhi }(x)=0, \quad \lim _{x\rightarrow +\infty }{\varPhi }(x)=1. \end{aligned}$$

If $\xi$ is an uncertain variable with regular uncertainty distribution ${\varPhi }(x)$, then we call the inverse function ${\varPhi }^{-1}(\alpha )$ the inverse uncertainty distribution of $\xi$. The uncertain variables $\xi _1,\xi _2,\ldots ,\xi _m$ are said to be independent if

for any Borel sets $B_1,B_2,\ldots ,B_m$ of real numbers.

An uncertain process is essentially a sequence of uncertain variables indexed by time for modeling the evolution of uncertain phenomena.

Definition 2

(Liu 2008) Let T be a totally ordered set and let be an uncertainty space. An uncertain process is a function $X_t(\gamma )$ from to the set of real numbers such that $\{X_t\in B\}$ is an event for any Borel set B of real numbers at each time t.

An uncertain process $X_t$ is said to have independent increments if $X_{t_0},\,X_{t_1}-X_{t_0},\,X_{t_2}-X_{t_1},\,\ldots ,\,X_{t_k}-X_{t_{k-1}}$ are independent uncertain variables where $t_0$ is the initial time and $t_1,t_2,\ldots ,t_k$ are any times with $t_0<t_1<\ldots <t_k$. An uncertain process $X_t$ is said to have stationary increments if, for any given $t>0$, the increments $X_{s+t}-X_{s}$ are identically distributed uncertain variables for all $s>0$.

Definition 3

(Liu 2009) An uncertain process $C_t$ is said to be a canonical Liu process if

• (i) $C_0=0$ and almost all sample paths are Lipschitz continuous;

• (ii) $C_t$ has stationary and independent increments;

• (iii) every increment $C_{s+t}-C_s$ is a normal uncertain variable with an uncertainty distribution

  $$\begin{aligned} {\varPhi }(x)=\left( 1+\exp \left( \frac{-\pi x}{\sqrt{3}t}\right) \right) ^{-1},\quad \ x\in \mathfrak {R}. \end{aligned}$$

Theorem 1

(Liu 2015) Let $C_t$ be a canonical Liu process. Then for each time $t>0$, the ratio $C_t/t$ is a normal uncertain variable with expected value 0 and variance 1. That is,

$$\begin{aligned} \frac{C_t}{t}\sim \mathcal{N}(0,1) \end{aligned}$$

for any $t>0$.

In order to deal with the integration and differentiation with respect to a canonical Liu process, the Liu integral was defined as follows.

Definition 4

(Liu 2009) Let $X_t$ be an uncertain process and let $C_t$ be a canonical Liu process. For any partition of closed interval [a, b] with $a=t_1<t_2<\ldots <t_{k+1}=b$, the mesh is written as

$$\begin{aligned} {\varDelta }=\max _{1\le i\le k}|t_{i+1}-t_i|. \end{aligned}$$

Then the Liu integral of $X_t$ with respect to $C_t$ is defined as

$$\begin{aligned} \int _a^bX_t\mathrm{d}C_t=\lim _{{\varDelta }\rightarrow 0}\sum _{i=1}^kX_{t_{i}}\cdot (C_{t_{i+1}}-C_{t_{i}}) \end{aligned}$$

provided that the limit exists almost surely and is finite. In this case, the uncertain process $X_t$ is said to be Liu integrable.

Definition 5

(Chen and Ralescu 2013) Let $C_t$ be a canonical Liu process and let $Z_t$ be an uncertain process. If there exist two uncertain processes $\mu _t$ and $\sigma _t$ such that

$$\begin{aligned} Z_t=Z_0+\int _0^t\mu _s\mathrm{d} s+\int _0^t\sigma _s\mathrm{d} C_s \end{aligned}$$

for any $t\ge 0$, then $Z_t$ is called a Liu process with drift $\mu _t$ and diffusion $\sigma _t$. Furthermore, $Z_t$ has an uncertain differential

$$\begin{aligned} \mathrm{d} Z_t=\mu _t\mathrm{d} t+\sigma _t\mathrm{d} C_t. \end{aligned}$$

Theorem 2

(Liu 2009) Let h(t, c) be a continuously differentiable function. Then $Z_t=h(t,C_t)$ is a Liu process and has an uncertain differential

$$\begin{aligned} \mathrm{d} Z_t=\frac{\partial h}{\partial t}(t,C_t)\mathrm{d} t+\frac{\partial h}{\partial c}(t,C_t)\mathrm{d} C_t. \end{aligned}$$

Uncertain field is a generalization of uncertain process when the index set T becomes a partially ordered set (e.g. time $\times$ space, or surface). A formal definition is given below.

Definition 6

(Liu 2014) Let T be a partially ordered set and let be an uncertainty space. An uncertain field is a function $X_t(\gamma )$ from to the set of real numbers such that $\{X_t\in B\}$ is an event for any Borel set B of real numbers at each t.

In order to describe uncertain field, Gao and Chen (2016) proposed the concepts of uncertainty distribution and inverse uncertainty distribution.

Definition 7

(Gao and Chen 2016) An uncertain field $X_t$ is said to have an uncertainty distribution ${\varPhi }_t(x)$ if for each t, the uncertain variable $X_t$ has an uncertainty distribution ${\varPhi }_t(x)$.

An uncertainty distribution ${\varPhi }_t(x)$ of uncertain field $X_t$ is said to be regular if for any t, it is a continuous and strictly increasing function with respect to x such that $0<{\varPhi }_t(x)<1$, and

$$\begin{aligned} \lim _{x\rightarrow -\infty }{\varPhi }_t(x)=0, \quad \lim _{x\rightarrow +\infty }{\varPhi }_t(x)=1. \end{aligned}$$

If $X_t$ is an uncertain field with regular uncertainty distribution ${\varPhi }_t(x)$, we call the inverse function ${\varPhi }^{-1}_t(\alpha )$ the inverse uncertainty distribution of $\xi$.

3 Uncertain partial differential equation

In this section, we propose the tool of uncertain partial differential equation, and give some examples.

Definition 8

Suppose $C_t$ is a canonical Liu process, and F is a function. Then

$$\begin{aligned} F\left( t,x_1,\ldots ,x_n,u,\frac{\partial u}{\partial t},\frac{\partial u}{\partial x_1},\ldots , \frac{\partial u}{\partial x_n},\frac{\partial ^2u}{\partial x_1^2},\ldots ,\frac{\partial ^2u}{\partial x_1\partial x_n},\ldots ,{\dot{C_t}}\right) =0 \end{aligned}$$

(1)

is called an uncertain partial differential equation, where

$$\begin{aligned} {\dot{C_t}}:=\frac{\mathrm{d}C_t}{\mathrm{d}t}. \end{aligned}$$

A solution is an uncertain field $u(t,x_1,x_2,\ldots ,x_n)$ that satisfies the Eq. (1) identically.

The order of the highest derivatives of Eq. (1) is called the order of uncertain partial differential equation.

Example 1

The partial differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}=t+x+{\dot{C_t}} \end{aligned}$$

is a first-order uncertain partial differential equation. And it has a solution

$$\begin{aligned} u(t,x)=\frac{1}{2}t^2+tx+C_t+f(x) \end{aligned}$$

where f(x) is an arbitrary function.

Example 2

The partial differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}=x+t+{\dot{C_t}} \end{aligned}$$

is a first-order uncertain partial differential equation. And it has a solution

$$\begin{aligned} u(t,x)=xt+C_t+u(0,0). \end{aligned}$$

Example 3

The partial differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}-\frac{\partial ^2 u}{\partial x^2}=-6x+{\dot{C_t}} \end{aligned}$$

is a second-order uncertain partial differential equation. And it has a solution

$$\begin{aligned} u(t,x)=x^3+C_t+u(0,0). \end{aligned}$$

Example 4

The partial differential equation

$$\begin{aligned} \frac{\partial ^2u}{\partial t^2}-\frac{\partial ^2 u}{\partial x^2}=-2+\exp (C_t){\dot{C_t}} \end{aligned}$$

is a second-order uncertain partial differential equation. And it has a solution

$$\begin{aligned} u(t,x)=x^2+\int _0^t\exp (C_s)\mathrm{d}s+u(0,0). \end{aligned}$$

Example 5

The partial differential equation

$$\begin{aligned} \frac{\partial ^2 u}{\partial x^2}={\dot{C_t}} \end{aligned}$$

is a second-order uncertain partial differential equation. And it has a solution

$$\begin{aligned} u(t,x)=\frac{1}{2}x^2{\dot{C_t}}+u(0,0). \end{aligned}$$

4 Uncertain heat equation

In this section, we investigate the heat conduction over an infinitesimally-thin wire of infinite length. Let u(t, x) denote the temperature of the wire at point $x\in \mathfrak {R}$ and at time $t>0$. There is a fluctuating heat source ${\tilde{q}}(t,x,{\dot{C_t}})$ with a disturbance (or white noise) that is denoted by ${\dot{C_t}}$.

By Fourier’s law, the rate of flow of heat energy per unit length is proportional to the negative temperature gradient,

$$\begin{aligned} -k\frac{\partial u}{\partial x}(t,x) \end{aligned}$$

where k is the thermal conductivity. So the change in internal energy in the interval $[x- {\varDelta }x, x+{\varDelta }x]$ during the period $[t-{\varDelta }t, t+{\varDelta }t]$ is

$$\begin{aligned} k\int _{t-{\varDelta }t}^{t+{\varDelta }t}\left( \frac{\partial u}{\partial x}(s,x+{\varDelta }x)-\frac{\partial u}{\partial x}(s,x-{\varDelta }x)\right) \mathrm{d}s= k\int _{t-{\varDelta }t}^{t+{\varDelta }t}\int _{x-{\varDelta }x}^{x+{\varDelta }x}\frac{\partial ^2 u}{\partial y^2}(s,y)\mathrm{d}y\mathrm{d}s. \end{aligned}$$

The total heat from uncertain fluctuating heat source in the interval $[x- {\varDelta }x, x+{\varDelta }x]$ during the period $[t-{\varDelta }t, t+{\varDelta }t]$ is

$$\begin{aligned} \int _{t-{\varDelta }t}^{t+{\varDelta }t}\int _{x-{\varDelta }x}^{x+{\varDelta }x}{\tilde{q}}\left( s,y,{\dot{C_t}}\right) \mathrm{d}y\mathrm{d}s. \end{aligned}$$

Note that the change of energy is proportional to the change in temperature, i.e., ${\varDelta }Q=c_{\rho }\rho {\varDelta }u,$ where $c_{\rho }$ is the specific heat capacity, $\rho$ is the mass density of the material. The change of energy in the interval $[x- {\varDelta }x, x+{\varDelta }x]$ of the material during the period $[t-{\varDelta }t, t+{\varDelta }t]$ is

$$\begin{aligned} c_{\rho }\rho \int _{x-{\varDelta }x}^{x+{\varDelta }x}u(t+{\varDelta }t,y)-u(t-{\varDelta }t,y)\mathrm{d}y =c_{\rho }\rho \int _{x-{\varDelta }x}^{x+{\varDelta }x}\int _{t-{\varDelta }t}^{t+{\varDelta }t}\frac{\partial u}{\partial s}(s,y)\mathrm{d}s\mathrm{d}y. \end{aligned}$$

By conservation of energy,

$$\begin{aligned} \begin{aligned}&k\int _{t-{\varDelta }t}^{t+{\varDelta }t}\int _{x-{\varDelta }x}^{x+{\varDelta }x}\frac{\partial ^2 u}{\partial y^2}(s,y)\mathrm{d}y\mathrm{d}s+ \int _{t-{\varDelta }t}^{t+{\varDelta }t}\int _{x-{\varDelta }x}^{x+{\varDelta }x}{\tilde{q}}\left( s,y,{\dot{C_t}}\right) \mathrm{d}y\mathrm{d}s\\&\quad =\, c_{\rho }\rho \int _{x-{\varDelta }x}^{x+{\varDelta }x}\int _{t-{\varDelta }t}^{t+{\varDelta }t}\frac{\partial u}{\partial s}(s,y)\mathrm{d}s\mathrm{d}y. \end{aligned} \end{aligned}$$

Then we have

$$\begin{aligned} \frac{\partial u}{\partial t}(t,x)=\frac{k}{c_{\rho }\rho }\frac{\partial ^2 u}{\partial x^2}(t,x)+\frac{1}{c_{\rho }\rho }{\tilde{q}}\left( t,x,{\dot{C_t}}\right) . \end{aligned}$$

Let

$$\begin{aligned} a^2=\frac{k}{c_{\rho }\rho },\quad q(t,x,{\dot{C_t}})=\frac{1}{c_{\rho }\rho }{\tilde{q}}(t,x,{\dot{C_t}}). \end{aligned}$$

Then the uncertain heat equation can be expressed by an uncertain partial differential equation

(2)

where $\varphi (x)$ is a given initial temperature at the initial time $t=0$. This problem is called a Cauchy problem for uncertain heat equation.

For each $\gamma \in {\varGamma }$, the uncertain heat Eq. (2) degenerates to a normal heat equation

(3)

whose solution is

$$\begin{aligned} u(t,x,\gamma )=\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)q(s,y,\dot{C_s}(\gamma ))\mathrm{d}y\mathrm{d}s \end{aligned}$$

where

$$\begin{aligned} K(t,x)=\frac{1}{2a\sqrt{\pi t}}\exp \left( -\frac{x^2}{4a^2t}\right) . \end{aligned}$$

Example 6

Assume the heat source is ${\dot{C_t}}$. Then the partial differential equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}\end{array}\right. \end{aligned}$$

(4)

is an uncertain heat equation.

Example 7

Assume the heat source is $\sin x\cdot e^{-t}+{\dot{C_t}}$. Then the partial differential equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+\sin x\cdot e^{-t}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\sin x, &{}x\in \mathfrak {R}\end{array}\right. \end{aligned}$$

(5)

is an uncertain heat equation.

Example 8

Assume the heat source is $-e^{-t}{\dot{C_t}}$. Then the partial differential equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}-e^{-t}{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}\end{array}\right. \end{aligned}$$

(6)

is an uncertain heat equation.

Example 9

Assume the heat source is $(\sin x+1){\dot{C_t}}$. Then the partial differential equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+(\sin x+1){\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}\end{array}\right. \end{aligned}$$

(7)

is an uncertain heat equation.

5 Solution of uncertain heat equation

In this section, we give the solution of Cauchy problem for uncertain heat Eq. (2). Write

$$\begin{aligned} C_b(\mathfrak {R})= & {} \{f:\mathfrak {R}\rightarrow \mathfrak {R}|f \text{ is } \text{ a } \text{ continuous } \text{ and } \text{ bounded } \text{ function, }\}\\&C_b^{1,2,1}(\mathfrak {R}^+\times \mathfrak {R}\times \mathfrak {R})\\= & {} \left\{ f(t,x,c):\mathfrak {R}^+\,{\times }\,\mathfrak {R}\,{\times }\,\mathfrak {R}\rightarrow \mathfrak {R}\Big |f, \frac{\partial f}{\partial t},\frac{\partial f}{\partial x},\frac{\partial ^2 f}{\partial x^2}, \frac{\partial f}{\partial c}\in C_b(\mathfrak {R}^+\,{\times }\mathfrak {R}{\times }\,\mathfrak {R})\right\} . \end{aligned}$$

Theorem 3

If $\varphi (x)\in C_b(\mathfrak {R})$ and $q(t,x,c)\in C_b^{1,2,1}(\mathfrak {R}^+\times \mathfrak {R}\times \mathfrak {R})$, then the uncertain field

$$\begin{aligned} u(t,x)=\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)q(s,y,\dot{C_s})\mathrm{d}y\mathrm{d}s \end{aligned}$$

(8)

is a solution of uncertain heat Eq. (2).

Proof

We first prove that u(t, x) satisfies the initial condition. Since $\varphi (x)$ is a bounded function on $\mathfrak {R}$, there exists a positive constant N such that $|\varphi (x)|\le N$. Then, we get

$$\begin{aligned} \begin{aligned}&\left| \int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\right| \\&\quad \le N\int _{-\infty }^{+\infty }K(t,x-y)\mathrm{d}y\\&\quad \le N\int _{-\infty }^{+\infty }\frac{1}{2a\sqrt{\pi t}}\exp \left( -\frac{(x-y)^2}{4a^2t}\right) \mathrm{d}y\\&\quad =N, \end{aligned} \end{aligned}$$

that is, the integral

$$\begin{aligned} \int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y \end{aligned}$$

is uniformly convergent with respect to x and t. Therefore,

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow 0^+}u(t,x)&=\lim _{t\rightarrow 0^+} \int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\\&=\lim _{t\rightarrow 0^+} \int _{-\infty }^{+\infty }\frac{1}{2a\sqrt{\pi t}}\exp \left( -\frac{(x-y)^2}{4a^2t}\right) \varphi (y)\mathrm{d}y\\&=\lim _{t\rightarrow 0^+} \int _{-\infty }^{+\infty }\frac{1}{\sqrt{\pi }}\exp \left( -z^2\right) \varphi (x+2a\sqrt{t}z)\mathrm{d}z\\&=\int _{-\infty }^{+\infty }\lim _{t\rightarrow 0^+}\left[ \frac{1}{\sqrt{\pi }}\exp \left( -z^2\right) \varphi (x+2a\sqrt{t}z)\right] \mathrm{d}z\\&=\int _{-\infty }^{+\infty }\frac{1}{\sqrt{\pi }}\exp \left( -z^2\right) \varphi (x)\mathrm{d}z\\&=\varphi (x). \end{aligned} \end{aligned}$$

Next we prove that u(t, x) satisfies Eq. (2). Since the function K(t, x) is infinitely differentiable with uniformly bounded derivatives of all orders on $\mathfrak {R}\times [\delta ,+\infty )$ for each $\delta >0$, we see that $u(t,x,\gamma )\in C^{1,2}(\mathfrak {R}^+\times \mathfrak {R})$ for any $\gamma \in {\varGamma }$ by Lebesgue dominated convergence theorem. Rewrite u(t, x) in following form

$$\begin{aligned} u(t,x)=\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(s,y)q(t-s,x-y,\dot{C}_{t-s})\mathrm{d}y\mathrm{d}s. \end{aligned}$$

Furthermore, $\dot{C}_{t-s}(\gamma )$ is a function of $t-s$ for any $\gamma \in {\varGamma }$, and we write

$$\begin{aligned} q(t-s,x-y,\dot{C}_{t-s}(\gamma ))=Q_\gamma (t-s,x-y). \end{aligned}$$

For any $\gamma \in {\varGamma }$, we can get

$$\begin{aligned} \frac{\partial u}{\partial t}(t,x,\gamma )= & {} \int _{-\infty }^{+\infty }\frac{\partial K}{\partial t}(t,x-y)\varphi (y)\mathrm{d}y +\int _{-\infty }^{+\infty }K(t,y)Q_\gamma (0,x-y)\mathrm{d}y\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(s,y)\frac{\partial Q_\gamma }{\partial t}(t-s,x-y)\mathrm{d}y\mathrm{d}s,\\ \frac{\partial ^2 u}{\partial x^2}(t,x,\gamma )= & {} \int _{-\infty }^{+\infty }\frac{\partial ^2 K}{\partial x^2}(t,x-y)\varphi (y)\mathrm{d}y \\&+\int _0^{t}\int _{-\infty }^{+\infty }K(s,y)\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\mathrm{d}y\mathrm{d}s. \end{aligned}$$

It is easy to check that the following equation holds

$$\begin{aligned} \frac{\partial K}{\partial t}(t,x)-a^2\frac{\partial ^2 K}{\partial x^2}(t,x)=0. \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned}&\frac{\partial u}{\partial t}(t,x,\gamma )-a^2\frac{\partial ^2 u}{\partial x^2}(t,x,\gamma )\\&\quad =\int _0^{t}\int _{-\infty }^{+\infty }K(s,y)\left[ \frac{\partial Q_\gamma }{\partial t}(t-s,x-y) -a^2\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\\&\qquad +\int _{-\infty }^{+\infty }K(t,y)Q_\gamma (0,x-y)\mathrm{d}y\\&\quad =\int _0^{\varepsilon }\int _{-\infty }^{+\infty }K(s,y)\left[ \frac{\partial Q_\gamma }{\partial t}(t-s,x-y) -a^2\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\\&\qquad +\int _\varepsilon ^{t}\int _{-\infty }^{+\infty }K(s,y)\left[ \frac{\partial Q_\gamma }{\partial t}(t-s,x-y) -a^2\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\\&\qquad +\int _{-\infty }^{+\infty }K(t,y)Q_\gamma (0,x-y)\mathrm{d}y\\ \end{aligned} \end{aligned}$$

(9)

where $0<\varepsilon <t$, and

$$\begin{aligned} \begin{aligned}&\left| \int _0^{\varepsilon }\int _{-\infty }^{+\infty }K(s,y)\left[ \frac{\partial Q_\gamma }{\partial t}(t-s,x-y)-a^2\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\right| \\&\quad \le \left( \left| \frac{\partial Q_\gamma }{\partial t}\right| +\left| \frac{\partial ^2 Q_\gamma }{\partial x^2}\right| \right) \int _0^{\varepsilon }\int _{-\infty }^{+\infty }K(s,y)\mathrm{d}y\mathrm{d}s\\&\quad =\varepsilon \left( \left| \frac{\partial Q_\gamma }{\partial t}\right| +\left| \frac{\partial ^2 Q_\gamma }{\partial x^2}\right| \right) . \end{aligned} \end{aligned}$$

(10)

Using integration by parts, we also have

$$\begin{aligned}&\int _\varepsilon ^{t}\int _{-\infty }^{+\infty }K(s,y)\left[ \frac{\partial Q_\gamma }{\partial t}(t-s,x-y) -a^2\frac{\partial ^2 Q_\gamma }{\partial x^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\nonumber \\&=\int _\varepsilon ^{t}\int _{-\infty }^{+\infty }K(s,y)\left[ -\frac{\partial Q_\gamma }{\partial s}(t-s,x-y) -a^2\frac{\partial ^2 Q_\gamma }{\partial y^2}(t-s,x-y)\right] \mathrm{d}y\mathrm{d}s\nonumber \\&=\int _\varepsilon ^{t}\int _{-\infty }^{+\infty }\left[ \frac{\partial K}{\partial s}(s,y) -a^2\frac{\partial ^2 K}{\partial y^2}(s,y)\right] Q_\gamma (t-s,x-y)\mathrm{d}y\mathrm{d}s\nonumber \\&\quad +\int _{-\infty }^{+\infty }K(\varepsilon ,y)Q_\gamma (t-\varepsilon ,x-y)\mathrm{d}y -\int _{-\infty }^{+\infty }K(t,y)Q_\gamma (0,x-y)\mathrm{d}y\nonumber \\&=\int _{-\infty }^{+\infty }K(\varepsilon ,y)Q_\gamma (t-\varepsilon ,x-y)\mathrm{d}y -\int _{-\infty }^{+\infty }K(t,y)Q_\gamma (0,x-y)\mathrm{d}y.\nonumber \\ \end{aligned}$$

(11)

By Eqs. (9)–(11), we obtain

$$\begin{aligned} \begin{aligned}&\left| \frac{\partial u}{\partial t}(t,x,\gamma )-a^2\frac{\partial ^2 u}{\partial x^2}(t,x,\gamma )-\int _{-\infty }^{+\infty }K(\varepsilon ,y)Q_\gamma (t-\varepsilon ,x-y)\mathrm{d}y\right| \\&\quad \le \varepsilon \left( \left| \frac{\partial Q_\gamma }{\partial t}\right| +\left| \frac{\partial ^2 Q_\gamma }{\partial x^2}\right| \right) , \quad \varepsilon \in (0,t). \end{aligned} \end{aligned}$$

Setting $\varepsilon \rightarrow 0^+$, we have

$$\begin{aligned} \begin{aligned} \frac{\partial u}{\partial t}(t,x,\gamma )-a^2\frac{\partial ^2 u}{\partial x^2}(t,x,\gamma )&=\lim _{\varepsilon \rightarrow 0^+}\int _{-\infty }^{+\infty }K(\varepsilon ,y)Q_\gamma (t-\varepsilon ,x-y)\mathrm{d}y\\&=Q_\gamma (t,x)=q(t,x,\dot{C}_{t}(\gamma )),\quad \forall \gamma \in {\varGamma }. \end{aligned} \end{aligned}$$

The theorem is proved. $\square$

Example 10

Consider the uncertain heat equation in Example 6,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 3 that the solution is

$$\begin{aligned} u(t,x)&=\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\dot{C_s}\mathrm{d}y\mathrm{d}s\\&=\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\mathrm{d}y\mathrm{d}C_s\\&=\int _0^{t}\int _{-\infty }^{+\infty }\frac{1}{2\sqrt{\pi (t-s)}}\exp \left( -\frac{(x-y)^2}{4(t-s)}\right) \mathrm{d}y\mathrm{d}C_s\\&=\int _0^{t}\int _{-\infty }^{+\infty }\frac{1}{\sqrt{\pi }}\exp \left( -z^2\right) \mathrm{d}z\mathrm{d}C_s\\&=\int _0^{t}\mathrm{d}C_s=C_t. \end{aligned}$$

Example 11

Consider the uncertain heat equation in Example 7,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+\sin x\cdot e^{-t}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\sin x, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 3 that the solution is

$$\begin{aligned} \begin{aligned} u(t,x)&=\int _{-\infty }^{+\infty }K(t,x-y)\sin y\mathrm{d}y\\&\quad +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left( \sin y\cdot e^{-s}+\dot{C_s}\right) \mathrm{d}y\mathrm{d}s\\&=\int _{-\infty }^{+\infty }K(t,x-y)\sin y\mathrm{d}y\\&\quad +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\sin y\cdot e^{-s}\mathrm{d}y\mathrm{d}s+C_t\\&=e^{-t}\sin x+te^{-t}\sin x+C_t\\&=(t+1)e^{-t}\sin x+C_t. \end{aligned} \end{aligned}$$

Example 12

Consider the uncertain heat equation in Example 8,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}-e^{-t}{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 3 that the solution is

$$\begin{aligned} \begin{aligned} u(t,x)&=-\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)e^{-s}\dot{C_s}\mathrm{d}y\mathrm{d}s\\&=-\int _0^{t}e^{-s}\int _{-\infty }^{+\infty }K(t-s,x-y)\mathrm{d}y\mathrm{d}C_s\\&=-\int _0^{t}e^{-s}\mathrm{d}C_s. \end{aligned} \end{aligned}$$

Example 13

Consider the uncertain heat equation in Example 9,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+(\sin x+1){\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 3 that the solution is

$$\begin{aligned} \begin{aligned} u(t,x)&=\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)(\sin (y)+1)\dot{C_s}\mathrm{d}y\mathrm{d}s\\&=\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)(\sin (y)+1)\mathrm{d}y\mathrm{d}C_s\\&=e^{-t}\sin x\int _0^{t}e^{s}\mathrm{d}C_s+C_t. \end{aligned} \end{aligned}$$

Corollary 1

If $\varphi (x)\in C_b(\mathfrak {R})$ and $f(t,x),\sigma (t,x)\in C_b^{1,2}(\mathfrak {R}^+\times \mathfrak {R})$, then the uncertain heat equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=a^2\frac{\partial ^2 u}{\partial x^2}+f(t,x)+\sigma (t,x){\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\varphi (x), &{}x\in \mathfrak {R}\end{array}\right. \end{aligned}$$

(12)

has a solution

$$\begin{aligned} \begin{aligned} u(t,x)=&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\sigma (s,y)\mathrm{d}y\mathrm{d}C_s. \end{aligned} \end{aligned}$$

(13)

Proof

Let $q(t,x,c)=f(t,x)+\sigma (t,x)c\in C_b^{1,2,1}(\mathfrak {R}^+\times \mathfrak {R}\times \mathfrak {R})$. It follows from Theorem 3 that the uncertain heat Eq. (12) has a solution

$$\begin{aligned} \begin{aligned} u(t,x)=&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left( f(s,y)+\sigma (s,y)\dot{C}_s\right) \mathrm{d}y\mathrm{d}s\\ =&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\sigma (s,y)\dot{C}_s\mathrm{d}y\mathrm{d}s\\ =&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\sigma (s,y)\mathrm{d}y\mathrm{d}C_s. \end{aligned} \end{aligned}$$

Thus, the corollary is proved. $\square$

6 Inverse uncertainty distribution of solution

In this section, we give the inverse uncertainty distribution of solution of Cauchy problem for uncertain heat equation.

Theorem 4

Let u(t, x) be the solution of the Cauchy problem for uncertain heat equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=a^2\frac{\partial ^2 u}{\partial x^2}+q(t,x,{\dot{C_t}}), &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\varphi (x), &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

If q(t, x, c) is a strictly increasing function with respect to c, then the solution u(t, x) has an inverse uncertainty distribution

$$\begin{aligned} {\varPsi }_{t,x}^{-1}(\alpha )=\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\,\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)q(s,y,{\varPhi }^{-1}(\alpha ))\mathrm{d}y\mathrm{d}s \end{aligned}$$

where

$$\begin{aligned} {\varPhi }^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \end{aligned}$$

is the inverse uncertainty distribution of standard normal uncertain variable.

Proof

On the one hand, we have

On the other hand, we have

Note that $\left\{ u(t,x)\le {\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\}$ and $\left\{ u(t,x)\,{\nleq }\,{\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\}$ are opposite with each other. By using the duality axiom, we get

It follows from

$$\begin{aligned} \left\{ u(t,x)>{\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\} \subset \left\{ u(t,x)\nleq {\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\} \end{aligned}$$

and the monotonicity theorem that

Thus, we obtain

The theorem is proved. $\square$

Theorem 5

Let u(t, x) be the solution of the Cauchy problem for uncertain heat equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=a^2\frac{\partial ^2 u}{\partial x^2}+q(t,x,{\dot{C_t}}), &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\varphi (x), &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

If q(t, x, c) is a strictly decreasing function with respect to c, then the solution u(t, x) has an inverse uncertainty distribution

$$\begin{aligned} {\varPsi }_{t,x}^{-1}(\alpha )= & {} \int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\\&+\,\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)q(s,y,{\varPhi }^{-1}(1-\alpha ))\mathrm{d}y\mathrm{d}s \end{aligned}$$

where

$$\begin{aligned} {\varPhi }^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \end{aligned}$$

is the inverse uncertainty distribution of standard normal uncertain variable.

Proof

On the one hand, we have

On the other hand, we have

Note that $\left\{ u(t,x)\le {\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\}$ and $\left\{ u(t,x)\nleq {\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\}$ are opposite with each other. By using the duality axiom, we get

It follows from

$$\begin{aligned} \left\{ u(t,x)>{\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\} \subset \left\{ u(t,x)\nleq {\varPsi }_{t,x}^{-1}(\alpha ),\forall t, \forall x\right\} \end{aligned}$$

and the monotonicity theorem that

Thus, we obtain

The theorem is proved. $\square$

Example 14

Consider the uncertain heat equation in Example 6,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 4 that the inverse uncertainty distribution of solution is

$$\begin{aligned} {\varPhi }_{t,x}^{-1}(\alpha )=\frac{\sqrt{3}t}{\pi }\ln \frac{\alpha }{1-\alpha } \end{aligned}$$

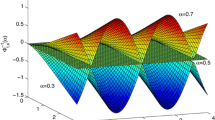
that is just the inverse uncertainty distribution of $C_t$, which is shown in (Fig. 1).

Example 15

Consider the uncertain heat equation in Example 7,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+\sin x\cdot e^{-t}+{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\sin x, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 4 that the inverse uncertainty distribution of solution is

$$\begin{aligned} {\varPhi }_{t,x}^{-1}(\alpha )=(t+1)e^{-t}\sin x+\frac{\sqrt{3}t}{\pi }\ln \frac{\alpha }{1-\alpha } \end{aligned}$$

that is just the inverse uncertainty distribution of $(t+1)e^{-t}\sin x+C_t$, which is shown in (Fig. 2).

Fig. 1

Inverse uncertainty distribution in Example 14

Example 16

Consider the uncertain heat equation in Example 8,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}-e^{-t}{\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 5 that the inverse uncertainty distribution of solution is

$$\begin{aligned} {\varPhi }_{t,x}^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\left( 1-e^{-t}\right) \ln \frac{\alpha }{1-\alpha } \end{aligned}$$

that is just the inverse uncertainty distribution of

$$\begin{aligned} -\int _0^{t}e^{-s}\mathrm{d}C_s, \end{aligned}$$

which is shown in Fig. 3.

Example 17

Consider the uncertain heat equation in Example 9,

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=\frac{\partial ^2 u}{\partial x^2}+(\sin x+1){\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=0, &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

It follows from Theorem 4 that the inverse uncertainty distribution of solution is

$$\begin{aligned} {\varPhi }_{t,x}^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\left( \sin x(1-e^{-t})+t\right) \ln \frac{\alpha }{1-\alpha } \end{aligned}$$

that is just the inverse uncertainty distribution of

$$\begin{aligned} e^{-t}\sin x\int _0^{t}e^{s}\mathrm{d}C_s+C_t, \end{aligned}$$

which is shown in Fig. 4.

Fig. 2

Inverse uncertainty distribution in Example 15

Fig. 3

Inverse uncertainty distribution in Example 16

Fig. 4

Inverse uncertainty distribution in Example 17

Corollary 2

Assume $\sigma (t,x)\ge 0,\forall t,x$ or $\sigma (t,x)\le 0,\forall t,x$, and let u(t, x) be the solution of the Cauchy problem for uncertain heat equation

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{\partial u}{\partial t}=a^2\frac{\partial ^2 u}{\partial x^2}+f(t,x)+\sigma (t,x){\dot{C_t}}, &{}t>0,x\in \mathfrak {R},\\ u(0,x)=\varphi (x), &{}x\in \mathfrak {R}. \end{array}\right. \end{aligned}$$

(14)

Then the solution u(t, x) has an inverse uncertainty distribution

$$\begin{aligned} \begin{aligned} {\varPsi }_{t,x}^{-1}(\alpha )=&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+\,{\varPhi }^{-1}(\alpha )\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left| \sigma (s,y)\right| \mathrm{d}y\mathrm{d}s. \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\varPhi }^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha } \end{aligned}$$

is the inverse uncertainty distribution of standard normal uncertain variable.

Proof

If $\sigma (t,x)\ge 0$, then $q(t,x,c)=f(t,x)+\sigma (t,x)c$ is a strictly increasing function with respect to c. From Theorem 4, the solution u(t, x) has an inverse uncertainty distribution

$$\begin{aligned} \begin{aligned} {\varPsi }_{t,x}^{-1}(\alpha )=&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left( f(s,y) +\sigma (s,y){\varPhi }^{-1}(\alpha )\right) \mathrm{d}y\mathrm{d}s\\ =&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+\,{\varPhi }^{-1}(\alpha )\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\sigma (s,y)\mathrm{d}y\mathrm{d}s.\\ \end{aligned} \end{aligned}$$

If $\sigma (t,x)\le 0$, then $q(t,x,c)=f(t,x)+\sigma (t,x)c$ is a strictly decreasing function with respect to c. From Theorem 5, the solution u(t, x) has an inverse uncertainty distribution

$$\begin{aligned} \begin{aligned} {\varPsi }_{t,x}^{-1}(\alpha )=&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y\\&+\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left( f(s,y) +\sigma (s,y){\varPhi }^{-1}(1-\alpha )\right) \mathrm{d}y\mathrm{d}s\\ =&\int _{-\infty }^{+\infty }K(t,x-y)\varphi (y)\mathrm{d}y +\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)f(s,y)\mathrm{d}y\mathrm{d}s\\&+{\varPhi }^{-1}(\alpha )\int _0^{t}\int _{-\infty }^{+\infty }K(t-s,x-y)\left| \sigma (s,y)\right| \mathrm{d}y\mathrm{d}s.\\ \end{aligned} \end{aligned}$$

Thus, the corollary is proved. $\square$

7 Some special uncertain partial differential equations

This section defines some special uncertain partial differential equations including uncertain parabolic equation, uncertain hyperbolic equation and uncertain elliptic equation.

Definition 9

Assume that $a_{ij}$, $b_{i}$, c and f are given functions, and

$$\begin{aligned} a_{ij}(t,x)=a_{ji}(t,x),\quad (t,x)\in \mathfrak {R}^+\times \mathfrak {R}^n,\quad i,j=1,2,\ldots ,n. \end{aligned}$$

The uncertain partial differential equation

$$\begin{aligned} \frac{\partial u}{\partial t}-\sum _{i,j=1}^n a_{ij}(t,x)\frac{\partial ^2u}{\partial x_ix_j} +\sum _{i=1}^n b_{i}(t,x)\frac{\partial u}{\partial x_i}+c(t,x)u=f(t,x,{\dot{C_t}}) \end{aligned}$$

(15)

is called parabolic if there exists a constant $\lambda >0$ such that

$$\begin{aligned} \sum _{i,j=1}^n a_{ij}(t,x)y_iy_j\ge \lambda |y|^2 \end{aligned}$$

for all $(t,x)\in \mathfrak {R}^+\times \mathfrak {R}^n$ and $y=(y_1,y_2,\ldots ,y_n)\in \mathfrak {R}^n$.

If $n=1, a_{11}(t,x)=1, b_1(t,x)=c(t,x)=0$, then uncertain parabolic partial differential equation becomes an uncertain heat equation

$$\begin{aligned} \frac{\partial u}{\partial t}-\frac{\partial ^2u}{\partial x^2}=f(t,x,{\dot{C_t}}). \end{aligned}$$

The function $f(t,x,{\dot{C_t}})$ means that heat source has an uncertain disturbance. The equation in Example 3 is an uncertain parabolic partial differential equation.

Definition 10

Assume that $a_{ij}$, $b_{i}$, c and f are given functions, and

$$\begin{aligned} a_{ij}(t,x)=a_{ji}(t,x),\quad (t,x)\in \mathfrak {R}^+\times \mathfrak {R}^n,\quad i,j=1,2,\ldots ,n. \end{aligned}$$

The uncertain partial differential equation

$$\begin{aligned} \frac{\partial ^2u}{\partial t^2}-\sum _{i,j=1}^n a_{ij}(t,x)\frac{\partial ^2u}{\partial x_ix_j}+\sum _{i=1}^n b_{i}(t,x)\frac{\partial u}{\partial x_i}+c(t,x)u=f(t,x,{\dot{C_t}}) \end{aligned}$$

(16)

is called hyperbolic if there exists a constant $\lambda >0$ such that

$$\begin{aligned} \sum _{i,j=1}^n a_{ij}(t,x)y_iy_j\ge \lambda |y|^2 \end{aligned}$$

for all $(t,x)\in \mathfrak {R}^+\times \mathfrak {R}^n$ and $y=(y_1,y_2,\ldots ,y_n)\in \mathfrak {R}^n$.

If $n=1, a_{11}(t,x)=1, b_1(t,x)=c(t,x)=0$, then uncertain hyperbolic partial differential equation becomes an uncertain wave equation

$$\begin{aligned} \frac{\partial ^2u}{\partial t^2}-\frac{\partial ^2u}{\partial x^2}=f(t,x,{\dot{C_t}}). \end{aligned}$$

The function $f(t,x,{\dot{C_t}})$ means that the force has an uncertain disturbance. The equation in Example 4 is an uncertain hyperbolic partial differential equation.

Definition 11

Assume that $a_{ij}$, $b_{i}$, c and f are given functions, and

$$\begin{aligned} a_{ij}(x)=a_{ji}(x),\quad x\in \mathfrak {R}^n,\quad i,j=1,2,\ldots ,n. \end{aligned}$$

The uncertain partial differential equation

$$\begin{aligned} -\sum _{i,j=1}^n a_{ij}(x)\frac{\partial ^2u}{\partial x_ix_j} +\sum _{i=1}^n b_{i}(x)\frac{\partial u}{\partial x_i}+c(x)u=f(x,{\dot{C_t}}) \end{aligned}$$

(17)

is called elliptic if there exists a constant $\lambda >0$ such that

$$\begin{aligned} \sum _{i,j=1}^n a_{ij}(x)y_iy_j\ge \lambda |y|^2 \end{aligned}$$

for all $x\in \mathfrak {R}^n$ and $y=(y_1,y_2,\ldots ,y_n)\in \mathfrak {R}^n$.

If $n=1, a_{11}(x)=1, b_1(x)=c(x)=0$, then uncertain elliptic partial differential equation becomes an uncertain Poisson’s equation

$$\begin{aligned} -\frac{\partial ^2u}{\partial x^2}=f(x,{\dot{C_t}}). \end{aligned}$$

The function $f(x,{\dot{C_t}})$ means that it has an uncertain disturbance. The equation in Example 5 is an uncertain elliptic partial differential equation.

8 Paradox of stochastic heat equation

Let us consider a one-dimensional stochastic heat equation over infinitesimally-thin wire with infinite length

$$\begin{aligned} \frac{\partial u}{\partial t}=a^2\frac{\partial ^2u}{\partial x^2}+q(t,x,\dot{W_t}) \end{aligned}$$

(18)

where $a^2$ is the constant thermal diffusivity, u(t, x) is the temperature at point $x\in \mathfrak {R}$ and time $t>0$, $q(t,x,\dot{W_t})$ is a stochastic heat source, $\dot{W_t}=\mathrm{d}W_t/\mathrm{d}t$ is a white noise, and $W_t$ is a standard Wiener process.

Although the stochastic heat Eq. (18) has been widely accepted, is such an equation really reasonable? Note that

$$\begin{aligned} \dot{W}_t\sim \mathcal {N}\left( 0,\frac{1}{\mathrm{d}t}\right) \end{aligned}$$

is a normal random variable whose expected value is zero and variance is $1/\mathrm{d}t$. Consider a special case, $q(t,x,\dot{W_t})=f(t,x)+\sigma (t,x)\dot{W_t}$, where f and $\sigma$ are bounded real-valued functions. Then, we can get

$$\begin{aligned} \frac{\partial u}{\partial t} =a^2\frac{\partial ^2u}{\partial x^2}+f(t,x)+\sigma (t,x)\dot{W_t} \end{aligned}$$

(19)

and

$$\begin{aligned} \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\sim \mathcal {N}\left( f,\sigma ^2\frac{1}{\mathrm{d}t}\right) . \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned}&\mathrm{Pr}\left\{ \left| \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\right| \ge N\right\} \\&=\mathrm{Pr}\left\{ \left( \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\ge N\right) \bigcup \left( \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\le -N\right) \right\} \\&=\mathrm{Pr}\left\{ \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\ge N\right\} +\mathrm{Pr}\left\{ \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\le -N\right\} \\&=\mathrm{Pr}\left\{ \frac{\frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}-f}{\sigma /\sqrt{\mathrm{d}t}}\ge \frac{N-f}{\sigma }\sqrt{\mathrm{d}t}\right\} \\&\quad +\mathrm{Pr}\left\{ \frac{\frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}-f}{\sigma /\sqrt{\mathrm{d}t}}\le -\frac{N+f}{\sigma }\sqrt{\mathrm{d}t}\right\} \\&=1-{\varPhi }\left( \frac{N-f}{\sigma }\sqrt{\mathrm{d}t}\right) +{\varPhi }\left( -\frac{N+f}{\sigma }\sqrt{\mathrm{d}t}\right) \\&\rightarrow 1\quad (\mathrm{d}t\rightarrow 0) \end{aligned} \end{aligned}$$

where N is any given large constant, and ${\varPhi }(\cdot )$ is the standard normal distribution function. This means,

$$\begin{aligned} \mathrm{Pr}\left\{ \left| \frac{\partial u}{\partial t}-a^2\frac{\partial ^2u}{\partial x^2}\right| \ge N\right\} =1, \end{aligned}$$

that is, at least one term is $\infty$ at any point x and any time t among $\partial u/\partial t$ and $\partial ^2u/\partial x^2$. However, from the physics point of view, those terms $\partial u/\partial t$ (heat transmission speed) and $\partial ^2u/\partial x^2$ (change rate of $\partial u/\partial x$ with respect to x) are bounded at every point x and every time t for any material in real life. Therefore, it is unreasonable that the temperature u(t, x) follows the stochastic heat equation like (18) from the above paradox.

As a summary, Eq. (18) can just be used to describe the heat conduct phenomenon with an infinite heat transmission speed or an infinite change rate of $\partial u/\partial x$ with respect to x. However, this heat conduct process does not exist at all because all the objects in nature have finite heat transmission speed and finite change rate of $\partial u/\partial x$ with respect to x. This means it is unreasonable to model the heat conduction process via stochastic heat equations.

9 Conclusion

At first, this paper proposed the uncertain partial differential equation driven by Liu process and investigated uncertain heat equation. And then, the solution of the Cauchy problem for uncertain heat equation was obtained and the inverse uncertainty distribution of solution was also derived. This paper also defined three kinds of uncertain partial differential equations. In addition, a paradox of stochastic heat equation was introduced.