1 Introduction

In power market, generation companies (GCs) first submit expected selling price (bidding) of their production, then a grid company determines the productive task to each GC considering future power load and the bidding of all GCs. Thus, the profit of each GC cannot be obtained until the gird company decides the power dispatch. Problems with such structure could be formed as bilevel programming (BP), in which a group of GCs manage the upper level and a market operator (MO) who not only guarantees supply system reliability, but also represents consumer’s will to minimize electricity purchasing cost, controls the lower level.

From the literature, the designation of BP was first used by Candler et al. [4], while its original formulation was introduced by Bracken and McGill [3]. The BP is distinguished from conventional approaches as this type of programs have a subset of decision variables constrained to be an optimal solution of other program parameterized by their remaining variables. Recent years, the development of BP has been strongly motivated by real-world applications, and it has been applied with remarkable success in a number of practical problems that involve a hierarchical decision making process, e.g. the applications in transportation [1], management [12] and especially power systems planning [2, 5, 24]. Zhang et al. [24] proposed a multi-leader one-follower bilevel model for day-ahead electricity markets, where the upper level is a game problem among every GC and the lower level is a cost minimization problem of an MO. Then, each GC chooses the bidding to maximize its individual profit, and an MO can find its minimal electricity purchasing fare, which is determined by the output of each unit and an unified market clearing price. However, the proposed method assumed that all of the generation units are always online and working independently, i.e. unit commitment (UC) optimization which aims to schedule the generation units to meet the system load at the lowest cost was not considered. Carrion et al. [5] presented a medium-term bilevel decision-making programming for a power retailer. This model helps the retailer decide his level of involvement in future market and in the pool as well as the selling price offered to its potential clients. Uncertainty on future pool prices, client demands, and rival-retailer prices is accounted for via stochastic programming. Fernandez-Blanco et al. [2] studied a general BP framework for alternative market-clearing procedures dependent on market-clearing prices. The bilevel formulation is investigated through a particular instance of price-based market clearing driven by consumer payment minimization. However, the future load uncertainty as well as the UC optimization were not considered.

The UC optimization which can increase the profit of a GC and more importantly, decrease the waste of social resources, has been wildly studied in the past decades. Generally, the UC is applied to minimize the generation cost via arranging the on/off states and outputs of all units over the scheduling horizon. A lot of constraints such as system power balance, reserve requirement, minimal/maximal output, initial condition, and minimal on/off limits are considered during the optimization process [10]. Therefore, the UC is a complicated but realistic problem to be addressed in the optimization process.

Some related studies [5, 17] describe the load uncertainty by using probability theory, then stochastic programming is applied to solve the optimization problems. However, on the one hand, the various inputs such as precipitation, humidity, wind speed and temperature that form the basis of load forecasting are often assessed with some uncertainty. This type of uncertainty is usually non-statistical and involves linguistic knowledge. On the other hand, the power load forecasted on historical data needs to be adjusted by experts based on their confidence about the future. Such human estimations can also involve imprecise information. The probability theory is used for analyzing a great amount of data, while fuzzy logic is used for the representation and using of linguistic knowledge. Therefore, it is reasonable to apply fuzzy set theory as an alternative tool of probability theory to handle the endogenous fuzzy uncertainty. Recently, fuzzy set theory has been applied in power systems by some researchers [16, 19]. Besides this, study [9] also introduced a fuzzy interaction regression method to short term load forecast, which provides a possible way to address the fuzzy load uncertainty in real applications.

Based on the above analysis, this study constructs a UC-based fuzzy bilevel electricity trading model (UC-BETM). The upper level are mixed-integer profit maximization problems of several GCs while the lower level is an electricity purchasing fare minimization problem of an MO: Each GC first provides an initial bidding for each scheduling period (usually 1 h), then the MO determines the generation amount of the GC according to the future load and the bidding. After this, the MO can obtain his payment and the GCs are able to calculate their profits after solving the UC problem. Such processes can be implemented repeatedly until an optimal solution is obtained. In contrast to [19] which merely solves the UC scheduling of one GC, the proposed model focuses on the electricity trading problem among various participants, includes not only the UC optimization, but also the MO’s response and reliability concern. In addition, the UC-BETM is formed as a bilevel structure, which is different from the two-stage model developed in [19]. Compared with [2, 24], we consider the upper level problem as a collaboration of all generation units, instead of working separately, i.e. the cost is obtained via the UC optimization. More importantly, we also take the load uncertainty into consideration and use different distributed fuzzy variables to describe the power loads.

The solution to UC has been studied extensively in the past several decades. Among the existing results, some optimization methods such as priority list (PL), branch-and-bound (BB) and Lagrangian relaxation (LR) have explicit formulations and can lead to exact solutions [16, 19], while the others are mainly meta-heuristic algorithms use iterative search techniques to find local optimal solutions or approximate global optima. From solution quality perspective, the first type of methods outperform the meta-heuristic ones, as the latter cannot guarantee a systematic exploration of the entire solution space. However, on the one hand, the UC-BETM developed in this study is a BP with several nonlinear sub-optimization problems: Besides a series of classical UC optimizations, the UC-BETM also includes a nonlinear cost minimization problem of a MO and a feedback process between the upper and lower levels, which make it difficult or impossible to be solved by methods with explicit formulations. On the other hand, research on the improvement of meta-heuristic computation shows that well-design algorithms could mitigate local convergency during iterations and provide reasonable assurance that the search has few overlooked promising regions. Therefore, it could be reasonable to apply meta-heuristic algorithm to find approximate global optima when the problem is difficult to be solved by approaches with explicit formulations. Based on the above reasons, we develop a particle swarm optimization (PSO)-based algorithm in this research, and some techniques proposed in previous study are employed as well to improve the search result.

The remainder of this paper is organized as follows: Sect. 2 introduces some knowledge of BP and fuzzy set theory. In Sect. 3, we describe the detailed problem of each level and build the UC-BETM. Section 4 provides a PSO-based algorithm to solve the proposed model. Then, the effectiveness of this study is illustrated by a test system-based numerical example in Sect. 5. Finally, Sect. 6 summarizes our conclusions.

2 Preliminaries

2.1 Bilevel programming

The general formulation of BP is given as follows:

$$\begin{aligned} \begin{array}{ll} \min \limits _{x\in X}\ \ \ F(x,y) \\ s.t. \ \ \ \ \ G(x,y)\le 0,\\ \end{array}\end{aligned}$$
(1)
$$\begin{aligned} \begin{array}{ll} \min \limits _{y}\ \ \ f(x,y) \\ s.t. \ \ \ \ \ g(x,y)\le 0.\\ \end{array} \end{aligned}$$
(2)

where Eq. (1) is the upper level problem controlled by the upper level variables \(x\in \mathbb {R}^{n_{1}}\), Eq. (2) is the lower level optimization determined by the lower level variables \(y\in \mathbb {R}^{n_{2}}\). \(F: \mathbb {R}^{n_{1}} \times \mathbb {R}^{n_{2}} \rightarrow \mathbb {R}\) and \(f: \mathbb {R}^{n_{1}} \times \mathbb {R}^{n_{2}} \rightarrow \mathbb {R}\) are the upper and lower level objective functions, while \(G: \mathbb {R}^{n_{1}} \times \mathbb {R}^{n_{2}} \rightarrow \mathbb {R}^{m_{1}}\) and \(g: \mathbb {R}^{n_{1}} \times \mathbb {R}^{n_{2}} \rightarrow \mathbb {R}^{m_{2}}\) are the upper and lower level constraints.

The constraint region of the above BP problem is:

$$\begin{aligned} \varOmega =\left\{ (x,y)\in \mathbb {R}^{n_{1}} \times \mathbb {R}^{n_{2}}: x\in X,\ G(x,y)\le 0, \ g(x,y)\le 0\right\} . \end{aligned}$$
(3)

Then, for a given solution \(\overline{x}\) of the upper level, the lower level feasible solution region is defined as:

$$\begin{aligned} \textit{LR}(\overline{x})=\{y\in \mathbb {R}^{n_{2}}: g(\overline{x},y)\le 0\}. \end{aligned}$$
(4)

And, the optimal solution of the lower level is expressed as:

$$\begin{aligned} y^{*}=\{y\in \textit{LR}(\overline{x}): \textit{argmin}\ f(\overline{x},y)\}, \end{aligned}$$
(5)

where \(y^{*}\) is called as a rational response of \(\overline{x}\), and \(R(\overline{x})\) is normally used to denote the reaction set of each \(y^{*}\) to every feasible value of \(\overline{x}\).

Now, we can conclude the feasible region of the upper level problem as:

$$\begin{aligned} \textit{UR}(\overline{x}, y^{*})=\{(\overline{x}, y^{*})\in \varOmega : (\overline{x}, y^{*})\in R(\overline{x}) \}. \end{aligned}$$
(6)

Based on the above knowledge, Colson et al. introduced the concepts of optimistic and pessimistic BP in [7], which provide a possible way to solve the bilevel optimization. The readers may refer to [1, 7] for more detailed information on BP.

2.2 Fuzzy set theory

In this study, fuzzy set theory is applied to address future load uncertainty, system reliability as well as develop the solution algorithm. Therefore, we provide some necessary concepts and features of fuzzy variables.

Suppose \(\xi \) is a fuzzy variable with membership function \(\mu _{\xi }\), \(r \) is a real number. Then, the possibility and necessity of event \(\xi \ge r\) are:

$$\begin{aligned} \hbox {Pos}\{\xi \ge r\}= & {} \sup \limits _{t\ge r}\mu _{\xi }(t),\end{aligned}$$
(7)
$$\begin{aligned} \hbox {Nec} \{\xi \ge r\}= & {} 1-\sup \limits _{t< r}\mu _{\xi }(t), \end{aligned}$$
(8)

The credibility measure [13] is formed on the basis of the possibility and necessity measures, and in the simplest case, it is taken as their average.

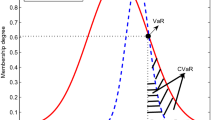
$$\begin{aligned} \hbox {Cr} \{\xi \ge r\}=\frac{1}{2}\left[ {\hbox {Pos}}\{\xi \ge r\}+{\hbox {Nec}}\{\xi \ge r\}\right] . \end{aligned}$$
(9)

Value-at-risk (VaR) of an investment is the likelihood of the greatest loss under a given confidence level [8]. Recently, researchers have introduced the VaR in fuzzy environment [15, 21], as follows:

Suppose \(\mathcal {L}\) is a variable that represents the fuzzy loss of one investment, then the VaR of \(\mathcal {L}\) under confidence level \((1-\beta )\) can be written as follows:

$$\begin{aligned} \hbox {VaR}_{1-\beta }={\hbox {sup}}\{\lambda | \hbox {Cr}(\mathcal {L}\ge \lambda )\ge \beta \}, \end{aligned}$$
(10)

where \(\beta \in (0, 1)\). This equation tells us that the greatest loss of \(\mathcal {L}\) under confidence level \(1-\beta \) is \(\lambda \).

The fuzzy VaR has been applied to build engineering optimization models [20–22]. In this study, we use this concept to measure the unexpected load risk and construct the lower level objective function.

3 Mathematical modeling of the UC-BETM

In this section, we first introduce the upper and lower level optimization problems respectively, then build the mathematical model of the UC-BETM. It is assumed that all the GCs are mutually independent thermal power plants, and no transmission loss is considered in this research.

3.1 Upper level problem

The upper level problem involves a series of sub-optimization problems of every GC, with the goal of maximizing the generation profit.

3.1.1 Objective function

$$\begin{aligned} \begin{array}{ll} \max \limits _{\textit{AP}_{t}^{m}} F=\sum \limits _{t=1}^{T}P_{t}^{m}\cdot \textit{UMCP}_{t}-F^{\prime }_{m}, \end{array} \end{aligned}$$
(11)

where \(\textit{UMCP}_{t}\) is the unified market clearing. price determined by the maximal value of all bidding in period \(t\) [24], \(\sum \nolimits _{t=1}^{T}P_{t}^{m}\cdot \textit{UMCP}_{t}\) calculates the revenue of GC \(m\) and \(F^{\prime }_{m}\) represents the generation cost obtained from the UC optimization.

Generally, the UC is modeled as a complicated nonlinear problem which aims to minimize the system generation cost subject to several constraints. The following problem is formed for the \(m\)th GC:

$$\begin{aligned} \hbox {min} \ F^{\prime }_{m}=\sum _{t=1}^{T}\sum _{j_{m}=1}^{N_{m}}u_{t}^{j_{m}}\cdot \left[ CT_{j_{m}}\left( G_{t}^{j_{m}}\right) +SC_{j_{m}}\cdot \left( 1-u_{t-1 }^{j_{m}}\right) \right] , \end{aligned}$$
(12)

where \(\textit{CT}_{j_{m}}(G_{t}^{j_{m}})\) is computed using the following equation:

$$\begin{aligned} \textit{CT}_{j_{m}}\left( G_{t}^{j_{m}}\right) =a_{j_{m}}+b_{j_{m}}\cdot G_{t}^{j_{m}}+c_{j_{m}}\cdot \left( G_{t}^{j_{m}}\right) ^{2}. \end{aligned}$$
(13)

In Eq. (13), the numerical values of \(a_{j_{m}}\), \(b_{j_{m}}\) and \(c_{j_{m}}\) are determined by the attributes of each generation unit.

Constraints

  1. a.

    Power demand balance

    $$\begin{aligned} \sum \limits _{j_{m}=1}^{N_{m}}G_{t}^{j_{m}}\cdot u_{t}^{j_{m}}=P_{t}^{m}. \end{aligned}$$
    (14)
  2. b.

    Spinning reserve requirement

    $$\begin{aligned} \sum \limits _{j_{m}=1}^{N_{m}}P_{j_{m}}^{max}\cdot u_{t}^{j_{m}}\ge P_{t}^{m}+R_{t}^{m}. \end{aligned}$$
    (15)

    The spinning reserve is usually taken as a pre-specified amount of the demand, e.g. \(0.1\cdot P_{t}^{m}\).

  3. c.

    Generation constraints

    $$\begin{aligned} P_{j_{m}}^{min}\cdot u_{t}^{j_{m}} \le G_{t}^{j_{m}} \le P_{j_{m}}^{max}\cdot u_{t}^{j_{m}}. \end{aligned}$$
    (16)
  4. d.

    Unit on/off limitations The unit on/off limits can be expressed by the following Eq. [14].

    $$\begin{aligned}&\sum \limits _{i=t}^{t+T_{j_{m}, \textit{up}}-1}u_{t}^{j_{m}}\ge x_{t}^{j_{m}}T_{j_{m}, \textit{up}}\nonumber \\&\qquad \forall j_{m}, \forall t=A_{j_{m}}+1,\ldots ,T-T_{j_{m}, \textit{up}}+1\nonumber \\&\sum \limits _{i=t}^{t+T_{j_{m}, \textit{down}}-1}\left( 1-u_{t}^{j_{m}}\right) \ge y_{t}^{j_{m}}T_{j_{m}, \textit{down}}\nonumber \\&\qquad \forall j_{m}, \forall t=B_{j_{m}}+1,\ldots ,T-T_{j_{m},\textit{down}}+1 \nonumber \\&\sum \limits _{i=t}^{T}\left( u_{t}^{j_{m}}-x_{t}^{j_{m}}\right) \ge 0\nonumber \\&\qquad \forall j_{m}, \forall t=T- T_{j_{m}, \textit{up}}+1,\ldots ,T \nonumber \\&\sum \limits _{i=t}^{T}\left( 1-u_{t}^{j_{m}}-y_{t}^{j_{m}}\right) \ge 0\nonumber \\&\qquad \forall j_{m}, \forall t=T- T_{j_{m}, \textit{down}}+2,\ldots ,T \nonumber \\&\sum \limits _{i=t}^{A_{j_{m}}}u_{t}^{j_{m}}= A_{j_{m}}\quad \forall j_{m}\nonumber \\&\sum \limits _{i=t}^{B_{j_{m}}}u_{t}^{j_{m}}= 0 \quad \forall j_{m}, \end{aligned}$$
    (17)

    where \(A_{j_{m}}={\hbox {min}}[T,U_{j_{m}}]\), \(B_{j_{m}}={\hbox {min}}[T,D_{j_{m}}]\), \(U_{j_{m}}\) and \(D_{j_{m}}\) are constants determined by the initial status of each unit. The reader may refer to [14] for the detailed explanation on this constraint.

  5. e.

    Unit ramp rate constraints

    $$\begin{aligned} -\textit{DR}_{j_{m}}\le G_{t}^{j_{m}}-G_{t-1}^{j_{m}}\le \textit{UR}_{j_{m}}, \end{aligned}$$
    (18)

    where \(\textit{DR}_{j_{m}}\) and \(\textit{UR}_{j_{m}}\) are positive values that measure the maximal downward and upward ramp rates of unit \(j_{m}\).

Economic load dispatch and gray zone state problems

The unit on/off state can be decided according to the above constraints. Then, the priority list [23] is generated to determine the exact output of each unit. This list is calculated on the average fuel cost (measured in $/MW) of each unit at its maximal output. Suppose \(\alpha _{j_{m}}\) is a priority index, then

$$\begin{aligned} \alpha _{j_{m}}=\frac{\textit{CT}_{j_{m}}(P_{j_{m}}^{\textit{max}})}{P_{j_{m}}^{\textit{max}}} = \frac{a_{j_{m}}}{P_{j_{m}}^{\textit{max}}}+b_{j_{m}}+c_{j_{m}}\cdot P_{j_{m}}^{\textit{max}}. \end{aligned}$$
(19)

The priority list is created according to the ascending order of \(\alpha _{j_{m}}\), in which a unit with the lowest \(\alpha _{j_{m}}\) holds the highest priority to be dispatched.

Another issue in UC could be the gray zone problem caused by the difference between cold and hot start-up costs (SC), the readers may refer to [19] for the detailed knowledge.

3.2 Lower level problem

The goal of an MO is to minimize the purchasing cost when guaranteeing the supply reliability. However, this object is usually hard to achieve as the future power loads normally cannot be exactly captured. In this study, we depict those uncertain loads as fuzzy variables and apply the following fuzzy VaR-based method to construct the lower level problem.

3.2.1 A fuzzy VaR-based unexpected load risk measurement

Suppose in a successfully operated system where no intrinsic emergency happens, \(\widetilde{L}_{t}\ (t=1,\ldots ,T)\) are fuzzy variables denote the forecasted loads of all period. Then, an MO will determine the total generation amount \(P_{t}\) of each period \(t\) and the exact generation task (\(P_{t}^{m}, m=1,\ldots ,M\)) to every GC, based on the future load \(\widetilde{L}_{t}\) and the bidding \(\textit{AP}_{t}^{m}\) submitted previously by each GC.

For a determined \(P_{t}\), the fuzzy variable describes the unexpected load of period \(t\) is calculated as:

$$\begin{aligned} \widetilde{\hbox {UL}}_{t}=\widetilde{L}_{t}-P_{t}, \quad \hbox {for}\, t=(1,\ldots ,T). \end{aligned}$$
(20)

Then, for a given confidence level of \(1-\beta \), we use fuzzy VaR to calculate the maximal power shortage of period \(t\) as:

$$\begin{aligned} \hbox {VaR}_{1-\beta }(\widetilde{\textit{UL}}_{t})=\hbox {sup}\{\lambda | \hbox {Cr}(\widetilde{\textit{UL}}_{t}\ge \lambda )\ge \beta \}. \end{aligned}$$
(21)

Normally, the generation cost of a thermal unit is taken for a quadratic function of the output, as shown in Eq. (13). Then, the marginal cost of unit \(j_{m}\) is obtained as

$$\begin{aligned}{}[\textit{CT}_{j_{m}}(G_{t}^{j_{m}})]'=b_{j_{m}}+2\cdot c_{j_{m}}\cdot G_{t}^{j_{m}}. \end{aligned}$$
(22)

Obviously, the marginal cost is linearly increasing to output \(G_{t}^{j_{m}}\) [24]. Therefore, when power shortage happens in period \(t\), the MO has to pay a higher unit price (\(\textit{HP}_{t}\)) than the bidding for those unexpected load. In this study, we first compute the marginal cost of each unit at the minimal output, then select the largest one as a base to obtain the \(\textit{HP}_{t}\).

$$\begin{aligned} \begin{array}{ll} \textit{HP}_{t}=k_{1}^{t}\cdot \max (b_{j_{m}}+2\cdot c_{j_{m}}\cdot P_{j_{m}}^{\textit{min}})+k_{2}^{t},\\ \quad (j_{m}=1,\ldots ,N_{m})\ \hbox {and} \ (m=1,\ldots ,M) \end{array} \end{aligned}$$
(23)

where \(k_{1}^{t}\) and \(k_{2}^{t}\) are coefficients with different values regard to different periods.

Based on the above analysis, we define the cost of the unexpected load risk as:

$$\begin{aligned} \textit{ULC}_{t}=\hbox {VaR}_{1-\beta }(\widetilde{\textit{UL}}_{t})\cdot \textit{HP}_{t}. \end{aligned}$$
(24)

Since the future loads are uncertain, for any \(P_{t}\in \widetilde{L}_{t}\) there exists possibility that the real power load is higher than \(P_{t}\). Then the above \({\hbox {VaR}}_{1-\beta }(\widetilde{\textit{UL}}_{t})\) can be viewed as a robust measurement of the maximal unexpected load of period t under confidence level \(1-\beta \).

3.2.2 Objective function of the lower level

We provide the following equation as the lower level objective function:

$$\begin{aligned} \min \limits _{P_{t}^{m}} f=\sum \limits _{m=1}^{M}\sum \limits _{t=1}^{T}P_{t}^{m}\cdot \textit{AP}_{t}^{m}+\alpha \cdot \sum \limits _{t=1}^{T}\hbox {VaR}_{1-\beta }(\widetilde{\textit{UL}}_{t})\cdot \textit{HP}_{t}. \end{aligned}$$
(25)

This function combines the power purchasing cost with the unexpected load risk, an MO then can minimize the cost via finding optimal \(P_{t}\) and \(P_{t}^{m}\) values for each scheduling period. In addition, \(\alpha \in [0,1]\) represents the risk attitude of an MO, and \(\textit{LB}_{t}\le P_{t} \le \textit{UB}_{t}\) for \(t=(1,\ldots ,T)\), i.e. any lower level decision should be made within these intervals.

3.2.3 Constraint caused by unit ramp rate

Equation (18) introduces the unit ramp rate constraints which influence the UC scheduling of the upper level problem. These constraints meanwhile, are also effects to the lower level decision, since an extreme changing of the generation amount between two contiguous periods may lead to infeasible UC planning or unexpected wear and tear of the units. Therefore, we use the following equation to handle the above problems, where \(\gamma _{m}\in (0, 1)\) are coefficients given by each GC after evaluating the intrinsic cost of generation unit wear.

$$\begin{aligned} -\gamma _{m}\cdot \sum \limits _{j_{m}=1}^{N_{m}}\textit{DR}_{j_{m}}\le P_{t+1}^{m}-P_{t}^{m}\le \gamma _{m}\cdot \sum \limits _{j_{m}=1}^{N_{m}}\textit{UR}_{j_{m}}. \end{aligned}$$
(26)

The above equation is essential to the bilevel electricity trading problem, however also changes the lower level optimization to be nonlinear.

3.3 Mathematical model of the UC-BETM

Based on the above knowledge, we introduce the mathematical model of the UC-BETM, as shown in Eq. (27).

The proposed model forms the electricity trading problem between the GCs and the MO as a bilevel programming. The UC optimization, the future load uncertainty as well as the unexpected load risk are addressed in this multi-leader one-follower model.

$$\begin{aligned} \left\{ \begin{aligned}&\hbox {for}\ m=1,\ldots ,M\\&\max \limits _{\textit{AP}_{t}^{m}} F_{m}=\sum \limits _{t=1}^{T}P_{t}^{m}\cdot \textit{UMCP}_{t}-F^{'}_{m}\\&\hbox {Subject to} \\&\qquad \sum \limits _{j_{m}=1}^{N_{m}}G_{t}^{j_{m}}\cdot u_{t}^{j_{m}}=P_{t}^{m}\\&\qquad \sum \limits _{j_{m}=1}^{N_{m}}P_{j_{m}}^{\textit{max}}\cdot u_{t}^{j_{m}}\ge P_{t}^{m}+R_{t}^{m}\\&\qquad P_{j_{m}}^{\textit{min}}\cdot u_{t}^{j_{m}} \le G_{t}^{j_{m}} \le P_{j_{m}}^{\textit{max}}\cdot u_{t}^{j_{m}}\\&\qquad -\textit{DR}_{j_{m}}\le G_{t}^{j_{m}}-P_{t-1}^{j_{m}}\le \textit{UR}_{j_{m}} \\&\qquad \textit{HP}_{t}=k_{1}^{t}\cdot \max (b_{j_{m}}+2\cdot c_{j_{m}}\cdot P_{j_{m}}^{\textit{min}})+k_{2}^{t}\\&\qquad k_{1}^{t}, k_{2}^{t}>0 \\&\qquad \textit{AP}_{t}^{m}\in (\textit{AP}_{t,-}^{m},\textit{HP}_{t}) \\&\mathrm{where} \ P_{t}^{m}\ \mathrm{solves}\ \\&\min \limits _{P_{t}^{m}} f=\sum \limits _{m=1}^{M}\sum \limits _{t=1}^{T}P_{t}^{m}\cdot \textit{AP}_{t}^{m}+\alpha \cdot \sum \limits _{t=1}^{T}{\hbox {VaR}}_{1-\beta }(\widetilde{UL}_{t})\cdot \textit{HP}_{t}\\&\hbox {Subject to} \\&\qquad -\gamma _{m}\cdot \sum \limits _{j_{m}=1}^{N_{m}}\textit{DR}_{j_{m}}\le P_{t+1}^{m}-P_{t}^{m}\le \gamma _{m}\cdot \sum \limits _{j_{m}=1}^{N_{m}}{ UR}_{j_{m}}\\&\qquad P_{t}^{m}+R_{t}^{m}\le P_{m}^{\textit{max}} \\&\qquad P_{t}=\sum \limits _{m=1}^{M} P_{t}^{m}\\&\qquad \textit{LB}_{t}\le P_{t} \le UB_{t}\\&\qquad 0\le \alpha ,\beta ,\gamma _{m}\le 1\\ \end{aligned} \right. \end{aligned}$$
(27)

3.4 A fuzzy maxmin-based convergence mechanism of the UC-BETM

As we know, the BP is always difficult to solve and there is no classical method for the proposed UC-BETM. Moreover, it is even hard to define the global optimal solution of the UC-BETM for two reasons: First, the upper level problem includes more than one decision-maker which makes it difficult to achieve an unified upper level solution. Second, the concept of the optimistic/pessimistic BP introduced in [7] cannot be employed directly to solve the problem due to the intrinsic conflict between the upper and lower levels. For example, if we use the global optimistic solution as the final decision, then the decision-making process will lead to the monopoly of the GCs, i.e. all of the GCs will increase their bidding more and more to obtain high profits. Conversely, the monopoly of the MO happens when we use global pessimistic solution principle. In real-life applications however, such monopolies are not realistic.

To overcome the above difficulties and direct the convergence of BP, [24] applied game theory to build the mathematical model and developed generalized Nash equilibrium-based solution. However, this type of approach has some drawbacks in real applications especially in the proposed UC-BETM: First, they define the Nash equilibrium solution as the choices from all the GCs are close enough to their corresponding rational reactions, which requires each GC knows the exact bidding of the others. In most applications however, it is difficult to achieve this object as they cannot have perfect information about each other’s decisions, and in a simplified but realistic case, the GCs only focus on personal profit. Second, the final solution in Nash equilibrium is mainly determined by the GCs themselves, as the MO can only dispatch the power based on the offered bidding. This is not consistent with the real application, since the electricity market structure is more akin to grid company oligopoly than perfect competition, due to special features of the electricity supply industry e.g. transmission monopoly which isolates consumers from the GCs. Therefore, the MO’s behavior such as cost control should be an affect on the final result. Third, even though the GCs will share information with each other, it is quite time-consuming to find the Nash equilibrium solution (basically, an additional heuristic algorithm is required, thus increase the computation time of the problem exponentially). Since the proposed model has been a BP with nonlinear upper and lower optimizations, it may not be reasonable to use game theory to solve a day-ahead UC-BETM problem.

On account of the above reasons, we apply a fuzzy maxmin approach [25], which only requires some straightforward assignments to the goal of each participant. Considering the GCs and the MO may have imprecise knowledge toward future trading such as the higher the better or the smaller the better, we use fuzzy variables and related membership functions to describe these goals and develop the following approach to solve the UC-BETM.

Step 1. Consider a MO’s decision \(P_{t}^{m}\) and the corresponding upper and lower level objective values are \(F_{m}\) and \(f\). Then, (\(P_{t}^{m}\), \(\textit{AP}_{t}^{m}\)) and (\(F_{m}, f\)) compose the possible solution set \(SS\) and the result set \(RS\).

Step 2. For the upper level problem, we assume each GC has an individual target profit (\(\widetilde{E}_{m}\)) towards future trading, denoted as a fuzzy variable with the following membership function:

(28)

where \(E_{m}^{l}\) means the lowest expected return that GC \(m\) can accept and \(E_{m}^{h}\) is the satisfied return. Obviously, for each upper level participant, it is expected that \(F_{m}\) maximizes \(\mu _{\widetilde{E}_{m}}(F_{m})\).

Step 3. For the lower level problem, the MO has a reservation budget \(\textit{RB}\) and an expected payment \(\textit{EP}\) of the trading, where these two values can be exactly estimated as the electricity market price is open and accurate. Then, we define the local feasible solutions of the UC-BETM as:

$$\begin{aligned} (P_{t}^{m}, \textit{AP}_{t}^{m})\in \textit{FS},\quad {\hbox {iff}}\ f\le \textit{RB}, \end{aligned}$$
(29)

where \(\textit{FS}\) is an aggregation of the local feasible solutions.

Moreover, we use fuzzy variable \(\widetilde{\textit{LC}}\) to measure the membership degree of each solution to the lower level goal:

$$\begin{aligned} \mu _{\widetilde{LC}}(f)=\left\{ \begin{array}{l@{\quad }l} 1, &{} f< \textit{EP}\\ (\textit{RB}-f)/(\textit{RB}-\textit{EP}), &{}\textit{EP} \le f\le \textit{RB}\\ \end{array} \right. \end{aligned}$$
(30)

Step 4. For each local feasible solution, we calculate \(\mu _{\widetilde{E}_{m}}(F_{m})\) and \(\mu _{\widetilde{\textit{LC}}}(f)\) by using Eqs. (28) and (30), then obtain a unified membership degree as \(\min _{m=1,\ldots ,M} \mu _{\widetilde{E}_{m}}(F_{m})\wedge \mu _{\widetilde{\textit{LC}}}(f)\).

Step 5. Finally, the global optimal solution \(GS\) of the UC-BETM is defined as the element in \(\textit{FS}\) that maximizes the unified membership degree as:

$$\begin{aligned} GS\longrightarrow \max \ \min \limits _{m=1,\ldots ,M} \mu _{\widetilde{E}_{m}}(F_{m})\wedge \mu _{\widetilde{LC}}(f). \end{aligned}$$
(31)

The above method is easier to be realized than conventional approaches and it can prevent the monopoly problems from occurring in the optimization process. Additionally, the MO’s cost control behavior is also addressed.

4 Solution method

Based on the above knowledge, we develop a bilevel PSO algorithm to solve the UC-BETM, named B-PSO.

The PSO algorithm was introduced by Kennedy et al. [11] in 1995. Suppose that \(S\) particles search in a \(K\)-dimensional space for \(\textit{IT}\) iterations, the position of particle \(s\) is denoted as \({\hbox {Pi}}_{s}=({\hbox {Pi}}_{s, 1},\ldots , {\hbox {Pi}}_{s, k},\ldots ,{\hbox {Pi}}_{s, K})\), \((s=1,2,\ldots ,S\ {\hbox {and}}\ k=1,2,\ldots ,K)\), then the velocity and position of each particle are updated as follows:

$$\begin{aligned} v_{s,k}= & {} w\cdot v_{s,k}+c1\cdot \textit{Rand}\cdot (\hbox {Pbest}_{s,k}-\hbox {Pi}_{s,k})\nonumber \\&+\, c2\cdot \textit{Rand}\cdot (\hbox {Gbest}_{t,k}-\hbox {Pi}_{s,k}), \end{aligned}$$
(32)
$$\begin{aligned}&\hbox {Pi}_{s, k}\leftarrow \hbox {Pi}_{s, k}+v_{s,k}. \end{aligned}$$
(33)

where \(v_{s,k}\) is the velocity of particle \(s\) at dimension \(k\) with an upper bound Vmax and a lower bound Vmin, \(w\) is an inertia weight, \(c1\) and \(c2\) are the learning rates, \(Rand\) is a randomly generated value in (0,1), \({\hbox {Pbest}}_{s,k}\) is the personal best which means the best position of particle \(s\) itself in the past iterations, and \({\hbox {Gbest}}_{t,k}\) is the global best which denotes the best position of all particles after \(t\) iterations. Recently, the PSO algorithm has been applied to solve the UC optimization problems [18, 19].

The UC-BETM proposed in this study contains two related optimization processes: The upper level problem includes a bidding optimization and a series of mix-integer nonlinear UC problems to maximize the profit of each GC, while the lower level determines the total generation amount and each GC’s involvement. Hence, to solve the proposed model, a B-PSO employs different particle swarms in the upper and lower levels is designed, in which the parameters, such as the maximal/minimal velocity, the inertia weight and the iteration number are assigned independently to each swarm. In contrast to the algorithm developed in [19], the B-PSO is in a bilevel structure and it solves not only the conventional UC, but also the market trading problem. We summarize the B-PSO as follows:

Step 1. Initialize particle swarm \(\Lambda \), where each particle includes \(T*M\) randomly generated values \(\textit{AP}_{t}^{m}\) in \((\textit{AP}_{t,-}^{m},\textit{HP}_{t})\), denotes the initial bidding of all GCs over the scheduling horizon:

$$\begin{aligned} \Lambda \rightarrow \left[ \begin{array}{l} \textit{AP}_{1}^{1}\ \textit{AP}_{1}^{2}\ \cdot \cdot \cdot \cdot \cdot \textit{AP}_{1}^{M}\\ \textit{AP}_{2}^{1}\ \textit{AP}_{2}^{2}\ \cdot \cdot \cdot \cdot \cdot \textit{AP}_{2}^{M}\\ \cdot \cdot \cdot \cdot \cdot \cdot \ \ \ \ \ \textit{AP}_{t}^{m} \ \ \ \cdot \cdot \cdot \cdot \\ \textit{AP}_{T}^{1}\ \textit{AP}_{T}^{2}\ \cdot \cdot \cdot \cdot \cdot \textit{AP}_{T}^{M}\\ \end{array} \right] . \end{aligned}$$
(34)

Step 2. Optimize the lower level problem based on each particle in \(\Lambda \), detailed as follows:

Step 2.1. Initialize particle swarm \(\mathcal {A}\): the \(s\)th particle \({\hbox {Pi}}_{\mathcal {A}}^{s}\) has \(T*M\) randomly generated nonnegative values \(P_{t}^{m}\).

$$\begin{aligned} {\hbox {Pi}}_{\mathcal {A}}^{s} \rightarrow \left[ \begin{array}{l} P_{1}^{1}\ P_{1}^{2}\ \cdot \cdot \cdot \cdot \cdot P_{1}^{M}\\ P_{2}^{1}\ P_{2}^{2}\ \cdot \cdot \cdot \cdot \cdot P_{2}^{M}\\ \cdot \cdot \cdot \cdot \ \ \ \ \ P_{t}^{m} \ \ \ \cdot \cdot \cdot \\ P_{T}^{1}\ P_{T}^{2}\ \cdot \cdot \cdot \cdot \cdot P_{T}^{M}\\ \end{array} \right] . \end{aligned}$$
(35)

Step 2.2. Each \({\hbox {Pi}}_{\mathcal {A}}^{s}\) must satisfy the following constraints:

  1. a.

    The power dispatch to each GC should not exceed its generation capacity. Check each \(P_{t}^{m}\) in \({\hbox {Pi}}_{\mathcal {A}}^{s}\), if \(P_{t}^{m}+R_{t}^{m}\ge P_{m}^{max}\), order \(P_{t}^{m}=P_{m}^{max}/1.1\) (suppose that \(R_{t}^{m}\) equals \(0.1\cdot R_{t}^{m}\)) and revise matrix \({\hbox {Pi}}_{\mathcal {A}}^{s}\).

  2. b.

    For each t, \(LB_{t}\le \sum _{m=1}^{M}P_{t}^{m}\le UB_{t}\).

Calculate \(\sum _{m=1}^{M}P_{t}^{m}\), if there is a violation, for example \(\sum _{m=1}^{M}P_{t}^{m}<\textit{LB}_{t}\), we first compute their difference as

$$\begin{aligned} \varDelta _{1} =\textit{LB}_{t}-\sum \limits _{m=1}^{M}P_{t}^{m}. \end{aligned}$$
(36)

Then, select a GC randomly and calculate

$$\begin{aligned} \varDelta _{2}=P_{m}^{\textit{max}}-P_{t}^{m}. \end{aligned}$$
(37)

If \(\varDelta _{2}>0\) and \(\varDelta _{2}<\varDelta _{1}\), then

$$\begin{aligned} \begin{array}{ll} \textit{temp}=\textit{Rand}\cdot \varDelta _{2}\\ P_{t}^{m}=P_{t}^{m}+\textit{temp}\\ \varDelta _{1}=\varDelta _{1}-\textit{temp}, \end{array} \end{aligned}$$
(38)

where \(\textit{temp}\) is a temporary variable.

If \(\varDelta _{2}>0\) and \(\varDelta _{2}\ge \varDelta _{1}\), then

$$\begin{aligned} \begin{array}{ll} P_{t}^{m}=P_{t}^{m}+\varDelta _{1}\\ \varDelta _{1}=0. \end{array} \end{aligned}$$
(39)

Repeat the above process until \(\varDelta _{1}=0\). Similar approach can be developed as well to revise \({\hbox {Pi}}_{\mathcal {A}}^{s}\) when \(\sum _{m=1}^{M}P_{t}^{m}> UB_{t}\).

  1. c.

    For each t and GC \(m\), \(-\gamma _{m}\cdot \sum _{j_{m}=1}^{N_{m}}\textit{DR}_{j_{m}}\le P_{t+1}^{m}-P_{t}^{m}\le \gamma _{m}\cdot \sum _{j_{m}=1}^{N_{m}}\textit{UR}_{j_{m}}\).

For a specified GC \(m^{*}\), calculate the generation amount variation of each \(t\ (t>1)\).

$$\begin{aligned} \varDelta _{3}=P_{t}^{m^{*}}-P_{t-1}^{m^{*}}. \end{aligned}$$
(40)

If \(\varDelta _{3}<-\gamma _{m^{*}}\cdot \sum _{j_{m^{*}}=1}^{N_{m^{*}}}\textit{DR}_{j_{m^{*}}}\), calculate

$$\begin{aligned} \varDelta _{4}=-\gamma _{m^{*}}\cdot \sum \limits _{j_{m^{*}}=1}^{N_{m^{*}}}\textit{DR}_{j_{m^{*}}}-\varDelta _{3}. \end{aligned}$$
(41)

Then, randomly generate \(m\) (\(m\le M\), \(m\ne m^{*}\)) and compute

$$\begin{aligned} \varDelta _{5}=P_{t}^{m}-P_{t-1}^{m}+\gamma _{m}\cdot \sum \limits _{j_{m}=1}^{N_{m}}\textit{DR}_{j_{m}}. \end{aligned}$$
(42)

If \(\varDelta _{5}>0\) and \(\varDelta _{5}<\varDelta _{4}\),

$$\begin{aligned} \begin{aligned} \textit{temp}&=\textit{Rand}\cdot \varDelta _{5}\\ P_{t}^{m^{*}}&=P_{t}^{m^{*}}+\textit{temp}\\ P_{t}^{m}&=P_{t}^{m}-\textit{temp}\\ \varDelta _{4}&=\varDelta _{4}-\textit{temp}. \end{aligned} \end{aligned}$$
(43)

If \(\varDelta _{5}>0\) and \(\varDelta _{5}\ge \varDelta _{4}\),

$$\begin{aligned} \begin{aligned} P_{t}^{m^{*}}&=P_{t}^{m^{*}}+\varDelta _{4}\\ P_{t}^{m}&=P_{t}^{m}-\varDelta _{4}\\ \varDelta _{4}&=0. \end{aligned} \end{aligned}$$
(44)

Repeat the above process until \(\varDelta _{4}=0\). Similar approach can be developed to handle \(\varDelta _{3}> \gamma _{m^{*}}\cdot \sum _{j_{m^{*}}=1}^{N_{m^{*}}}\textit{UR}_{j_{m^{*}}}\).

Step 2.3. For each \({\hbox {Pi}}_{\mathcal {A}}^{s}\), calculate the lower level objective value based on fuzzy VaR and \(\Lambda \).

Step 2.4. For each particle in swarm \(\mathcal {A}\), repeat Steps 2.2–2.3 to obtain different lower level responses and the corresponding objective values.

Step 2.5. Initialize personal best and global best of swarm \(\mathcal {A}\): The personal best and global best of each particle \(P_{\mathcal {A}}\) are determined by the lower level objective function \(f\). Then, we update the position of each particle in swarm \(\mathcal {A}\) using Eqs. (32) and (33).

Step 2.6. Repeat Steps 2.2–2.5 until all the iterations of swarm \(\mathcal {A}\) are accomplished. Among the iterations, the escape speed and particle restart position techniques [20] are employed to mitigate the local convergence problem. Finally, we can obtain the lower level optimal value \(f\) and related decision on \(P_{t}^{m}\) regards to the bidding matrix \(\Lambda \).

Step 3. Return the optimal \(P_{t}^{m}\) to the upper level, then solve the UC optimization to maximize the profit of each GC. This step is similar to the solution developed in our previous study [19], except that the ramp rate constraint is also considered in this research. Therefore, in what follows, we only provide the ramp rate realization method, the readers may refer to [19] for other knowledge of this step.

The ramp rate constraints actually represent the maximal increment or decrement of the output of unit \(j_{m}\) in a unit time (usually 1 h). Then, the following approach is used to avoid any illegal output variation:

Step 3.1. Set \(t=1\), find the committed units of period 1, and check the output of these unit \(j_{m}\) at the initial states (\(t=0\)).

Step 3.2. Each of the committed unit are first assigned to a minimal output as \(G_{t}^{j_{m}}={\hbox {max}}[G_{t-1}^{j_{m}}-\textit{DR}_{jm},\ P_{j_{m}}^{min}]\).

Step 3.3. Calculate \(\varDelta =P_{t}^{m}-\sum _{j_{m}}^{N_{m}}G_{t}^{j_{m}}\cdot u_{t}^{j_{m}}\).

Step 3.4. Then, we use the priority list-based method to disperse the \(\varDelta \) value to each committed unit, while the largest output of unit \(j_{m}\) is \({\hbox {min}}[G_{t-1}^{j_{m}}+\textit{UR}_{jm},\ P_{j_{m}}^{max}]\).

Step 3.5. Repeat the above process until \(t=T\).

Step 4. Execute Step 3 for \(M\) times to obtain the optimal schedules and profit \(F_{m}\ (m=0,\ldots ,M)\) of all the GCs.

Step 5. The bidding matrix \(\Lambda \) and the lower level response \(P_{t}^{m}\) (determined in Step 2) can be taken as a feasible solution of the UC-BETM if \(f\le RB\). Then, we record this solution in \(\textit{FS}\) and calculate \(\min \limits _{m=1,\ldots ,M} \mu _{\widetilde{E}_{m}}(F_{m})\wedge \mu _{\widetilde{\textit{LC}}}(f)\) as the fitness value.

Step 6. Use PSO strategy again, we revise each particle in \(\Lambda \), thus construct a swarm of new bidding matrix.

Step 7. Repeat Steps 1–6 for a given iterations \(\textit{IT}\), and record all the feasible solutions and related fitness values in \(\textit{FS}\).

Step 8. For each member in \(\textit{FS}\), we compare the fitness value and select the one with the highest unified membership degree as the global optimal solution of the UC-BETM.

5 Computational experience

The performance of this study is illustrated by using a test system-based three-GC one-MO day-ahead electricity trading problem.

5.1 Problem description

We first introduce the test system data of each GC based on [10]. Table 1 lists the detailed attributes of 10 generation units, which forms the base of the upper level UC problems. Suppose each upper level GC has 8 different units among Table 1, e.g. GC 1 holds units 1–4, 6–7, 9–10.

In the lower level problem, the future load of each period is described as triangular or trapezoidal fuzzy variable, as these distributions are frequently used and can simulate lots of uncertainties. Of course, variables with Gaussian distribution or some other irregular distributions can be applied as well to describe the future load in different environment. For the sake of convenience in computation, we assume the future loads as deviations on the exact data provided in [10, 23], as listed in Table 2 below, where \((x,\ y,\ z)\) denotes a triangular fuzzy variable, \((x,\ y_{l},\ y_{r},\ z)\) represents a trapezoidal fuzzy variable, and the spinning reserve \(R_{t}^{m}\) equals \(0.1\cdot P_{t}^{m}\).

Table 1 Attributes of the generation units in GCs
Full size table
Table 2 Day-ahead forecasted loads \(\widetilde{L}_{t}\) (MW) of the supply system
Full size table

Other parameter settings, such as the target profit \(\widetilde{E}_{m}\), the empirical lower bound \(\textit{AP}_{t,-}^{m}\) and the reservation budget RB are listed in Table 3.

Table 3 Parameter settings of the UC-BETM
Full size table

5.2 Experimental results

The fuzzy maxmin-based B-PSO is applied to solve the UC-BETM, where all of the experiments were implemented with C code on a Dell 3.40-GHz CPU personal computer. Table 4 gives the parameter settings of the B-PSO and the iteration times \(\textit{IT}\) (introduced in Step 7) is assigned as 600 while the particle number of swarm \(\Lambda \) is 20. Then, the following Table 5 provides the global optimal solution of this problem which includes the profit of each GC, the payment of the MO and the maximal unified membership degree. Table 6 lists the final bidding and the MO’s decision on power dispatch. This solution satisfies every participant most in the proposed electricity trading problem.

Table 4 Parameter settings of the B-PSO
Full size table
Table 5 Global optimal solution of the UC-BETM ($)
Full size table
Table 6 Market operator’s decision on \(P_{t}^{m}\) (MW) and the final bidding of generation companies ($/MW)
Full size table

5.3 Discussions on the experiment results

Based on the above experimental results, we provide the following discussions to illustrate the effectiveness of the UC optimization and the fuzzy maxmin-based algorithm.

1. In this study, the global optima of the UC-BETM is defined as the solution in \(\textit{FS}\) that maximizes the unified membership degree. Then, Table 7 lists some of the local feasible solutions obtained by B-PSO, where No. 1 is the global optima.

Table 7 Some local feasible solutions of the UC-BETM ($)
Full size table

Comparing the global optima with solutions No. 2 and 3, we find that higher MO payment does not mean higher profit of each GC, e.g. the total/individual profit of all GCs of No. 1 are higher than the others, even though its payment is the lowest. The reason lies in the differences of the power dispatch \(P_{t}^{m}\) to each GC: A small increment (decrement) of the \(P_{t}^{m}\) alters the GC’s revenue little, but may lead to a different UC scheduling, e.g. a de-committed(committed) unit need to be committed (de-committed), thus increases (decreases) the generation cost by a relative high value. Then, an optimal power dispatch will lead to not only a lower MO payment but also proper UC scheduling of all GCs, thus increases their profits. Nevertheless, such conclusion cannot be achieved if we only use some approximate calculations of the generation cost. Therefore, we can say that, it is essential to include the UC optimization in electricity trading problem and the MO’s decision on \(P_{t}^{m}\) is significant to be investigated.

In view of No. 4–7, these solutions provide either higher profit of some GC or lower MO payment than that of No. 1. However, in this study, we only search for the solution that satisfies all participants most when the MO’s payment is lower than the reservation budget.

2. To test the performance of the B-PSO, we set \(\textit{IT}=1500\) and 5 trials were carried out. Figure 1 depicts the optimal results to different iteration times (also different runtime costs) of each trial, while Table 8 analyzes their average value and standard deviation.

In the case of trial 1, a total of 13,642 local feasible solutions were found, while the largest fitness value is 0.728. According to the knowledge provided in Fig. 1 and Table 8, we can conclude that the B-PSO is robust to different trials as the deviations of the final optima are small, and 600 is the most suitable iteration times for our problem while the related runtime cost is also appropriate for solving a day-ahead UC-BETM problem.

Fig. 1
figure 1

Optimal result to different iteration and runtime cost of 5 trials

Full size image
Table 8 Average value and standard deviation of 5 trials ($)
Full size table

5.4 Social welfare maximization

In this part, we analyze the above solutions from social welfare perspective [6]. The inherence relationship between the unified membership degree and social welfare is illustrated below.

If we only consider the electricity trading between GCs and MO (no power consumers), social welfare can be measured from two aspects: one is the total profit of all participants in the trading (SW-P), in this case GCs and MO; another is the cost of the commodity (SW-C), i.e. the negative value of all money paid for the power generation. Then, we use the summation of all GCs’ profits minus the MO’s payment \(\sum \nolimits _{m=1}^{M}F_{m}-f\) as the measurement from the first aspect and the total generation cost of the GCs \(\sum \nolimits _{m=1}^{M}F_{m}^{'}\) as an estimation from another perspective. Figures 2 and 3 show their relationship with the unified membership degree reflected by all of the solutions in \(\textit{FS}\), where the point in asterisk is the global optima.

Fig. 2
figure 2

Social welfare and unified membership degree: SW-P

Full size image
Fig. 3
figure 3

Social welfare and unified membership degree: SW-C

Full size image

From Fig. 2, we can find that the growth of \(\sum \nolimits _{m=1}^{M}F_{m}-f\) basically keep identical with the increasing of the unified membership degree, which means that the B-PSO guides the bidding and the power dispatch toward social welfare maximization. Figure 3 shows that the increasing of the unified membership degree generally results in the decreasing of \(\sum \nolimits _{m=1}^{M}F_{m}^{\prime }\), which also proves the effectiveness of the UC: the power dispatch optimized during the iteration process becomes more and more proper for all GCs to generate nearly the same quality of electricity at a relatively low cost, thus reduce social resource waste.

However, it is also noticed that, a global optima that satisfies all the participants most does not with the highest social welfare, as reflected by the dash line in these figures. Ideally, the structure and management mechanisms or rules in an electricity market could be sufficiently well designed to direct the operation towards social welfare maximization. Nevertheless, as explained before, the electricity market structure is more akin to oligopoly and most of the participants are profit-push, which hamper the realization of the above objective. Based on the knowledge revealed in Figs. 2 and 3, we suggest that a trading which balances the satisfaction of each participant and social welfare, for example the one with maximal social welfare when the unified membership degree is larger than a predefined value, can be selected as the final decision.

5.5 Comparisons with conventional methods

The main contribution of this study exists in the application of fuzzy set theory to describe the load uncertainty, measure the unexpected load risk and develop the fuzzy maxmin-based algorithm. Therefore, in this portion, we compare the performance of the UC-BETM as well as the B-PSO with conventional methods.

From future load uncertainty perspective: Existing studies [2, 24] ignore the UC optimization and most of the traditional UC problems are solved based on exact future demands [10, 23], which are considered to be a special decision made on the interval data provided in Table 2. Therefore, we first compare the experimental result of the crisp load-based method, i.e. the expected value of the fuzzy variables, with the global optima of the UC-BETM. From solution algorithm perspective: As we mentioned, a generalized Nash equilibrium-based solution algorithm [24] was developed to solve such problem. Therefore, we also discuss about the experimental results as well as the runtime cost of the B-PSO with the existing algorithm, where the swarm used to find the rational reaction in [24] is considered as 10 particles with 100 iterations. We conducted 5 trials for each method and the best results after 600 iterations are listed in Table 9 while the same type of parameters are set as uniform values in each algorithm.

Table 9 Comparisons with conventional method ($)
Full size table

Table 9 shows that the solution of the proposed UC-BETM dominates that of the crisp load-based model, as the profits, the cost as well as the social welfare are better. For example, from social welfare aspect, the total profit is increased by 3.07 % while the generation cost of all GCs is decreased by 3.58 %. Therefore, it can be proven that the operation on load uncertainty is of important to the electricity trading problems. When comparing the B-PSO with the Nash equilibrium-based algorithm, we find that both of the two approaches lead to profit maximization of each GC while minimizing the MO’s payment. However, the solution of B-PSO shows advantages in most of the evaluations, especially the payment and the social welfare. More importantly, the runtime cost of the latter one is quite huge (almost 50 times of the B-PSO), which makes it infeasible to solve a day-ahead UC-BETM problem. Therefore, it can be concluded that the fuzzy maxmin-based B-PSO is better than the existing method when solving this complicated optimization.

We also noticed that, there have been a number of studies applied stochastic theory to address the load uncertainty, whereas none of them focus on our topic due to the inherent complexity of the bilevel model itself. Therefore, in this research, we only compare the UC-BETM with the crisp load-based method. However, our future work may work on the stochastic model and investigate its difference from the UC-BETM.

6 Conclusions

This study introduced a unit commitment-based bilevel electricity trading model. Experimental and comparison results show that the UC is essential when calculating the generation cost of a series of collaborated units, and fuzzy set theory is effective to address the imprecise knowledge and develop the algorithm. We also prove that a trading better satisfies all participants basically leads to higher social welfare. Moreover, the using of fuzzy value-at-risk to measure the supply reliability and the construction of the bilevel model provide researchers and market operators with effective approaches when analyzing the electricity trading problems in real industry. However, due to the complexity of the optimization problem and the high runtime cost of the algorithm, the parameter settings of the B-PSO were not sufficiently analyzed in this paper. Our future work will focus on the application of some tuning process to derive well-working parameters, when the solution algorithm can be implemented within a reasonable period of time..