Comparison of optimal buffer allocation in flow lines under installation buffer, echelon buffer, and CONWIP policies

Abstract

We compare the optimal buffer allocation of a manufacturing flow line operating under three different production control policies: installation buffer (IB), echelon buffer (EB), and CONWIP (CW). IB is the conventional policy where each machine may store the parts that it produces only in its immediate downstream buffer if the next machine is occupied. EB is a more flexible policy where each machine may store the parts that it produces in any of its downstream buffers. CW is a special case of EB where the capacities of all buffers, except the last one, are zero. The optimization problem that we consider is to maximize the average gross profit (AGP) minus the average cost (AC), subject to a minimum average throughput constraint. AGP is defined as the average throughput of the line weighted by the gross marginal profit (selling price minus production cost per part), and AC is the sum of the average WIP plus total buffer capacity plus transfer rate of parts to remote buffers, weighted by the inventory holding cost rate, the cost of storage space, and the marginal cost of transferring parts to remote buffers, respectively. Numerical results show that the optimal EB policy generally outperforms the optimal IB and CW policies. They also show that as the production rates of the machines decrease, the relative advantage in performance of the EB policy over the other two policies increases. When the cost of transferring parts to remote buffers increases, the dominance of the EB policy over the IB policy decreases while the dominance of the EB policy over CW increases.

1 Introduction

The most common type of manufacturing system used in mass-production is the flow line. A flow line consists of machines in series that are visited sequentially by all parts. Often, the unpredictable variation in the processing times of the parts causes congestion and adversely affects the efficiency of the line. One of the ways of improving efficiency is to provide buffer space between the machines. With such space, if a machine stops, then the other machines can continue working undisturbed; without buffers, every machine is forced to work at the rate of the slowest machine.

Because buffers are expensive and occupy valuable space, it is important to use them as efficiently as possible. Recently, Liberopoulos (2018) considered a production control policy aimed at increasing the utilization of buffers by allowing each machine to store the parts that it produces in any of its downstream buffers, if the next machine is occupied. He referred to the ensemble of all the downstream buffers and the next machine as echelon buffer and to the resulting policy as echelon buffer (EB) policy. Under the EB policy, the buffers can contain parts that are in different stages of completion. In this case, it is not possible to evaluate the total buffer inventory in common units and to have a single unit cost for each buffer. Moreover, a machine is blocked from processing a part if the number of parts that have been processed by it but have not yet departed from the line is equal to the capacity of the echelon buffer following the machine. This means that the release of parts in each production stage is based on global information. If the capacity of each buffer except possibly the last one is zero, the EB policy is equivalent to CONWIP (henceforth, CW), as is explained in Liberopoulos (2018).

Liberopoulos (2018) juxtaposed the EB policy with the conventional production control policy in which each machine may store the parts that it produces only in its immediate downstream buffer if the next machine is unavailable. He referred to the ensemble of that buffer and the space in the next machine as installation buffer, and to the resulting policy as installation buffer (IB) policy. Under the IB policy, a machine is blocked from processing a part if the installation buffer downstream of it is full. In this case, the release of parts in each stage is based on local information.

Clearly, the utilization of buffer space under the EB policy is higher than it is under the IB policy. Consequently, the EB policy is expected to yield higher average throughput—at the cost of higher average WIP—than the IB policy. Moreover, the EB policy is expected to incur an additional transfer cost for storing parts to remote downstream buffers. Numerical results in Liberopoulos (2018) confirm these expectations. The question that we address in this paper is whether the benefit of the throughput increase under the EB policy outweighs the disadvantage of the WIP increase and transfer cost, also considering that a smaller total buffer space is needed under EB than under IB to achieve the same throughput level.

To answer this question, we consider a constrained optimization problem whose objective is to determine the optimal buffer sizes to maximize the average net profit (ANP) of the line subject to a minimum average throughput constraint, under any production control policy. ANP is defined as the average gross profit (AGP) minus the average cost (AC), where AGP is the average throughput of the line weighted by the gross marginal profit (selling price minus production cost per part), and AC is the sum of the average WIP plus total buffer capacity plus transfer rate of parts to remote buffers, weighted by the inventory holding cost rate, the cost of storage space, and the marginal cost of transferring parts to remote buffers, respectively.

We numerically solve the constrained optimization problem for numerous instances of a 20-machine and an 8-machine line operating under the IB, EB, and CW policies. In all instances, we adopt the Bernoulli reliability model for the machines, i.e., we assume that the machines have geometrically distributed processing times. The Bernoulli reliability model leads to a simpler mathematical description than other models and is adequate for production systems where the downtime is short and comparable with the cycle time. The Bernoulli machine model has been successfully applied in many manufacturing system studies (e.g., Diamantidis and Papadopoulos 2004; Li and Meerkov 2000; Meerkov and Zhang 2008, 2011; Biller et al. 2009). The instances that we investigate differ in the production rates of the machines and the parameters of the constrained optimization problem. For the 20-machine line, these parameters are chosen randomly within a reasonable range. For the 8-machine line, they are chosen in a systematic way for sensitivity analysis.

To find the optimal buffer allocation for each instance under each policy, we use a two-phase optimization algorithm. Phase 1 is an adaptation of the two-step Lagrangean relaxation-type gradient algorithm presented in Shi and Gershwin (2009). Phase 2 is a simple neighborhood search that aims to improve the allocation obtained in phase 1 by adding, subtracting, or transferring a unit of storage capacity to one buffer at a time, on a trial basis. It only applies to the IB and EB policies where multiple buffer capacities must be optimized. Recall that in CW, only the capacity of the last buffer is optimized.

For each of the considered policies, the performance of the line for given buffer sizes is evaluated using an approximation method that is based on decomposing the original multiple-machine line into many 2-machine 1-buffer elementary lines that can be analyzed in isolation. The buffer in each elementary line represents one of the buffers in the original line, and the upstream and downstream machines represent in an aggregate way the segments of the original line that are upstream and downstream of that buffer. The parameters of these two machines are determined by relationships among the flows of parts through the buffers in the original line. The idea is to set these parameters so that the behavior of the buffer in each elementary line mimics as closely as possible the behavior of the buffer that it represents in the original line.

For the IB policy, we use a decomposition-based approximation method that is conceptually similar to the algorithm developed in Li and Meerkov (2009) for the Bernoulli machine case but is more elaborate than that algorithm as far as the modeling of the machines of the elementary lines is concerned. For the EB and CW policies, we employ the decomposition-based approximation method developed and specialized for the Bernoulli reliability model in Liberopoulos (2018). Using these methods, various performance measures of the line can be evaluated. The measures that are of interest for the purposes of the optimization are the average throughput, the average WIP levels at each processing stage, and the average transfer rate of parts to remote buffers.

The main question that we try to answer in this paper is not whether the performance evaluation and optimization algorithms that we used are good or better than other algorithms, but whether the optimal EB policy outperforms the optimal IB and CW policies under different problem scenarios. The contribution of this paper, therefore, lies mainly in setting up the numerical study for the comparison of the three policies, carrying it out and obtaining and discussing the results, and to a much lesser extent in assessing the efficiency of the algorithms used to obtain the results.

The remainder of this paper is organized as follows. In Sect. 2, we review the related literature on the buffer allocation problem and on the comparison of different production policies. In Sect. 3, we describe the IB, EB, and CW policies. In Sect. 4, we give the formulation of the constrained optimization problem under consideration, and in Sect. 5, we present the algorithm that we use to solve it. In Sect. 6, we present the numerical results. First, we describe the setup of the numerical experiments that we run to compare the optimal IB, EB, and CW policies. Then, in Sect. 6.1, we present the results on the comparison of the optimal IB, EB, and CW policies, for a 20-machine line with randomly chosen input parameters. In Sect. 6.2, we present more results on the comparison of the optimal IB, EB, and CW policies, for an 8-machine line with systematically chosen input parameters for sensitivity analysis. Finally, we conclude in Sect. 7.

2 Literature review

The role of intermediate storage buffers in mitigating the adverse effect of process time variability on the efficiency of manufacturing flow lines has been researched for over five decades. Most of the issues that have been studied throughout these years fall into one of three areas: (1) modeling, (2) performance evaluation, and (3) optimization. A review of the first two areas can be found in Liberopoulos (2018) and references therein. Below, we briefly review the area of optimization.

One of the most widely researched problems in flow line optimization is the buffer allocation problem (BAP). BAP deals with allocating storage capacity to intermediate storage buffers to meet a given criterion under given constraints. In a recent survey on this topic, Demir et al. (2014) identified three main BAP variants. In one variant, which is often referred to as primal BAP in the literature, the goal is to minimize the total buffer size to achieve a given desired average throughput. In another variant, which is often referred to as dual BAP, the goal is to maximize the average system throughput for a given fixed total buffer size. In the third variant, the goal is to minimize the average system WIP subject to total buffer size and average throughput constraints. A more recent review of the BAP can be found in Weiss et al. (2018). According to Tempelmeier (2003), who raised important practical considerations in the optimization of flow production systems, planners normally treat average throughput as a datum and therefore usually consider the primal BAP variant.

Relatively recently, Shi and Gershwin (2009) considered an extension of the primal BAP whose objective is to maximize the average profit of the line subject to a given minimum average throughput constraint. The average profit is defined as the weighted average throughput of the system minus the sum of the weighted average WIP plus total buffer capacity. In this paper, we consider this variant except that we also include the weighted average transfer rate of parts to remote buffers as an additional cost term in the objective function. The resulting constrained problem is quite general and includes as special cases the unconstrained problem, when the minimum average throughput is zero, and the primal BAP, when the weights of the average throughput and the total buffer capacity in the objective function are zero. Note that the unconstrained problem has been studied for over 30 years (e.g., Kramer and Love 1970; Smith and Daskalaki 1988; Altiok 1997).

Demir et al. (2014) and Shi and Gershwin (2014) also categorized the BAP literature based on the search and performance evaluation techniques used. The search techniques include analytical methods (e.g., Enginarlar et al. 2005), DP (e.g., Diamantidis and Papadopoulos 2004), heuristics (e.g., Tempelmeier 2003) and meta-heuristics (e.g., Spinellis et al. 2000), among others. In this paper, we employ an adaptation of the NLP gradient search technique that was used in Shi and Gershwin (2009). Previous works that also use gradient search for optimization and decomposition for performance evaluation include Gershwin and Schor (2000), Levantesi et al. (2001), and Helber (2001).

To date, performance evaluation and parameter optimization have been studied as separate problems for the most part. One exception is a recent stream of research that uses mathematical programming approaches for the simultaneous simulation and optimization of discrete event dynamic systems, based on the seminal work of Chan and Schruben (2008) (e.g., Helber et al. 2011; Alfieri and Matta 2012, 2013; Weiss and Stolletz 2015; Tan 2015).

As we wrote in the introduction, this paper is about comparing the optimal performance of three policies for operating flow lines. Most of the literature on the comparison of different production control policies has focused on systems where production is driven by demand for finished goods. Such systems are often referred to as pull systems. The two pull control policies that have appeared most frequently in such comparisons are kanban and CW. A kanban-controlled line is often viewed as being equivalent to a flow line with finite buffers, i.e., to the IB policy. There are also many researchers that view kanban as being equivalent to the minimal blocking (MB) policy (Mitra and Mitrani 1989), where each machine or workstation has an input buffer in addition to its output buffer (see Liberopoulos and Dallery 2000).

Framinan et al. (2003) presented a summary of papers addressing the comparison of CW with other policies and noted that the vast majority of papers concluded on the superiority of CW over kanban in both performance and robustness. The only authors that concluded differently were Gstettner and Kuhn (1996) who found that kanban achieves a given throughput with less WIP that CW.

Bonvik et al. (1997) compared five pull control policies for a 4-machine line with constant and time-varying deterministic demand rate. They considered the problem of minimizing total average inventory subject to a minimum service-level constraint. To evaluate the performance of each policy they used simulation. The policies that they compared are kanban, MB, basestock, CW and a kanban/CW hybrid control policy introduced in Van Ryzin et al. (1993). They found that the kanban/CW hybrid policy had superior performance, closely followed by CW and basestock. It is worth noting that their definitions of the kanban and basestock coincide with the definitions of the IB and EB policies, respectively. The kanban/CW hybrid is essentially an IB policy where the release of parts in the line is controlled with a CW loop.

Gaury et al. (2000) designed a generic control system that combines the features of kanban, CW and hybrid kanban/CW, and proposed a simulation-based evolutionary algorithm for selecting the best combined policy. Their numerical results on three examples with 6, 8, and 10 machines showed that for the problem of minimizing average WIP subject to a minimum service-level constraint, the best policy is a simplified kanban/CW policy.

Koukoumialos and Liberopoulos (2005) developed an analytical approximation method for the performance evaluation of a multi-stage production inventory system operated under an echelon kanban (EK) policy, which, as explained in Liberopoulos (2018), is similar to but not identical to the EB policy. The main difference between the two policies is that EK considers a system of manufacturing stages instead of machines, where each stage may be a single machine or a network of machines and has an input buffer in addition to its output buffer. They used their method to optimize the EK policy and compare it against CW, which is a special case of the EK policy. They considered a constrained optimization problem whose objective is to minimize the WIP plus finished goods inventory holding cost subject to a service level constraint (they considered two different service level definitions), where the inventory holding costs are increasing in the stages. Their numerical results for a 5-machine line showed that the superiority in performance of the EK policy over the CW policy can be quite significant, particularly when the relative increase in inventory holding costs from one stage to the next downstream stage is high and/or the quality of service is low.

Finally, Lavoie et al. (2010) optimized and compared kanban, CW, and hybrid kanban/CW policies for lines with 4 to 7 machines, using simulation, design of experiments, and response surface methodology. The performance measure that they used for the optimization was the weighted average inventory, backlog, and storage space cost. They found that the hybrid policy always outperforms CW and kanban when storage space and inventory costs are considered explicitly. However, the hybrid policy turns out to be equivalent to CW when storage space costs are not considered explicitly but are aggregated with the inventory costs in the holding costs. Furthermore, with the increase of storage space cost and the number of machines, kanban outperforms CW.

From the above analysis, to the best of our knowledge, the only papers that compare the EB policy against other policies are Bonvik et al. (1997) and Koukoumialos and Liberopoulos (2005). The latter paper compares the EK policy (which is similar to EB) against CW but not against the kanban policy, which is identical or similar to IB, depending on its definition. Both papers solve a simple optimization problem whose objective is to minimize the inventory holding costs subject to a minimum service-level constraint for demand-driven production lines with up to 5 machines. Both papers investigate a limited number of scenarios concerning the values of the problem parameters. In our numerical study, we consider a different optimization problem whose objective is to maximize the ANP subject to a minimum average throughput constraint. In addition to the inventory holdings costs, which are generally assumed to be increasing in the stages, we also consider the cost of buffer space and the cost of transferring parts to remote buffers. Our study is performed on larger lines with 8 machines and 20 machines and for a very large number of problem instances. For the 20-machine line with randomly chosen input parameters, we report results for 80 instances. For the 8-machine line with systematically chosen input parameters for sensitivity analysis, we report results for 396 parameter scenarios.

3 Description of IB, EB, and CW policies

We consider a flow line consisting of $N$ machines in series denoted by $M_{n} ,n = 1, \ldots ,N$, with $N - 1$ finite intermediate buffers denoted by $B_{n} ,n = 1, \ldots ,N - 1$. Parts are processed sequentially by all the machines, starting at $M_{1}$ and finishing at $M_{N}$. Time is broken in discrete periods. In each period, machine $M_{n} , n = 1, \ldots ,N,$ produces a part with probability $p_{n}$ unless it is starved or blocked; hence, the processing time of a part on machine $M_{n}$ is geometrically distributed with mean $1/p_{n}$. Probability $p_{n}$ is referred to as the production probability or rate of machine $M_{n}$ in isolation. Every machine has unit capacity, while the capacity of buffer $B_{n}$ is denoted by $C_{n} ,n = 1, \ldots ,N - 1$.

The union of $B_{n}$ and $M_{n + 1}$ constitutes the installation buffer following $M_{n}$. Its capacity is $1 + C_{n}$. The number of parts that have been processed by $M_{n}$ but have not yet departed from the next machine, $M_{n + 1}$, is referred to as the installation WIP following $M_{n}$ and is denoted by $i_{n}$. The union of $B_{n} , \ldots ,B_{N - 1} ,$ and $M_{n + 1}$ constitutes the echelon buffer following $M_{n}$. Its capacity is $1 + \mathop \sum \nolimits_{m = n}^{N - 1} C_{m}$. The number of parts that have been processed by $M_{n}$ but have not yet departed from the last machine, $M_{N}$, is referred to as the echelon WIP following $M_{n}$ and is denoted by $e_{n}$. With the above notation in mind, the IB, EB, and CW policies are defined as follows (see also Liberopoulos 2018):

Definition 1

(IB policy) In a flow line with $N$ machines and $N - 1$ intermediate buffers with capacities $C_{n} ,n = 1, \ldots ,N - 1,$ under the IB policy, machine $M_{n} ,n = 1, \ldots ,N - 1,$ releases the parts that it produces to installation buffer $B_{n} \cup M_{n + 1}$, and is blocked from processing a part if $i_{n} = 1 + C_{n}$.

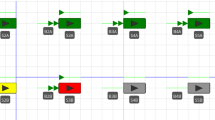
Figure 1 shows a flow line with $N = 4$ machines operated under IB. The different line-types of the arrows indicate the flow of parts between different machines. For instance, the solid-line arrows indicate the flow of parts that have been processed by machine $M_{2}$ but have not yet been processed by machine $M_{3} .$ These parts can be stored only in buffer $B_{2}$.

Fig. 1

Flow line operated under an IB policy

Definition 2

(EB policy) In a flow line with $N$ machines and $N - 1$ intermediate buffers with capacities $C_{n} ,n = 1, \ldots ,N - 1,$ under the EB policy, machine $M_{n} ,n = 1, \ldots ,N - 1,$ releases the parts that it produces to echelon buffer $B_{n} \cup \cdots \cup B_{N - 1} \cup M_{n + 1}$, and is blocked from processing a part if $e_{n} = 1 + \mathop \sum \nolimits_{m = n}^{N - 1} C_{m}$.

Figure 2 shows the 4-machine flow line of Fig. 1 operated under an EB policy. Again, the different line-types of the arrows indicate the flow of parts between different machines. As in Fig. 1, the solid-line arrows indicate the flow of parts that have been processed by machine $M_{2}$ but have not yet been processed by machine $M_{3} .$ These parts can be stored either in buffer $B_{2}$ or in buffer $B_{3}$.

Fig. 2

Flow line operated under an EB policy

If the capacities of all intermediate buffers, except possibly the last one, are zero (i.e., if $C_{n} = 0,n = 1, \ldots ,N - 2$, and $C_{N - 1} \ge 0$), then under the EB policy, machine $M_{n} ,n = 1, \ldots ,N - 1,$ can store the parts that it produces in the last and only buffer $B_{N - 1}$ if $M_{n + 1}$ is occupied. To simplify notation, we denote this buffer by $B$ and its capacity by $C$, i.e., $B \equiv B_{N - 1}$ and $C = C_{N - 1}$. It is easy to see that in this case, $M_{1}$ is blocked from processing a part if $e_{1} = 1 + C$ and that no other machine can ever be blocked. This way of operation is identical to the operation of CW where parts are not allowed to be released into the system if the total WIP is at the WIP-cap (Spearman et al. 1990). For the purposes of this paper, we will henceforth use the following definition for CW:

Definition 3

(CW policy) In a flow line with $N$ machines and $N - 1$ intermediate buffers with capacities $C_{n} = 0,n = 1, \ldots ,N - 2,$ and $C_{N - 1} = C \ge 0,$ the EB policy is equivalent to a CW policy with a WIP-cap of $1 + C$.

Figure 3 depicts the 4-machine flow line of Figs. 1 and 2 operated under CW, where the last buffer is shown as a common storage area on the side of the machines.

Fig. 3

Flow line operated under a CW policy

To analyze the operation of a flow line under the EB policy, Liberopoulos (2018) modelled it as a token-based queueing network and developed a decomposition-based approximation method for evaluating its performance. This network consists of the $N$ machines of the line, $M_{1} , \ldots ,M_{N}$, separated by $N - 1$ infinite capacity buffers, denoted by $Y_{1} , \ldots ,Y_{N - 1}$, as shown in Fig. 4, for $N = 4$. The number of parts in buffer $Y_{n} ,n = 1, \ldots ,N - 1,$ including the part in machine $M_{n + 1}$, is referred to as the stage WIP following $M_{n}$ and is denoted by $y_{n}$; $y_{n}$ represents the number of parts that have been produced by $M_{n}$ but have not yet departed from $M_{n + 1}$. As was mentioned earlier, in the physical system shown in Fig. 2, these parts may reside anywhere in echelon buffer $B_{n} \cup \cdots \cup B_{N - 1} \cup M_{n + 1}$.

Fig. 4

Queueing network model of a flow line operated under an EB policy

When a part flows from machine $M_{n}$ to buffer $Y_{n} ,$ a token is generated and is placed in an associated finite buffer denoted by $E_{n} , n = 1, \ldots ,N - 1$. The capacity of $E_{n}$ is equal to $1 + \mathop \sum \nolimits_{m = n}^{N - 1} C_{m}$, i.e., it is equal to the capacity of echelon buffer $B_{n} \cup \cdots \cup B_{N - 1} \cup M_{n + 1}$ following $M_{n} ,n = 1, \ldots ,N - 1$, in the physical line shown in Fig. 2. The long vertical line at the end of the system in Fig. 4 represents a synchronization station that synchronizes parts exiting the line with tokens from buffers $E_{n} , n = 1, \ldots ,N - 1$. More specifically, when a part is produced by machine $M_{N}$, it draws a token from each of buffers $E_{1} , \ldots ,E_{N - 1}$. The finished part departs from the line, and the tokens are discarded. Clearly, the number of tokens in $E_{n}$ equals the echelon WIP downstream of $M_{n} ,n = 1, \ldots ,N - 1$, in the physical line shown in Fig. 2; it is therefore denoted by $e_{n}$. The echelon WIP and the stage WIP levels are related as follows:

$$e_{n} = \mathop \sum \limits_{m = n}^{N - 1} y_{m} , n = 1, \ldots ,N - 1;$$

To further clarify the difference between the EB and IB policies, Fig. 5 shows a token-based queuing network model of a flow line operated under IB which is analogous to the model of the EB policy in Fig. 4. In the IB model, when a part flows from machine $M_{n}$ to buffer $Y_{n} ,$ a token is generated and is placed in an associated finite buffer denoted by $I_{n} , n = 1, \ldots ,N - 1$. When a part is produced by machine $M_{n + 1}$, it draws a token from buffer $I_{n}$. The capacity of $I_{n}$ is equal to $1 + C_{n}$, i.e., it is equal to the capacity of installation buffer $B_{n} \cup M_{n + 1}$ following $M_{n} ,n = 1, \ldots ,N - 1$, in the physical line shown in Fig. 1. The part moves further downstream the line, and the token is discarded. Clearly, the number of tokens in $I_{n}$ equals the installation WIP downstream of $M_{n} ,n = 1, \ldots ,N - 1$; it is therefore denoted by $i_{n}$. Note that in the IB policy, the stage WIP levels are identical to the installation WIP levels, i.e.,

Fig. 5

Queueing network model of a flow line operated under an IB policy

$$y_{n} = i_{n} ,n = 1, \ldots ,N - 1.$$

To evaluate the performance of the EB policy, Liberopoulos (2018) developed an approximation method that is based on: (1) decomposing the original queueing network model of the line with $N$ machines and $N - 1$ echelon buffers (see Fig. 4) into $N - 1$ nested segments, and (2) approximating each segment with a 2-machine subsystem that can be analyzed in isolation. For the case where the machines have geometrically distributed processing times, each subsystem is modelled as a 2D Markov chain that is solved numerically. The parameters of the 2-machine subsystems are determined by relationships among the flows of parts through the echelon buffers in the original system. These relationships are solved using an iterative algorithm. Liberopoulos (2018) demonstrated that this method is highly accurate and computationally efficient. In this paper, we use the same method to evaluate the performance of the EB and CW policies.

4 Formulation of the buffer allocation problem

We consider an optimization problem similar to that presented in Shi and Gershwin (2009). The objective is to determine the buffer sizes of a flow line to maximize the average net profit of the line subject to a minimum throughput constraint, for the three considered policies, namely, IB, EB, and CW. The average net profit is defined as the weighted average throughput of the line minus the average cost. The latter is defined as the sum of the weighted average WIP plus total buffer capacity plus transfer rate of parts to remote downstream buffers. The mathematical formulation of the problem is as follows:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{C_{1} , \ldots ,C_{N - 1} }} P\left( {C_{1} , \ldots ,C_{N - 1} } \right) & = r \nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) \\ & \quad - \,\left( {\mathop \sum \limits_{n = 1}^{N - 1} h_{n} \bar{y}_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right) + b\mathop \sum \limits_{n = 1}^{N - 1} C_{n} + t\mathop \sum \limits_{n = 1}^{N - 2} \theta_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right)} \right) \\ \end{aligned}$$

(1)

$${\text{subject}}\;{\text{to}}\quad \quad \quad \nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) \ge \nu_{min} ,$$

(2)

where we have used the following notation:

• $P\left( {C_{1} , \ldots ,C_{N - 1} } \right){:}$ average net profit of the line as a function of $C_{1} , \ldots ,C_{N - 1}$ ($ per unit time);

• $\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right){:}$ average throughput of the line as a function of $C_{1} , \ldots ,C_{N - 1}$ (parts per unit time);

• $\bar{y}_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right){:}$ average value of stage WIP $y_{n} , n = 1, \ldots ,N - 1$, as a function of $C_{1} , \ldots ,C_{N - 1}$ (parts);

• $\theta_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right){:}$ overflow rate of stage WIP buffer $Y_{n}$, as a function of $C_{1} , \ldots ,C_{N - 1}$; (parts per unit time)—to be defined shortly;

• $r{:}$ gross profit rate per final part produced by the line ($ per part);

• $h_{n}{:}$ inventory holding cost rate of parts comprising stage WIP $y_{n}$, $n = 1, \ldots ,N - 1$ ($ per part per unit time);

• $b{:}$ cost rate of storage space ($ per storage space for one part per unit time);

• $t{:}$ cost rate of transferring parts to remote buffers ($ per part transferred to a remote buffer);

• $\nu_{min}{:}$ minimum required average throughput (parts per unit time).

The overflow rate $\theta_{n}$ is defined as the joint probability that machine $M_{n}$ produces a part and $y_{n} \ge C_{n} + 1$. It represents the flow rate of parts that are produced by $M_{n}$ and are transferred for storage to a remote downstream buffer, i.e., a buffer which is different from $B_{n}$, because $B_{n}$ is full (hence the term “overflow”). Recall that under the IB policy, parts are never transferred for storage to remote downstream buffers but are stored locally. In this case, $\theta_{n} = 0,n = 1, \ldots ,N - 1$. Under the EB and CW policies, on the other hand, the overflow rates of all stage WIP buffers except $Y_{N - 1}$ are positive, i.e., $\theta_{n} > 0,n = 1, \ldots ,N - 2$, and $\theta_{N - 1} = 0$. The overflow rate of $Y_{N - 1}$ is zero, because the parts in it represent parts that have been produced by machine $M_{N - 1}$ but have not yet departed from machine $M_{N}$ in the physical system. These parts can only be stored locally in the immediate downstream buffer $B_{N - 1}$ and not in any other remote buffer in the physical system.

5 Optimization algorithm for solving the buffer allocation problem

Problem (1)–(2) is a constrained non-linear integer optimization problem. To solve it, we use the following two-phase optimization algorithm.

Phase 1 Phase 1 is an adaptation of the two-step gradient algorithm presented in Shi and Gershwin (2009). That algorithm is basically an implementation of the Lagrange multiplier method for solving non-linear constrained optimization problems.

Step 1 of phase 1 In step 1, we solve problem (1)–(2) without taking into account constraint (2). This problem is referred to as the unconstrained problem. To solve this problem, we use the following iterative “gradient-like” technique.

We start with an initial design where all buffer capacities are zero, i.e., $C_{n} = 0,n = 1, \ldots ,N - 1$. In each iteration, given the current design $C_{1} , \ldots ,C_{N - 1}$ and the corresponding average net profit $P\left( {C_{1} , \ldots ,C_{N - 1} } \right)$, we compute the increase in the average net profit that would result if we incremented the value of $C_{n}$ by one unit to $C_{n} + 1$, for each $n = 1, \ldots ,N - 1$.

If the increase in the average net profit is negative for all $n = 1, \ldots ,N - 1,$ then there are no more gains to make by incrementing the buffer capacities one at a time; therefore, we stop and keep the current design as the final one for the unconstrained problem.

Otherwise, we update the current design to a new design in which the capacity of the intermediate buffer that yielded the largest increase in the average net profit is incremented by one unit and all other capacities remain the same, and we move on to the next iteration.

If the final solution of the unconstrained problem solved in step 1 satisfies constraint (2), then it is also the final solution of the constrained problem (1)–(2); hence, we keep it as the final design of phase 1 and move on to phase 2. Otherwise, we proceed to step 2.

Step 2 of phase 1 Step 2 is implemented if the final solution of the unconstrained problem solved in step 1 violates constraint (2). In this case, if the decision variables $C_{n} ,n = 1, \ldots ,N - 1,$ were continuous, making $\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right)$ continuous too, the constraint would be binding at the optimal solution. Because the buffer capacities are discrete, $\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right)$ increases in jumps, and it is unlikely that any of its values exactly equal $\nu_{min}$. In this case, the optimal buffer capacities are the smallest values of $C_{n} ,n = 1, \ldots ,N - 1,$ such that $\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) \ge \nu_{min}$. To find them, we introduce a Lagrange multiplier $\lambda$ and try to solve the following modified unconstrained problem:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{C_{1} , \ldots ,C_{N - 1} ,\lambda }} P\left( {C_{1} , \ldots ,C_{N - 1} ,\lambda } \right) & = r \nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) \\ & \quad - \,\left( {\mathop \sum \limits_{n = 1}^{N - 1} h_{n} \bar{y}_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right) + b\mathop \sum \limits_{n = 1}^{N - 1} C_{n} + t\mathop \sum \limits_{n = 1}^{N - 2} \theta_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right)} \right) \\ & \quad + \,\lambda \left( {\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) - v_{min} } \right), \\ \end{aligned}$$

which is equivalent to:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{C_{1} , \ldots ,C_{N - 1} ,\lambda }} P\left( {C_{1} , \ldots ,C_{N - 1} ,\lambda } \right) & = r'\nu \left( {C_{1} , \ldots ,C_{N - 1} } \right) \\ & \quad - \,\left( {\mathop \sum \limits_{n = 1}^{N - 1} h_{n} \bar{y}_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right) + b\mathop \sum \limits_{n = 1}^{N - 1} C_{n} + t\mathop \sum \limits_{n = 1}^{N - 2} \theta_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right)} \right), \\ \end{aligned}$$

(3)

where $r'$ is a modified gross profit rate, given by:

$$r^{\prime} = r + \lambda .$$

(4)

To solve problem (3) in step 2, we use the following iterative technique.

We start with the initial design where all buffer capacities are set equal to the values of the final design of phase 1 and $r^{\prime} = r$, which from (4) implies that $\lambda = 0$.

In each iteration, we slightly increment the value of the gross profit rate $r'$ and resolve the modified unconstrained problem (3) with the incremented value of $r'$. Essentially, by increasing $r'$, we are increasing the Lagrange multiplier $\lambda$ introduced in (3), since $\lambda = r^{\prime} - r$ from (4).

If the final solution of the modified unconstrained problem (3) with the new value of $r'$ satisfies constraint (2), then it is also the solution of the original constrained problem (1)–(2); hence, we keep it as the final design of phase 1 and move on to phase 2. Otherwise, we increment the value of $r'$ again and repeat the process until the solution of problem (3) with the updated value of $r'$ satisfies constraint (2). The resulting design solves the constrained problem too, and so we keep it as the final design of phase 1. To evaluate the average net profit that this design yields we use the original value of $r$ in (1). We then move on to phase 2.

A block diagram of phase 1 is shown in Fig. 6, where we have used the following notation:

Fig. 6

Block diagram of phase 1 of the optimization algorithm

• ${\mathbf{C}} = \left( {C_{1} , \ldots ,C_{N - 1} } \right){:}\,\, \left( {N - 1} \right)$-element vector of current buffer capacities;

• $1_{n} = ( {0, \ldots ,\underbrace {1}_{{n{\text{th}}\;{\text{position}}}}, \ldots ,0} ){:} \,\,(N - 1)$-element vector with 1 in position n and zeros elsewhere, n = 1,…,N − 1

• $P\left( {{\mathbf{C}};r^{\prime}} \right){:}$ Average net profit as a function of buffer capacity vector ${\mathbf{C}}$ for given modified gross profit rate $r^{\prime}$;

• $\nu \left( {\mathbf{C}} \right){:}$ Average throughput as a function of buffer capacity vector ${\mathbf{C}}$;

• $\varepsilon{:}$ A very small positive number, e.g., $\varepsilon = 0.01$.

Phase 2 Phase 2 is a simple iterative neighborhood search that tries to improve the solution obtained in phase 1. Throughout phase 2, we use the original gross profit rate $r$ in (1). In each iteration, given the current design $C_{1} , \ldots ,C_{N - 1}$ and the corresponding average net profit $P\left( {C_{1} , \ldots ,C_{N - 1} } \right)$, we compute the increase in the average net profit that would result if we made the following perturbations to the buffer capacities: (1) decrement the value of $C_{n}$ by one unit to $C_{n} - 1,n = 1, \ldots ,N - 1$, (2) increment the value of $C_{n}$ by one unit to $C_{n} + 1,n = 1, \ldots ,N - 1$, and (3) transfer one unit of capacity from buffer $C_{n}$ to buffer $C_{m} ,n = 1, \ldots ,N - 1,$$m = 1, \ldots ,N - 1,m \ne n$.

If the increase in the average net profit is negative for all the above perturbations, then there are no more gains to make by perturbing the buffer capacities; therefore, we stop and keep the current design as the final one.

Otherwise, we update the current design to the perturbed design that yielded the highest increase in average profit and we move on to the next iteration.

Although the optimization problem that we consider is similar to the problem considered in Shi and Gershwin (2009), there are several differences between our work and the work of Shi and Gershwin.

Firstly, in the line that we consider, the machines have geometrically distributed processing times, whereas in the line that Shi and Gershwin consider, the machines have unit production times and geometrically distributed up times and downtimes.

Moreover, Shi and Gershwin study only the traditional IB policy, whereas we also consider the alternative EB policy and its special case, CW. Because the transferring of parts to remote buffers does not apply to the IB policy, Shi and Gershwin do not include in the objective function the weighted average transfer rate of parts to remote buffers, $t\mathop \sum \nolimits_{n = 1}^{N - 2} \theta_{n} \left( {C_{1} , \ldots ,C_{N - 1} } \right)$, whereas we consider it for the EB and CW policies.

Finally, we treat the buffer capacities as integers. Throughout the optimization method, we move in the direction the steepest ascent of the average net profit, by making the smallest possible step, to be on the safe side, as the focus of our work is not to assess the efficiency of the optimization algorithm but to compare the optimal performance of the three considered policies. Namely, in each iteration of step 1 of phase 1, we increment the capacity of only one buffer (the buffer that yields the highest increase in profit) by only one unit. Similarly, in each iteration of phase 2, we decrement or increment the capacity of one buffer by one unit or we transfer one unit of capacity from one buffer to another.

Shi and Gershwin, on the other hand, employ an approximation method that allows them to treat the buffer capacities as continuous variables. Hence, in the optimization, they use a classical gradient method where in each iteration they modify the capacities of all buffers in the direction that yields the steepest ascent in the objective function. The goal of their work is to demonstrate the accuracy and efficiency of this method. Moreover, they do not have the equivalent of phase 2 for improving the solution obtained in phase 1; at the end of the two-step method (phase 1) they simply round the final continuous buffer capacity solutions to the closest integers.

Shi and Gershwin (2009) point out that the method that they use—as any gradient method—is based on the assumption that the net average profit is concave and has a single maximum. They cite several references that substantiate this assumption for similar lines based on numerical evidence and intuition. In their conclusions, they write that the rigorous proof of this assumption is an issue for future research.

In our work we also assume that the net average profit is concave and has a single maximum, for the classical IB policy. For the EB policy, we run some additional numerical tests that validate this assumption. More specifically, for a selected set of the instances of problem (1)–(2) that we solved for the 8-machine line, we rerun the iterative two-phase optimization algorithm, except that this time, for each design that we evaluated, we also computed the Hessian matrix of partial derivatives of the average net profit with respect to the buffer capacities. In all cases, all the eigenvalues of this matrix turned out to be negative. This indicates that the Hessian matrix is negative definite, and therefore the net average profit is concave for all the design points that we evaluated. The results of these tests are presented in “Appendix 1”.

6 Numerical results

We used the algorithm outlined in the previous section to solve problem (1)–(2) for numerous instances of a 20-machine and an 8-machine flow line, operating under the IB, EB, and CW policies. The instances differ in the production rates of the machines, $p_{n} ,n = 1, \ldots ,N$, and in the main parameters of optimization problem (1)–(2), namely, $r,b,t,h_{n} ,n = 1, \ldots .,N$, and $\nu_{min}$. These parameters depend on the production costs of the line, the interest rate and profit margin used by the firm that runs the line, and other problem parameters which we refer to as “basic”. To choose realistic and reasonable values for the main optimization parameters we used the following basic parameters:

• $c_{0}{:}$ cost per raw-material part ($ per part).

• $c_{n}{:}$ total cost per part produced by machine $M_{n}$, $n = 1, \ldots ,N - 1,$ ($ per part).

• $c_{N}{:}$ total cost per finished part exiting the line ($ per part).

• $I_{c}{:}$ value-added rate per production stage as a percentage of $c_{0}$ ($ per $). A value of $I_{c} = 0.5$ means that processing at machine $M_{n}$ adds a cost (value) equal to 50% of $c_{0}$ to each part, i.e., $c_{n} = c_{n - 1} + I_{c} c_{0} ,n = 1, \ldots ,N$.

• $I_{h}{:}$ interest rate of capital ($ per $ per unit time).

• $I_{r}{:}$ gross profit margin ($ per $) defined as follows: $I_{r} = \left( {s - c_{N} } \right)/c_{N}$, where $s$ is the selling price per finished part ($ per part). A value of $I_{r} = 0.1$ means that the selling price of a finished part is 10% higher than the total cost of the part, $c_{N}$.

• $I_{b}{:}$ buffer capacity cost rate defined as a multiple of inventory holding cost rate $h_{1}$ (parts per storage space). A value of $I_{b} = 2$ means that the per period “rental” cost of space for storing one part in an intermediate buffer is equal to the cost of holding two parts in stage-1 WIP inventory for one period.

• $I_{t}{:}$ transfer cost rate as a multiple of raw material cost $c_{0} .$ A value of $I_{t} = 0.01$ means that the cost of transferring a part to a remote installation buffer and back is 1% of $c_{0} .$

• $I_{\nu }{:}$ minimum required flow line efficiency. A value of $I_{\nu } = 0.8$ means that $\nu_{min}$ is 80% of the production probability (rate) of the slowest machine in isolation.

Based on the above definitions, the total cost per part in stage $n$, $c_{n} \left( {n = 1, \ldots ,N} \right)$, and parameters $r,b,t,h_{n} ,n = 1, \ldots .,N$, and $\nu_{min}$ in optimization problem (1)–(2) are computed as follows:

$$c_{n} = c_{n - 1} + I_{c} c_{0} = c_{0} \left( {1 + nI_{c} } \right), n = 1, \ldots ,N,$$

(5)

$$h_{n} = I_{h} c_{n} = I_{h} c_{0} \left( {1 + nI_{c} } \right), n = 1, \ldots ,N - 1,$$

(6)

$$r = I_{r} c_{N} = I_{r} c_{0} \left( {1 + NI_{c} } \right),$$

(7)

$$b = I_{b} h_{1} = I_{b} I_{h} c_{1} = I_{b} I_{h} c_{0} \left( {1 + I_{c} } \right),$$

(8)

$$t = I_{t} c_{0} ,$$

(9)

$$\nu_{min} = I_{\nu } \mathop {\hbox{min} }\limits_{n = 1, \ldots ,N} \left\{ {p_{n} } \right\}.$$

(10)

In all instances of the 20-machine line that we investigated, we randomly chose different values for the production rates of the machines and the basic variables $c_{0} ,I_{c} ,I_{h} ,I_{r} ,I_{b} ,I_{t}$, and $I_{v}$. In the instances of the 8-machine line, these values were chosen in a structured way because we wanted to perform a more systematic sensitivity analysis. In both cases, the chosen production rates and basic variables were then used to determine the values of the optimization parameters $r,b,t, \nu_{min} ,$ and $h_{n} ,n = 1, \ldots ,N - 1$, in problem (1)–(2) from expressions (5)–(10). All instances were run on a PC with an Intel(R) Core(TM) i3-7100U CPU @ 2.40 GHz with 4.00 GB RAM. The input parameters and the results for both the 20-machine and the 8-machine line instances are presented in the next sections.

6.1 20-Machine line with randomly chosen input parameters

For the 20-machine line example, we considered 80 different instances. In each instance, the values of the production rates of the machines, $p_{n} ,n = 1, \ldots ,N$, and the basic parameters $I_{c} ,I_{h} ,I_{r} ,I_{b} ,I_{v}$, and $I_{t}$ were chosen randomly from a uniform distribution over a given interval. The value of $c_{0}$ was equal to 100 in all instances. Table 1 shows the range of values for each parameter, and Table 2 shows the randomly generated parameter values for the first 40 instances. The parameter values for the remaining 40 instances are shown in Table 23 in “Appendix 2”, for space considerations.

Table 1 Range of values of the basic input parameters for the 20-machine line

Table 2 Values of production rates $p_{n} ,n = 1, \ldots ,N$, and basic parameters $I_{c} ,I_{h} ,I_{r} ,I_{b} ,I_{\nu }$ and $I_{t}$ for instances 1–40 of the 20-machine line

Table 3 shows the optimization results for the first 40 instances. The optimization results for instances 41–80 are shown in Table 24 in “Appendix 2”. Each row in Table 3 (and Table 24) shows the instance number, the optimal buffer sizes ($C_{1}^{*}$–$C_{19}^{*}$ for the IB and EB policies and $C^{*}$ for the CW policy), the maximum profit $P^{*}$, the computational time in minutes (cpu), and the number of iterations of steps 1 and 2 of phase 1 and of phase 2 of the optimization algorithm, for each policy (iter). The last two elements ($\% \Delta P^{*}$) show the percent gain in the net average profit of the optimal EB policy w.r.t. the optimal IB policy (E–I) and w.r.t. the optimal CW policy (E–C). These gains are computed as follows:

Table 3 Numerical results for instances 1–40 of the 20-machine line

$$\% \Delta P^{*} \left( {E{-}I} \right) = \frac{{P_{EB}^{*} - P_{IB}^{*} }}{{\left| {P_{IB}^{*} } \right|}} \times 100,$$

(11)

$$\% \Delta P^{*} \left( {E{-}C} \right) = \frac{{P_{EB}^{*} - P_{CW}^{*} }}{{\left| {P_{CW}^{*} } \right|}} \times 100.$$

(12)

We should note that once we run all 80 instances, we renumbered them as follows. First, we sorted instances 1–80 in decreasing order of E–I values. We kept the first 20 sorted instances and renumbered them as 1–20. Then, we resorted the remaining instances 21–80 in decreasing order of E–C values. We kept the first 20 resorted instances and renumbered them as 21–40. Next, we resorted instances 41–80 in decreasing order of E–I values. Again, we kept the first 20 resorted instances and renumbered them as 41–60. Finally, we resorted the last 20 remaining instances in decreasing order of E–C values and renumbered them 61–80. Tables 2, 3, 23, and 24 show the input data and the results for the renumbered instances.

Note that in a few instances the profit is negative for one or more policies, because the gross profit margin is not high enough to cover the costs. Table 4 shows the average, minimum, and maximum values of the maximum profit, computational time, and number of iterations for all instances in Tables 3 and 24.

Table 4 Average, minimum, and maximum values of maximum profit, computational time, and number of iterations for instances 1–80 of the 20-machine line

Based on the results shown in Tables 3 and 4 as well as Table 24 in “Appendix 2”, we make the following observations regarding the optimal buffer allocation designs:

• 1. In all instances, the maximum profit under the optimal EB policy is higher than the respective profit under the optimal IB policy. From Table 4, the percent gain in the net average profit of the optimal EB policy w.r.t. the optimal IB policy (“E–I”) ranges between 1.4 and 401.9% with an average of 15.9%. This implies that for the range of parameters considered, the benefit of the throughput increase under the EB policy significantly outweighs the disadvantage of the WIP increase and transfer cost, also taking into account the fact that a smaller buffer space is needed under the EB policy than under the IB policy to achieve the same throughput level.

• 2. In all instances, the maximum profit under the optimal EB policy is higher than the respective profit under the optimal CW policy. This is expected given that CW is a special case of EB. From Table 4, the percent gain in the net average profit of the optimal EB policy w.r.t. the optimal CW policy (“E–C”) ranges between 0.04 and 12.71% with an average of 1.23%.

• 3. In three out of four instances, the total buffer capacity of the optimal EB policy is significantly smaller than that of the optimal IB policy (on average by 7 units). This is expected given that the EB policy utilizes buffer space more efficiently that the IB policy does.

• 4. In all instances, the total buffer capacity of the optimal EB policy is exactly equal or almost equal (within a unit) to the total capacity of the optimal CW policy. Based on this observation, one could use the following two-stage heuristic for finding the optimal buffer allocation under the EB policy. Stage 1: Find the optimal capacity of the last buffer for the CW policy. This is an easy problem, because there is only one parameter to optimize. Stage 2: Reallocate this capacity to all the buffers to increase the net average profit through an iterative algorithm that is similar to phase 2.

Regarding the computational effort needed to get to the optimal buffer allocation, we make the following observations:

• 5. The number of iterations of step 1 of phase 1 of the optimization algorithm is generally higher for the IB policy than it is for the EB and CW policies. This is because in each iteration of step 1, the capacity of a single buffer is incremented by one unit until there are no more gains to make. Because the total optimal buffer capacity is generally higher for the IB policy (recall that it is higher in three out of four instances), more iterations of this step are performed for the IB policy than for the other policies. More specifically, from Table 4, the number of iterations of step 1 of phase 1 ranges from 3 to 57 with an average of 24 for the IB policy. For the EB policy, it ranges from 7 to 31 with an average of 16, and for the CW policy it is similar, ranging from 7 to 30 with an average of 16.

• 6. The number of iterations of step 2 of phase 1 of the optimization algorithm is higher for the IB policy than it is for the EB and CW policies. This is because each time the capacity of a buffer is incremented by one unit in step 1 of phase 1, the resulting increase in throughput is much higher for the EB and CW policies than it is for the IB policy. Therefore, the increase in the gross profit rate $r'$ that is necessary to satisfy the minimum throughput constraint (step 2 of phase 1) is smaller in the EB and CW policies than it is in the IB policy. More specifically, from Table 4, the number of iterations of step 2 of phase 1 of the optimization algorithm ranges from 0 to 913 with an average of 101, for the IB policy. For the EB and CW policies, it ranges from 0 to 412 with an average of 46.

• 7. The number of iterations of phase 2 of the optimization algorithm is higher for the IB policy than it is for the EB policy (for the CW policy, it is always zero). More specifically, from Table 4, the number of iterations of phase 2 ranges from 0 to 19 with an average of 4, for the IB policy. For the EB policy, it ranges from 0 to 5 with an average of 1. Still, for both policies this number is generally quite low, indicating that phase 1 often leads to the optimal buffer allocation or close to it.

• 8. The CPU time to reach the optimal solution is much higher for the IB policy than it is for the EB and CW policies. This is because the IB policy requires more iterations in all the steps of the optimization algorithm, as was mentioned earlier, but also because the algorithm used for the performance evaluation of the IB policy is more time consuming that the algorithm used for the performance evaluation of the EB and CW policies.

6.2 8-Machine line with systematically chosen input parameters for sensitivity analysis

For the 8-machine line example, we considered four scenarios, denoted $L_{1} , \ldots ,L_{4}$, regarding the production rates of the machines. These scenarios are shown in Table 5. Scenario $L_{1}$ represents a totally balanced line where all the machines have the same base production probability of 0.6. Scenarios $L_{2}$–$L_{4}$ represent lines where all the machines have the same base production probability of 0.6 except for one machine which has a lower probability, making it the slowest machine. That machine may be upstream, in the middle, or downstream the line. The production probability of the slowest machine is shown in bold.

Table 5 Production rate scenarios with base production probability 0.6 for the 8-machine line

We also considered three different scenarios, denoted $T_{1} ,T_{2} ,T_{3}$, regarding basic parameter $I_{t}$ which determines the cost rate of transferring parts to remote buffers, $t$, via expression (9). These scenarios are shown in Table 6. Note that $T_{1}$ represents the scenario where $I_{t} = 0$, meaning that $t = 0$.

Table 6 Scenarios of basic parameter I_t and resulting optimization problem parameter t

Finally, we considered 11 different scenarios, denoted $O_{1} , \ldots O_{11}$, regarding basic parameters $c_{0} ,I_{c} ,I_{h} ,I_{r} ,I_{b} ,$ and $I_{\nu }$ which determine the main optimization parameters $r,b,$ and $h_{1} , \ldots ,h_{7}$ in problem (1)–(2) according to expressions (5)–(8) and (10). These scenarios are shown in Table 7.

Table 7 Scenarios of basic problem parameters $c_{0} ,I_{c} ,I_{h} ,I_{r} ,I_{b} ,I_{\nu }$ and resulting optimization parameters $r,b,$ and $h_{1} , \ldots ,h_{7}$

Scenario $O_{1}$ is the base scenario. The optimization parameters for this scenario are computed from expressions (6)–(8) as follows:

$$h_{n} = I_{h} c_{0} \left( {1 + nI_{c} } \right) = \left( {0.001} \right)\left( {100} \right)\left( {1 + 0.5n} \right) = 0.1 + 0.05n\; \${\text{per part per unit time}}, n = 1, \ldots ,N - 1,$$

$$r = I_{r} c_{0} \left( {1 + NI_{c} } \right) = \left( {0.1} \right)\left( {100} \right)\left( {1 + \left( {0.5} \right)\left( 8 \right)} \right) = 50\;\$ {\text{ per part}},$$

$$b = I_{b} I_{h} c_{0} \left( {1 + I_{c} } \right) = \left( 2 \right)\left( {0.001} \right)\left( {100} \right)\left( {1 + 0.5} \right) = 0.3\; \${\text{per storage space per unit time}}.$$

$O_{2}$–$O_{11}$ are scenarios in which we have changed one of the basic parameters of the base scenario. The changed parameter is shown in bold. Note that $O_{2} ,O_{9} ,$ and $O_{11}$ represent situations where $I_{c} ,I_{b} ,$ and $I_{\nu }$ are zero, respectively. Consequently, under $O_{2}$, all WIP inventory holding cost rates $h_{1} , \ldots ,h_{7}$ are equal. Similarly, under $O_{9}$, the cost rate of storage space $b$ is zero. Finally, under $O_{11}$, the minimum required average throughput $\nu_{min}$ is zero.

We solved problem (1)–(2) for all combinations of scenarios L₁–L₄, T₁–T₃, and O₁–O₁₁, i.e., for a total of $4 \times 3 \times 11 = 132$ instances. Tables 8, 9, 10 and 11 show the optimization results for all these instances. More specifically, each table shows the results for a specific production rate scenario, $L_{1} , \ldots ,L_{4}$, and all combinations of scenarios T₁–T₃, and O₁–O₁₁. Each row in each table shows the scenario combination, the optimal buffer sizes ($C_{1}^{*}$–$C_{7}^{*}$ for the IB and EB policies and $C^{*}$ for the CW policy), the maximum profit $P^{*}$, the computational time (cpu) in minutes, and the number of iterations of steps 1 and 2 of phase 1 and of phase 2 of the optimization algorithm that were needed to get to the optimal solution, for each policy (iter). The last two elements (“$\% \Delta P^{*}$”) show the percent gain in the net average profit of the optimal EB policy w.r.t. the optimal IB policy (“E–I”) and the optimal CW policy (“E–C”), computed from (11) and (12), respectively.

Table 8 Numerical results for scenario $L_{1}$ of the 8-machine line

Table 9 Numerical results for scenario $L_{2}$ of the 8-machine line

Table 10 Numerical results for scenario L₃ of the 8-machine line

Table 11 Numerical results for scenario L₄ of the 8-machine line

Based on the results, we make the following observations, some of which coincide with observations 1–4 listed in Sect. 6.1:

• 1. In almost all instances, the maximum profit under the optimal EB policy is higher than the respective profit under the optimal IB policy. The only instances where the optimal IB policy outperforms the optimal EB policy are the instances where $I_{b} = 0$ (scenario $O_{9}$). Indeed, when the cost of buffer capacity is zero, the efficiency in buffer space utilization under EB becomes irrelevant and does not bring any advantage over IB.

• 2. In all instances, the maximum profit under the optimal EB policy is higher than the respective profit under the optimal CW policy. When I_t = 0, meaning that t = 0 (scenario T₁), the difference in maximum profit between the two policies is negligible; however, as t increases (scenarios T₂ and T₃), the difference in the maximum profit becomes quite significant. This is expected, because CW results in a higher transfer rate of parts to remote buffers than EB does, since in CW, there is only one buffer, and that buffer is remote for all machines except $M_{N - 1}$.

• 3. In almost all instances, the total buffer capacity of the optimal EB policy is significantly smaller than that of the optimal IB policy. The only cases where the two capacities are equal are a few instances where $I_{\nu } = 0$ (scenario $O_{11}$). In these instances, $v_{min} = 0$, which means that constraint (2) is redundant.

• 4. In most instances, the total buffer capacity of the optimal EB policy is exactly equal or almost equal (within a unit) to the total capacity of the optimal CW policy.

• 5. In all instances, as I_t increases, implying that the cost rate of transferring parts to remote buffers, t, increases, the dominance of the EB policy over the IB policy fades. This is expected, because the cost of transferring parts to remote buffers applies only to the EB policy.

• 6. Scenarios O₂, O₆, and O₈ result in the lowest net average profit under all policies. The reason for this differs depending on the scenario. In the case of O₂ and O₈, the reason is that the gross profit rate r is low compared to the cost rates. In the case of O₆, the reason is that the inventory holding cost rates $h_{n} ,n = 1, \ldots ,N - 1$, are high. Given that in these three scenarios the profit is the lowest (and in some cases, even negative), it is not surprising that the noted increase in the net average profit of the optimal EB policy over the other two policies is the highest in percentage terms.

• 7. A careful comparison among scenarios L₂, L₃, L₄, which represent lines with a slow machine, shows that the further downstream the slow machine, the lower the optimal average net profit of the line and the lower the optimal total buffer capacity under any policy. This is expected since a slow machine causes congestion upstream the line; therefore, the further downstream the slow machine, the more extensive the propagation of the congestion—and its adverse effect—upstream the line.

We also run two additional sets of scenarios for the production rates of the 8-machine line in which we used a base production probability of 0.4 and 0.8, respectively, instead of 0.6, which was used in the set shown in Table 5. The input parameters and results for these sets are shown in “Appendix 3”. Qualitatively, these results are similar to the results that were obtained for the base production probability of 0.6, discussed above. Quantitatively, they differ. By comparing the results for the three scenario sets, we observe that as the base production probability decreases from 0.8 to 0.6 to 0.4, the optimal buffer capacities and the maximum profit also decrease for all policies. This is natural, because as the base production probability decreases, the average throughput of the line drops and so do the profits.

At the same time, however, the percent gain in the net average profit of the optimal EB policy w.r.t. the optimal IB policy (E–I) and w.r.t. the optimal CW policy (E–C) increases (we only consider the instances where the profit is positive). This can probably be explained by the fact that as the maximum profit decreases in absolute terms for all policies, the relative differences in maximum profit between the policies become more prominent.

A closer look at the results further reveals that in most instances as the base production probability decreases, the relative gain of EB over IB rises more sharply than does the relative gain of EB over CW. One possible explanation for this is that as the base production probability decreases, the production times of the machines have higher variability (the coefficient of variability of the production times of a Bernoulli machine with production probability $p_{n}$ is $1 - p_{n}$); EB, being a policy that releases parts based on global information, copes better with increased variability than does IB, where the release of parts is based on local information.

7 Conclusions

We set up and carried out an extensive numerical study for the optimization and comparison of the EB policy for operating flow lines with intermediate finite-capacity buffers against two well-known and well-studied policies: IB and CW. Compared to IB, EB aims to increase the utilization of the intermediate buffers by controlling the release of parts in each stage based on the echelon WIP level associated with that stage. CW, which is a special case of EB, also results in increasing the utilization of the intermediate buffers but in a less regulated way, because it only controls the release of parts at the beginning of the line.

Our numerical results indicate that the optimal EB policy generally outperforms the optimal IB and CW policies, the difference in performance being striking in some cases. The results also show that as production probabilities of the machines decrease, the relative advantage in performance of the EB policy over the other two policies increases. When the cost of transferring parts to remote buffers is negligible, the optimal EB policy slightly outperforms the optimal CW policy but significantly outperforms the optimal IB policy. Therefore, in such cases, CW is a good performer. Finally, when the cost of transferring parts to remote buffers is noticeable, the dominance of EB over CW increases while the dominance of EB over IB decreases.

While some of our results were expected, other results were less obvious at the onset of this study. For example, the result that the EB policy outperforms CW was expected, since CW is a special case of EB. However, the magnitude of the difference in performance between the two policies was not obvious. Similarly, the result that EB outperforms IB when the cost of transferring parts to remote buffers is negligible was not apparent, because EB, besides incurring additional costs for transferring parts to remote buffers, also results in higher WIP levels than IB does.

We believe that the EB policy performs well primarily because it increases the utilization of the existing buffers but can still block machines from producing if the number of parts that they have already produced but are still in the system is large. An obvious advantage of the EB policy is that it uses global information for releasing parts at any stage whereas IB uses local information. It is likely for this reason that as the variability of the machine production times increases, the relative advantage in performance of the EB policy over the IB policy increases sharply.

A shortcoming of the EB policy is that it has increased material handling requirements compared to the IB policy. As is explained in Liberopoulos (2018), technology can handle such increased requirements at affordable costs. Today, there exist several modular reconfigurable material handling solutions that can be assembled flexibly to transport parts in the manufacturing floor. Many of the material handling ideas and equipment that are used in flow lines with reentrant flows (e.g., in semiconductor manufacturing) can also be used to implement the EB policy. The material handling technology for implementing the EB policy can also be found in classical flexible manufacturing systems and their successors, reconfigurable manufacturing systems, where typically pallets are sent back and forth to the work centers.

Having established that the EB has advantages over the IB and CW policies in serial flow lines, a future research direction would be to explore if these advantages carry over to other system configurations, for example, assembly/disassembly lines, lines with fork/join stations, reentrant flows, etc., as well as lines producing multiple products. Another direction would be to consider more general machine reliability models than the Bernoulli model.

Appendices

Appendix 1: Numerical tests for the 8-machine line verifying the concavity of the net average profit under the EB policy

Tables 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22 present the buffer capacity designs under the EB policy that resulted in each iteration of the two-phase optimization algorithm, for scenarios $L_{1} ,T_{3} ,$ and $O_{1}$–$O_{11}$ of the 8-machine line. Each row shows the iteration number, the buffer capacity design at that iteration, and the eigenvalues corresponding to the Hessian matrix of partial derivatives of the average net profit with respect to the buffer capacities at that design. The buffer capacity design in the last row of each table is the optimal design shown in Table 8. In all cases, all the eigenvalues of the Hessian matrix are negative, indicating that the average net profit at the buffer capacity designs examined is concave.

Table 12 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{1}$ of the 8-machine line, under the EB policy

Table 13 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{2}$ of the 8-machine line, under the EB policy

Table 14 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{3}$ of the 8-machine line, under the EB policy

Table 15 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{4}$ of the 8-machine line, under the EB policy

Table 16 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{5}$ of the 8-machine line, under the EB policy

Table 17 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{6}$ of the 8-machine line, under the EB policy

Table 18 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{7}$ of the 8-machine line, under the EB policy

Table 19 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{8}$ of the 8-machine line, under the EB policy

Table 20 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{9}$ of the 8-machine line, under the EB policy

Table 21 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{10}$ of the 8-machine line, under the EB policy

Table 22 Numerical results per iteration for scenario $L_{1} ,T_{3} ,O_{11}$ of the 8-machine line, under the EB policy

Appendix 2: Additional numerical results for the 20-machine line with randomly chosen input parameters

Table 23 shows the randomly generated parameter values for instances 41–80 of the 20-machine line, and Table 24 and shows the optimization results for all these instances.

Table 23 Values of production rates $p_{n} ,n = 1, \ldots ,N$, and basic parameters $I_{c} ,I_{h} ,I_{r} ,I_{b} ,I_{\nu }$ and $I_{t}$ for instances 41–80 of the 20-machine line

Table 24 Numerical results for instances 41–80 of the 20-machine line

Appendix 3: Numerical results for the 8-machine line with base production probabilities 0.4 and 0.8

Table 25 shows eight additional scenarios for the production rates of the 8-machine flow line example considered in Sect. 6.2. These scenarios are denoted $L_{5} , \ldots ,L_{12}$ and are similar to scenarios $L_{1} , \ldots ,L_{4}$ shown in Table 5, except that they use a different base production probability than 0.6, which is used in scenarios $L_{1} , \ldots ,L_{4}$. More specifically, scenarios $L_{5} , \ldots ,L_{8}$ use base production probability 0.4, while scenarios $L_{9} , \ldots ,L_{12}$ use base production probability 0.8.  As in Table 5, the production probabilities of the slowest machine in scenarios L₆-L₈ and L₁₀-L₁₂ are shown bold.

Table 25 Production rate scenarios with base production probability 0.4 and 0.8 for the 8-machine line

We solved problem (1)-(2) for all combinations of scenarios L₅–L₁₂, T₁–T₃, and O₁–O₁₁, i.e., for a total of $8 \times 3 \times 11 = 264$ instances. Tables 26, 27, 28, 29, 30, 31, 32 and 33 show the optimization results for all these instances.

Table 26 Numerical results for scenario $L_{5}$ of the 8-machine line

Table 27 Numerical results for scenario L₆ of the 8-machine line

Table 28 Numerical results for scenario $L_{7}$ of the 8-machine line

Table 29 Numerical results for scenario L₈ of the 8-machine line

Table 30 Numerical results for scenario L₉ of the 8-machine line

Table 31 Numerical results for scenario L₁₀ of the 8-machine line

Table 32 Numerical results for scenario L₁₁ of the 8-machine line

Table 33 Numerical results for scenario L₁₂ of the 8-machine line