1 Introduction

The intercontinental container liner shipping service, also called the long-haul service in some literature, is defined as the cyclic shipping route covering ports belonging to more than one continent, with fixed port rotation and visiting schedule followed by a series of similar container ships (Wang et al. 2018). Figure 1 depicts a typical example of the intercontinental service, CC1 from the former G6 Alliance. This service covers 4 Asian ports including Qingdao, Shanghai, Kwangyang and Pusan and 2 North American ports including Los Angeles and Oakland. Following the traditions of the liner shipping industry, an intercontinental shipping service consists of two types of shipping legs, the “Intracontinental Port (IP)” leg with the departure and arrival ports within the same continent (e.g., the leg from Qingdao to Shanghai in CC1) and the “Long Haul (LH) leg” that connects two continents (e.g., the leg from Pusan to Los Angeles in CC1). Despite the cyclic route for a service, a starting port (e.g., Qingdao in CC1) is often selected for the convenience of the shipping company. Hence, the direction from the continent containing the starting port to the other continent is defined as “Head Haul (HH)” direction, while the reverse is defined as the “Back Haul (BH)” direction. The two LH legs are further classified as “HH leg” and “BH leg” depending on the directions they belong to. In addition, a complete round trip completed by a container ship in this service is called a “voyage”.

Fig. 1
figure 1

Service CC1 from G6 alliance

Full size image

To satisfy the container shipping demand, before the start of each ship voyage, the liner shipping company usually opens available container slots of the ship for customers booking several weeks ahead. If a customer wants to transport his cargos to the destination port on the other continent by this ship voyage, he first contacts the company to book container slots for the containers. Then the shipping company accepts the booking, and lets the customer load his cargos into the containers and deliver them to the container yard before the gate-in time. Finally, after the gate-in time, the containers are loaded to the ship and are transported to the destination port for customer collection. The whole procedure can be intuitively shown in Fig. 2. We call the time interval between the booking opening day and the ship gate-in day the “booking period” of this voyage meaning that the shippers can freely book and cancel the container ship slots during this period; after this period, no bookings can be accepted or cancelled for this voyage. The length of the booking period varies from one to several months. The gate-in date is usually quite close to the ship departure date, usually 1 or 2 days before the ship departure.

Fig. 2
figure 2

Container slot booking procedure for the intercontinental service

Full size image

During the booking period of each voyage, the shipping company would like to know the amount of containers transported by this voyage in an intercontinental shipping service, which is often used to support many tactical/operational decisions in the decision support system of a shipping company, such as capacity exchange in alliance, empty container relocation between continents, and container freight rate adjustment, all of which are vital to the profitability of the shipping company. However, as the customers can freely book and cancel the container slots during the booking period, this value fluctuates and is unknown until the gate-in time. Therefore, during the booking period, there remains a problem how to predict this finalized slot booking amount that will be transported by this incoming voyage. As the intercontinental service mainly transports containers across different continents, this problem can be also defined as: how to predict the realized shipping demand actually transported through the HH and BH legs respectively, based on the currently arrived booking information during the booking period. Note that here we actually aggregate the ports in the same continent and assume the same booking period for these ports. This is reasonable because the sailing durations between the ports in the same continent are usually quite small compared with those in the LH legs. It is also an industry practice to aggregate the demand from the ports in the same continent because it has more stable pattern and is easier to forecast than that from a single origin and destination (OD) port pair. Also noted that we separately forecast the demands through the HH and BH legs. This is because the demands through these two legs have the opposite origin and destination continents and are thus almost unrelated. In addition, the booking period for the HH and BH legs in the same voyage are also considered different because of the long sailing time between these two continents.

This paper thus solves the container slot booking forecasting problem for an intercontinental shipping service, that is, during the booking period of each ship voyage, how to predict the realized container slot booking amounts through the LH legs by the incoming voyage based on the current booking information for this voyage and the historical data for the completed voyages belonging to the same service. An integrated container slot booking forecasting method is developed in this paper. This method combines the predictions from the different forecasting models such as piecewise linear regression (PLR) model, autoregressive (AR) model and artificial neural network (ANN) model by assigning weights to these models. Test results show the satisfactory forecasting precision of this forecasting model.

The remainder of this paper is organized as follows. In Sect. 2, we review the literature on demand forecasting and analyse the uniqueness of demand forecasting in the intercontinental liner shipping services. In Sect. 3, we introduce the demand forecasting problem considered in this study. In Sect. 4, the tangible forecasting method is developed. The demand forecasting procedure, as well as the model building and training technique, are also presented in this section. Section 5 tests the efficiency of the developed forecasting model on the real-case container slot booking log data. Section 6 gives the conclusions of this study.

2 Literature review

This topic belongs to the area of the container shipping demand forecasting, which can be divided into the aggregate-level forecasting and the disaggregate-level forecasting. The aggregate-level forecasting focuses on the long-term variation of the total number of containers, such as forecasting the annual container throughput of a port. On the other hand, the disaggregate-level forecasting deals with the short-term variation of the container shipping demand for a specific service, which is the focus of this study. Currently, lots of studies focusing on the aggregate-level forecasting for the container shipping demand including Chen and Chen (2010), Fung (2001), Gao et al. (2016), Peng and Chu (2009), Russo and Musolino (2013), Tavasszy et al. (2015), Winston (1981), Woo et al. (2016) and Xie et al. (2013). For example, Fung (2001) used a vector error correction time series model (VECM) with structural identification to forecast the demand for container handling services and analyzed the competition between Hong Kong and Singapore in the East and Southeast Asian market. Tavasszy et al. (2015) investigated the modeling methods and techniques for the analyses of the future global container shipping demand. However, as far as we are concerned, there exist no studies discussing the disaggregate-level forecasting on the container slot booking. This reveals the necessity to study the disaggregate-level container slot booking forecasting for intercontinental liner shipping services.

As a matter of fact, the disaggregate-level demand forecasting has been extensively discussed in the land and airline transportation. For example, in the truck freight transportation, Garrido and Mahmassani (2000) modeled the freight transportation demand for the truckload carrier by means of the space–time multinomial probit model for the tactical and operational plannings. This model considers spatially and temporally correlated error structure. In the study by Al-Deek (2002), the back-propagation (BP) artificial neural network (ANN) model and time series model were combined to forecast the inbound and outbound heavy truck movement using the vessel freight data. Nuzzolo and Comi (2014) developed the demand forecasting models to estimate the Origin–Destination matrices by the transport service, the delivery time period, the tour departure time and the vehicle type. The airline industry is the most successful area for the disaggregate-level demand forecasting and modeling. The earliest study can be traced back to the work by Beckmann and Bobkoski (1958), which examined Poisson, Negative Binomial and Gamma distributions for the stochastic passenger arrivals and concluded that Gamma distribution best fits the data. After that, many studies formulated the airline passenger arrival pattern as the general point process (Gallego and van Ryzin 1994, 1997; Li and Sheng 2016) and different versions of Poisson process, such as non-homogeneous Poisson process (Lee 1990; Zhao 1999), stuttering Poisson process (Rothstein 1968, 1971) and censored Poisson process (Lee 1990). For a comprehensive review on the airline demand modeling and forecasting, we here recommend the review by McGill and van Ryzin (1999).

However, in spite of the sufficient studies conducted in the land and airline transportation, the following characteristics of the liner container shipping make the container slot booking forecasting a worthy research topic:

  1. 1.

    Due to the large capacity of a container ship (up to several thousands of TEUs), compared with the airline and land transportation, the booking amount from a single customer varies more widely, ranging from a few TEUs to tens of TEUs. At the same time, the canceling behaviors of the customers are quite unique. Some customers cancel their bookings completely while some customers cancel part of their bookings. According to our preliminary study with a global shipping company, a considerable percentage of customers choose to cancel half of their bookings during the booking period. Moreover, some customers even recover their bookings after their bookings have been canceled. This increases the challenge in modeling the customer booking behaviors.

  2. 2.

    In the airline seat booking, the seats are classified into different classes by the airline operators, such as first class, business class and economic class, each with specific fare and service level. However, in the liner shipping industry, the services are more customized. For example, the freight rate is usually determined through the negotiation between the customers and sale department of the liner shipping companies. Customers are also different in their container handling priorities, such as the timeliness in handling the delayed containers. Thus, it is generally hard to classify the customers into different classes.

  3. 3.

    In the airline seat booking, the customer may be charged a penalty if he decides to cancel his booking. However, in the liner shipping industry, customers can cancel their bookings without any penalty. This also leads to high canceling rates and large variations in the realized demand.

In the airline demand forecasting, the customer booking arrivals can be formulated as different analytical distributions or stochastic processes, such as Poisson distribution, as is mentioned in above paragraphs. However, for the liner shipping industry, due to the above three reasons, we find it hard to formulate the customer booking/canceling behaviors as specific analytical distributions and stochastic processes from the real booking data. On the other hand, it is interesting to observe that similar patterns exist in the container slot booking among different directions in different services. Figure 3 shows the variations of the container slot booking levels for different voyages in two directions, HH and BH, of an intercontinental service, within 28 days before the gate-in day. Each line in the subfigure represents the container slot booking of a voyage for the corresponding direction during its booking period. It can be seen that, for the two directions, HH and BH, the container slot booking amount generally increases in early days of booking period, reaches the peak and decreases near the gate-in time. This can be explained that when the shipping company starts accepting slot bookings, the booking arrival rate is much higher than the canceling rate. Hence, the cumulative booking will increase fast. For the days quite near the gate-in time, however, more bookings are canceled. As a result, the cumulative booking level will increase more and more slowly or even decrease near the gate-in time. In this study, the pattern existing in the container slot booking data is used for the forecasting model development to predict the booking levels for future voyages. At the same time, it can be also observed that the exact patterns for the two directions, HH and BH, are different (see Fig. 3). Therefore, to give precise results, the forecasting models are separately developed for these two directions, based on the exact pattern in each direction.

Fig. 3
figure 3

Variations of container slot booking levels for different voyages in a service. a Head haul and b back haul

Full size image

3 Container slot forecasting

Consider a liner shipping company that intends to forecast the realized shipping demands in both directions, HH and BH, for the intercontinental shipping services during their booking periods. According to the industrial practice, for each intercontinental shipping service, the shipping company usually starts forecasting when there are T days remaining in the booking period instead of forecasting across the whole booking period, where T is smaller than the booking period length. For example, the booking period can be as long as several months while T is often within 1 month. This is because, at the beginning of the booking period, the booking amount is too small to show a strong pattern. In addition, predicting a value too long time ahead usually incurs large errors and is thus unreliable. The days for the demand prediction can thus be expressed as \(t \in \{ - T, - T + 1, \ldots , - 1\}\). \(t = - T\) means the day when shipping company starts prediction, and \(t = 0\) means the gate-in day of the voyage when the bookings will no longer be accepted or canceled for this voyage.

The shipping company has the historical data depicting the variations of the container slot booking levels across the booking periods for all completed voyages in this service (see Fig. 3 as an example). Denote by V the set of all completed voyages in the historical data. For each voyage \(v \in V\), denote by \(x_{v}^{HH} (t)\) and \(x_{v}^{BH} (t)\) the cumulative slot booking levels for the two directions, HH and BH, respectively on the day \(t \in \{ - T, - T + 1, \ldots , - 1,0\}\). This cumulative container slot booking level is calculated as the total amount of the arrival slot bookings minus the total amount of the bookings canceled by the customers from the start of the booking period day T to the day t. It is thus easy to know that the finalized slot booking level (or the realized container shipping demand) after the booking period is equal to the cumulative container slot booking level on day 0, i.e., \(x_{v}^{HH} (0)\) and \(x_{v}^{BH} (0)\), \(\forall v \in V\). This is because, after the gate-in day \(t = 0\), no bookings can be accepted or canceled. The slot booking level is thus fixed.

Based on the above illustrations, the problem considered in this study can be elaborated here. For the incoming ship voyage \(v_{0}\) in an intercontinental service, on each day \(t_{v0} \in \{ - T, - T + 1, \ldots , - 1\}\) of its booking period, we can collect the current booking information, i.e., the cumulative booking value, \(x_{{_{v0} }}^{HH} (t)\) and \(x_{{_{v0} }}^{BH} (t)\) from the day \(t = - T\) to \(t = t_{v0}\). At the same time, we also have the historical slot booking data of the completed ship voyages in this service, i.e., \(x_{v}^{HH} (t),x_{v}^{BH} (t)\), for all \(t \in \{ - T, - T + 1, \ldots , - 1\}\) and \(v \in V\). In this regard, the forecasting problem in this paper considers, on each day \(t_{v0} \in \{ - T, - T + 1, \ldots , - 1\}\) of the booking period of the incoming shipping voyage \(v_{0}\), how to predict the finalized container slot booking demand \(x_{{_{v0} }}^{HH} (0)\) and \(x_{{_{v0} }}^{BH} (0)\) for the two directions, HH and BH, respectively, based on the historical booking log data \(x_{v}^{HH} (t),x_{v}^{BH} (t),\)\(\forall t \in \{ - T, - T + 1, \ldots , - 1,0\} ;v \in V\) and the currently arrived demand information \(x_{{_{v0} }}^{HH} (t),x_{{_{v0} }}^{BH} (t)\)\(\forall t \in \{ - T, - T + 1, \ldots ,t_{v0} \}\) of the voyage \(v_{0}\). This means that we need to establish a series of forecasting models for \(t_{v0} \in \{ - T, - T + 1, \ldots , - 1\}\) that map \(x_{{_{v0} }}^{HH} (t)\) and \(x_{{_{v0} }}^{BH} (t)\) to \(x_{{_{v0} }}^{HH} (0)\) and \(x_{{_{v0} }}^{BH} (0)\), for the two directions, HH and BH, respectively, namely:

$$\hat{x}_{v0}^{k} (0,t_{v0} ) = f_{{t_{v0} }}^{k} (x_{v0}^{k} (t),t = - T, \ldots ,t_{v0} );\quad t_{v0} \in \{ - T, - T + 1, \ldots , - 1\} ,\quad k \in \{ HH,BH\}$$
(1)

where \(\hat{x}_{v0}^{k} (0,t_{v0} )\) stands for the prediction of the revealed container booking demand made on the day \(t_{v0}\) for direction k using the arrived container slot booking data from the day \(t = - T\) to \(t = t_{v0}\). \(f_{{t_{v0} }}^{k} ( \cdot )\) is the forecasting model for the prediction made on the day \(t_{v0}\) for direction k which can be calibrated from the historical booking data \(x_{v}^{HH} (t),\;x_{v}^{BH} (t);\;t \in \{ - T, - T + 1, \ldots , - 1,0\} ,\;v \in V\). Note that, in Eq. (1), we separately forecast the finalized container slot bookings for the two directions, HH and BH. The value of \(t_{v0}\) is also determined separately for each direction based on its own gate-in day. Equation (1) can be intuitively depicted in Fig. 4.

Fig. 4
figure 4

Container slot booking forecasting on each day \(t_{v0} \in \{ - T, - T + 1, \ldots , - 1\}\)

Full size image

4 Forecasting model building logic

In order to solve the problem defined in Sect. 3, an integrated forecasting model is developed, which combines several different forecasting models (called “member models”) by calculating the weighted average of all these models. Hence, this integrated model is able to reflect the merits of these member models in formulating the patterns of the container slot bookings existing in the historical data. We first briefly introduce these member models. We then show how to build the integrated model and give procedures to use this model for prediction. In addition, some key techniques concerned with this model, such as the model calibration methods and the weight determination methods for these member models are also introduced.

In this study, three member models are considered, i.e., the PLR model, the AR model and the ANN model. The reasons for choosing these three models are illustrated as follows. As is mentioned in Sect. 2, the variations of the container slot booking levels across different voyages share similar patterns. The PLR model is used to formulate the general trend of the slot booking data as a piecewise linear function. The PLR model can be viewed as a macro level forecasting model on the finalized container slot booking amount. The ANN model is also widely used in forecasting. It is able to directly model the relationship between the container slot booking level on each day of the booking period and the finalized container slot booking amount for each voyage in a service. Therefore, it can be viewed as a meso level forecasting model. In addition, it is also able to model the effect of unknown or unclear factors on the forecasting results. Finally, the AR model is a time series model to represent the effect of the previous values on the current value. It reflects the deviations of the container slot booking levels away from the general trend represented by PLR. It can be viewed as a micro level forecasting model on the finalized container slot booking amount. We can see that these three models focus on the slot booking predictions from three different levels, i.e., macro level, meso level and micro level, respectively. Hence, the integrated model combining all these three models is able to give predictions simultaneously reflecting the characteristics of the container slot booking from all three levels. The integrated forecasting model can be shown in Fig. 5. In this model, the prediction result is calculated as the weighted average of the predictions from these three models, which can be expressed as

$$\hat{x}_{vo}^{k} (0,t_{v0} ) = \sum\limits_{{i \in \{ PLR,AR,ANN\} }} {w_{i}^{k} (t_{v0} )\hat{x}_{vo,i}^{k} (0,t_{v0} )} ;\quad t_{v0} \in \{ - T, - T + 1, \ldots , - 1\} ,\quad k \in \{ HH,BH\}$$
(2)

where \(\hat{x}_{v0}^{k} (0,t_{v0} )\) is the prediction result of the integrated model in Eq. (1); \(\hat{x}_{vo,i}^{k} (0,t_{v0} )\) stands for the prediction from the member model \(i \in \{ PLR,AR,ANN\}\) made on the day \(t_{v0}\); \(w_{i}^{k} (t_{v0} )\) is the weight assigned to this member model \(i \in \{ PLR,AR,ANN\}\). We can see that the integrated forecasting model is quite flexible, i.e., the forecasting models used in the integrated method are not exclusive. Other forecasting models can be easily embedded into this forecasting framework by means of the integrated model training method developed in this paper, if readers consider them helpful for precise prediction (and their contributions will be reflected by the weight determined in the modelling training method).

Fig. 5
figure 5

Integrated forecasting model

Full size image

It should be noted that, to capture the time-varying performance of each model across the booking period, the weights \(w_{i}^{k} (t_{v0} )\) in Eq. (2) are day-based, which means that the weights assigned to these three models may not be the same on the different days during the booking period. In addition, seasonality also has a significant effect on the container slot demand level. For example, the number of laden containers from Asia to Europe often increases significantly in the fourth quarter of each year (Meng and Wang 2011). In order to incorporate the effect of seasonality on the forecasting results, a time window is maintained for the historical data. When the booking data of newly finished ship voyages are available, the time window moves forward to incorporate these new data and to remove too old data. The member models are retrained with their weights recalculated for the subsequent forecasts in a rolling-horizon manner. Also noted that the appropriate time window may vary service by service according to the characteristics of the service considered. For example, by default, the time window can be set as 3 months to reflect the seasonal changes in the container shipping demand. For the service with a stable pattern across different seasons, this time window can be expanded in order to incorporate more data for a more precise prediction. On the contrary, if service has large variations in different seasons, the time window should be shortened so that only the data from the recently completed voyages are included to reflect the up-to-date trend of the service. The whole process including model training and forecasting is shown in Fig. 6.

Fig. 6
figure 6

Prediction process for the integrated model

Full size image

The remaining content in this section illustrates how to calibrate the integrated model (as is highlighted by the dotted line in Fig. 6) including the training method for the member models (PLR, AR, and ANN) and the weight determination method for these three models. Finally, a step-by-step forecasting procedure is presented.

4.1 Member model training

4.1.1 Piecewise linear regression (PLR) model

To reflect the pattern shown in the cumulative container slot bookings, the piecewise linear regression (PLR) method is adopted. The PLR, also the called segmented regression, is a regression technique to fit the data with a piecewise linear function. The piecewise function with n breakpoints (or equally, \(n + 1\) line segments) for the container slot booking for the direction \(k \in \{ HH,BH\}\) can be expressed as

$$f_{PLR}^{k} (t) = \beta_{0}^{k} + \beta_{1}^{k} t + \sum\limits_{i = 1}^{n} {\beta_{i + 1}^{k} (t - \alpha_{i}^{k} )sign(t - \alpha_{i}^{k} )} ;\quad t \in \{ - T, - T + 1, \ldots ,0\} ,\quad k \in \{ HH,BH\}$$
(3)

where \({\varvec{\upalpha}}^{{\mathbf{k}}} : = [\alpha_{1}^{k} , \ldots ,\alpha_{n}^{k} ]\) and \({\varvec{\upbeta}}^{{\mathbf{k}}} : = [\beta_{0}^{k} , \ldots ,\beta_{n + 1}^{k} ]\) are parameters to be estimated; t is the independent variable representing the day before the gate-in day; \(Sign( \cdot )\) is a sign function, i.e.

$$Sign(x) = \left\{ \begin{aligned} 1,\quad x > 0 \hfill \\ 0,\quad x = 0 \hfill \\ - 1,\quad x < 0 \hfill \\ \end{aligned} \right.$$
(4)

It can be easily seen that \(\alpha_{1}^{k} , \ldots ,\alpha_{n}^{k}\) represent the n breakpoints of the piecewise linear function. The parameters \({\varvec{\upalpha}}^{{\mathbf{k}}}\) and \({\varvec{\upbeta}}^{{\mathbf{k}}}\) can be estimated by minimizing the sum of squared errors (SSE) of the function (3), \(f_{PLR}^{k} (t)\), with respect to container slot booking data value, \(x_{v}^{k} (t)\). That is

$$\mathop {\hbox{min} }\limits_{{{\varvec{\upalpha}}^{{\mathbf{k}}} ,{\varvec{\upbeta}}^{{\mathbf{k}}} }} SSE^{k} = \sum\limits_{t = - T}^{ - 1} {\sum\limits_{v \in V} {\left( {x_{v}^{k} (t) - f_{PLR}^{k} (t)} \right)^{2} } } ;\quad k \in \{ HH,BH\}$$
(5)

It can be observed that this minimization model is nonconvex and nonsmooth due to the existence of the function \(Sign( \cdot )\). Thus in order to obtain the global optimal solution, the genetic algorithm (GA) is used. As the number of variables in this problem is not very large (e.g., six variables for PLR with two break points and three line segments), GA is able to find the solution quite close to the global optimal solution in a reasonable time. We will not present here the detailed procedure of the GA due to the length of this paper. By solving the minimization model (5), the piecewise linear function can be determined.

Another question related to the PLR model is how to choose the proper number of line segments. Too small number of segments does not sufficiently represent the trend of the slot booking levels. On the other hand, the excessive line segments cause overfitting problem, which also severely affects the prediction precision. In this study, we select the number of line segments according to the Akaike’s Information Criterion (AIC). The AIC simultaneously combines the information theory, maximum likelihood theory and the entropy of information in model assessment. The model with lower AIC value is believed to better represent the actual patterns of the container slot booking (Motulsky and Christopoulos 2004). The AIC value of the PLR model for direction \(k \in \{ HH,BH\}\) can be calculated as

$$AIC_{PLR}^{k} = N^{k} \ln \left( {\frac{{SSE^{k} }}{{N^{k} }}} \right) + 4(n + 1)$$
(6)

where \(N^{k}\) is the total number of data points used in the PLR model; \(SSE^{k}\) is the optimal sum of squared errors in the optimization problem (5); n is the number of breakpoints for the piecewise linear function. To find the proper number of line segments, for each direction \(k \in \{ HH,BH\}\) of a service, we calibrate PLR models with the number of breakpoints n varying from 1 to 5. Then the PLR model with the smallest AIC value is selected as the most proper model for PLR forecasting. Also noted that there exist some other selection criteria for the number of breakpoints, such as BIC and HQIC. These criteria give similar results to AIC in this study and we do not illustrate them in detail.

We take the data shown in Fig. 3 as an example, the AICs under different numbers of breakpoints are shown in Table 1. For head haul (HH), the PLR with three break points has the lowest AIC while, for back haul (BH), the PLR with two break points is the best. The piecewise linear functions for BH and HH are given in Fig. 7 and Table 2.

Table 1 AICs for PLR with different numbers of breakpoints
Full size table
Fig. 7
figure 7

Piecewise linear regression results for cumulative booking level. a Head haul and b back haul

Full size image
Table 2 Parameters \({\varvec{\upalpha}}^{{\mathbf{k}}}\) and \({\varvec{\upbeta}}^{{\mathbf{k}}}\) for the PLR
Full size table

Based on the PLR model, the finalized container shipping demand can be predicted as

$$\hat{x}_{vo,PLR}^{k} (0,t_{v0} ) = x_{v0}^{k} (t_{v0} ) + f_{PLR}^{k} (0) - f_{PLR}^{k} (t_{v0} );\quad t_{v0} \in \{ - T, - T + 1, \ldots , - 1\} ,\quad k \in \{ HH,BH\}$$
(7)

where \(x_{v0}^{k} (t_{v0} )\) is the container slot booking level of the voyage \(v_{0}\) for the direction \(k\) on the forecasting day \(t_{v0}\). \(f_{PLR}^{k} (0) - f_{PLR}^{k} (t_{v0} )\) can be viewed as the incoming booking amount from day \(t_{v0}\) to the gate-in time estimated by PLR model.

4.1.2 Autoregressive (AR) model

The cumulative booking level can be split into two components, the trend and the fluctuation. The trend can be viewed as a long-term pattern of the cumulative booking for all ship voyages, which has been formulated by the PLR model presented in Sect. 4.1.1. The fluctuation, on the contrary, represents the short-term effects on the cumulative booking. In this study, the autoregressive (AR) model is used to formulate this fluctuation component.

Denote by \(f_{PLR}^{k} (t)\) the long-term trend value obtained on the day \(t \in \{ - T, - T + 1, \ldots ,0\}\) for leg \(k \in \{ HH,BH\}\) represented by the PLR model in Sect. 4.1.1. The fluctuation component, \(\tilde{x}_{v}^{k} (t)\), contained in historical data can be obtained by subtracting the trend value from the real data. This operation is called “detrending”.

$$\tilde{x}_{v}^{k} (t) = x_{v}^{k} (t) - f_{PLR}^{k} (t);\quad t \in \{ - T, - T + 1, \ldots ,0\} ,\quad v \in V$$
(8)

It should be noted that the long-term trend can be expressed by other models, such as moving average model and cubic smoothing spline model (see e.g., Hyndman and Athanasopoulos 2014). According to our preliminary tests, these trending models do not affect the prediction power of the AR model. The AR model with the order of n (i.e., n look-back periods, AR(n)) is expressed as

$$\tilde{x}_{v}^{k} (t) = \gamma_{0}^{k} + \sum\limits_{i = 1}^{n} {\gamma_{i}^{k} \tilde{x}_{v}^{k} (t - i)} + \varepsilon ;\quad t \in \{ - T + n, \ldots ,0\} ,\quad v \in V$$
(9)

where \({\varvec{\upgamma}}^{{\mathbf{k}}} : = [\gamma_{0}^{k} , \ldots ,\gamma_{n}^{k} ]\) are parameters to be determined and \(\varepsilon\) is the white noise term. The parameters \({\varvec{\upgamma}}^{{\mathbf{k}}}\) can be easily estimated by linear regression, or equivalently, by minimizing the sum of squared errors (SSE) for each direction k, i.e.,

$$\mathop {\hbox{min} }\limits_{{{\varvec{\upgamma}}^{{\mathbf{k}}} }} SSE^{k} = \sum\limits_{t = - T + n}^{0} {\sum\limits_{v \in V} {\left( {\tilde{x}_{v}^{k} (t) - \gamma_{0}^{k} - \sum\limits_{i = 1}^{n} {\gamma_{i}^{k} \tilde{x}_{v}^{k} (t - i)} } \right)^{2} ;} } \quad k \in \{ HH,BH\}$$
(10)

As this minimization model is convex, the optimal solution can be precisely obtained by the convex optimization algorithms such as gradient method. It should be noted that the order of the AR model, n, also significantly affects the prediction precision. Observe that the numbers of data points used to calibrate the AR model are different for different orders of the AR model. Therefore, different from the PLR model, the AIC cannot be used to select the best order of the AR model as it makes no sense to compare two AICs with different numbers of data points. In this regard, we calculate the p value of the F test in the analysis of variance (ANOVA) for the linear regression (10) for each order \(n \in \{ 1, \ldots ,10\}\) and select the best order of AR model with the lowest p value.

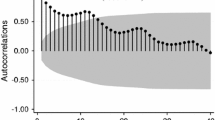
We take the data in Fig. 3 as an example. First, we remove the trend obtained in PLR (see Fig. 7) from the original cumulative booking data. Then we vary the order of the AR model from 1 to 10, calibrate the AR model and select the best order with the lowest p value. For HH direction, the best order is 1 and \(\gamma_{0}^{k} = 0.1048\) and \(\gamma_{1}^{k} = 0.8912\), with \(R^{2} = 0.7985\), and for BH direction, the best order is 1 and \(\gamma_{0}^{k} = 0.3263\) and \(\gamma_{1}^{k} = 0.8227\), with \(R^{2} = 0.7652\). The histograms for white noise term \(\varepsilon\) for these two directions are shown in Fig. 8. We also conducted the autocorrelation analysis for the white noise as shown in Fig. 9. We can see that there exist no autocorrelations in the residuals of the AR models. This means that the AR model is able to sufficiently reflect the autocorrelations of the booking levels in different time periods.

Fig. 8
figure 8

Histogram for the white noise. a Head haul and b back haul

Full size image
Fig. 9
figure 9

Autocorrelation analysis for the white noise. a Head haul and b back haul

Full size image

After the AR model is calibrated, on each day \(t_{v0}\), the realized demand for the incoming voyage, \(\hat{x}_{v0,AR}^{k} (0)\), can be predicted by iteratively calculating the next-day value using the AR(n) from \(t = t_{v0}\) to \(t = 0\). The detailed procedure is illustrated as follows by taking AR(2) as an example: First, on the day \(t_{v0}\) for each direction k, we remove the trend from \(x_{v0}^{k} (t_{v0} )\) and \(x_{v0}^{k} (t_{v0} - 1)\), i.e., \(\tilde{x}_{v0}^{k} (t_{v0} ) = x_{v0}^{k} (t_{v0} ) - f_{PLR}^{k} (t_{v0} )\) and \(\tilde{x}_{v0}^{k} (t_{v0} - 1) = x_{v0}^{k} (t_{v0} - 1) - f_{PLR}^{k} (t_{v0} - 1)\). Then, we calculate the predicted cumulative booking level without the trend for the day \(t_{v0} + 1\) by Eq. (9), i.e., \(\hat{\tilde{x}}_{v0}^{k} (t_{v0} + 1) = \beta_{1}^{k} \tilde{x}_{v0}^{k} (t_{v0} ) + \beta_{2}^{k} \tilde{x}_{v0}^{k} (t_{v0} - 1)\). We repeat this calculation by using the predicted value obtained in previous calculations to predict the value for the next day until we reach the day \(t = 0\) and get the value \(\hat{\tilde{x}}_{v0}^{k} (0)\). Finally, the trend value \(f_{PLR}^{k} (0)\) is added to \(\hat{\tilde{x}}_{v0}^{k} (0)\) to get the predicted value \(\hat{x}_{vo,AR}^{k} (0,t_{v0} )\). The whole process illustrated above can generally be represented as follows

$$\hat{x}_{vo,AR}^{k} (0,t_{v0} ) = f_{{_{AR} }}^{k} (t_{v0} ,x_{v0}^{k} (t_{v0} ), \ldots ,x_{v0}^{k} (t_{v0} - n));\quad t_{v0} \in \{ - T + n, \ldots ,0\} ,\;\quad \in \{ HH,BH\}$$
(11)

4.1.3 Artificial neural network (ANN) model

The ANN is also used for the container shipping demand prediction. The ANN model uses a series of linear relationships to approximate the highly nonlinear and/or unclear relationship between the input parameters and the explained parameter. The readers can refer to the book by Haykin (2009) for the detailed information for the ANN. Here, we adopt the ANN model to formulate the relationship between the current cumulative booking level and the realized container shipping demand.

For the ANN model used in this study, we consider two input variables, i.e., the days before gate-in day \(t_{v0}\) and the cumulative booking level on this day, \(x_{v0}^{k} (t_{v0} )\). We also consider the output variable to be the cumulative booking level on the ship gate-in day, \(x_{v0}^{k} (0)\). In addition, the ANN model has single node layer with 10 nodes, which is enough to represent the relationship between input and output in most cases. The configuration of this ANN model is illustrated in Fig. 10. The ANN model is trained based on the historical booking data: the input \((t,x_{v}^{k} (t))\) and output \(x_{v}^{k} (0)\) for all \(v \in V\). Due to the length of this paper, we will not introduce how to train ANN. The readers can find the training method in the book by Haykin (2009). As an example, we take the data shown in Fig. 3 to train the ANN model.

Fig. 10
figure 10

Structure of artificial neural network model

Full size image

Figure 11 shows the histogram of the ANN fitting errors of the historical booking data on HH and BH directions respectively.

Fig. 11
figure 11

Fitting errors of the ANN model for HH and BH legs. a Head haul and b back haul

Full size image

The realized container shipping demand for the incoming voyage \(v_{0}\), \(\hat{x}_{v0,ANN}^{k} (0)\), can be predicted by putting the day \(t_{v0}\) and current cumulative booking level \(x_{v0}^{k} (t_{v0} )\) into the ANN, i.e.,

$$\hat{x}_{v0,ANN}^{k} (0,t_{v0} ) = f_{ANN}^{k} (t_{v0} ,x_{v0}^{k} (t_{v0} ));\quad t_{v0} \in \{ - T, \ldots ,0\} ,\quad \in \{ HH,BH\}$$
(12)

4.2 Weight determination

Now we determine the day-based weights in Eq. (2) so as to combine all forecasting results from the three models. There exist a series of combination methods, such as simple average combination method, variance–covariance method, discounted mean square forecast error method and information-based method (see e.g., Cang and Yu 2014; Gao et al. 2016; Shen et al. 2008; Wong et al. 2007). Shen et al. (2008) examine that the variance–covariance method gives the best performance. Therefore, in this paper, the variance–covariance method is adopted to determine the weights for the three member models.

This method determines the optimal weights assigned to these three models that minimize the sum of the squared distance between the actual data value \(x_{v,i}^{k} (0)\) and the weighted average of the fitted values \(\hat{x}_{v,i}^{k} (0,t_{v} )\)\(i \in \{ PLR,AR,ANN\}\) for all voyages of a service in the training data (see Shen et al. 2008). For the direction \(k \in \{ HH, \, BH\}\), this can be expressed as

$$\mathop {\hbox{min} }\limits_{{{\mathbf{w}}^{k} }} \sum\limits_{t = - T}^{ - 1} {\sum\limits_{v \in V} {\left( {x_{v}^{k} (0) - \sum\limits_{{i \in \{ PLR,AR,ANN\} }} {w_{i}^{k} (t)\hat{x}_{v,i}^{k} (0,t)} } \right)^{2} } }$$
(13)

subject to

$$\sum\limits_{{i \in \{ PLR,AR,ANN\} }} {w_{i}^{k} (t)} = 1;\quad t_{v} \in \{ - T, \ldots , - 1\}$$
(14)
$${\mathbf{w}}^{k} \ge 0$$
(15)

where the weights vector \({\mathbf{w}}^{k} : = [w_{i}^{k} (t)|t = - T, \ldots , - 1;\;i \in \{ PLR,AR,ANN\} ]\) is the decision variables. \(\hat{x}_{v,i}^{k} (0,t_{v} )\) represents the fitted value from model i for the actual data \(x_{v}^{k} (t),t = - T, \ldots ,t_{v}\), i.e.

$$\hat{x}_{v,i}^{k} (0,t_{v} ) = f_{i}^{k} (x_{v}^{k} (t),t = - T, \ldots ,t_{v} );\quad i \in \{ PLR,AR,ANN\} ,\quad t_{v} \in \{ - T, \ldots , - 1\} ,\quad k \in \{ HH,BH\}$$
(16)

The first item in the bracket of the objective function (13) refers to the realized booking value in the historical data; the second item is the weighted average of the fitted values from the three forecasting models. Constraint (14) guarantees that the sum of the weights assigned to these three models should equal to 1. The constraint (15) is the non-negativity constraint. It is easy to see that this model is convex with respect to the decision variables \({\mathbf{w}}^{k}\). Thus it can be efficiently solved by the convex optimization algorithms.

4.3 Step-by-step forecasting procedure

For the incoming ship voyage \(v_{0}\) in the intercontinental shipping service, we now give the step-by-step forecasting procedure for the realized container slot booking. Note that in this procedure, Step 0 updates the historical data to incorporate the seasonality in a rolling horizon manner. If new data are added to the historical data, the forecasting model is retrained as is shown in Step 1 and Step 2.

Forecasting procedure

 

Input:

Current day index \(t_{v0}\); the direction k; the arrived booking information \(x_{v0}^{k} (t)\) for \(t \in \{ - T, - T + 1 \ldots ,t_{v0} \}\).

Output:

Prediction for the realized container slot booking level, \(\hat{x}_{v0}^{k} (0,t_{v0} )\).

Step 0.

(Historical data updating) If there exists a newly finished ship voyage \(v_{new}\) in this service that is not contained in \(V\), add \(v_{new}\) into \(V\), i.e., \(V = V \cup \{ v_{new} \}\). Also remove the oldest voyage \(v_{old}\) from \(V\), i.e., \(V = V\backslash\{ v_{old} \}\). If \(V\) is updated, go to Step 1. Otherwise, go to Step 3.

Step 1.

(Member model training) Train the three models, PLR, AR and ANN, based on the newly updated historical data according to Sects. 4.1.1–4.1.3.

Step 2.

(Weight determination) Determine the day-based weights for the three models, PLR, AR, and ANN, based on the updated historical data according to Sect. 4.2.

Step 3.

(Member model forecasting) Calculate the forecasting value \(\hat{x}_{v0,i}^{k} (0);i \in \{ PLR,AR,ANN\}\) by these three models according to Sects. 4.1.1–4.1.3.

Step 4.

(Integrated model forecasting) Calculate the weighted average \(\hat{x}_{v0}^{k} (0,t_{v0} )\) of the forecasting value \(\hat{x}_{v0,i}^{k} (0)\)\(i \in \{ PLR,AR,ANN\}\) by these three models according to Eq. (2) based on the weights assigned to these three models.

Step 5.

(Output) Return the value \(\hat{x}_{v0}^{k} (0,t_{v0} )\).

5 Numerical test

In this section, the efficiency of the integrated forecasting model is evaluated based on the real-case container slot booking data from a global liner shipping company. The data record slot bookings within 1 year (from mid-2015 to mid-2016) for the 17 intercontinental services from the typical trade lanes including Asia-Europe, Asia-North America (west coast), Asia-North America (east coast), North–South America etc. For the sake of confidentiality, we do not show the names and port call sequences of all these services. In the container slot booking data, we have removed the irregular voyages with the structural changes. For example, in some voyage, the ship type or the port rotation is changed. For each service, we randomly choose the voyages data for model training and testing, which are shown in Table 3. We also assume \(T = 28\), which means that shipping company starts forecasting when there are 28 days left for the booking period.

Table 3 Intercontinental services used for efficiency test
Full size table

For each shipping service and each direction (HH or BH), an integrated forecasting model is calibrated based on the training voyages data of this service (so there are 34 models calibrated in total). The average weight of the model for each service and each direction is shown in Table 4. We can see that the ANN model makes the most contributions among the three to the final predictions. This can be explained that the ANN model gives good predictions at most time in the booking period compared with the remaining two models. But the other two models (PLR, AR) indeed have positive weights indicating that they also contribute to the final results.

Table 4 Average weights of the three models (PLR, AR and ANN) for each shipping service
Full size table

Then the forecasting efficiency is tested on the testing voyages. On day \(t \in \{ - T, \ldots , - 1\}\) during the booking period of the testing voyages, we make the predictions on the realized container shipping demand and compare it with the actual value to calculate the forecasting error according to following formula

$${\text{Error}} = \left| {{\text{Actual}}\;{\text{value}} - {\text{Predicted}}\;{\text{value}}} \right| / {\text{Actual}}\;{\text{value}} \times 100\%$$
(17)

where \(\left| x \right|\) means the absolute value of x.

The average forecasting errors (i.e., mean absolute percentage error, MAPE) are reported in Table 5 for the forecasts made 1–4 week(s) ahead of the gate-in time for the test voyages. Note that the satisfactory error limits for the liner shipping company are 20% for forecasts made 3–4 weeks ahead and 10% for forecasts made 1–2 weeks ahead. It can be seen that most of the forecasting errors satisfy the requirement. This demonstrates the high precision of the developed forecasting model. In addition, the forecasting errors tend to be smaller for the forecasts made just a few days before the gate-in day (e.g. 1 week ahead) than those with quite long time ahead (e.g. 4 weeks ahead). This can be easily explained that forecasting an uncertain value too long time before its realization suffers large uncertainties and thus incurs large prediction error. Finally, it can be also noticed that, although the overall forecasting precisions are satisfactory for both the HH and BH directions, the predictions for the HH direction are generally better than those for the BH direction. This is because the data for the HH direction show clearer pattern than those for the BH direction, which makes it harder to predict the container shipping demand on the BH direction than the HH direction.

Table 5 MAPE of the integrated model on testing data
Full size table

To further investigate the forecasting efficiency of the forecasting method developed in this paper, we move to compare the forecasting results between the integrated method and each of the three member models. The forecasting results of these models on the test data can be seen in Table 6. We can see that the ANN model generally shows a better forecasting precision than the other two member models (PLR and AR), which is consistent with the observations in Table 4. This may be because of its ability to directly model the relationship between booking value on the day of prediction and the finalized booking amount and to incorporate unknown factors affecting the prediction. In addition, the integrated model outperforms the other methods in both HH and BH directions for all four-week forecastings. This means that the integrated model is able to combine the merits of the three member models in representing the pattern of the container slot booking data. Above results show the satisfactory forecasting efficiency of the integrated model.

Table 6 MAPE for different forecasting methods
Full size table

6 Conclusions and discussions

Intercontinental shipping services operated transport containers between different continents. This paper discussed how to forecast the realized container slot booking amount between two continents by the intercontinental service for the incoming ship voyage. Considering the patterns existing in the historical container slot booking data, an integrated forecasting model was developed for this problem. This model combines the forecasting powers from the piecewise linear regression (PLR) model, the autoregressive (AR) model, and the artificial neural network (ANN) model by calculating the weighted average of the results from these three models. We also introduced the training methods for the models and discussed how to determine the weights assigned to these three models in the integrated model. The test results based on the real-case booking data showed the satisfactory precision of the developed model.

Future research extending this study can be conducted as follows. First, this forecasting model is developed based on the data pattern and does not consider the effects of exogenous variables on the container slot booking, such as the general economic condition, the market share of a shipping company and market competition. Therefore, future studies can incorporate these factor for more precise predictions. In addition, this model only focuses the number of containers to transport in each of the two directions and cannot predict the utilization rate of a container ship. Therefore, future studies can consider the ship utilization prediction.