A mathematical model for the optimization of agricultural supply chain under uncertain environmental and financial conditions: the case study of fresh date fruit

Abstract

In recent years, due to the rapid growth of the world’s population, the demand for agricultural products and food is growing increasingly. Therefore, the agricultural supply chain optimization has been grabbed by researchers to reduce food security concerns. On the other hand, the production amount of farmers is affected by various factors, including environmental conditions. In this paper, a supply chain network is investigated by developing a Mixed-Integer Linear Programming (MILP) model to effectively improve economic objectives under uncertainty. Then, a scenario-based robust optimization approach is employed to deal with the uncertainty. One of the novelities of our paper is considering weather conditions and economic fluctuations in different scenarios. The effectiveness of the proposed mathematical model has been confirmed by a real case study of dates farms. Dates and its by-products have a significant role in GDP, job creation, export, and the creation of various packaging and processing. Moreover, three meta-heuristic algorithms including Whale Optimization Algorithm (WOA), Particle Swarm Optimization (PSO), and a hybrid algorithm based on them (WOA–PSO) are adapted to deal with the NP-hardness of the problems. Moreover, the parameters of the proposed algorithms are improved by the Taguchi method, and to achieve more exact measurements, sensitivity analysis is performed. Finally, the numerical results confirmed that the accuracy of the hybrid algorithm was between 1.9 and 2.8%. Therefore, this approach could be practical and efficient for solving large-sized problems. The obtained outcomes demonstrated that the planned model provides tactical considerations for the related managers.

1 Introduction

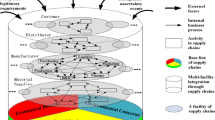
Nowadays, many countries consider agricultural supply chain (ASC) management an essential research topic (Roghanian and Cheraghalipour, 2019). Many researchers have distinguished the ASC from other products’ supply chains, due to their notable differences, such as corruption and different product qualities (Jolai, 2022). Moreover, the agriculture sector faces new challenges, such as an uncertain environment that complicates managerial decision-making (Borodin et al., 2016). According to Food and Agriculture Organization (FAO) in 2010, agricultural products have a significant role in GDP, job creation, export, and the creation of various packaging and processing industries (Seif et al., 2023). Recently, agriculture is also considered one of the major drivers of economic growth in many countries (Cheraghalipour et al., 2019). While a large portion of the harvested product is consumed fresh, lower-quality products are used in the processing industry to make products such as juice, jam, jelly, powder, syrup, etc. (Oladzad et al., 2021). In addition, agricultural residues are rich in carbohydrates, making them a suitable feedstock to make a variety of value-added products (Oladzad et al., 2021). The agricultural products value chain includes production, processing, wholesaling, and retailing (Fatima et al., 2016) (see Fig. 1).

Fig. 1

Structure of agricultural products value chain (Fatima et al., 2016)

Due to the unique characteristics and the unstable environment of ASC, managers should consider the uncertainty in decision-making processes (Gholian-Jouybari et al., 2023). In the real world, there are some uncertain paramerters such as fluctuations in the product price (Boronoos et al., 2021). The demand for agricultural products is strongly influenced by the price and quality of the product, and climate change also has a significant effect on the farmer’s yield (Cheraghalipour and Roghanian, 2022). Besides, the production cost of this product could experience a high fluctuation rate during the cultivation period for its farmers (Rajabi-Kafshgar et al., 2023). Therefore, the demand for these products, their price, production cost, and the amount of harvested products are affected by environmental uncertainty. Considering the importance of environmental, economic, and social effects in the decision-making process, it is necessary to use analytical tools for quantitative evaluation of different options (Cheraghalipour et al., 2019).

Robust optimization is an appropriate and proven methodology for dealing with uncertainty. Mulvey et al. (1995) used scenario-based robust optimization approach to predict the scenarios that date supply chain managers consider to predict future conditions. In this research, we attempt to present a robust model by considering scenario-based stochastic programming, which optimize the robustness, by utilizing the variance of the objective function. However, the literature review shows a research gap in ASC optimization by using this approach. One of the innovations of this research is to design a supply chain for agricultural products and their by-products, considering uncertain weather conditions and economic fluctuations, which has been rarely investigated.

In this study, a Mixed-Integer Linear Programming model (MILP) is planned to optimize the ASC supply chain’s profit. In order to fill the research gap mentioned above, some parameters are uncertain, including the demand, price, production cost, and the amount of the harvested crop. One of the novelities of our paper is considering weather conditions and economic fluctuations in different scenarios. A scenario-based robust technique is used to reduce the impacts of uncertainty. In addition, three meta-heuristic algorithms are employed as the solution methods, namely, Particle Swarm Optimization Algorithm (PSO), Whale Optimization Algorithm (WOA), and a new hybrid algorithm based on them (PSO–WOA). Furthermore, the validity of the proposed is checked using a real case study. Therefore, the novelities of this paper are presented in three significant aspects:

• Designing a supply chain network for agricultural products considering their by-products.

• Developing a mathematical model to optimize total profit under uncertainty including demand, weather conditions, and economic fluctuations in different scenarios.

• Presenting a hybrid meta-heuristic algorithm based on PSO and WOA to solve the planned model in large-sized scale.

This article is organized into six sections so that an overview of the literature related to the research background is provided in Sect. 2. The scenario-based robust approach is detailed in Sect. 3, and the proposed network and robust model are presented in Sect. 4. The solution methods and meta-heuristic algorithms are described in Sect. 5. Moreover, the evaluation of the planned model is checked on a real case of date fruit supply chain in Iran, and the model parameters are tuned. Moreover, the numerical results are analyzed in this section. Finally, conclusions and managerial insights are provided in Sect. 6.

As stated, the main goal of this research is to optimize an ASC under uncertainty. In this section, an introduction to this topic was given. In the next sections, the mathematical model used to optimize the objectives and its solution approach, and the obtained results will be stated and described.

2 Literature review

Most recently, many researchers have proposed various mathematical models for optimizing many agricultural products logistics (Shafiee Roudbari et al., 2023). From the literature review, researchers can identify the barriers, enablers, and performance indicators of ASC and propose different methodologies to enhance the ASC performance (Srikanta and Astajyoti, 2016). However, ASC management will be more complex due to unpredictable weather conditions, uncertainty in harvest yield, being perishable, and having characteristics like the seasonality of agriculture production (Aramyan et al., 2006).

The current research aims to study the ASC under uncertainty. Given that agricultural products are of economic importance in the countries that produce them, there are numerous articles in the literature that evaluate and analyze agricultural products such as Castillo et al. (2023), Chandrasekaran and Bahkali (2013), and Oladzad et al. (2021); however, according to our knowledge, a few research studies have been performed proposing a mathematical model for optimizing the ASC under uncertainty. Therefore, some papers published in the scope of agricultural products are examined in two categories: papers in the scope of ASC and papers considering uncertainty in ASC optimization models.

2.1 ASC

In developing countries, ASC plays a vital role in social, economic, and environmental attitudes (Cheraghalipour et al., 2018). So, operational mathematical approaches were improved the structure of this sector, since the late 1940s. In the first attempt to reveal this field, van Berlo (1993) planned a mathematical model for vegetable supply chain optimization and used an objective programming approach for solving the model. Addressing the fresh food supply chain network was another research performed by Tsao (2013). In this paper, a mathematical model was planned for the optimal discovery of appropriate services for agricultural markets.

Ge et al. (2016) studied the possibility of cost minimizing in wheat logistics by planning a simulation model in Canada. Mogale et al. (2018) designed the food grain logistics network and presented a mathematical model to obtain optimal transportation, allocation, and capacity of silos in India. Cheraghalipour et al. (2018) designed a mathematical model for the citrus supply chain. In other research, Cheraghalipour et al. (2019) addressed the rice supply chain network and used meta-heuristic algorithms to optimize the chain’s costs. Furthermore, Anderson and Monjardino (2019) discussed arranging supply chain contracts, considering performance risk to reduce wheat prices in Australia. The results of their research showed that this arrangement is related to the risk aversion of farmers. Some meta-heuristics algorithms are employed to optimize the chain’s costs. Salehi-Amiri et al. (2021a, 2021b) formulated a new model to optimize walnut logistics costs. They used some hybrid meta-heuristics algorithms to solve the planned model. Computational results confirmed the supremacy of hybrid approach. Baratsas et al. (2021) presented a novel circular economy system engineering framework and decision-making tool for the modeling and optimization of food supply chains. Rajabi-Kafshgar et al. (2023) considered environmental impacts of agricultural wastes and proposed a MILP model for an agriculture supply chain network to minimize total costs. Some well-known meta-heuristic algorithms are used to solve their model. Gholipour et al. (2023) presented an agricultural closed-loop supply chain aiming at minimizing the costs of supply chains and reducing the supply risks considering intelligence technology.

2.2 Uncertainty in ASC

Since the production of agricultural products is affected by climatic conditions, and the market for agricultural products is susceptible to economic fluctuations, ASC managers should consider the uncertainty (Motevalli-Taher et al., 2020). In many studies in the field of ASC optimization, uncertainty in the model has been considered. For example, Grillo et al. (2019) designed a model for optimizing the oranges supply chain in Spain. They used a triangular fuzzy method for managing uncertainty.

Carvajal et al. (2019) proposed an efficient model for managing the sugarcane logistics, which included many operational and strategic choices for optimizing the factories’ profit. Also, a robust technique was applied to deal with the uncertain weather conditions in Colombia. Wang and Chan (2020) planned a combined decision model, in agricultural production systems. Motevalli-Taher et al. (2020) developed a model to optimize wheat production considering sustainability aspects. Gilani and Sahebi (2021) proposed a bi-objective model to optimize total profit and minimize the pollutants in pistachio supply chain, considering uncertainity of demand and cost. In their research, a robust fuzzy optimization approach was used to handle uncertainty. Gholian-Jouybari et al. (2023) addressed an ASC network considering marketing practices. A stochastic mathematical model was formulated to optimize total costs and environmental factors under uncertainty. Some meta-heuristics algorithms were used to solve their model. D’Adamo (2022) used the analytic hierarchy process method to assign relevance to sustainability criteria in ASC and proposed stakeholder engagement as an order winner for sustainable strategies.

3 Research gap

In this section, to identify the research gaps related to the agricultural logistics network, a brief overview of the past studies is reported in Table 1. Reviewing previous studies, we conclude that there are few researches focusing dates supply chain considering uncertainty. Moreover, employing robust approaches to deal with uncertainty especialy in environmental conditions in the scope of ASC is rarely seen. To fill the research gap, in this paper, a scenario-based robust optimization model is planned for ASC optimization. The model’s objective is to obtain the maximum profit, considering uncertainty on some parameters. By solving this model, the optimal flow of products between facilities, inventory level, and the amount of by-products production will be determined in each period.

Table 1 Some previous studies were published in ASC scope

4 Robust optimization

Several approaches are used to control the uncertainty in mathematical models by different researchers. The robust approach can help controlling system perturbations and is considered a reliable technique to tackle uncertainty (Sahinidis, 2004). There are two types of robustness: solution and model robustness. The solution stays near-optimal by considering the solution robustness type, and it is relatively achievable in a scenario set for the model robustness type. Before providing a robust model, we define two sets of variables:

• $x \in R^{n1}$: Design variables vector

• $y \in R^{n2}$: Control variables vector

The structure of the scenario-based robust optimization model is defined below:

$$Min c^{T} x + d^{T} y$$

(1)

$$Ax{ } = { }b{ }$$

(2)

$$Bx + Cy{ } = {\text{ e}}$$

(3)

$$x.y \ge 0\quad {\text{and}}\quad x \in R^{n1} ; y \in R^{n2}$$

(4)

Equation (2) represents the structural constraint, whose coefficients are constant and have no noise. Equation (3) defines the control constraint with noise in the coefficients. Non-negative vectors are maintained in Eq. (4). A series of scenarios including $\Omega = \left\{ {1,2, . . ., S} \right\}$ are defined so that $p_{s}$ is the chance of each scenario occurring and $\mathop \sum \nolimits_{s = 1}^{S} p_{s} = 1$. In general, the scenario-based robust model is formulated as follows:

$$\min z = \sigma \left( {x.y_{1} .y_{2} { }. \ldots .y_{s} } \right) + \omega \times {\Sigma }\rho \left( {\delta_{1} . \ldots .\delta_{s} } \right)$$

(5)

$$Ax = b$$

(6)

$$B_{s} x + C_{s} ys + \delta_{s} = e_{s} ,\quad s \in \Omega$$

(7)

$$x \ge 0 \cdot y_{s} \ge 0,\quad s \in {\Omega }$$

(8)

The model robustness principles are formulated in the second segment of the above objective function. It denotes that specific scenarios can result in inapplicable designs, based on an input parameter set, where ω means the scenario's inapplicable weight (Safaei et al., 2017). Yu and Li (2000) proposed an appropriate formulation for this objective function's first term, which is defined as below:

$$Minz = \mathop \sum \limits_{s \in S} p_{s} \xi_{s} + \lambda \mathop \sum \limits_{s \in S} p_{s} \left[ {\left( {\xi_{s} - \mathop \sum \limits_{s^{\prime} \in S} p_{s^{\prime}} \xi_{s^{\prime}} } \right) + 2\theta_{s} } \right]$$

(9)

$$\xi_{s} - \mathop \sum \limits_{s \in S} P_{s} \xi_{s} + \theta_{s} \ge 0$$

(10)

5 Problem definition

Although, the production of agricultural products shows an increase in many countries, due to the inefficiency and lack of logistics management, vast amounts of these products are rotten. Therefore, optimal supply chain control with minimal loss of quantity and quality during transportation and production and its by-products is critical.

In this paper, a five-level supply chain network for agricultural products is desiged. Moreover, a MILP mathematical model for optimizing the chain’s profits is presented. The multi-period network includes farmers, sorting centers (SCs), distribution centers (DCs), processing industries (PIs), valorization industries (VIs), and markets (customers). As illustrated in Fig. 2, in the proposed network, farmers at the lowest level send their harvested products to the SCs for packaging in the harvest periods. Then, low- and high-quality products are sent to the DCs, and the rotten products are sent to the VIs for processing into various value-added products. The DCs can hold products for a limited time. Then, low-quality products are shipped to the PIs, and high-quality products are sent to the markets to meet customer’s demands. Moreover a portion of the stored products is rotten which is sent to the VIS. After that, PIs produce some kinds of by-products, such as syrup and sent them to the markets. Moreover, the refined product residues such as seeds are sent to the valorization industries. It is assumed that all of the locations are fixed except for new PIs. The proposed model seeks to find optimum flows of products transferred between different facilities in each period under uncertainty of demand, price, production cost, and the amount of the harvested crop.

Fig. 2

The proposed supply chain for agricultural products

5.1 Assumption

• 1. Both facility capacities and transportation costs are predetermined.

• 2. Each farmer sends its products to only one SCs.

• 3. The locations of all facilities are known, but some potential sites for opening new PIs are considered.

• 4. A time horizon of 1 year is considered.

5.2 MILP model

5.2.1 Indices

$i \in I$::

Index for farmers

$j \in J$::

Index for SCs

$d \in D$::

Index for DCs

$n_{1} \in N1$::

Index for current PIS

$n_{2} \in N2$::

Index for new PIS

$n \in N = N1 \cup N2$::

Index for all PIs

$q \in Q$::

Index for the quality of products

$c \in C$::

Index for by-product types

$m \in M$::

Index for markets

$v \in V$::

Index for VIs

$t \in T = \left\{ {1.2 \ldots .t^{\prime} \ldots .t} \right\}$::

Index for time periods

$s \in S$::

Index for scenarios

5.2.2 Parameters

$fc_{n2}$::

Fixed cost of establishing PI n₂

$cpa_{i}^{s}$::

Production cost per unit for farmer i under scenario s

$cha_{d}$::

Holding cost for per unit of product by Dc d

$cpc_{cn}$::

Producing cost per unit of by-product c in the PI n

$cta_{ij}$::

Shipping cost from farmer i to the PC j

$ctb_{jd}$::

Shipping cost from SC $j$ to the DC $d$

$ctc_{jc}$::

Shipping cost from SC $j$ to the VI $c$

$ctg_{dm}$::

Shipping cost from DC $d$ to PC m

$ctk_{dv}$::

Shipping cost from DC $d$ to VI v

$ctf_{dn}$::

Shipping cost from DC d to PI $n$

$cth_{nv}$::

Shipping cost from PI n to VI v

$cti_{nm}$::

Shipping cost from PI $n$ to market m

$cap_{cnt}$::

Production capacity of PI $n$ for by-product c in time period t

$capd_{d }$::

Holding capacity of DC $d$

$capf_{n }$::

Holding capacity of PI $n$

$a_{i}^{s}$::

Waste percentage of the harvested product by farmer i under scenario s

$da_{mt}^{s}$::

Demand for fresh productwith by market m in period t under scenario s

$db_{cmt}^{s}$::

Demand for by-product c by market m in time period t under scenario s

$ca_{t}^{s}$::

High-quality product price in period t under scenario s

$cc_{t}^{s}$::

By-product c price in period t under scenario s

$M$::

A big positive number

$P_{s}$::

The probability of occurrence of scenario s

$\varphi$::

Waste percentage of the received product in SCs

$\beta$::

Waste percentage of held products in DCs

$\sigma_{c}$::

The conversion rate of low-quality product to by-product c

5.2.3 Decision variables

$Xha_{{qjt^{s} }}$::

Quantity of the product with quality q stored in DC d in period t under scenario s

$Xa_{{ijt{^{\prime}}^{s} }}$::

Quantity of the product transported from farmer $i$ to SC $j$ under scenario $s$ in period $t\prime$

$Xb_{{qjdt{^{\prime}}^{s} }}$::

Quantity of the product with quality q transported from SC $j$ to DC d under scenario $s$ in period $t\prime$

$Xg_{dmt^{\prime}}^{s}$::

Quantity of high-quality product transported from DC d to market m in period $t\prime$ under scenario $s$

$Xf_{dnt}^{s}$::

Quantity of low-quality product transported from DC d to PI n in period $t$ under scenario $s$

$Xc_{{jvt{^{\prime}}^{s} }}$::

Quantity of the rotten product shipped from SC $j$ to VI v under scenario $s$ in period $t\prime$

$Xk_{{dvt{^{\prime}}^{s} }}$::

Quantity of the rotten product shipped from DC $d$ to VI v under scenario $s$ in period $t\prime$

$Xh_{{nvt{^{\prime}}^{s} }}$::

Quantity of the rotten product shipped from PI $n$ to VI v under scenario $s$ in period $t\prime$

$Xi_{cnmt}^{s}$::

Quantity of by-product c transported from PI $n$ to markets $m$ in period $t$ under scenario $s$

$\theta_{s}$::

Linearization variable under scenario $s$

5.2.4 Binary variables

$$W_{{n_{2} }} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\;{\text{new}}\;{\text{PI}}\;n2\;{\text{is}}\;{\text{estblished}}} \hfill \\ 0 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$

$$V_{ij} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\;{\text{farmer}}\;i\;{\text{sends}}\;{\text{goods}}\;{\text{to}}\;{\text{SC}}\;j} \hfill \\ 0 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$

Aiming at maximizing total profit, the objective function is defined as follows:

$$\begin{aligned} z & = \mathop \sum \limits_{m \in M} \mathop \sum \limits_{{{\text{d}} \in D}} \mathop \sum \limits_{t \in T} ca{}_{t}^{s} \times Xg_{dmt}^{s} + \mathop \sum \limits_{c \in C} \mathop \sum \limits_{p \in P} \mathop \sum \limits_{t \in T} cc_{ct}^{s} \times Xq_{cpt}^{s} \\ & - \mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} \mathop \sum \limits_{{t{^{\prime}} \in T}} cta_{ij} \times Xa_{{ijt{^{\prime}}}}^{s} - \mathop \sum \limits_{j \in J} \mathop \sum \limits_{d \in D} \mathop \sum \limits_{t \in T} \mathop \sum \limits_{q \in Q} ctb_{jd} \times Xb_{qjdt}^{s} - \mathop \sum \limits_{d \in D} \mathop \sum \limits_{m \in M} \mathop \sum \limits_{t \in T} ctg_{dm} \times Xg_{dmt}^{s} \\ & - \mathop \sum \limits_{d \in D} \mathop \sum \limits_{n \in N} \mathop \sum \limits_{t \in T} ctg_{dn} \times Xf_{dnt}^{s} - \mathop \sum \limits_{v \in V} \mathop \sum \limits_{j \in J} \mathop \sum \limits_{{t^{\prime} \in T}} ctc _{jv} \times Xc_{{jvt{^{\prime}}^{s} }} - \mathop \sum \limits_{d \in D} \mathop \sum \limits_{v \in V} \mathop \sum \limits_{t \in T} ctk_{dv} \times Xk_{{dvt^{\prime s} }} \\ & - \mathop \sum \limits_{n \in N} \mathop \sum \limits_{v \in V} \mathop \sum \limits_{t \in T} cth_{nv} \times Xh_{{nvt{ }^{s} }} - \mathop \sum \limits_{c \in C} \mathop \sum \limits_{n \in N} \mathop \sum \limits_{m \in M} \mathop \sum \limits_{{t^{\prime} \in T}} cti_{nm} \times Xi_{cnmt}^{s} - \mathop \sum \limits_{c \in C} \mathop \sum \limits_{n \in N} \mathop \sum \limits_{m \in M} \mathop \sum \limits_{{{\text{t}} \in T}} cp_{ct}^{s} \times Xi_{cnmt}^{s} \\ & - \mathop \sum \limits_{n2 \in N2} fc_{{n_{2} }} \times w_{{n_{2} }} + \mathop \sum \limits_{q \in Q} \mathop \sum \limits_{d \in D} \mathop \sum \limits_{t \in T} cha_{d} \times Xha_{qdt}^{s} - \mathop \sum \limits_{i \in I} \mathop \sum \limits_{j \in J} \mathop \sum \limits_{{t^{\prime} \in T}} cpa_{i}^{s} \times Xa_{{ijt^{\prime}}}^{s} \\ \end{aligned}$$

(11)

The objective function (11) seeks to find the maximum profit, which includes the selling value of the product and by-products minus the shipping cost between facilities, the production cost for farmers and PIs, the holding cost for DCs, and fixed opening costs. We present the model and constraints as follows:

$$\max z = \mathop \sum \limits_{s \in S} p_{s} \cdot z + \lambda \times \mathop \sum \limits_{s \in S} p_{s} \left\{ {{\text{z}} - \mathop \sum \limits_{s \in S} p_{s} \cdot z_{ } + 2 \theta_{s} } \right\} - \omega *\mathop \sum \limits_{s \in S} \delta \left( s \right)$$

(12)

5.2.5 Constraints

$${\text{min}}cap_{{it{^{\prime}}}} \le \mathop \sum \limits_{j \in J} Xa_{{ijt{^{\prime}}}}^{s} \le \left( {1 - a_{i}^{s} } \right) \times cap_{{it{^{\prime}}}} \quad \forall i \in I.t^{\prime} \in T.s \in S$$

(13)

$$\mathop \sum \limits_{i \in I} \mathop \sum \limits_{{t{^{\prime}} \in T{^{\prime}}}} Xa_{{ijt{^{\prime}}}}^{s} = \mathop \sum \limits_{d \in D} \mathop \sum \limits_{t \in T} \mathop \sum \limits_{q \in Q} Xb_{qjdt}^{s} + \mathop \sum \limits_{v \in V} \mathop \sum \limits_{t \in T} Xc_{jvt}^{s} \quad \forall j \in J.s \in S$$

(14)

$$Xha_{qdt}^{s} = Xha_{qdt - 1}^{s} + \mathop \sum \limits_{j \in J} Xb_{qjdt}^{s} - \mathop \sum \limits_{m \in M} Xg_{dmt}^{s} - \mathop \sum \limits_{n \in N} Xf_{dnt}^{s} - \delta \left( s \right)\quad \forall q \in Q,j \in J,s \in S,t,t^{\prime} \in T$$

(15)

$$\mathop \sum \limits_{j \in J} \mathop \sum \limits_{q \in Q} \mathop \sum \limits_{t^{\prime} \in T^{\prime}} Xb_{qjdt}^{s} = \mathop \sum \limits_{n \in N} Xf_{dnt}^{s} + \mathop \sum \limits_{m \in M} Xg_{dmt}^{s} - \delta \left( s \right) \quad \forall d \in D,s \in S$$

(16)

$$\varphi \times \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{t{^{\prime}} \in T{^{\prime}}}} Xa_{ijt\prime }^{s} = \mathop \sum \limits_{v \in V} \mathop \sum \limits_{t \in T} Xc_{{jvt\prime^{s} }} - \delta \left( s \right)\quad \forall j \in J.s \in S$$

(17)

$$\mathop \sum \limits_{j \in J} Xk_{{dvt\prime^{s} }} = \beta \times Xha_{qdt - 1}^{s} - \delta \left( s \right)\quad \forall q \in Q.d \in D,t \in T.s \in S$$

(18)

$$\mathop \sum \limits_{j \in J} Xg_{dmt}^{s} = \mathop \sum \limits_{j \in J} \mathop \sum \limits_{j \in J} Xi_{cnmt}^{s} - \delta \left( s \right)$$

(19)

$$\mathop \sum \limits_{ d \in D} Xf_{dnt}^{s} = \mathop \sum \limits_{c \in C} \mathop \sum \limits_{v \in V} (1 - \sigma_{c} ) \times Xh_{{nvt{^{\prime}}^{s} }} - \delta \left( s \right)\quad \forall n \in N_{ } .t \in T,s \in S$$

(20)

$$\sigma_{c} \times \mathop \sum \limits_{d \in D} \mathop \sum \limits_{t \in T} Xf_{dnt}^{s} = \mathop \sum \limits_{m \in M} \mathop \sum \limits_{t \in T} Xi_{cnmt}^{s} - \delta \left( s \right)\quad \forall c \in C. n \in N,t \in T,s \in S_{ }$$

(21)

$$\mathop \sum \limits_{d \in D} \mathop \sum \limits_{t \in T} Xf_{{dn_{2} t}}^{s} \le M \times w_{{n_{2} }} \quad \forall n_{2} \in N_{2} .s \in S$$

(22)

$$\mathop \sum \limits_{t^{\prime} \in T} Xa_{ijt^{\prime}}^{s} \le M \times v_{{ij_{ } }} \quad \forall j \in J,i \in I, s \in S$$

(23)

$$\mathop \sum \limits_{j \in J} v_{{ij_{ } }} = 1\quad \forall i \in {\rm I}$$

(24)

$$\mathop \sum \limits_{m \in M} Xi_{cnmt}^{s} \le capc_{cnt } \quad \forall c \in C, n \in N,t \in T . s \in S$$

(25)

$$\mathop \sum \limits_{j \in J} \mathop \sum \limits_{q \in Q} Xb_{qjdt}^{s} \le capd_{d } \quad \forall d \in D,t \in {\rm T}.s \in S$$

(26)

$$\mathop \sum \limits_{j \in J} \mathop \sum \limits_{q \in Q} Xf_{{dn_{1} t}}^{s} \le capf_{n1 } \quad \forall n_{1} \in {\text{N}}_{1} .t \in T.s \in S$$

(27)

$$\mathop \sum \limits_{j \in J} \mathop \sum \limits_{q \in Q} Xf_{{dn_{2} t}}^{s} \le capf_{n2} \times w_{{n{}_{2}^{{}} }} \quad \forall n \in N_{2} .t \in T.s \in S$$

(28)

$$\mathop \sum \limits_{d \in D} Xg_{dmt}^{s} \ge da_{mt}^{s} \quad \forall m \in M.s \in S.t \in T$$

(29)

$$\mathop \sum \limits_{n \in N} Xi_{cnmt}^{s} \ge db_{cmt }^{s} \quad \forall c \in C.t \in T.s \in S,m \in M$$

(30)

$$z - \mathop \sum \limits_{s^{\prime}} p_{s^{\prime}} . z + \theta_{s} \ge 0\quad \forall s \in S$$

(31)

$$Xa_{qijt^{\prime}} ,Xb_{qjdt}^{s} ,Xc_{jvt}^{s} ,Xg_{dmt}^{s} ,Xf_{dnt}^{s} ,Xi_{cnmt}^{s} , Xha_{qdt}^{s} \ge 0,w_{{n_{2} }} , v_{ij} \in \left\{ {0.1} \right\}$$

(32)

Considering the product quality, constraint (13) guarantees that the amounts of transported products from farmers to DCs are between the minimum and maximum anticipated production rates. Constraint (14) ensures that the amount of product received in SCs should be equal to the amounts of product transported to the DCs under scenarios. Constraint (15) balances the inventory level in DCs. So, the stored product amount should be equal to the stored amount of the previous month and the quantity of received product minus the amount of product transported to DCs and Vis. Constraint (16), similar to the constraint (14), balances the flow in DCS. Constraints (17), (18), (19), (20), and (21) state that the amount of rotten product sent to the VIs is equal to the amount of received product multiplied by its conversion rate to waste. Constraint (21) states that the amount of by-products shipped to the markets is equal to the amount of received product multiplied by its convertion rates to each by-products. We define constraint (22) ensures that the products are transported to new PIs, if it is opened. Constraint (23) allows shipping product to SCs, if the farmers decide to send to them. Constraint (24) ensures that each farmer sends its products to only one DC. Constraint (25) ensures that the amount of shipped by-products is limited to the maximum production rate under scenarios. Constraints (26), (27), and (28) ensure that the quantity of the transported product to the DCs and PIs should be less than or equal to their capacities. Constraints (29) and (30) ensure that the quantity of the transported product and its by-prodcuts to the markets should be more than or equal to their demands. Finally, we define a linearization constraint (31) with the robust model, and constraint (32) presents the type of decision variables.

6 Solution approach

In this paper, a MILP model was planned for maximizing total profit in ASC. Also, GAMS software is applied to achieve optimal solutions for problems with small-scale approximation. This software cannot solve large-scale problems, so we should use several effective meta-heuristics approaches to find the best solutions. Here, the proposed solution approaches with both encoding and decoding are detailed. In this respect, we employ WOA, PSO, and a new hybrid based on them (WOA–PSO) to find the best solution. The mentioned approach is detailed in the next section.

6.1 Encoding and decoding

In this study, we employ a priority-based encoding, using the presented approach in Gen et al. (2006) study, representing the solution as an array in implementing the meta-heuristic algorithms. In this method, an answer is displayed as a array with $\left| {K + J} \right|$ cells, where K represents the number of origins, and J represents the number of destinations. Then, random numbers between zero and one are generated, and after sorting, they are assigned to each cell as a priority (see Tables 2 and 3). At one of the supply chain network levels with four suppliers and three customers, encoding is based on a permutation of the number of nodes, as shown in this figure as 2–5–3–7–4–1–6. It has been shown that the priorities (4–1–6) are customer-related and (2–5–3–7) supplier-related. The following two steps must be taken to encoding.

Table 2 Capacity and demand and transportation costs

Table 3 The priority-based encoding in the example

6.1.1 Step 1

First, the largest priority among the selected suppliers (priority 7 to the fourth supplier), and if this supplier can meet all customer demand, the priority of the rest of the donation centers will be reduced to zero. In the example, the fourth supplier capacity is 850, while the total customer demand is 1050. In that case, the next supplier will be selected with the next largest priority (priority 5 to the second supplier). Now, the capacity of two suppliers (1600 amount) is greater than the total customer demand (1050 amount). In this case, the priorities of the first and third suppliers will be reduced to zero.

6.1.2 Step 2

After determining the number and location of suppliers, the optimal allocation is made between the selected suppliers and the customers. At this stage, the highest priority (priority 7 to the fourth supplier) is selected, and the lowest shipping cost associated with this supplier is identified (the first customer cost is 11.42) and the minimum amount of capacity selected, and customer determined as optimal allocation (minimum value is 300). Priority is reduced to zero after updating residual capacity or unmet demand. Repeat the second step until all values of all priorities are reduced to zero.

Examine a small-size case to evaluate the solutions, and how the proposed procedure can satisfy the constraints. Presume that the numbers of farmers, PCs, DCs, PIs, and VIs and markets be 2 1,1,2,1, and 1, respectively. The presented array is a twelve-row and i + 3j + 2d + 2m + 3n + v + 5 column matrix. As shown in Fig. 3, the proposed array consists of two parts; one part is related to the allocation sequence between levels, and another one corresponds to each scenario. Each row is related to one period ($t$).

Fig. 3

The schematic description of the presented array

For clarification, segment 1 shows the amount of transported product from farmers to SPs in scenarios. After generating this array, the cells of this matrix are filled randomly, with some numbers in the interval [0, 1]. After ordering these numbers, we introduce a priority-based matrix and sort these numbers separately for each sub-segment, according to Fig. 4. In addition, the corresponding sector of each scenario will be filled by discrete numbers between [1, S]. Constraints (13), (14), and (23) can be satisfied according to the allocation procedures of part 1 described in Fig. 5. Also, the inventory level can be controlled in DCs by allocation procedures of segment three described in the “Appendix.” The amount of inventory is recorded in another matrix and applied in the next period. Other constraints will be satisfied similarly.

Fig. 4

Proposed priority-based array of the first part in the first time period and random key

Fig. 5

Decoding procedure considering priority for part one

6.2 Particle swarm optimization (PSO)

PSO is a meta-heuristics algorithm, based on the social behavior of birds' flocks. In this algorithm, the particles move in the search space as a population of candidate solutions, which we obtain from basic mathematical formulas with respect to the velocity of the particle and its position, as below formulation. In every iteration, particles update their position and velocity by Eqs. (33) and (34).

$$V_{ij} \left( {t + 1} \right) = W \times V_{ij} \left( t \right) + c_{1} r_{1j} \left( t \right)\left[ {p_{ij} \left( t \right) - x_{ij } \left( t \right)} \right] + c_{2} r_{2j} \left( t \right)\left[ {g_{j} \left( t \right) - x_{ij } \left( t \right)} \right]$$

(33)

$$x_{ij} \left( {t + 1} \right) = x_{ij} \left( t \right) + V_{ij} \left( {t + 1} \right)$$

(34)

where $V_{ij} \left( {t + 1} \right)$ and $x_{ij} \left( t \right)$ are the particle’s velocity and position, respectively.$p_{ij} \left( t \right)$ is the individual local of best position, and $g_{j} \left( t \right)$ is the global best solution at that iteration. Moreover, W is the inertia weight factor, C₁ and C₂ represent the acceleration constants, and $x_{ij} \left( {t + 1} \right)$ is the particle’s position in the next iteration. The process will continue till obtaining the best possible solution in $p_{ij} \left( t \right)$ and $g_{j} \left( t \right)$. Otherwise, we should update the particles’ velocity and position.

6.3 Whale optimization algorithm (WOA)

Mirjalili and Lewis (2016) created WOA by simulating the hunting process of humpback whales. Whales follow a spiral of bubble-net attacking mechanism while encircling prey during chasing. They make spiral form bubbles, encircle prey, and then pursue the bubbles. In the following subsections, the mathematical models of spiral bubble-net feeding maneuver, circling prey, and prey scanning are discussed.

6.3.1 Encircling prey

The humpback whale searches to hunt the prey and then updates its spot according to the most suitable solution using the following equations:

$$\vec{D} = \left| {\left. {C \cdot \vec{X}*\left( t \right) - X\left( t \right)} \right|} \right.$$

(35)

$$\vec{X}\left( {t + 1} \right) = \overrightarrow {X*} \left( t \right) - \overrightarrow {A} \cdot \vec{D}$$

(36)

where A and D are coefficient vectors, t is a current iteration, $\overrightarrow {X*} \left( t \right)$ is the position vector of the best solution, and $X\left( t \right)$ is the position vector in iteration t. The vectors A and D are computed according to the below formulation (Mirjalili and Lewis, 2016):

$$\vec{A} = { }2\vec{a} \times r - \vec{a}$$

(37)

$$\vec{C} = 2 \times r$$

(38)

where a is a variable linearly reduced from 2 to 0 during the iterations, and $r$ is a random vector in the interval [0, 1].

6.3.2 Bubble-net attacking method

This algorithm designs a mathematical model for the bubble-net behavior of humpback whales in two ways:

• (a) Shrinking encircling mechanism: This strategy is defined by lowering the value from 2 to 0 and specifying a randomized value for vector A in the interval [− 1, 1].

• (b) Spiral updating position: This approach measures the related distance between the whale and the prey and gives a helix-shaped equation between them, as shown below:

  $$\vec{X}\left( {t + 1} \right) = \vec{D} \times e^{bt} \times \cos \left( {2\pi l} \right) + \vec{X}\left( t \right)$$

  (39)

  where l is a random number in the interval [− 1, 1], and b is a constant that defines the logarithmic spiral shape.

$\overrightarrow {D^{\prime}} = \vec{X}*\left( t \right) - \vec{X}\left( t \right)$ shows the distance between whale and prey, which means the best-obtained solution so far. It is assumed that the whales choose to shrink encircling and the logarithmic path with the probability of $Pe\%$ and $1 - Pe\%$ to update their positions, respectively, and mathematically formulate as follows (Mirjalili and Lewis (2016)):

$$\vec{X}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\vec{X}\left( t \right) - \overrightarrow {A.} \vec{D} } \hfill & {\quad {\text{if}}\;p < 0.5} \hfill \\ {\vec{D} \times e^{bt} \times \cos \left( {2\pi l} \right) + \vec{X}\left( t \right)} \hfill & {\quad {\text{if}}\;p \ge 0.5} \hfill \\ \end{array} } \right.$$

(40)

where p is a random number in the interval [0, 1].

6.3.3 Searching for prey

We can also use vector $\overrightarrow {{A{ }}}$ to locate prey which can also take values greater than one or less than − 1. There are two prerequisites for the examination:

$$\mathop {\vec{D}}\limits^{ } = \left| {\vec{C} \cdot \vec{X}rand - \vec{X}} \right|$$

(41)

$$\vec{X}\left( {t + 1} \right) = \vec{X}rand - \overrightarrow {A} \cdot \vec{D}1$$

(42)

Throughout the iterations for updating the search agents’ position, a random search agent is chosen if |A|> 1, and the best solution is selected if |A|< 1 (Manzoor et al., 2018). The pseudo-code of this algorithm is presented in Fig. 20 in “Appendix.”

6.4 Hybrid approach

In the current study, a hybrid algorithm based on WOA and PSO meta-heuristic algorithms is presented to get better results. We use the formulas and operators of WOA and PSO algorithms to formulate the mentioned hybrid algorithm. The proposed algorithm begins with a population of candidate whales at random positions and corresponding velocities within the search space. They can memorize their positions and both pbest and gbest similar to the PSO algorithm. We perform WOA with several secondary sub-iterations for each prior iteration just before reaching the exploitation step. If the fitness of the leader whale is greater than the fitness of the gbest, the leader whale is awarded the WOA global best position. Following that, tertiary sub-iteration starts with updating the location, velocity, pbest, and gbest using the PSO framework described by Eqs. (33) and (34). The gbest of WOA is assigned as the gbest of PSO during every tertiary sub-iteration. The fitness of the global best obtained by PSO and the best obtained by WOA is compared. If the global best fitness of PSO is greater than the global fitness of WOA, the global best position of WOA is allocated to the global best position of PSO, and vise versa, before the primary iterations are completed. Figure 21 in “Appendix” illustrates the proposed flowchart of the WOA–PSO.

6.5 Computational experiments and results

Here, a real case study of dates industry in Iran is employed to justify the applicability of the planned model. Moreover, ten test problems are generated to examine the performance of the model. Furthermore, a comparison is made between the obtained results from GAMS and the mentioned algorithms. Finally, a sensitivity analysis is performed to achieve a more exact measurement.

6.5.1 Case study

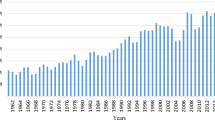
Here, the accuracy of the planned model is checked using a real case study in dates (date fruit) industry in Iran. Since 7000 years ago, date fruit has been one of the most valuable crops grown in subtropical and tropical regions and has been of great importance to farmers (Chandrasekaran and Bahkali, 2013). South Asia, the Middle East, and Africa widely plant the date fruit (Oladzad et al., 2021). According to FAO, in some of its major producing countries, the production of this product has increased, which is shown in Fig. 6. Dates have a significant role in GDP, job creation, export, and the creation of various packaging and processing industries (Sarraf et al., 2021). Recently, palm growing is also considered one of the major drivers of economic growth in its producing countries. In addition, dates residues are rich in carbohydrates, making them a suitable feedstock for making a variety of value-added products (see Fig. 7). The dates garden, some fresh dates, date syrup, and DCs are shown in Fig. 8.

Fig. 6

Dates production per country (FAO)

Fig. 7

Date palm fruit by-products and wastes

Fig. 8

Dates garden, fresh dates, date syrup, and DC

Iran is classified as the second producer of date fruit by FAO reports. To gather data, some cities in Kerman Province of Iran, namely, Bam, Jiroft, Narmashir, Fahraj, and Rigan are considered as farmers, SPs, and DCs. Moreover, some other cities of Iran are the customer zones and current and new PIs ' locations, which are presented in Figs. 9 and 10. As shown in Table 4, ten test problems are generated to evaluate the performance of the planned model. These test problems are classified based on the number of farmers (I), the number of SCs (J), DCs (D), PIs (N), markets (M), and VIs (V). The shipment costs between farmers and DCs are presented in Table 5. These costs are gathered from date farmers and correspond to distances between the mentioned cities and fare rates in Iran. Table 6 shows the other defined parameters of the proposed model.

Fig. 9

Location of farmers, PCs, and DCs

Fig. 10

Markets, VIS, and PIs

Table 4 The generated test problems

Table 5 Shipment cost between the DCs and location of customers (unit: Dollar per ton)

Table 6 Other generated parameters

We consider three types of date by-products, including date cookie $\left( {c1} \right)$, date syrup $\left( {c2} \right)$, and date coffee $\left( {c3} \right)$ which are produced in the current PIs and new ones. Table 7 shows the conversion rate of low-quality date fruit to by-product c. For example, 0.3 kg of low-quality date fruit is used for making 1 kg of date cookies. Also, Tables 8 and 9 present date fruit and its by-product prices in accordance with actual data in 2018 in Iran, respectively.

Table 7 Conversion rate of low-quality dates to by-product type c

Table 8 High-quality dates price in period t (unit: Dollar per kilogram)

Table 9 By-product c price in period t (unit: Dollar per kilogram)

Four scenarios are defined based on the past data, considering price, demand, and waste percentage of harvested products as uncertain parameters. The increase or decrease in the parameters will be according to Tables 10 and 11, and we can assume future scenarios to fit one of the following four scenarios. In the first scenario, the production cost for farmers is increased to 5% higher. The waste percentage of harvested products for farmers is between 10 and 20%, and the price is decreased by 8%. Due to the price reduction, consumers’ demand values show an increase. In the other scenarios, we assume, the product price increases consequently, the demand will decrease as well. The occurring probability for each scenario is equal to 0.25.

Table 10 Percentage of increase in dates and by-products price in different scenarios

Table 11 Amount of post-harvest waste, product demand and by-products, and production costs in different scenarios

6.5.2 Parameter tuning

In this sub-section, the Taguchi method is performed to obtain the mentioned algorithms’ efficiency using parameter tuning. This method contains a few experiments to determine the optimum value of each parameter, instead of full factorial experiments (Cheraghalipour et al., 2019). It employs orthogonal arrays to investigate many decision variables with fewer experiments (Cheraghalipour et al., 2018). This approach uses signal-to-noise (S/N) ratio, where the “signal” term implies the desired value and is the response component. Furthermore, "noise" refers to the adverse value, which is the standard deviation (Gharye Mirzaei et al., 2022). Consequently, the S/N ratio indicates the amount of variance in the response variable. Using Eq. (43), the S/N ratio should be optimized to the maximum value.

$$SN = - 10 \log \left( { \frac{{\mathop \sum \nolimits_{i = 1}^{n} Y^{2} }}{n}} \right)$$

(43)

In this equation, Y and n represent the observed data and the number of observations, respectively (Cheraghalipour et al., 2019). This method also uses the relative percentage deviation (RPD) as the response variable and computes it as the following:

$${\text{RPD}} = \frac{{{\text{Bestsol}} - {\text{Algsol}}}}{{{\text{Bestsol}}}}$$

(44)

where Bestsol is the best solution among all solutions, and Algsol is the output of the algorithm. Less value for RPD is desirable (Liao et al., 2020). A Taguchi design is created by identifying the specified level of the factors. Three levels are considered for each factor, which is presented in Table 12. Figures 11, 12, and 13 show these plots. For example, the best value of the max-iteration parameter in the PSO algorithm is 150. We can use these suitable levels for all test problems.

Table 12 Algorithm parameters and their levels

Fig. 11

SN ratio plot for PSO

Fig. 12

SN ratio plot for WOA

Fig. 13

SN ratio plot for WOA–PSO

6.5.3 Numerical results

To run the mentioned algorithms and test the proposed models, a PC with 4-GB RAM and 2.2-GHz CPU is used. Moreover, ten test problems 1–5 and 6–10 are generated as small- and medium-sized problems, respectively, and the efficiency of algorithms is investigated in terms of objective functions. Initially, the small-sized problems are solved by GAMS software, and then, the mentioned algorithms are encoded in MATLAB software to solve the small- and medium-sized problems. The values of the objective function and CPU time of the mentioned algorithms are shown in Figs. 14, 15, and 16, respectively. According to the graphical solution, the hybrid WOA–PSO provides better results by investigating the objective function value.

Fig. 14

The performance of algorithms in terms of the objective function

Fig. 15

Comparison of the objective values for meth-heuristics and GAMS

Fig. 16

The performance of algorithms in terms of CPU time

Moreover, the relative percent deviation (RPD) is used to compare the obtained results by GAMS and mentioned algorithm in Tables 13 and 14. The gap between solutions is between 1.9 and 2.8% for all test problems. Furthermore, PSO and WOA are faster regarding CPU time, as shown in Table 15 and Fig. 16.

Table 13 The obtained results with various algorithms in test problems

Table 14 The results obtained by algorithms in different test problems

Table 15 The performance of algorithms in terms of computational time (min)

6.6 Sensitivity analysis

Here, for further evaluation of the planned model, the sensitivity analysis has been done on two parameters including robustness weight coefficient and demand for the first test problem. The obtained results are presented in the following sub-sections.

6.6.1 Sensitivity analysis (robustness weight coefficient)

Here, the sensitivity of the variance effect factor ($\lambda$) values on the proposed model is examined. In all experiments, it is assumed that the weight coefficient ($\omega$) is constant. According to Sect. 3, a weight coefficient ($\omega$) is used to illustrate a trade-off between model robustness and the solution robustness in the objective function. When $\omega$ is very large, the model cannot generate impossible solutions. Therefore, a large number is assigned to $\omega$ in this research ($\omega$ = 500). The variance of the solution gains relative importance by $\lambda$ increasing. Figure 17 assesses the presented robust model with several $\lambda$ values in the first test problem. As seen, the objective function increases with an increase in the $\lambda$ value.

Fig. 17

Sensitivity analysis on the variance effect factor (landa)

6.6.2 Sensitivity analysis on demand

Here, sensitivity analysis has been done on the demand parameter. This experiment is performed under five cases in which the demand for a product decreases and increases by 10% and 20%, and the third state is consistent with the base case. The obtained results are displayed in Fig. 18, and according to this figure, as the demand increases by 10%, the objective function also increases about 2%.

Fig. 18

Sensitivity analysis on demand for dates

7 Conclusion, suggestions for future studies, and managerial insights

Agriculture is considered one of the major economic sectors for its producing countries and provides income and employment to their rural farmers. While the subject of supply chain network optimization of date fruit has rarely been explored in related literature, this paper addressed this issue and provided a framework for distributing this product and reusuing its by-product. In this paper, a three-level supply chain network was designed, in which the farmers and SPs were defined as the first and second levels. The third level was DCs for holding the products. Then, they sent the product to the PIs and VIs then to the markets for meeting customer’s demand. A MILP model was formulated to optimize total profit under uncertainty, and a scenario-based robust approach was used to handle uncertainty associated with production cost, demand, price, and wasted percentage of the harvested product. One of the novelities of our paper is considering weather conditions and economic fluctuations in different scenarios. Also, an exact method and three meta-heuristic algorithms including PSO, WOA, and a new hybrid algorithm based on them, namely, WOA–PSO were utilized for solving the mentioned model, then their obtained results were compared.

Moreover, the Taguchi method was used for calibrating the parameters of the mentioned algorithms to achieve better results. A real-world case study in dates industry in Iran along with some test problems was applied for validating the effectiveness of the planned model. According to the obtained numerical results, the hybrid WOA–PSO showed the best results by investigating the objective function so that its results had a difference between 0.9 and 2.8% with the exact method. Therefore, this approach could be practical and efficient for solving large-sized problems.

7.1 Managerial insights

The outcomes demonstrated that the planned model provides tactical considerations for the related managers and an efficient plan for the date fruit logistics network. The findings of this research in the areas of uncertainty in ASC can be stated as follows:

7.1.1 Uncertainty in ASC

Decision-making under uncertainty is one of the main issues of the agricultural sector. The management of agricultural production is confronted with weather conditions, interregional disparities in climate, and quality of the soil. Moreover, the agricultural market is extremely sensitive to economic and financial fluctuations. The current research dealt with this issue and designed a supply chain network for dates industry and formulated a MILP to make strategic decisions about dates logistics under uncertainty.

7.2 Limitations and future studies

Although the main goal of this research was to design a general framework for the proper distribution of dates and its waste, it has many limitations. For example, sustainability aspects were not addressed in the current research, which should be investigated in the future research due to its importance. Another issue is considering coordination decisions in the ASC, such as advertising and pricing, which have rarely received the attention of researchers. In addition, utilizing other methods for dealing with uncertainty such as stochastic and fuzzy planning or other robust programming approaches can also be used for modeling this problem in uncertain environments. Finally, adding some topics such as operational risks, disruption, water resources, etc., to the proposed model and solving it with other heuristics or meta-heuristics methods can also motivate researchers in this field.

Appendix

See Figs. 19, 20, and 21.

Fig. 19

Decoding procedure considering inventory levels (part 3)

Fig. 20

The pseudo-code of WOA

Fig. 21

The proposed flowchart of the hybrid WOA–PSO algorithm