1 Introduction

Piezoelectricity is an electromechanical effect resulting from a linear coupling between mechanical stress and strain on one hand and an electric field and displacement field on the other. The name originates from the Greek word piezos meaning pressure and expresses the observation that electricity is generated on applying pressure to a piezoelectric material. The opposite also occurs: applying an electric field generates a deformation. A piezoelectric material will aggregate electrical charges when mechanical stress is applied in certain classes of crystalline materials, which is called the piezoelectric effect. One of the surprising features of the piezoelectric effect is its reversible nature, which suggests that materials exhibit the direct piezoelectric effect (the internal generation of electrical charge resulting from an applied mechanical force), and also exhibit the reverse piezoelectric effect (the internal generation of a mechanical strain resulting from an applied electrical field). This inherent electromechanical coupling is widely exploited in the design of numerous devices like transducers, sensors and actuators [1,2,3,4,5].

It is a well-known fact that surface acoustic waves (SAWs) are extensively used in sensors and transducers, especially viscous liquid sensors because of their lower damping and smaller dimension. Piezoelectric materials are used to manufacture SAW devices; for example, a thin film lying on a substrate is currently adopted to achieve high performance. Numerous investigations have been undertaken for analysing the characteristics of SAW or Love-type waves in layered piezoelectric structures by many researchers in various disciplines because of its important applications in SAW devices. With the wider applications of SAW sensors, the studies on horizontally polarized shear (SH) wave propagation under various working conditions have become hotspots in this field. The propagation of SH waves in piezoelectric material composites generally exhibits dispersion behaviours, i.e., the phase velocity is dependent on the wave number [6,7,8]. The dispersion behaviour is a significant factor affecting the performances of SAW sensors; most researchers in this area focus their attention on the dispersion relations. First, Love [9] investigated the shear horizontal surface wave in an isotropic composite structure composed of a homogeneous isotropic layer of finite width lying over a homogeneous isotropic half-space. This shear horizontal surface wave is known as a Love wave and refers to a shear wave that is polarized horizontally and propagates at the surface of the medium. Curtis and Redwood [10] proposed a solution for dispersion characteristics of Love waves in a piezoelectric material and the conditions for the existence of various modes. Liu et al. [11] discussed the propagation behaviour of Love waves in layered piezoelectric/piezomagnetic structures. The dispersion of Love wave propagation in a composite structure consisting of the finite piezoelectric and viscoelastic layers on the size-dependent half-space was examined by Goyal and Kumar [12], and surface wave frequency in piezo-composite structure is discussed by Singhal et al. [13]. A theoretical method for analyzing Love waves in a structure with a viscoelastic guiding layer bounded on a piezoelectric substrate is developed by Liu et al. [14] and Liu [15]. The study of shear acoustic waves in piezoelectric cylindrically layered composite structure is also a subject of great interest. The circulation of shear harmonic waves around a long metallic cylinder covered with a piezoelectric layer was presented by Wang et al. [16], and shear wave propagation in a cylindrically layered piezoelectric structure with initial stress is studied by Du et al. [17]. The axisymmetric vibration of a piezoelectric laminated hollow circular cylinder has been studied by Paul and Nelson [18]. The propagation of elastic waves through piezoelectric structures has been in the forefront of the present era because of the continued utilization of piezoelectric materials in various functional devices, namely, sensors, actuators, filters, delay lines, oscillators, amplifiers, microbalances and air-coupled ultrasonic transducers, which are widely used in electronic technology.

To enhance the effect of piezoelectric material, functionally graded piezoelectric materials (FGPMs) are utilised, which can solve practical problems arising from production and application of a new type of composite materials. FGPMs possess a gradual variation in composition and structure over volume, which may change their properties [19, 20]. These materials find numerous applications in engineering fields because of their high performance and multifunctional role. The desire to develop materials for specific functions, their practical applications and research on them has turned into the foundation of current material science. It is because of the increased interdisciplinary interactions and rapid invention of theories, methods and experimental techniques [21,22,23]. The effect of initial stress on the propagation behaviour of Love waves in a layered piezoelectric structure was investigated by Liu et al. [24] and Zhu et al. [25]. Hryniewicz [26] studied the propagation of Love-type waves in a randomly non-homogeneous layer over a homogeneous half-space. The propagation of shear horizontal surface acoustic waves in a functionally graded magneto-electro-elastic half-space was studied by Shodja [27]. Sahu et al. [28] investigated the transference of Love-type waves in an FGPM layer bonded between viscous liquid and a piezoelectric half-space. The influence of functional gradedness and anisotropy on the propagation of surface waves has been studied by Mahanty et al. [29], and shear wave propagation in an isotropic and fibre-reinforced cylindrical layered media was investigated by Kumar et al. [30] and Mahanty et al. [31]. Singhal et al. [32] analysed the dispersion characteristics of Love wave propagation in an FGPM composite layered structure. The structures based on FGPMs are being extensively utilised in the engineering domain due to their inherent properties, indispensable characteristics and exceptional ability of sensing, actuating and controlling.

A common feature of the above-mentioned papers is that they discussed the problems based on perfectly bonded interfaces. It is known that the interfaces of practical piezoelectric composite structures may become damaged or imperfect after a long time of service under harsh circumstances. Imperfect bonding often occurs in surface acoustic wave (SAW) devices because of the aging of glue applied to two conjunct solids, micro-defects, diffusion impurities, and other forms of damages. Also, two dissimilar materials cannot be perfectly bonded, and there exists an interphase or transition with a thickness typically within a nanometre range across the interface. The existence of the interface layer or interphase significantly affects interface mechanical behaviour, such as the inability to transfer stresses effectively, etc.; hence, this kind of interface is called an imperfect interface. Owing to the above, many eminent researchers have developed an analytical model of imperfect bonding in their studies [33,34,35,36,37]. Chen et al. [38] provided the exact three-dimensional solutions of laminated orthotropic piezoelectric rectangular plates featuring inter-laminar imperfections bonding modelled by a general spring layer. Wang et al. [39] displayed the scattering of anti-plane shear waves by a piezoelectric circular cylinder having an imperfect interface. Chaudhary et al. [40] investigated shear waves in a piezoelectric layer laid over a substrate with imperfect interface. Li and Yong Lee [41] studied the propagation of SH waves in a piezoelectric sensor with an imperfect interface. Kumar et al. [42] discussed the effect of interfacial imperfection on shear wave propagation in a piezoelectric composite structure. After this detailed literature survey, it is found that there are number of articles concerned with the propagation of transverse waves in a homogeneous/functionally graded piezoelectric layered structure with a rectangular frame of reference, and very few articles are published concerned with the propagation of shear waves in homogeneous/heterogeneous cylindrical piezoelectric structures. It is worth mentioning that, to date, no investigations have been made on the propagation of shear acoustic waves in a piezoelectric cylindrical layered structure composed of a piezoelectric material cylinder coated by a concentric functionally graded cylindrical piezoelectric material (FGPM) layer of finite width in which the said inner cylinder is imperfectly bonded with the said cylindrical layer. In view of the undertaken geometry and configuration along with the consideration of imperfect bonding, the present manuscript provides a novel feature.

In this paper, shear acoustic wave propagation behaviour in a piezoelectric cylindrical layered structure consisting of a piezoelectric material cylinder coated by a concentric FGPM cylindrical layer with an imperfect bonding interface has been analysed. The functional gradient in the FGPM cylindrical layer varies simultaneously along the radial direction, and the imperfection of the cylindrical structure’s interface is taken into account which may practically exist due to some mechanical and/or electrical damage. An analytical treatment has been employed to determine the dispersion relations of propagating shear acoustic waves for both electrically short and electrically open conditions. The deduced results are validated by pre-established results and the classical Love wave equation as a special case of the problem. Numerical calculation and graphical delineation have been carried out to unravel the effect of functional gradient parameter, radii ratio, wave number, order of Bessel’s function and mechanical/electrical imperfection parameters associated with the imperfect bonding of a piezoelectric material cylinder and a concentric FGPM cylindrical layer on the phase velocity of shear acoustic waves.

2 Methodology adopted for the mathematical model

The following methodology is used to obtain dispersion relations of a propagating wave for both electrically short and open cases in the undertaken model:

  • In view of the geometry of the problem and considered frame of reference, the mathematical condition of propagation of a shear acoustic wave is taken into account.

  • With the aid of a constitutive relation, the governing equation of motion and Gauss’s law concerned with the electrical displacements are derived.

  • Keeping in mind the shear imperfection existing between the inner cylinder and outer cylindrical layer, the boundary conditions for electrically short and open conditions of the undertaken model are identified.

  • By adopting separation of the variable technique, the solution of the non-vanishing equation of motion for propagation of shear acoustic waves in the considered geometrical model has been obtained in terms of Bessel’s function of the first and second kind. Furthermore, with aid of boundary conditions, we obtain two distinct dispersion relations for short and open conditions.

  • For the sake of validation, the obtained dispersion relations for short and open conditions are matched with the classical and pre-established results.

3 Mathematical formulation of the problem

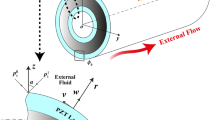
Let us assume shear acoustic wave propagation in a piezoelectric cylindrical layered structure composed of a piezoelectric material cylinder imperfectly bonded to a concentric functionally graded piezoelectric material (FGPM) cylindrical layer of finite width. The width of the FGPM cylindrical layer is \(h\left( =r_2 -r_1 \right) \) where \(r_1\) and \(r_2\) are inner and outer radii of the cylindrical structure, respectively. Let us introduce a cylindrical coordinate system in such a way that the wave propagation is along the \(\theta \) direction; the poling of the linearly transversely isotropic piezoelectric material cylinder and FGPM layer is along the \(z\hbox {-axis;}\), the \(r\hbox {-axis}\) is the radial direction of the cylinder and O is the centre of the cylindrical structure as shown in Fig. 1.

Fig. 1
figure 1

Schematic of the problem a piezoelectric cylindrical structure, b cross-section of the piezoelectric cylindrical structure

Full size image

The constitutive relations for piezoelectric material [1] are given by

$$\begin{aligned} \sigma _{ij} = c_{ijkl} S_{kl} -e_{kij} E_k , \qquad D_j = e_{jkl} S_{kl} +\varepsilon _{jk} E_k, \end{aligned}$$
(1)

where \(\sigma _{ij} , S_{kl} , D_j \) and \(E_k \) denote the stress tensors, strain tensors, electric displacements and intensity of the electric field, respectively; \(c_{ijkl} , e_{jkl} \) and \(\varepsilon _{jk} \) are elastic, piezoelectric and dielectric constants.

In view of Eq. (1), the constitutive equations for a piezoelectric medium can also be expanded in terms of cylindrical coordinates as

$$\begin{aligned} \left( {{\begin{array}{c} {\sigma _{rr} } \\ {\sigma _{\theta \theta } } \\ {\sigma _{zz} } \\ {\sigma _{\theta z} } \\ {\sigma _{rz} } \\ {\sigma _{r\theta } } \\ \end{array} }} \right)= & {} \left( {{\begin{array}{cccccc} {c_{11} }&{}\quad {c_{12} }&{}\quad {c_{13} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ {c_{12} }&{}\quad {c_{11} }&{}\quad {c_{13} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ {c_{13} }&{}\quad {c_{13} }&{}\quad {c_{33} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad {c_{44} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {c_{44} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {\frac{c_{11} -c_{12} }{2}} \\ \end{array} }} \right) \left( {{\begin{array}{c} {S_{rr} } \\ {S_{\theta \theta } } \\ {S_{zz} } \\ {S_{\theta z} } \\ {S_{rz} } \\ {S_{r\theta } } \\ \end{array} }} \right) -\left( {{\begin{array}{ccc} 0&{}\quad 0&{}\quad {e_{31} } \\ 0&{}\quad 0&{}\quad {e_{31} } \\ 0&{}\quad 0&{}\quad {e_{33} } \\ 0&{}\quad {e_{15} }&{}\quad 0 \\ {e_{15} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right) \left( {{\begin{array}{c} {E_r } \\ {E_\theta } \\ {E_z } \\ \end{array} }} \right) , \end{aligned}$$
(2)
$$\begin{aligned} \left( {{\begin{array}{c} {D_r } \\ {D_\theta } \\ {D_z } \\ \end{array} }} \right)= & {} \left( {{\begin{array}{cccccc} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {e_{15} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad {e_{15} }&{}\quad 0&{}\quad 0 \\ {e_{31} }&{}\quad {e_{31} }&{}\quad {e_{33} }&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \right) \left( {{\begin{array}{l} {S_{rr} } \\ {S_{\theta \theta } } \\ {S_{zz} } \\ {S_{\theta z} } \\ {S_{rz} } \\ {S_{r\theta } } \\ \end{array} }} \right) +\left( {{\begin{array}{ccc} {\varepsilon _{11} }&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\varepsilon _{11} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\varepsilon _{33} } \\ \end{array} }} \right) \left( {{\begin{array}{l} {E_r } \\ {E_\theta } \\ {E_z } \\ \end{array} }} \right) . \end{aligned}$$
(3)

The strain components in terms of mechanical displacement components and intensity of the electric field in terms of electric potential with cylindrical coordinates are defined as

$$\begin{aligned} S_{r r}= & {} \frac{\partial u}{\partial r},\qquad S_{r \theta } =\left[ {\frac{\partial v}{\partial r}-\frac{v}{r}+\frac{1}{r}\frac{\partial u}{\partial \theta }} \right] ,\qquad S_{r z} =\left[ {\frac{\partial w}{\partial r}+\frac{\partial u}{\partial z}} \right] ,\qquad S_{\theta \theta } =\frac{1}{r}\left[ {u+\frac{\partial v}{\partial \theta }} \right] ,\nonumber \\ S_{\theta z}= & {} \left[ {\frac{1}{r}\frac{\partial w}{\partial \theta }+\frac{\partial v}{\partial z}} \right] ,\qquad S_{z z} =\frac{\partial w}{\partial z} , \qquad E_r =-\frac{\partial \phi }{\partial r},\qquad E_\theta =-\frac{1}{r}\frac{\partial \phi }{\partial \theta },\qquad E_z =-\frac{\partial \phi }{\partial z}, \end{aligned}$$
(4)

where u, v and w are the mechanical displacement components along the \(r, \theta \) and z directions, respectively, and \(\phi \) represents the electric potential.

In the absence of body force, the equation of motion in a cylindrical coordinate system in terms of stress components [9] and Gauss’s law of electrostatics without charge are written as

$$\begin{aligned}&\frac{\partial \sigma _{r r} }{\partial r}+\frac{1}{r}\frac{\partial \sigma _{r \theta } }{\partial \theta }+\frac{\partial \sigma _{r z} }{\partial z}+\frac{\sigma _{r r} -\sigma _{\theta \theta } }{r}=\rho \frac{\partial ^{2}u}{\partial t^{2}}, \end{aligned}$$
(5)
$$\begin{aligned}&\frac{\partial \sigma _{r \theta } }{\partial r}+\frac{1}{r}\frac{\partial \sigma _{\theta \theta } }{\partial \theta }+\frac{\partial \sigma _{\theta z} }{\partial z}+\frac{2\sigma _{r\theta } }{r}=\rho \frac{\partial ^{2}v}{\partial t^{2}}, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\partial \sigma _{r z} }{\partial r}+\frac{1}{r}\frac{\partial \sigma _{\theta z} }{\partial \theta }+\frac{\partial \sigma _{z z} }{\partial z}+\frac{\sigma _{r z} }{r}=\rho \frac{\partial ^{2}w}{\partial t^{2}}, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{\partial D_r }{\partial r}+\frac{1}{r}\frac{\partial D_\theta }{\partial \theta }+\frac{\partial D_z }{\partial z}+\frac{D_r }{r}=0, \end{aligned}$$
(8)

where \(\rho \) is the material’s mass density.

On the assumption that the shear acoustic wave propagates along the \(\theta \hbox {-direction,}\) the mechanical displacements and electric potential can be characterised as

$$\begin{aligned} u=v=0, \qquad w=w\left( {r, \theta , t} \right) ,\qquad \phi =\phi \left( {r, \theta , t} \right) \hbox { and }\quad \frac{\partial \left( \right) }{\partial z}\equiv 0. \end{aligned}$$
(9)

On substituting of Eqs. (4) and (9) into Eqs. (2) and (3), the following relations yield:

$$\begin{aligned} \sigma _{rz} =c_{44} \frac{\partial w}{\partial r}+e_{15} \frac{\partial \phi }{\partial r}, \qquad \sigma _{\theta z} =\frac{1}{r}\left( {c_{44} \frac{\partial w}{\partial \theta }+e_{15} \frac{\partial \phi }{\partial \theta }} \right) \end{aligned}$$
(10)

and

$$\begin{aligned} D_r =e_{15} \frac{\partial w}{\partial r}-\varepsilon _{11} \frac{\partial \phi }{\partial r}, \qquad D_\theta =\frac{1}{r}\left( {e_{15} \frac{\partial w}{\partial \theta }-\varepsilon _{11} \frac{\partial \phi }{\partial \theta }} \right) . \end{aligned}$$
(11)

In view of Eqs. (9)–(11), the equation of motion (Eqs. (5) and (6)) becomes identically zero, while Eqs. (7) and (8) take the form as

$$\begin{aligned} c_{44} \nabla ^{2}w+e_{15} \nabla ^{2}\phi= & {} \rho \frac{\partial ^{2}w}{\partial t^{2}}, \end{aligned}$$
(12)
$$\begin{aligned} e_{15} \nabla ^{2}w-\varepsilon _{11} \nabla ^{2}\phi= & {} 0, \end{aligned}$$
(13)

where

$$\begin{aligned} \nabla ^{2}=\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}}{\partial \theta ^{2}} \end{aligned}$$

is the two-dimensional Laplace operator in polar coordinates.

The layer \(\left( {r_1 <r\le r_2 } \right) \) is functionally gradient and it enhances the properties of piezoelectric material, therefore, by considering all the material parameters of the FGPM layer in the radial variation (along the r-direction), the functional gradedness in the FGPM layer is introduced as

$$\begin{aligned} c_{44} =c_{44}^{\left( F \right) } \left( {\frac{r}{r_2 }} \right) ^{\ell },\qquad e_{15} =e_{15}^{\left( F \right) } \left( {\frac{r}{r_2 }} \right) ^{\ell },\qquad \varepsilon _{11} =\varepsilon _{11}^{\left( F \right) } \left( {\frac{r}{r_2 }} \right) ^{\ell } ,\qquad \rho =\rho ^{\left( F \right) }\left( {\frac{r}{r_2 }} \right) ^{\ell }, \end{aligned}$$
(14)

where \(c_{44} , e_{15} , \varepsilon _{11}\) and \(\rho \) indicate the shear elastic modulus, piezoelectric constant, dielectric coefficients and mass density of the FGPM layer, respectively; \(c_{44}^{\left( F \right) } , e_{15}^{\left( F \right) } , \varepsilon _{11}^{\left( F \right) }\) and \(\rho ^{\left( F \right) }\) are the associated values at \(r=r_2 \), and \(\ell \) is the dimensionless functional gradient parameter.

Assuming the displacement components and electric potential for an FGPM layer \(\left( {r_1 <r\le r_2 } \right) \) as \(w^{\left( F \right) }, \quad \phi ^{\left( F \right) }\) and Eqs. (12) and (13) with aid of Eq. (14) result in

$$\begin{aligned}&c_{44}^{\left( F \right) } \left[ {r^{2}\frac{\partial ^{2}w^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial w^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}w^{\left( F \right) }}{\partial \theta ^{2}}} \right] +e_{15}^{\left( F \right) } \left[ {r^{2}\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial \phi ^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial \theta ^{2}}} \right] \nonumber \\&\quad =\frac{r^{2}}{\rho ^{\left( F \right) }}\frac{\partial ^{2}w^{\left( F \right) }}{\partial t^{2}}, \end{aligned}$$
(15)
$$\begin{aligned}&e_{15}^{\left( F \right) } \left[ {r^{2}\frac{\partial ^{2}w^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial w^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}w^{\left( F \right) }}{\partial \theta ^{2}}} \right] -\varepsilon _{11}^{\left( F \right) } \left[ {r^{2}\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial \phi ^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial \theta ^{2}}} \right] =0. \end{aligned}$$
(16)

On simplifying of Eqs. (15) and (16), the following Eqs. (17) and (18) will serve the field equations in terms of mechanical displacement and electric potential function as

$$\begin{aligned}&r^{2}\frac{\partial ^{2}w^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial w^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}w^{\left( F \right) }}{\partial \theta ^{2}}=\frac{r^{2}}{\beta _1^2 }\frac{\partial ^{2}w^{\left( F \right) }}{\partial t^{2}}, \end{aligned}$$
(17)
$$\begin{aligned}&r^{2}\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial r^{2}}+r\left( {\ell +1} \right) \frac{\partial \phi ^{\left( F \right) }}{\partial r}+\frac{\partial ^{2}\phi ^{\left( F \right) }}{\partial \theta ^{2}}=\frac{e_{15}^{\left( F \right) } r^{2}}{\varepsilon _{11}^{\left( F \right) } \beta _1^2 }\frac{\partial ^{2}w^{\left( F \right) }}{\partial t^{2}}, \end{aligned}$$
(18)

where

$$\begin{aligned} \beta _1 =\sqrt{\frac{\bar{{c}}_{44} }{\rho ^{\left( F \right) }}} \quad {\text {and}} \quad \bar{{c}}_{44} =c_{44}^{\left( F \right) } +\frac{\left( {e_{15}^{\left( F \right) } } \right) ^{2}}{\varepsilon _{11}^{\left( F \right) } }. \end{aligned}$$

For the sake of simplicity and noting the superscript \(\left( P \right) \) of material constants, density, mechanical displacement and electric potential of the piezoelectric cylinder become \(c_{44}^{\left( P \right) } , e_{15}^{\left( P \right) } , \varepsilon _{11}^{\left( P \right) } , \rho ^{\left( P \right) },w^{\left( P \right) } \) and \(\phi ^{\left( P \right) }\), respectively, and therefore, the field equations of piezoelectric cylinder \(\left( {0<r\le r_1 } \right) \) on simplifying Eqs. (12) and (13) reduce to

$$\begin{aligned}&r^{2}\frac{\partial ^{2}w^{\left( P \right) }}{\partial r^{2}}+r\frac{\partial w^{\left( P \right) }}{\partial r}+\frac{\partial ^{2}w^{\left( P \right) }}{\partial \theta ^{2}}=\frac{r^{2}}{\beta _2^2 }\frac{\partial ^{2}w^{\left( P \right) }}{\partial t^{2}}, \end{aligned}$$
(19)
$$\begin{aligned}&r^{2}\frac{\partial ^{2}\phi ^{\left( P \right) }}{\partial r^{2}}+r\frac{\partial \phi ^{\left( P \right) }}{\partial r}+\frac{\partial ^{2}\phi ^{\left( P \right) }}{\partial \theta ^{2}}=\frac{r^{2}e_{15}^{\left( P \right) } }{\beta _2^2 \varepsilon _{11}^{\left( P \right) } }\frac{\partial ^{2}w^{\left( P \right) }}{\partial t^{2}}, \end{aligned}$$
(20)

where

$$\begin{aligned} \beta _2 =\sqrt{\frac{\bar{{\bar{{c}}}}_{44} }{\rho ^{\left( P \right) }}} \quad {\text {and}} \quad \bar{{\bar{{c}}}}_{44} =c_{44}^{\left( P \right) } +\frac{\left( {e_{15}^{\left( P \right) } } \right) ^{2}}{\varepsilon _{11}^{\left( P \right) } }. \end{aligned}$$

The outer surface \(\left( {r>r_2 } \right) \) of the FGPM layer is in the air where the dielectric constant \(\left( {\varepsilon _0 } \right) \) is much smaller as compared to piezoelectric medium, and therefore, the air can be regarded as a vacuum and the electric potential \(\phi _0 \) satisfies the Laplacian equation, i.e.

$$\begin{aligned} \nabla ^{2}\phi _0 =0, \end{aligned}$$
(21)

where the subscript 0 specifies the quantities in the vacuum.

4 Boundary conditions

The outer surface of the FGPM cylindrical layer (i.e. \(r=r_2\)) is mechanically traction-free and subjected to two different kinds of boundary conditions; one is an electrically short condition and the other is an electrically open condition. These boundary conditions can be expressed by the following mathematical formulae:

  1. (i)

    Mechanical traction-free condition at the free surface of the FGPM layer common for both open and short cases is given by

    $$\begin{aligned} \sigma _{rz}^{\left( F \right) } =0 \quad \hbox {at}\quad r=r_2 . \end{aligned}$$
    (22)
  2. (ii)

    Electrically short condition at the free surface of the FGPM layer is given by

    $$\begin{aligned} \phi ^{\left( F \right) }=0 \quad \hbox {at}\quad r=r_2 . \end{aligned}$$
    (23)
  3. (iii)

    Electrically open condition at the free surface of the FGPM layer is given by

    $$\begin{aligned} \phi ^{\left( F \right) }=\phi _0 \quad \hbox {at}\quad r=r_2 \end{aligned}$$
    (24)

    and

    $$\begin{aligned} D_r^{\left( F \right) } =-\varepsilon _0 \frac{\partial \phi _0 }{\partial r} \quad \hbox {at}\quad r=r_2 . \end{aligned}$$
    (25)
  4. (iv)

    It is assumed that the interface (i.e. \(r=r_1 )\) of the FGPM layer and piezoelectric cylinder is assumed to be damaged electrically and/or mechanically and becomes imperfect. According to an imperfect interfacial model, the stresses and electrical displacements are continuous, but the mechanical displacements and electric potentials are jumped across the interface, which complies with the following relations:

    $$\begin{aligned} \sigma _{rz}^{\left( F \right) }= & {} \alpha _1 \left( {w^{\left( F \right) }-w^{\left( P \right) }} \right) \quad \hbox {at}\quad r=r_1 , \end{aligned}$$
    (26)
    $$\begin{aligned} D_r^{\left( F \right) }= & {} -\,\alpha _2 \left( {\phi ^{\left( F \right) }-\phi ^{\left( P \right) }} \right) \quad \hbox {at}\quad r=r_1 , \end{aligned}$$
    (27)
    $$\begin{aligned} \sigma _{rz}^{\left( F \right) }= & {} \sigma _{rz}^{\left( P \right) }\quad \hbox {at}\quad r=r_1 , \end{aligned}$$
    (28)
    $$\begin{aligned} D_r^{\left( F \right) }= & {} D_r^{\left( P \right) }\quad \hbox {at}\quad r=r_1, \end{aligned}$$
    (29)

    where the superscripts \(\left( F \right) \hbox {and} \left( P \right) \) in stresses and electric displacement components stand for the FGPM layer and piezoelectric cylinder, respectively. The two imperfect interface parameters \(\alpha _1\; \hbox {and}\; \alpha _2 \) are uniform and non-negative constants. Obviously, if \(\alpha _1 \rightarrow \infty \; \hbox {and}\; \alpha _2 \rightarrow \infty ,\) the interface is perfectly bonded and conducting, otherwise it is mechanically and/or dielectrically imperfect.

  5. (v)

    As the mechanical displacement and electric potential of the piezoelectric cylinder will become finite at the origin of the cylinder, i.e.

    $$\begin{aligned} r\rightarrow 0, \qquad w^{\left( P \right) },\qquad \phi ^{\left( P \right) }\rightarrow \hbox {finite}\,\hbox {value.} \end{aligned}$$
    (30)

5 Solution of the problem

To find the displacement components, electric potentials of both the FGPM layer and piezoelectric cylinder and the electric potential of the vacuum, we dealt with the Eqs. (17)–(21).

As shear acoustic wave is propagating steadily along the circumferential direction, on assuming the solutions of Eqs. (17) and (18) in the form

$$\begin{aligned} w^{\left( F \right) }\left( {r,\theta ,t} \right)= & {} W^{\left( F \right) }\left( r \right) \cos \left( {n\theta -\omega t} \right) r^{-\ell /2}, \end{aligned}$$
(31)
$$\begin{aligned} \phi ^{\left( F \right) }\left( {r,\theta ,t} \right)= & {} \varphi ^{\left( F \right) }\left( r \right) \cos \left( {n\theta -\omega t} \right) r^{-\ell /2}, \end{aligned}$$
(32)

where \(W^{\left( F \right) }\left( r \right) , \varphi ^{\left( F \right) }\left( r \right) \) are unknown functions and n is a non-negative real number.

In view of Eqs. (31) and (32), Eqs. (17) and (18) lead to

$$\begin{aligned} r^{2}\frac{d^{2}W^{\left( F \right) }\left( r \right) }{{\text {d}}r^{2}}+r\frac{{\text {d}}W^{\left( F \right) }\left( r \right) }{{\text {d}}r}+\left[ {\frac{r^{2}\omega ^{2}}{\beta _1^2 }-\left( {n^{2}+\frac{\ell ^{2}}{4}} \right) } \right] W^{\left( F \right) }\left( r \right) =0 \end{aligned}$$
(33)

and

$$\begin{aligned}&r^{2}\frac{d^{2}\varphi ^{\left( F \right) }\left( r \right) }{{\text {d}}r^{2}}+r\frac{{\text {d}}\varphi ^{\left( F \right) }\left( r \right) }{{\text {d}}r}-\left( {n^{2}+\frac{\ell ^{2}}{4}} \right) \varphi ^{\left( F \right) }\left( r \right) \nonumber \\&\quad =\frac{e_{15}^{\left( F \right) } }{\varepsilon _{11}^{\left( F \right) } }\left[ {r^{2}\frac{d^{2}W^{\left( F \right) }\left( r \right) }{{\text {d}}r^{2}}+r\frac{{\text {d}}W^{\left( F \right) }\left( r \right) }{{\text {d}}r}-\left( {n^{2}+\frac{\ell ^{2}}{4}} \right) W^{\left( F \right) }\left( r \right) } \right] . \end{aligned}$$
(34)

Equation (33) is in the form of Bessel’s differential equation of order \(p\Big ( {=\sqrt{n^{2}+\frac{\ell ^{2}}{4}}} \Big ),\) and the solution of Eq. (33) is given by

$$\begin{aligned} W^{\left( F \right) }\left( r \right) =C_1 J_p \left( {\frac{\omega r}{\beta _1 }} \right) +C_2 Y_p \left( {\frac{\omega r}{\beta _1 }} \right) , \end{aligned}$$
(35)

where \(C_1 \), \(C_2 \) are undetermined constants and \(J_p \left( \cdot \right) , Y_p \left( \cdot \right) \) are the pth order Bessel’s function of the first and second kind, respectively.

In view of Eq. (35), the solution of Eq. (34) can be represented by

$$\begin{aligned} \varphi ^{\left( F \right) }\left( r \right) =C_1^{*} r^{-p}+C_2^{*} r^{p}+\frac{e_{15}^{\left( F \right) } }{\varepsilon _{11}^{\left( F \right) } }\left( {C_1 J_p \left( {\frac{\omega r}{\beta _1 }} \right) +C_2 Y_p \left( {\frac{\omega r}{\beta _1 }} \right) } \right) , \end{aligned}$$
(36)

where \(C_1^{*} \) and \(C_2^{*} \) are undetermined constants.

Thus, the displacement component and electric potential of a functionally graded piezoelectric material (FGPM) layer \(\left( {r_1 <r\le r_2 } \right) \) are as follows:

$$\begin{aligned} w^{\left( F \right) }= & {} \left[ {C_1 J_p \left( {\frac{\omega r}{\beta _1 }} \right) +C_2 Y_p \left( {\frac{\omega r}{\beta _1 }} \right) } \right] r^{-\ell /2}\cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(37)
$$\begin{aligned} \phi ^{\left( F \right) }= & {} \left[ {C_1^{*} r^{-p}+C_2^{*} r^{p}+\frac{e_{15}^{\left( F \right) } }{\varepsilon _{11}^{\left( F \right) } }\left( {C_1 J_p \left( {\frac{\omega r}{\beta _1 }} \right) +C_2 Y_p \left( {\frac{\omega r}{\beta _1 }} \right) } \right) } \right] r^{-\ell /2}\cos \left( {n\theta -\omega t} \right) . \end{aligned}$$
(38)

Similarly, the displacement component and electric potential of the piezoelectric cylinder \(\left( {0<r\le r_1 } \right) \) will be served as

$$\begin{aligned} w^{\left( P \right) }= & {} \left[ {D_1 J_n \left( {\frac{\omega r}{\beta _2 }} \right) +D_2 Y_n \left( {\frac{\omega r}{\beta _2 }} \right) } \right] \cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(39)
$$\begin{aligned} \phi ^{\left( P \right) }= & {} \left[ {D_1^{*} r^{-n}+D_2^{*} r^{n}+\frac{e_{15}^{\left( P \right) } }{\varepsilon _{11}^{\left( P \right) } }\left( {D_1 J_n \left( {\frac{\omega r}{\beta _2 }} \right) +D_2 Y_n \left( {\frac{\omega r}{\beta _2 }} \right) } \right) } \right] \cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(40)

where \(D_1 , D_2 , D_1^{*} \) and \(D_2^{*} \) are undetermined constants and \(J_n \left( \cdot \right) \) and \(Y_n \left( \cdot \right) \) are the nth order Bessel’s function of the first and second kind, respectively.

With the aid of the boundary condition (Eq. (30)), the mechanical displacement and electric potential of the piezoelectric cylinder \(\left( {0<r\le r_1 } \right) \) result in

$$\begin{aligned} w^{\left( P \right) }= & {} D_1 J_n \left( {\frac{\omega r}{\beta _2 }} \right) \cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(41)
$$\begin{aligned} \phi ^{\left( P \right) }= & {} \left[ {D_1^{*} r^{-n}+\frac{e_{15}^{\left( P \right) } }{\varepsilon _{11}^{\left( P \right) } }D_1 J_n \left( {\frac{\omega r}{\beta _2 }} \right) } \right] \cos \left( {n\theta -\omega t} \right) . \end{aligned}$$
(42)

The solution of Eq. (21) for electric potential in the vacuum can be assumed as

$$\begin{aligned} \phi _0 =\varphi _0 \left( r \right) \cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(43)

where \(\varphi _0 \left( r \right) \) is the undetermined function.

On substituting Eq. (43) into Eq. (21) and taking note of the fact that the electric potential in the vacuum approaches zero as \(r\rightarrow \infty ,\) the electric potential of a vacuum is given by

$$\begin{aligned} \phi _0 =A_0 r^{-n}\cos \left( {n\theta -\omega t} \right) , \end{aligned}$$
(44)

where \(A_0 \) is the undetermined constant.

6 Dispersion relations

6.1 Frequency equation for the case of an electrically short condition

Substitution of Eqs. (37), (38), (41) and (42) and their corresponding stresses and electrical displacement components into boundary conditions Eqs. (22), (23) and (25)–(28) will provide the following algebraic equations with unknowns \(C_1 , C_2 , C_1^{*} , C_2^{*} , D_1\) and \(D_1^{*} \) as follows:

$$\begin{aligned}&M_{11} C_1 +M_{12} C_2 +M_{13} C_1^{*} +M_{14} C_2^{*} +M_{15} D_1 +M_{16} D_1^{*} =0, \end{aligned}$$
(45)
$$\begin{aligned}&M_{21} C_1 +M_{22} C_2 +M_{23} C_1^{*} +M_{24} C_2^{*} +M_{25} D_1 +M_{26} D_1^{*} =0, \end{aligned}$$
(46)
$$\begin{aligned}&M_{31} C_1 +M_{32} C_2 +M_{33} C_1^{*} +M_{34} C_2^{*} +M_{35} D_1 +M_{36} D_1^{*} =0, \end{aligned}$$
(47)
$$\begin{aligned}&M_{41} C_1 +M_{42} C_2 +M_{43} C_1^{*} +M_{44} C_1^{*} +M_{45} D_1 +M_{46} D_1^{*} =0, \end{aligned}$$
(48)
$$\begin{aligned}&M_{51} C_1 +M_{52} C_2 +M_{53} C_1^{*} +M_{54} C_2^{*} +M_{55} D_1 +M_{56} D_1^{*} =0, \end{aligned}$$
(49)
$$\begin{aligned}&M_{61} C_1 +M_{62} C_2 +M_{6 3} C_1^{*} +M_{64} C_2^{*} +M_{65} D_1 +M_{66} D_1^{*} =0, \end{aligned}$$
(50)

where \(M_{ij} \) are defined in Appendix A.

In order to find the non-trivial solution of the arbitrary constants \(C_1 , C_2 , C_1 ^{*}, C_2 ^{*}, D_1\) and \(D_1 ^{*}\), the determinant of the coefficient matrix \(M\left( {=\left| {M_{ij} } \right| } \right) \) obtained from the algebraic system of equations (Eqs. (45)–(50)) must be zero, i.e.

$$\begin{aligned} \left| {M_{ij} } \right| _{6\times 6} =0. \end{aligned}$$
(51)

Equation (51) will serve the dispersion equation for the electrically short case for shear acoustic wave propagation in a piezoelectric cylinder coated by an FGPM layer.

6.2 Frequency equation for the case of an electrically open condition

For the electrically open case, Eq. (46) will be substituted by the following two equations:

$$\begin{aligned} N_{21} C_1 +N_{22} C_2 +N_{23} C_1^{*} +N_{24} C_2^{*} +N_{25} D_1 +N_{26} D_1^{*} +N_{27} A_0= & {} 0, \end{aligned}$$
(52)
$$\begin{aligned} N_{31} C_1 +N_{32} C_2 +N_{33} C_1^{*} +N_{34} C_2^{*} +N_{35} D_1 +N_{36} D_1^{*} +N_{37} A_0= & {} 0. \end{aligned}$$
(53)

For the non-trivial solution of this system of equations with coefficients \(C_1 , C_2 , C_1 ^{*}, C_2 ^{*}, D_1 , D_1 ^{*}\) and \(A_0 \) , the determinant of the coefficient matrix derived from Eq. (45), Eqs. (47)–(50), Eqs. (52) and (53) will be zero, i.e.

$$\begin{aligned} \left| {N_{ij} } \right| _{7\times 7} =0, \end{aligned}$$
(54)

where \(N_{ij} =M_{ij} ;\) for \(i=1, \quad N_{ij} =M_{\left( {i-1} \right) j} \); for \(i=4\ldots 7\) and \(N_{ij} \) for \(i=2,3\) are defined in Appendix A.

Equation (54) is the dispersion equation for electrically open case for shear acoustic wave propagation in the considered cylindrical structure.

The expansions of Eqs. (51) and (54) will result in a quite lengthy expression and, hence, has not been presented here. Moreover, Eqs. (51) and (54) indicate that the expanded expression contains only real terms which will lead to dispersion relations for the electrically short and open conditions, respectively, for the propagation of the shear acoustic wave in a piezoelectric cylindrical structure with imperfect bonding of the cylinder and concentric layer. It is worth mentioning that the dispersion relations, Eqs. (51) and (54) relating the phase velocity of the shear acoustic wave with wave number, which is our prime interest, will be considered for further study to unearth distinct characteristics associated with the shear acoustic wave propagation in the considered model.

7 Special cases

7.1 Case 1

When in the considered structure, the outer layer becomes free from the functional gradient, i.e. \(\ell =0,\) and the dispersion relations, Eqs. (51) and (54), associated with electrically short condition and electrically open condition, respectively, reduce to

$$\begin{aligned} \left| {{\overline{M}} _{ij} } \right| =0 \end{aligned}$$
(55)

and

$$\begin{aligned} \left| {{\overline{N}} _{ij} } \right| =0, \end{aligned}$$
(56)

where \({\overline{M}} _{ij}\) and \({\overline{N}} _{ij} \) are defined in Appendix B.

Equations (55) and (56) are the dispersion relations for the propagation of the shear acoustic wave in the cylindrical structure composed of a piezoelectric cylinder bonded imperfectly to a piezoelectric layer of finite width for both electrically short condition and electrically open condition, respectively.

7.2 Case 2

When in the considered structure, the outer layer becomes free from the functional gradient and the inner piezoelectric cylinder becomes dielectric, i.e. \(\ell =0 \;\hbox {and}\; e_{15}^{\left( P \right) } =0.\) Then the dispersion relations, Eqs. (51) and (54), associated with electrically short and open conditions, respectively, reduce to

$$\begin{aligned} \left| {\overline{{\overline{M}}} _{ij} } \right| =0 \end{aligned}$$
(57)

and

$$\begin{aligned} \left| {\overline{{\overline{N}}} _{ij} } \right| =0, \end{aligned}$$
(58)

where \(\overline{{\overline{M}}} _{ij}\) and \(\overline{\overline{N}} _{ij} \) are defined in Appendix B.

Equations (57) and (58) represent the dispersion relations for shear acoustic wave propagation in the cylindrical structure composed of a dielectric cylinder bonded imperfectly to a piezoelectric layer of finite width for electrically short and electrically open conditions, respectively, which are found to be in good agreement with the result obtained by Li and Lee [41].

7.3 Case 3

When in the considered structure, the outer layer becomes free from the functional gradient and is bonded perfectly (welded contact) to the inner elastic cylinder, i.e. \(\ell =0, \varepsilon _{11}^{\left( P \right) } =0, e_{15}^{\left( P \right) } =0,c_{44}^{\left( P \right) } =\mu _2 \) and \(\alpha _1 \rightarrow \infty , \alpha _2 \rightarrow \infty .\) Then the dispersion relations, Eqs. (51) and (54), associated with electrically short and open conditions, respectively, reduce to

$$\begin{aligned} \left| {\overline{\overline{{\overline{M}} }} _{ij} } \right| =0 \end{aligned}$$
(59)

and

$$\begin{aligned} \left| {\overline{\overline{{\overline{N}} }} _{ij} } \right| =0 \end{aligned}$$
(60)

where \(\overline{\overline{{\overline{M}}} } _{ij}\) and \(\overline{\overline{{\overline{N}}} } _{ij} \) are defined in Appendix B.

Equations (59) and (60) are the dispersion relations for shear acoustic wave propagation in the cylindrical structure composed of an elastic cylinder perfectly bonded to a piezoelectric layer of finite width for electrically short and electrically open conditions, respectively, which are found to be in good agreement with the result obtained by Du et al. [17] on neglecting initial stress in the study.

7.4 Case 4

When the FGPM layer and piezoelectric cylinder become homogeneous, isotropically elastic and are perfectly bonded with each other, i.e. \(\ell =0, e_{15}^{\left( F \right) } =e_{15}^{\left( P \right) } =\varepsilon _{11}^{\left( F \right) } =\varepsilon _{11}^{\left( P \right) } =0, \quad \alpha _1 \rightarrow \infty , \alpha _2 \rightarrow \infty \) and \(c_{44}^{\left( F \right) } =\mu _1 , c_{44}^{\left( P \right) } =\mu _2,\) then both the dispersion relations (51) and (54) for both electrically short condition and electrically open condition, respectively, reduce to

$$\begin{aligned} \tan \left( {kh\sqrt{\frac{c^{2}}{\beta _1^2 }-1}} \right) =\frac{\mu _2 \sqrt{1-\frac{c^{2}}{\beta _2^2 }}}{\mu _1 \sqrt{\frac{c^{2}}{\beta _1^2 }-1}}, \end{aligned}$$
(61)

which is the classical Love wave equation [43].

8 Numerical simulation and discussion

In this section, numerical simulation and graphical demonstration are carried out to illustrate the analytical results obtained for shear acoustic wave propagation in a piezoelectric cylindrical structure composed of a piezoelectric material cylinder imperfectly bonded to a concentric FGPM cylindrical layer. The materials PZT-5H and AlN are used for FGPM cylindrical layer [24] and inner piezoelectric material cylinder [44], respectively. The values of the material constants and densities in the computation part are listed in Table 1, and the value of the dielectric parameter \(\left( {\varepsilon _0 } \right) \) for the vacuum is \(8.85\times 10^{-12}\) C/Nm\(^{2}\). For numerical computation purposes, the mechanical and electrical imperfection parameters are made dimensionless as

$$\begin{aligned} R_1 =\frac{\alpha _1 r_1 }{{\left( {e_{15}^{\left( F \right) } } \right) ^{2}}/{\varepsilon _{11}^{\left( F \right) } }}\quad {\text {and}} \quad R_2 =\frac{\alpha _2 r_1 }{\varepsilon _{11}^{\left( F \right) }}, \end{aligned}$$

respectively.

Table 1 Material constants used for the FGPM layer and piezoelectric cylinder
Full size table

The influence of the functional gradient parameter \(\left( \ell \right) ,\) mechanical imperfection parameter \(\left( {R_1 } \right) ,\) electrical imperfection parameter \(\left( {R_2 } \right) ,\) radii ratio \(\left( {{r_2 }/{r_1 }} \right) \) and order of Bessel’s function \(\left( n \right) \) on the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of shear acoustic wave propagation in the considered piezoelectric cylindrical structure with respect to the dimensionless wave number \(\left( {kh} \right) \) has been delineated through Figs. 2, 3, 4, 5 and 7 for both electrically short and electrically open conditions. The analysis of different modes of the phase velocity of the shear acoustic wave is delineated in Fig. 6. An overview of Figs. 2, 3, 4, 5, 6 and 7 shows that the phase velocity of the shear acoustic wave decreases when the wave number increases.

Fig. 2
figure 2

Effect of functional gradient parameter \(\left( \ell \right) \) associated with the FGPM layer on the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of shear acoustic wave propagation against dimensionless wave number \(\left( {kh} \right) \) for a electrically short condition, b electrically open condition

Full size image
Fig. 3
figure 3

Effect of mechanical imperfection parameter \(\left( {R_1 } \right) \) associated with the imperfectly bonded interface of the layer and cylinder on the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of shear acoustic wave propagation against dimensionless wave number \(\left( {kh} \right) \) for a electrically short condition, b electrically open condition

Full size image
Fig. 4
figure 4

Effect of electrical imperfection parameter \(\left( {R_2 } \right) \) associated with the imperfectly bonded interface between the layer and cylinder on the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of shear acoustic wave propagation against dimensionless wave number \(\left( {kh} \right) \) for a electrically short condition, b electrically open condition

Full size image
Fig. 5
figure 5

Effect of radii ratio parameter \(\left( {{r_2 }/{r_1 }} \right) \) on the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of shear acoustic wave propagation against dimensionless wave number \(\left( {kh} \right) \) for a electrically short condition, b electrically open condition

Full size image
Fig. 6
figure 6

Dispersion curves for first three modes, viz., first mode, second mode and third mode for a electrically short condition, b electrically open condition

Full size image
Fig. 7
figure 7

Variation of order of Bessel’s function of the first and second kind appearing in the dispersion relation for a electrically short condition, b electrically open condition

Full size image

8.1 Effect of functional gradient parameter on phase velocity

The pronounced effect of the functional gradient parameter associated with the FGPM layer on the phase velocity of shear acoustic wave propagation in a piezoelectric cylindrical structure is delineated by Fig. 2. The dispersion curve 1 is traced out by considering the FGPM layer as a homogeneous piezoelectric layer, whereas curves 2 and 3 are associated to the effect of the gradient parameter of the FGPM layer. Figure 2a and b exhibits the impact of the gradient parameter on the phase velocity of the shear acoustic wave through the piezoelectric cylindrical structure for electrically short and electrically open conditions, respectively. The variation of phase velocity increases with the increment of gradient parameter for the electrically short case, while for the electrically open case, the gradient parameter has decreasing effect on the phase velocity. Also, a comparative study of Fig. 2a and b depicts that the impact of gradient parameter for the electrically short condition is more as compared to the electrically open condition.

8.2 Effect of imperfection parameter on phase velocity

Figures 3 and 4 demonstrate the remarkable impact of the mechanical imperfection parameter \(\left( {R_1 } \right) \) and electrical imperfection parameter \(\left( {R_2 } \right) \) associated to the imperfect bonding of the FGPM layer and piezoelectric cylinder on the phase velocity of a shear acoustic wave. The interface of the structure is perfectly bonded and conducting when the imperfection parameters are very large or tends to infinity; otherwise, it is mechanically or electrically imperfect. Thus the smaller values of imperfection parameter lead to more interfacial imperfection. The dispersion curve 1 in both the figures is drawn for high imperfection in the interface, while curve 2 and curve 3 in Figs. 3 and 4 are associated to the weak imperfection and perfectly bonded/conducted interface, respectively.

Figure 3a and b reveals the influence of the mechanical imperfection parameter on the phase velocity of a shear acoustic wave for electrically short and electrically open conditions, respectively. The values of the mechanical imperfection parameter have an encouraging effect on the phase velocity for both electrically short and open conditions, and, therefore, the phase velocity is maximum when the interface is perfectly bonded. Also, a comparative study of Fig. 3a and b indicates that the effect of the mechanical imperfection parameter for a short case is more as compared to the open case. The influence of the electrical imperfection parameter on the phase velocity of shear acoustic wave is portrayed in Fig. 4a and b for both electrically short and electrically open conditions, respectively. The phase velocity of the shear acoustic wave decreases when values of the electrical imperfection parameter increase for electrically short condition, whereas it has an encouraging impact on the phase velocity of shear acoustic wave propagation for an electrically open condition.

8.3 Effect of radii ratio parameter on phase velocity

The effect of the radii ratio parameter on the phase velocity of shear acoustic wave propagation in a piezoelectric cylindrical structure is manifested through Fig. 5. In particular, Fig. 5a and b corresponds to the electrically short and electrically open conditions, respectively. The dispersion curves 1, 2 and 3 are traced out to show the effect of radii ratio on the phase velocity for shear acoustic wave propagation in both the figures. Figure 5a and b demonstrates the impact of radii ratio parameter on the phase velocity of shear acoustic wave propagation in the aforesaid structure. The radii ratio parameter has a favourable effect on the phase velocity for both electrically short condition and electrically open condition. Also, a subtle examination discussing on the comparative study of Fig. 5a and b indicates that the influence of the radii ratio parameter for an electrically open condition is greater as compared to that of an electrically short condition.

8.4 Analysis of distinct mode of phase velocity

Dispersion curves for the first three modes, viz., first mode, second mode and third mode, are plotted for both electrically short and open conditions in Fig. 6a and b, respectively. As per the validity condition of the propagation of a shear acoustic wave in the considered piezoelectric cylindrical structure, the common wave velocity \(\left( c \right) \) lies between the shear velocities of the wave in an FGPM cylindrical layer \(\left( {\beta _1 } \right) \) and piezoelectric cylinder \(\left( {\beta _2 } \right) \) where \(\beta _2 >\beta _1 .\) For the data taken into consideration, the dimensionless phase velocity \(\left( {c/{\beta _1 }} \right) \) of the propagating shear acoustic wave lies in the range \(1<c/{\beta _1 }<2.75\) in both conditions. Therefore, for the admissible range of phase velocity, the range of dimensionless frequency for the first mode, second mode and third mode is (1.5, 4.6), (2.3, 6.6) and (2.7, 7.6), respectively, for an electrically short condition. On the other hand, for the electrically open condition, the range of dimensionless frequency for the first mode, second mode and third mode are (0.3, 1), (1, 3) and (1.5, 4.2), respectively. It has been found that the fundamental (first) mode lies in the lower-frequency region, and the higher mode lies in the higher-frequency region.

Figure 7 shows the effect of the order of Bessel’s function of the first and second kind appearing in the dispersion relation on the phase velocity of a shear acoustic wave for both electrically short and electrically open conditions. In particular, Fig. 7a stands for the electrically short condition, whereas Fig. 7b is associated to the electrically open condition. It is revealed from Fig. 7a and b that the phase velocity of the shear acoustic wave increases with the increment of the order of Bessel’s function of the first and second kind appearing in the dispersion relation.

A common observation drawn from the comparative study of all Figs. 2a, 3, 4, 5, 6 and 7b is that the phase velocity of a shear acoustic wave is found to be greater in the case of an electrically short condition as compared to the electrically open condition.

9 Conclusion

The present work emphasizes study of the propagation behaviour of a shear acoustic wave through a piezoelectric cylindrical layered structure composed of a piezoelectric material cylinder imperfectly bonded to a concentric FGPM cylindrical layer of finite width. Two distinct dispersion relations for electrically short and electrically open conditions are obtained with the aid of some mathematical treatment. Numerical simulation and graphical demonstration have been done to show the effect of the functional gradient parameter, radii ratio parameter, order of Bessel’s functions appearing in the dispersion relations and mechanical and electrical imperfection parameters on the phase velocity of a propagating wave. A comparative analysis is also carried out to examine the dispersion relations for short and open conditions. The outcome of the current study can be encapsulated as follows:

  • Wave number disfavours the phase velocity of a propagating wave in the considered piezoelectric cylindrical layered structure.

  • The functional gradient parameter has an increasing effect on the phase velocity of a propagating wave for an electrically short condition, while for an electrically open condition, phase velocity decreases when the functional gradient parameter increases.

  • The mechanical imperfection parameter enhances the phase velocity of shear acoustic wave propagation for both electrically short and open conditions.

  • The electrical imperfection parameter disfavours the phase velocity of a propagating wave for an electrically short condition, while for an electrically open condition, phase velocity is enhanced when the electrical imperfection parameter increases.

  • The radii ratio of the piezoelectric cylinder and concentric FGPM cylindrical layer favours the phase velocity of a shear acoustic wave for both electrically short and open conditions.

  • It has been observed that the fundamental (first) mode exists in the lower-frequency region, and the higher modes exist in the higher-frequency region.

  • The deduced dispersion relations are matched with the pre-established results and classical Love wave equation.

It is revealed that based on the material properties of a piezoelectric cylinder imperfectly bonded with a concentric FGPM cylindrical layer, a propagating shear acoustic wave (along the azimuthal direction) can be entrapped in the cylindrical structure for a longer duration in both electrically short and open conditions. Numerical results show that the transient electromechanical responses are also sensitive to the weakness of the mechanically and/or electrically imperfect interface. Therefore, by involving the functional gradient in the layer and the extent of imperfection in the bonding of the concentric cylindrical piezoelectric material medium, we may enhance the confinement of the shear acoustic wave in the structure. As it is a well-known fact that the principle of surface acoustic wave (SAW) devices relies on phase delay, therefore, from an applicative point of view, the consequences of the present study can be employed in the design of Love wave or shear acoustic wave sensors/transducers. The present problem is an important foundation in engineering science for evaluating the interfacial properties, such as non-destructive testing, structural health monitoring, etc.