1 Introduction

The mictostructure of the porous cylinder considered in this paper consists of the matrix phase (solid phase) and the fluid that fills in the pores. Both the solid and the fluid phases are assumed incompressible. The fluid can move within the pore space and can flow out of the body or it can flow into the body. When the latter happens the volume of the body changes although the individual phases are incompressible.

The fluid can experience stress under the load so there is a quantity called the fluid pressure. When the fluid leaves the body, in the long term the fluid pressure usually goes to zero.

When the fluid pressure is small (or when the pores are empty), one can refer to the remaining structure consisting of the voids and the solid phase as the skeleton. The skeleton itself is usually considered as a compressible material since the volume of the pores should decrease, for example, when the fluid flows out of the body.

Ogden material model for incompressible materials is introduced in [1]. In this model the strain energy of the material is assumed to be a function of strain invariants \((\lambda _{1}^{\alpha }+ \lambda _{2}^{\alpha }+ \lambda _{3}^{ \alpha }- 3)/\alpha \), where \(\alpha \) is one of the material parameters and \(\lambda _{i}\) are principal stretches. In particular, if \(\alpha =1\), Varga material is recovered, and if \(\alpha =2\), the neo-Hookean material is obtained.

Many strain energy functions can be used to describe elastic behavior of the compressible skeleton of the poroelastic body. The most famous one is neo-Hookean strain energy function (with \(\alpha =2\)). For this case the shear modulus \(\mu \) and the compressibility parameter \(D\) are the two remaining elastic parameters that need to be specified. In this paper we focus on Ogden strain energy function, which can be considered as the generalization of the neo-Hookean material. In addition to two material constants \(\mu \) and \(D\), there is a third parameter \(\alpha \).

In the recent paper by Selvadurai and Suvorov [2] the large twist deformation of a porous fluid-saturated cylinder was considered. The twist is assumed to be applied to the cylinder within a relatively short interval of time so that the rate effects associated with the fluid motion are present. In [2] the authors assumed the neo-Hookean material model for the skeleton.

Two distinct responses of the poroelastic body can usually be identified in the situation when the deformation is applied suddenly (in a fast rate). The first one is the short-term response or instantaneous response. The second one is the long-term response.

In the instantaneous response the fluid cannot move relative to the skeleton of the poroelastic body. Thus, it cannot leave the body and the volume of the cylinder remains unchanged. Furthermore, any point which had the radial coordinate \(R\) will have the same radial coordinate after the deformation. Due to this simple geometrical description of the deformation, studying the instantaneous response is usually much simpler than the analysis of the long-term response.

In the long-term response the role of the fluid in supporting the overall stress is usually small, the pressure in the fluid is small. This process of fluid pressure reduction is often referred to as fluid pressure dissipation. However, the volume of the cylinder has now been changed due to the fluid migration. In this case the radial coordinate of a point after the deformation \(r\) will not be equal to the initial radial coordinate \(R\) of this point.

This paper focuses only on the instantaneous response of the cylinder subjected to the suddenly applied large twist deformation. The material of the skeleton is assumed to be of Ogden type. It should be noted that the analysis presented in this paper can also be applied to a homogeneous incompressible cylinder subjected to the finite twist deformation.

Horgan and Murphy [3] considered in detail pure torsion of an incompressible (and homogeneous) cylinder with Ogden-type strain energy function. They obtained closed form expressions for the axial force and twisting moment for a prescribed amount of twist (angle of rotation) of the cylinder. Since the cylinder is a simple homogeneous material, there is no fluid pressure in it. In contrast this paper does not include the results for the axial force and the twisting moment, but rather presents expressions for the stresses and fluid pressure in the cylinder subjected to a twist.

As was mentioned above studying the long-term response of the poroelastic body (or the transient response) is more difficult and usually involves finite element simulations. Certain analytical results, however, can be obtained if the skeleton is assumed to be only slightly compressible. Small et al [4] solved the problem of finite torsion of fluid-saturated poroelastic cylinder for this case. They obtained analytical results for slightly compressible hyperelastic skeleton using the perturbation techniques and verified the solution using the FEBio finite element software.

Possible application areas for which the present theory of large torsional deformations is relevant include: torsion of rock specimens in laboratory described in [5], torsion of marine cables and their buckling due to torsional instability studied in [6] and [7], supercoiling of long DNA molecules in a cell ([7]), torsion of biological tissues both in normal condition and in pathological condition. Torsional instability of solid cylinders was studied in [8] and [9].

Finally, it is important to mention, that except torsion problem, Selvadurai and Suvorov studied application of many other deformation modes to porous fluid-saturated bodies with hyperelastic skeleton. For example in [10] they studied compression of porous fluid-saturated 1D column and a sphere. Their another paper [11] is devoted to inflation of fluid-saturated cylindrical shell (tube).

2 General Equations for a Twisted Cylinder

Consider a cylinder with radius \(A\) and length \(L\) cccupying the region \(0\le R\le A\), \(0\le Z \le L\). Each point has the coordinates \(R\), \(\Theta \), \(Z\) in the cylindrical coordinate system.

When the cylinder is twisted each cross-section of the cylinder is rotated by a certain angle. We assume that the angle of rotation is linearly changing along the length of the cylinder. Define \(\tau \) as the difference in angles of rotation of the cross-sections of the cylinder at a unit distance apart from each other. Then, the deformed coordinates of the cylinder \(r\), \(\theta \), \(z\) (in the cylindrical coordinate system) can be described by the following functions

$$\begin{aligned} r = r(R), \quad \theta = \Theta + \tau Z, \quad z = Z. \end{aligned}$$
(1)

If the cylinder volume does not change, as in case of the short-term response of the cylinder subjected to a sudden twist, then \(r=R\).

In Fig. 1 we show the initial and twisted configurations of the cylinder and also some imaginary fibers that are initially vertical. For the example shown in the figure, in the twisted state the upper cross-section is rotated by an angle \(\pi /2\) (or \(\pi \)), the cross-section at mid-length is rotated by an angle twice smaller and so on. For the geometry shown in the picture with \(L/A=3.2\), \(\tau A = 0.491\) for the middle cylinder and \(\tau A =0.9817\) for the right cylinder.

Fig. 1
figure 1

Initial and deformed configurations of the cylinder when the upper cross-section is rotated by an angle equal \(\pi /2\) and \(\pi \)

Full size image

Taking into account (1), the deformation gradient tensor is given by

$$\begin{aligned} \mathbf{{F} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & \tau R \\ 0 & 0 & 1 \end{pmatrix}. } \mathbf{ } \end{aligned}$$
(2)

Therefore, if we take a vector parallel to the \(Z\)-axis with the coordinates \((0,0,1)^{T}\) lying on a lateral surface of the cylinder \(R=A\) and observe how it deforms, after the deformation it will have the coordinates \((0, \tau A, 1)^{T}\) (according to the third column of the tensor \(\mathbf{{F}}\)). The last two coordinates are measured on the lateral surface of the cylinder \(R=A\) along the axes \(\Theta \) and \(Z\). Also, the vector tangent to the circumferential direction with the coordinates \((0,1,0)^{T}\) transforms to \((0,1,0)^{T}\) according to the second column of the tensor \(\mathbf{{F}}\) (see also Fig. 3).

The deformation gradient can be represented as the product of a symmetric stretch tensor \(\mathbf{{V}}\) and some rotation matrix \(\mathbf{{R}}\), i.e., \(\mathbf{{F}= }\mathbf{{V} }\mathbf{{R}}\). Let the eigenvalues of the stretch tensor \(\mathbf{{V}}\) be denoted by \(\lambda _{1}\), \(\lambda _{2}\), \(\lambda _{3}\). These are so-called principal stretches. The eigenvectors are called principal directions.

The left Cauchy-Green strain tensor \(\mathbf{{B}}\) is defined as \(\mathbf{{B} = }\mathbf{{F} }\mathbf{{F}^{T}}\) and thus is given by

$$\begin{aligned} \mathbf{{B} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1+\tau ^{2} R^{2} & \tau R \\ 0 & \tau R & 1 \end{pmatrix}. } \mathbf{ } \end{aligned}$$
(3)

We can find eigenvalues and eigenvectors of the tensor \(\mathbf{{B}}\). It is clear that the eigenvalues of the tensor \(\mathbf{{B}}\) are the squares of the eigenvalues of the tensor \(\mathbf{{V}}\), i.e., the squares of the principal stretches \(\lambda _{1}^{2}\), \(\lambda _{2}^{2}\), \(\lambda _{3}^{2}\). The eigenvectors of the tensor \(\mathbf{{B}}\) and the tensor \(\mathbf{{V}}\) are the same, and thus also the principal directions.

By solving the eigenvalue problem for the tensor \(\mathbf{{B}}\), it can be shown that the principal stretches can be found as

$$\begin{aligned} \lambda _{1} = \lambda _{r} = 1, \\ \lambda _{2} = \frac{1}{2} (\tau R + \sqrt{4 + \tau ^{2} R^{2})}, \\ \lambda _{3} = \lambda _{2}^{-1} = \frac{1}{2} (-\tau R +\sqrt{4 + \tau ^{2} R^{2})}. \end{aligned}$$
(4)

Also

$$\begin{aligned} &\lambda _{2}^{2} = 1 + \frac{1}{2} (\tau ^{2} R^{2} + \tau R \sqrt{4 + \tau ^{2} R^{2}}), \\ &\lambda _{3}^{2} = 1 + \frac{1}{2} (\tau ^{2} R^{2} - \tau R \sqrt{4 + \tau ^{2} R^{2}}). \end{aligned}$$
(5)

The following connections hold between the principal stretches

$$\begin{aligned} \lambda _{2} - \frac{1}{\lambda _{2}} = \tau R, \qquad \lambda _{3} - \frac{1}{\lambda _{3}} = - \tau R. \end{aligned}$$
(6)

Also

$$\begin{aligned} \lambda _{2}^{2} - \lambda _{3}^{2} = \tau R \sqrt{4 + \tau ^{2} R^{2}}, \quad \lambda _{2}^{2} + \lambda _{3}^{2} = 2 + \tau ^{2} R^{2}, \quad \lambda _{2}^{2} \lambda _{3}^{2} = 1. \end{aligned}$$
(7)

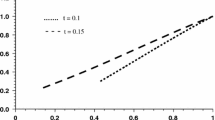
Figure 2 shows dependence of the principal stretch \(\lambda _{2}\) on parameter \(\tau A\) for the surface \(R=A\), as given by (5). We note that when \(\tau A \rightarrow \infty \), the principal stretch is well approximated by \(\tau A\). When \(\tau A \rightarrow 0\), \(\lambda _{2}\) is well approximated by \(\frac{1}{2} \tau A + 1\).

Fig. 2
figure 2

Principal stretch \(\lambda _{2}(A)\) as a function of \(\tau A\)

Full size image

In addition, it can be shown that in cylindrical coordinate system (\(r, \theta , z\)) the principal directions have the following vector representation

$$\begin{aligned} \vec{n}_{1} = (1, 0 , 0)^{T}, \quad \vec{n}_{2} = (0, n, m)^{T}, \quad \vec{n}_{3} = (0,-m, n)^{T}, \end{aligned}$$
(8)

where \(m^{2}+n^{2}=1\) and \(m\), \(n\) can be found from

$$\begin{aligned} &m^{2} = \frac{2}{4 + \tau ^{2} R^{2} + \tau R \sqrt{4 + \tau ^{2} R^{2}}} = \frac{1}{\lambda _{2}^{2} + 1}, \\ &n^{2} = \frac{2}{4 + \tau ^{2} R^{2} - \tau R \sqrt{4 + \tau ^{2} R^{2}}} = \frac{1}{\lambda _{3}^{2} + 1}. \end{aligned}$$
(9)

Figure 3 shows deformed shapes of a rectangle lying on unfolded \(\theta Z\)-plane for the values of twist \(\tau A\) equal to 0.5, 1, 1.5 and 2 (with a solid line). Direction of the vertical side of the rectangle after the specified deformation was found using the third column of the deformation gradient tensor (2). This inclined side of the deformed rectangle coincides with the direction of the fiber, shown in Fig. 1. Note also that the tangent of the angle that this fiber makes with the horizontal axis is equal to \(1/\tau A\).

Fig. 3
figure 3

Deformed rectangle lying on a \(\theta Z\) - surface (solid line) and the principal direction \(\vec{n}_{2}\) (dashed line) for \(\tau A = 0.5, 1, 1.5\) and 2

Full size image

Along with that, this figure shows principal directions (dashed line) corresponding to the principal stretch \(\lambda _{2}\) for the same values of \(\tau A\). The principal direction \(\vec{n}_{2}\) was found using (9). It can be observed that if \(\tau A\) is small, then the principal direction is close to the main diagonal of the deformed rectangle, but when \(\tau A\) becomes larger, the principal direction is more aligned with the side of the deformed rectangle.

In a poroelastic body the total normal stresses are usually represented as the sum of the stresses supported by the skeleton of the body and the stresses in the fluid. If we define the fluid pressure \(p\) as the stress in the fluid multiplied by −1, then this decomposition for all the normal stresses takes the form

$$\begin{aligned} \sigma _{normal} = \sigma _{normal}^{\prime }- p, \quad \sigma _{shear} = \sigma _{shear}^{\prime}. \end{aligned}$$
(10)

Here the stresses with the prime sign are the effective stresses or the stresses supported by the skeleton. The stresses without prime are the total stresses. The fluid pressure affects only the normal stresses.

Similar decomposition can be written down for homogeneous and incompressible cylinder, separating the total stresses into two components \(\sigma _{normal}^{\prime}\) and \(-p\) but in this case it is not easy to find the physical meaning for \(p\) (for example, it is called an arbitrary scalar field in [3]) and for the stresses with prime sign. For convenience, we would still refer to the stresses with prime as effective stresses.

The effective normal stresses along the principal directions are called the principal stresses and denoted by \(\sigma _{1}^{\prime}\), \(\sigma _{2}^{\prime}\), \(\sigma _{3}^{\prime}\). Since the first principal direction is coincident with the radial direction, \(\sigma _{1}^{\prime }= \sigma _{rr}^{\prime}\).

With the knowledge of the principal directions and principal stresses, the effective stresses in the cylindrical coordinate system can be derived by using usual transformation rules as

$$\begin{aligned} & \sigma _{rr}^{\prime }= \sigma _{1}^{\prime}, \\ &\sigma _{\theta \theta}^{\prime} = n^{2} \sigma _{2}^{\prime} + m^{2} \sigma _{3}^{\prime} = \frac{1}{\lambda _{3}^{2} + 1} \sigma _{2}^{ \prime} + \frac{1}{\lambda _{2}^{2} + 1} \sigma _{3}^{\prime}, \\ &\sigma _{zz}^{\prime} = m^{2} \sigma _{2}^{\prime} + n^{2} \sigma _{3}^{ \prime} = \frac{1}{\lambda _{2}^{2} + 1} \sigma _{2}^{\prime} + \frac{1}{\lambda _{3}^{2} + 1} \sigma _{3}^{\prime}. \end{aligned}$$
(11)

Here \(n\) is the cosine of the angle between the principal direction \(\vec{n}_{2}\) and the \(\theta \)-axis. Similarly, it can be treated as the cosine of the angle between the principal direction \(\vec{n}_{3}\) and the \(z\)-axis.

Therefore, the effective normal stress along an arbitrary direction defined by an angle \(\beta \) with respect to the principal direction \(\vec{n}_{2}\) can be evaluated as

$$\begin{aligned} \sigma _{d}^{\prime }= \cos ^{2} {\beta} \sigma _{2}^{\prime }+ \sin ^{2} {\beta} \sigma _{3}^{\prime}. \end{aligned}$$
(12)

Similarly, if \(\beta \) is the angle between the desired direction and the principal direction \(\vec{n}_{3}\), then the normal stress along the desired direction is given by

$$\begin{aligned} \sigma _{d}^{\prime }= \sin ^{2} {\beta} \sigma _{2}^{\prime }+ \cos ^{2} {\beta} \sigma _{3}^{\prime}. \end{aligned}$$
(13)

Note that for large \(\tau \), \(\lambda _{2} \rightarrow \infty \) and \(\lambda _{3} \rightarrow 0\), and thus \(\sigma _{\theta \theta}^{\prime }\rightarrow \sigma _{2}^{\prime}\) and \(\sigma _{zz}^{\prime }\rightarrow \sigma _{3}^{\prime}\).

Consider now equilibrium equation in the radial direction. The equilibrium equation in terms of the total stresses can be written as

$$\begin{aligned} \frac{d \sigma _{rr}}{dr} + \frac{1}{r} (\sigma _{rr} - \sigma _{ \theta \theta}) = 0, \end{aligned}$$
(14)

and we can assume again that \(r=R\). On the other hand, this equation can be written in terms of the effective stresses

$$\begin{aligned} \frac{d \sigma _{rr}^{\prime}}{dr} + \frac{1}{r} (\sigma _{rr}^{ \prime }- \sigma _{\theta \theta}^{\prime}) - \frac{dp}{dr} = 0. \end{aligned}$$
(15)

On the external surface of the cylinder \(R=A\), the total radial stress is assumed zero

$$\begin{aligned} \sigma _{rr} (A) = 0. \end{aligned}$$
(16)

Therefore, from (14) the total radial stress can be found as

$$\begin{aligned} \sigma _{rr} = \int _{R}^{A} \frac{\sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}}{R} dR, \end{aligned}$$
(17)

where we have used the fact that \(\sigma _{rr} - \sigma _{\theta \theta} = \sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}\) due to definition of the effective stress.

Therefore, for evaluation of the radial stress we need first to evaluate

$$\begin{aligned} \sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime }= \sigma _{1}^{ \prime} - \frac{1}{\lambda _{3}^{2} + 1} \sigma _{2}^{\prime} - \frac{1}{\lambda _{2}^{2} + 1} \sigma _{3}^{\prime} = \sigma _{1}^{ \prime} - \frac{\lambda _{2}^{2}}{\lambda _{2}^{2} + 1} \sigma _{2}^{ \prime} - \frac{1}{\lambda _{2}^{2} + 1} \sigma _{3}^{\prime}, \end{aligned}$$
(18)

where we have used (11).

The fluid pressure is then found using the definition of the effective radial stress

$$\begin{aligned} p = \sigma _{rr}^{\prime }- \sigma _{rr} = \sigma _{rr}^{\prime }- \int _{R}^{A} \frac{\sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}}{R} dR. \end{aligned}$$
(19)

Note that the fluid pressure does not have to be zero at the external surface for the short-term response of the cylinder to the sudden twist.

After finding the fluid pressure, the axial and hoop stresses can be found as

$$\begin{aligned} &\sigma _{zz} = \sigma _{zz}^{\prime }- p = \frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- p = \frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- \sigma _{rr}^{ \prime }+ \sigma _{rr}, \\ &\sigma _{\theta \theta} = \sigma _{\theta \theta}^{\prime }- p = \frac{1}{1+\lambda _{3}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{2}^{2}} \sigma _{3}^{\prime }- p = \frac{1}{1+\lambda _{3}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{2}^{2}} \sigma _{3}^{\prime }- \sigma _{rr}^{ \prime }+ \sigma _{rr}. \end{aligned}$$
(20)

The shear stress is easier to find than the normal stresses. Using the transformation rules for stress tensor components, similar to (11), and the fact that there is no shear stress on the principal planes, the shear stress \(\sigma _{\theta z}\) can be found as

$$\begin{aligned} \sigma _{\theta z} = n m \sigma _{2}^{\prime }- nm \sigma _{3}^{ \prime }= n m (\sigma _{2}^{\prime }- \sigma _{3}^{\prime}). \end{aligned}$$
(21)

From (9) it can be shown that

$$\begin{aligned} n m = \frac{1}{\sqrt{4 + \tau ^{2} R^{2} }}. \end{aligned}$$
(22)

3 Specializing Results to Ogden Material

Assume now that the skeleton of the poroelastic cylinder is a nearly incompressible material of Ogden type. Its strain energy is given in terms of the principal stretches as

$$\begin{aligned} W_{1} = \frac{2\mu}{\alpha ^{2}} (J_{3}^{-\alpha /3} (\lambda _{1}^{ \alpha }+ \lambda _{2}^{\alpha }+ \lambda _{3}^{\alpha}) - 3) + \frac{1}{D} (J_{3}-1)^{2}, \end{aligned}$$
(23)

where \(\mu \), \(D\), \(\alpha \) are the material constants and \(J_{3} = \lambda _{1} \lambda _{2} \lambda _{3}\). Due to the fact that the volume of the twisted cylinder does not change, \(J_{3}=1\). If \(\alpha =2\), we recover the case of neo-Hookean material.

The effective principal stresses (the stresses in the skeleton) are derived from the strain energy function as

$$\begin{aligned} \sigma _{1}^{\prime }= \frac{\lambda _{1}}{J} \frac{dW}{d\lambda _{1}}, \quad \sigma _{2}^{\prime }= \frac{\lambda _{2}}{J} \frac{dW}{d\lambda _{2}}, \quad \sigma _{3}^{ \prime }= \frac{\lambda _{3}}{J} \frac{dW}{d\lambda _{3}}. \end{aligned}$$
(24)

Therefore, for the skeleton with the strain energy function \(W_{1}\) we can find the effective principal stresses as

$$\begin{aligned} &\sigma _{1}^{\prime} = \sigma _{rr}^{\prime }= \frac{2\mu}{\alpha ^{2}} (-\frac{\alpha}{3} (1 + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha}) + \alpha ), \\ &\sigma _{2}^{\prime} = \frac{2\mu}{\alpha ^{2}} (-\frac{\alpha}{3} (1 + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha}) + \alpha \lambda _{2}^{ \alpha} ), \\ &\sigma _{3}^{\prime} = \frac{2\mu}{\alpha ^{2}} (-\frac{\alpha}{3} (1 + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha}) + \alpha \lambda _{3}^{ \alpha}). \end{aligned}$$
(25)

We have derived these equations by substituting the strain energy (23) into (24). We have also taken into account the fact that \(\lambda _{1}=1\), \(\lambda _{2} \lambda _{3}=1\). From (25) it follows that all effective stresses are equal to zero at the center of the cylinder \(R=0\) since at the center \(\lambda _{1} = \lambda _{2} = \lambda _{3} = 1\) and all the stretches are equal to 1.

In case of a totally incompressible and homogeneous material, the strain energy of Ogden type is given by

$$\begin{aligned} W_{0} = \frac{2\mu}{\alpha ^{2}} (\lambda _{1}^{\alpha }+ \lambda _{2}^{ \alpha }+ \lambda _{3}^{\alpha }- 3). \end{aligned}$$
(26)

When the strain energy function \(W_{0}\) is used, the effective stresses can be obtained from (24) as

$$\begin{aligned} &\sigma _{1}^{\prime} = \sigma _{rr}^{\prime }= \frac{2\mu}{\alpha}, \quad \sigma _{2}^{\prime} = \frac{2\mu}{\alpha} \lambda _{2}^{\alpha}, \quad \sigma _{3}^{\prime} = \frac{2\mu}{\alpha} \lambda _{3}^{\alpha}. \end{aligned}$$
(27)

Note that these effective stresses are not equal to zero at the center of the cylinder \(R=0\).

We now proceed to evaluation of the total radial stress \(\sigma _{rr}\). When substituting the principal stresses \(\sigma _{2}^{\prime}\), \(\sigma _{3}^{\prime}\) for the Ogden material from (25) into (18)

$$\begin{aligned} \sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime }= \sigma _{1}^{ \prime} - \frac{\lambda _{2}^{2}}{\lambda _{2}^{2} + 1} \sigma _{2}^{ \prime} - \frac{1}{\lambda _{2}^{2} + 1} \sigma _{3}^{\prime}, \end{aligned}$$

we find that the terms than contain \((1 + \lambda _{2}^{\alpha} + \lambda _{3}^{\alpha})\) cancel out. After a few simplifications and using the fact that \(\lambda _{2} \lambda _{3} = 1\), we can obtain

$$\begin{aligned} \sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime }= - \frac{2\mu}{\alpha} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)}. \end{aligned}$$
(28)

The total radial stress can then be obtained by integration of \(\sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}\) as follows

$$\begin{aligned} &\sigma _{rr} = \int _{R}^{A} \frac{\sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}}{R} dR = \\ &-\frac{2\mu}{\alpha} \int _{R}^{A} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} \frac{dR}{R}. \end{aligned}$$
(29)

Note that this expression for the total radial stress is also valid for a totally incompressible material of Ogden type with the strain energy function \(W_{0}\).

To compute this integral, the change of variables \(R \rightarrow \lambda _{2}\) must be made. Using the fact that (see [3])

$$\begin{aligned} \lambda _{2} - \lambda _{2}^{-1} = \tau R, \end{aligned}$$

we can easily find that

$$\begin{aligned} dR = \frac{1}{\tau} (1+\frac{1}{\lambda _{2}^{2}}) d \lambda _{2}, \end{aligned}$$
(30)

and consequently

$$\begin{aligned} \frac{dR}{R} = \frac{1+\lambda _{2}^{2}}{\lambda _{2}^{2}-1} \frac{d\lambda _{2}}{\lambda _{2}}. \end{aligned}$$
(31)

Therefore, after the change of variables under the sign of the integral, we obtain the radial stress as

$$\begin{aligned} &\sigma _{rr} = -\frac{2\mu}{\alpha} \int _{\lambda _{2}(R)}^{ \lambda _{2}(A)} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} \frac{1+\lambda _{2}^{2}}{\lambda _{2}^{2}-1} \frac{d\lambda _{2}}{\lambda _{2}} = \\ & -\frac{2\mu}{\alpha} \int _{\lambda _{2}(R)}^{\lambda _{2}(A)} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha +1} (\lambda _{2}^{2}-1) } d\lambda _{2}. \end{aligned}$$
(32)

Here the limits of integration are the stretches \(\lambda _{2}\) evaluated at the location \(R\) and at the external surface \(R=A\) for a given twist \(\tau \)

$$\begin{aligned} \lambda _{2} (R) = \frac{1}{2} ( \tau R + \sqrt{4+\tau ^{2} R^{2}}), \quad \lambda _{2} (A) = \frac{1}{2} ( \tau A + \sqrt{4+\tau ^{2} A^{2}} ). \end{aligned}$$
(33)

For \(\alpha \) which is an even integer, i.e., \(\alpha =2,4,6\ldots \), the integral defined as

$$\begin{aligned} I = \int \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha +1} (\lambda _{2}^{2}-1) } d\lambda _{2} \end{aligned}$$
(34)

can be evaluated as

$$\begin{aligned} &\alpha = 2: \frac{1}{2} (\lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}}), \\ &\alpha = 4: \frac{1}{2} (\lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}}) + \frac{1}{4} (\lambda _{2}^{4} + \frac{1}{\lambda _{2}^{4}}), \\ &\alpha = 6: \frac{1}{2} (\lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}}) + \frac{1}{4} (\lambda _{2}^{4} + \frac{1}{\lambda _{2}^{4}}) + \frac{1}{6} (\lambda _{2}^{6} + \frac{1}{\lambda _{2}^{6}}), \\ &\alpha = 8: \frac{1}{2} (\lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}}) + \frac{1}{4} (\lambda _{2}^{4} + \frac{1}{\lambda _{2}^{4}}) + \frac{1}{6} (\lambda _{2}^{6} + \frac{1}{\lambda _{2}^{6}}) + \frac{1}{8} (\lambda _{2}^{8} + \frac{1}{\lambda _{2}^{8}}), \end{aligned}$$
(35)

and so on. For \(\alpha \) which is an odd integer, i.e., \(\alpha =1,3,5\ldots \), the integral takes the form

$$\begin{aligned} &\alpha = 1: (\lambda _{2} + \frac{1}{\lambda _{2}}) + \ln{ \frac{\lambda _{2}}{(1+\lambda _{2})^{2}}}, \\ &\alpha = 3: (\lambda _{2} + \frac{1}{\lambda _{2}}) + \frac{1}{3} ( \lambda _{2}^{3} + \frac{1}{\lambda _{2}^{3}}) + \ln{ \frac{\lambda _{2}}{(1+\lambda _{2})^{2}}}, \\ &\alpha = 5: (\lambda _{2} + \frac{1}{\lambda _{2}}) + \frac{1}{3} ( \lambda _{2}^{3} + \frac{1}{\lambda _{2}^{3}}) + \frac{1}{5} ( \lambda _{2}^{5} + \frac{1}{\lambda _{2}^{5}}) + \ln{ \frac{\lambda _{2}}{(1+\lambda _{2})^{2}}}, \\ &\alpha = 7: (\lambda _{2} + \frac{1}{\lambda _{2}}) + \frac{1}{3} ( \lambda _{2}^{3} + \frac{1}{\lambda _{2}^{3}}) + \frac{1}{5} ( \lambda _{2}^{5} + \frac{1}{\lambda _{2}^{5}}) + \frac{1}{7} ( \lambda _{2}^{7} + \frac{1}{\lambda _{2}^{7}}) + \ln{ \frac{\lambda _{2}}{(1+\lambda _{2})^{2}}}, \end{aligned}$$
(36)

and so on.

For example, if \(\alpha =6\), the radial stress can be computed as

$$\begin{aligned} &\sigma _{rr} (R) = -\frac{\mu}{3} [ \frac{1}{2} \lambda _{2}^{2}(A) - \frac{1}{2}\lambda _{2}^{2}(R) + \frac{1}{4} \lambda _{2}^{4} (A) - \frac{1}{4}\lambda _{2}^{4} (R) + \frac{1}{6} \lambda _{2}^{6} (A) - \frac{1}{6} \lambda _{2}^{6} (R) + \\ &\frac{1}{2\lambda _{2}^{2} (A)} - \frac{1}{2\lambda _{2}^{2} (R)} + \frac{1}{4 \lambda _{2}^{4} (A)} - \frac{1}{4 \lambda _{2}^{4} (R)} + \frac{1}{6 \lambda _{2}^{6} (A)} - \frac{1}{6 \lambda _{2}^{6} (R)}]. \end{aligned}$$
(37)

Note that the radial stress is negative since the terms like \(\frac{1}{n\lambda _{2}^{n} (A)} - \frac{1}{n\lambda _{2}^{n} (R)}\) are small, and \((\lambda _{2}^{n}(A) - \lambda _{2}^{n}(R))/n\) are positive.

Significant simplifications are possible if \(\alpha =2\) and \(\alpha = 4\). This is true due to the fact that

$$\begin{aligned} \lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}} = 2 + \tau ^{2} R^{2}, \qquad (\lambda _{2}^{2} + \frac{1}{\lambda _{2}^{2}})^{2} = \lambda _{2}^{4} + \frac{1}{\lambda _{2}^{4}} + 2. \end{aligned}$$

For these cases, it can be shown that

$$\begin{aligned} &\alpha =2: \hspace{2pt} \sigma _{rr} = -\mu \int _{R}^{A} \tau ^{2} R^{2} \frac{dR}{R} = - \frac{\mu}{2} \tau ^{2} A^{2} (1 - (\frac{R}{A})^{2}), \\ &\alpha =4: \hspace{2pt} \sigma _{rr} = - \frac{\mu}{2} \int _{R}^{A} [\tau ^{4} R^{4} + 3 \tau ^{2} R^{2}] \frac{dR}{R} = \\ &- \frac{3\mu}{4} \tau ^{2} A^{2} (1 - (\frac{R}{A})^{2}) - \frac{\mu}{8} \tau ^{4} A^{4} (1 - (\frac{R}{A})^{4}). \end{aligned}$$
(38)

Note that the radial stress is negative.

After finding the radial stress, the fluid pressure can be found as

$$\begin{aligned} p = \sigma _{rr}^{\prime }- \sigma _{rr} = \sigma _{1}^{\prime }- \int _{R}^{A} \frac{\sigma _{rr}^{\prime }- \sigma _{\theta \theta}^{\prime}}{R} dR. \end{aligned}$$
(39)

Using (20) the axial stress can be expressed in terms of the principal stresses as follows

$$\begin{aligned} \sigma _{zz} = \sigma _{zz}^{\prime }- p = \frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- p = \frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- \sigma _{rr}^{ \prime }+ \sigma _{rr}. \end{aligned}$$

The term \(\frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- \sigma _{rr}^{ \prime}\) can be found by substituting the expressions for the principal stresses for the Ogden material (25). After a few simplifications one can again show that all the terms containing \((1+\lambda _{2}^{\alpha} + \lambda _{3}^{\alpha})\) disappear and we have

$$\begin{aligned} \frac{1}{1+\lambda _{2}^{2}} \sigma _{2}^{\prime }+ \frac{1}{1+\lambda _{3}^{2}} \sigma _{3}^{\prime }- \sigma _{rr}^{ \prime }= \frac{2 \mu}{\alpha} \frac{(1-\lambda _{2}^{-\alpha})(\lambda _{2}^{\alpha }- \lambda _{2}^{2})}{1+\lambda _{2}^{2}}. \end{aligned}$$
(40)

Therefore, the axial stress is given by

$$\begin{aligned} &\sigma _{zz} = \frac{2 \mu}{\alpha} \frac{(1-\lambda _{2}^{-\alpha})(\lambda _{2}^{\alpha }- \lambda _{2}^{2})}{1+\lambda _{2}^{2}} + \sigma _{rr} = \\ &\frac{2 \mu}{\alpha} \frac{(1-\lambda _{2}^{-\alpha})(\lambda _{2}^{\alpha }- \lambda _{2}^{2})}{1+\lambda _{2}^{2}} -\frac{2\mu}{\alpha} \int _{R}^{A} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} \frac{dR}{R}. \end{aligned}$$
(41)

Similarly, one can derive the hoop stress as

$$\begin{aligned} & \sigma _{\theta \theta} = \frac{2\mu}{\alpha} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} + \sigma _{rr} = \\ & \frac{2\mu}{\alpha} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} -\frac{2\mu}{\alpha} \int _{R}^{A} \frac{(1-\lambda _{2}^{\alpha}) (1-\lambda _{2}^{2+\alpha})}{\lambda _{2}^{\alpha }(\lambda _{2}^{2} + 1)} \frac{dR}{R}. \end{aligned}$$
(42)

After the radial stress has been found, evaluation of these stress components should not cause any problems.

It is important to note that the expressions for the total stresses are also valid for a totally incompressible and homogeneous cylinder with the strain energy function \(W_{0}\). This is true due to the fact that in all our derivations for the total stresses in the porous cylinder (with nearly incompressible skeleton) all the terms \((1+\lambda _{2}^{\alpha} + \lambda _{3}^{\alpha})\) present in the expressions for the principal stresses in the skeleton disappear. But these terms are the only ones that distinguish these stresses from the stresses in the material with the strain energy function \(W_{0}\).

Since the total stresses presented here for porous cylinder are the same as for homogeneous incompressible cylinder, the overall axial force \(N\) and the overall twisting moment \(M\) will also be the same. The expressions for the axial force and twisting moment were obtained by Horgan and Murphy [3] and will not be repeated here.

The shear stress can be found using (21) as

$$\begin{aligned} \sigma _{\theta z} = n m \sigma _{2}^{\prime }- nm \sigma _{3}^{ \prime }= n m (\sigma _{2}^{\prime }- \sigma _{3}^{\prime}) = \frac{1}{\sqrt{4 + \tau ^{2} R^{2} }} (\sigma _{2}^{\prime }- \sigma _{3}^{ \prime}). \end{aligned}$$

For the Ogden material from (25)

$$\begin{aligned} \sigma _{2}^{\prime }- \sigma _{3}^{\prime }= \frac{2\mu}{\alpha} ( \lambda _{2}^{\alpha }- \lambda _{3}^{\alpha}). \end{aligned}$$
(43)

Therefore,

$$\begin{aligned} \sigma _{\theta z} = \frac{2\mu}{\alpha} \frac{1}{\sqrt{4 + \tau ^{2} R^{2} }} (\lambda _{2}^{\alpha }- \lambda _{3}^{\alpha}) = \frac{2\mu}{\alpha} \frac{\tau R}{\lambda _{2}^{2} - \lambda _{3}^{2}} (\lambda _{2}^{ \alpha }- \lambda _{3}^{\alpha}), \end{aligned}$$
(44)

and no integration is needed to find the shear stress. Significant simplifications are possible for several values of \(\alpha \). For example, in case \(\alpha =2\)

$$\begin{aligned} \sigma _{\theta z} = \mu \tau R, \end{aligned}$$
(45)

and if \(\alpha =4\)

$$\begin{aligned} \sigma _{\theta z} = \frac{\mu}{2} \tau R (2 + \tau ^{2} R^{2}), \end{aligned}$$
(46)

due to the fact that

$$\begin{aligned} \lambda _{2}^{2} + \lambda _{3}^{2} = 2 + \tau ^{2} R^{2}. \end{aligned}$$

4 Discussion of the Stress State

Before presenting numerical results, it is useful to give the qualitative picture for the total stresses induced in the porous fluid-saturated cylinder subjected to a sudden twist or in a totally incompressible and homogeneous cylinder. We have shown that for these two cases the total stresses will be identical.

Consider a set of fibers shown in Fig. 1 as vertical in the initial configuration. For convenience, we number these fibers as \(0, 1, 2, \ldots \) starting from the fiber in the center. It is clear that the fiber 0 does not rotate or move during the twist. During the deformation, fiber 1 is wrapped around fiber 0 causing some normal stress at the surface of contact between these fibers. This contact stress is obviously compressive and coincides with the direction of the radial stress. Now the second fiber is wrapped around the first two fibers. This will increase the existing contact stress on the surface of contact between the 0-th and the first fibers, and create the new contact stress between the first and the second fibers.

Continuing this procedure, we will eventually obtain the final stress field as a superposition of all normal contact stresses at the fibers’ surfaces. This stress can be identified as the radial stress in the cylinder; obviously, the radial stress will be maximum at the center and zero on the external surface.

Recall now the equilibrium equation in the radial direction

$$\begin{aligned} \frac{d \sigma _{rr}}{dr} + \frac{1}{r} (\sigma _{rr} - \sigma _{ \theta \theta}) = 0. \end{aligned}$$

The central fiber is very thin and thus the radial stress can be assumed uniform inside this fiber, i.e., \(\frac{d \sigma _{rr}}{dr}=0\). Therefore, the hoop stress \(\sigma _{\theta \theta}\) must be equal to the radial stress in the center, and thus the hoop stress is negative at \(R=0\). Closer to the external surface \(R=A\), the radial stress becomes smaller but the gradient of the radial stress gets larger. Since the radial stress is compressive (negative) and decreasing in magnitude towards the external surface, the gradient of the radial stress must be a positive quantity. From the same equilibrium equation, given that \(\frac{d \sigma _{rr}}{dr}>0\) and large but \(\sigma _{rr}<0\) and small, it follows that the hoop stress \(\sigma _{\theta \theta}\) at the external surface must be a positive quantity, and thus, it is tensile.

Having determined the signs for the radial and hoop stresses, we move on to the axial stress determination \(\sigma _{zz}\). It is the most difficult part of the stress state. Since in our picture the external fibers are wrapped around the internal ones, we can expect that these fibers will experience tensile stress along their respective axes, and this tensile stress will be the most significant for the external fibers, and the least significant for the fibers closer to the center. But we also note that the direction of the fibers’ axes after the twist is not exactly coincident with the \(z\)-axis and therefore, the tensile stress in these fibers will not be exactly equal to the axial stress \(\sigma _{zz}\).

On the other hand, when the external fibers are wrapped around the internal ones, some Poisson’s ratio effect is expected to arise in the internal fibers since the internal fibers will tend to elongate in the direction of the \(z\)-axis when they are acted upon the compressive contact stresses equal to \(\sigma _{rr}\). Since the fibers are actually constrained in the direction of the \(z\)-axis, the negative component of the stress \(\sigma _{zz}\) will be induced, especially closer to the center. Of course, when the Poisson’s coefficient is small, this negative component of the axial stress is also small, but for incompressible body the Poisson’s ratio is the largest.

The final axial stress can be viewed as a superposition of the positive and negative components described above. But we expect that at the center the axial stress is more likely to be compressive, and closer to the external surface the axial stress is probably tensile. But this is not always true, and for example, for \(\alpha =2\), the axial stress remains compressive and never becomes tensile at the external surface (it is equal to zero on the external surface (see Fig. 4)).

Fig. 4
figure 4

Normalized stresses \(\sigma _{RR}\), \(\sigma _{ZZ}\), \(\sigma _{\theta \theta}\), \(\sigma _{\theta Z}\) and fluid pressure \(p\) at the center \(R=0\) (largest circles), at the external surface \(R=A\) (smallest circles) and in the middle of the radius \(R=A/2\) (circles of middle size) for \(\tau A = 0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image

Let us evaluate the normal stress along the axes of the fibers that were vertical in the initial configuration. Denote this stress as \(\sigma _{f}\). It was already noted that the angle \(\beta _{f}\) that the fiber makes with the \(\theta \)-direction after the deformation can be evaluated from

$$\begin{aligned} \tan{\beta _{f}} = \frac{1}{\tau r}, \end{aligned}$$
(47)

where \(r\) is the coordinate of the fiber in the radial direction. Using now usual transformation rules for the stresses when changing coordinate systems, we can obtain the desired fiber stress as

$$\begin{aligned} \sigma _{f} = \cos ^{2} \beta _{f} \sigma _{\theta \theta} + sin^{2} \beta _{f} \sigma _{zz} + 2\cos \beta _{f} \sin \beta _{f} \sigma _{ \theta z}. \end{aligned}$$
(48)

For example, for new-Hookean material, with \(\alpha =2\), the stress components are given by

$$\begin{aligned} \sigma _{\theta \theta} = \frac{1}{2} \mu \tau ^{2} (3 r^{2} - A^{2}), \quad \sigma _{zz} = \frac{1}{2} \mu \tau ^{2} (r^{2} - A^{2}), \quad \sigma _{\theta z} = \mu \tau r. \end{aligned}$$
(49)

Substituting (49) into (48) and using the fact that

$$\begin{aligned} \cos ^{2} \beta _{f} = \frac{\tau ^{2} r^{2}}{1+\tau ^{2} r^{2}}, \quad \sin ^{2} \beta _{f} = \frac{1}{1+\tau ^{2} r^{2}}, \end{aligned}$$
(50)

we can obtain, after some simplifications, that the fiber stress is

$$\begin{aligned} \sigma _{f} = \frac{1}{2} \mu \tau ^{2} (3 r^{2} - A^{2}) + \mu \frac{\tau ^{2} r^{2}}{1+\tau ^{2} r^{2}} = \sigma _{\theta \theta} + \mu \frac{\tau ^{2} r^{2}}{1+\tau ^{2} r^{2}}. \end{aligned}$$
(51)

Thus, the fiber stress is found to be even larger than the hoop stress \(\sigma _{\theta \theta}\), and therefore, it is strongly tensile for the external fibers, as expected, but remains compressive for the fibers in the center.

5 Numerical Results

Figure 4 shows the total stresses \(\sigma _{RR}\), \(\sigma _{\theta \theta}\), \(\sigma _{ZZ}\), \(\sigma _{\theta Z}\) and fluid pressure \(p\) in the poro-hyperelastic cylinder evaluated at three points along the radius of the cylinder: \(R=0\) (shown with the largest circles), \(R=A/2\), and \(R=A\) (the smallest circles). The twist is prescribed by \(\tau A=0.6\). The stresses and the fluid pressure are normalized with respect to the shear modulus \(\mu \). All quantities are shown for the values of the material parameter \(\alpha \) equal to 2, 4, 6 and 8 (the value of \(\alpha \) is increased from left to right in each group). For plotting this graph, the radial stress must be found first using an expression similar to (37), given for \(\alpha =6\). Then the fluid pressure is found from (39). The axial and hoop stresses are obtained from (41) and (42), respectively. The shear stress is determined from (44). The expression for the principal stretch \(\lambda _{2}\) in terms of \(R\), given by (4), is used in evaluation of all stress components.

Plotting the stress distributions in this simplified form is possible due to the fact that all the stresses and the fluid pressure are monotonous functions of \(R\), i.e., the maximum or minimum occur either at the external surface of the cylinder \(R=A\), or at the center \(R=0\). For example, the maximum value for the shear stress \(\sigma _{\theta Z}\) is found at external surface, \(R=A\), and the minimum of the shear stress (zero) is at the center.

Note that all the stresses and the fluid pressure grow in magnitude with the increase in the material’s parameter \(\alpha \). Also note that among all normal stresses the magnitude of the hoop stress \(\sigma _{\theta \theta}\) is actually the largest; the hoop stress at the external surface is always large and tensile.

The axial stress \(\sigma _{ZZ}\) is always compressive at the center but becomes actually tensile on the external surface for \(\alpha =4,6,8\). For large values of \(\alpha \) this tensile stress at the surface will be larger in absolute value than the compressive stress at the center. This eventually leads to the negative Poynting’s effect discovered for the materials with large \(\alpha \) by Horgan and Murphy [3].

Figure 5 shows how the value of the total normal stress changes as a function of the angle \(\beta \) that this stress makes with the hoop direction (or \(\theta \) direction) in the \(\theta z\)-plane on the surface of the cylinder, \(R=A\). Thus, the horizontal axis of this plot, where \(\beta =0\), corresponds to the hoop stress, \(\sigma _{\theta \theta}\), and the vertical axis, where \(\beta =\pi /2\), corresponds to the axial stress, \(\sigma _{zz}\). As before, \(\tau A=0.6\) and parameter \(\alpha \) equal to 2, 4, 6 and 8. The normal stress in a given direction is evaluated using the usual transformation rules between the stresses, i.e.,

$$\begin{aligned} \sigma (\beta ) = \cos ^{2} \beta \sigma _{\theta \theta} + sin^{2} \beta \sigma _{zz} + 2\cos \beta \sin \beta \sigma _{\theta z}. \end{aligned}$$
(52)

As before, the stresses shown on the graph are normalized with respect to the shear modulus \(\mu \). The pale circles mark the specific values of the normal stress equal to -0.5, 0, 0.5, 1 and so on.

Fig. 5
figure 5

Normalized normal stresses on the \(\theta z\)-plane versus the angle between the \(\theta \) (hoop) direction and direction of the stress evaluated at the surface of the cylinder \(R=A\) for \(\tau A=0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image

Dotted lines show the principal directions and it is apparent that the principal directions are the same for all values of \(\alpha \). The larger principal stress is always tensile and grows rapidly with the parameter \(\alpha \). The smaller principal stress is always compressive and of much smaller magnitude, between -0.5 and 0.

Figure 6 shows detailed distribution of the fluid pressure \(p\) along the radius of the cylinder \(0\le R/A \le 1\) for the amount of twist \(\tau A=0.6\). The fluid pressure is found from (39). The maximum, minimum values of this distribution are also shown in Fig. 4. It is seen that the fluid pressure is a monotonous function reaching its positive maximum at the center of the cylinder. At the external surface the fluid pressure has a negative sign.

Fig. 6
figure 6

Normalized fluid pressure \(p\) along the radius of the cylinder for \(\tau A=0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image

Figures 7, 8 and 9 show distributions of the effective radial, hoop and axial stresses, respectively, along the radius of the cylinder for the twist \(\tau A=0.6\). The effective stresses can be found by adding the fluid pressure to the total stresses, which have been already found. Recall that the effective stresses are supported by the skeleton of the poroelastic body. The effective stress are all equal to zero at the center of the cylinder since the compressive stress at the center is supported by the fluid. The effective radial stress is always compressive along the radius, the effective hoop stress is always tensile, and the axial stress is mostly compressive but may change the sign for large \(\alpha \). Note that the magnitude of the effective axial stress gets smaller compared to the effective radial or hoop stresses as the parameter \(\alpha \) increases.

Fig. 7
figure 7

Effective radial stress \(\sigma _{rr}^{\prime}\) along the radius of the cylinder for \(\tau A=0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image
Fig. 8
figure 8

Effective hoop stress \(\sigma _{\theta \theta}^{\prime}\) along the radius of the cylinder for \(\tau A=0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image
Fig. 9
figure 9

Effective axial stress \(\sigma _{zz}^{\prime}\) along the radius of the cylinder for \(\tau A=0.6\). Parameter \(\alpha =2,4,6,8\)

Full size image

6 Conclusions

In this paper we have derived analytical expressions for the stresses and the fluid pressure arising in the porous fluid-saturated cylinder subjected to a sudden twist of large magnitude. We have shown that for large twists, not only the usual shear stress emerges in the cylinder, but the normal stresses and fluid pressure as well. Since the behavior of the porous fluid-saturated body is usually time-dependent, we have concentrated only on the initial stress state in the cylinder, existing only for a short period of time after the twist was applied.

Material of the skeleton of this poroelastic cylinder is assumed hyperelastic of Ogden type and nearly incompressible. In addition to two usual material parameters, the shear modulus \(\mu \) and compressibility parameter \(D\), the Ogden material also has the third material parameter \(\alpha \). This material was chosen because the analytical expressions for the stresses due to a finite twist deformation were not available for arbitrary value of \(\alpha \).

In particular, we have obtained that, for example, when \(\alpha =6\), the total radial stress in the cylinder can be found as

$$\begin{aligned} &\sigma _{rr} (R) = -\frac{\mu}{3} [ \frac{1}{2} \lambda _{2}^{2}(A) - \frac{1}{2}\lambda _{2}^{2}(R) + \frac{1}{4} \lambda _{2}^{4} (A) - \frac{1}{4}\lambda _{2}^{4} (R) + \frac{1}{6} \lambda _{2}^{6} (A) - \frac{1}{6} \lambda _{2}^{6} (R) + \\ &\frac{1}{2\lambda _{2}^{2} (A)} - \frac{1}{2\lambda _{2}^{2} (R)} + \frac{1}{4 \lambda _{2}^{4} (A)} - \frac{1}{4 \lambda _{2}^{4} (R)} + \frac{1}{6 \lambda _{2}^{6} (A)} - \frac{1}{6 \lambda _{2}^{6} (R)} ]. \end{aligned}$$

Consequently, the fluid pressure for this material can be determined from

$$\begin{aligned} &p = \frac{\mu}{9} (2-\lambda _{2}^{6}(R)- \frac{1}{\lambda _{2}^{6}(R)}) + \\ &\frac{\mu}{3} [ \frac{1}{2} \lambda _{2}^{2}(A) - \frac{1}{2} \lambda _{2}^{2}(R) + \frac{1}{4} \lambda _{2}^{4} (A) - \frac{1}{4} \lambda _{2}^{4} (R) + \frac{1}{6} \lambda _{2}^{6} (A) - \frac{1}{6} \lambda _{2}^{6} (R) + \\ &\frac{1}{2\lambda _{2}^{2} (A)} - \frac{1}{2\lambda _{2}^{2} (R)} + \frac{1}{4 \lambda _{2}^{4} (A)} - \frac{1}{4 \lambda _{2}^{4} (R)} + \frac{1}{6 \lambda _{2}^{6} (A)} - \frac{1}{6 \lambda _{2}^{6} (R)} ]. \end{aligned}$$

Analytical expression for the shear stress for arbitrary value of \(\alpha \) was obtained as well,

$$\begin{aligned} \sigma _{\theta z} = \frac{2\mu}{\alpha} \frac{\tau R}{\lambda _{2}^{2} - \lambda _{3}^{2}} (\lambda _{2}^{ \alpha }- \lambda _{3}^{\alpha}). \end{aligned}$$

We have given a qualitative picture for the total stresses induced in the twisted cylinder. By following the deformation of some imaginary fibers that were vertical in the initial configuration, we have explained why the total radial stress in the twisted cylinder is compressive, the hoop stress on the external surface is tensile and the axial stress in the center is likely to be compressive. Moreover, we have derived the expression for the normal stress along the axes of the fibers after the deformation. In particular, for \(\alpha =2\), we have shown that this fiber stress is larger than the hoop stress by some positive quantity.

We have also investigated the effective stresses, arising in the skeleton of the poroelastic body, and established that all of them are equal to zero at the center. The effective radial stress is always compressive along the radius of the cylinder, and the effective hoop stress is always tensile; they increase in magnitude as the parameter \(\alpha \) increases.

It appears that even if the skeleton of the fluid-saturated cylinder is assumed to be totally incompressible, to find the effective stresses and the fluid pressure in this cylinder, one must still use the strain energy function for a nearly incompressible material (corresponding to that incompressible material). It is only when one is interested solely in the total stresses, then it suffices to use the strain energy function of a totally incompressible material \(W_{0}\). In the latter case, when using \(W_{0}\), separation of the total stress field into the effective stress and the scalar field \(p\) has no clear physical interpretation.