Homogenization of the Nernst-Planck-Poisson System by Two-Scale Convergence

Abstract

This work focuses on performing the homogenization of the Nernst-Planck-Poisson system, in order to obtain an efficient modelling of the ionic transfer and electrocapillary effects at the macroscopic scale for saturated porous media. The homogenization is performed with the powerful two-scale convergence method, which enables to obtain both the homogenized model and the associated convergence result.

1 Introduction

Ionic transfers in saturated porous media and the associated electrocapillary adsorption effect (electric double layer phenomenon) are generally modelled by the partial differential evolution system of Nernst-Planck-Poisson with Cauchy and boundary conditions. Using a decomposition of the concentrations of ionic species, keeping the concentration of the anions c− and of the cations c+ separate with a Boltzmann distribution, we classically obtain the Nernst-Planck-Poisson-Boltzmann system of equations [10–13, 28, 29]. The two equations of ionic transfer (for the cations and for the anions) are coupled with the Poisson-Boltzmann equation describing the electrical potential, the latter being generally decomposed into the bulk potential and the electrical double layer potential. This model is often used in civil-engineering to study the migration of chlorides in mortars or in concrete structures [1, 2, 10–13], responsible of severe damages due to corrosion, or to study the coupled electro-chemo-mechanical phenomena in expansive clays [28, 29]. Numerical analysis and convergent discretizations for the nonstationary Nernst-Planck-Poisson system are detailed in [32, 33]. Let us cite also the recent work [34], that discusses a related topic using two-scale convergence in order to investigate the influence of different boundary conditions and variables choices of scalings in ε. Various classes of up-scaled model equations are obtained.

The main goal of this work is to deduce, from the micro-local Nernst-Planck-Poisson equations, an efficient modelling of ionic transfers and electrocapillary effects at the macroscopic scale in saturated porous media.

The homogenization is performed with the powerful two-scale convergence method, presented in Sect. 3. One of the interests of this method is to obtain both the search homogenized model and the convergence result, without assuming a priori the form of the asymptotic expansion of the unknowns, as classically with periodic homogenization technique [5, 7, 35]. Moreover, with this approach, it is not necessary to decompose the electrical potential into the bulk potential and the electrical double layer potential as in the Nernst-Planck-Poisson-Boltzmann equations [10–13, 28, 29]. Furthermore, the present approach may be generalized to a multi-species formalism, without considering only monovalent cations and anions.¹

With the formalism proposed here, the electric potential due to the migration of ionic species, and the electrical double layer potential are contained in the total potential $\varPsi_{\varepsilon}^{*}$ (Sect. 2). Once the homogenization performed and the efficient macroscopic model obtained by two-scale convergence method, with the associated convergence result (Sect. 3.2), it is proved that the steady states have the form of the classical Poisson-Boltzmann expression of the ionic concentrations (Sect. 4).

The originality of the present work lies on the consideration of electrocapillary adsorption effect: important phenomena occur on the boundaries of the pores and introduce into the model problem strongly nonlinear terms defined on a periodic surface and leading to memory effects, described by a macroscopic Grahame’s law.

2 The Ionic Drift-Diffusion Problem

2.1 The General Framework

Let Ω be a bounded connected open set of R ^d with a Lipschitz boundary ∂Ω, with d=2 or d=3 for the classical applications concerned in this paper. We introduce the classical functional spaces V=H ¹(Ω) and H=L ²(Ω) which are Hilbert spaces with the usual scalar products, the embedding of V in H being dense and compact. Classically, we identify the pivot space H with its topologic dual, such as V′, the dual of V, can be identified with an over-espace of H. Finally, we note 〈. ,.〉 the duality bracket between V and V′. For a couple of regular functions, this duality bracket coincides with the usual scalar product of L ²(Ω).

For parabolic time depending problems, it is also classical to introduce the space (cf. [25], Chap. 3, [26])

$$\biggl\{ v\in L^{2} \bigl( [ 0,T ] ;H^{1} ( \varOmega) \bigr) ,\ \frac{\partial v}{\partial t}\in L^{2} \bigl( [ 0,T ] ;L^{2} ( \varOmega) \bigr) \biggr\} $$

which is a Hilbert space for its natural topology that can be identified with H ¹(Q), with Q=]0,T[×Ω. Moreover, the injection of H ¹(Q) in L ²([0,T];H) (identified with L ²(Q)) is compact ([26], p. 57), and the injection of H ¹(Q) in C ⁰([0,T];H) is continuous provided an appropriate choice of a representative element.

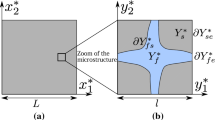
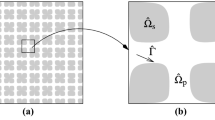
Using the classical notations of [3, 4, 23, 24] for periodic homogenization problems, we denote by Y the unit reference cube [0,1]^d, Y _s an open set of Y representing the solid phase, and $Y_{f}=Y\smallsetminus\overline{Y_{s}}$ its complementary (assumed to be connected) representing the fluid phase. The Lipschitzian boundary Γ=Γ ^sf∪Γ ^ss is composed of the internal boundary Γ ^sf between the fluid and the solid phases and of the boundary Γ ^ss between the solid parts of two adjacent unit cubes constituting the microstructure of the material (Figs. 1 and 2). Equivalently, we denote by Γ ^ff the boundary between the fluid phases of two adjacent unit cubes. Finally, in the sequel, we will still denote by Y, Y _s ,Y _f and Γ ^sf the extensions of Y, Y _s , Y _f and Γ ^sf to R ^d by Y-periodicity.

Fig. 1

Modelling of the material microstructure with a periodic elementary cell. (a) Porous media at the macroscopic scale. (b) Elementary reference cell

Fig. 2

Periodic microstructure constructed from the elementary reference cell considered

Introducing now a sequence ε of positive reals converging to 0, we define the whole fluid phase where the fluid can circulate

$$ \varOmega_{\varepsilon}^f= \biggl\{ x\in \varOmega,\ \frac {x}{\varepsilon}\in Y_{f} \biggr\} $$

(1)

and its complementary representing the whole solid phase

$$ \varOmega_{\varepsilon}^s= \biggl\{ x\in \varOmega,\ \frac {x}{\varepsilon}\in Y_{s} \biggr\} $$

(2)

of the microstructure of the material (Fig. 2). We denote by $\varGamma_{\varepsilon}^{sf}$ the inner boundary of Ω between the fluid and the solid phases, periodic surface of dimension (d−1) such as:

$$ \varGamma_{\varepsilon}^{sf}= \biggl\{ x\in \varOmega,\ \frac {x}{\varepsilon}\in\varGamma^{sf} \biggr\} . $$

(3)

The connected porosity is denoted by $\varPhi=\frac{\mathcal {L}^{d}-\mathrm{measure} ( Y_{f} ) }{\mathcal{L}^{d}-\mathrm{measure} ( Y ) }$.

Classically, in the sequel we will denote $Q_{\varepsilon}^{f}= \mathopen{]}0,T\mathclose{[} \times\varOmega_{\varepsilon}^{f}$ and $V_{\varepsilon}=H^{1} ( \varOmega^{f}_{\varepsilon} )$, $H^{1} ( Q^{f}_{\varepsilon } )$, $L^{\infty} ( Q^{f}_{\varepsilon} )$, etc., the expressions of the functional spaces which now depend on ε.

2.2 Coupled Transport Equations in Saturated Porous Media

We consider a heterogeneous saturated porous medium, whose microstructure contains two phases: a solid phase $\varOmega_{\varepsilon}^{s}$ (of cement paste for example and eventually aggregates in case of mortars or concrete), and a liquid phase $\varOmega_{\varepsilon}^{f}$ (see Fig. 2). The boundary between the solid and the liquid phases is denoted $\varGamma_{\varepsilon}^{sf}$.

In what follows, ∇, div or ∇. and Δ will denote respectively the gradient, divergence and Laplacian operator in the sense of distributions on R ^d.

The diffusion in the fluid phase is described by Nernst-Planck equation² coupled with the Poisson equation characterizing the electrical field accelerating or slowing down the ionic transfer. Nernst-Planck equation is generally written for an isotropic diffusivity assumed in the fluid phase [6, 9, 10, 27, 29, 30]

$$ \frac{\partial c_{\pm,\varepsilon}}{\partial t} - \mathrm{div} \biggl( D_\pm\nabla c_{\pm,\varepsilon} + D_\pm\frac {F}{R\varTheta} z_\pm c_{\pm,\varepsilon} \nabla\varPsi^*_\varepsilon\biggr) =0 \quad \mbox{in} \ \varOmega_\varepsilon^f , \ t>0 , $$

(4)

where c _±,ε denotes the concentration of the cations (respectively anions) of valence z _±, D _± their molecular diffusion coefficient in the liquid phase,³ $E^{*}_{\varepsilon}= - \nabla\varPsi^{*}_{\varepsilon}$ the total electrical field in the solution. Note that the electrical potential $\varPsi^{*}_{\varepsilon}$ results both from the evolution of the repartition of concentrations of electrical species (cations and anions), and of the effect of the double electrical layer. When an external electrical potential is applied, it may be also included in the total potential $\varPsi^{*}_{\varepsilon}$. Finally, F and R denote respectively, the Faraday and the ideal gas constant, and Θ the temperature of the fluid.

Let us denote ε _f (resp. ε _s ) the dielectric constant of the fluid phase $\varOmega _{\varepsilon}^{f}$ (resp. of the solid phase $\varOmega _{\varepsilon}^{s}$). In a general way, ε _f et ε _s may depend on x for very heterogeneous media, with ε _f >0,ε _s ≥0.

The Poisson equation characterizing the potential Ψ ^∗ in the fluid phase and in the solid phase (that can be conductive also) is stated as

$$ \mathrm{div}\bigl(\varepsilon_f \nabla\varPsi ^*_\varepsilon \bigr) = - {\rho^*} \quad\mbox{in}\ \varOmega_\varepsilon^f , $$

(5)

where ρ ^∗=F(z ₊ c _+,ε −z ₋ c _−,ε ) denotes the total electrical charge density in the fluid phase. In the solid phase, the Poisson equation reduces to

$$ \mathrm{div}\bigl(\varepsilon_s \nabla\varPsi ^*_\varepsilon \bigr) = 0 \quad\mbox{in} \ \varOmega_\varepsilon^s , $$

(6)

as the concentrations of ionic species are only defined in the fluid phase $\varOmega_{\varepsilon}^{f}$. The existence of the electric potential $\varPsi^{*}_{\varepsilon}$ and (5)–(6) result from Maxwell’s equations.

Introducing the function

$$ \kappa=\varepsilon_{f}\chi_{Y_{f}}+ \varepsilon_{s}\chi_{Ys} , $$

(7)

representing the dielectric values on the whole domain Ω through the characteristic phase functions $\chi_{Y_{f}}$ and $\chi_{Y_{s}}$, (5) and (6) can be written in the global formulation in the sense of distributions as

$$ \mathrm{div}\biggl(\kappa\biggl(\frac {x}{\varepsilon }\biggr) \nabla \varPsi^*_\varepsilon\biggr) = - F (z_+ c_{+,\varepsilon} - z_- c_{-,\varepsilon}) \chi_{\varOmega_\varepsilon^{f}} + g(\varepsilon,t,x) \delta_{(\varGamma_\varepsilon^{sf})} \quad\mbox{in}\ \varOmega,\ t>0 , $$

(8)

where the last term denotes a measure, with support on $\varGamma _{\varepsilon}^{sf}$, governing the jump of the electrical flux through the interface $\varGamma_{\varepsilon}^{sf}$. Here is the key of understanding and modelling the electrocapillary phenomena on the boundary of the pores. This term will be explained later by the assertions (11), (12) and the Grahame relation.

To complete (4)–(8), let us write the associated boundary conditions. First, we assume that we have homogeneous Neumann boundary conditions associated with the Nernst-Planck equation

$$ D_\pm\biggl( \nabla c_{\pm,\varepsilon} + \frac{F}{R\varTheta} z_\pm c_{\pm,\varepsilon} \nabla\varPsi ^*_\varepsilon \biggr).n =0 \quad\mbox{on} \ \varGamma_\varepsilon^{sf}\cup \varGamma_\varepsilon^{f\mathrm{ext}} , $$

(9)

where $\varGamma_{\varepsilon}^{f\mathrm{ext}}=\partial\varOmega\cap \varOmega _{\varepsilon}^{f}$ denotes the external fluid boundary to $\varOmega _{\varepsilon}^{f}$ and n denotes the external unit normal to $\varOmega _{\varepsilon}^{f}$. Moreover, as the system is assumed to be insulated with respect to the exterior, we have

$$ \frac{ \partial\varPsi^*_\varepsilon }{\partial n} = 0 \quad\mbox{on} \ \varGamma_\varepsilon^{f\mathrm{ext}} \cup\varGamma_\varepsilon^{s\mathrm{ext}} , $$

(10)

where $\varGamma_{\varepsilon}^{s\mathrm{ext}}=\partial\varOmega\cap \varOmega _{\varepsilon}^{s}$ denotes the external solid boundary to $\varOmega _{\varepsilon}^{s}$.

Finally, the electrical double layer phenomenon at the interface $\varGamma_{\varepsilon}^{sf}$ will be modelled through the boundary condition involving the surface charge density σ. In the general case, accounting for the jump of the electrical flux through the interface⁴ $\varGamma_{\varepsilon}^{sf}$, noted $[ [ \kappa(\frac{x}{\varepsilon})\nabla\varPsi^{\ast }_{\varepsilon}( t,x ) ] ].n$, we have:

$$ \biggl[ \biggl[ \kappa\biggl(\frac{x}{\varepsilon }\biggr)\nabla \varPsi^{\ast }_\varepsilon( t,x ) \biggr] \biggr] .n=\varepsilon \sigma\bigl( \varPsi^{\ast}_\varepsilon(t,x) \bigr) ,\quad x\in \varGamma_{\varepsilon}^{sf} . $$

(11)

A bijective relation between the surface charge density σ and the potential $\varPsi^{\ast}_{\varepsilon}$ may be given by the Grahame relation coming from the Gouy-Chapman theory (cf. [17, 21] and [22], p. 474). The electrocapillary adsorption phenomenon at the substrate interface may be modelled for a very general class of material by the relation [4, 14–16, 20]

$$ \sigma\bigl(\varPsi^*_\varepsilon(t,x)\bigr) = -\lambda \biggl( \frac{x}{\varepsilon} \biggr) \tau\bigl( \varPsi^{\ast }_\varepsilon ( t,x ) \bigr) ,\quad x\in\varGamma_{\varepsilon}^{sf} , $$

(12)

where λ denotes the dielectric permittivity coefficient⁵ at the interface Γ ^sf, possibly heterogeneous, extended by Y-periodicity, verifying λ∈L ^∞(Γ ^sf), λ≥λ ₀>0. The function τ must be a monotonic continuously differentiable Lipschitz-function satisfying the properties:

$$\tau( 0 ) =0,\qquad \tau^{\prime} ( r ) \geq\alpha,\quad \alpha >0 ,\ r\in \mathbb{R}. $$

Obviously, it may depend on several physical parameters (pH, temperature, water content, etc.). As an example, in [22], p. 474, the practically useful restriction of the function is considered:

$$r \mapsto\tau( r ) =K_{1}\sinh K_{2\ }r , \quad K_{1}>0,\ K_{2}>0 ,\ r\in\mathbb{R}. $$

Remark 1

The scaling at the right hand side of (11) enables the double layer effects to be involved at the main order of the homogenized model of ionic transfer that will be obtained in Theorem 1. It may be justified physically considering orders of magnitude of the electrical double layers and surface charge density that may be encountered experimentally in some configurations.

2.3 Associated Weak Formulation

The equivalent weak formulation associated to (4)–(11) takes the variational form:

Find (c _±,ε )=(c _+,ε ,c _−,ε ) in $L^{\infty} ( [ 0,T ] ;H^{1} ( \varOmega_{\varepsilon}^{f} ) )^{2}\cap H^{1} ( Q_{\epsilon}^{f} )^{2}$ and $\varPsi_{\varepsilon}^{\ast} \in L^{\infty} ( [ 0,T ] ;\allowbreak H^{1} ( \varOmega) )$ verifying ∀t>0, $\forall v \in H^{1} ( \varOmega^{f}_{\varepsilon} )$ and ∀w∈H ¹(Ω):

(13)

(14)

(15)

The establishment of this weak formulation does not constitute any difficulty and is left to the reader. Let us just notice that the integral of the left-hand side of the Poisson equation is on the whole domain Ω whereas the right-hand side only involves the integral on the fluid domain $\varOmega_{\varepsilon}^{f}$.

The preliminary framework is stated by the following global well-posedness result:

Proposition 1

If the boundary of Ω is smooth enough,⁶ for all initial data $( c_{\pm,\varepsilon}^{0} ) = ( c_{+,\varepsilon}^{0},c_{-,\varepsilon}^{0} )$ in $L^{\infty} ( \varOmega^{f}_{\varepsilon} )^{2}\cap H^{1} ( \varOmega^{f}_{\varepsilon} )^{2}$, such as $( c_{\pm,\varepsilon}^{0} ) \geq0$, problem (13)–(15) admits a unique solution $(c_{\pm,\varepsilon}, \varPsi_{\varepsilon}^{\ast})$ with (c _±,ε )=(c _+,ε ,c _−,ε ) in $L^{\infty} ( [ 0,T ] ;H^{1} ( \varOmega^{f}_{\varepsilon} ) )^{2}\cap$ $H^{1} ( Q_{\epsilon}^{f} )^{2}$ and $\varPsi_{\varepsilon}^{\ast} \in C^{0} ( [ 0,T ] ;H^{1} ( \varOmega) )$. The potential $\varPsi_{\varepsilon}^{\ast}$ is continuous in time since the left-hand side of the Poisson equation is continuous in time $( c_{\pm,\varepsilon} \in\mathcal{C}^{0} ( [ 0,T ] ; \varOmega^{f}_{\varepsilon} ) )$.

Proof

The proof of this proposition is rather technical and does not constitute the main point of this article. It can be obtained from the Schauder-Tikhonov fixed-point method [8, 18–20]. In order to use a fixed point method, we introduce

$$W_\varepsilon(0,T) = \biggl\{ v\in L^{2} \bigl( [ 0,T ] ; V_\varepsilon\bigr) ,\ \frac{\partial v}{\partial t}\in L^{2} \bigl( [ 0,T ] ; V_\varepsilon' \bigr) \biggr\}, $$

a separable Hilbert space under its natural topology.

For f=(f ₋,f ₊)∈W _ε (0,T)², we consider $\varPsi ^{*}_{\varepsilon}(f)$ the unique solution of the nonlinear generalized Poisson equation (14) where the right-hand side is written:

$$F\int_{\varOmega_{\varepsilon}^f} ( z_{+}\ f_+ -z_{-}\ f_- ) w\,dx. $$

Then, we consider the parabolic equations with a drift term in the form, as preparatory,

$$D_{\pm} \frac{F}{R\varTheta}\int_{\varOmega^f_{\varepsilon}} z_{\pm} \min\bigl( (\ c_{\pm,\varepsilon})^+,M \bigr) \nabla \varPsi_{\varepsilon}^{\ast}(f).\nabla v\,dx , $$

with r ⁺=max(r,0), and where M>0 is a “large” parameter which will be specified later. The application

$$(f_-,f_+) \in W_\varepsilon(0,T)^2 \mapsto( c_{+,\varepsilon}, c_{-,\varepsilon} ) \in W_\varepsilon(0,T)^2 $$

admits a fixed point (a convex closed bounded nonempty set $\mathcal {K}$ is stable and the application is weakly-weakly sequentially continuous from $\mathcal{K}$ to $\mathcal{K}$). Independently of M, the boundedness of the obviously positive concentrations can be proved with Moser’s iteration technique ([20], pp. 21–24), such that

$$\min\bigl( (c_{\pm,\varepsilon})^+,M \bigr) = c_{\pm ,\varepsilon}\quad \hbox{for a suitable}\ M. $$

Under the assumptions on the initial data and the regularity of Ω, $\frac{ \partial c_{\pm,\varepsilon}}{\partial t}$ is proved to belong to $L^{2} ( [ 0,T ] ; L^{2}(\varOmega_{\varepsilon}^{f}) )$. Uniqueness and local stability are proved by using the Gronwall’s lemma and Young’s inequality. □

As a consequence of Proposition 1, the concentrations c _±,ε and the potential $\varPsi_{\varepsilon }^{\ast}$ satisfy the properties for all t>0

(16)

(17)

consequence of (13) with the test function $v=1_{\varOmega ^{f}_{\varepsilon}}$,

$$ F\int_{\varOmega^f_{\varepsilon}} \bigl( z_{+} c_{+,\varepsilon} ( t ) -z_{-} c_{-,\varepsilon } ( t ) \bigr) \,dx=\varepsilon \int _{\varGamma^{sf}_{\varepsilon}} \lambda\biggl( \frac {x}{\varepsilon} \biggr) \tau\bigl( \varPsi_{\varepsilon }^{\ast} \bigr) ( t ) \,ds_{\varepsilon} , $$

(18)

consequence of (14) with the test function w=1 _Ω . Therefore, the quantity

$$\varepsilon \int_{\varGamma^{sf}_{\varepsilon}} \sigma\bigl(\varPsi^*_\varepsilon(t,x)\bigr) \,ds_{\varepsilon}=-\varepsilon \int_{\varGamma^{sf}_{\varepsilon}} \lambda\biggl( \frac{x}{\varepsilon} \biggr) \tau\bigl( \varPsi_{\varepsilon }^{\ast} \bigr) ( t ) \,ds_{\varepsilon} $$

is constant with respect to time t and we have ∀t≥0:

$$ \varepsilon\int_{\varGamma^{sf}_{\varepsilon}} \sigma\bigl (\varPsi^*_\varepsilon(t,x) \bigr) \,ds_{\varepsilon}=-F z_{+}\int_{\varOmega^f _{\varepsilon}}c_{+,\varepsilon}^{0} ( x ) \,dx+F z_{-} \int_{\varOmega^f_{\varepsilon }}c_{-,\varepsilon}^{0} ( x ) \,dx. $$

(19)

3 Homogenization by Two-Scale Convergence of the Nernst-Planck-Poisson System

3.1 The Main Principle of the Method

The homogenization method by two-scale convergence that will be used in the sequel has been developed first by G. Nguetseng [31] and then by G. Allaire [3]. This new type of convergence enables to capture at the limit the oscillations of a function in resonance with another one of the type of $x\rightarrow\varphi( x,\frac{x}{\varepsilon} )$. This method has the advantage to avoid to postulate the form of an asymptotic expansion of the unknowns, and to obtain for non-linear problems in the same time both the limit homogenized model and the result of convergence. For more details on this homogenization method by two-scale convergence, refer to [3, 4, 15, 23, 24, 31].

3.2 The Homogenized Model of Ionic Drift-Diffusion

The homogenization by two-scale convergence of ionic drift-diffusion equations (4)–(12) or (13)–(15) leads to the results:

Theorem 1

The concentrations of anions and cations in the solution (c _±)=(c ₊,c ₋), and the electrical potential Ψ ^∗ are solution of the homogenized ionic diffusion problem in Q=]0,T[×Ω

(20)

(21)

where Φ denotes the porosity of the material. The symmetric positive definite tensor of homogenized diffusion ϒ is defined as follows

$$ \varUpsilon_{kl}=\int_{Y_{f}} ( \nabla_{y}\omega_{k}+e_{k} ) . ( \nabla_{y}\omega_{l}+e_{l} ) \,dy , $$

(22)

where (ω _k ) is the family of the solutions defined by the cell problem:

$$ E_{\mathrm{cell}}^{c_{\pm}} \begin{cases} ( \omega_{k} ) \in H_{\sharp}^{1} ( Y ) \\ -\operatorname{div}_{y} ( \nabla_{y}\omega_{k}+e_{k} ) =0\quad \text{\textit{in} }Y_{f}\\ ( \nabla_{y}\omega_{k}+e_{k} ) .n=0\quad\text{\textit{on} }\varGamma^{sf}. \end{cases} $$

(23)

In a similar way, the symmetric definite positive tensor Λ is defined as

$$ \varLambda_{kl}=\int_{Y} \kappa(y) ( \nabla_{y}\varsigma_{k}+e_{k} ) ( \nabla_{y}\varsigma_{l}+e_{l} ) \,dy , $$

(24)

where (ς _k ) is the family of the solutions defined by the cell problem:

$$ E_{\mathrm{cell}}^{\varPsi^{\ast}} \begin{cases} ( \varsigma_{k} ) \in H_{\sharp}^{1} ( Y ) \\ -\operatorname{div}_{y} ( \kappa( y ) ( \nabla_{y}\varsigma_{k}+e_{k} ) ) =0\quad\text{\textit{in} }Y . \end{cases} $$

(25)

The weak formulation of the homogenized equations of Theorem 1 may be written equivalently as follows:

Theorem 2

For an insulated system from outside, with positive Cauchy data in L ^∞(Ω)∩H ¹(Ω) and homogeneous Neumann conditions given on the parabolic boundary of Q, there exists a unique vectorial function

$$( c_{\pm} ) = ( c_{+},c_{-} ) \in L^{\infty } \bigl( [ 0,T ] ;H^{1} ( \varOmega) \bigr)^{2}\cap H^{1} ( Q )^{2} $$

representing the concentrations of anions and cations in the electrolyte, and a unique function

$$\varPsi^{\ast} \in C^{0} \bigl( [ 0,T ] ;H^{1} ( \varOmega) \bigr) \cap H^{1} ( Q ) $$

representing the electrical potential, such that for all t>0, for all test function v∈H ¹(Ω), w∈H ¹(Ω)

(26)

(27)

(28)

The following properties of physical equilibrium are satisfied for t>0:

(29)

(30)

As a consequence, the quantity

$$\varpi(t) =- \biggl( \int_{ \varGamma^{sf}} \lambda( y ) \,ds ( y ) \biggr) \int_{\varOmega} \tau\bigl( \varPsi^{\ast} \bigr) ( t,x ) \,dx , \quad t\in[0,T] $$

is constant with respect to time t and satisfies to the global electric equilibrium:

$$\varpi(t) =-F z_{+}\varPhi\int_{\varOmega}c_{+}^{0} ( x ) \,dx+F z_{-}\varPhi\int_{\varOmega }c_{-}^{0} ( x ) \,dx , \quad t\in[0,T]. $$

Proof

We give here the main steps of the proof of Theorems 1 and 2.

(i) Uniform estimates and two-scale convergence of c _±,ε

By standard methods, we have the estimates

$$\bigl\|\nabla\varPsi_{\varepsilon}^{\ast} ( t ) \bigr \|_{L^{2} ( \varOmega) ^{d}}\leq C \bigl( \bigl\|c_{+,\varepsilon } ( t ) \bigr \|_{_{L^{2} ( \varOmega _{\varepsilon}^{f} ) }}+\bigl\|c_{-,\varepsilon} ( t ) \bigr \|_{L^{2} ( \varOmega_{\varepsilon}^{f} ) } \bigr) , \quad t>0, $$

and by formal derivation of the Poisson equation (assumptions on the function τ are essential here):

$$\biggl\|\nabla\frac{\partial\varPsi_{\varepsilon}^{\ast} ( t ) }{\partial t}\biggr\|_{L^{2} ( \varOmega) ^{d}}\leq C \biggl( \biggl\|\frac{\partial c_{+,\varepsilon} ( t ) }{\partial t}\biggr\|_{_{L^{2} ( \varOmega_{\varepsilon}^{f} ) }}+\biggl\| \frac{\partial c_{-,\varepsilon} ( t ) }{\partial t}\biggr\| _{L^{2} ( \varOmega_{\varepsilon}^{f} ) } \biggr) , \quad t>0. $$

Therefore, we deduce the inequality, after integration by parts in the drift term:

By using the Gonwall’s and Young’s inequalities, we prove a priori estimates:

for a constant C independent of ε. □

According to the well-known extension result (see [14], p. 505; [15], Lemma 2.1, p. 617; [16], Lemma 2.1, p. 7) under the assumptions on connectedness and regularity properties of Y _f , let us introduce the extension operators $\mathcal{P}_{\varepsilon}$ in Q outside of $Q^{f}_{\varepsilon}$, equi-bounded of $H^{1} ( Q^{f}_{\varepsilon} )$ in H ¹(Q). We then extend the functions c _±,ε into $\widetilde {c_{\pm,\varepsilon}} =\mathcal{P}_{\varepsilon} ( c_{\pm ,\varepsilon } )$. Moreover, we quote that the function τ involved in the expression of the electrical double layer is a Lipschitz function, null for zero, which operates from H ¹(Ω) in itself. Therefore, we have also the new a priori estimates, for a new constant C independent of ε:

Now, let us write again for t>0 the system (13)–(14) with integrals in Q, for any test functions v taken in $\mathcal{D} ( \mathopen{]} 0,T \mathclose{[} ;V )$

(31)

(32)

From the sequence $\widetilde{ c_{\pm,\varepsilon}}$, we can extract a subsequence, still noted $\widetilde{ c_{\pm,\varepsilon}}$ that converges to an element c _±, weakly in H ¹(Q)², weakly-∗ in L ^∞(0,T;H ¹(Ω))², strongly in L ²(Q)² and C ⁰([0,T];L ²(Ω))², and $\mathcal{L}^{d+1}$-a.e. in Q using a result of compactness [26]. For t>0 fixed, the quantity $\widetilde { c_{\pm,\varepsilon}} ( t )$ has a sense and defines an element of H ¹(Ω) uniformly bounded with respect to t, because $\widetilde{ c_{\pm,\varepsilon}}$ is continuous from [0,T] to H ¹(Ω) endowed with the weak topology. Moreover, $\widetilde{ c_{\pm,\varepsilon}}$ two-scale converges (weakly) in Q to an element c _± and there exists an other element c _±,1(t,x,y) of $L^{2} ( Q;H_{\sharp}^{1} ( Y ) / R )$ such that $\nabla\widetilde{ c_{\pm,\varepsilon}}$ two-scale converges (weakly) to ∇ _x c _±(t,x)+∇ _y c _±,1(t,x,y).

(ii) Expression of Ψ ₁(t,x,y)

For t>0 fixed, the expression $\varPsi_{\varepsilon}^{\ast} ( t )$ has a sense and defines and element of H ¹(Ω), uniformly bounded with respect to t. Thus we can extract a subsequence $\varPsi_{\varepsilon_{ ( t ) }}^{\ast}$ a priori dependent of t, such that $\varPsi_{\varepsilon_{ ( t )}}^{\ast}$ converges to an element denoted Ψ ^∗(t), weakly in H ¹(Ω) and strongly in L ²(Ω), and therefore two-scale converges also. Moreover, there exists an element Ψ ₁(t,x,y) of $L^{2} ( \varOmega;H_{\sharp}^{1} ( Y ) / R )$ such that $\nabla\varPsi_{\varepsilon_{ ( t ) }}^{\ast}$ two-scale converges to ∇ _x Ψ ^∗(t)+∇ _y Ψ ₁(t,x,y). As τ is a Lipschitz function, $\tau( \varPsi_{\varepsilon _{ ( t )}}^{\ast} )$ converges to τ(Ψ ^∗(t)) weakly in H ¹(Ω) and strongly in L ²(Ω). Finally, $\lambda( \frac {x}{\varepsilon (t)}) \tau( \varPsi_{\varepsilon(t)}^{\ast} ) ( t )_{\mid\varGamma ^{sf}_{\varepsilon(t)}}$ two-scale converges to λ(y)τ(Ψ ^∗(t)), as defined by ([4], Theorem 2.1)

(33)

for any continuous function $(x,y) \mapsto\psi(x,y) \in\mathcal {C} ( \overline{\varOmega}; C_{\sharp}(y) )$.

The second part of the proof consists in introducing a test-function of the form $\psi( x ) +\varepsilon\psi_{1} ( x,\frac{x}{\varepsilon} )$ with $\psi \in\mathcal{D} ( \overline{\varOmega} )$ and $\psi_{1}\in \mathcal{D} [ \varOmega;C_{\sharp}^{\infty} ( Y ) ]$. Passing at the two-scale limit for ε tending to zero in (32), it stands:

As $\mathcal{D} ( \overline{\varOmega } )$ is dense in H ¹(Ω), using a general result for elliptic monotone partial differential equations in the Hilbert space H ¹(Ω)× $L^{2} ( \varOmega;H_{\sharp}^{1} ( Y ) / R )$, we can prove that the accumulation point (Ψ ^∗(t,.),Ψ ₁(t,. ,.)) obtained by this process is unique. As a consequence, we deduce a posteriori that it was not necessary to extract a subsequence dependent on t: all the sequence converges independently of t. Moreover, the weakly measurable function t→Ψ ^∗(t,.) is in fact measurable according to Pettis theorem as V is a separable space.

Using this previous results, we deduce that at the two-scale limit, the homogenized problem obtained from the Poisson equation reduces to:

(34)

(35)

From (34), we deduce classically that Ψ ₁ can be expressed, for all t>0, introducing functions ζ defined by (25) on the elementary cell $E_{\mathrm{cell}}^{\varPsi^{\ast}}$:

$$ \varPsi_{1} ( t,x,y ) = \sum _i \frac{\partial\varPsi^{\ast} ( t,x ) }{\partial x_{i}} \zeta _{i} ( y ). $$

(36)

Indeed, with this expression of ζ, it is easy to verify that:

(iii) Homogenized Poisson equation

Replacing expression (36) of Ψ ₁ in the homogenized Poisson equation (35), we have to compute the expression:

(37)

Using the definition (24)–(25) of the tensor Λ (Theorem 1), we deduce that we have for all t>0 in Ω

$$-\operatorname{div} \bigl[ \boldsymbol{\varLambda}\nabla\varPsi ^{\ast} ( t ) \bigr] + \biggl( \int_{ \varGamma^{sf}} \lambda( y ) \,ds ( y ) \biggr) \tau\bigl( \varPsi^{\ast} \bigr) ( t ) =F \varPhi\bigl( z_{+} c_{+} ( t ) -z_{-}c_{-} ( t ) \bigr) , $$

which constitutes the second homogenized equation of Theorem 1.

(iv) Homogenized Nernst-Planck equation

To finish, we have to compute the two-scale limit of the Nernst-Planck equation from the weak formulation (31). To do this, we first have to notice that $\chi_{\varOmega^{f}_{\varepsilon}}\nabla\varPsi_{\varepsilon }^{\ast} ( t )$ two-scale converges to $\chi_{Y_{f}} ( y ) [ \nabla_{x}\varPsi^{\ast} ( t,x ) +\nabla_{y}\varPsi_{1} ( t,x,y ) ]$, i.e., to

$$ \chi_{Y_{f}} ( y ) \biggl[ \nabla_{x} \varPsi^{\ast} ( t,x ) + \sum_i \frac{\partial\varPsi^{\ast} ( t,x ) }{\partial x_{i}} \nabla _{y}\zeta_{i} ( y ) \biggr]. $$

(38)

Replacing expression (36) of Ψ ₁ in (38), the calculations are equivalent to the developments of (37) by considering that $\kappa( \frac{x}{\varepsilon} ) =\chi_{Y_{f} } ( \frac{x}{\varepsilon} )$. This leads to introduce naturally the homogenized tensor ϒ defined by (22)–(23) in Theorem 1. The other calculations are similar than those to establish the homogenized equation (21) and are left to the reader.

(v) Uniqueness of the limit

In points (i) to (iv), we proved the existence of the two-scale limit leading to the homogenized equations (20)–(21) of Theorem 1. To establish the uniqueness, we must define a Lipschitz continuation (at the left and at the right) of the graph of the function τ outside of its domain of validity by two half-lines passing through the origin. We observe that the non-linear expression with respect to Ψ ^∗

$$\bigl( \varPsi^{\ast},w \bigr) \rightarrow\big\langle\mathcal {A}_{\tau } \bigl( \varPsi^{\ast} \bigr) ,w\big\rangle= \int_{\varOmega} \boldsymbol{\varLambda}\nabla\varPsi^{\ast}.\nabla w\,dx+ \int _{ \varGamma^{sf}} \lambda( y ) \,ds ( y ) \int_{\varOmega} \tau\bigl( \varPsi^{\ast} \bigr) w\, d\sigma $$

defined on H ¹(Ω)×H ¹(Ω), enables to define a strongly monotone operator $\mathcal{A}_{\tau}$ from H ¹(Ω) into its dual V′. Indeed, we have:

$$\exists\eta>0,\forall u,\forall v\in H^{1} ( \varOmega) , \quad\big \langle \mathcal{A}_{\tau} ( u ) -\mathcal{A}_{\tau} ( v ) ,v-u\big\rangle \geq \eta\|u-v\|_{H^{1} ( \varOmega ) }^{2}. $$

The other theoretical results, in particular the uniqueness of the solution of Theorem 2, derive from the application of monotone methods (see [26], Chap. 2) and from Gronwall lemma.

The uniqueness of the obtained accumulation point (c _±,Ψ ^∗) implies the convergence of the sequences $\widetilde{\ c_{\pm,\varepsilon}}$ and $\varPsi_{\varepsilon }^{\ast} ( t )$ without needing to extract subsequences.

Remark 2

It is important to notice that the source or well term (according to the sign of the potential) resulting from the homogenization of the electrical double layer term in the Nernst-Planck-Poisson system ((20) of Theorem 1) has an equivalent in the homogenization modelling of porous media in oil-engineering [4, 14–16]. When the coefficient λ is constant, the term $\int_{ \varGamma^{sf}} \lambda( y ) \,ds ( y )$ writes λ|Γ ^sf| where |Γ ^sf| denotes the area of Γ ^sf in dimension d=3, that traduces an effect of memory conservation of the micro-local geometry by the homogenization process.

4 Steady Solutions and Asymptotic Solutions

In this section, we establish the general expressions of the concentrations for a very long time (steady and asymptotic solutions of the homogenized Nernst-Planck-Poisson system). They are given in the following result:

Theorem 3

The steady solutions of the homogenized Nernst-Planck-Poisson system (26)–(27) can be written in the form

$$ C_{\pm}=\varkappa_{\pm}\exp\biggl( - \frac{F}{R\varTheta} z_{\pm} \varPsi^{\ast\ast } \biggr) ,\quad \varkappa_{\pm}>0 , $$

(39)

where (ϰ _±) are two strictly positive constants. The potential $\varPsi^{\ast\ast}=\varPsi_{\varkappa _{\pm}}^{\ast\ast}$ is the unique (steady) solution in L ^∞(Ω)∩H ¹(Ω) of the variational Liouville equation:

(40)

Moreover, in order that the functions C _± are asymptotic solutions as well, the principle of conservation of the concentrations must be preserved. Therefore, the constants ϰ _± must be solutions of the non-linear strongly coupled system:

$$ \varkappa_{\pm} \int_{\varOmega} \exp\biggl( - \frac{F}{R\varTheta} z_{\pm} \varPsi_{\varkappa_{\pm }}^{\ast\ast} ( x ) \biggr) \,dx=\int_{\varOmega}C_{\pm}^{0} ( x ) \,dx. $$

(41)

Proof

Let us search a vectorial function C=(C _±) in H ¹(Ω)²∩L ^∞(Ω)² such that for all v=(v _±) in H ¹(Ω)², and for Ψ ^∗∗ representing the potential in H ¹(Ω)∩L ^∞(Ω):

$$ \int_{\varOmega} \boldsymbol{\varUpsilon}\nabla C_{\pm}.\nabla v_{\pm}\,dx+\ \frac {F}{R\varTheta}\int _{\varOmega} z_{\pm} C_{\pm}\boldsymbol{ \varUpsilon}\nabla\varPsi^{\ast\ast }.\nabla v_{\pm}\,dx=0. $$

(42)

Setting $Z_{\pm}=\frac{F}{R\varTheta} z_{\pm}$, (42) may be written again:

$$ \int_{\varOmega} \bigl( \exp\bigl( -Z_{\pm} \varPsi^{\ast\ast} \bigr) \bigr) \boldsymbol{\varUpsilon}\nabla \bigl( C_{{\pm}}\exp\bigl( Z_{_{\pm}}\varPsi^{\ast\ast } \bigr) \bigr) .\nabla v_{\pm}\,dx=0. $$

(43)

Choosing a test-function $v_{_{\pm}}=C_{_{\pm}}\exp( Z_{_{\pm}}\varPsi^{\ast\ast} )$, that is possible in Banach algebra H ¹(Ω)∩L ^∞(Ω), it stands:

$$ \int_{\varOmega} \bigl( \exp\bigl( -Z_{\pm} \varPsi^{\ast\ast} \bigr) \bigr) \boldsymbol{\varUpsilon }\nabla\bigl( C_{{\pm}}\exp\bigl( Z_{{\pm}}\varPsi^{\ast\ast} \bigr) \bigr) .\nabla\bigl( C_{{\pm}}\exp\bigl( Z_{_{\pm} } \varPsi^{\ast\ast} \bigr) \bigr) \,dx=0. $$

(44)

As the matrix ϒ is definite positive, the admissible solutions are necessary of the Maxwellian form:

$$ C_{{\pm}}=\varkappa_{_{\pm}}\exp\biggl( - \frac{F}{R\varTheta} z_{{\pm}} \varPsi^{\ast\ast} \biggr) ,\quad \varkappa_{{\pm}}\geq0. $$

(45)

Finally, in order that the concentrations C _± are also asymptotic solutions, the conservation principle of the concentrations imposes that:

$$ \varkappa_{\pm} \int_{\varOmega} \exp \biggl( -\frac{F}{R\varTheta} z_{\pm} \varPsi_{\varkappa_{\pm }}^{\ast\ast} ( x ) \biggr) \,dx=\int_{\varOmega}C_{\pm}^{0} ( x ) \,dx. $$

(46)

Obviously, in the system (46) the constants ϰ _± depend on Cauchy data. Now, replacing expression (45) of the concentrations in the homogenized Poisson equation (21), the potential Ψ ^∗∗ is proved to be a solution of the Liouville equation (40). As the function

$$\varPsi\rightarrow-F\varPhi\biggl( \sum_{\pm}z_{\pm} \varkappa_{\pm} \exp\biggl( -\frac{F}{R\varTheta} z_{\pm} \varPsi^{\ast\ast } \biggr) \biggr) + \biggl( \int _{ \varGamma^{sf}} \lambda( y ) \,ds ( y ) \biggr) \tau\bigl( \varPsi^{\ast\ast} \bigr) $$

is strictly monotonic, using general results on non-linear strongly monotone elliptic partial differential equations [26], we can prove that (40) admits a unique solution in H ¹(Ω)∩L ^∞(Ω), which concludes the proof of Theorem 3. □

5 Conclusion

The homogenization of the Nernst-Planck-Poisson system by two-scale convergence has made it possible to obtain a consistent model describing the ionic transfers, coupled with the electrocapillary effects, at the macroscopic scale for saturated porous media. The electrocapillary effects are taken into account in the homogenized Poisson equation through a source or a well term (according to the sign of the potential). With the approach used, not only it is not necessary to assume a priori an asymptotic expansion of the unknowns of the problem (the concentrations and the potential), but also we obtain a convergence result associated with the homogenized model. Moreover, the present formalism avoids using the Poisson-Boltzmann formalism, which considers generally monovalent ions, and may be easily extended to a multi-species approach. The Poisson-Boltzmann distribution of concentrations is recovered as the general form of the asymptotic steady solutions of the homogenized Nernst-Planck-Poisson system.