Abstract
Asymptotic multiple scale homogenisation allows to determine the effective behaviour of a porous medium by starting from the pore-scale description, when there is a large separation between the pore-scale and the macroscopic scale. When the scale ratio is “small but not too small”, the standard approach based on first-order homogenisation may break down since additional terms need to be taken into account in order to obtain an accurate picture of the overall response of the medium. The effect of low scale separation can be obtained by exploiting higher-order equations in the asymptotic homogenisation procedure. The aim of the present study is to investigate higher-order terms up to the third order of the advective–diffusive model to describe advection–diffusion in a macroscopically homogeneous porous medium at low scale separation. The main result of the study is that the low separation of scales induces dispersion effects. In particular, the second-order model is similar to the most currently used phenomenological model of dispersion: it is characterised by a dispersion tensor which can be decomposed into a purely diffusive component and a mechanical dispersion part, whilst this property is not verified in the homogenised dispersion model (obtained at higher Péclet number). The third-order description contains second and third concentration gradient terms, with a fourth-order tensor of diffusion and with a third-order and an additional second-order tensors of dispersion. The analysis of the macroscopic fluxes shows that the second- and the third-order macroscopic fluxes are distinct from the volume averages of the corresponding local fluxes and allows to determine expressions of the non-local effects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Most studies in the theory of flow and transport in porous media are based on the exploitation of the continuum theory implying that the original heterogeneous medium behaves like a homogeneous one characterised by macroscopic fluid flow and transport equations with certain effective properties. Such an approach requires that the condition of separation of scales be fulfilled: the microscopic size l of heterogeneities must be essentially smaller than the macroscopic characteristic length L : \(l \ll L\). In this definition, length L represents either the size of the whole sample, or a macroscopic characteristic length of the phenomenon, which means that the condition of separation of scales must be fulfilled geometrically and also and with respect to loading conditions.
The multiple-scale asymptotic homogenisation method which can be traced to Sanchez-Palencia (1980), Bensoussan et al. (1978), and Bakhvalov and Panasenko (1989) can be used as a systematic tool of averaging so as to derive such continuum models: first-order models obtained by asymptotic homogenisation are thus accurate for media with large scale separation between the pore scale and the macroscale. But when the ratio l / L is “small but not too small”, microstructural scale effects may occur which result in specific non-local phenomena. Then, the “local action” assumption of classical continuum mechanics, which postulates that the current state of the medium at a given point is only affected by its immediate neighbours and that there are no physical mechanisms that produce action at a distance, is no longer satisfied. Consequently, additional terms need to be taken into account in order to obtain an accurate picture of the overall response of the medium, which cannot be predicted in the frame of first-order homogenisation theory. Thus, the study of so-called higher-order or non-local effects in the overall behaviour of heterogeneous media is motivated by the need to account for the scale effects observed in the behaviour of multiple-scale heterogeneous media where the scales are separated widely but not “too widely”, and these scale effects can be systematically analysed by considering higher-order correctors in the asymptotic homogenisation method.
Mathematical aspects of higher-order homogenisation have been developed in Smyshlyaev and Cherednichenko (2000) and Cherednichenko and Smyshlyaev (2004). The role of higher-order terms has been investigated for heat conduction in heterogeneous materials in Boutin (1995) and for elastic composite materials subjected to static loading in Gambin and Kroner (1989) and Boutin (1996). In these studies, it is shown that the heterogeneity of the medium causes non-local effects on a macrolevel: instead of the homogenised equilibrium equations of continuum mechanics, new equilibrium equations are obtained that involve higher-order spatial derivatives and thus represent the influence of the microstructural heterogeneity on the macroscopic behaviour of the material. In dynamic problems, application of higher-order homogenisation provides a long-wave approach valid in the low-frequency range (Boutin and Auriault 1993; Fish and Chen 2001; Bakhvalov and Eglit 2005; Chen and Fish 2001; Andrianov et al. 2008). In Boutin and Auriault (1993), it is demonstrated that higher-order terms successively introduce effects of polarisation, dispersion and attenuation.
Transport in porous media with low scale separation has thus far received relatively little attention. However, two important works on fluid flow have been performed. In Goyeau et al. (1997, 1999), the authors investigate the permeability in a dendritic mushy zone, which is generally a non-homogeneous porous structure. They make use of the volume averaging method to obtain corrector terms to Darcy’s law. In Auriault et al. (2005), the validity of Darcy’s law is investigated by higher-order asymptotic homogenisation up to the third order.
The focus of the present study is on solute transport by advection–diffusion in porous media with low scale separation, which can occur in the two following situations (Auriault et al. 2005): (i) when large gradients of concentration are applied to macroscopically homogeneous porous media; (ii) when the porous medium is macroscopically heterogeneous and the macroscopic characteristic length L associated with the macroscopic heterogeneities is not “very” large compared to the characteristic length l of the pores. The scope of the present work is to derive higher-order homogenised models of advection–diffusion in macroscopically homogeneous porous media and is therefore aimed at describing the situations where large concentration gradients are applied. This may for example happen during soil-column experiments, where soil samples are necessarily limited in size and are subjected to large concentration gradients, especially at early stages of the tests. In these situations, the macroscopic characteristic length \(L \approx C/\mid \mathbf {\nabla }C \mid \) associated with this gradient of concentration is not “very” large compared to l (Auriault and Lewandowska 1997). Homogenisation of convection-diffusion equations on the pore scale leads to three macroscopic transport models, accordingly to the order of magnitude of the Péclet number (Auriault and Adler 1995): (i) a diffusion model; (ii) an advection–diffusion model; (iii) an advection–dispersion model. Whilst the first two models are first-order models, the dispersive model requires to account for the first corrector. The purpose of the present work is to derive the second- and third-order homogenised models in the case where the model of advection diffusion is obtained at the first order.
The paper is organised as follows. Section 2 presents the existing phenomenological and homogenised macromodels and their properties for describing solute transport in rigid porous media. The input transport problem is formulated in Sect. 3: the medium geometry is described in Sect. 3.1, and the pore-scale governing equations for fluid flow and solute transport are then presented and non-dimensionalised in Sect. 3.2. The results from Auriault et al. (2005) for higher-order homogenisation up to the third order of the fluid flow equations, and which are required for the developments that follow, are briefly summarised in Sect. 4. Section 5 is devoted to higher-order homogenisation up to the third order of solute transport equations in the advective–diffusive macroregime. The physical meaning of the volume averages of local fluxes which arise with the homogenisation procedure is analysed in Sect. 6, and the writing of the second- and third-order homogenised models in terms of the macroscopic fluxes provides expressions of the non-local effects. Finally, Sect. 7 presents a summary of the main theoretical results contained in this work and highlights conclusive remarks.
2 About Phenomenological and Homogenised Models of Solute Transport in Porous Media
2.1 Phenomenological Macromodels
Let consider a rigid porous medium saturated by an incompressible Newtonian fluid. When the fluid is at rest, transient solute transport within the medium is described by the model of diffusion:
in which \(\phi \) denotes the porosity, C represents the concentration, and \({\bar{\bar{D}}}^{{{\tiny {\mathrm{eff}}}}}\) is the tensor of effective diffusive. When the fluid is in motion, solute transport may either be described by the model of advection–diffusion
or by the model of advection–dispersion
In both models, \(\overrightarrow{V}\) denotes the macroscopic fluid velocity and verifies:
where \(\bar{\bar{K}}\) denotes the tensor of permeability, \(\mu \) is the fluid viscosity, and P represents the fluid pressure. For the sake of simplicity, gravity is neglected in Eq. (2.4). Tensor \({\bar{\bar{D}}}^{{{{\tiny {\mathrm{disp}}}}}}\) in model Eq. (2.3) is the tensor of hydrodynamic dispersion: it depends on the fluid velocity. In the most currently used model of dispersion (Bear 1972; Bear and Bachmat 1990), the tensor of dispersion is decomposed into the sum of a diffusive term and a term of mechanical dispersion which depends on the fluid velocity:
Whilst the regime of advection–diffusion is rarely mentioned in the geosciences literature, it is of particular relevance for modelling electro-chemo-mechanical coupling in swelling porous media (Moyne and Murad 2006). Advection–diffusion is furthermore the usual transport regime observed in biological tissues (Becker and Kuznetsov 2013; Ambard and Swider 2006; Swider et al. 2010; Lemaire and Naili 2013).
2.2 Homogenised Models
Homogenisation of the convection–diffusion equations on the pore scale allows to find the three above-mentioned transport regimes (Auriault and Adler 1995) and to give their respective range of validity by means of the order of magnitude of the Péclet number
where L denotes the characteristic macroscopic length and \(v_\mathrm{c}\) and \(D_\mathrm{c}\) are characteristic values of the local fluid velocity and of the coefficient of molecular diffusion. The results of Auriault and Adler (1995) are the following:
where \(\varepsilon =l/L \), with l being the pore-scale characteristic length, is the small parameter of the asymptotic homogenisation method and a parameter \(\mathbb {P}\) is said to be of order \(\varepsilon ^p \), \(\mathbb {P}={\mathscr {O}}(\varepsilon ^p) \), when
The homogenised models of diffusion and of advection–diffusion are first-order models and are rigorously identical to models Eqs. (2.1)–(2.2). On the other hand, however, the homogenised model of advection–dispersion is different from the classical phenomenological model Eq. (2.3). It is a second-order model, which in particular implies that Darcy’s law is no longer valid (Auriault et al. 2005). Furthermore, the homogenised tensor of dispersion does not verify relationship Eq. (2.6) and is not symmetric (Auriault and Adler 1995; Auriault et al. 2010). At high Péclet number, \({{\mathbb {P}}}e\ge {\mathscr {O}}(\varepsilon ^{-2})\), the problem becomes dependent upon the macroscopic boundary conditions. Consequently, there exists no continuum macromodel to describe solute transport within this regime.
3 Problem Statement for Homogenisation of Solute Transport Within the Advective–Diffusive Regime
3.1 Geometry
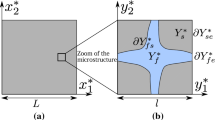
Consider a rigid porous medium with connected pores. We assume it to be periodic with period \(\hat{\Omega }\). The fluid occupies the pores \(\hat{\Omega }_\mathrm {p}\), and \(\hat{\Gamma }\) represents the surface of the solid matrix \(\hat{\Omega }_\mathrm {s}\). We denote as \({\hat{l}}\) and \({\hat{L}}\) the characteristic length of the pores and the macroscopic length (Fig. 1). We assume the scales to be separated, and we define
Using the two characteristic lengths, \({\hat{l}}\) and \({\hat{L}}\), two dimensionless space variables are defined
where \({\overrightarrow{{\hat{X}}}}\) is the physical spatial variable. Invoking the differentiation rule of multiple variables, the gradient operator with respect to \({\overrightarrow{{\hat{X}}}}\) is written as
where \(\overrightarrow{\nabla }_y\) and \(\overrightarrow{\nabla }_x\) are the gradient operators with respect to \(\overrightarrow{y}\) and \(\overrightarrow{x}\), respectively.
3.2 Governing Equations on the Pore Scale and Estimates
The pores are saturated with a viscous, incompressible and Newtonian fluid containing a low concentration of solute \({\hat{c}}\). The fluid is in slow steady-state isothermal flow, so that the solute is transported by diffusion and convection.
3.2.1 Fluid Flow
The equations governing velocity \(\overrightarrow{{\hat{v}}}\) and pressure \({\hat{p}}\) of an incompressible viscous fluid of viscosity \(\hat{\mu }\) in slow steady-state flow within the pores are the following:
-
Stokes equation
$$\begin{aligned} \hat{\mu }\varDelta _X\overrightarrow{{\hat{v}}} - \overrightarrow{\nabla }_{{\hat{X}}} {\hat{p}}=\overrightarrow{0} \quad \hbox {within }\hat{\varOmega }_{\mathrm {p}}, \end{aligned}$$(3.5) -
the conservation of mass
$$\begin{aligned} \overrightarrow{\nabla }_{{\hat{X}}}\cdot \overrightarrow{{\hat{v}}} = 0 \quad \hbox {within }\hat{\Omega }_{\mathrm {p}}, \end{aligned}$$(3.6) -
the no-slip condition
$$\begin{aligned} \overrightarrow{{\hat{v}}} = \overrightarrow{0}\quad \hbox {over } \hat{\Gamma }. \end{aligned}$$(3.7)
3.2.2 Solute Transport
The transport of solute by diffusion–convection in the pore domain is described by conservation of mass
and the no-flux boundary condition
where \({\hat{c}}\) is the solute concentration (mass of solute per unit volume of fluid), t is the time, \( {\hat{D}}_0\) denotes the coefficient of molecular diffusion, and \(\overrightarrow{n}\) is the unit vector giving the normal to \(\hat{\Gamma }\) exterior to \(\hat{\Omega }_\mathrm {p}\).
3.2.3 Non-dimensionalisation and Estimates
Introducing into Eqs. (3.5)–(3.9)
where quantities with subscript \(\mathrm {c}\) denote characteristic quantities, we can write the microscopic description in dimensionless form as
with
In the above writing, the dimensionless counterpart of any dimensional quantity \(\hat{\varPsi }\) is \(\varPsi =\hat{\varPsi }/\varPsi _\mathrm {c}\). In particular, the characteristic time \(t_\mathrm {c}\) is the time over which we intend to describe the solute transport: it is the characteristic time of the observation. We have arbitrarily chosen the macroscopic length \({\hat{L}}\) as the reference length for normalising the gradient operator. Consequently, according to Eq. (3.4), the corresponding dimensionless gradient operator reads
We may now estimate the three dimensionless parameters, \( \mathbb {F}\), \(\mathbb {N}\) and the Péclet number \(\mathbb {P}e\), with respect to powers of the small parameter \(\varepsilon \) and for this purpose we shall apply the rule defined by Eq. (2.8). Parameter \(\mathbb {F}\), which arises from Stokes equation Eq. (3.10), is the ratio of the viscous term to the pressure gradient. We shall consider the case where homogenisation of Stokes equations leads to Darcy’s law on the sample scale. As shown in Auriault (1991), this happens when the local flow is balanced by a macroscopic pressure gradient, which in an order-of-magnitude sense reads
and yields
The order of magnitude of the Péclet number \(\mathbb {P}\mathrm {e}\) characterises the regime of solute transport. Indeed, it is the ratio of characteristic times of diffusion and convection
where
We consider
which leads to the homogenised advective–diffusive model at the first order (Cf. Sect. 2.2). The dimensionless number \(\mathbb {N}\) is such that:
Since \( \mathbb {P}\mathrm {e} = {\mathscr {O}}(\varepsilon ^0)\) means that \(t^{\scriptscriptstyle \mathrm {diff}}= t^{\scriptscriptstyle \mathrm {conv}}\) , we take \(t_\mathrm {c}=t^{\scriptscriptstyle \mathrm {diff}}= t^{\scriptscriptstyle \mathrm {conv}}\), which yields
Note that taking \(t_\mathrm {c}=t^{\scriptscriptstyle \mathrm {diff}}= t^{\scriptscriptstyle \mathrm {conv}}\) ensures a macroscopic transient regime, while \( t_\mathrm {c}> t^{\scriptscriptstyle \mathrm {diff}}\) would lead to a macroscopic steady-state regime and that when \(t_\mathrm {c}<t^{\scriptscriptstyle \mathrm {diff}}\), the transport mechanism is not sufficiently developed for its evolution be described by means of a continuum model.
4 Higher-Order Homogenisation of Fluid Flow
Homogenisation of the fluid flow equations has been performed up to the third order in Auriault et al. (2005). Equations (3.10)–(3.13) are considered with Eq. (3.17), which leads to the following set of flow equations
where
The homogenisation procedure consists in looking for the pressure and the velocity in the form of asymptotic expansions in powers of \(\varepsilon \) (Bensoussan et al. 1978; Sanchez-Palencia 1980):
For a macroscopically homogeneous medium, the results can be summarised as follows
with
where \(\langle .\rangle \) denotes the volume average and is defined by
The third-order tensor \(N_{ijk}\) is symmetric with respect to its last two indices and antisymmetric with respect to its first two indices. Then, since \(N_{ijk}\) is symmetrical with respect to its last two indices, it is equal to zero when the medium is isotropic.
Functions \(p^0\), \(p^1\) and \(p^2\) are such that
Note that functions \({\bar{p}}^1\) and \({\bar{p}}^2\), which appear in Eqs. (4.7) and (4.8), are particular solutions involved in the definitions of \(p^1\) and \(p^2\), Eqs. (4.11) and (4.12), respectively. Combining Eq. (4.5) with the averaged velocities, the second-gradient terms vanish as a result of the antisymmetry of \(N_{ijk}\). Thus, the following flow descriptions are obtained
5 Higher-Order Homogenisation of Solute Transport in the Advective–diffusive Regime
5.1 Local Dimensionless Description
We consider Eq. (3.12) with estimates Eqs. (3.21) and (3.23) and boundary conditions Eqs. (3.13)–(3.14). This leads to the following set of equations:
We look for solutions to the unknowns c and \(\overrightarrow{v}\) of the form:
where functions \(c^n(\overrightarrow{y}, \overrightarrow{x})\) and \(\overrightarrow{v}^n(\overrightarrow{y}, \overrightarrow{x})\) are \(\varOmega \)-periodic in \(\overrightarrow{y}\). Furthermore, because of the two spatial variables \(\overrightarrow{x}\) and \(\overrightarrow{y} = \varepsilon ^{-1}\overrightarrow{x}\), the spatial derivation takes the form Eq. (4.4). The homogenisation technique involves the introduction of these expansions into the dimensionless equations Eqs. (5.1)–(5.3) and the identification of the powers of \(\varepsilon \).
5.2 First-Order Homogenisation
5.2.1 Boundary Value Problem for \(c^0\)
At the first order, the boundary value problem Eqs. (5.1)–(5.3) lead to:
from which it is clear that the concentration \(c^0\) is constant over the period
5.2.2 Boundary Value Problem for \(c^1\)
We now consider the second order of Eqs. (5.1)–(5.3). Then, noticing that (see Eq. (4.2))
we obtain the following boundary value problem for \(c^1\):
By virtue of linearity, the solution reads:
where \({\bar{c}}^1(\overrightarrow{x}, t)\) is an arbitrary function. The exact definition of the vector \(\overrightarrow{\chi }\) is reported in “Appendix A.1”. Note that, to render the solution unique, we impose that \(\overrightarrow{\chi }\) is average to zero (Bensoussan et al. 1978; Sanchez-Palencia 1980; Mei and Vernescu 2010):
Note further that, since we are considering a macroscopically homogeneous medium, \(\overrightarrow{\chi }\) doesn’t depend on variable \(\overrightarrow{x}\): \(\overrightarrow{\chi }=\overrightarrow{\chi }(\overrightarrow{y})\).
5.2.3 Derivation of the First-Order Macroscopic Description
Let consider the boundary value problem Eqs. (5.1)–(5.3) at the third order:
The homogenisation procedure consists now in integrating Eq. (5.14) over \(\varOmega _\mathrm {p}\). This leads to the so-called compatibility condition, which is a necessary and sufficient condition for the existence of solutions. Furthermore, it represents the first-order macroscopic description. Invoking Gauss’ theorem, the integration yields:
where \(\delta \varOmega _{\mathrm {p}}=\varGamma \cup (\delta \varOmega \cap \delta \varOmega _\mathrm {p})\) denotes the bounding surface of \(\varOmega _{\mathrm {p}}\). The second term of Eq. (5.17) is thus the sum of two surface integrals, and it actually cancels out: the integral over the surface \(\varGamma \) vanishes because of boundary conditions Eqs. (5.15)–(5.16), while the integral over the cell boundary, \(\delta \varOmega \cap \delta \varOmega _\mathrm {p} \), vanishes by periodicity. Hence, Eq. (5.17) reduces to
where
denotes the porosity. Using Eq. (5.12), we can write:
where
Taking Eq. (4.5) into account, Eq. (5.18) can be rewritten as follows:
where
is the tensor of effective diffusion. It can be shown that the second-order tensor \(D_{ij}\) is positive and symmetric (Cf. “Appendix A.2”).
Defining the first-order macroscopic concentration and average fluid velocity by
the first-order macroscopic description thus reads
In dimensional variables, it becomes
where
is the tensor of effective diffusion. The fluid velocity verifies (Cf. Sect. 4):
The first-order behaviour is thus described by the classical advection–diffusion transport equation, in which the fluid velocity verifies Darcy’s law.
5.3 Second-Order Homogenisation
5.3.1 Boundary Value Problem for \(c^2\)
The third-order boundary value given by Eqs. (5.14)–(5.16) can be transformed (Cf. “Appendix B.1”) so as to obtain the following boundary value problem for \(c^2\):
We observe that the solution must depend on three forcing terms, which are associated with \({\partial ^2 c^0}/{\partial x_j \partial x_k} \), \({\partial c^0}/{\partial x_j}\) and \({\partial {\bar{c}}^1}/{\partial x_j} \), respectively. By virtue of linearity, the solution is a linear combination of particular solutions associated with each of the three forcing terms. Note that the problem linked to \({\partial {\bar{c}}^1}/{\partial x_j} \) is identical to that observed at the first order for \({\partial c^0}/{\partial x_j}\) in the boundary value problem which defines \(c^1\) (Eqs. (5.9)–(5.10)). Therefore, the solution reads
where \({\bar{c}}^2(\overrightarrow{x}, t)\) is an arbitrary function and
The detailed definitions of \(\eta _{jk}\) and \(\pi _j\) are reported in “Appendix B.2”.
5.3.2 Derivation of the First Corrector
At the fourth order, the boundary value problem made of Eqs. (5.1)–(5.3) yields:
The first corrector of the macroscopic description is obtained by integrating Eq. (5.36) over \(\varOmega _\mathrm {p}\). This leads to
Using the expressions obtained for \(c^1\) and \(c^2\), Eqs. (5.12) and (5.33), we get
with
Then, noticing that
Equation (5.39) becomes:
where
The third-order tensor \(E_{ijk}\) is symmetric with respect to its last two indices and antisymmetric with respect to its first two indices (Cf. “Appendix B.3”). Note further that \(E_{ijk}\) can be determined from vector \(\chi _i\), without determining tensor \(\eta _{jk}\) (Cf. “Appendix B.3”). As a result of the antisymmetry property of \(E_{ijk}\), the second-order gradient term of Eq. (5.43) vanishes. Thus, the first corrector finally reads:
From its definition Eq. (5.45), we see that the second-order tensor \(D'_{ij}\) contains a convective term: it is therefore a dispersion tensor. It is a non-symmetric tensor which can be decomposed into a symmetric and an antisymmetric parts (Cf. “Appendix B.4”). Furthermore, it can be determined from vectors \(v_i^0\) and \(\chi _j\), without solving boundary value problem Eqs. (5.36)–(5.38) (Cf. “Appendix B.4”).
5.3.3 Second-Order Macroscopic Description
Let add Eqs. (5.22)–(5.46) multiplied by \(\varepsilon \). We get:
Defining the second-order macroscopic concentration and average fluid velocity by
the second-order macroscopic description is written as follows
When cast in dimensional variables, Eq. (5.50) becomes
where
The second-order fluid velocity is such that (Cf. Sect. 4):
Note that combining both above equations leads to:
Therefore, the second-order macroscopic transport description is a model of advection–dispersion, in which the tensor of dispersion is non-symmetric (Cf. “Appendix B.4”) and follows property Eq. (2.6) of the phenomenological model of dispersion. The fluid velocity verifies a second-order law Eq. (5.53), which reduces to Darcy’s law in case of an isotropic medium. In other words, the second-order macroscopic transport model is similar to the phenomenological dispersion transport equation (2.3).
5.4 Third-Order Homogenisation
5.4.1 Boundary Value Problem for \(c^3\)
The fourth-order boundary value problem, Eqs. (5.36)–(5.38), can be transformed into the following boundary value problem for \(c^3\) (Cf. “Appendix C.1”):
From the above boundary value problem and its variational formulation (Cf. “Appendix C.2”), it can be seen that the solution must depend on the following forcing terms: \({\partial ^3 c^0}/{\partial x_j \partial x_k \partial x_l}\), \({\partial ^2 c^0}/{\partial x_k\partial x_l} \), \({\partial ^2 {\bar{c}}^1}/{\partial x_k \partial x_l}\), \({\partial c^0}/{\partial x_j}\), \({\partial {\bar{c}}^1}/{\partial x_j}\) and \( {\partial {\bar{c}}^2}/{\partial x_j}\). We note that the problem linked to \( {\partial {\bar{c}}^2}/{\partial x_j}\) is identical to that associated with \({\partial c^0}/{\partial x_j}\) in the boundary value problem for \(c^1\) Eqs. (5.9)–(5.10). Furthermore, the problem associated with \({\partial {\bar{c}}^1}/{\partial x_j}\) is identical to that linked to \({\partial c^0}/{\partial x_j}\) in the boundary value problem for \(c^2\), Eqs. (5.31)–(5.32), and the problem linked to \({\partial ^2 {\bar{c}}^1}/{\partial x_k \partial x_l}\) is identical to that obtained for \({\partial ^2 c^0}/{\partial x_k\partial x_l} \) in the boundary value problem for \(c^2\). Consequently, the solution reads:
where \({\bar{c}}^3 (\overrightarrow{x}, t)\) is an arbitrary function and
The exact definitions of \(\xi _{jkl}\), \(\tau _{kl} \) and \(\theta _j\) are reported in “Appendices C.3, C.4 and C.5”, respectively. Let us recall that \(\chi _j\) is related to the definition of \(c^1\) Eq. (5.12), while \(\eta _{jk}\) and \(\pi _j \) have been introduced in the definition of \(c^2\) Eq. (5.33). Note that in expression Eq. (5.58), \(\xi _{jkl}\), \(\eta _{jk}\), \(\chi _j\) are only related to the diffusion mechanism, while \(\tau _{kl}\), \(\theta _j\) and \(\pi _j\) contain both diffusive and convective terms.
5.4.2 Derivation of the Second Corrector
Let now consider the boundary value problem Eqs. (5.1)–(5.3) at the fifth order:
Integrating Eq. (5.62) over \(\varOmega _\mathrm {p}\), we get:
Using Eqs. (5.33) and (5.58), we deduce that
where
Then, noticing that:
Equation (5.64) becomes:
where
Tensor \(F_{ijkl}\) is a fourth-order tensor of diffusion. It can be calculated from vector \(\overrightarrow{\chi }\) and tensor \(\bar{\bar{\eta }} \), without solving the boundary value problem Eqs. (5.56)–(5.57) (Cf. “Appendix C.8”). The third-order tensor \(E'_{ijk}\) and the second-order tensor \(D''_{ij}\) are tensors of dispersion. They can also be determined without solving the boundary value problem Eqs. (5.56)–(5.57) (Cf. “Appendices C.6, C.7”). Finally, we conclude that the second corrector can be determined from \(\bar{\bar{\eta }} \), \(\overrightarrow{\chi }\), \(\overrightarrow{\pi }\), \(\overrightarrow{v}^0\) and \(\overrightarrow{v}^1\).
5.4.3 Third-Order Macroscopic Description
Let add Eqs. (5.47)–(5.68) multiplied by \(\varepsilon ^2\):
Defining the third-order macroscopic concentration and fluid velocity by
the third-order macroscopic description is written as follows
In dimensional variables, we get:
where
The third-order fluid velocity verifies (Cf. Sect. 4):
Note that when combining both above equations, the second-gradient term vanishes, due to the antisymmetry property of tensor \({\hat{N}}_{ijk}^{{{\tiny {\mathrm{eff}}}}}\).
The third-order transport model Eq. (5.76) introduces a fourth-order tensor of diffusion, and a third-order and an additional second-order tensors of dispersion.
6 Macroscopic Fluxes
6.1 Volume Versus Surface Averages
With the homogenisation averaging procedure, macroscopic descriptions are expressed in terms of variables which are systematically defined as volume averages. Specifying the meaning of the macroscopic variables, i.e. determining whether the use of volume averages is appropriate or not is thus an important issue (Hassanizadeh and Gray 1979; Costanzo et al. 2005; Hill 1972). In the particular context of solute transport in porous media, since a solute flux is physically defined over a specific area, macroscopic fluxes should thus be defined as surface averages.
6.2 Writing of Local and Homogenised Equations in Terms of Fluxes
In order to address the above described issue, we may rewrite the local and the homogenised equations in terms of fluxes. We shall thus rewrite Eq. (5.1) as follows
where the local flux \(\overrightarrow{q} \) is defined by
The no-flux boundary condition now reads
Flux \( \overrightarrow{q}\) is looked for in the form of the following asymptotic expansion in powers of \(\varepsilon \)
This leads to the following perturbations equations for Eqs. (6.1)–(6.2) at the successive orders of powers of \(\varepsilon \):
and
As for the homogenised equations at the first three orders, Eqs. (5.18), (5.46) and (5.68), they are re-expressed as follows
First-order
Second-order corrector
Third-order corrector
To analyse whether volume averages of local fluxes have the properties of macroscopic fluxes, we consider the following identity to transform volume averages into surface averages (Auriault et al. 2005)
6.3 First-Order Macroscopic Flux
Let take \( q_i = q_i^0\) in Eq. (6.17) and then integrate over \(\varOmega _p\). Since by Eq. (6.8) \(q_i^0\) is solenoidal according to \(\overrightarrow{y}\), it reduces to
Applying the divergence theorem and the no-flux boundary condition Eq. (6.3) of order \(\varepsilon ^0\) leads to:
Let \(l_i\) be the dimensionless length of the period along the \(y_i\) axis. We denote by \(\varSigma _i^0\) and \(\varSigma _i\) the cross-sections of the period at \(y=0\) and \(y_i=l_i e_i\), respectively. \(\varSigma _{p_i}^0\) and \(\varSigma _{p_i}\) are the fluid parts of \(\varSigma _i^0\) and \(\varSigma _i\), respectively (Cf. Fig. 2). We firstly note that \(y_j q_i^0\) is \(\varOmega \)-periodic in the \(y_k (k\ne j)\) direction. Consequently, only integrals over boundaries \(\varSigma _j^0\) and \(\varSigma _j\) (where the normal unit vectors are \(\pm e_j \)) remain; the others cancel out. Furthermore, \(y_j q_i^0=0\) for \(y_j=0\). Therefore, the integral over \(\varSigma _j^0\) is zero. We are left with
(without summation over j), and we define
Hence, we have
which means that the volume average of \(q_j^0\) is equal to a surface average. Therefore, \(\langle q_j^0\rangle \) has the properties of a macroscopic flux. As a consequence, from the expression of \(\overrightarrow{q}^0\), Eq. (6.5), we deduce that
which means that the volume average of \(\overrightarrow{v}^0\) has the properties of a Darcy’s velocity. Note that the equalities between volume averages and surface averages of \(q_j^0\) and \(v_j^0\) are consequences of the solenoidal character of \(\overrightarrow{q}^0\) and \(\overrightarrow{v}^0\), according to variable \(\overrightarrow{y}\).
Therefore, Eqs. (6.11)–(6.12) can be rewritten as
and the first-order macroscopic description Eq. (5.26) can be expressed as
where the first-order macroscopic solute flux and fluid velocity are defined by
Finally, in dimensional variables the first-order transport model reads
6.4 Second-Order Macroscopic Flux
To analyse the volume average of \(\overrightarrow{q}^1\), let consider identity Eq. (6.17) with \(q_i=q_i^1\) and integrate over \(\varOmega _\mathrm {p}\). This yields
Now, by Eq. (6.9), we get that \(\overrightarrow{q}^1\) is non-solenoidal
Consequently, the volume average of \(\overrightarrow{q}^1\) is not equal to its surface average
which means that \(\langle \overrightarrow{q}^1\rangle \) is not a macroscopic flux.
By starting from Eq. (6.32) and then using Eq. (6.33) to get the term \(\langle y_i{\partial q_j^1}/{\partial y_j}\rangle \), we obtain the following expression for \(\langle \overrightarrow{q}^1\rangle _{\varSigma _{p_i}}\) (Cf. “Appendix D.1”):
where
Using Eq. (6.32), the first corrector of the macroscopic description, Eq. (6.13), can be rewritten in terms of the second-order macroscopic flux as follows:
Then, using Eqs. (D.4), (D.9), (6.36) and (6.37), it becomes
Now, in order to obtain the corresponding second-order macroscopic description, let firstly add Eqs. (6.24)–(6.39) multiplied by \(\varepsilon \). We get
Next, we add Eqs. (6.25)–(6.35) multiplied \(\varepsilon \), and we obtain
In the above equations, the second-order macroscopic solute flux and fluid velocity are defined by
respectively. In dimensional variables, Eqs. (6.40) and (6.41) read
where
6.5 Third-Order Macroscopic Flux
Proceeding in the same manner as in Sect. 6.4, we also conclude that
and we show that in dimensional variables, the third-order transport model expressed in terms of the macroscopic flux reads (Cf. “Appendix D.2”):
where (Cf. “Appendix D.2”)
Since \(\langle {\hat{q}}_i\rangle _{\varSigma _{p_i}} \) has the properties of a macroscopic flux, the right-hand sides of the mass-balance equations, Eqs. (6.44) and (6.50), represent source terms, which are actually expressions of the second-order and third-order non-local effects, respectively.
7 Conclusions
In the present paper, higher-order asymptotic homogenisation up to the third order of solute transport in the advective–diffusive regime is performed. The main result of the study is that low scale separation induces dispersion effects. At the second order, the transport model is similar to the classical model of dispersion: the dispersion tensor is the sum of the diffusion tensor and a mechanical dispersion tensor, while this property is not verified in the homogenised dispersion model obtained at higher Péclet number. The velocity is governed by a second-order law which reduces to Darcy’s law in case of isotropy. Thus, the second-order model of advection–diffusion is similar to the phenomenological model of dispersion. The third-order description contains second and third concentration gradient terms, with a fourth-order tensor of diffusion and with a third-order and an additional second-order tensors of dispersion. Hence, these results show that when employing the first-order model while \(\varepsilon \) is not “very” small would, for example, lead to a wrong estimate of the tensor of effective diffusion from experimental data. We generally admit that a first-order model, whose degree of precision is \({\mathscr {O}}(\varepsilon )\), is valid for a value of \(\varepsilon \) up to \(\varepsilon \approx 0.1\). Consequently, we may estimate that the p-order model is required when \(\varepsilon ^p\approx 0.1 \). The analysis of the macroscopic fluxes shows that the second- and the third-order macroscopic fluxes are distinct from the volume averages of the corresponding local fluxes. From the writing of the second- and third-order models in terms of the macroscopic fluxes arise expressions of the non-local effects. All theses results are valid for macroscopically homogeneous media, and macroscopic heterogeneity would lead to stronger non-local effects.
The results at Péclet number \({\mathscr {O}}(\varepsilon )\) can quite easily be deduced from the above analysis. This leads to the model of diffusion at the first order and the model of advection–diffusion at the second order, and dispersion effects appear at the third order. Eventually, we may conclude that scale separation is a crucial issue whenever the fluid is in motion, since low scale separation induces a modification of the apparent transport regime (Royer 2018).
An important property of higher-order homogenised models is that edge effects are induced: the boundary layer created by the heterogeneity may affect the homogenised solution inside the domain in higher orders with respect to \(\varepsilon \). Numerical simulations of the above-derived effective higher-order equations thus require a specific treatment of these edge effects (Smyshlyaev and Cherednichenko 2000; Buannic and Cartraud 2001; Dumontet 1990). A discussion on that topic is complex and beyond the scope of this paper.
Since the advection–diffusion equation is a Fokker-Planck type equation, the higher-order transport homogenised equations may appear to be similar to a generalised Fokker-Planck equation (Risken 1989). Such equation which describes the time evolution of a probability density function is obtained by a Kramers–Moyal expansion which transforms an integro-differential master equation. Pawula (1967) has proved that finite truncations of the generalised Fokker–Planck equation at any order greater than the second leads to a logical inconsistency, as the function must then have negative values at least for sufficiently small times and in isolated regions. This argument may be used to put into question the validity of higher-order homogenised transport models (Mauri 1991). In this regard, the work of van Kampen (1981) provides the framework for the introduction of a small parameter which allows for the construction of a modified Kramers–Moyal expansion. Then, one can approximate the expansion by a finite number of terms which involves derivatives of order higher than two, using an appropriate perturbation technique. In this case, the contribution from higher-order terms diminishes, because of their order in the small parameter. Such an expansion is admittedly questionable in view of Pawula’s theorem, but can be controlled when manipulated with care (Popescu and Lipan 2015). Thus, the theorem of Pawula does not necessarily restrict the truncation of higher-order terms, when we can formally obtain high-order perturbative equations (Kanazawa 2017) and nonvanishing higher-order coefficients have been observed in various systems (Anvari et al. 2016; Friedrich et al. 2011; Prusseit and Lehnertz 2007; Tutkun and Mydlarski 2004; Lim et al. 2008; Petelczyc et al. 2009, 2015). Therefore, though higher-order perturbative models might, in some cases, have negative values at some isolated times and positions, this does not invalidate the models derived in the study, which are valid only in zones where large concentration gradients are applied.
References
Ambard, D., Swider, P.: A predictive mechano-biological model of the bone-implant healing. Eur. J. Mech. A Solids 25, 927–937 (2006)
Andrianov, I.V., Bolshakov, V.I., Danishvskyy, V.V., Weichert, D.: Higher order asymptotic homogenisation and wave propagation in periodic composite materials. Proc. R. Soc. A 464, 1181–1201 (2008)
Anvari, M., Tabar, M.R., Peinke, J., Lehnertz, K.: Disentangling the stochastic behavior of complex time series. Sci. Rep. 6, 35435 (2016). https://doi.org/10.1038/srep35435
Auriault, J.-L.: Heterogeneous medium. Is an equivalent macroscopic description possible? Int. J. Eng. Sci. 29(7), 785–795 (1991)
Auriault, J.-L., Adler, P.M.: Taylor dispersion in porous media: analysis by multiple scale expansions. Adv. Water Resour. 18(4), 217–226 (1995)
Auriault, J.-L., Lewandowska, J.: On the validity of diffusion/dispersion tests in soils. Eng. Trans. 45(3–4), 395–417 (1997)
Auriault, J.-L., Geindreau, C., Boutin, C.: Filtration law in porous media with poor separation of scales. Transp. Porous Media 60, 89–108 (2005)
Auriault, J.-L., Moyne, C., Amaral Souto, H.P.: On the asymmetry of the dispersion tensor in porous media. Transp. Porous Media 85(3), 771–783 (2010)
Bakhvalov, N.S., Eglit, M.E.: Equations of higher order of accuracy describing the vibrations of thin plates. J. Appl. Math. Mech. 69, 593–610 (2005)
Bakhvalov, N.S., Panasenko, G.P.: Homogenization: Averaging processes in Periodic Media. Kluwer, Dordrecht (1989)
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier, New York (1972)
Bear, J., Bachmat, Y.: Introduction to Modeling of Transport Phenomena in Porous Media. Kluwer, Dordrecht (1990)
Becker, S., Kuznetsov, A.: Transport in Biological Media. Elsevier, Amsterdam (2013)
Bensoussan, A., Lions, J.-L., Papanicolaou, G.: Asymptotic Analysis for Periodic Structures. North-Holland Publishing Company, Amsterdam (1978)
Boutin, C.: Microstructural influence on heat conduction. Int. J. Heat Mass Transf. 38(17), 3181–3195 (1995)
Boutin, C.: Microstructural effects in elastic composites. Int. J. Solids Struct. 33(7), 102–1051 (1996)
Boutin, C., Auriault, J.-L.: Rayleigh scattering in elastic composite materials. Int. J. Eng. Sci. 31, 1669–1689 (1993)
Buannic, N., Cartraud, P.: Higher-order effective modelling of periodic heterogeneous beams—part 2: derivation of the proper boundary conditions for the interior asymptotic solution. Int. J. Solids Struct. 38, 7163–7180 (2001)
Chen, W., Fish, J.: A dispersive model for wave propagation in periodic heterogeneous media based on homogenisation with multiple spatial and temporal scales. J. Appl. Mech. 68, 153–161 (2001)
Cherednichenko, K.D., Smyshlyaev, V.P.: On full two-scale expansion of the solutions of nonlinear periodic rapidly oscillating problems and higher-order homogenised variational problems. Arch. Ration. Mech. Anal. 174, 385–442 (2004)
Costanzo, F., Gray, G.L., Andia, P.C.: On the definitions of effective stress and deformation gradient for use in MD: Hill’s macro-homogeneity and the virial theorem. Int. J. Eng. Sci. 43, 533–555 (2005)
Dumontet, H.: Homogénéisation et effets de bords dans les matériaux composites. Thèse d’Etat, Université Paris 6 (1990)
Fish, J., Chen, W.: Higher-order homogenization of initial/ boundary-value problem. J. Eng. Mech. 127(12), 1223–1230 (2001)
Friedrich, R., Peinke, J., Sahimi, M., Tabar, M.R.R.: Approaching complexity by stochastic methods: from biological systems to turbulence. Phys. Rep. 506(5), 87–162 (2011)
Gambin, B., Kroner, E.: High order terms in the homogenised stress-strain relation of periodic elastic media. Phys. Stat. Sol. 6(151), 513–519 (1989)
Goyeau, B., Benihaddadene, T., Gobin, D., Quintard, M.: Averaged momentum equation for flow through a nonhomogeneous porous structure. Transp. Porous Media 28, 19–50 (1997)
Goyeau, B., Benihaddadene, T., Gobin, D., Quintard, M.: Numerical calculation of the permeability in a dendritic mushy zone. Met. Mater. Trans. B 30B, 613–622 (1999)
Hassanizadeh, M., Gray, W.: General conservation equations for multi-phase systems: 1. Averaging procedure. Adv. Water Resour. 2, 131–144 (1979)
Hill, R.: On constitutive macro-variables for heterogeneous solids at finite strain. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 326, 131–147 (1972)
Kanazawa, K.: Statistical Mechanics for Athermal Fluctuation Springer Theses. Springer, Singapore (2017)
Lemaire, T., Naili, S.: Multiscale approach to understand the multiphysics phenomena in bone adaptation. In: Gefen, A. (ed.) Multiscale Computer Modeling in Biomechanics and Biomedical Engineering, Studies in Mechanobiology, Tissue Engineering and Biomaterials, vol. 14. Springer, Berlin (2013)
Lim, G., Kim, S., Scalas, E., Kim, K., Chang, K.-H.: Analysis of price fluctuations in futures exchange markets. Phys. A 387, 2823–2830 (2008)
Mauri, R.: Dispersion, convection, and reaction in porous media. Phys. Fluids A 3, 743–756 (1991)
Mei, C.C., Vernescu, B.: Homogenization Methods for Multiscale Mechanics. World Scientific Publishing, Hackensack (2010)
Moyne, C., Murad, M.: A two-scale model for coupled electro-chemo-mechanical phenomena and Onsager’s reciprocity relations in expansive clays: I homogenization analysis. Transp. Porous Media 62, 333–380 (2006)
Pawula, R.F.: Approximation of the linear Boltzmann equation by the Fokker–Planck equation. Phys. Rev. 162, 186–188 (1967)
Petelczyc, M., Żebrowski, J.J., Baranowski, R.: Kramers–Moyal coefficients in the analysis and modeling of heart rate variability. Phys. Rev. E 80, 031127 (2009)
Petelczyc, M., Żebrowski, J.J., Orlowska-Baranowska, E.: A fixed mass method for the Kramers–Moyal expansion—application to time series with outliers. Chaos 25, 033115 (2015)
Popescu, D.M., Lipan, O.: A Kramers–Moyal approach to the analysis of third-order noise with applications in option valuation. PLoS ONE 10, e0116752 (2015)
Prusseit, J., Lehnertz, K.: Stochastic qualifiers of epileptic brain dynamics. Phys. Rev. Lett. 98, 138103 (2007)
Risken, H.: The Fokker–Planck Equation. Springer, Berlin (1989)
Royer, P.: Low scale separation induces modification of apparent solute transport regime in porous media. Mech. Res. Commun. 87, 29–34 (2018)
Sanchez-Palencia, E.: Non-homogeneous Media and Vibration Theory. Lecture Notes in Physics, vol. 127. Springer, Berlin (1980)
Smyshlyaev, V.P., Cherednichenko, K.D.: On rigorous derivation of strain gradient effects in the overall behaviour of periodic heterogeneous media. J. Mech. Phys. Solids 48, 1325–1357 (2000)
Swider, P., Accadbled, F., Laffosse, J.M., Sales de Gauzy, J.: Influence of fluid-flow direction on effective permeability of the vertebral end plate: an analytical model. Comput. Methods Biomech. Biomed. Eng. 15(2), 151–156 (2010)
Tutkun, M., Mydlarski, L.: Markovian properties of passive scalar increments in grid-generated turbulence. New J. Phys. 6, 49 (2004)
van Kampen, N.G.: Stochastic Processes in Physics and Chemistry. North-Holland, Amsterdam (1981)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
First-Order Homogenisation
1.1 Definition of Vector \({\chi _j}\)
Let multiply the local problem defined by Eqs. (5.9)–(5.10) by a test function \(\alpha \) satisfying the condition of having zero average, and then, let integrate over \(\varOmega _\mathrm {p}\). We obtain the following variational formulation
Vector \(\chi _j\) is the solution for \(c^1\) when \({\partial c^0}/{\partial x_i}=\delta _{ij}\). Therefore, the variational formulation associated with \(\chi _j\) is
and \(\chi _j\) must satisfy
1.2 Symmetry of Tensor \(D_{ij}\)
To demonstrate the symmetry of \(D_{ij}\), we firstly take
into Eq. (A.1). This leads to:
Next, we consider
into Eq. (A.1), which leads to:
By Eqs. (A.5) and (A.7), we deduce that:
Consequently, we have:
which proves the symmetry of \(\bar{{\bar{D}}}\).
Second-Order Homogenisation
1.1 Boundary Value Problem for \(c^2\)
The third-order boundary value given by Eqs. (5.14) and (5.16) can be written as follows:
Now, using Eq. (5.8), and the second order of Eq. (4.2)
while bearing in mind Eq. (5.7), the second and the third terms of the left-hand side of Eq. (B.1) can be transformed as follows:
Next, using Eq. (5.22) we get
and from Eq. (5.12), we obtain
Substituting Eqs. (B.4)–(B.7) into Eqs. (B.1)–(B.2), and then using the expression Eq. (5.20), we get the boundary value problem Eqs. (5.31)–(5.32).
1.2 Definitions of Tensor \(\eta _{jk}\) and Vector \(\pi _j\)
By multiplying the local problem Eqs. (5.31)–(5.32) by a test function \(\alpha \) of zero average, and then integrating over \(\varOmega _\mathrm {p}\), we obtain its variational formulation:
\(n_{lm}\) is the particular solution for \(c^2\) when
Therefore, the variational formulation associated with \(n_{jk}\) reads
and \(n_{jk}\) must satisfy
From its definition, we see that \(\eta _{lm}\) is a parameter related to the diffusion mechanism.
\(\pi _k\) is the solution for \(c^2\) when
The variational formulation associated with \(\pi _k\) is thus
and \(\pi _k\) must satisfy
From the above definition, it is clear that vector \(\overrightarrow{\pi }\) depends on both the diffusive and the convective phenomena, which characterises the presence of dispersive effects.
1.3 Properties of the Third-Order Tensor \(E_{ijk}\)
1.3.1 Symmetry by Construction of a Third-Order Tensor with Respect to Its Last Two Indices
By construction, \(E_{ijk}\) is symmetric with respect its last two indices:
Consequently:
In case of isotropy, third-order tensors are scalar multiples of the permutation tensor
Since \(\epsilon _{ijk}=-\,\epsilon _{ikj}\), Eq. (B.14) induces that: \(E=0\). Thus, any third-order tensor which is symmetric with respect to its last two indices is equal to zero in case of isotropy.
1.3.2 Antisymmetry with Respect to the First Two Indices
Let take \(\alpha =\eta _{lm}\) in the variational formulation associated with functions \(\chi _j\) Eq. (A.2). We obtain
Let now take \(\alpha =\chi _j\) in the variational formulation associated with \(\eta _{lm}\) Eq. (B.9). We get
From Eqs. (B.16) and (B.17), we deduce
Thus, from the definition of \(E_{jlm} \) Eq. (5.44), we have
and
Therefore
Since the medium is macroscopically homogeneous, \(E_{ijk}\) does not depend on the macroscopic variable \(\overrightarrow{x}\). Consequently, the antisymmetry with respect to the two first indices implies that
From Eq. (B.19), we further note that tensor \(E_{jlm}\) can be determined from vector \(\overrightarrow{\chi }\).
1.4 Properties of Tensor \(D'_{ij}\)
Let take \(c^2= \pi _k\) and \(\alpha =\chi _l\) in the variational formulation of the second-order local problem Eq. (B.8). We obtain
Now, by taking \(c^1=\chi _l\) and \(\alpha =\pi _k\) in the variational formulation of the first-order problem Eq. (A.1), we get
From Eqs. (B.23) and (B.24), we deduce
Now, by considering the definition of \(\bar{{\bar{D}}}'\), Eq. (5.45), with the above expression, it comes
from which we deduce
Therefore, \(\bar{{\bar{D}}}'\) is not symmetric:
From Eq. (B.26), tensor \(\bar{{\bar{D}}}'\) can be decomposed as
where
is symmetric and
is antisymmetric.
Furthermore, from Eq. (B.26), it can be seen that tensor \(D'_{lk}\) can be determined from vectors \(\overrightarrow{\chi }\) and \(\overrightarrow{v}^0\).
Third-Order Homogenisation
1.1 Boundary Value Problem for \(c^3\)
From Eqs. (5.36)–(5.38), we get the following boundary value problem for \(c^3\):
Using Eqs. (5.8), (B.3) and (4.2) at the third order
we deduce that
Then, substituting Eqs. (C.4)–(C.8) into Eq. (C.1) while using Eqs. (5.20) and (5.40) yields
We may now determine an expression for \({\partial c^1}/{\partial t}\). From the definition of \(c^1\) (Eq. (5.12)), we have
Now, using the expression of \({\partial c^0}/{\partial t}\) (Eq. (B.6)) and deducing \({\partial {\bar{c}}^1}/{\partial t}\) from Eq. (5.46), the above equation finally becomes
Then, from the expression obtained for \(c^2\), Eq. (5.33), we get
Finally, substituting Eqs. (C.11) and (C.12) into Eq. (C.9), we get Eq. (5.56), and the boundary condition Eq. (C.2) over \(\varGamma \) becomes Eq. (5.57).
1.2 Variational Formulation of the Local Boundary Value Problem
The variational formulation of the local problem defined by Eqs. (5.56) and (5.57) is obtained by multiplying both equations by a test function \(\alpha \) of zero average and by integrating over \(\varOmega _p\):
1.3 Definition of the Third-Order Tensor \(\xi _{lmp}\)
\(\xi _{lmp}\) is the solution for \(c^3\) when
while the other forcing terms are set to zero. Thus, \(\xi _{lmp}\) must satisfy
From Eq. (C.13), we deduce the corresponding variational formulation:
1.4 Definition of the Second-Order Tensor \({\tau _{lm}} \)
\(\tau _{lm}\) is the solution for \(c^3\) when
Thus, it is the solution to
and the associated variational formulation reads
1.5 Definition of Vector \(\theta _k \)
\(\theta _k \) is the solution for \(c^3\) when
Therefore, it must satisfy
The corresponding variational formulation is
1.6 Properties of the Second-Order Tensor \(D''_{jk}\)
By taking \(\alpha =\theta _k\) in the variational formulation associated with \(\overrightarrow{\chi }\) (Eq. (A.2)), we get:
Next, we consider \(\alpha =\chi _j\) in the variational formulation associated with \(\overrightarrow{\theta }\) (Eq. (C.19)):
Then, from Eqs. (C.20)–(C.21), we deduce that:
From the above relationship and from the expression of \(D''_{jk}\), Eq. (5.71), we get:
from which we see that \(D''_{jk}\) can be determined from \(\overrightarrow{\chi }\), \(\overrightarrow{\pi }\), \(\overrightarrow{v}^0\) and \(\overrightarrow{v}^1\).
1.7 Properties of the Third-Order Tensor \(E'_{jlm}\)
Let us consider \(\alpha =\tau _{lm} \) in the variational formulation associated with \(\overrightarrow{\chi }\) (Eq. (A.2)):
We may now take \(\alpha =\chi _j\) in the variational formulation associated with \({{\bar{\bar{\tau }}}} \) (Eq. (C.17)):
From the above two equations, we get:
From the definition of \(E'_{jlm}\), Eq. (5.70), and the above relationship, we finally obtain:
Therefore, tensor \(E'_{jlm}\) can be determined from \(\overrightarrow{\chi }\), \(\overrightarrow{\pi }\), \({\bar{\bar{\eta }}}\), \(\overrightarrow{v}^0\) and \(\overrightarrow{v}^1\).
1.8 Properties of the Fourth-Order Tensor \(F_{jlmp}\)
Let firstly take \(\alpha =\xi _{lmp} \) in the variational formulation associated with \(\overrightarrow{\chi }\) (Eq. (A.2)):
Next, by considering \(\alpha =\chi _j\) in the variational formulation associated with \({\bar{\bar{\bar{\xi }}}} \) (Eq. (C.15)), we get:
From the above two relationships, and from the definition of \( F_{jlmp} \) (Eq. (5.69)), we deduce that:
which shows that \(F_{jlmp}\) is determined from \(\overrightarrow{\chi }\) and \({\bar{\bar{\eta }}}\).
Macroscopic Fluxes
1.1 Derivation of \(\langle q_i^1 \rangle _{\varSigma _{p_i}} \)
To determine \(\langle q_i^1 \rangle _{\varSigma _{p_i}} \), we see from Eq. (6.32), that the term \(\langle y_i{\partial q_j^1}/{\partial y_j}\rangle \) must be determined. This can be done by starting from Eq. (6.33). By Eq. (6.5), we firstly deduce that
and then from Eq. (5.22), we get
Reporting expressions Eqs. (D.1) and (D.2) into Eq. (6.33), we get:
from which we deduce
Now, reporting the above expression together with Eq. (6.14) into Eq. (6.32), we obtain the following expression for the surface average of \(q_i^1\):
To be physically meaningful, the macroscopic fluid velocity must also be defined by a surface average. In order to determine \(\langle v_i^1\rangle _{\varSigma _{\mathrm {p}_i}}\), let consider the identity
Integrating over \(\varOmega _\mathrm {p}\), we get
Now, since by Eq. (4.2) at \({\mathscr {O}}(\varepsilon ^0)\)
we deduce that
Substituting Eq. (D.9) into Eq. (D.5) and bearing in mind Eq. (6.23), we finally get Eq. (6.35) with Eqs. (6.36)–(6.37).
1.2 Derivation of \(\langle q_i^2 \rangle _{\varSigma _{p_i}} \)
Let consider Eq. (6.17) with \(q_i=q_i^2\) and integrate over \(\varOmega _\mathrm {p}\):
From Eq. (6.10), we get
Using the definition of \( \overrightarrow{q}^1\) (Eq. (6.6)), we deduce:
and by Eq. (5.46), we get
Using Eqs. (D.11)–(D.13), we deduce
Using Eq. (6.17) successively for \(q_i= v_i^1 \) and \(q_i=v_i^2\), and integrating both resulting equations over \(\varOmega _p\), we can easily show that
By Eqs. (D.10) and (D.14), and using both above equations, together with the expression of \(\langle q_i^2 \rangle \), Eq. (6.16) yields
in which
From Eqs. (5.68) and (D.10), we get the following writing for the second corrector of the macroscopic mass-balance equation
Then, using the expression of \(\langle y_i \displaystyle \frac{\partial q_j^2}{\partial y_j}\rangle \), Eq. (D.14), it becomes
To obtain the expression of the third-order macroscopic description with respect to the macroscopic flux, let firstly add Eqs. (6.12)–(6.39) multiplied by \(\varepsilon \) and to Eq. (D.22) multiplied by \(\varepsilon ^2\):
and then let add Eqs. (6.12)–(6.35) multiplied by \(\varepsilon \) and Eq. (D.17) multiplied by \(\varepsilon ^2\)
where
Rights and permissions
About this article
Cite this article
Royer, P. Advection–Diffusion in Porous Media with Low Scale Separation: Modelling via Higher-Order Asymptotic Homogenisation. Transp Porous Med 128, 511–551 (2019). https://doi.org/10.1007/s11242-019-01258-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01258-2