Transition flow regime on stepped spillways: air–water flow characteristics and step-cavity fluctuations

Abstract

Stepped spillways are man-made hydraulic structures designed to control the release of flow and to achieve a high energy dissipation. The flow pattern for a given stepped chute geometry can be distinguished into different regimes. Herein, the transition flow regime occurs at a range of intermediate discharges and is characterised by strong hydrodynamic fluctuations and intense splashing next to the free-surface. Up to date, only minimal experimental data is available for the transition flow. As this flow regime is likely to occur on stepped spillways designed for skimming flow operation, a knowledge of the transition flow characteristics is important to ensure safe operation. The present article investigates the hydraulics of the transition flow regime on a laboratory spillway, presenting a detailed characterisation of air–water flow properties and an image-based analysis of pool depth fluctuations within successive step-cavities. The results show two different void fraction and turbulence intensity profiles, indicating the existence of an upper and a lower transition flow sub-regime. The image-based analysis suggests the presence of a rapidly and a gradually varied flow region downstream of the inception point for both sub-regimes, whereas full equilibrium flow was not reached in the physical model. Overall, the study contributes towards improving the characterisation of the transition flow by assembling analytical solutions for different two-phase flow parameters, including void fraction, interfacial velocity and step-cavity pool height.

1 Introduction

The self-aerated flow on stepped chutes or spillways has been intensively researched within the last two decades. The main focus of the research was on the skimming flow, whereas less attention was paid to intermediate flow conditions between nappe flows at low discharges and skimming flow at large flow rates. This intermediate regime is classified as transition flow. Characteristics of the transition flow regime include substantial air entrainment, presence of air cavities within pools of recirculating waters, significant spray and water deflection immediately downstream of the stagnation point, strong hydrodynamic fluctuations and an overall chaotic appearance [5].

The transition flow regime was first denoted as the onset of skimming flow and characterised by different criterions. Chanson [4] described the dissapearence of the air-cavity beneath the free-falling nappes and the water flowing as a quasi-homogeneous stream, whereas Chamani and Rajaratnam [3] assumed that the skimming flow begins when the falling nappe has a slope equal to that of the stepped spillway. Ohtsu and Yasuda [19] defined the concept of the transition flow regime, but no further work on the flow properties was undertaken. Nowadays, the common definition of the flow regimes implies that nappe flow represents a succession of distinct free-falling nappes, whereas skimming flow is characterised by a coherent flow over the pseudo-bottom and a full submergence of the step cavities [6]. The transition flow ranges between those regimes without having the quasi-smooth appearance of skimming flows, nor the distinct succession of free-falling jets [11].

Chanson and Toombes [11] conducted a comprehensive investigation of the transition flow regime on stepped chutes with slopes of $\theta = 3.4^\circ$, 15.9$^\circ$ and 21.8$^\circ$ (Table 1). Their measurements highlighted two sub-regimes of the transition flow. The first sub-regime TRA1 occurred at lower flow rates and was characterised by a irregular succession of small and large air cavities at each step, associated with almost linear air concentration distributions. The sub-regime TRA2 was observed in the upper range of the transition flow rates. The longitudinal pattern of the second sub-regime was characterised by an irregular alternance of air pockets and filled step-cavities and the air concentration profiles had a shape similar to skimming flow observations. The air concentration distributions at the step edges were fitted by analytical solutions of the air bubble advective diffusion equation for both sub-regimes.

Concerning the practical design of a stepped spillway, three failure cases within transition flow conditions have been reported in literature [5]: Lahontan Dam (USA, 1930–1940), New Croton Dam (USA, 1955) and Gyrandra Weir (Australia, 1989). As the flow conditions in the transition flow regime are unstable and rapidly changing, it is emphasised that these conditions should be avoided or that additional hydraulic and structural tests should be considered [5]. However, if a stepped spillway is designed for a skimming flow regime, transition flow conditions will occur for discharges lower than the design flow.

In summary, the transition flow is characterised by substantial air entrainment and strong hydrodynamic fluctuations. In order to ensure a safe operation of stepped spillways, a scientifically sound knowledge of the transition flow characteristics is required, especially as significant loads might be imposed to the structure. Up to date, only few experimental data is available within this flow regime. To close the existing gap in research and to improve the design of hydraulic spillways, the current study presents systematic investigations of the transition flow regime on a large stepped chute with a slope of $\theta = 45^\circ$. Table 1 shows the experimental conditions of the present study together with a summary of earlier laboratory investigations (including the year of publication). Herein, $\theta$ is the chute slope, W is the channel width, q is the specific water discharge, $d_c/h$ is the dimensionless discharge with $d_c$ the critical water depth and h the step height, Re is the Reynolds number and $\phi$ is the diameter of the probe tips.

Table 1 Laboratory studies of the transition flow regime on stepped spillways

2 Physical modelling and experimental setup

2.1 Dimensional analysis

In hydraulic engineering, physical models are commonly used at the planning stage of hydraulic structures to predict their behaviour at different operating conditions and to optimise their geometry, e.g. in terms of energy dissipation or aeration efficiency. For the extrapolation of laboratory data to prototype application, scale dependent effects have to be taken into account by ensuring similarity between model and nature, implying geometrical, kinematic and dynamic similarity.

Air–water flows on stepped spillways are characterised by air entrainment and strong turbulence. The description of the motion of these high-velocity flows relies on physical constants, fluid properties, geometrical constraints, inflow conditions and air–water flow properties. A simplistic dimensional analysis of the air–water flow down a stepped spillway in a rectangular prismatic channel yields the following relationship between air–water flow properties and a number of relevant dimensionless numbers:

$$\begin{aligned} C, \frac{V_x}{V_c}, \frac{u'}{V_c}, \frac{F \times d_c}{V_c}, \frac{d_p}{h},\ldots = f \left( \frac{x}{d_c}, \frac{y}{d_c},\frac{z}{d_c}, \frac{d_c}{h},Re,Mo,\theta ,\frac{W}{d_c},\frac{k'_s}{d_c} \right) \end{aligned}$$

(1)

where C is the void fraction, $V_x$ is the streamwise water velocity, $u'$ is the turbulent streamwise velocity fluctuation, $d_c$ is the critical flow depth: $d_c = (q^2/g)^{1/3}$ with q the specific water discharge and g the gravitational acceleration, $V_c$ is the critical flow velocity: $V_c = \sqrt{g \times d_c}$ , F is the bubble count rate, $d_p$ is the step-cavity pool height, h is the step-cavity height, x, y, z are the longitudinal, normal and transversal coordinates, $d_c/h$ is the dimensionless discharge proportional to a Froude number defined in terms of the step height since: $d_c/h = ((q^2/(gh^3))^{1/3}$, Re is the Reynolds number defined in terms of the hydraulic diameter: $Re = (\rho _wV_xD_h)/\mu _w$ with $\rho _w$ the water density, $D_h$ the hydraulic diameter and $\mu _w$ the dynamic viscosity of water, Mo is the Morton number: $Mo = g\mu _w^4/(\rho _w\sigma _w^3)$ with $\sigma _w$ the surface tension between air and water, $\theta$ is the spillway slope, W is the width of the channel and $k'_s$ is the step surface roughness height.

In Eq. 1, the two-phase flow properties at a given location (x, y, z) are expressed as functions of geometrical constraints of the spillway and of dimensionless numbers, namely the Froude, Reynolds and Morton number. Note that the Morton number represents a relation between the Reynolds, Froude and Weber number. Physical models of air–water flows are usually operated with the same fluids (air, water) as in prototype applications. Therefore, Froude and Reynolds similitude cannot be satisfied simultaneously while the Morton number is an invariant. As viscous forces are inferior compared to gravity and inertia forces, free-surface flows are typically scaled with Froude similitude. Assuming geometrical similarity and a two-dimensional air–water flow down a stepped spillway, Eq. 1 yields for a given physical model:

$$\begin{aligned} C, \frac{V_x}{V_c}, \frac{u'}{V_c}, \frac{F \times d_c}{V_c}, \frac{d_p}{h},\ldots = f \left( \frac{x}{d_c}, \frac{y}{d_c}, \frac{d_c}{h}, Re \right) \end{aligned}$$

(2)

Using a Froude similitude, the Reynolds number in the model becomes much smaller compared to the protoype and possible scale effects are implied in terms of the measured two-phase flow parameters. In order to minimise those effects, the present experiments were undertaken in a large-size facility with Reynolds numbers ranging between $1.3 \times 10^5 \le Re \le 2.7 \times 10^5$. Limitations of the Reynolds number in order to avoid scale effects in air–water flow model investigations are presented in [21]. In this context, scale effects always refer to a set of specific two-phase flow parameters and some parameters (e.g. bubble count rate, interfacial turbulence intensities) tend to be more affected than others (e.g. void fraction, interfacial velocities) [8, 14, 20].

2.2 Stepped spillway facility

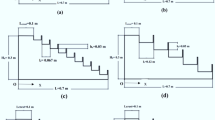
Experimental investigations were conducted on a large-size model of a steep stepped spillway with a slope of $\theta = 45^\circ$. A definition sketch of the spillway is shown in Fig. 1. The physical model consisted of an inlet section followed by a 12.4 m long and 0.985 m wide channel and ended with a free overfall into a recirculation sump. The model had an independent open water circuit and the recirculation was adjusted by three centrifugal pumps, operating at variable rotational speed. The inlet section was made up of a 5 m wide and 2.7 m long basin, contracting with a ratio of 5.08:1 towards the channel (Fig. 2a). The length of the sidewall convergent was 2.8 m. The inlet basin was equipped with a variety of longitudinal flow straighteners in order to provide smooth inflow conditions for the test section.

Fig. 1

Definition sketch of the broad crested weir and the stepped spillway; note the numbering of step-edges and step-cavities

Fig. 2

Physical model of the stepped spillway; $d_c/h = 0.8$; $Re = 2.7 \times 10^5$; $\theta = 45^\circ$. a (Left) top view; inlet basin, side-wall convergent and stepped chute. b (Right) lateral view; flow direction from right to left

Spillway discharge was controlled by a broad crested weir, located at the head of the channel. The crest was made of PVC and had dimensions of $L_{\mathrm {crest}} = 0.60$ m, $W_{\mathrm {crest}} = 0.985$ m and $H_{\mathrm {crest}} = 1.20$ m. To reduce flow separation, the upstream and downstream edges of the broad crested weir were rounded with radii of 0.058 and 0.012 m, respectively.

The spillway consisted of 12 steps with a step length of $l = 0.1$ m and a step height of $h = 0.1$ m. The width of the steps corresponded to the channel width of $W = 0.985$ m and the steps were made of plywood. The step-edges were increasingly numbered, where step-edge 0 corresponded to the rounded downstream edge of the broad crested weir, see Fig. 1. A trolley system was mounted perpendicular to the pseudo-bottom of the spillway allowing for the implementation of measurement devices such as phase-detection probes. The trolley could be moved in longitudinal direction alongside the pseudo-bottom and also enabled vertical and transversal positioning of the probes. Figure 2b shows a lateral view of the physical model. Note that the step-edges are marked in Fig. 2b for clarity.

2.3 Instrumentation

The clear-water flow depth upstream of the weir was measured with a pointer-gauge on the channel centreline at a longitudinal location of $x_1/L_{\mathrm {crest}} = -\,0.92$. The location of the pointer-gauge fulfilled the requirement of $l_1/d_1 =$ 3–4 [1]. Herein, $d_1$ is the flow depth related to the weir crest height and $l_1$ is the horizontal distance between crest and measurement location (Fig. 1). The accuracy of the pointer-gauge was within ±1 mm in the non-aerated flow region.

Air–water flow properties were measured with a double-tip phase-detection probe at the centreline of the channel. Each tip had an inner diameter of 0.25 mm, an outer diameter of 0.8 mm and the longitudinal separation of the probe tips was $\Delta x = 4.7$ mm. The conductivity probe was mounted on the trolley and excited by an electronic air bubble detector having a response frequency greater than 100 kHz. Key parameters for the signal acquisition of phase-detection probe measurements in self aerated free-surface flows included the sampling rate and the sampling duration. Felder and Chanson [13] carried out a sensitivity analysis and recommend a sampling rate of 20 kHz and a sampling duration of 45 s. In the current study, the signals of the conductivity probe were scanned at 20 kHz for a duration of 90 s and therefore met the recommended criteria.

Two-phase flow properties within successive step-cavities were recorded with a high-speed Casio EX-10 camera. The distance between camera and side-wall amounted 0.3 m and the lens of the camera was aligned with the centre of the step-cavity. The camera was focussed on the flow in direct proximity to the inner side-wall of the spillway model and images ($512 \times 384$ pixels) were recorded for a duration of 45 s at a frame rate of 240 Hz. The flow was illuminated with two LED light sources placed next to the channel.

2.4 Signal processing

2.4.1 Phase-detection probe signals

The physical measuring principle of the phase-detection probe relies on different electrical resistivities of air and water. A single threshold technique is commonly applied to the raw signals of the probe in order to identify the instantaneous void fraction. In this study, the threshold was selected to be 50% of the span between the identified peaks of the signals probability mass function. Time-averaged void fraction and bubble count rate were calculated based on the thresholded instantaneous void fraction data. Further analysis of the probe output provided important information such as interfacial velocities and interfacial turbulence intensities [10, 16]. The raw signals of the probe tips were divided into 30 sub-segments and cross- and auto-correlation analyses were performed on these sub-segments. An extensive description of the instrumentation and the signal processing can be found in Toombes [25], Chanson and Carosi [7] and Felder and Chanson [13].

2.4.2 Image-based water-level detection

The fluctuations of the water-level near the riser of the step-cavities were examined based on an analysis of the recorded video sequences. In the recent past, non-intrusive free-surface detection methods involving edge detection filters were used to characterise the surface roughness in the aerated region of the skimming flow regime [2]. The current investigation examined the air–water surface within the step-cavity and implied the particle mask correlation method to extract the water-level elevation. The methodology consisted of the following steps:

• 1. Image pre-processing

Image pre-processing was conducted in order to improve the results of the water-level detection algorithm. The first pre-processing tasks included image rotation and (if necessary) distortion correction. Subsequently, a background image was calculated from the whole image sequence (10.800 frames per sequence) and subtracted from the processed image. The subtraction of the mean image was followed by a contrast enhancement. Fig. 3 shows these pre-processing steps for a representative image recorded at step-cavity 5 with a dimensionless flow rate of $d_c/h = 0.5$.

Fig. 3

Image pre-processing steps; flow direction from left to right; step-cavity 5; $Re = 1.3 \times 10^5$; $d_c/h = 0.5$. a (Left) original image. b (Middle) background substraction. c (Right) contrast enhancement

• 2. ROI selection, particle and cavity pool depth detection

After pre-processing the video sequence, a region of interest (ROI) was defined within the image plane. The ROI consisted of a narrow streak with a typical width of 10 pixels, located close to the riser of the steps and stretching over the total step height on the image plane (Fig. 4a). In order to identify air bubbles within the water column, the particle mask correlation method [24] was applied to the selected ROI. Herein, a brightness pattern of a particle image is referred to a particle mask and was scanned over the entire ROI. The particle mask was approximated as a centred peak with concentrically decreasing brightness, following a two-dimensional Gaussian distribution:

$$\begin{aligned} I(x,y) = M \times \exp \left[ -\frac{(x-x_C)^2+(y-y_C)^2}{2\sigma ^2}\right] \end{aligned}$$

(3)

where I(x, y) is the brightness value, M is the peak brightness, $x_C$ and $y_C$ are the coordinates of the particle mask image centre and $\sigma$ is the standard deviation, referring to the radius of the particle image.

Fig. 4

Image-based water-level detection; flow direction from left to right; step-cavity 7; $Re = 2.2 \times 10^5$; $d_c/h = 0.7$. a (Left) ROI and detected particles. b (Right) ROI and resulting water-level elevation

Figure 4a shows a representative result of the particle mask correlation algorithm. Herein, the white markers are detected image features representing small bubbles, droplets and foam in the vicinity of the water-surface. The vast majority of the particles was located above a visual detected water-level. Consequently, the water-level elevation could be determined based on the distribution function of the particles. It was found that the elevation of the water-level corresponded to a quantile of the particle distribution, where a probability of 0.2 was the most suitable value for all processed image sequences. This assumption was justified based on a visual control of the detected water-level elevations, compare Fig. 4b.

Possible drawbacks of the proposed method may include circumstances where a small amount of air bubbles is advected from the stagnation point towards the riser of the step. If the air bubbles are located below the water-level and within the ROI, the algorithm may detect these particles (depending on their brightness intensity) and underestimate the water-level elevation. Note that the clear water depth would only differ slightly from the air–water-surface elevation, whereas the algorithm detects an elevation with higher deviations. However, only a small number of frames was affected by this phenomenon and the effects were considered to be negligible.

• 3. Scaling

The detected water-level elevations on the image plane were scaled from pixel units to the length units of the physical model by means of a previously determined conversion factor.

2.5 Investigated flow conditions

The experiments were conducted for discharges of $0.5 \le d_c/h \le 0.8$ within the transition flow regime. Table 2 summarises the experimental flow conditions of the conducted experiments, including a classification of the transition flow sub-regimes as defined in Chanson and Toombes [11]. Herein, $L_i$ indicates the longitudinal position of the inception point of air entrainment.

Table 2 Experimental conditions for the conducted measurements

3 Results (1): Flow patterns

The transition flow observations were largely in accordance with earlier studies [11], even so the slope was steeper herein. Downstream of the spillway crest, the first steps showed an undulating pattern with a wave length of approximately twice the step-cavity length $L_\mathrm {cav}$. The first and the second step-cavity were not aerated for all investigated flow rates and the surface above these steps appeared glossy.

Fig. 5

Experimental observations of lower and upper limits of transition flows. Data from [3, 11, 12, 15, 17,18,19, 22, 26]

The third and the fourth step-cavity next to the inception point instead showed a different appearance with regard to the particular flow rate. For the lower flow rates of $d_c/h = 0.5$ and 0.6, the third step-cavity was almost completely filled with air and the fourth step-cavity was partially air-filled. At higher flow rates of $d_c/h = 0.7$ and 0.8, the third and the fourth step-cavity were filled with an air–water mixture and showed a stable recirculation between the edges of adjacent steps. This pattern seemed to have similarities with the recirculating cavity flow sub-regime (SK3) of the skimming flow, described by Chanson [5]. Downstream of the third step-cavity, the falling nappes were almost parallel to the pseudo-bottom of the chute (Fig. 4) and air pockets beneath the nappes were observed for all discharges. These air cavities/pockets were fluctuating and their size increased with decreasing $d_c/h$. In contrast to observations reported in [11], the shape of the air pockets did not exhibit an alternating pattern within the current study. As the ratio of step length to step height equaled unity, the nappes rather skipped from edge to edge instead of impacting onto the steps and a stagnation point was not visible for the majority of the cavities. Intense splashing and spray ejection occurred for all investigated flow rates within the rapidly and gradually varied flow regions of the transition flow.

Chanson and Toombes [11] proposed two empirical relationships which define the lower and the upper limit of the transition flow regime:

$$\begin{aligned} d_c/h > 0.9714 - 0.381 \times (h/l) \end{aligned}$$

(4)

$$\begin{aligned} d_c/h \,<\, 0.9821/(h/l+0.388)^{0.384} \end{aligned}$$

(5)

Note that Eq. 4 defines the lower limit for $0\,<\,h/l\,<\,1.7$ and Eq. 5 the upper limit for $0\,<\,h/l\,<\,1.5$, respectively. Figure 5 includes both equations together with collected data from literature and the results of the present study. It is concluded that the presented empirical equations are in agreement with the experimental data and provide a reasonable prediction of the flow regime, although derived for different slopes.

The existence of two sub-regimes within the transition flow was first proposed in [11] and was based on a different flow appearance as well as on different shapes of the measured void fraction profiles. The current investigations confirmed this sub-classification as both types of void fraction profiles were likewise observed. However, the flow appearance differed from the one reported in [11], possibly because of differences in chute slope.

Within the lower sub-regime TRA1, the longitudinal flow pattern consisted of fluctuating air pockets which had similar geometrical dimensions in the gradually varied flow region. In the upper sub-regime TRA2, the air-pockets were much smaller and sometimes disappeared during the measurement. The filling of the cavities was accompanied by a step-cavity recirculation. However, this recirculation was much less stable compared to skimming flow conditions.

4 Results (2): Air–water flow properties

4.1 Void fraction

The void fraction, presented as the time-averaged air concentration at each particular measurement location, is a fundamental parameter within the description of aerated flows. Figure 6 shows the longitudinal distribution of the time and cross-sectional averaged void fraction along the chute. Herein, two different flow regions, denoted as rapidly varied flow (RVF) and gradually varied flow (GVF), were seen. The RVF region was located close to the inception point and was characterised by a sudden change of air–water flow parameters, whereas these changes were less pronounced within the GVF region. The measured mean air concentrations of the GVF region were in a range of $C_\mathrm {mean} = 0.45$–0.69 and a general trend of increasing mean air concentration with decreasing discharge was observed. The mean void fraction of the discharges $d_c/h =$ 0.5 and 0.6 did not show a sudden increase. This behaviour was related to the aeration of the cavities of the third and fourth step and has already been pointed out in Sect. 3.

Fig. 6

Longitudinal distributions of the mean void fraction; inception point for all measurements at $L_ {i}/L_\mathrm {cav} = 2.0$; $\theta = 45^\circ$

The void fraction profiles for all discharges at successive step-edges are examined in Fig. 7. Herein, the dimensionless distance $y/Y_{90}$ from the pseudo-bottom is plotted on the ordinate against the void fraction on the abscissa, with $Y_{90}$ being the characteristic depth where the void fraction equals $C = 0.9$. The shape of the void fraction profiles showed a clear distinction between the different sub-regimes TRA1 and TRA2 of the transition flow. For the dimensionless discharges $d_c/h = 0.5$ and 0.6, the void fraction profiles were straight and flat, whereas the profiles for the discharges $d_c/h = 0.7$ (majority) and $d_c/h = 0.8$ had an S-shape curvature being similar to void fraction profiles within the skimming flow regime. A sudden change of the void fraction was observed for all sub-regimes close to the pseudo-bottom, indicating the existence of air-pockets within the step-cavities. The void fraction profiles could be described based on analytical solutions of the advection-diffusion equation for air in water, where different shapes are modelled by the assumption of a non-constant air-bubble diffusivity. Within the transition flow sub-regimes TRA1 and TRA2, the void fraction profiles at the step-edges may be fitted by the following solutions [10, 11]:

$$\begin{aligned} C = K' \times \exp \left( 1 - \exp \left( - \lambda ' \times \frac{y}{Y_{90}} \right) \right) \end{aligned}$$

(6)

$$\begin{aligned} C = 1 - \tanh ^2 \left( K'' - \frac{y/Y_{90}}{2 \times \lambda ''} + \frac{(y/Y_{90}-1/3)^3}{3 \times \lambda ''} \right) \end{aligned}$$

(7)

where C is the modelled void fraction of the sub-regimes TRA1 (Eq. 6) and TRA2 (Eq. 7), $K'$ and $K''$ are integration constants and the parameters $\lambda '$ and $\lambda ''$ describe the dependency between the dimensionless bubble diffusivity and the void fraction.

Fig. 7

Void fraction distributions of the transition flow sub-regimes TRA1 and TRA2; $d_c/h = 0.5$, 0.6, 0.7 and 0.8; $\theta = 45^\circ$

It is worthwhile to mention that both models are only valid for void fraction distributions at step-edges. The theoretical solutions for both sub-regimes are plotted in Fig. 7, where the underlying mean void fractions are equally indicated. These mean void fractions represent a streamwise averaged mean air concentration along the step-edges 5–11 and therefore were representative for the GVF region. Overall, the theoretical solutions were in good agreement with the experimental data. Note that Eq. 7 has also been successfully applied to skimming flow conditions and a comprehensive overview of air diffusion models within the skimming flow regime is presented in [28].

4.2 Bubble count rate

The bubble count rate F is defined as the frequency of air bubbles detected by the probe sensor. Figure 8 shows representative dimensionless bubble count rates for both transition flow regimes TRA1 and TRA2. Only little difference was observed between the different sub-regimes. The number of bubbles was small in proximity to the pseudo bottom of the spillway and increased with increasing $y/Y_{90}$ or higher void fractions, respectively. The recorded data followed typical bell shaped distributions with maxima around $y/Y_{90} = 0.3$–0.5, corresponding to void fractions between $C = 0.35$–0.5.

Fig. 8

Dimensionless bubble count rate distributions for the transition flow sub-regimes TRA1 and TRA2; $d_c/h = 0.5$ and 0.8; $\theta = 45^\circ$

Within the upper flow region, the bubble count rates decreased as the probe tips were only hit by few ejected droplets. The presented data were consistent with previous studies, where a strong correlation between the bubble frequency and the air concentration was documented (e.g. [9, 10, 28]). The longitudinal distribution of the measured bubble frequencies shows that the number of detected bubbles increased with further distance from the inception point of air entrainment. This indicated the presence of a gradually varied flow region within the lower section of the spillway model, whereas full equilibrium flow was not reached.

4.3 Velocity distribution

Interfacial velocities were calculated based on the cross-correlation analysis between the raw voltage signals of the two phase-detection probe tips, separated by the longitudinal distance $\Delta x = 4.71$ mm. Figure 9 shows dimensionless velocities for both transition flow sub-regimes TRA1 and TRA2. Herein, the elevations perpendicular to the pseudo-bottom and the interfacial velocities are normalised by the characteristic depth $Y_{90}$ and the characteristic velocity $V_{90}$.

Power law functions are often applied to characterise the velocity distribution within the skimming flow regime of stepped spillways. In skimming flow, different values of the reciprocal power law exponent have been observed, depending e.g. on chute slope, roughness height and dimensionless discharge. For example, Chanson and Toombes [10] found a value of N = 6 for slopes of $\theta = 15.9^\circ$ and 21.8$^\circ$, whereas Takahashi and Ohtsu [23] identified N-values ranging between $3 \le N \le 14$ for chute slopes of $\theta = 19^\circ$, 30$^\circ$ and 55$^\circ$. It is also known that the reciprocal power law exponent may vary between different step-edges. This behaviour is believed to be caused by interference between adjacent shear layers and cavity flows.

Within the transition flow regime, only little work has been undertaken so far. Chanson and Toombes [11] presented empirical correlations for the velocity distribution in both sub-regimes of the transition flow. These empirical correlations are shown in Fig. 9 as dotted lines. Note that the chute slope in the latter study was between $\theta = 3.4^\circ$ and 21.8$^\circ$. The data of the current study differed from these previous observations. Instead, the present data indicated an application of the power law concept for both transition flow sub-regimes. The data for $0 \le y/Y_{90} < 1$ were best described with:

$$\begin{aligned} \frac{V_x}{V_{90}} = \left( \frac{y}{Y_{90}} \right) ^{1/N} \end{aligned}$$

(8)

where $V_x$ is the streamwise interfacial velocity, y is the distance perpendicular to the mean flow direction, $Y_{90}$ is the distance where $C = 0.9$ and N is the reciprocal value of the power law exponent.

Fig. 9

Dimensionless interfacial velocity distribution for the transition flow sub-regimes TRA1 and TRA2 at step-edges 4–11; $\theta = 45^\circ$

The reciprocal of the power law exponent was $N = 14.2$ for the transition flow sub-regime TRA1 and $N = 12.8$ for the transition flow sub-regime TRA2. At dimensionless depths of $y/Y_{90} >1$, the dimensionless velocities satisfied an uniform profile of $V_x/V_{90}=1$ for both sub-regimes. Compared to N-values of the skimming flow regime [10, 23], the observed N-values (transition flow) were in the upper range and were increasing with decreasing dimensionless discharge $d_c/h$.

4.4 Interfacial turbulence intensity

The interfacial turbulence intensity was calculated based on descriptive parameters of the cross- and auto-correlation functions of the raw conductivity probe signals. Figure 10 shows the turbulence intensity distribution for both transition flow sub-regimes TRA1 and TRA2.

Within the sub-regime TRA1, the interfacial turbulence intensity had a maximum near the pseudo-bottom of the spillway and was decreasing monotonically with increasing distance from the step invert. The high turbulence intensities close to the pseudo-bottom might be caused by a developing shear region in the wake of the steps. Perpendicular to the pseudo-bottom, the turbulence decreased at higher elevations as a results of decreasing shear.

In contrast, the interfacial turbulence intensities within the sub-regime TRA2 had local peaks at elevations of $y/Y_{90} = 0.5$–0.8 and near the pseudo-bottom. The shape of the interfacial turbulence distribution of the sub-regime TRA2 was similar to those observed within the skimming flow regime, e.g. [13]. A physical reasoning for the second peak might be a continuous breakdown of entrained air [27].

Fig. 10

Distributions of interfacial turbulence intensities for transition flow sub-regimes TRA1 and TRA2 at step-edges 4–11; $\theta = 45^\circ$

5 Results (3): Step-cavity measurements

5.1 Pool height and pool length

Macroscopic parameters describing the transition flow within step-cavities are the pool height $d_p$, the pool length $L_p$ and the impact angle $\alpha$. The pool length is defined as the length of the air–water-surface between the pool of circulating water and the air-cavity beneath the nappe. Figure 11a shows a time-averaged image of the video sequence recorded at $d_c/h = 0.5$, including the definition of macroscopic parameters. The pool height $d_p$ was calculated as the mean of the time-resolved signals, e.g. presented in Fig. 11b. The signals were obtained using the image based water-level detection algorithm described in Sect. 2.4.2. Overall there was a good agreement between the extracted mean value and a visible pool height within Fig. 11a.

Fig. 11

Macroscopic flow parameters of step-cavities within the transition flow; $d_c/h = 0.5$. a (Left) time-averaged image of the cavity 5; flow direction from left to right. b (Right) time-resolved cavity pool depth (extracted from image sequence)

Figure 12a shows dimensionless pool heights and cavity pool depth fluctuations for the discharges $d_c/h = 0.5$, 0.6 and 0.7, plotted against the step-cavity number. Due to a very small size and a temporary disappearance of air-pockets, no image-based analysis was conducted for $d_c/h = 0.8$.

Fig. 12

Characteristics of the step-cavity within the transition flow regime; $\theta = 45^\circ$. a (Left) dimensionless pool heights and cavity pool depth fluctuations. b (Right) dimensionless pool lengths

For $d_c/h = 0.7$, the cavity of the fourth step was completely filled with an air–water mixture. Downstream of step-cavity 5, the water-level elevations within the step-cavities only showed slight changes for all discharges, indicating the presence of a GVF region. The pool heights increased with increasing flow-rates and the dimensionless standard deviations were almost constant for all measurements. The pool lengths are examined in Fig. 12b and the data showed an opposed pattern compared to the pool heights. This is physically correct as greater pool heights imply a smaller air-cavity length.

5.2 Characteristic frequencies

Characteristic frequencies of the oscillating cavity pool depth were investigated along the stepped chute. The power spectral density (PSD) function was evaluated based upon a fast Fourier transform (FFT) and dominant frequencies showed distinct peaks within the frequency domain of the signals. Figure 13a shows a typical PSD function of the original signal and a smoothed function, highlighting a dominant frequency of around 2.7 Hz.

Fig. 13

Characteristic frequencies of water-level fluctuations within step-cavities of the transition flow regime; $\theta = 45^\circ$. a (Left) power spectral density function of water level-elevations within the step-cavity. b (Right) characteristic frequencies in longitudinal direction of the chute

The longitudinal distributions of the dominant cavity pool depth fluctuation frequencies for the discharges $d_c/h = 0.5$, 0.6 and 0.7 are shown in Fig. 13b. The data indicated an increase next to the inception point, whereas the frequency remained almost constant within the GVF region of the stepped spillway. Some secondary frequencies were also noted and believed to be the effect of an intermittent impact of the lower nappes on the step treads. Overall, the present data yielded dimensionless cavity frequencies ranging from $(f_\mathrm {cav} \times h)/V_c = 0.26$–0.38.

6 Discussion: Pool height in the step-cavity

Within the transition flow regime on steep sloped chutes, a major portion of the air–water mixture appeared to flow almost parallel to the pseudo bottom formed by the step edges. The upper streamlines rather overflowed the step cavities, whereas the lower streamlines impacted on the tread close to the brink of the steps (Fig. 11a). Due to this impact, a backward facing hydraulic jump occurred, forming a liquid pool within the step-cavity.

An estimate of the pool height was obtained by resolving the momentum equation for the water phase in horizontal direction of the step-cavity (Fig. 14a):

$$\begin{aligned} V_x^2d \cos \alpha + g \frac{d_p^2}{2} = V_x^2d \cos \beta \end{aligned}$$

(9)

where $d_p$ is the pool height, d the clear-water depth of the free-stream, $V_x$ the mean velocity, $\alpha$ the impact angle, g the gravitation acceleration and $\beta$ the downstream flow angle.

The presented equation is based on the assumptions that the flow entering and leaving the control volume has approximately the same depth and velocity and that shear forces on the surfaces are insignificant. Furthermore, the pressure forces of the entering and the leaving flow are considered identical and a hydrostatic pressure distribution is assumed at the step-riser. A simplification of Eq. 9 leads to an expression of the pool height:

$$\begin{aligned} d_p = \sqrt{-\frac{4}{g} V_x^2 d \sin \left( \frac{\beta + \alpha }{2}\right) \sin \left( \frac{\beta - \alpha }{2} \right) } \end{aligned}$$

(10)

where $d_p$ is the pool height, d the clear-water depth, $V_x$ the mean velocity, $\alpha$ the impact angle, g the gravitation acceleration and $\beta$ the downstream flow angle.

Fig. 14

Pool heights within the transition flow regime; $\theta = 45^\circ$. a (Left) control volume for the momentum equation. b (Right) comparison of measured pool heights with Eq. 10; $\alpha = 48^\circ$–51$^\circ$ (extracted from images) and $\beta = 45^\circ$

Impact angles were extracted based on time-averaged images of the step-cavity flow, compare Fig. 11a. The impact angles were similar for all investigated discharges and lied within a range of $\alpha = 48^\circ$–51$^\circ$. The downstream flow angle of the fluid leaving the step-cavity was set in a first approximation to $\beta = 45^\circ$. Figure 14b shows a comparison of the measured pool heights and the results of Eq. 10, demonstrating a reasonable agreement between measured and calculated values. It is acknowledged that the angles of the lower nappe leaving the step might be smaller than the chosen value of $\beta = 45^\circ$. However, the upper nappes did not impact onto the treads and therefore, the deflection of 3$^\circ \le (\alpha - \beta ) \le$ 6$^\circ$ might be interpreted as an average deflection of the entire nappe.

7 Conclusion

The transition flow regime is a flow pattern occurring on stepped chutes at intermediate discharges and is characterised by strong free-surface aeration, some chaotic motion and intense droplet ejection. This study presents detailed laboratory investigations on a steep sloped spillway ($\theta = 45^\circ$) to enhance the understanding of the physical characteristics of the transition flow.

Two-phase flow properties were measured with an intrusive phase-detection probe and suggested the presence of two transition flow sub-regimes. The lower and the upper sub-regime TRA1 and TRA2 were clearly identified by different void fraction and interfacial turbulence intensity distributions. The air concentration distributions were in accordance with earlier solutions of the advection-diffusion equation for air in water and the interfacial velocities of both sub-regimes were best fitted with power law functions.

Time-resolved elevations of the pool depth within the step-cavities were measured based on a novel image-based analysis approach using the particle mask correlation method. Distinct peaks within the frequency domain of the signals revealed characteristic pool depth fluctuation frequencies and showed the existence of a rapidly varied flow region close to the inception point and a gradually varied flow region further downstream. The pool heights within the step-cavities were successfully compared to a proposed solution of the momentum equation resolved along the step-cavity. Overall, the study presents new insights into the hydraulics of the transition flow regime on stepped chutes and aims to provide useful tools for an improved spillway design.