1 Introduction

Algorithmic thinking refers to the thinking or reasoning involved in designing, testing, improving, or making sense of an algorithm independent of a programming language that might be used to execute it (Futschek, 2006; Stephens & Kadijevich, 2020). Developing algorithmic thinking is emerging as an objective of mathematics education because it equips students with skills necessary to thrive in a world defined by complex systems and widespread use of digital technologies (Blannin & Symons, 2019; Stephens, 2018; Wing, 2006). Incorporating algorithmic thinking into mathematics curricula coincides with the broader recognition that computational thinking, which encompasses algorithmic thinking among other key practices including coding, is an essential competence for all students to develop across the school curriculum (Wing, 2006, 2008).

Many countries, such as England, France, and Japan, have already begun incorporating algorithmic thinking into school curricula (Stephens, 2018). In Australia, the national curriculum authority answered calls to incorporate algorithmic thinking by including graph theory topics in the recently revised national mathematics curriculum (Australian Curriculum, Assessment and Reporting Authority [ACARA], 2022). For instance, year 10 students investigate “how networks and network diagrams can be used to model authentic situations” and “design, test and refine solutions to spatial problems using algorithms” (ACARA, 2022). Graph theory is a domain of mathematics that has long been used as a modelling tool in mathematics and computer science (Medová et al., 2019), and problems in this domain provide many opportunities for students to develop algorithmic thinking (Rosenstein, 2018). However, the incorporation of algorithmic thinking in this way is occurring at a time when research into the teaching and learning of algorithmic thinking is not keeping pace with curriculum reform.

Mathematics education researchers have suggested using mathematical modelling as a vehicle for eliciting algorithmic thinking, particularly in relation to graph theory (Hart & Martin, 2018; Medová et al., 2019), which is plausible given that researchers from across disciplines describe algorithm design as a cyclical, modelling-like process (Futschek & Moschitz, 2010; Hart, 1998; Standl, 2017). However, there appears to be little empirical evidence that supports these strong recommendations. The aim of the present study was to address this gap by investigating how mathematical modelling elicits the algorithmic thinking of students as they design an algorithm to solve a minimum spanning tree problem. To achieve this aim, I conducted a series of task-based interviews with eight year 12 students in which they leveraged their competence in the mathematical modelling cycle to formulate a model of the problem using abstraction and decomposition, design an algorithm to solve the problem during the working mathematically transition, and debug their algorithms during their validating transition. The findings extend the field by providing insights into how teachers and researchers might recognize the algorithmic thinking of their students and design tasks that intentionally elicit algorithmic thinking through mathematical modelling.

2 Review of related literature

2.1 Algorithmic thinking

Researchers across the disciplines of education frame algorithmic thinking in terms of a subset of cognitive skills from computational thinking (Blannin & Symons, 2019; Ritter & Standl, 2023; Stephens, 2018; Stephens & Kadijevich, 2020). These cognitive skills include decomposition, abstraction, algorithm design, pattern recognition, debugging, and generalization. Table 1 contains elaborations for each of these cognitive skills, which are used throughout this study.

Table 1 Definition of cognitive skills of algorithmic thinking
Full size table

Although there has been considerable effort to identify the cognitive skills involved in algorithmic and computational thinking (Shute et al., 2017), there appears to be very little research across the domains of educational research into how these cognitive skills are learned by students, particularly in relation to graph theory. However, recent research into novice mathematics students’ attempts at algorithmatising tasksFootnote 1 offers some preliminary insights into tasks that might elicit aspects of algorithmic thinking. Moala (2021) examined approaches to algorithm design used by two small groups of novice year 12 (group A) and first-year undergraduate (group B) mathematics students in response to a maximum Hamiltonian path algorithmatising task. The analysis showed that students developed a set of rules based on features of their solution, a mechanism that Moala (2021) called “accounting for features of the solution” (p. 264). However, only group B wrote a sufficient set of features that would produce the optimal arrangement, which Moala (2021) attributed to two strategies used by this group: “1) finding a sub-optimal arrangement and then improving it; and 2) trying to improve the optimal arrangement, but not being able to do so” (p. 282). In a similar study, Moala et al. (2019) examined the debugging practices used by a group of three pre-degree students in response to another Hamiltonian path-type optimization task involving three unweighted vertex-edge graphs. They found that the students solved the first problem using an exhaustive search and then based their initial algorithm on the attributes of that solution. However, the students’ initial algorithm did not produce an optimal solution for the second two graphs and the students responded by retaining elements of their algorithm that they deemed apt (local considerations) and removed or added instructions (patching) when the algorithm was inapt, although the students were ultimately unsuccessful at designing an algorithm that would guarantee an optimal solution. These two case studies illustrate how algorithmatising tasks can be used to elicit and analyse algorithm design and debugging approaches by novice students. However, it is unclear if these or similar approaches are used by students who have comparatively more experience with graph theory or for problems beyond the Hamiltonian-type problems used in these studies, for which exhaustive searches are typically necessary.

A study by Greefrath et al. (2022) illustrates how an Eulerian-path modelling activity can elicit the algorithmic thinking skill of abstraction in the context of graph theory. Two groups of four grade 9 students, without experience in graph theory, were invited to find an optimum route for a city street cleaning service. The analysis showed how the students collected relevant information about a local road network from a street map and built a representation of that road network using vertex-edge graph concepts, including weighted edges and considerations for graph traversal, which reflect the two key aspects of abstraction in algorithmic thinking. Although the study did not address how the students found a Eulerian path—because it was not their intent—the study is instructive in that it illustrates how a modelling activity can elicit an abstract representation of a problem for which an algorithmic solution could be designed. In the present study, my aim was to build on this modelling approach by combining it with the algorithmatising approach described above (Moala, 2021; Moala et al., 2019) to elicit a broader set of algorithmic thinking skills.

2.2 Mathematical modelling

The purpose of mathematical modelling is to use mathematics to understand a real-world phenomenon and explain, make predictions about, or organize some aspect of that phenomenon (Niss, 2015). A mathematical modelling process refers to the phases used to develop a mathematical model, which include identifying a messy or ill-defined real-world problem, formulating an appropriate mathematical representation, finding a mathematical solution, interpreting the solution in the context of the original problem, and validating and evaluating the solution (Stillman et al., 2007). This process is cyclical because it is often necessary to refine a model after evaluating the intermediate solution or results.

There are numerous interpretations of the mathematical modelling process, which are typically represented by a cyclical diagram such as the one in Fig. 1 used in this study (Stillman et al., 2007). Such diagrams, however, are idealized descriptions of the phases of the modelling process used to analyse the actual process followed by an individual modeller in response to a modelling problem (Niss & Blum, 2020). Figure 1 shows the phases of the process, which are labelled A–G, and the transitions between these phases, which are shown as bolded arrows labelled 1–7 and described briefly in the accompanying key. The double-headed arrows depict possible backwards and forwards iterations of the phases resulting from a modeller’s evaluative activity between phases (Geiger et al., 2022). The phases of the process and iterations might be accomplished in any order, but all permutations are omitted for simplicity.

Fig. 1
figure 1

Modelling process of Stillman et al. (2007)

Full size image

Irrespective of the process used, teachers can use mathematical modelling as a vehicle to support students’ learning of mathematical ideas, ways of reasoning (Julie & Mudaly, 2007; Reinke, 2019), or, in the present case, algorithmic thinking. A goal of mathematical modelling can also be for students to develop algorithms, which can be interpreted as formal models emerging from the modelling process that apply beyond the original problem situation (Reinke, 2019). For example, researchers suggest that modelling tasks can be used to elicit students’ invention of algorithms for solving minimum spanning tree problems (Hart, 1998; Medová et al., 2019). However, there is little analysis of students’ responses to such tasks, which would otherwise provide insights into how students use their mathematical modelling competencies to design algorithms and illustrate how teachers might recognize students’ algorithmic thinking as they engage in the modelling process. The research question that guided this study was:

How does mathematical modelling elicit students’ algorithmic thinking?

3 Conceptual framework

The conceptual framework that I devised to investigate how mathematical modelling elicits students’ algorithmic thinking contains two parts that reflect these two cognitive activities. First, I used the framework formulated by Stillman et al. (2007) outlined above (see Fig. 1) to interpret students’ modelling processes from a cognitive modelling perspective (Kaiser, 2017; Stillman, 2011). The cognitive modelling perspective foregrounds students’ modelling process and thinking to reconstruct individual modelling pathways. Second, I interpreted algorithmic thinking as a competency model, which is a set of knowledge, skills, and other attributes that comprise a construct, such as algorithmic thinking (Messick, 1994; Shute et al., 2017). Table 1 contains the set of cognitive skills that comprise this competency model of algorithmic thinking. The elaborations in this table describe the behaviours and performance that are indicative of these cognitive skills, which cannot be directly observed. These indicators are drawn from the existing literature and may be subject to revision given the generative nature of this study.

3.1 Minimum spanning trees

Minimum spanning trees are a class of problems for which novice students are likely to design algorithms independently as they attempt to model and solve the problem, indicating an alignment between the modelling process and algorithmic concepts (Hart, 1998; Medová et al., 2019). In this section, I present a brief conceptual discussion of how the modelling process may elicit algorithmic thinking skills in relation to the minimum spanning tree problems used for this study (see Appendices 1 and 2).

The cyclical mathematical modelling process is reminiscent of several attempts by researchers across education disciplines to describe the algorithmic thinking process. In Table 2, I used the transitions from the mathematical modelling process to compare proposed processes of algorithmic thinking from the mathematics (Mingus & Grassl, 1998), computer science (Futschek & Moschitz, 2010), and computational thinking (Standl, 2017) education literature. This latter process suggests links between the cyclical process of algorithmic thinking and the cognitive skills of algorithmic thinking, which I show in the right-hand column.

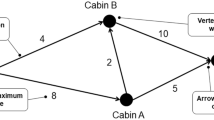
Table 2 Perspectives on algorithmic thinking process
Full size table

Each of the algorithmic thinking processes begins with an understanding and formulating phase, which elicits decomposition and abstraction, and results in an abstract representation of the real-world problem. The vertex-graph in Appendix 2 is an abstract representation of the network of electrical cables for the school fete, which shows how the stalls can be linked directly as well as how much cable is needed using the given map of the school. It is not possible to run a cable between each stall because of various obstacles in the layout of the school. The labelled vertices represent the stalls, and two vertices are connected by an edge if the stalls can be connected directly. The weight of each edge represents the length of cable in metres that connects the two stalls. The goal of the problem is to find the minimum length of cable needed to connect each of the stalls.

The next phase in the process is to design an algorithm that will solve the problem, which aligns with the working mathematically transition. The models developed during this phase are an algorithm for finding a minimum spanning tree and the minimum spanning tree itself. A minimum spanning tree is a subgraph that includes all the vertices and has a minimum total weight, which is calculated by summing the weight of each edge. The minimum spanning tree for the graph in Appendix 2 is shown in step (iii) of Fig. 2, which has a weight of 98 m. The tree has no circuits (a set of edges that joins a vertex to itself such as E—F—G—E) because each vertex only needs one connection. There are several algorithms for finding a minimum spanning tree, including Kruskal’s (1956) and Prim’s (1957) algorithms, which work by adding the next available edge with minimum weight. Figure 2 is an illustration of Kruskal’s algorithm and algorithmic concepts are shown in bold. The processes of Mingus and Grassl (1998) and Futschek and Moschitz (2010) indicate that the algorithm design phase requires ongoing monitoring of outputs to ensure the algorithm is working. This aligns with the interpreting mathematical output transition in mathematical modelling and may trigger iterations of the modelling phases.

Fig. 2
figure 2

Illustrated steps of Kruskal’s algorithm

Full size image

The algorithmic thinking processes end with a validating phase, which elicits debugging skills. This phase involves validating an algorithm, possibly with the use of another example or counterexample (Moala et al., 2019).

4 Methodology

Clinical methods are appropriate for a generative study such as this because my purpose was to “generate new observation categories and new elements of a theoretical model in the form of descriptions of mental structures or processes that can explain the data” (Clements, 2000, p. 557). Task-based interviews (Goldin, 2000; Maher & Sigley, 2020) are one clinical method that mathematics education researchers use to explore students’ mathematical thinking as they attempt mathematical tasks. Hence, I conducted a set of two, 50–80-min one-on-one task-based interviews with eight year 12 student (16 interviews in total; mean time total = 118 min) to make systematic observations of students’ verbal and nonverbal behaviours as they used the modelling process to design an algorithm to solve the minimum spanning tree problem.

4.1 Participants and curriculum context

The eight year 12 students (mean age = 17.5 years) were enrolled at a large, high-socioeconomic secondary school in Queensland, Australia. They were in their second quarter of year 12 at the time of the study. I recruited these students because they were studying General Mathematics (QCAA, 2019), which is a 2-year course designed for students who do not require knowledge of calculus for their future work or study. Two features of this syllabus provided a suitable context for investigating students’ use of mathematical modelling to design algorithms. First, the syllabus embeds the development of mathematical modelling competence throughout the course and recommends that teachers use modelling as a vehicle for learning mathematics. The first column of Table 3 contains a summary of the students’ previous modelling experience, as well as a summary of the criteria used to assess students’ modelling competence through a high-stakes modelling task worth 20% of their final grade. All eight students had achieved a grade of either 19 or 20 on this summative assessment task and hence had well-developed modelling competence according to the criteria in Table 3.

Table 3 Relevant syllabus descriptors (QCAA, 2019)
Full size table

The second feature of the syllabus that made the context and students suitable for this study is the graph theory and algorithm content contained in Table 3, which the students had learned in the four weeks immediately preceding this study. I expected that the students’ experience in using vertex-edge graphs to model real-world networks and familiarity with basic algorithmic concepts, such as inputs, fundamental operations, loops, branching, and outputs, would support their algorithmic thinking in response to the minimum spanning tree problem.

4.2 Task-based interviews

I conducted the one-on-one task-based interviews with each student individually using Zoom because the study coincided with locally mandated COVID-19 restrictions that prohibited students from attending interviews in person. The students participated in the Zoom interviews from their homes, and I accessed Zoom from my home office. During the interviews, I observed the students via the speaker view while they used the Share Screen function to show their working. The students used Word to document their modelling process, and the whiteboard functions in Zoom to show their working out.

Table 4 contains the interview protocol that I used to conduct the interviews, which is organized according to the phases of the modelling process. In general, the students were asked to think aloud during the interviews and as will be shown below, were accustomed to this because they had completed several task-based interviews before.

Table 4 Interview protocol
Full size table

I captured screenshots of the students’ work using the Save Whiteboard function in Zoom. The interviews were recorded using the application’s recording function. The data collected for the study included the following: audio and video recordings of the sessions generated by Zoom; the screenshots of all written responses produced by the students; transcriptions of the audio recordings; and students’ Word documents.

4.3 Data analysis

I used content analysis (Patton, 2002) to interpret the students’ responses. I developed a dual coding system to interpret the students’ responses in terms of their mathematical modelling process and algorithmic thinking. I coordinated the dual analysis of the audio/video recordings using MaxQDA, a screenshot of which is shown in Fig. 3.

Fig. 3
figure 3

Screenshot of MaxQDA analysis of Oakley’s validating/debugging

Full size image

The data were first analysed to reconstruct each students’ mathematical modelling process. I used the descriptors of the transition between the phases in the modelling process of Stillman et al. (2007) as codes to interpret each students’ modelling activity. For brevity, these codes were truncated to the following: understanding; formulating; working mathematically; interpreting; validating; revisiting; and communicating. These seven codes were used to code the video footage as well as the transcriptions. For example, I coded the scene shown in Fig. 3 as “validating” because Oakley was checking her algorithm by applying it to the revised graph. The corresponding excerpt from the transcription, shown in Table 5, was also coded as validating. An experienced mathematics educator coded the responses independently and we resolved any conflicting interpretations through discussion.

Table 5 Transcription analysis of Oakley’s validating/debugging
Full size table

After each student’s modelling processes were coded, I turned to their algorithmic thinking. The same video and transcription data were analysed to determine when and how the students used the cognitive skills of algorithmic thinking, which involved both deductive and inductive analyses (Saldaña, 2021). First, I coded each student’s modelling activity according to the six cognitive skills: decomposition; abstraction; algorithm design; pattern recognition; debugging; and generalization. For example, the same scene shown in Fig. 3 was coded as “debugging” because Oakley was testing her algorithm.

The inductive analysis involved creating codes that characterized how the students used the cognitive skill in response to the task. I came to interpret these codes as subskills because they explained the way the students used the broader cognitive skill, and I use this term in the presentation of the findings. To generate these subskills, I first wrote my interpretation of the students’ actions or utterances as a memo, as shown in the final column of Table 5. For example, my memo for line 31:36 of Table 5 was “detects error” because this was the exact moment that Oakley realized that her draft algorithm could yield a circuit. I grouped qualitatively similar types of memos together and assigned them a code. My code for all instances in which a student identified an error while they were executing their draft algorithm was, for example, “detect error”. The same experienced mathematics educator reviewed my interpretations of the students’ algorithmic thinking and we again resolved disagreements through discussion. During these discussions, we found instances when students’ responses could not be characterized by the indicators of algorithmic thinking in Table 1. For example, the students made various assumptions about how the cable would be laid while determining the essential components of the system but making assumptions was not a subskill under the initial abstraction skill in the conceptual framework. To handle these instances, we created new subskills, and these subskills represent developments in the conceptual framework for algorithmic thinking.

After the data were coded, I generated a Modelling Transition Diagram (Czocher, 2016) for each student. Figure 4 shows Oakley’s Modelling Transition Diagram, which also shows how I added the algorithmic thinking skills to the diagram. The purpose of this was to analyse how the mathematical modelling process elicited the students’ algorithmic thinking.

Fig. 4
figure 4

Oakley’s modelling transition diagram

Full size image

5 Findings

Each of the eight students followed a different modelling pathway to formulate a reasonable model of the network and designed an algorithm that found a minimum spanning tree, although they used algorithmic thinking in slightly different ways. Table 6 contains a summary of the algorithmic (sub)skills elicited throughout the modelling process, which are based on the Modelling Transition Diagrams. In the remainder of this section, I present the findings according to each of the cognitive skills and use the final algorithms designed by Wyatt and Paxton, reproduced in Fig. 5, as examples throughout.

Table 6 Alignment of transitions between modelling phases and algorithmic thinking skills
Full size table
Fig. 5
figure 5

a Wyatt’s and b Paxton’s final algorithms

Full size image

5.1 Decomposition

The modelling task elicited students’ use of decomposition in two ways. First, instructing the students to use mathematical modelling appeared to elicit their use of decomposition (DEC1) because they first broke down the task into the phases of the modelling process during the understanding transition. Figure 6 is a screenshot of Remington’s Word document taken at minute 10:24 of her first interview and shows how she broke the task down into three phases, Formulate, Solve; and Evaluate and Verify. Second, five of the students used decomposition to break down the method for finding a minimum spanning tree into subgoals (DEC2) during the working mathematically transition. For example, Wyatt’s algorithm in Fig. 5 shows how she broke down the algorithm into three separate subgoals: (1) listing the weights; (2) finding the minimum spanning tree; (3) adding the weights of the spanning tree edges. Four other students also used decomposition in this way to structure their final algorithms.

Fig. 6
figure 6

Screenshot of Remington’s Word document (“Formulate”, “Solve”, and “Evaluate and Verify” are the abbreviations that the students routinely used to describe the modelling process.)

Full size image

5.2 Abstraction

The modelling process elicited students’ use of abstraction as they translated the real-world problem into a mathematical model. The students used implicit criteria to determine the relevant information about the fete (AB1), consistent with the existing first subskill of abstraction in the algorithmic thinking framework (Table 1), and illustrated by Remington’s document in Fig. 6 where she listed relevant information under the heading, “Observations”. Remington’s document also illustrates two additional subskills for abstraction that emerged from the students’ use of their mathematical modelling competencies. The students identified the length between stalls as the relevant variable that they would quantify (AB2), although this variable was clearly implied by the task statement. The students also made various assumptions about information not contained in the task (AB3), such as how the cable would be laid and the location of the stalls.

All students chose a vertex-edge graph to represent the distances between each stall (AB4), although five students initially attempted to use a matrix. As these students began searching for the minimum spanning tree during the working mathematically transition, they found it difficult to identify a cycle. In response to this “red flag” (Goos, 2002, p. 286), the students engaged their revisiting competence by cycling back to the formulate transition and revising their model by using a graph.

Having selected an appropriate representation, the students determined how to represent the essential information about the network using the graph (AB5). For example, Spencer explained how she intended to represent the essential components as follows:

1

09:06

Spencer:

Well, obviously…you’d show the names of all of the stalls and distances to each location [moves mouse to show distance]

2

09:14

Researcher:

Okay

3

09:16

Spencer:

I don’t know. If we would have direct numbers…but if we’re using it on a graph, you can actually see length, distance to each location from each other location

4

09:29

Researcher:

Okay

5

09:34

Spencer:

So, measure them. Like with a ruler. We could use the map scale, but it won’t matter because they are in the same proportions

In lines 1 and 3, Spencer described how she intended to use the names of the stalls as the vertices and the distances between the stalls as the edges. She then explained in line 5 how she intended to quantify the distances by measuring the lengths on the map with a ruler. Spencer did not use the map scale, although the other seven students converted their measurements using the scale.

Figure 7 a is a screenshot from Wyatt’s interview that shows how she used the online drawing tool to indicate the locations of the stalls and how she envisaged the cable would be laid along the ground from the source to stall B. She measured the length of these lines to reach a total of approximately 8 cm, which she converted to 80 m and represented as a straight line in her final vertex-edge graph (Fig. 7b).

Fig. 7
figure 7

Wyatt’s a use of drawing tools, b vertex-edge graph, and c solution

Full size image

5.3 Generalization

The modelling task elicited generalization in two ways. First, the students applied the mathematical modelling process (GEN1), which, for these students, reflected a generalization of the process to accomplish a goal (design an algorithm) different from previous modelling tasks (see Table 3). GEN1 was most evident during the understanding transition when the students planned their process, as illustrated by Remington’s headings and subheadings in Fig. 6. These headings reflect Remington’s adaptation of the modelling process to the algorithm design task in which she initially planned to write the algorithm during the “solve” transition. However, all students’ actual modelling pathways were iterative (see for example Fig. 4) as they adapted their validating/evaluating competence to algorithm design.

Second, the students applied their emerging skills at constructing vertex-edge graphs (GEN2) during the formulation and revisiting transitions, as illustrated by Wyatt’s graphs in Fig. 7. Specifically, Wyatt applied the conventions for representing vertices and edges, and assigning weights to the edges. The students had previous experience interpreting graphs and modelling shortest path problems (see Table 3), which suggests that previous experience and some level of competence is a prerequisite for generalising algorithmic thinking skills across problem types.

5.4 Algorithm design

The students expressed their final algorithms as a sequence of ordered steps (AD6) during the communicating transition. There were two types of algorithm designs that emerged from this study, although both types are greedy algorithms because they involve making locally optimal choices at each iteration of selecting the next shortest edge (Maurer & Ralston, 1991; Medová et al., 2019). The first type focuses on the edges in the graph, as exemplified by Wyatt’s final algorithm in Fig. 5, whereas the second type focuses on the vertices, as exemplified by Paxton’s final algorithm in Fig. 5. Irrespective of the type, the modelling task elicited students’ use of algorithmic concepts and I will address each of these in turn.

Both algorithm designs used the weighted vertex-edge graph as input (AD1). However, five students used a separate list or matrix of weights that made their use of the weights as inputs explicit. For example, the first step in Wyatt’s algorithm is to, “List out all weights in ascending order”. The use of the weights as inputs in this way are shown in Wyatt’s written response in Fig. 7c and Oakley’s response in Fig. 3. In addition to the weights, the students implicitly used the edges and vertices as inputs. For instance, Wyatt used the phrase, “Select the edge” and Paxton used the phrase “Choose the edge” in their second steps, which instructs the user to use the edges as inputs. Similarly, the students used the vertices as inputs that govern the branching statements and loops.

The second subskill used by the students to design their algorithm was to devise a fundamental operation (AD2), which refers to the specific action that a user must execute to transform an input into an output. For example, Wyatt’s fundamental operation is “Select the edge with the lowest available weight” and “highlight it on the graph and cross it off the list”. The students devised their fundamental operation as they were working mathematically. For example, Wyatt explained her fundamental operation as follows:

1

40:05

Wyatt:

Well, it’s reasonably consistent, because most of the options are just longer. So, it is obvious, you always choose the shortest possible option

2

40:16

Researcher:

Talk me through how you worked that out

3

40:21

Wyatt:

So, G to H is obvious because it’s the shortest possible option out of everything. So just sort of starting there. Then when you get to the point where D needs to connect to something its 15. Basically, it’s just the same step over and over

4

40:55

Researcher:

Tell me what you mean by same step?

5

41:00

Wyatt:

Go through the list and it will tell you the shortest one where there are ulterior [sic] options

In line 1, Wyatt noticed that there is always a shortest option, and the fundamental operation is to choose that option. In line 3, she explained that the algorithm starts with the lowest weight and then continues with the next lowest weight, as indicated in the list of all available weights (line 5).

In contrast to Wyatt’s algorithm, Paxton relied on graph traversal and focused on vertices rather than a list of weights:

1

56:17

Paxton:

You’ve got to visit each stall. Wait, did I visit each one? [pause to check] Yeah, I did

2

56:45

Researcher:

Tell me how you solved it

3

56:50

Paxton:

The rule is you’ve got to choose the shortest edge going onto the next vertex

4

56:54

Researcher:

What do you mean by the rule?

5

56:58

Paxton:

I started at M, and it has to have at least one connection. So, I chose the shortest one. Then you go around to each vertex and always choose the shortest one to get there

In line 1, Paxton explained that each vertex must be visited and in line 3, stated her fundamental operation of choosing the shortest edge leading to the next vertex. In line 5, Paxon explained the application of the fundamental operation by starting at one vertex (M) and then traversing the graph to the next vertex by choosing the edge with the lowest weight.

Subskill AD3 refers to recognising that the fundamental operation can be repeated to work towards the solution. Examples of loops can be found in step 3 of both Wyatt’s and Paxton’s algorithms (Fig. 5), each of which contain an instruction to repeat the fundamental operation and the condition that the loop be terminated when all vertices are connected/visited. As for the fundamental operation, the need for a loop arose while the students were working mathematically.

Branching statements were used by all students to create an exception to the application of the fundamental operation (AD4). The purpose of these branching statements was to ensure that the fundamental operation did not result in a circuit. Wyatt’s branching statement in step 2 (Fig. 5a) specifically includes a reference to a circuit as the condition that stops the user from applying the fundamental operation. In contrast, Paxton’s branching statement in step 2 (Fig. 5b) contains two conditions, the first of which is to not apply the fundamental operation if the vertex is already connected. These branching statements emerged for five students while they were solving the original problem and during the validating transition for the other three students.

The modelling task elicited students’ interpreting and validating competencies, which gave rise to subskill AD5, determine and verify outputs. The students’ models contained two outputs: the minimum length of cable and a plan for how the cable would be laid so that each stall would have electricity, as shown in Wyatt’s solution (Fig. 7c). The students made each of these outputs explicit in their final algorithms. First, step 4 in both Wyatt’s and Paxton’s algorithms contain an instruction to add the weights of all minimum spanning tree edges to find the minimum length. Second, step 2 in both algorithms contains an instruction to highlight the selected edges, which cumulatively results in the formation of the minimum spanning tree.

Additionally, the students verified their outputs in two ways. First, the students evaluated the reasonableness of the output by relating their minimum spanning tree back to the real-world, as illustrated by the following excerpt from Wyatt’s interview:

1

68:50

Wyatt:

It means you have to go all the way to the pool lawn [A—G] then dangle the chord back to the fifth floor. You should probably just go to toasties [F] direct [from A]

2

69:33

Researcher:

Okay

3

69: 40

Wyatt:

It’s like for cupcakes [H] to brownies [I]. It’s got that big tree in the way. So probably shouldn’t have that [edge] in there because I was never going to go that way

Wyatt noticed that the minimum spanning tree included edges A—G—F but in line 1 decided that this was unreasonable because of how the cable would need to “dangle” over several floors of an adjacent building. Similarly, in line 3, Wyatt explained that she did not select the H—I edge because of an obstructing tree (shown in the map of the school), which otherwise is an equivalent solution, and suggested that this edge should not be in the network. Several students made similar adjustments to their graph because of their evaluation. The second way that three students verified their solution was by finding an online minimum spanning tree calculator, which was an established technique that students had learned to verify their models.

5.5 Pattern recognition

The two pattern recognition subskills (PR1 and PR2) emerged during the working mathematically transition and appeared to complement the algorithm design subskills, AD2 and AD3, respectively. PR1 provided the reasoning for AD2 in that the students devised a fundamental operation when they recognized that the minimum spanning tree is found by always choosing the shortest option. Similarly, PR2 provided the reasoning for AD3 when students devised a loop. For example, Wyatt recognized that the fundamental operation can be repeated “over and over” in line 3 of her excerpt above, and Paxton recognized the need to repeat her fundamental operation when she stated that, “you go around to each vertex”.

5.6 Debugging

The validating transition elicited two debugging subskills consistent with the detecting and fixing errors elaboration in the algorithmic thinking framework. There were three types of errors that the students detected (BUG1) and fixed (BUG2) as they tested their draft algorithm on the revised network (Appendix 2): omitting a branching statement, listing steps in an incorrect order, and non-terminating loop.

Oakley’s screenshot in Fig. 3 is an example of omitting a branching statement. Oakley detected an error after executing her fundamental operation of selecting the next lowest weight in the list of weights, as shown in the excerpt in Table 3. In line 8, Oakley highlighted the G—F edge and then realized that this formed a circuit (line 9). In response, she asserted that she needed to include a branching statement that creates an exception for edges that result in a circuit (line 12–14).

The second type of error that students detected was steps in a wrong order. For example, Paxton draft algorithm in Fig. 8 contains a branching statement at step 4, which she discovered instructed the user to reject an edge if it formed a circuit after a circuit had been formed. In response to detecting this error, Paxton re-wrote step 2 of her algorithm to include the branching statement in this step, as shown in her final algorithm (Fig. 5b).

Fig. 8
figure 8

Paxton’s draft algorithm

Full size image

The third type of error that students detected was non-terminating loops. Step 3 in Paxton’s draft algorithm (Fig. 8) contains a non-terminating loop, which she fixed by adding the condition, “until all vertices are visited”.

6 Discussion

The aim of this study was to investigate how mathematical modelling can be a vehicle for eliciting students’ algorithmic thinking. The findings show that each students’ use of the modelling process activated modelling competences that were critical in eliciting their algorithmic thinking. The resultant algorithmic thinking subskills documented in this study extend and contrast with findings from the limited existing research into algorithmic thinking, which suggest that there are advantages in using modelling as a vehicle for eliciting students’ algorithmic thinking.

First, the need to formulate a model elicited abstraction subskills to make the problem tractable. Each student spent considerable time determining the relevant information from the given map and building an abstract representation of the network, consistent with the findings of Greefrath et al. (2022). However, the students in this study also explicitly identified the relevant variable (AB2) and made assumptions (AB3), which were adaptations of modelling competences critical to the students’ success in formulating abstract representation and then evaluating the spanning tree once it was found. Although the importance of using abstraction to make problems tractable in algorithmic thinking is well-documented, the findings of the present study demonstrate the specific role that mathematical modelling can play in eliciting these skills among students.

Second, the design of a fundamental operation that transforms inputs into outputs was central to each student’s final algorithm. Each student devised a way of choosing the next shortest available edge during the working mathematically transition of the modelling process and expressed this fundamental operation in their final algorithm. This finding contrasts with the strategy used by group B in the study by Moala (2021) who wrote a sufficient set of features for their algorithm by first finding a suboptimal spanning tree and then improving it until no further improvements could be made. The greedy approach that emerged for the students in the present study probably reflects their experience with traversing graphs and familiarity with an algorithm for solving shortest path problems.

In addition to devising a fundamental operation, the students in this study used branching, which previous studies have not documented. The students’ use of branching emerged during either the working mathematically and/or interpreting phases as the students evaluated the intermediate outputs returned by their fundamental operations. The modelling process appeared to trigger the students’ validating competence because they monitored the outputs to ensure that they avoided circuits, in the same way that a student might monitor an evolving model to check that the solution satisfies the conditions of the problem (Czocher, 2018). The students also used their validating competence to evaluate the minimum spanning tree by comparing it to the real world and revise their graphs accordingly.

Finally, the modelling process triggered the students’ use of decomposition and generalization in ways not documented previously in the literature. Although I instructed the students to use mathematical modelling to complete the task, the students independently responded by decomposing the task into subgoals and applying their modelling competences throughout the cycle. Similarly, their use of a vertex-edge graph in response to the task was likely due to their recent experiences in learning about networks. Further research into how students use decomposition and generalization without these prompts would extend our understanding of how these cognitive skills develop.

The findings of this study have three practical implications for using mathematical modelling as a vehicle for eliciting algorithmic thinking. First, teachers might first provide students with an opportunity to learn that an algorithm is a sequence of steps composed of fundamental algorithmic concepts such as loops and branching conditions because this appeared to enhance the students’ attempts at designing their own algorithm. Second, the subskills in existing algorithmic thinking frameworks (Table 1) and new subskills documented in this study (Table 6) may help teachers recognize the algorithmic thinking of their students. Finally, teachers might design modelling tasks set in authentic real-world contexts that compel students to formulate a model because this offers students an opportunity to develop a broader set of cognitive skills. Although previous researchers have used preformulated graphs to study students’ algorithm design and debugging approaches in research settings (Medová et al., 2019; Moala, 2021; Moala et al., 2019), such tasks may not develop students’ abstraction competence, which is at the heart of mathematical modelling, and algorithmic and computational thinking (Wing, 2008).

7 Limitations

The findings of this study are limited in four significant ways. First, opportunities to examine students’ cognitive barriers throughout the mathematical modelling process were limited because the design of an algorithm to solve a minimum spanning tree problem is relatively straightforward when compared with the design of algorithms to solve other graph problems (cf Moala, 2021; Moala et al., 2019). Further research might focus on whether the subskills identified in this study apply to the successful design of algorithms for other graph problems, or indeed, in other domains. Second, the reproducibility of the responses to the modelling task used in this study by students in other cohorts will be limited because the context of the school fete was familiar to the students in this study. However, similar minimum spanning problems can be designed by adapting the task to networks familiar to students in other contexts. Third, the generalizability of the study is limited because the students in this study had well-developed mathematical modelling competence, experience in graph theory, and used standard graph algorithms. Although existing studies into graph algorithm design involve novice student participants, further research might involve more experienced participants to enhance research into algorithmic thinking. Finally, the competency model of algorithmic thinking developed for this study is based on the existing literature, which is limited. Hence, my reliance on provisional definitions and indicators of the cognitive skills of algorithmic thinking is a limitation of this study, which further research in this field should address.