Sharing a Fish Stock When Distribution and Harvest Costs are Density Dependent

Abstract

We studied cooperative and competitive solutions for managing a trans-boundary fish stock that has a stock-size dependent distribution and harvesting costs, using Norwegian spring-spawning (NSS) herring (Clupea harengus) as a case study. This is among the first studies to investigate the effect of a dynamic distribution in a partition function game framework, i.e., including externalities. The special feature of NSS herring is that it comes under the sole ownership of Norway when the stock size is sufficiently low. The three players in our game are differentiated by stock ownership, cost per unit effort and stock elasticity of harvest. We find that cost asymmetry improves the likelihood of forming a stable grand coalition as harvesting load can be assigned to each fishing zone according to a player’s relative cost level and the density of fish. A dynamic distribution increases the bargaining power of Norway because of her ability to control both the total stock and the stock shares in different zones, especially during the stock transition years. However, the bargaining power of Norway may disappear if her cost of harvesting exceeds that of the other players. This loss of bargaining power can take on two forms: first, a dynamic distribution may encourage a minor player to free ride because Norway, needing a coalition partner to improve her cost-effectiveness, would be less inclined to retaliate as retaliation hurts her ally as much as the free-rider; second, in a stable grand coalition, Norway is not guaranteed to receive an allocation of benefit shares in proportion to (not to say in excess of) her stock ownership. At the current stock condition, the strategy where Norway reduces stock abundance below the level where the stock becomes non-migratory is found attractive only if the discounting rate is sufficiently high.

1 Introduction

Trans-boundary fishery resources challenge effective fishery management. The challenge becomes even greater if the distributions of the targeted fish stocks vary over time, or more dramatically, migration patterns change. Several commercial fish stocks have shown considerable shifts in their distribution. For example, Pacific salmon in Alaska increased sharply in abundance from the mid 1970s, whereas salmon stocks along the U.S. west coast and in southern British Columbia showed strong declines; the situation represented a complete reversal compared to that in the 1960s and early 1970s (Mantua et al. 1997). Atlantic mackerel is a recent example where the stock that used to visit Icelandic waters only occasionally in recent years has become abundant enough to support a sizeable Icelandic commercial fishery (ICES 2010). Finally, Norwegian spring-spawning (NSS) herring, the focal stock of this study, has undergone profound distributional shifts. During years of high stock abundance, NSS herring stock can occupy five exclusive economic zones (EEZ) as well as international waters, but when the stock collapsed in the 1960s, the stock became confined to the Norwegian EEZ (Dragesund et al. 1997; Holst et al. 2004). The underlying reasons for such distributional changes are multifaceted and can involve exogenous drivers such as climatic changes (Toresen and Østvedt 2000; Perry et al. 2005) and endogenous drivers such as density-dependent habitat selection (Holst et al. 2004; Planque et al. 2011).

Overlooking distributional shifts can lead to distorted fisheries management decisions (Hannesson 2007; Johnson and Welch 2010; Liu and Heino 2013). Most of the trans-boundary fisheries agreements are based on the “zonal attachment” principle, that is, a country’s share of the total quota is proportional to its share of the total stock in its EEZ. The displacement of fish from one zone to another can then threaten the stability of existing agreements; further, it may incite uncoordinated fishing practices that potentially harm the biological stocks and economic outcomes. Pacific salmon moving from Canada to Alaska triggered a breakdown of the cooperative harvest agreement (Miller and Munro 2004), and Scottish fishermen called for a “war” against the new entrant to the mackerel fishery, Iceland.

Game theory has been widely used to tackle questions in international fishery management (see Bailey et al. 2010; Hannesson 2011 for reviews), often using herring fisheries as the case study (Arnason et al. 2000; Lindroos and Kaitala 2000; Bjørndal et al. 2004; Lindroos 2004; Hannesson 2006). All these earlier studies assumed a fixed stock distribution. Studies addressing the implications of stock distributional shift on trans-boundary fisheries management have only started emerging recently. Hannesson (2007) and Liu and Heino (2013) used biomass models to study non-cooperative solutions in the presence of a dynamic stock distribution. Ekerhovd (2010) and Hannesson (2013) used age-structured models and allowed for co-operative solutions, but these studies also had some important shortcomings. Ekerhovd (2010) only compared two static distribution scenarios (with and without a distributional shift) for blue whiting, finding that the scenario with distributional shift showed an increased likelihood of a stable coastal state agreement. The study by Hannesson (2013) allowed for a dynamic distribution and found that density-dependent distribution weakens the bargaining position of the minor player in the Northeast Atlantic mackerel fishery. His model, however, is based on a characteristic function game approach that ignores the free-rider problem (Greenberg 1994), an important feature for shared fisheries. Our study expands on these earlier studies by combining age-structured population modelling, distributional changes, and consideration of externalities through the use of a partition function game. Further, we include many details in our models that are very rarely seen in fisheries games, e.g., harvesting cost is dependent on the stock density experienced by fishers, and we define reference fishing mortality as a decision variable. In the next section, we will elaborate on these concepts.

We chose NSS herring fishery as the case study because distributional changes have been prominent for this stock. The stock came under Norwegian sole ownership when the stock collapsed to low abundance, but expanded to EEZs of other countries when the stock recovered. The expansions and contractions in the range of NSS herring are driven by many factors, but an important driver is believed to be competition for prey during the summer feeding migration. The migration is energetically costly for herring, but when the stock is large, competition for food drives the stock to expand its range further away from its spawning and overwintering areas (Holst et al. 2004; Varpe and Fiksen 2010).

Intriguingly, cooperative management of NSS herring has not always been stable; the Coastal States agreement (i.e., the grand coalition in game parlance) was suspended from 2003 to 2006, primarily because Norwegian fishermen were not satisfied with the share (53 %) they received, given that the stock spends critical stages of its life cycle near the Norwegian coast (Sissener and Bjørndal 2005). A new coastal states’ agreement was reached in 2007–2012, and Norway received 61 % of the herring quota.¹ The agreement broke down again in 2013 (Norwegian Ministry of Fisheries and Coastal Affairs 2013).

This paper aims to study the stability of the self-enforcing grand coalition (full cooperation) for NSS herring, and the optimal benefit sharing rule for the stable grand coalition. We approach our research question through a three-player coalition game where Norway and Russia are envisioned as independent players, and the remaining players (Iceland, the Faroe Islands, and the EU, hereafter referred to as IFE) are grouped as the third player. Given the unique strategic position Norway has in the game, it is important to treat Norway as an independent player (some earlier studies have merged Norway and Russia). Merging IFE countries is not ideal but helps to limit the complexity of the game. The players in our model are asymmetric; in particular, only Norway could monopolize the stock. In the model, optimal harvest policies are derived via the partition function game (P-game) approach, in which environmental externalities such as the free-riding problem are taken into account in the coalition formation. We compare out results across two different benefit sharing rules, namely the “almost ideal sharing scheme” (Eyckmans and Finus 2004) and the “externality-free” Shapley value modified for P-games (see Sect. 3.3).

2 The Model Set-Up

2.1 General Introduction

We apply a three-player coalition game framework built upon an age-structured biological model. We use the biological model developed and parameterized by Patterson (1998) for NSS herring. The model is intended to capture the essence of the dynamics of this stock, as an example of a long-lived fish with stock-size dependent distribution, rather than to provide an accurate description of dynamics of NSS herring. The same model (albeit without including a dynamic distribution) has been used by many earlier studies (Lindroos and Kaitala 2000; Touzeau et al. 2000; Bjørndal et al. 2004; Lindroos 2004). We deviate from these earlier works in one important aspect: we use the new fisheries sub-model (catch equation) introduced by Steinshamn (2011) that accounts for non-linear harvest costs in a mechanistically sound way; we modify his model by defining a more realistic condition for stock exhaustion. Model parameters and variables are summarized in the Appendix.

2.2 Stock Size-Dependent Distribution

The life cycle of NSS herring has the following pattern: in the beginning of a fishing season (year $t$), adult herring spawn along the Norwegian coast, the only spawning area for NSS herring and the main habitat for juvenile herring. After spawning, the feeding seasons starts. Adult herring may feed in Norwegian waters (when stock is small) or migrate further away for foraging (Holst et al. 2004; ICES 2013). Fishing takes place after the stock is redistributed. In our setting, players are only allowed to harvest in their own exclusive economic zones (EEZ)—even under the full cooperation case. Towards the end of the fishing season, NSS herring from different zones merge again in the Norwegian EEZ before a new spawning season ($t+1$) starts. The herring can also be accessible in the international waters but our model ignored this component.

The spatial distribution of herring is modeled following Patterson (1998) where the share of total stock abundance ($\theta$) available to each player is a piece-wise linear function of total spawning stock biomass ($B$):

$$\begin{aligned} \theta _{j,t} = \left\{ \begin{array}{ll} \frac{d_{j,t_1}+d_{j,t_2}+d_{j,t_4}}{3} &{} \quad \text{ if } B_t>B_{high}\\ \phi {\frac{d_{j,t_1}+d_{j,t_2}+d_{j,t_4}}{3}}+(1-\phi )d_{j,t_3} &{}\quad \text{ if } B_{low}\le B_t\le B_{high}\\ d_{j,t_3}&{} \quad \text{ if } B_t<B_{low}, \end{array} \right. \end{aligned}$$

(1)

where $d_{j,t_{n=1:4}}$ denotes empirically observed stock share in a zone $j$ in a reference year, averaged over all age classes, and $\phi =\frac{B_{t}-B_{low}}{B_{high}-B_{low}}$. Equation 1 suggests that stock distribution is fixed if the biomass level is below the low threshold ($B_{low}$) or above the high threshold ($B_{high}$) level. $t_3$ in the equation represents a year when the herring fishery is confined to the Norwegian water (the coastal regime, here 1972), whereas the other years represent years when the stock had a broad, trans-boundary distributions (the oceanic regime). Following Patterson (1998), we set reference years $t_n=(1950, 1959, 1972, 1983)$ for $n=1,\ldots ,4$, see Table 1 for their distributions. The actual distribution of herring naturally is more complex. In our simplified model, we focus on the transition between the two regimes.

Table 1 Observed stock shares in representative years (following Patterson 1998)

2.3 Concave Density Effect

In the classic harvest production function, instantaneous catch rate is assumed to be linear in stock abundance $N$; that is: $\frac{d{\mathbb {C}}}{dt}=qEN$, where ${\mathbb {C}}$, $E$ and $q$ denote catch, effort rate and catchability coefficient, respectively. However, this is often known to be not true (Clark 1990; Hilborn and Walters 1992; Harley et al. 2001), especially for schooling species where the catch rate can stay high even though the total abundance is strongly reduced. Because Norwegian spring-spawning herring is a schooling species, we follow an alternative formulation (Clark 1990; Steinshamn 2011; Liu and Heino 2014) where the catch rate is linear in local stock density $\rho$:

$$\begin{aligned} \frac{d{\mathbb {C}}}{dt}=s E \rho , \quad \text { with } \rho =h \left( \frac{N}{N^*}\right) ^{b} \quad \text{, } b \ge 0\text{. } \end{aligned}$$

(2)

Here $s$ denotes selectivity, $h$ is a scaling parameter, and $sh$ can be seen as catchability defined in terms of density. The formulation above suggests that the density $\rho$ as experienced by fishers depends on stock abundance $N$ and stock elasticity of harvest $b$. In the equation $N$ is normalized with respect to non-fishing stock equilibrium $N^*$ such that $\frac{N}{N^*}\le 1$. In our age-structured model, $s, h, {\mathbb {C}}, N$ and $N^*$ in Eq. 2 are age-specific, and $E$, $\rho$ and $b$ are zone-specific. Fish density in zone $j$ follows $\rho _j=h\left( \frac{N_j}{\theta _j N^*}\right) ^{b_j}$, where $\theta _j$ indicates stock share in zone $j$.

Parameter $b$ typically has a value between 0 (Bjørndal 1988) and 1 (Bjørndal 1987), depending on the behaviour of the targeted fish as well as the ability of fishermen to find the fish. $b=0$ represents an extreme schooling species and where fishermen can find even the last fish school with ease. $b =1$ refers to a non-schooling fish which is uniformly distributed, or that the encounters between fishable schools and fishermen are random.

We chose the $b$ values to reflect the characteristics of herring. Considering the schooling nature of NSS herring and that the aggregation of herring stock is highly predictable in coastal spawning grounds, we assume $b =0$ for the Norwegian zone. In contrast, we chose an intermediate level of aggregation, $b=\frac{1}{2}$, for the other two zones because (1) outside the spawning grounds, aggregation is not as extreme, and (2) the distribution of NSS herring schools is less predictable further away from the Norwegian coast, and fishermen thus have more difficulty locating the schools; more pragmatically, the catch expression for $b=\frac{1}{2}$ is relatively simple (Steinshamn 2011). Although our exact values of $b$ are somewhat arbitrary, these values qualitatively reproduce herring characteristics better than those used in earlier studies that have assumed $b=1$ either explicitly or implicitly, through the use of the standard Beverton-Holt population model (Steinshamn 2011; Liu and Heino 2014; known as the Baranov catch equation in fisheries science), a questionable choice for a schooling stock.

2.4 Stock Dynamics and Harvest Function

Defining catch rate in terms of local density gives rise to a new form of stock dynamics. Steinshamn (2011) derived an age-structured but spatially unstructured model for stock dynamics under such conditions. We extend his model by allowing fishing in more than one zone and by defining a more realistic condition for stock exhaustion. ²

We specify stock dynamics as follows:

$$\begin{aligned} N_{i+1,j,t+1}&= \left\{ \left[ N_{i,j,t}^{1-b_j}+\frac{s_i h_i E_{j,t}}{M_i \theta _{j,t}^{b_j} (N_i^*)^{b_j}}\right] e^{-M_i \left( 1-b_j\right) \tau _{i,j,t}} -\frac{s_i h_i E_{j,t}}{M_i \theta _{j,t}^{b_j} (N_i^*)^{b_j}}\right\} ^{\frac{1}{1-b_j}},\nonumber \\&\quad 0\le b_j<1, \quad i\in [0,1,\ldots ,15], \end{aligned}$$

(3)

where $N_{i,j,t}$ denotes initial stock abundance, $i$ age, $j$ zone and $t$ year; its value depends on total stock abundance and $j$th stock share, i.e., $N_{i,j,t}=N_{i,t} \theta _{j,t}$. Effort $E$ is assumed to be constant within a season $t$ and in a zone $j$. $M$ is age-specific natural mortality. $s$ is a knife-edge selectivity parameter defined such that only fish $i \ge 3$ years of age are fully fishable ($s=1$) and fish $i\le 2$ are fully protected ($s=0$). $\tau _{i,j,t}$ denotes the length of a fishing season, which ends when abundance at age $i$ becomes zero or the maximum season length $(=1)$ is reached:

$$\begin{aligned} \tau _{i,j,t}=\min \left[ 1, \frac{1}{M_i (1-b_j)} \log {\left( 1+\frac{{M_i {\theta _{j,t}^{b_j}} {(N_i^*)^{b_j}} N_{i,j,t}}^{1-b_j}}{s_i h_i E_{j,t}}\right) }\right] \end{aligned}$$

(4)

NSS herring in our model distribute themselves in multiple EEZs but spawning only occurs in one of the zones. In a new season, the total stock abundance is simply a sum of unharvested fish over all zones: $N_{i+1,t+1} = \sum _{j=1}^{j=3} N_{i+1,j,t+1}, i\in [0,1,\ldots ,15]$. The abundance of newly spawned recruits follows the Beverton–Holt stock-recruitment model:

$$\begin{aligned} B_t&= \sum _{i}{O_i W_i^S N_{i,t}}, \nonumber \\ N_{0,t}&= \frac{\beta B_t}{1+\frac{B_t}{\gamma }}, \end{aligned}$$

(5)

where $B_t$ is total spawning stock biomass in year $t$, and $i$ denotes a spawning age class. We assume that NSS herring at age $2$ and younger do not spawn; $O_i$ is maturity ogive (proportion of maturity individuals) at age $i$; here herring are considered fully mature when $i\ge 6$. $W_i^S$ is the (stock) weight at age $i$, and $N_{0,t}$ is the total stock abundance at age $0$. The respective values for parameter $\beta$ and $\gamma$ are taken from Patterson (1998), see the Appendix.

The seasonal harvest is obtained through integrating the instantaneous catch rate in Eq. 2 over the effective fishing season specified in Eq. 4. For some specific values of $b$, explicit harvest functions can be derived (Steinshamn 2011):

$$\begin{aligned} {\mathbb {C}}_{i,j,t} (E_{j,t}) = \left\{ \begin{array}{ll} s_i h_i E_{j,t} \tau _{i,j,t} &{} b=0\\ \frac{2s_i h_i E_{j,t}}{M_i} \sqrt{\frac{{N_{j,t}}}{\theta _{j,t} N_i^*}} \left( 1-e^{-\frac{M_i \tau _{i,j,t}}{2}}\right) +\frac{(s_i h_i E_{j,t})^2}{{M_i}^2\theta _{j,t} N_i^*} \left( 2-2e^{-\frac{M_i \tau _{i,j,t}}{2}}-M_i \tau _{i,j,t}\right) &{} b=\frac{1}{2} \\ \end{array} \right. \end{aligned}$$

(6)

An insight from the harvest equations above is that when $b=0$, marginal productivity of effort ($\frac{d{\mathbb {C}}}{dE}$) is constant, whereas when $b=\frac{1}{2}$, it depends on stock size $N$ in an EEZ (the lower $N$, the lower the catch a player can get from additional unit of effort). We also note that $\frac{d{\mathbb {C}}}{dE}$ is reduced as $b$ increases.

2.5 Decision Rule

We consider a NSS herring management model with two decision levels. First, fishery managers in each country choose their policy, a reference fishing mortality $F_j^{ref}$ that determine the catch quota. The fishermen in each country then ‘decide’ the total effort $E_{j,t}$ which yields a total catch that satisfies the quota for season $t$.

The fisheries managers’ objective is to choose a zone-specific management target $F^{ref}$, so as to maximize the net present value $\textit{NPV}$ of their herring fisheries. We assume that $F^{ref}$ remains constant over the entire decision horizon (here 40 years). It is common in real fisheries management to express harvest policies in terms of a fixed target fishing mortality (Hilborn and Walters 1992). The chosen $F^{ref}$ also determines total catch quota ($C^{tot}$) for a fishing zone; i.e., $C_{j,t}^{tot}=(1-e^{-F_j^{ref}})N_{j,t}^{tot}$, where $N_{j,t}^{tot}$ refers to the fishable stock abundance which is season and zone-specific but not age-specific.³

The exact form of a $\textit{NPV}$ function varies according to coalition structure, for the grand coalition, the problem can be specified as follows:

$$\begin{aligned} {\textit{NPV}}=\max _{F_j^{ref}} \sum _{j}\sum _{t}{\overbrace{\frac{{p_0 \sum _{i=0}^{16}{W_{i}^{C} {\mathbb {C}}_{i,j,t}(E_{j,t})}-c_j E_{j,t} \tau _{j,t}^e}}{(1+r)^{t-1}}}^{\text {Seasonal profit}}} \end{aligned}$$

(7)

$$ \begin{aligned} {\text{ Subject } \text{ to }}\left\{ \begin{array}{ll} &{} \hbox {Eqs. }3 \quad \& \quad 5,\\ &{} C_{j,t}^{tot} =\sum \nolimits _{i}{{\mathbb {C}}_{i,j,t}(E_{j,t})} \end{array}\right. \end{aligned}$$

(8a)

where $p_{0}$ is an exogenous price, $W^C$ is age-specific catch weight, and constant $c$ denotes player/zone-specific cost per unit effort. $\tau _{j,t}^e=\max _{i}(\tau _{i,j,t})$ is the effective season length, determined by the age class that sustains fishing longest.⁴ If an age class is depleted before a season ends ($t=1$), fishing of that class terminates but fishing of the remaining classes will continue. Total catch ${\mathbb {C}}_{i,j,t}(E_{j,t})$ is specified in Eq. 6. Equations 3 and 5 are biological production constraints and Eq. 8a is a quota compliance constraint. Because the population’s age structure is not fixed, total effort $E_{j,t}$ cannot be derived directly from the catch quota; instead, it is necessary to solve it iteratively from Eq. 8a using a root finding technique.

Notice that we have assumed equality in Eq. 8a. This implies that fishermen are forced to fish, even if resource rent is negative in some years. We have made this assumption in order to avoid a situation in which a manager chooses an unsustainable level of $F^{ref}$, such that the stock is diminished early on, and fishing ceases when it is no longer profitable. Thus, we force the fisheries managers to adopt a long-term perspective in their management policies.

Our formulation is different from typical open-loop fishery game-theoretic models where fishing effort is used as the control variable and kept constant over time. In fisheries management, it is customary to express management targets in terms of maximum allowable fishing mortality. While the solutions we are aiming at are open-loop game equilibria—the control variables $F_{t}^{ref}$ are constant over the decision horizon—the seasonal effort $E_t$ will vary over time with the biological stock. Allowing effort to be dynamic is realistic and important for the research question of our interest, emphasizing the effect of dynamic stock distribution.

3 Partition Function Game and Sharing Rules

3.1 Game Theoretic Model

The three players in our coalition game are asymmetric. They are differentiated by stock ownership ($\theta$), cost per unit effort ($c$), and stock elasticity of harvest ($b$) that reflect different local stock densities experienced by fishermen. Our three-player coalition game belongs to the class of partition function games (P-game) according to Thrall and Lucas (1963). A P-game is based on the assumption of transferable utility, or transferable side payments in a risk neutral world. We assume a simultaneous move, “open-membership” game (Yi and Shin 2000), where a player is free to join or leave a coalition. Different coalitions adopt Nash strategies in a competitive game.

We compute optimal solutions for each player under all possible coalition strategies using a gradient ascent algorithm. Gradient ascent in a single player maximization is a standard first-order optimization algorithm: given an initial search point, step size, and error tolerance, the search path follows the steepest ascent to a maximum after a finite number of iterations. The exact procedure followed here depends on the coalition structure. In the singleton case where all players maximize their own NPV (subject to the other players’ strategies), the gradient ascent is in a player’s own NPV, with step sizes being proportional to the gradients of each player. For partial coalitions, for example when players 2 and 3 are in the same coalition, and player 1 remains the singleton, the optimal policy is found with simultaneous gradient ascent in player 2 and 3’s joint NPV, and in the single-player’s NPV function of player 1. For a grand coalition, the gradient ascent is in the joint NPV function of all players. We overcome the problem of local maxima by considering several initial conditions. The method of simultaneous gradient ascent is commonly used in evolutionary game theory (Brown and Vincent 1987; Dieckmann and Law 1996).

3.2 Stability Conditions

Formally, our coalition game consists of a set of three players $\mathcal {N}=\{1,2,3\}$. A coalition $S$ is a subset of $\mathcal {N}$: $S\subseteq \mathcal {N}$; a partition $P$ is a set of disjointed coalitions which covers the whole set of players, $S\in P$; and $\mathcal {P}$ is a set of all partitions, $P\in \mathcal {P}$. A coalition $S$ being a part of a partition $P$ is called an embedded coalition and denoted by $(S; P)$. For convenience, we define $S_{-j}\mathop {=}\limits ^{\tiny \text {def}}S\backslash \{j\}$, similarly, $P_{-S}\mathop {=}\limits ^{\tiny \text {def}}P\backslash \{S\}$.

We distinguish two functions in a partition function game: (i) partition function $\pi$, e.g., $\pi (S;P)$ denotes the aggregate payoff of coalition $S$, and the value also depends on how the rest of the players ($P_{-S}$) are organized; (ii) valuation function $v$, which specifies the distribution of the aggregate payoff within an embedded coalition. For $\forall j \in S$, $v_j(S;P)$ denotes the share of coalition payoffs $j$ receives and is sharing-rule-specific. The following relationships hold: $\sum _{j\in S}{v_j(S;P)}=\pi (S;P)$, and $v_j(S;P)=\pi (S;P)$ if $S$ is a singleton.

Stability conditions can be defined in terms of $v$ or $\pi$ function. According to D’Aspremont et al. (1983), a coalition $S$ is stable with respect to a valuation function $v$ if and only if

$$\begin{aligned} \text{ Internal } \text{ stability } \text{(IS) }:&v_j(S;P)\ge v_j(j;\{j\cup {S_{-j}}\cup {P_{-S}}\}),\quad \forall {j}\in S,\end{aligned}$$

(9)

$$\begin{aligned} \text{ External } \text{ stability } \text{(ES) }:&v_{j'}(j';\{j'\cup S \cup P_{-(S+j')}\})\ge v_{j'}(S_{+j'};P), \quad \forall {j'}\notin S.\quad \end{aligned}$$

(10)

That is, a coalition $S$ is stable if no insider is interested in leaving the coalition to form a singleton coalition,⁵ nor any outsider wants to join the coalition.

Potential internal stability (PIS) is an alternative stability condition that only relates to the partition functions $\pi$ (Eyckmans and Finus 2004). A coalition is considered PIS if and only if

$$\begin{aligned} \pi (S; P)\ge \sum _{j\in S}{\pi (j; \{j\cup {S_{-j}}\cup {P_{-S}}\})}. \end{aligned}$$

(11)

That is, a coalition is PIS if the aggregated payoff to the coalition is no less than the sum of free-rider payoffs of its members.

It is easy to see that PIS is the sum of the IS condition in (9) over all $j\in S$. If PIS holds for a coalition, it implies IS can be achieved under some (but not all) sharing rules. If PIS does not hold, no sharing rule can ensure the internal stability (Pintassilgo et al. 2010). PIS alone is sufficient to determine whether the grand coalition is stable because there is no player outside the grand coalition, and ES is always satisfied. The advantage of PIS is that we do not need to introduce any specific sharing rule in order to discuss the stability of a coalition.

3.3 Sharing Rules

We consider two different sharing rules in this paper: the “externality-free” Shapley value that is generalized for a partition function game (Pham Do and Norde 2007; De Clippel and Serrano 2008) and the “almost ideal sharing scheme” by Eyckmans and Finus (2004).

The classic Shapley value (Shapley 1953) assumes that players in the game enter a coalition one by one in a random order and that the player receives her share of benefits that is an average of the sum of all her marginal contributions resulting from different orders of arrival. Note that the classic Shapley value is associated with the characteristic function where a coalition payoff is independent of how the rest of the players in the game are organized (Greenberg 1994). In the literature extending the Shapley value for partition function games, an important contribution is the “average approach” (Macho-Stadler et al. 2007). In line with the classic Shapley value, this approach allocates the benefits based on the players’ marginal contributions. However, the payoff by coalition $S$ also depends on the coalition strategies of other players in a partition $P$, and $P$ that contains $S$ is not unique. Macho-Stadler et al. (2007) proposed taking a weighted average of the payoffs generated by all possible partitions where $S$ is embedded.

A drawback is that this “average approach” does not produce a unique solution, due to the unspecified weight parameter. Pham Do and Norde (2007) took an extreme stance and gave full weight to a partition where players outside of coalition $S$ remain singletons. De Clippel and Serrano (2008) justify this treatment by proposing a two-step process. In the first step, player $j$ leaves the coalition $S$ and remains alone, and in the second step, $j$ joins the coalition from $P_{-S}$. They argue that only the first step is the intrinsic marginal contribution, and the externality which arises from merging with the coalition in the second step is an external effect, and hence should not be captured. Using this “externality-free” Shapley value (hereafter termed the modified Shapley value) as the main solution concept, we can specify the sharing rule of our three-player partition function game as follows:

$$\begin{aligned} {\varphi _{j=x}^{Shap}}&= \frac{\pi (x;\{x,y,z\})}{3}+\frac{\pi (xy;\{xy,z\}) -\pi (y;\{x,y,z\})}{6}\nonumber \\&\quad +\frac{\pi (xz;\{xz,y\})-\pi (z;\{x,y,z\})}{6}+\frac{\pi (xyz;\{xyz\}) -\pi (yz;\{yz,x\})}{3}\qquad \end{aligned}$$

(12)

where $x$, $y$ and $z$ are the players.

The other sharing rule, “almost ideal sharing scheme” (AISS), ascertains that players in the coalition at least receive their free-riding payoff, formally: ${\varphi _j}^{AISS}=v_j(j;\{j\cup S_{-j}\cup P_{-S}\})+\lambda _j(S)\Delta (S)$ where $\lambda _j$ is a weight parameter. This can only be achieved if the surplus $\Delta (S)$ is non-negative (coalition payoff less the sum of free-rider payoffs), or $\Delta (S)\mathop {=}\limits ^{\tiny \text {def}} \pi _{j\in S}(S; P)-\sum _{j\in S}v_j(j;\{j\cup S_{-i}\cup P_{-S}\})$ is non-negative. Because the weight parameter, $\lambda _j$, can be any value between 0 and 1, AISS does not give a unique solution. Hence, we follow the Kronbak and Lindroos (2007) definition and let the surplus be evenly distributed among players after each of them have secured their free-rider payoffs (i.e., let $\lambda _j=\frac{1}{3}$ for all players).

4 Results

4.1 Cost Asymmetry and Stability of the Grand Coalition

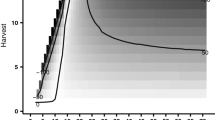
In this section, we examine the role of asymmetry in shaping the stability of the grand coalition—in the sense of potential internal stability (Eq. 11). Recall that players exhibit asymmetry in up to three dimensions: stock ownership, cost per unit effort and stock elasticity. To begin with, we study the case in which players are only differentiated by their stock ownership, represented by the point (1,1) in Fig. 1a. Note that the ownership is dynamic, but Norway always owns the largest stock share ($\ge$54 %), followed by IFE countries ($\le 28$ %), and then Russia ($\le$18 %). Results are summarized in Table 2a.

Fig. 1

Influence of cost asymmetry on the stability of the grand coalition and benefit sharing. $c_2/c_1$ and $c_3/c_1$ are player’s relative cost ratios. We assume $c_1=2.0$, $B_0=5.86$ Mt, $r=5$ %, and $p_0=1.3$ NOK/kg in all panels. The grey colour marks the unstable grand coalition. a The boundaries of the stable grand coalition, drawn when the grand coalition payoffs ($\pi _{1,2,3}$) approximate the sum of free-rider payoffs ($\sum \pi _j$); b changes in benefit allocation when $c_2=c_3$ and $b=[0,\frac{1}{2},\frac{1}{2}]$ (i.e., moving along the diagonal in a); c comparison of Shapley value with outsider option payoffs, $c_2=c_3$ and $b=[0,\frac{1}{2},\frac{1}{2}]$; d changes in payoff functions ($\pi _{1,2,3}$, $\pi _j$ and $\sum \pi _j$) when $c_2=c_3$ and $b_j=[0, 0, 0]$; $F^{ref}$ denotes optimal policy set under the coalition structure $\{(1,2); 3\}$

Table 2 Heterogeneous players and grand coalition stability

In a singleton game, Norway applies the lowest harvest rate of $F^{ref}=0.115$ and Russia is the heaviest exploiter with $F^{ref}=0.253$. This reiterates a familiar phenomenon, namely that in competitive games the major owner (herewith Norway) has a larger conservation incentive than the minor owners (IFE and Russia), a result often seen in fisheries games (Kaitala and Lindroos 2004; Hannesson 2007). Another feature is that players in the same coalition adopt similar harvest policies, mostly due to the same cost per unit effort we have assumed. Notice that the most aggressive harvest policy a player adopts is not in a fully competitive singleton game, but when she is playing against a two-player coalition.

The intuition is as follows: when players are in a coalition, they harvest more responsibly than they would do in a non-cooperative game; this creates a positive externality in the form of more stock spill-over to the zone of the free-rider in the following period. If the free-rider is also a minor owner, she gains more from positive stock spill-over because the proportion of total stock that migrates into her zone may also increase (because of the dynamic distribution). According to Eq. 8a, this means that the free-rider can raise her catch quota and catch more fish. When $b=0$, the seasonal profit is linear in catch. The spilled stock can be fully exploited by the free-rider.

In the next case, we allow heterogeneity both in stock ownership ($\theta$) and cost per unit effort ($c$), keeping everything else unchanged; an example is presented in Table 2b. In contrast to the previous example, harvesting load is tilted towards the players with lower harvesting costs, and noticeably, the grand coalition becomes stable under this specific setting. The stability of the grand coalition under a more generic setting is also tested in Fig. 1a where we vary the players’ relative cost ratios, $\frac{c_2}{c_1}$ and $\frac{c_3}{c_1}$, while keeping $c_1$ at a given level.⁶ The results show that the area representing an unstable grand coalition is roughly circular in shape and the further a point deviates from (1,1), where all players have identical $c$, the more likely it is that the grand coalition is stable, unless the unit effort cost gets so high that a player chooses not to fish.⁷ The evidence suggests that cost asymmetry among the players improves the stability of the grand coalition. The result can be seen as follows: in the presence of heterogeneous costs, a coalition can assign a harvesting policy among members in a more cost-effective way, leading to enhanced aggregated coalition payoffs and greater incentive to cooperate. The set-up of our model allows such cost-effectiveness to take place: (a) we allow side-payment; (b) we account for spatial variation of fish density in each zone and density dependent harvesting costs; (c) each player in a coalition can choose its own harvest policy, instead of applying one common policy for the entire coalition, a common practice in the coalition game literature. This way we expand the policy space for the 3-player grand coalition from one dimension to three dimensions.

The aforementioned result is still true if we add the third dimension of asymmetry, asymmetry in stock elasticity of harvest $b$. In this case, we set parameter $b=\frac{1}{2}$ both for Russia and IFE countries, and keep $b=0$ for Norway. Comparing with the case with identical $b$’s, we observe that: (i) the area in which the grand coalition is unstable tends to shrink; and (ii) the instability occurs in the area where both minor players have a lower unit effort cost, see Fig. 1a marked as $b=[0, \frac{1}{2}, \frac{1}{2}]$. The results are intuitive: unit harvesting costs are now stock-dependent for Russia and IFE, implying they will suffer more (rent dissipation) than Norway from their own overexploitation, thus they have a greater incentive to cooperate. The second observation indicates that if they are able to overcome the disadvantage of a higher $b$ by making their fishing effort cheaper, their free-riding incentive still remains.

If the grand coalition were not stable as the example in Table 2a shows, which coalition would become the equilibrium coalition structure? The singleton is stable by definition, but it is deemed inefficient in a common-pool game such as ours. Among three partial coalitions, some or all of them can be the equilibrium, depending on the model configuration. For the example shown in Table 2, the partial coalition formed by Norway and IFE is unstable, because the PIS condition cannot be satisfied. The situation for other two partial coalitions is the opposite, hence either of them can be the equilibrium coalition.

4.2 Sharing Benefits

In the following, we focus on the optimal benefit allocation when the grand coalition is stable. We are particularly interested in benefit sharing scenarios in which Norway’s unique position and her inherent advantage in the herring fishery are fully realized.

Table 3 provides an example where Norway, in addition to being the largest owner, is the only player whose unit harvesting cost is independent of stock size, that is $b=0$ for Norway and $b=\frac{1}{2}$ for the other two players. The results show that the respective shares received by Norway, IFE and Russia are 38, 34 and 28 % according to the modified Shapley value, and 37, 30 and 33 % according to the Almost Ideal Sharing Scheme (AISS) with equal weights. Neither of these two sharing schemes gives Norway an allocation of shares in excess of or in proportion to her stock ownership, which is $\ge 54$ % of the total stock.

Table 3 Benefits sharing of the stable grand coalition

A seasonal breakdown of the modified Shapley values—i.e., the benefits that each player is entitled to, broken down by season and after being discounted—sheds some light on these results: compared to the two minor players, Norway earns much more seasonal benefits during the years when the stock is approaching an equilibrium (Fig. 2a). As the stock stabilizes, the differences in the players’ seasonal Shapley values become less profound. The stock in transition is volatile regardless of the coalition structure (Fig. 2b); the volatility is due to the age structure that slows down the equilibration of the biological model. The reason that the transition stock gives Norway an advantage over her competitors is twofold: first, a higher fishable stock in the Norwegian zone, because the Norwegian stock share is the highest (Fig. 2c) during the transition years relative to the other years, and the total abundance of the fishable stock stays high (because there are many young fish); second, the two minor players have to reduce their yield because fishable stocks in their zones are smaller, and instantaneous unit harvest cost increases as stock declines due to $b=\frac{1}{2}$. As further proof, the optimal effort allocation for the competitive game (Fig. 2d) shows that Norway increases her effort during the transition, but the minor owners do the opposite.

Fig. 2

Model dynamics depicted in a seasonal Shapley value, b spawning stock biomass, c the stock share in the Norwegian zone, and d seasonal effort,. Two horizontal lines in b indicate two critical biomass levels; seasonal Shapley value in a is after discounting. Parameter values: $r=5$ %, $b_j=[0,\frac{1}{2},\frac{1}{2}]$, $c_j=[2,0.875,0.875]$, $j\in \{\text {Nor}, \text {Rus}, \text {IFE}\};\, B_0=5.58$ Mt

To what extent can a lower cost per unit effort ($c$) help the two minor players to offset their inherent disadvantages, namely smaller stock ownership and stock-dependent unit harvest cost? Figure 1b depicts how the benefit shares received by each country vary with their relative costs of effort ($c_2/c_1$), assuming identical $c$ for IFE and Russia ($c_2=c_3$). It shows that the benefit shares for Norway, using the modified Shapley value, sway from approximately 31 to 100 %, depending on relative unit effort cost level. If Norway’s effort cost level were far above that of her competitors’ (e.g., $c_2/c_1 \lessapprox 0.4$), her benefit shares may go below what IFE countries, the second largest owner, would obtain.

PIS (defined in Eq. 11) only guarantees the existence of a sharing scheme that ensures the stability of a grand coalition. Thus, if a wrong sharing scheme were used, the coalition that is PIS could still break down. After comparing the modified Shapley values (${\textit{Shap}}_j$) that each player receives with their outside option payoffs ($\pi _j$, $j \in \{ 1, 2, 3 \}$), we are reassured that the area satisfying ${\textit{Shap}}_j \ge \pi _j$ largely coincides with the area marking the stable grand coalition, except for $c_2/c_1 \le 0.34$ when Russia’s free-riding payoff is below (albeit marginally so) her Shapley benefit shares (see Fig. 1c). This largely justifies our choice of using the modified Shapley values as our primary sharing scheme.

4.3 The Influence of a Dynamic Distribution

The dynamic distribution defined in our model increases the bargaining power of Norway through two mechanisms: Norway can influence the total stock and, indirectly, the stock shares in other zones. More specifically, this means that if Norway were to increase her harvesting effort, both the total stock and the proportion of stock migrating over to other zones would decline, and vice versa. We have showed in Fig. 2 that such dual effect leads to higher competitive advantage for Norway during the stock transition years. From the perspective of a minor player, the dynamic distribution makes her more vulnerable to a retaliation by the major player, especially if her cost per unit effort relative to the major player is higher or her cost of harvesting is density-dependent ($b>0$). This forces minor players to be more conservation oriented.

However, the bargaining power of Norway can be undermined by her high relative cost of harvesting. This can take on two forms: by constraining Norway’s ability to retaliate against a more cost-efficient free-rider, which may lead to the break down of the grand coalition, or by constraining Norway’s ability to exploit the stock, resulting in lower realized fisheries value in her zone and lower benefit shares than she would be entitled to based on her stock share. This loss of bargaining power is best showcased in Fig. 1d where the two minor players’ free-riding payoffs flip when $c_2/c_1$ increases from $0.72 \rightarrow 0.75$ (points b and c in Fig. 1d). The flipping effect is intriguing and two conditions are needed for this to occur:

• First, Norway still relies substantially on a more cost-efficient player, IFE or Russia, to exploit the stock for the coalition that she is part of, implying $c_2/c_1<1$ .⁸ Indeed at point c where $c_2/c_1=0.75$, the corresponding fishing mortalities for Norway ($F_{Nor}^{ref}$) and Russia ($F_{Ru}^{ref}$) are 0.04 and 0.31, respectively. Under this circumstance, it is in Norwegian interests to reduce her own fishing effort ($F_{Nor}^{ref}$ reduced from $0.07$ in b $\rightarrow$ 0.04 in c), and let stock grow and spill-over to the zones of more cost-efficient allies. The downside of such scenario is that it increases the free-riding incentive of a minor player; Norway would be disincentivized to retaliate because retaliation would hurt her ‘foe’ as well as her ‘friend’.

• Second, $c_2/c_1$ has to increase (meaning a relatively low harvesting cost for Norway) to a level such that Norway is capable to divert the stock in favor of her ally. This also explains why the flips observed in $\pi _2$ and $\pi _3$ do not occur at a lower level of $c_2/c_1$ in Fig. 1d. The argument is also supported by our finding in Sect. 4.2, in which the benefit shares received by a player in the grand coalition can change drastically with cost of unit effort, and a player’s benefit share is not necessarily proportional to the share of her stock ownership. High cost diminishes the value of fisheries in the Norwegian zone, leading to a weakening of her leverage over the competitors.

In short, the dynamic distribution in our model increases the bargaining power of Norway, but it is not necessarily translated into higher benefit shares for Norway nor into a higher likelihood to form the stable grand coalition. It all depends on Norway’s relative cost of harvesting.

4.4 Sensitivity

The justification and sensitivity of key specific parameters, namely stock elasticity of effort ($b$) and relative cost per unit efforts ($\frac{c_2}{c_1}$ and $\frac{c_3}{c_1}$), are reported in Sect. 2.3 and throughout the results Sects. 4.1–4.3. In this section, we focus on the following parameters: the initial stock biomass, the lower critical biomass level, and the discount rate. The example in Table 3 is our reference scenario that emphasizes Norway’s unique position in the game.

So far, all results are based on the assumption that the initial stock ($B_0=5.58$ Mt) is slightly above the high critical biomass level ($B_{high}=5.0$ Mt). Due to the discounting of future payoffs, the initial state is expected to be important. Indeed, we find that a low initial stock leads to greater benefit shares for Norway, whereas a high initial stock does the opposite. The reason is threefold: first, when a stock with age structure is sufficiently small, it takes time to recover and the period during which the herring stock remains in the Norwegian EEZ is prolonged; second, it is more costly for IFE and Russia to harvest a small stock due to lower fish density experienced in their zones ; third, as the stock recovers to a certain critical level beyond which the two minor players can enjoy high fish density in their zones, the limiting effect of a higher $b$ starts diminishing and their advantage of having low unit effort costs begins to gain momentum. Figure 3 supports this reasoning based on examples from two extreme years: in the year 1969 when the initial stock was extremely low ($B_0=0.086$ Mt), Norway’s seasonal Shapley value surpasses her competitors’ by a great margin until the stock recovers. As a result, Norway gets as much as 44 % of the total benefits; in the year 1950 when initial stock was extremely high ($B_0=16.6$ Mt), Norway, whose unit effort cost is the highest, receives less than a third of the total benefits.

Fig. 3

Effect of initial stock biomass on the seasonal Shapley values (after discounting), assuming $b_j=[0,\frac{1}{2},\frac{1}{2}]$, and $c_j=[2.0, 0.875, 0.875]$, $j\in \{\text {Nor}, \text {Rus}, \text {IFE}\}$. a With the low initial biomass from year 1969 $B_0=86 Kt, \varphi _j^{Shap}=[44\%, 25\%, 31\%]$; b with the high initial biomass example from year 1950: $B_0=16.6$ Mt, $\varphi _j^{Shap}=[28\%, 31\%, 41\%$]

Is it in the interest of Norway to keep the herring stock so low that she can enjoy the sole ownership? To investigate this question, we vary the lower critical biomass level ($B_{low}$) from 0.3 to 4.0 Mt, keeping the upper critical biomass level unchanged ($B_{high}=5.0$ Mt). The singleton solutions are computed for our focal scenario in Table 3. The results indicate that, in a fully competitive game, the stock biomass in the terminal year ($B_{40}$) always stays above $B_{low}$;⁹ there are complementary policy shifts by the major and minor owners (e.g., the minor players reduce their fishing mortality if the major player increases it). If the stock distribution were static, we would expect the minor owners to free-ride on the major owner’s conservation incentive and leave behind as little as they can. In the presence of a dynamic distribution, the future stock shares for IFE and Russia very much depend on what is left behind today; they have to act conservatively. The low biomass threshold thus functions as a threat point.

What is the role of the discount rate? In our model, the major owner does not compete with her competitors on price (exogenous) and her unit harvesting cost is fixed (because $b=0$), the rule of optimality simply results from the trade-off between the rate of temporal discounting and the marginal rate of stock productivity. Building upon our base scenario in Table 3 (5 % discount rate, $b=[0, 0.5, 0.5]$, Norway has the highest cost per unit effort $c$), the discount rate has to increase to as high as 80 % to make it optimal for Norway to adopt the non-migratory strategy. If we assume all players have identical $c$, other things being equal to the base scenario, then the rate can go down to approximately 50 %. With a more moderate discounting rate, Norway is primarily interested in a relatively large, productive stock. Whether the fish will spill over to other zones is immaterial for her.

5 Discussion and Concluding Remarks

We have studied cooperative and non-cooperative outcomes in the presence of a dynamic stock distribution, using Norwegian spring-spawning (NSS) herring as the case study. This is one of very few studies where age-structured population modelling, distributional changes and a partition function game are combined. Furthermore, our model combines many features that are rarely seen in fisheries games, in particular, density-dependent and potentially zone-dependent harvesting cost and the use of reference fishing mortality as the decision variable.

We find that the likelihood of forming a stable three-player grand coalition is positively correlated with the degree of asymmetry in the players’ cost per unit effort ($c$). The finding contributes to the recent and growing body of literature on international agreements (McGinty 2007; Fuentes-Albero and Rubio 2010; Pintassilgo et al. 2010) that supports the postulate ‘asymmetry improves cooperation’. The underlying mechanism in our model, however, differs from theirs. In our case, the combination of allowing side payments, accounting for spatial variation of harvesting costs and fish density, and letting coalition members to take zone-specific policies enables harvesting to take place in a more cost-efficient way, resulting in much improved aggregated coalition payoffs. This also explains our finding that, when the grand coalition is not stable, a partial coalition always stands out as a more favorable equilibrium solution than the singleton solution.

The dynamic distribution increases the bargaining power of Norway because of her ability to control both the total stock and the stock shares in different zones. For a minor player, the dynamic distribution makes her more vulnerable to the major player’s retaliation against free-riding, hence becoming more conservation oriented. However, the bargaining power of Norway may disappear if her cost per unit effort ($c$) exceeds that of the other players. This loss reflects two influences: the cost constrains the ability of Norway to punish a free-rider and the grand coalition breaks down, and it constrains Norway’s ability to divert the stock movement in her favor. We show that if Norway were the player with the highest $c$, it can happen that the IFE countries and Russia would receive higher benefit shares than Norway. Notice that assuming a higher $c$ for Norway is not unrealistic; e.g., for years, the Norwegian fisheries industry has been facing a recruitment problem due to labour competition with the oil-supply fleet and changing regulation of coastal fleet that increased the demand for specialized crew (Sandberg and Olafsen 2006; Sønvisen 2013). Hannesson (2013) also found that density-dependent distribution weakens the small players’ bargaining power. But much of the embedded dynamics were missed out in his model because the problem was framed in a characteristic function game without accounting for the free-rider problem.

The benefit allocation rule is also sensitive to the initial stock state: a low initial stock level brings greater benefit shares to Norway, while a high initial stock does the opposite. A problematic effect can arise from a high stock: we found cases where a stable grand coalition breaks down when the initial stock is sufficiently high. A similar observation has been made by Hannesson (2006). Indeed, when stock is abundant, cooperation becomes less important for minor players, and a more lucrative deal would probably have to be offered in order to ensure their participation.

Whether the strategy where Norway pushes down the stock to become the sole owner of a non-migratory stock is optimal for Norway depends on the trade-off between the rate of temporal discounting and the marginal rate of stock productivity. Under a moderate discounting rate it will not pay off for Norway to adopt such a strategy, because she is primarily interested in a large and productive stock, and the fisheries in the EEZ of a minor player(s) is valuable for the coalition that Norway belongs to.

Earlier herring studies are based on static distribution and their model configurations differ. Bjørndal et al. (2004) showed the non-migratory strategy is not attractive for Norway because ‘open access with closures’ gives better outcomes. Their result is based on one particular critical biomass level and discount rate ($B_{low}=500$ kt and $r=0.04$). We have shown that the outcome can go both directions, depending on the discount rate and the stock condition. With a moderate discounting rate, their result holds also for other levels of $B_{low}$. Hannesson (2006) indicated that it can be optimal for Norway to keep stock at the $B_{low}$ level, assuming that $B_{low}$ is high enough. He used a biomass model and all players had constant unit harvesting costs. With an age-structured model and allowing asymmetric unit harvest costs, we found that under current stock conditions the discount rate has to be very high, e.g., as high as 50 % or more, to make the sole owner strategy attractive. Nevertheless, our model has its own limitations, for instance, the management regime in the model is quite rigid. In future research one could allow players to fish both in their own exclusive economic zones and the high seas, and to stop fishing when it is not profitable.

Despite some simplifications, our model is able to reproduce some important aspects of the actual history of NSS herring management. Between 2007 and 2012, NSS herring was managed based on an agreement that involved all coastal states. This grand coalition, however, broke down when quotas for 2013 were negotiated. At the moment, the management is based on a partial coalition that excludes the Faroes Islands. Our results suggest that, as long as the herring fishery is relatively productive, Norway should not retaliate by fishing down and confining the stock to its own waters. On the other hand, with side payments, the prospects of the stable grand coalition for NSS herring could be increased if the spatial variation of harvesting cost were to be fully explored while allocating fishing effort among coalition members. This can be relieving news given that the negotiations for full cooperation of the herring fishery are still underway.

Appendix

See Tables 4, 5 and 6.

Table 4 Age-specific parameters

Table 5 Notational summary

Table 6 Age-unspecific parameters