Supervisory control and reactive synthesis: a comparative introduction

Abstract

This paper presents an introduction to and a formal connection between synthesis problems for discrete event systems that have been considered, largely separately, in the two research communities of supervisory control in control engineering and reactive synthesis in computer science. By making this connection mathematically precise in a paper that attempts to be as self-contained as possible, we wish to introduce these two research areas to non-expert readers and at the same time to highlight how they can be bridged in the context of classical synthesis problems. After presenting general introductions to supervisory control theory and reactive synthesis, we provide a novel reduction of the basic supervisory control problem, non-blocking case, to a problem of reactive synthesis with plants and with a maximal permissiveness requirement. The reduction is for fully-observed systems that are controlled by a single supervisor/controller. It complements prior work that has explored problems at the interface of supervisory control and reactive synthesis. The formal bridge constructed in this paper should be a source of inspiration for new lines of investigation that will leverage the power of the synthesis techniques that have been developed in these two areas.

1 Introduction

The goal of this paper is to introduce and present a formal connection between synthesis problems that have been considered, largely separately, in the two research communities of control engineering and formal methods. By making this connection mathematically precise in a paper that attempts to be as self-contained as possible, we hope to introduce these two research areas to non-expert readers and at the same time inspire future research that will further bridge the gap between them and leverage their complementarity. Given the pedagogical nature of this paper, we focus on connecting the most basic synthesis problem in supervisory control, for safety and non-blockingness in the case of full observation, with a suitably-defined analogous problem in the field of reactive synthesis. We start our discussion with a general introduction to the two research areas under consideration.

1.1 Supervisory control of discrete event systems

Feedback control of dynamic systems is an essential element of our technological society. Control theory was originally developed for systems with continuous variables that evolve in time according to dynamics described by differential or difference equations. Since the 1980s, the field of Discrete Event Systems (DES) in control engineering has been concerned with the application of the feedback paradigm of control theory to the class of dynamical systems with discrete state space and event-driven dynamics.

The DES community has been investigating feedback control of DES using models from computer science, such as automata and Petri nets. The body of control theory developed in DES has been for specifications that are expressible as regular languages, in the case of DES modeled by automata, or in terms of constraints on the state (marking vector), in the case of DES modeled by Petri nets. Control-theoretic frameworks have been developed for both of these modeling formalisms. In this paper, we focus on the supervisory control theory for systems modeled by finite-state automata and subject to regular language specifications. Both the plant and the specification are represented as finite-state automata over a common event set. The foundations for this framework were developed in the seminal work of Ramadge and Wonham (1987), Wonham and Ramadge (1987). Since then, a whole body of theory has been developed that covers a wide variety of control architectures and information structures, with vertical and horizontal modularity. The reader is referred to Cassandras and Lafortune (2008), Wonham (2015) for textbook expositions of this theory; other relevant references are the monograph (Kumar and Garg 1995), the survey papers (Ramadge and Wonham 1989; Thistle 1996), and the recent edited book (Seatzu et al. 2013). The focus of this theory is on the synthesis of provably safe and non-blocking controllers for a given uncontrolled system, or plant in control engineering terminology, despite limited actuation and limited sensing capabilities. In automated manufacturing applications for instance, the plant would be the joint operation of a set of robots, conveyors, Automated Guided Vehicles (AGVs), and numerically controlled machines, and the controller would be implemented using one or more Programmable Logic Controllers (PLCs). Safety properties are expressed in terms of bad states where robots and/or AGVs collide for instance, or bad sequences of events that correspond to incorrect assembly for instance. Non-blockingness captures the fact that product assembly should be completed in its entirety, followed by a return of all components to their initial states.

1.2 Reactive synthesis

It is widely acknowledged that many design defects originate in the failure of the implementation to accurately capture the designer’s intent. Underlying the reactive synthesis approach is the realization that many requirements can be expressed as formal temporal assertions, capturing intended system functionality in a declarative fashion. Assertions can express both safety properties, such as “a Grant is always followed by Busy”, and liveness properties, such as “a Request is eventually followed by a Grant”. Thus, the functional specification of a system can be expressed as a set of temporal assertions.

The assertion-based approach to system specification underlays early work on program verification (Francez 1992), whose focus was on input/output properties. This was later extended to temporal properties of ongoing computations (Pnueli 1977), which enabled the application of formal verification techniques to reactive systems–systems that have ongoing interactions with their environments (Harel and Pnueli 1985). One of the most successful applications of the assertion-based approach has been model checking, an algorithmic formal-verification technique (Clarke and Emerson 1981; Clarke et al. 1986; Lichtenstein and Pnueli 1985; Queille and Sifakis 1982; Vardi and Wolper 1986); see (Clarke et al. 2000) for an in depth coverage.

The design of reactive systems, systems that engage in an ongoing interaction with their environment, is one of the most challenging problems in computer science (Harel and Marelly 2003; Harel and Pnueli 1985). The assertion-based approach constitutes a significant progress towards addressing this challenge. While there has been impressive recent progress on applying formal methods in verification (Jackson 2009), in current design methodology, design and verification are distinct phases, typically executed by separate teams. Substantial resources are spent on verifying that an implementation conforms to its specifications, and on integrating different components of the system. Not only do errors discovered during this phase trigger a costly reiteration of design and programming, but more importantly, verification offers only quality control, not quality improvement, and hence, current design methodology does not produce systems that are safe, secure, and reliable.

Currently, when formal assertions are being used, it is in testing and verification, after a significant effort has already gone into the development effort. When errors are found, significant effort has to be expended on design change. An old dream in computer science is that of design automation, in which the process of converting formal specification to implementation is, to a major extent, automated. The implication is that a major portion of the manual design effort should go into the development of high-level specifications, since much of the implementation effort can then be automated. The technique of compiling high-level formal requirements to low-level system code is referred to as synthesis, and was proposed already in Church (1957), Green (1969). Follow up work in Büchi and Landweber (1969), Rabin (1972) addressed the problem mathematically, but it seemed quite far from being applicable to real-life problems.

In the late 1980s, several researchers realized that the classical approach to system synthesis (Green 1969), where a system is extracted from a proof that the specification is satisfiable, is well suited to closed systems (systems with no inputs), but not to reactive systems. In reactive systems, the system interacts with the environment, and a correct system should then satisfy the specification no matter how the environment behaves, i.e., no matter which inputs the environment provides to the system. If one applies the techniques of Emerson and Clarke (1982), Manna and Wolper (1984) to reactive systems, one obtains systems that are correct only with respect to some environment behaviors. Pnueli and Rosner (1989a), Abadi et al. (1989), and Dill (1989) argued that the right way to approach synthesis of reactive systems is to use the model of a, possibly infinite, game between the environment and the system. A correct system can be then viewed as a winning strategy in this game. It turns out that satisfiability of the specification is not sufficient to guarantee the existence of such a strategy. Abadi et al. called specifications for which a winning strategy exists realizable. Since then, the subject of reactive synthesis has been an active area of research, attracting a considerable attention, for example (Kupferman and Vardi 2000; Pnueli and Rosner 1989b; Vardi 1995; Wong-Toi and Dill 1991).

1.3 Contributions and organization of this paper

We start in Section 2 by presenting technical introductions to supervisory control (Section 2.1) and reactive synthesis (Section 2.2). We have tried to make Section 2 as self-contained as possible, so that readers who are not experts in either domain could follow the ensuing results connecting these two areas. However, these introductions are not meant to be thorough and readers interested in learning these areas in more depth should consult the references mentioned above.

The main results connecting supervisory control and reactive synthesis are contained in Section 3. That section is organized into several parts. First, we present in Section 3.1 a simplification of the basic supervisory control problem, non-blocking version, to one where the safety specification has been absorbed into the plant model. We then show that the resulting Simple Supervisory Control Problem (SSCP) has a state-based solution. The results on SSCP will facilitate bridging the gap in the remainder of Section 3. Second, for bridging reactive synthesis with supervisory control, we need two technical steps: the first step is to consider reactive synthesis with plants; the second step is to bring in the issue of maximal permissiveness into this reactive synthesis setting. These two steps are covered in Section 3.2. With the above technical results established, we establish the formal reduction from SSCP to a reactive synthesis problem with plants and maximal permissiveness in Section 3.3. This formal reduction is the main technical contribution of this paper. Section 3.4 discusses algorithmic issues and Section 3.5 discusses links between the reactive synthesis problem with plants and the more standard reactive synthesis problem without plants.

Finally, some concluding comments and directions for future work are given in Section 4. A preliminary and partial version of this paper, without proofs, appears in Ehlers et al. (2014).

1.4 Related works

This paper is not the first to explore connections between supervisory control and reactive synthesis. On the supervisory control side, several authors have considered control of discrete event systems subject to temporal logic specifications; see, e.g.,Thistle and Wonham 1986, Lin (1993), Jiang and Kumar (2006). Supervisory control of discrete event systems with infinite behavior, i.e., modeled by languages over E ^ω instead of E ^∗ for a given event set E, has also been considered by many researchers; see, e.g., Ramadge (1989), Kumar et al. (1992), Thistle and Wonham (1994a), Thistle and Wonham (1994b), Thistle (1995), Thistle and Malhamé (1998), Lamouchi and Thistle (2000). On the other hand, several researchers in the formal methods community have investigated supervisory control of fully- and partially-observed discrete event systems, in untimed, timed, and hybrid system settings; see, e.g., Hoffmann and Wong Toi (1992), Maler et al. (1995), Asarin et al. (1995), Henzinger and Kopke (1997), Kupferman et al. (2000), Madhusudan (2001), Cassez et al. (2002), Arnold et al. (2003), Riedweg and Pinchinat (2003). Researchers from both the supervisory control and formal methods communities have also studied problems of distributed or decentralized controller synthesis, where more than one controllers are (simultaneously) synthesized, e.g., see Pnueli and Rosner (1990), Rudie and Wonham (1992), Barrett and Lafortune (1998), Lamouchi and Thistle (2000), Overkamp and van Schuppen (2000), Ricker and Rudie (2000), Tripakis (2004), Lustig and Vardi (2009), Komenda et al. (2012), Seatzu et al. (2013).

In the present paper, we restrict attention to the basic problem of centralized supervisory control for fully-observed systems modeled by languages of finite strings. Our goal is to establish a precise connection of this classical work with problems of reactive synthesis, by showing how specific problem instances reduce to each other. While more advanced connections have been discussed in the above-cited references, our goal is pedagogical in nature and aims at establishing a bridge between these two areas at the most elementary level. Still, to the best of our knowledge, the formal reduction presented in Section 3 has not been published elsewhere. Our results therefore complement existing works from a technical standpoint.

2 Classical frameworks

In this section, we present technical introductions to the fields of supervisory control and reactive synthesis. These introductions are not meant to be comprehensive, but rather their goal is to allow readers who are not experts in either or both of these fields to follow the later results in Section 3 on establishing a precise connection between basic synthesis problems in these two fields.

2.1 Supervisory control

In supervisory control of Discrete Event Systems (DES), the system to be controlled, i.e., the plant, is typically modeled as a set of interacting finite-state automata coupled by common events or as a Petri net. In order to obtain a monolithic model that will be used for analysis and control synthesis purposes, the parallel composition of the set of interacting automata is performed or the reachability graph of the Petri net is constructed. We restrict attention to plants with finite state spaces. Also, we assume full event observability.

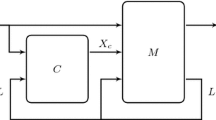
Let the plant be denoted by G. (Formal definitions will follow.) G captures the entire set of possible behaviors of the plant and it is called the “uncontrolled system.” In general, some of this behavior is not acceptable in the sense that it is not safe with respect to a given specification or that it results in deadlock or livelock. Consequently, we wish to restrict the behavior of G by means of a feedback controller, or supervisor in DES terminology. The standard feedback loop of supervisory control theory is shown in Fig. 1. The “input” to the supervisor S is the string of events generated so far by G. All the events of G are observed by S. The “output” of S is a control action that tells G which event(s) it is allowed to do at that moment. The supervisor may allow more than one event, in which case the system will decide which allowed event to execute next. The mechanism by which G chooses which allowed event to execute next is not modeled. One may think of G as a semi-autonomous system for instance. In general, the supervisor may not have full actuation capabilities, i.e., there may be events of G that it cannot disable. These events are called uncontrollable. How to deal with uncontrollable events is one of the contributions of supervisory control theory.

Fig. 1

Closed-loop system S/G, where S issues control actions in response to the events generated by G

Example 1 (Coffee Machine)

For the sake of illustration, assume that our plant G is a coffee machine that can grind coffee beans, brew coffee, and deliver a cup of coffee. Its interface with the user is a “coffee button” that generates an event, denoted by c, when it is pressed by the user. The automaton representation of that machine is shown in Fig. 2. We give the formal definition of an automaton below; for now, we explain the transition structure. The initial state is 1 (this is denoted by the fact that state 1 has an incoming arrow). State 1 is also an accepting or marked state (denoted by the fact that the state is drawn as a double circle). Upon occurrence of event c, the coffee machine moves to a new state in which it can execute an arbitrary number of “grind” events, which are denoted by g, as well as an arbitrary number of “brew” events, which are denoted by b; these events self-loop at state 2. Finally, when grinding and brewing are completed, the coffee is delivered (poured in cup) and the machine returns to its initial state; this is represented by event r. For simplicity, we assume that the machine ignores further pressing of the coffee button while it is grinding and brewing, i.e., until event r occurs. This is modeled by the self-loop for event c at state 2.

Fig. 2

Automaton G: uncontrolled coffee machine

G represents the physical capabilities of the machine, without an appropriate control protocol, i.e., without a specification. As given, this behavior is unsafe: first, brewing should always be preceded by grinding; second, no grinding should occur after brewing has started.

Moreover, one may wish to follow special coffee recipes, parameterized by the number of g events (more events means finer ground coffee) and the number of b events (more events for stronger coffee). One such recipe could be that coffee is prepared by one grinding step followed by two brewing steps. Another recipe for stronger coffee could call for two grinding steps followed by three brewing steps.

We wish to synthesize a supervisor S that will restrict the behavior of G in order to satisfy the above safety constraints and allow the two possible recipes. In this example, event c is uncontrollable, as the supervisor cannot tell the plant to ignore a request for coffee when it is in state 1. (Note that such requests are ignored while the plant is in state 2, as captured in the model in Fig. 2.) The other events are assumed to be controllable, as the coffee machine has actuators for grinding, brewing, and delivering a cup of coffee; hence, the control protocol can decide when to activate or de-active these actuators. For instance, after the occurrence of event c, S needs to tell G that it should execute a g event, not a b event, as grinding must precede brewing. Hence, immediately after event c occurs, S should disable event b. Similarly, after the first b event, S should disable event g until the next cup is prepared. As for event r, it should remain disabled until a recipe is completed. Here, in the spirit of supervisory control, we assume that the supervisor will not force one of the allowed recipes. Namely, after one occurrence of g, S can enable both g and b and let the plant “randomly” choose to do either another g event or to start brewing, i.e., randomly choose which recipe to implement (perhaps on the basis of some other features not included in this simple model). If the plant chooses to execute b, then further occurrences of g will be disabled by S. On the other hand, after two consecutive occurrences of event g, S needs to tell G that it should not execute any more g events for the current cup under preparation, as no recipe calls for three grinding steps; i.e., S must disable the third consecutive occurrence of event g. When the plant has completed either recipe, S disables both g and b and enables r in order to allow the plant to deliver the cup of coffee.

In supervisory control, the objective is to automatically synthesize a supervisor S that provably satisfies all given specifications. The inputs to the synthesis process are: (i) the model G; (ii) the sets of controllable and uncontrollable events; and (iii) an automaton model of the specifications imposed on G. In the rest of this section, we present the main concepts needed before we can proceed to bridging the gap with reactive synthesis.

2.1.1 Plant model

In supervisory control theory, plants are typically modeled as deterministic finite-state automata. A deterministic finite-state automaton (DFA) is a 5-tuple

$$G = (X,x_{0},X_{m},E,\delta) $$

where

• X is a finite set of states, x ₀∈X is the initial state, and X _m ⊆X is the set of marked (i.e., accepting) states;

• E is a finite set of events. E is (implicitly) partitioned into two disjoint subsets:

  $$E = E_{c} \cup E_{uc} $$

  where E _c models the set of controllable events and E _{u c} the set of uncontrollable events.

• δ:X×E→X is the transition function, which in general will be partial.

The reason for the transition function to be partial is the fact that G models the physically possible behavior of a DES, as a generator of events. Selection of the states to “mark,” i.e., to be included in X _m , is a modeling consideration to capture strings that represent that the system has completed some task. In many systems with cyclic behavior, such as our coffee machine, the initial state is marked, as returning to it means that a task has been completed and a new one can start.

A state x∈X is called a deadlock state if for all e∈E, δ(x,e) is undefined.

It is useful to “lift” the transition function δ to a function

$$\delta^{*} : X \times E^{*} \rightarrow X $$

defined as follows:

$$\begin{array}{@{}rcl@{}} \delta^{*}(x,\varepsilon) & = & x \\ \delta^{*}(x,\sigma\cdot e) & = & \delta(\delta^{*}(x,\sigma),e) \end{array} $$

where ε denotes the empty string and ⋅ denotes string concatenation. (We usually omit writing ⋅ unless needed for clarity of notation.) Note that since δ is partial, δ ^∗ is also partial. Since we always extend δ to δ ^∗, we shall drop the “*” superscript hereafter and simply refer to the extended function as δ.

The DES G defines the following languages:

$$\mathcal{L}(G) = \{ \sigma\in E^{*} \mid \delta(x_{0},\sigma) \text{ is defined}\} \quad\quad\text{and}\quad\quad \mathcal{L}_{m}(G) = \{ \sigma\in E^{*} \mid \delta(x_{0},\sigma)\in X_{m} \}. $$

Given K⊆E ^∗, let $\overline {K}$ denote the prefix-closure of K:

$$\overline{K} = \{ \sigma \mid \exists \sigma^{\prime} \in E^{*} : \sigma \sigma^{\prime} \in K \} $$

In the definition above σ ^′ can be the empty string, so $K\subseteq \overline {K}$ for all K.

Moreover, for any DES G:

$$\mathcal{L}_{m}(G) \subseteq \overline{\mathcal{L}_{m}(G)} \subseteq \mathcal{L}(G) = \overline{\mathcal{L}(G)} $$

Note that $\overline {\mathcal {L}_{m}(G)} \neq \mathcal {L}(G)$ in general. This is because $\mathcal {L}(G)$ may contain strings that cannot be extended to yield strings in $\mathcal {L}_{m}(G)$. In other words, G may contain reachable states that cannot reach any marked state.

2.1.2 Supervisors

A supervisor for G is a function S:E ^∗→2^E. It reads a string σ representing the history of what has happened so far and returns the set of controllable events that are allowed to occur. To ensure that S never disables an uncontrollable event, we require that E _{u c} ⊆S(σ) for all σ∈E ^∗ (alternatively, we could also define S to be a function $S: E^{*} \rightarrow 2^{E_{c}}$). Note that S(σ)∩E _c may be empty.

Sometimes S is required to satisfy the following property:

$$ \forall \sigma,c \in E_{c} : c\in S(\sigma) \implies \delta(x_{0},\sigma c) \text{ is defined} $$

(1)

which states that S allows a controllable event e only if e is feasible in G. This is not an essential requirement on S: we can simply ignore controllable events that S allows but are not feasible in G. The same comment applies to enabled but infeasible uncontrollable events.

When S is a supervisor specifically designed for G, the history σ can only be generated by G, therefore S can also be defined as a function

$$S : \mathcal{L}(G) \rightarrow 2^{E} $$

However, in general, it is more convenient to define S to be a function over E ^∗, since this allows us to use the same supervisor for different plants, as long as E _c and E _{u c} remain the same.

Remark 1 (Full observability)

In the current framework, a plant is fully observable by a supervisor, for two reasons. First, the supervisor, defined as a function with domain E ^∗, observes the entire sequence of events generated by the plant (in partial observability frameworks, only a subset of events are observed). Second, the plant itself is a deterministic automaton. Therefore, given the sequence of observed events, the supervisor can uniquely determine the current state of the plant.

2.1.3 Closed-loop system

Given a plant G=(X,x ₀,X _m ,E,δ) and a supervisor S:E ^∗→2^E for G, the closed-loop system S/G, according to the feedback loop in Fig. 1, is a DES that is formally defined as follows:

$$S/G = (X^{\prime},x_{0}^{\prime},X_{m}^{\prime},E,\delta^{\prime}) $$

where

• $X^{\prime } = X \times \mathcal {L}(G)$

• $x_{0}^{\prime } = (x_{0},\varepsilon )$

• $X_{m}^{\prime } = X_{m} \times \mathcal {L}(G)$

• $\delta ^{\prime }\left ( (x,\sigma ), e \right ) = \left \{\begin {array}{ll} (\delta (x,e), \sigma e) & \text { if }\delta (x,e)\text { is defined and } e\in S(\sigma )\\ \text {undefined} & \text { otherwise.} \end {array}\right .$

A state in S/G is a pair (x,σ) where x∈X is a state of the plant G and $\sigma \in \mathcal {L}(G)$ is the history observed so far. Thus, S/G is an infinite-state automaton, except for the special case that G is loop-free. This need not worry us for now. At this point, we are mainly interested in defining the synthesis problem, and not the algorithm to solve it. The initial state of S/G is (x ₀,ε), since x ₀ is the initial state of G and the history is initially empty. $X_{m}^{\prime }$ is defined as $X_{m} \times \mathcal {L}(G)$, meaning that a behavior of the closed-loop system is marked iff it is marked by G. In other words, we only consider supervisors that do not affect the marking of states in the plant. The definition of the transition function δ ^′ is explained as follows. Given current state (x,σ) and event e:

• when δ(x,e) is undefined (i.e., the plant does not have a transition from x for e), then δ ^′((x,σ),e) is also undefined

• otherwise, assuming δ(x,e) = x ^′,

  • if e is uncontrollable, i.e., e∈E _{u c} , then e is allowed by the supervisor and the next state is (x ^′,σ e), i.e., the plant moves to x ^′ and the supervisor observes e,

  • if e is controllable and allowed by the supervisor S, i.e., e∈E _c ∩S(σ), then the next state is again (x ^′,σ e),

  • otherwise (i.e., if e∈E _c ∖S(σ), meaning that e is controllable but not allowed by S), δ ^′((x,σ),e) is undefined. This is the only case when an event e which is allowed in G is forbidden in the closed-loop system.

Note that when δ(x,e) is defined, $\sigma \in \mathcal {L}(G)$ implies $\sigma e\in \mathcal {L}(G)$. This ensures that if (x,σ) is a valid state of S/G, i.e., (x,σ)∈X ^′, then δ ^′((x,σ),e) is also a valid state of S/G, so that the state-space of S/G is well defined.

S/G is an automaton (albeit an infinite-state one), therefore, languages $\mathcal {L}(S/G)$ and $\mathcal {L}_{m}(S/G)$ are defined as stated above. Note that, by definition, S/G is a restriction of G, therefore,

$$\mathcal{L}(S/G) \subseteq \mathcal{L}(G) \quad\text{ and }\quad \mathcal{L}_{m}(S/G) \subseteq \mathcal{L}_{m}(G) $$

Moreover, it is easy to verify that

$$\mathcal{L}_{m}(S/G) = \mathcal{L}(S/G) \cap \mathcal{L}_{m}(G) $$

since a marking in S/G is completely determined by a marking in G. When S is applied to G as described above, the definition of S(σ) for $\sigma \in E^{*} \setminus \mathcal {L}(S/G)$ is irrelevant, since the controlled behavior will never exceed $\mathcal {L}(S/G)$.

As an example, consider the plant G ₁ shown in Fig. 3. Let E _c ={c ₁,c ₂} and E _{u c} ={u} (we generally use the convention that events c,c ^′,c ₁,c ₂,... are controllable, while events u,u ^′,u ₁,u ₂,... are uncontrollable). Consider two supervisors S ₁ and S ₂ for G ₁, defined as follows:

$$\begin{array}{ccc} S_{1}(\sigma) = \{c_{1}, u\} \text{ for all } \sigma & & S_{2}(\sigma) = \left\{\begin{array}{ll} \{c_{1}, u\} & \text{ if } \sigma = \varepsilon \\ \{c_{2}, u\} & \text{ otherwise} \end{array}\right. \end{array} $$

Fig. 3

Plant G ₁ and two closed-loop systems

The closed-loop systems S ₁/G ₁ and S ₂/G ₁ are shown in Fig. 3. For simplicity, states in the closed-loop systems are labeled as in the original plant G ₁, instead of being labeled as pairs (x ₀,ε), (x ₁,c ₁), (x ₃,u), and so on.

Remark 2 (Supervisors vs. controllers)

Supervisory control theory typically uses the term “supervisor” instead of “controller”. The term “supervisor” is well-chosen because in this framework supervisors are like “parents”: they can disable options, but they cannot “make things happen”. For instance, a supervisor cannot force the plant to take a certain transition, even when this transition is controllable. The supervisor can only allow a controllable transition. If this is the only outgoing transition from the current state, then presumably this will happen (although the state may be marked, with the interpretation that the plant “stops” there). But if there are multiple (controllable or uncontrollable) transitions from that state, the plant could choose any of them, without the supervisor having any control over this choice.

2.1.4 A trivial synthesis problem

A supervisor is needed because without it the plant may generate illegal behaviors. The supervisor aims at restricting the plant’s behaviors, so that they are all contained in a set of “good”, or “legal” behaviors.

One way to formalize this idea is to assume that we are given a language of “good” behaviors, L _{a m} , called the admissible marked language. Then we could define a synthesis problem where we ask for a supervisor S (if it exists) such that $\mathcal {L}_{m}(S/G) \subseteq L_{am}$. This, however, is not a very interesting problem, for a number of reasons.

First, in terms of synthesis, the problem is trivial. Indeed, instead of searching for an arbitrary supervisor S, it suffices to simply check whether the most-restrictive (or least-permissive) supervisor works. The most-restrictive supervisor S _{m r} is the supervisor that disables everything that it can disable, i.e., S _{m r} (σ) = E _{u c} , for any σ. If S _{m r} satisfies $\mathcal {L}_{m}(S_{mr}/G) \subseteq L_{am}$, then we have found a solution to the above synthesis problem. Otherwise, it is easy to see that no solution exists. Indeed, any other supervisor S is bound to allow more behaviors than S _{m r} , that is, $\mathcal {L}_{m} (S_{mr}/G) \subseteq \mathcal {L}_{m}(S/G)$. Therefore, if $\mathcal {L}_{m}(S_{mr}/G)$ is not a subset of L _{a m} , neither can $\mathcal {L}_{m}(S/G)$ be.

The fact that this problem is trivial (indeed, it is not really a synthesis problem, but a verification problem) should not necessarily deter us. On the contrary, the easier the problem, the better. However, the second and most important reason why the above problem is not the right one is the fact that the most-restrictive supervisor is rarely what we want. Indeed, the most-restrictive supervisor may be far too restrictive. It may, for example, introduce deadlocks. For the plant G ₁ in Fig. 3, S _{m r} will result in a new deadlock at state 3 of G ₁, since the only events out of that state are controllable events that are disabled by S _{m r} . We therefore need a richer way to specify desirable supervisors. Toward this goal, we introduce next the notion of non-blockingness.

2.1.5 Non-blockingness

Let G be a plant and S a supervisor for G. S is said to be non-blocking for G iff

$$\overline{\mathcal{L}_{m}(S/G)} = \mathcal{L}(S/G). $$

Note that, as mentioned above, $\overline {\mathcal {L}_{m}(S/G)} \subseteq \mathcal {L}(S/G)$ always holds. Therefore, non-blockingness is equivalent to $\mathcal {L}(S/G) \subseteq \overline {\mathcal {L}_{m}(S/G)}$. Non-blockingness says that the closed-loop system should not contain behaviors that cannot be extended to marked behaviors. More precisely, there should be no deadlock states that are not marked, and there should be no absorbing strongly connected components that do not contain a marked state; the latter situation corresponds to a livelock.

As an example, consider again plant G ₁ and supervisors S ₁,S ₂ of Fig. 3. It can be seen that S ₁ is blocking since ($u c_{1}\in \mathcal {L}(S_{1}/G)$ but $\overline {\mathcal {L}_{m}(S_{1}/G)}= \{\varepsilon ,c_{1}\}$); on the other hand, S ₂ is non-blocking.

The following is a useful characterization of non-blockingness. Its proof is straightforward from the definition of non-blockingness.

Lemma 1

S is a non-blocking supervisor for G iff from every reachable state of S/G there is a path to a marked state of S/G.

2.1.6 Safety properties and admissible marked languages

Before we can give a formal statement of the basic supervisory control problem defined below (in Section 2.1.8), we need to formalize the notions of admissible (marked) language and of maximal permissiveness. This is done in this and the next subsections.

An admissible marked language in supervisory control, denoted L _{a m} , captures the set of “legal”, or “good”, behaviors. Typically, the designer first comes up with a prefix-closed regular language L _a (i.e., a regular language such that $\overline {L_{a}}=L_{a}$). L _a captures the set of safe behaviors. For safety properties, such sets are prefix-closed, since for every unsafe behavior σ, every extension σ⋅σ ^′ of σ is also unsafe. Conversely, if σ is safe, every prefix of σ is also safe. Once L _a is defined, the designer typically sets L _{a m} to be the intersection $L_{am} := L_{a} \cap \mathcal {L}_{m}(G)$, so that L _{a m} captures the set of all safe behaviors that can be generated and are marked by the plant. L _{a m} has two useful properties:

• 1. $L_{am} \subseteq \mathcal {L}_{m}(G)$ (by definition, since $L_{am} = L_{a} \cap \mathcal {L}_{m}(G)$).

• 2. L _{a m} is “$\mathcal {L}_{m}(G)$-closed”. Given languages K and L with K⊆L⊆E ^∗, we say that K is L-closed iff

  $$K = \overline{K} \cap L . $$

  Notice that since K⊆L and $K\subseteq \overline {K}$, $K\subseteq \overline {K} \cap L$ always holds. Therefore requiring L-closure is requiring that $\overline {K} \cap L \subseteq K$. Then, it is easy to see that if $L_{am} = L_{a} \cap \mathcal {L}_{m}(G)$ then $\overline {L_{am}} \cap \mathcal {L}_{m}(G) \subseteq L_{am}$.

In the sequel we will assume that the given admissible marked language L _{a m} satisfies conditions 1 and 2 above, i.e., $L_{am} \subseteq \mathcal {L}_{m}(G)$ and L _{a m} is $\mathcal {L}_{m}(G)$-closed. Moreover, we will assume that L _{a m} is regular and we will be using a finite-state automaton to represent it.

Given DES G and $L_{am}\subseteq \mathcal {L}_{m}(G)$, a supervisor S is said to be safe for G with respect to L _{a m} if $\mathcal {L}_{m}(S/G) \subseteq {L_{am}}$, i.e., the only marked strings allowed under control are safe marked strings. We often drop the reference to L _{a m} and simply say that a supervisor is “safe” if it is clear from the context which safety specification is being referred to.

As an example, consider plant G ₁ of Fig. 3. Let L ₂={u c ₂}, which can be interpreted as capturing the safety property “ c ₁ should never occur”. (As explained above, L ₂ is obtained by taking the intersection of $\mathcal {L}_{m}(G_{1})$ with the prefix-closed language containing all strings not including c ₁, i.e., ε, u, c ₂, u u, c ₂ c ₂, and so on.) L ₂ is $\mathcal {L}_{m}(G_{1})$-closed. L ₂ is also a strict subset of $\mathcal {L}_{m}(G_{1})$. Therefore, L ₂ is a valid admissible marked language. Consider the supervisor S ₃ defined as follows:

$$S_{3}(\sigma) = \left\{\begin{array}{ll} \{ u\} & \text{ if } \sigma = \varepsilon \\ \{c_{2}, u\} & \text{ otherwise} \end{array}\right. $$

It can be seen that S ₃ is non-blocking for G ₁ and satisfies $\mathcal {L}_{m}(S_{3}/G_{1}) \subseteq L_{2}$; therefore, S ₃ is safe w.r.t. L ₂.

Remark 3

$L_{am} \subseteq \mathcal {L}_{m}(G)$ is not a restrictive assumption, even for arbitrary L _{a m} , i.e., not necessarily satisfying $L_{am} = L_{a} \cap \mathcal {L}_{m}(G)$. If $L_{am} \not \subseteq \mathcal {L}_{m}(G)$, we can set $L_{am}^{\prime } := L_{am}\cap \mathcal {L}_{m}(G)$ (thus achieving the condition $L_{am}^{\prime } \subseteq \mathcal {L}_{m}(G)$) and ask for a supervisor such that $\mathcal {L}_{m}(S/G) \subseteq L_{am}^{\prime }$. Any such supervisor S also satisfies $\mathcal {L}_{m}(S/G) \subseteq L_{am}$, since $L_{am}^{\prime } \subseteq L_{am}$. Conversely, any supervisor which satisfies $\mathcal {L}_{m}(S/G) \subseteq L_{am}$ also satisfies $\mathcal {L}_{m}(S/G) \subseteq L_{am}^{\prime }$, since $\mathcal {L}_{m}(S/G) \subseteq \mathcal {L}_{m}(G)$. Therefore, asking for a supervisor such that $\mathcal {L}_{m}(S/G) \subseteq L_{am}$ is equivalent to asking for a supervisor such that $\mathcal {L}_{m}(S/G) \subseteq L_{am}^{\prime }$. Thus, we can assume $L_{am} \subseteq \mathcal {L}_{m}(G)$ without loss of generality.

On the other hand, an arbitrary L _{a m} is not necessarily $\mathcal {L}_{m}(G)$-closed, as the following example illustrates.

Consider the plant G ₂ shown in Fig. 4, where $\mathcal {L}_{m}(G_{2})=\{c,cc\}$. Let L ₁={c c}. L ₁ is not $\mathcal {L}_{m}(G_{2})$-closed. Indeed, $c\in \overline {L_{1}}\cap \mathcal {L}_{m}(G_{2})$ but c∉L ₁. It is easy to find a blocking supervisor that ensures $\mathcal {L}_{m}(S/G_{2}) \subseteq L_{1}$. In fact, the most-restrictive supervisor S _{m r} achieves $\mathcal {L}_{m}(S_{mr}/G_{2}) = \emptyset \subseteq L_{1}$. This supervisor is blocking, because ε is in $\mathcal {L}(S_{mr}/G_{2})$ but not in $\overline {\mathcal {L}_{m}(S_{mr}/G_{2})} = \emptyset$. A non-blocking supervisor S that ensures $\mathcal {L}_{m}(S/G_{2}) \subseteq L_{1}$ does not exist. Indeed, S can only disable transitions, and it cannot disable both transitions of G ₂ because this would be blocking. Thus, at least one of c or c c must be in $\mathcal {L}_{m}(S/G_{2})$. But $c \in \mathcal {L}_{m}(S/G_{2})$ is not allowed, because this would imply $\mathcal {L}_{m}(S/G_{2}) \not \subseteq L_{1}$. Therefore it must be that $\mathcal {L}_{m}(S/G_{2})=\{cc\}$. But it is impossible to have S allow c c while it forbids c, since c is a marked prefix of c c. Indeed, this would require S being able to “unmark” some marked states of the plant, which it cannot do.

Fig. 4

Plant G ₂

2.1.7 Maximal permissiveness and uniqueness

An important requirement in the basic supervisory control problem defined below (Section 2.1.8) is maximal permissiveness, namely, the fact that the supervisor must disable events only when strictly necessary to enforce the other requirements (non-blockingness or safety). This is a reasonable requirement, as it forces the supervisor to “disturb” the plant as little as possible, and only when strictly necessary. An important feature of the basic supervisory control framework is that a unique maximally-permissive supervisor always exists. As we shall see, this is not generally the case in the reactive synthesis framework. In this section, we establish this uniqueness property.

First, we define what it means for a supervisor to be more permissive than another supervisor. Consider a plant G and two supervisors S ₁, S ₂ for G. We say that S ₁ is no more permissive than S ₂ iff S ₁(σ) ⊆ S ₂(σ) for any σ. We say that S ₂ is strictly more permissive than S ₁ iff S ₁ is no more permissive than S ₂ and S ₁≠S ₂.

Now, consider an admissible marked language L _{a m} satisfying: (1) $L_{am} \subseteq \mathcal {L}_{m}(G)$ and (2) L _{a m} is $\mathcal {L}_{m}(G)$-closed. A supervisor S which is non-blocking for G and safe w.r.t. L _{a m} is said to be maximally-permissive with respect to G and L _{a m} if there is no supervisor S ^′ which is non-blocking for G, safe w.r.t. L _{a m} , and strictly more permissive than S. Note that, a-priori, there could be more than one maximally-permissive supervisor, as the definition itself does not imply uniqueness. The theorem below shows that, for non-blockingness and safety, a unique maximally-permissive supervisor exists, provided that a supervisor exists at all.

Theorem 1

Consider a plant G, and an admissible marked language L _am satisfying: (1) $L_{am} \subseteq \mathcal {L}_{m}(G)$ and (2) L _am is $\mathcal {L}_{m}(G)$ -closed. If there exists a supervisor which is non-blocking for G and safe w.r.t. L _am then there exists a unique maximally-permissive supervisor S _mpnb which is non-blocking for G and safe w.r.t. L _am .

Proof

The books (Cassandras and Lafortune 2008; Wonham 2015) and the original papers (Ramadge and Wonham 1987; Wonham and Ramadge 1987) contain proofs of Theorem 1, as well as statements of necessary and sufficient conditions for the existence of a safe and non-blocking supervisor and algorithmic procedures for computing S _{m p n b} , given G and given an automaton representation of L _{a m} . These proofs are normally done by defining the property of controllability of languages, showing that it is necessary and sufficient for the existence of a supervisor that exactly achieves a given language, and then proving the existence of the supremal controllable sublanguage.

For the reader interested in understanding the existence of a unique maximally permissive safe and non-blocking supervisor without reading more detailed treatments of supervisory control theory, we provide in Appendix A a direct proof based on disjunction of supervisors. This proof does not require the notions of controllable languages and of supremal controllable languages.

In the sequel, the unique maximally-permissive non-blocking and safe supervisor will be denoted by S _{m p n b} and its associated closed-loop marked language by $\mathcal {L}_{m}(S_{mpnb}/G) = L_{am}^{mpnb}$. Since S _{m p n b} is non-blocking, then $\mathcal {L}(S_{mpnb}/G) = \overline {L_{am}^{mpnb}}$. Moreover, as a consequence of the maximal permissiveness property of S _{m p n b} , the language $L_{am}^{mpnb}$ must contain the closed-loop marked language $\mathcal {L}_{m}(S_{other}/G)$ of any safe and non-blocking supervisor S _{o t h e r} for G wrt L _{a m} .

As an example, consider again plant G ₁ of Fig. 3, admissible marked language L ₂={u c ₂}, and supervisor S ₃ defined above. S ₃ is maximally-permissive w.r.t. G ₁ and L ₂. Indeed, any other supervisor, in order to be strictly more permissive than S ₃, would have to either allow c ₁ initially, which would violate safety w.r.t. L ₂, or allow c ₂ initially, which would violate non-blockingness, or allow c ₁ after u, which again would be blocking.

Remark 4 (Non-uniqueness of supervisors achieving maximal behavior)

Note that, although S _{m p n b} is unique, there are generally more than one supervisors that result in the same maximal closed-loop marked behavior $L_{am}^{mpnb}$ since, by definition, S _{m p n b} might enable infeasible controllable events. As an example, consider the plant G ₃ shown in Fig. 5, where both c ₁,c ₂ are controllable events. Note that all states of G are accepting and as a result, $\mathcal {L}_{m}(G)$ is prefix-closed and $\mathcal {L}_{m}(G)=\mathcal {L}(G)=\{\varepsilon ,c_{1},c_{1} c_{2}\}$.

Fig. 5

Plant G ₃

Let L _{a m} :={ε,c ₁}, which can be interpreted as “ c ₂ should never occur”. The maximally-permissive supervisor w.r.t. G ₃ and L _{a m} defined as above is

$$S_{mpnb}(\sigma) = \left\{\begin{array}{ll} \{c_{1}\} & \text{ if } \sigma = c_{1} \\ \{c_{1}, c_{2}\} & \text{ otherwise} \end{array}\right. $$

Another, less permissive supervisor, is one that always disables c ₂. Both these two supervisors, however, achieve the same maximal closed-loop behavior, which is exactly L _{a m} .

2.1.8 BSCP-NB: basic supervisory control problem with non-blockingness

We are now ready to define the standard supervisory control problem:

Definition 1 (BSCP-NB)

Given DES G and admissible marked language $L_{am} \subseteq \mathcal {L}_{m}(G)$, with L _{a m} assumed to be $\mathcal {L}_{m}(G)$-closed, find, if it exists, or state that there does not exist, a supervisor for G which is non-blocking for G, safe w.r.t. L _{a m} , and maximally-permissive.

Observe that from the safety property $\mathcal {L}_{m}(S/G)\subseteq L_{am}$, we get $\overline {\mathcal { L}_{m}(S/G)}\subseteq \overline {L_{am}}$. Also, from non-blockingness we know that $\mathcal {L}(S/G) = \overline {\mathcal {L}_{m}(S/G)}$. These two properties imply $\mathcal {L}(S/G) \subseteq \overline {L_{am}}$ and thus in BSCP-NB the controlled behavior always stays within the prefix-closure of the admissible marked behavior.

As an example, consider again plant G ₁ of Fig. 3, admissible marked language L ₂={u c ₂}, and supervisor S ₃ defined above. S ₃ is a solution to this BSCP-NB instance, since it is non-blocking, safe, and maximally-permissive, as explained above.

It may happen that BSCP-NB has no solution. For instance, suppose that $\mathcal {L}(G) = \overline { \{ucuc \}}$ and $\mathcal {L}_{m}(G) = \{ uc, ucuc \}$ with E _c ={c} and E _{u c} ={u}. Take L _{a m} ={u c}. Then no safe and non-blocking supervisor exists. Any supervisor will allow uncontrollable event u at the beginning of system operation. But enabling c after observing string u will violate safety, since string u c u will be in the closed-loop language. On the other hand, disabling c after observing string u causes deadlock. Hence, BSCP-NB has no solution in this example.

This shows that the set of uncontrollable events E _{u c} plays a central role in BSCP-NB. Algorithmic procedures that solve BSCP-NB must account for both uncontrollability and non-blockingness, and these two requirements are interdependent.

We postpone the discussion of algorithms to solve BSCP-NB to Section 3.4.1.

Example 2 (Coffee Machine Revisited)

We revisit the coffee machine example at the beginning of Section 2.1, where the “plant” is the automaton G in Fig. 2. To obtain an instance of BSCP-NB, we formalize the specifications of safety and the two allowed recipes described earlier in the form of a language $L_{am} \subseteq \mathcal {L}_{m}(G)$. It is not hard to see that L _{a m} is marked by the non-blocking automaton H shown in Fig. 6. This automaton ensures that grinding precedes brewing, that no grinding occurs after brewing has started, and it allows either one of the two recipes: g b b or g g b b b. Its marked language is also a sublanguage of $\mathcal {L}_{m}(G)$ as we have included self-loops for event c at the states where the coffee machine is not idle, consistent with the structure of G. Observe that automaton H needs to count the number of g and b events, something that is not done in G. It is also straightforward to verify from Fig. 6 that L _{a m} satisfies the $\mathcal {L}_{m}(G)$-closure condition.

Fig. 6

Automaton H that marks the language L _{a m} for the coffee machine example

If E _{u c} ={c} but all other events are controllable, then the solution of BSCP-NB achieves L _{a m} exactly under control, i.e., the maximally permissive non-blocking supervisor S _{m p n b} is such that $\mathcal {L}_{m} (S_{mpnb}/G) = L_{am}$. In other words, in this simple example, the synthesis step is trivial since the specification language is exactly achievable by disabling g, b, or r at the right moment along each run of the plant. Hence, the closed-loop language $\mathcal {L}(S_{mpnb}/G) = \overline {L_{am}}$ is also equal to $\mathcal {L}(H)$. (This is of course not true in general.) Indeed, initially, S _{m p n b} (ε)={c,b,g,r}: only c is feasible and it is uncontrollable, so it must be enabled; the other events are infeasible but added according to the definition of S _{m p n b} . Then the supervisor issues the following control actions for the given observed strings of G: S _{m p n b} (c)={c,g} (i.e., b and r must be disabled to allow grinding to start); S _{m p n b} (c g)={c,g,b} (i.e., r must be disabled until a recipe is completed); S _{m p n b} (c g b)={c,b} (i.e., b must continue since the first recipe is being followed); S _{m p n b} (c g g)={c,b} (i.e., b must start since the second recipe is being followed); S _{m p n b} (c g b b)={c,r} (i.e., r must start since the first recipe is completed); S _{m p n b} (c g g b)={c,b} (i.e., b must continue since the second recipe is being followed); S _{m p n b} (c g g b b)={c,b} (i.e., b must continue since the second recipe is being followed); S _{m p n b} (c g g b b b)={c,r} (i.e., r must start since the second recipe is completed); S _{m p n b} (c g b b r) = S _{m p n b} (c g g b b b r)={c,b,g,r} (i.e., a new cycle can begin); and so forth.

If either event g, b, or r were uncontrollable, then BSCP-NB would have no solution. In the case where g∈E _{u c} for instance, the strings c g ⁿ, n≥3, which are in $\mathcal {L}(G)$, cannot be prevented by control, and they are outside $\overline {L_{am}}$. Similarly for string c b if b is uncontrollable, and for string c r if r is uncontrollable.

2.2 Reactive synthesis

In reactive synthesis, we build correct-by-construction controllers from declarative specifications. Controllers are open dynamical systems. A controller is open in the sense that it has inputs and outputs, and its behavior (its dynamics) depends on the inputs that the controller receives. These inputs come from the controller’s environment (which may also be an open system, receiving as inputs the controller’s outputs). A specification is declarative in the sense that it states how a controller must behave, but is not concerned with its internal structure. Rather, the specification only describes the desired behavior of the controller on the interface level, i.e., using its sets of inputs and outputs.

Let us illustrate the reactive synthesis framework by re-stating the coffee maker example (Section 2.1) in this framework. Consider the interface of the controller of a coffee maker that is depicted in Fig. 7.

Fig. 7

The interface of a controller for a coffee maker

The controller is meant to trigger the mechanical components of the coffee maker. The interface shows that we have one input signal, c. In this example, it is supposed to represent whether the user of the coffee maker has pressed the coffee button. There are also two output signals, namely b and g. While b is supposed to represent whether the brewing unit of the coffee maker is activated, g represents whether the grinding unit is activated.

In reactive synthesis, we assume that the controller evolves in steps, i.e., the controller communicates via input and output signals, which all have some value assigned in every time step. For simplicity, we assume Boolean signals where all values are Boolean. Controllers can therefore be viewed as state machines of type Moore or Mealy. In typical targets for reactive synthesis such as on-chip controllers, this assumption is well-justified, as there is typically a global clock generator in such systems. In the scope of our coffee maker, which serves mainly as an introductory example, we just choose a reasonable step duration.

A reactive system has no designated time of going out-of-service, i.e., for every number of time steps n, we should not synthesize a controller that only works under the assumption that it runs for at most n steps, as letting it run for n+1 time steps is also conceivable. To abstract from this problem, we assume that the controller never goes out of service, and thus runs for an infinite duration. Such an execution produces a trace, which describes in which steps which inputs and outputs are set (i.e., have value t r u e). Formally, a trace is an infinite word w = w ₀ w ₁ w ₂…, where for every $i \in \mathbb {N}$, we have w _i ⊆A P _I ∪A P _O , where A P _I is the set of input signals, and A P _O is the set of output signals. In the case of the coffee maker, A P _I ={c} and A P _O ={g,b}. The following example shows an example trace of a coffee maker controller:

$$ w = \left(\begin{array}{l} c \mapsto \mathbf{false}\\ g \mapsto \mathbf{false}\\ b \mapsto \mathbf{false} \end{array}\!\right)\! \!\left( \begin{array}{l} c \mapsto \mathbf{true}\\ g \mapsto \mathbf{true}\\ b \mapsto \mathbf{false} \end{array}\!\right)\! \!\left( \begin{array}{l} c \mapsto \mathbf{false}\\ g \mapsto \mathbf{true}\\ b \mapsto \mathbf{false} \end{array}\!\right)\! \!\left( \begin{array}{l} c \mapsto \mathbf{false}\\ g \mapsto \mathbf{false}\\ b \mapsto \mathbf{true} \end{array}\!\right)\! \!\left( \begin{array}{l} c \mapsto \mathbf{false}\\ g \mapsto \mathbf{false}\\ b \mapsto \mathbf{true} \end{array}\!\right)\! \!\left( \begin{array}{l} c \mapsto \mathbf{false}\\ g \mapsto \mathbf{false}\\ b \mapsto \mathbf{true} \end{array}\!\right) \ldots $$

(2)

In this trace, the coffee button is pressed in the second step, and grinding is performed in the two steps starting with the second one. Then, the brewing unit of the coffee maker is triggered for three steps.

This behavior of the controller could be one that satisfies its specification. For example, a specification for a coffee maker controller could be that once the coffee button is pressed, grinding should happen for two steps, and afterwards brewing should be done for three time steps while the grinding unit is idle.

To now perform synthesis from this specification, we need to formalize it. In reactive synthesis, this is typically done by describing the specification in a logic. The logic CTL ^⋆ (Emerson and Halpern 1986) is well-suited for this purpose and extends standard Boolean logic by temporal operators and path quantifiers that intuitively allow us to connect the system’s signal valuations in one step with the actions in other, future time steps. In the context of logic, we also call the signals atomic propositions. (CTL stands for Computation Tree Logic.) The informal specification from the previous paragraph would be formalized into CTL ^⋆ as follows:

$$\psi = \mathsf{A} \mathsf{G} \left( c \rightarrow ( g \wedge \mathsf{X} g \wedge \mathsf{X} \mathsf{X} ( (b \wedge \neg g) \wedge \mathsf{X} (b \wedge \neg g) \wedge \mathsf{X} \mathsf{X} (b \wedge \neg g) ) \right) $$

The formula starts with the path quantifier A, which denotes that the expression right of the operator should hold along all executions of a system to be synthesized. It is followed by the temporal operator G, which is called the globally operator. For some formula G ϕ to hold at some point in the execution of a system, ϕ needs to hold for all steps from that point onward.

A specification is required to hold right from the start of the system. Thus, prefixing our coffee maker specification ψ with A G means that the implication c→… has to hold at every step of the system’s execution. The implication in turn describes that (g∧X g∧…) shall happen whenever we have c, i.e., the coffee button has been pressed. The consequent of the implication now is (g∧X g∧X X((b∧¬g)∧X(b∧¬g)∧X X(b∧¬g)), which is a Boolean formula in which the temporal operator X (next) is used. It describes that we need to look one step into the future in the trace of the system to test if some sub-formula holds. So X g holds in the first step in a trace of the system if g holds in the second step of the trace. Likewise, X X g holds in the first step in a trace if g holds in the third step of the trace. This example also shows that the operators in CTL ^⋆ can be chained, which makes it a rich modeling formalism for specifications. Note that the consequent of the implication in ψ describes the informal statement of what shall happen upon a coffee button press from above in a formal way.

To actually synthesize a system from a specification, the specification needs to be realizable, i.e., there has to exist a system implementation for the given interface that ensures that every trace of the system satisfies the specification. Most synthesis algorithms also check realizability, i.e., they do not only synthesize an implementation for realizable specifications, but also detect unrealizability. As a consequence, there is often no distinction between the two steps in the literature.

While testing realizability appears to be trivial and unnecessary, in the practice of synthesis, it is not. For example, the coffee maker specification from above is unrealizable, and despite its short length, this fact is easily overlooked. The reason for unrealizability here is that we might press the coffee button in the first two successive steps of the system’s execution. The specification part X g then requires that grinding is performed in the third step (as the implication is triggered by the second button press), but at the same time the specification part X X((b∧¬g)∧…) requires that grinding does not happen in the third step. This is a contradiction that the system to be synthesized cannot avoid, as the input is not under its control. Therefore, this specification is unrealizable.

There are two ways to fix the specification. One is to allow the system to delay the production of the next cup until a grinding and brewing cycle has finished. This can be done using the eventually operator ( F) of CTL ^⋆. Intuitively, a CTL ^⋆ formula F ϕ holds at a point in a trace of the system if at some point in the future, ϕ holds. The modified specification then looks as follows:

$$\psi = \mathsf{A} \mathsf{G} \left( c \rightarrow \mathsf{F} ( g \wedge \mathsf{X} g \wedge \mathsf{X} \mathsf{X} ( (b \wedge \neg g) \wedge \mathsf{X} (b \wedge \neg g) \wedge \mathsf{X} \mathsf{X} (b \wedge \neg g) ) \right) $$

It is now realizable, partly because there is no requirement that the number of coffees produced matches the number of button presses. Note that the eventually operator does not impose a bound on the number of steps by which a brewing cycle might be delayed. Thus, a system that satisfies this specification could react with a delay that gets longer and longer the more coffees are made. However, none of the contemporary synthesis algorithms produces such implementations, as such a behavior would require an infinite-state implementation, but they only compute finite-state ones. As it can be shown that whenever there exists an implementation for a CTL ^⋆ specification, there also exists a finite-state one, this is also not necessary. So using the eventually operator in this context instead of imposing a maximal bound on the number of steps until when grinding should start is reasonable.

Another possibility to fix the specification is to add an assumption to the specification that expresses that the coffee button cannot be pressed when brewing or grinding is already happening. The new realizable specification would be:

$$\begin{array}{@{}rcl@{}} \psi^{\prime} &=& \mathsf{A} \left( \mathsf{G}((g \vee b) \rightarrow \neg \mathsf{X} c)\rightarrow \mathsf{G} \left( c \rightarrow \mathsf{F} ( \mathsf{X} g \wedge \mathsf{X} \mathsf{X} g \wedge \mathsf{X} \mathsf{X} \mathsf{X} ( (b\! \wedge\! \neg g)\! \wedge\! \mathsf{X} (b\! \wedge\! \neg g)\! \wedge \mathsf{X} \mathsf{X} (b\! \wedge\! \neg g) ) \right) \right) \end{array} $$

An assumption of course always has to be reasonable in practice to make sense in synthesis. If we know that the coffee maker in which the controller is supposed to work ensures that the button cannot be pressed while the maker is running (or alternatively ignores the button press), then the assumption is justified.

After this short introduction to the aims of reactive synthesis, let us now discuss more formally how we specify the intended behavior of the system to be synthesized and how such a system is actually represented.

2.2.1 Computation trees

A reactive system has to satisfy a specification regardless of the input to the system. To get an overview about the possible behaviors of a system, for the scope of synthesis, we typically view a system implementation as a computation tree, as these describe all system behaviors of a reactive system at once. Formally, for some interface (A P _I ,A P _O ) of a reactive system, a computation tree is a tuple 〈T,τ〉, where $T = (2^{\mathsf {AP}_{I}})^{*}$ and $\tau : T \rightarrow 2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}}$. The tree describes all the possible traces by having τ map every input sequence to the system to an output signal valuation that the system produces after having read the input sequence. Without loss of generality, we assume that every node in the computation tree is also labeled by the last input, i.e., we have $\phantom {\dot {i}\!}\tau (t_{0} \ldots t_{n})|_{\mathsf {AP}_{I}} = t_{n}$ for every $t_{0} \ldots t_{n} \in (2^{\mathsf {AP}_{I}})^{+}$. While labeling the nodes in the tree according to the last direction seems to be unnecessary, it allows us to define the logic CTL ^⋆ below in a way that generalizes to applying the logic to Kripke structures (which we define in Section 3.2.1) as well. Note that $\phantom {\dot {i}\!}\tau (\epsilon )|_{\mathsf {AP}_{I}}$ is not constrained in any way and can be freely set by the computation tree.

Figure 8 shows an example computation tree of a coffee maker controller.

Fig. 8

A computation tree of a coffee maker controller. Taking a branch to the left always refers to the input {c↦f a l s e}, whereas the right branches always refer to the input {c↦t r u e}

2.2.2 The temporal logic CTL ^⋆

Let A P be a set of atomic propositions. Expressions in CTL ^⋆ can either be state formulas or path formulas. We define the set of path formulas in the temporal logic CTL ^⋆ inductively by the following rules:

• every CTL ^⋆ state formula is also a CTL ^⋆ path formula

• For every CTL ^⋆ path formula ψ, we have that ¬ψ, G ψ, F ψ, and X ψ are also CTL ^⋆ path formulas;

• For all CTL ^⋆ path formulas ψ and ψ ^′, we have that ψ U ψ ^′, ψ R ψ ^′, ψ∨ψ ^′, and ψ∧ψ ^′ are also CTL ^⋆ path formulas.

The set of state formulas is defined as follows:

• For every p∈A P, p is a CTL ^⋆ state formula;

• For all CTL ^⋆ state formulas ϕ and ϕ ^′, we have that ϕ∨ϕ ^′, ϕ∧ϕ ^′ and ¬ϕ ^′ are also CTL ^⋆ state formulas;

• Given a CTL ^⋆ path formula ψ, A ψ and E ψ are CTL ^⋆ state formulas.

The semantics of CTL ^⋆ is defined over computation trees. Let A P be a set of atomic propositions for A P=A P _I ∪A P _O , ψ be a CTL ^⋆ formula over A P, and 〈T,τ〉 be a computation tree. A branch in 〈T,τ〉 starting in some node t∈T is defined to be a sequence b = b ₀ b ₁ b ₂… such that (1) b ₀ = t, (2) for every $i \in \mathbb {N}$, we have b _i ∈T, and (3) for every $i \in \mathbb {N}$, we have b _i+1 = b _i x for some x⊆A P _I . We denote the suffix of a string b starting at position $j \in \mathbb {N}$ by b ^j, i.e., for b = b ₀ b ₁ b ₂…, we have b ^j = b _j b _j+1 b _j+2….

Given some node t = t ₀…t _n of 〈T,τ〉, we evaluate the validity of a CTL ^⋆ state formula at point t by recursing over the structure of the CTL ^⋆ state formula (where ψ is a CTL ^⋆ path formula and ϕ and ϕ ^′ are CTL ^⋆ state formulas):

• 〈T,τ〉,t⊧p for some p∈A P _I ∪A P _O if p∈τ(t);

• 〈T,τ〉,t⊧¬ϕ if and only if not 〈T,τ〉,t⊧ϕ;

• 〈T,τ〉,t⊧ϕ∨ϕ ^′ if and only if 〈T,τ〉,t⊧ϕ or 〈T,τ〉,t⊧ϕ ^′;

• 〈T,τ〉,t⊧ϕ∧ϕ ^′ if and only if 〈T,τ〉,t⊧ϕ and 〈T,τ〉,t⊧ϕ ^′;

• 〈T,τ〉,t⊧A ψ if for all branches b starting from t, we have 〈T,τ〉,b⊧ψ;

• 〈T,τ〉,t⊧E ψ if for some branch b starting from t, we have 〈T,τ〉,b⊧ψ.

Likewise, given some branch b = b ₀ b ₁… of 〈T,τ〉, we evaluate the validity of a CTL ^⋆ path formula on b by recursing over the structure of the CTL ^⋆ path formula (where ψ and ψ ^′ are CTL ^⋆ path formulas and ϕ is a CTL ^⋆ state formula):

• 〈T,τ〉,b⊧ϕ if and only if 〈T,τ〉,b ₀⊧ϕ;

• 〈T,τ〉,b⊧¬ψ if and only if not 〈T,τ〉,b⊧ψ;

• 〈T,τ〉,b⊧ψ∨ψ ^′ if and only if 〈T,τ〉,b⊧ψ or 〈T,τ〉,b⊧ψ ^′;

• 〈T,τ〉,b⊧ψ∧ψ ^′ if and only if 〈T,τ〉,b⊧ψ and 〈T,τ〉,b⊧ψ ^′;

• 〈T,τ〉,b⊧X ψ if and only if 〈T,τ〉,b ¹…⊧ψ;

• 〈T,τ〉,b⊧G ψ if and only if for all $j \in \mathbb {N}$, we have 〈T,τ〉,b ^j⊧ψ;

• 〈T,τ〉,b⊧F ψ if and only if for some $j \in \mathbb {N}$, we have 〈T,τ〉,b ^j⊧ψ;

• 〈T,τ〉,b⊧ψ U ψ ^′ if and only if for some $j \in \mathbb {N}$, we have 〈T,τ〉,b ^j⊧ψ ^′, and for all 0≤i<j, we have 〈T,τ〉,b ⁱ⊧ψ;

• 〈T,τ〉,b⊧ψ R ψ ^′ if either for all $j \in \mathbb {N}$, we have 〈T,τ〉,b ^j⊧ψ ^′, or there exists some $j \in \mathbb {N}$ such that 〈T,τ〉,b ^j⊧ψ, and for all i≤j, we have 〈T,τ〉,b ⁱ⊧ψ ^′.

We define the set of trees for which all children of the root node satisfy some CTL ^⋆ state formula ϕ to be the models of ϕ.¹

Given some CTL ^⋆ state formula ϕ, we say that ϕ is realizable for some interface $\mathcal {I} = (\mathsf {AP}_{I},\mathsf {AP}_{O})$ if there exists an $2^{\mathsf {AP}_{O} \cup \mathsf {AP}_{I}}$-labeled $2^{\mathsf {AP}_{I}}$-tree that is a model of ϕ (and that copies the last input correctly to its node labels).

CTL is the subset of CTL ^⋆ obtained by restricting the path formulas to be X ϕ, F ϕ, G ϕ, and ϕ U ϕ ^′, where ϕ,ϕ ^′ are CTL state formulas. LTL is the subset of CTL ^⋆ consisting of the formulas A ϕ in which the only state subformulas in ϕ are atomic propositions.

Definition 2 (Realizability Problem)

Given some system interface $\mathcal {I} = (\mathsf {AP}_{I},\mathsf {AP}_{O})$ and some CTL ^⋆ state formula ϕ (the specification), the realizability problem is to test if there exists some computation tree 〈T,τ〉 with $T = (2^{\mathsf {AP}_{I}})^{*}$ and $\tau : T \rightarrow 2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}}$ that copies the respective last input to its node labels correctly and such that 〈T,τ〉 is a model of ϕ.

2.2.3 Transducers

The definition of the realizability problem above has one slight problem: while it clearly defines what constitutes a computation tree that represents a solution to the synthesis problem, such computation trees have infinitely many nodes. Thus, the model is not directly usable for actually synthesizing systems, which have to be finite-state in order to be implementable in the field. As a remedy to this problem, we define (deterministic) transducers here, which serve as finite generators for computation trees. It can be shown that for every realizable specification, there exists a computation tree that is generated by a transducer, and thus for the scope of synthesis, it suffices to search for a transducer that generates a suitable computation tree.

Formally, a transducer over some set of input atomic propositions A P _I and output atomic propositions A P _O is defined as a tuple $\mathcal {T} = (S,2^{\mathsf {AP}_{I}},2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}},\delta ,s_{0},L)$, where S is a (finite) set of states, $\delta : S \times 2^{\mathsf {AP}_{I}} \rightarrow S$ is the transition function, s ₀∈S is the initial state of the system, and $L : S \rightarrow 2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}}$ assigns to each state its labeling. We require that the states always represent the last input to the transducer, i.e., we have $\phantom {\dot {i}\!}L(s)|_{\mathsf {AP}_{I}} = x$ for every s∈S such that for some s ^′∈S, we have δ(s ^′,x) = s. The definition of a transducer corresponds to the definition of a Mealy machine that is common in the practice of hardware design, but with the addition that the transducer always produces the last output.

We say that some word $w = w_{0} w_{1} \ldots \in (2^{\mathsf {AP}_{O}} \times 2^{\mathsf {AP}_{I}})^{\omega }$ is a trace of $\mathcal {T}$ if there exists some sequence of states π = π ₀ π ₁…∈S ^ω such that π ₀ = s ₀, and for all $i \in \mathbb {N}$, we have π _i+1 = δ(π _i ,x) for some x⊆A P _I and w _i = L(π _i ). We call π a run of the transducer in this context. We can obtain a computation tree 〈T,τ〉 from a transducer $\mathcal {T} = (S,2^{\mathsf {AP}_{I}},2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}},\delta ,s_{0},L)$ by setting $T = (2^{\mathsf {AP}_{I}})^{*}$ and τ(t ₀ t ₁…t _n ) = L(δ(…δ(δ(s ₀,t ₀),t ₁),…,t _n )) for all t ₀ t ₁…t _n ∈T.

To illustrate the concept of transducers, Fig. 9 shows an example transducer for a coffee maker controller that could have the same set of traces as the computation tree in Fig. 8. As the computation tree in Fig. 8 is not fully shown (after all, it is infinite), we can however not be sure about that.

Fig. 9

An example transducer structure for a coffee maker controller with A P _I ={c} and A P _O ={b,g}. The initial state is marked with an incoming arrow. Edges are labeled by simple Boolean formulas that represent the conditions over the input characters under which the transition is taken

2.2.4 Reactive Synthesis Problem (RSP)

Definition 3 (RSP)

Given some system interface $\mathcal {I} = (\mathsf {AP}_{I},\mathsf {AP}_{O})$ and some CTL ^⋆ state formula ϕ (the specification), the reactive synthesis problem (RSP) for $\mathcal {I}$ and ϕ is to compute a transducer over $\mathcal {I}$ whose computation tree satisfies ϕ whenever it exists, and to deduce that no such transducer exists whenever this is the case.

We postpone a discussion of algorithms to solve RSP to Section 3.4.2.

2.2.5 Maximal permissiveness in RSP

The reader may have noted that in the definition of the supervisory control problem, we are concerned with computing maximally permissive controllers, but in the reactive synthesis problem, we just search for any controller that satisfies the specification. There are two reasons for this difference. First of all, the reactive synthesis problem was originally defined in this form by Church (1963). The second, more important reason is however that in general, maximally-permissive controllers do not exist.

To actually discuss maximally-permissiveness in the context of the reactive synthesis problem, we first of all need to change our transducer definition, as the transducers currently dealt with are deterministic. For a transducer $\mathcal {T} = (S,2^{\mathsf {AP}_{I}},2^{\mathsf {AP}_{O}},\delta ,s_{0},L)$, we redefine δ to map from $S \times 2^{\mathsf {AP}_{I}}$ to a subset of S. This way, whenever the controller is in some state s and reads some input x⊆A P _I , then it can transition to any of the states in δ(s,x). We require that for all s∈S and x⊆A P _I , δ(s,x) is non-empty. We furthermore allow more than one initial state and modify the definition of a computation tree of account for these facts.

Computation trees for such non-deterministic transducers $\mathcal {T} = (S,2^{\mathsf {AP}_{I}},2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}},\delta ,s_{0},L)$ are then tuples 〈T,τ〉 with T⊆S ^∗ such that for some s ₀∈S ₀, we have:

• 1.1. τ(𝜖) = L(s ₀)

• 1.2. $|\{ s \in S \mid s \in T \}| = |2^{\mathsf {AP}_{I}}|$ and $\{L(s)|_{2^{\mathsf {AP}_{I}}} : s \in S \wedge s \in T\} = 2^{\mathsf {AP}_{I}}$

• 1.3. For all s∈S with s∈T, we have $s \in \delta (s_{0},L(s)|_{2^{\mathsf {AP}_{I}}})$

• 2.1. For all t = t ₀…t _n ∈T∖{𝜖}, we have τ(t ₀…t _n ) = L(t _n )

• 2.2. For all t = t ₀…t _n ∈T∖{𝜖}, we have that $|\{ s \in S \mid ts \in T \}| = |2^{\mathsf {AP}_{I}}|$ and $\{L(ts)|_{2^{\mathsf {AP}_{I}}} : ts \in T\} = 2^{\mathsf {AP}_{I}}$

• 2.3. For all t = t ₀…t _n ∈T∖{𝜖} with n≥1, we have $t_{n} \in \delta (t_{n-1}, L(t_{n})|_{2^{\mathsf {AP}_{I}}})$.

Note that we actually only have three different conditions, but for the sake of completeness need one copy of each condition for the root and one copy for the other nodes. The conditions together ensure that all the possible computation trees of a transducer are input-complete, i.e., from every node, they have one possible successor for every next input. We say that a non-deterministic transducer satisfies some CTL* state formula ϕ if every input-complete computation tree induced by the transducer satisfies ϕ (at the root).

We furthermore say that two computation trees 〈T,τ〉 and 〈T ^′,τ ^′〉 are isomorphic if there exists some bijective function f:T→T ^′ with |f(t)|=|t| for all t∈T and τ(t) = τ ^′(f ^′(t)) for all t∈T. Isomorphic trees effectively represent the same behavior of a reactive system although the internal structure of the transducers from which the trees are possibly generated may be different.

We call a non-deterministic transducer maximally permissive for some CTL* state formula specification ϕ and interface $\mathcal {I} = (\mathsf {AP}_{I},\mathsf {AP}_{O})$ if (1) the transducer branches over A P _I and satisfies ϕ on all trees induced by the transducer, and (2) every input-responsive computation tree for $\mathcal {I}$ that satisfies ϕ (at the root) has an isomorphic computation tree that is induced by the transducer.

Note that maximally permissive finite-state controllers/transducers do not exist in general for RSP. For example, let A P _I ={r}, A P _O ={g}, ϕ=A G F g, and $\mathcal {T} = (S,2^{\mathsf {AP}_{I}},2^{\mathsf {AP}_{I} \cup \mathsf {AP}_{O}},\delta ,s_{0},L)$ be any transducer that satisfies ϕ. Since $\mathcal {T}$ satisfies ϕ, there has to be some upper bound $b \in \mathbb {N}$ on the number of steps until g is set to true by the controller for the first time, as otherwise, there exists some path in some computation tree induced by $\mathcal {T}$ on which G F g is not satisfied. However, since a controller that sets g to true every (b+1)th cycle satisfies ϕ as well, $\mathcal {T}$ cannot be maximally permissive. As we started with an arbitrary finite-state transducer, this proves that no controller can be maximally permissive.

Section 3.2.5 contains a more detailed discussion of maximal permissiveness in the reactive synthesis context.

3 Bridging the gap

In this section, we discuss how to bridge the gap between the synthesis problems considered in supervisory control and reactive synthesis. We do this by establishing relations (e.g., reductions) between some specific problems studied in these frameworks. The general situation is described in Fig. 10, where the basic supervisory control problem (BSCP-NB) and the reactive synthesis problem (RSP) are the cases at the cliffs of the gap. We introduce problems that conceptually lie in between BSCP-NB and RSP in order to bridge the gap. These problems always differ in one aspect from their neighbors, and we can perform reductions between these problems. As a result, we can move gently between the BSCP-NB and RSP problems, which simplifies understanding the concepts to follow.

Fig. 10

Relations between different synthesis and control problems

However, our bridge does not exactly meet in the middle. The reason is that the aim of supervisory control and the aim of reactive synthesis slightly differ. In supervisory control, we always want our supervisor to be maximally permissive (being a “parent”), as it should only block undesired actions. In reactive synthesis, on the other hand, where maximal permissiveness is unachievable in general, we want our controller to actively enforce certain properties, possibly at the expense of preventing certain overall system behavior that is unproblematic. This mismatch, and the lack of study of the general reactive synthesis problem with maximal permissiveness, RSCP _max (see Definition 8 that follows), prevent us from performing a sequence of reductions that map the problems completely onto each other.

Our focus in this paper is on the left-side of the bridge: we present formal reductions from BSCP-NB to a special instance of RSCP _max. Specifically, we show in Section 3.1 that BSCP-NB is equivalent to a simpler supervisory control problem in which only non-blockingness is required, called SSCP, and which simplifies the reduction to the reactive synthesis setting. In Section 3.2 we define a reactive synthesis problem with an explicit notion of plants, called RSCP. This makes it easier to capture supervisory control problems where the plant is an input to the problem. RSCP does not generally admit maximally-permissive solutions, but does so for the non-blocking requirement, which is the only requirement of SSCP. In Section 3.3 we show how SSCP can be reduced to a variant of RSCP which requires maximal permissiveness.

Regarding the right side of the bridge, we discuss in Section 3.5 the links between reactive synthesis with plants and reactive synthesis without plants.

The center of the bridge is represented as an “automaton vehicle.” This vehicle captures the fact that at an algorithmic level, the problems on either side of the gap are solved by applying automata-theoretic techniques, as discussed in Section 3.4.2.

3.1 Simplifying the supervisory control problem

In view of reducing BSCP-NB to the reactive synthesis framework, we first reduce BSCP-NB to a simpler problem. In particular, we will eliminate the safety specification L _{a m} by incorporating it into the plant. This can be done by taking as new plant the product of the original plant G and an automaton recognizing L _{a m} . The simpler problem asks for a non-blocking supervisor for the new plant. We next formalize this idea.

3.1.1 Incorporating safety into the plant

Let G=(X,x ₀,X _m ,E,δ) be a DES plant. Let $L_{am}\subseteq \mathcal {L}_{m}(G)$ and let L _{a m} be $\mathcal { L}_{m}(G)$-closed. Let $A=(X^{A},{x_{0}^{A}},{X_{m}^{A}},E,\delta ^{A})$ be a deterministic finite-state automaton such that $\mathcal { L}_{m}(A)=L_{am}$ and $\mathcal {L}(A) = E^{*}$. We can assume without loss of generality that A is complete in the sense that its transition function δ ^A is total. Therefore, every string in E ^∗ has a unique run in A, although only some runs will generally end up in a marked state; in fact, A is generally a blocking automaton, since strings outside $\overline {L_{am}}$ will never reach a marked state. (The fact that $\mathcal {L}(A) \not \subseteq \mathcal {L}(G)$ is not a problem; this will become apparent below.)

The product of G and A, denoted by G×A, is defined to be the automaton

$$G\times A = (X\times X^{A}, (x_{0},{x_{0}^{A}}), X_{m}\times {X_{m}^{A}}, E, \delta^{\prime}) $$

such that

$$\delta^{\prime}\left( (x,x^{A}),e\right) = \left\{\begin{array}{l} \left( \delta(x,e),\delta^{A}(x^{A},e)\right) \\ \text{if}\,\delta(x,e)\,\text{is defined}\,(\delta^{A}\text{ is total, so }\delta^{A}(x^{A},e)\text{ is always defined)} \\ \text{undefined}\quad \text{otherwise} \end{array}\right. $$

It follows from the construction of A and the assumptions on L _{a m} and A that

$$\begin{array}{@{}rcl@{}} \mathcal{L}(G \times A) & = & \mathcal{L}(G) \cap \mathcal{L}(A) = \mathcal{L}(G) \cap E^{*} = \mathcal{L}(G) \quad\text{ and }\quad \\ \mathcal{L}_{m}(G \times A) & = & \mathcal{L}_{m}(G) \cap \mathcal{L}_{m}(A) = \mathcal{L}_{m}(G) \cap L_{am} = L_{am}. \end{array} $$

G and G×A have the same set of events E, thus also the same subsets of controllable and uncontrollable events. Therefore, any supervisor S for G is also a supervisor for G×A, and vice versa. This allows us to state the following result.

Theorem 2

Let G=(X,x ₀ ,X _m ,E,δ), $L_{am}\subseteq \mathcal {L}_{m}(G)$ , and assume that L _am is $\mathcal {L}_{m}(G)$ -closed. Let A be a complete DFA such that $\mathcal {L}_{m}(A)=L_{am}$. Let S be a supervisor for G, and therefore also for G×A. Then, the following statements are equivalent:

• 1. S solves BSCP-NB for plant G with respect to admissible marked language L _am .

• 2. S solves BSCP-NB for plant G×A with respect to admissible marked language $\mathcal {L}_{m}(G \times A)$.

Proof

The proof is given in Appendix B.

To the best of our knowledge, the result in Theorem 2 does not appear explicitly in the published literature, although it can be inferred rather straightforwardly from the algorithmic procedure for solving BSCP-NB originally presented in Ramadge and Wonham (1987), Wonham and Ramadge (1987). Our proof in Appendix B is direct and relies only on the concepts introduced so far in this paper.

3.1.2 SSCP: simple supervisory control problem

Theorem 2 allows to reduce BSCP-NB to a simpler problem, namely, that of finding a maximally-permissive non-blocking supervisor for a given plant, with no external admissible marked behavior. We call the resulting problem the Simple Supervisory Control Problem (SSCP) and restate it formally:

Definition 4 (SSCP)

Given DES G, find (if it exists, or state that none exists) a maximally-permissive non-blocking supervisor for G, that is, a supervisor S which is non-blocking for G, and such that there is no supervisor S ^′ which is non-blocking for G and strictly more permissive than S.

Corollary 1

BSCP-NB and SSCP are equivalent problems, i.e., each one can be reduced to the other with a polynomial-time reduction.

Proof

SSCP is equivalent to the special case of BSCP-NB with $L_{am} := \mathcal {L}_{m}(G)$. This is because $\mathcal { L}_{m}(G)$ is trivially $\mathcal {L}_{m}(G)$-closed and $\mathcal {L}_{m}(S/G)\subseteq \mathcal {L}_{m}(G)$ always holds. Obviously this special case of BSCP-NB can be reduced to BSCP-NB. Conversely, Theorem 2 demonstrates that BSCP-NB can be reduced to this special case of BSCP-NB. This reduction is polynomial-time because G×A can be computed in polynomial time from G and A. Therefore all three problems, BSCP-NB, BSCP-NB with $L_{am} := \mathcal {L}_{m}(G)$, and SSCP are equivalent with polynomial-time reductions.

It also follows from the above results and Theorem 1 that if a solution to SSCP exists, then this solution is unique, i.e., the maximally-permissive non-blocking supervisor is unique.

3.1.3 Finite-memory, state-based supervisors

We will use SSCP to establish a precise connection between supervisory control and reactive synthesis. In this regard, we prove a useful property for the type of supervisors that need to be considered in solving SSCP.

A supervisor is a function S:E ^∗→2^E. The domain of this function is E ^∗, which is an infinite set. This makes it a priori possible for S to require infinite memory. Fortunately, it can be shown that finite-memory, and in particular state-based supervisors, are sufficient for SSCP.

Definition 5

Let G=(X,x ₀,X _m ,E,δ) be a DES plant with E = E _c ∪E _{u c} and let S:E ^∗→2^E be a supervisor for G. S is said to be state-based if

$$\forall \sigma_{1},\sigma_{2}\in E^{*} : \delta(x_{0},\sigma_{1}) = \delta(x_{0},\sigma_{2}) \implies S(\sigma_{1}) = S(\sigma_{2}). $$

That is, S is state-based if it outputs the same decision for two behaviors σ ₁,σ ₂ of G that end up in the same state. Therefore, S only needs to know the current state of the plant in order to decide which controllable events should be allowed. Note that we assume that, when one or both of δ(x ₀,σ ₁),δ(x ₀,σ ₂) are undefined, the equality δ(x ₀,σ ₁) = δ(x ₀,σ ₂) is false, and therefore in that case the implication is trivially true. Given that, Definition 5 does not constrain the structure of S outside of $\mathcal {L}(G)$, i.e., for strings in $E^{*} \setminus \mathcal {L}(G)$. This is because we do not need to make any assumptions regarding the form of S over $E^{*} \setminus \mathcal {L}(G)$, since these control actions will never be invoked when S is applied to G.

Let S be a state-based supervisor for G, and assume all states of G are reachable, that is, ∀x∈X:∃σ∈E ^∗:δ(x ₀,σ) = x; note that unreachable states can be removed from X without affecting SSCP. Then the action of S on G can be viewed as a function S ^′:X→2^E, where S ^′(x) = S(σ) where σ is any string such that δ(x ₀,σ) = x ( x is reachable, so at least one such σ exists). Because S is state-based, it returns the same choice S(σ ^′) = S(σ) for any other string σ ^′ such that δ(x ₀,σ ^′) = x. Therefore, S ^′ is well-defined. Thus, we can assume, without loss of generality, that a state-based supervisor for G is a function S:X→2^E. As in the case of general supervisors, we assume that E _{u c} ⊆S(x), for all x∈X, to ensure that a state-based supervisor never disables an uncontrollable event.

In addition, the definition of the closed-loop system S/G can be simplified in the case of state-based supervisors. In particular, S/G can be defined as $S/G = (X^{\prime },x_{0}^{\prime },X_{m}^{\prime },E,\delta ^{\prime })$ where X ^′ = X (instead of X×L(G)), $x_{0}^{\prime } = x_{0}$, $X_{m}^{\prime } = X_{m}$, and

$$\delta^{\prime}(x, e) = \left\{\begin{array}{ll} \delta(x,e) & \text{ if }\delta(x,e)\text{ is defined and } e\in S(x) \\ \text{undefined} & \text{ otherwise.} \end{array}\right. $$

The following result states that in order to solve the SSCP it suffices to consider only state-based supervisors.

Theorem 3

The solution to SSCP, if it exists, is a state-based supervisor.

Proof

Let S _{m p n b} be the unique solution of SSCP. Suppose that δ(x ₀,σ ₁) = δ(x ₀,σ ₂) = x _p but that S _{m p n b} (σ ₁)≠S _{m p n b} (σ ₂). Then there must exist e _c ∈E _c such that e _c ∈S _{m p n b} (σ ₁) ∖ S _{m p n b} (σ ₂). (Recall that we assume that all uncontrollable events are always enabled by a supervisor.) Since δ(x ₀,σ ₁) = δ(x ₀,σ ₂) = x _p , the post-languages in G from x _p are the same, i.e.,

$$\begin{array}{@{}rcl@{}} \mathcal{L}(G) / \sigma_{1} & = & \mathcal{L}(G) / \sigma_{2} \\ \mathcal{L}_{m}(G) / \sigma_{1} & = & \mathcal{L}_{m}(G) / \sigma_{2} \end{array} $$

Since in SSCP the control problem involves the simple safety specification ${\mathcal {L}_{m}(G)}$ and the non-blocking property, as captured by the marked states of G, the decision to enable or not an event after a given (safe) string σ depends entirely on the post-language after σ, equivalently, on the state δ(x ₀,σ) reached by σ, since the states of G are equivalence classes for future behavior. (Recall Lemma 1.) Thus, no such e _c can exist at state x _p , otherwise S _{m p n b} (σ ₁) would be incorrect or S _{m p n b} (σ ₂) would not be maximally permissive. Hence, S _{m p n b} is a state-based supervisor.

The consequence of Theorem 3 is that in order to solve SSCP, it suffices to search over state-based supervisors. The state-based supervisor that satisfies the requirements of SSCP among all state-based supervisors will be equal to S _{m p n b} , the solution of SSCP.

As an illustration of state-based supervisors, consider our running example, and supervisors S ₁ and S ₂ defined in Section 2.1.3 and illustrated in Fig. 3. Both S ₁ and S ₂ are state-based and can be equivalently defined as follows:

$$\begin{array}{ccc} S_{1}(x) = \{c_{1}, u\} \text{ for all } x\in\{x_{0},x_{1},x_{2},x_{3}\} & & S_{2}(x) = \left\{\begin{array}{ll} \{c_{1} , u\} & \text{ if } x = x_{0} \\ \{c_{2}, u\} & \text{ if } x\in\{x_{1},x_{2},x_{3}\} \end{array}\right. \end{array} $$

Also consider supervisor S ₃ defined in Section 2.1.6. S ₃ is also state-based and can be equivalently defined as follows:

$$\begin{array}{ccc} S_{3}(x) = \left\{\begin{array}{ll} \{ u \} & \text{ if } x = x_{0} \\ \{c_{2} , u\} & \text{ if } x\in\{x_{1},x_{2},x_{3}\} \end{array}\right. \end{array} $$

3.2 Reactive synthesis with plants

Most classical reactive synthesis frameworks (Manna and Wolper 1984; Pnueli and Rosner 1989a) do not have a notion of plant. In Pnueli and Rosner (1989a), the realizability problem is defined as the problem of synthesizing, given a temporal logic specification ϕ, an input-output strategy that implements ϕ. This is also how the reactive synthesis problem (RSP) is defined in Section 2.2. An exception to the above is the work of Madhusudan (2001), where the control problem for non-reactive environments ² is defined as the problem of synthesizing a controller for a given plant modeled as a finite-state Kripke structure, so that the closed-loop system satisfies a specification in CTL or CTL ^⋆.

In view of building a bridge between supervisory control and reactive synthesis, in this section we recall Madhusudan’s reactive synthesis problem with an explicit notion of plant, giving it the name reactive synthesis control problem (RSCP). In Section 3.5 we discuss links between RSCP and RSP.

3.2.1 Plants as kripke structures

As done in Madhusudan (2001), a plant can be captured as a transition system, specifically a form of Kripke structure:

$$P = (W, w_{0}, R, AP, L) $$

where

• A P is a set of atomic propositions.

• W is a set of states, w ₀∈W being the initial state. W is (implicitly) partitioned into two disjoint subsets

  $$W = W_{s} \cup W_{e} $$

  W _s models the system states (where the system must choose a move). W _e models the environment states (where the environment must choose a move).

• R⊆W×W is the transition relation.

• L:W→2^AP is a labeling function mapping every state w to a set of propositions true in this state. L must be total.

We assume that R is total, that is, for any w∈W, there exists w ^′∈W such that (w,w ^′)∈R. We define s u c c _P (w)={w ^′∣(w,w ^′)∈R}. Because R is total, s u c c _P (w)≠∅ for all w∈W. When P is clear from context we write s u c c instead of s u c c _P .

As an example, consider the Kripke structure P ₁ shown in Fig. 11. States drawn as circles are system states. The square state is an environment state (it is also the initial state). The arrows between states represent the transition relation. Notice that there is at least one outgoing transition from every state, which ensures that the transition relation is total. P ₁ has a single atomic proposition p holding only at state 3.

Fig. 11

Kripke structure P ₁

A Kripke structure plant is called finite when its set of states is finite.

3.2.2 Using CTL ^⋆ for Kripke Structures

We have introduced the temporal logic CTL ^⋆ for the specification of a system to be synthesized in Section 2.2.2. This logic is equally useful for specifying control objectives in plants. In this context, we evaluate the CTL ^⋆ formula on the tree that is induced by the Kripke structure.

Let P=(W,w ₀,R,A P,L) be a Kripke structure. We say that P induces a computation tree 〈T,τ〉 if the following conditions hold:

• T⊆W ^∗

• {t∈T:|t|=1}={w∈W:(w ₀,w)∈R}

• τ(𝜖) = L(w ₀)

• For all t = t ₀ t ₁…t _n ∈T, the set of t ^′ s children is precisely {t ₀ t ₁…t _n t _n+1∣t _n+1∈W,(t _n ,t _n+1)∈R}

• For all t = t ₀ t ₁…t _n ∈T, we have τ(t) = L(t _n ).

In a nutshell, the computation tree that is induced by a Kripke structure represents all possible paths in the Kripke structure at the same time. A path of P is an infinite sequence π = w ₀ w ₁⋯, such that w _i ∈W and (w _i ,w _i+1)∈R, for all i≥0.

Given some CTL ^⋆ state formula ϕ, we say that some state w∈W satisfies ϕ if the computation tree for the Kripke structure P _w =(W,w,R,A P,L) that only differs from P by its initial state, satisfies ϕ. We say that a plant satisfies a CTL ^⋆ state formula ϕ, written formally as P⊧ϕ, if the tree induced by P satisfies ϕ.

3.2.3 Strategies

A plant P may not generally satisfy a CTL ^⋆ specification ϕ. A strategy aims to restrict P so that it satisfies ϕ. Let P=(W,w ₀,R,A P,L) with W = W _s ∪W _e . A strategy for P is a (total) function

$$f : W^{*} \times W_{s} \rightarrow 2^{W} $$

such that for all u∈W ^∗,w∈W _s , f(u,w) is a non-empty subset of s u c c(w). The intuition is that f observes the history of all states visited previously, u∈W ^∗, as well as the current system state w∈W _s , and chooses to allow moves to only a subset (but a non-empty subset) of the successors of w.

A strategy f is state-based if for all u ₁,u ₂∈W ^∗, and for all w∈W _s , we have f(u ₁,w) = f(u ₂,w). This means that the strategy only depends on the current state w and not on the previous history u.

A strategy f defines a new (infinite-state) Kripke structure P ^f:

$$P^{f} = (W^{f},{w_{0}^{f}},R^{f},AP,L^{f}) $$

where

• W ^f = W ^∗×W

• ${w_{0}^{f}} = (\epsilon ,w_{0})$

• R ^f={((u,w),(u⋅w,w ^′))∣(w∈W _e ∧(w,w ^′)∈R)∨(w∈W _s ∧w ^′∈f(u,w))}

• L ^f(u,w) = L(w) for all u∈W ^∗, w∈W.

Note that R ^f is guaranteed to be total. This is because R is assumed to be total, and f is required to be such that f(u,w)≠∅.

Some strategies for P ₁ are shown in Fig. 12. The strategies f ₁,f ₂,f ₃ are state-based, where f ₂ disables the transition 2→1, f ₃ disables the transition 1→2, and f ₁ disables both of these transitions.

Fig. 12

Some strategies enforcing A F p on the Kripke structure P ₁ of Fig. 11

3.2.4 Reactive Synthesis Control Problem (RSCP)

Given Kripke structure plant P and CTL ^⋆ formula ϕ, we say that a strategy f enforces ϕ on P if it is the case that P ^f⊧ϕ. The reactive synthesis control problem (RSCP) is the following:

Definition 6 (RSCP)

Given finite Kripke structure plant P and CTL ^⋆ formula ϕ, find (if it exists, or state that there does not exist) a strategy which enforces ϕ on P.

RSCP-CTL denotes RSCP where ϕ is required to be a CTL formula; RSCP-LTL denotes RSCP where ϕ is required to be an LTL formula. (Similarly for RSP.)

3.2.5 Maximal permissiveness in RSCP

The reader may have observed that in the definition of RSCP above, we did not require that the strategy f be maximally-permissive in any way. The reason is that unique maximally-permissive strategies do not always exist. An example is given below. Let us first introduce some terminology.

Let f ₁,f ₂ be two strategies for a plant P. f ₁ is said to be no more permissive than f ₂ iff for all u∈W ^∗, w∈W _s such that u w is a sequence of states that can be a prefix of a run in $\phantom {\dot {i}\!}P^{f_{2}}$, f ₁(u,w)⊆f ₂(u,w). f ₂ is said to be strictly more permissive than f ₁ if f ₁ is no more permissive than f ₂ and f ₁(u,w)≠f ₂(u,w) for some u∈W ^∗, w∈W _s such that u w is a sequence of states that can be a prefix of a run in $\phantom {\dot {i}\!}P^{f_{2}}$.

f ₁ is said to be maximally permissive with respect to specification ϕ if f ₁ enforces ϕ and there is no strategy f ₂ which enforces ϕ and is strictly more permissive than f ₁.

Let us return to the example of Figs. 11 and 12. Suppose we wish to find a strategy that makes the plant P ₁ meet the specification A F p. The latter states that all executions must eventually reach a state satisfying p. Since state 3 is the only state satisfying p in P ₁, we want all executions to reach state 3. On its own, P ₁ does not satisfy A F p, because it contains two executions “oscillating” between states 1 and 2.

All three strategies f ₁,f ₂,f ₃ of Fig. 12 enforce A F p on P ₁. Strategies f ₂ and f ₃ are strictly more permissive than f ₁, and are the two (incomparable) most permissive state-based strategies for A F p. However, there are infinitely many other, more permissive strategies which also enforce A F p, not shown in Fig. 12. In particular, any (non-state-based) strategy which allows a finite number of transitions between states 1 and 2 before forbidding them, enforces A F p.

There is a set of increasingly permissive such strategies, but the limit of this set is the strategy that forbids nothing, and this strategy no longer enforces A F p. This example shows that a unique maximally-permissive strategy does not generally exist for the RSCP problem.

In Section 3.3.2, we will be concerned with CTL ^⋆ specifications of the form A G E F q, where q is a CTL ^⋆ or CTL state formula without any temporal operator. For these, maximally-permissive strategies do exist, and they are at the same time state-based. Let us conclude the discussion of maximal permissiveness by proving this fact.

Lemma 2

Let P=(W,w ₀ ,R,AP,L) be a Kripke structure, and q be a CTL state formula without temporal operators. If there exists a strategy enforcing A G E F q on P, then there exists a unique, maximally-permissive strategy enforcing A G E F q on P; moreover, this strategy is state-based.

Proof

Let A be the set of states of P from which there is no state reachable in P that satisfies q. Then any strategy f that allows to eventually visit a state of A in P ^f cannot induce a computation tree that satisfies A G E F q, as there exists at least one node in the tree from which E F q is false (i.e., one node in A).

On the other hand, if a strategy only leads to visiting states other than A, then every node in the computation tree for P ^f satisfies E F q (by the definition of A). Therefore, in order for P ^f to satisfy A G E F q, it suffices for the strategy f to avoid visiting a state in A.

We prove that there exists a maximally-permissive, state-based strategy by showing that we can compute a set of bad states B that over-approximates A, and precisely the strategies that stay out of B lead to never having a path in P ^f that eventually visits A.

We build B gradually, starting with A. We add some state w∈W _s to B whenever there exists no successor of w that is not in B yet. Furthermore, we add some state w∈W _e to B whenever there is some successor of w that is in B. As we only add states to B in this process, and never remove states, B converges to some well-defined set.

It can be shown by induction over the step of the computation in which a state is added to B that from all of them, E F q cannot be enforced. For step 0, in which we initialize B with A, the claim is trivial. For step i+1, we can assume that the claim is true for $i \in \mathbb {N}$. If there is a state w∈W _s from which no matter what the strategy does, we land in a state in B, then obviously, once a run entered B, we cannot avoid to visit a state in A in the future (by induction), so adding w to B is justified. Likewise, if there is a state w∈W _e with a successor in B, then we cannot avoid that after one step, we land in a state in B, so adding w to B is again justified.

Now assume that we have a strategy of the following form: we set $f(\overline {w},w) = \{w^{\prime } \in W \mid (w,w^{\prime }) \in R, w^{\prime } \notin B \}$ if w∉B, and $f(\overline {w},w) = \{w^{\prime } \in W \mid (w,w^{\prime }) \in R\}$ otherwise. By definition, there is no strategy f ^′ that has $f(\overline {w},w) \subset f^{\prime }(\overline {w},w)$ for some $\overline {w}$ and w such that $\overline {w}w$ is a path in the run tree of $P^{f^{\prime }}$ and at the same time prevents visiting B from a state that is not in B, as it allows any transition to states not in B. As we have proven already that any strategy that allows visiting B from w ₀ cannot enforce A G E F q, there is no strategy that allows a move that is not allowed by f and enforces A G E F q. Thus, f is the unique maximally-permissive strategy enforcing A G E F q if f is actually winning. Note that f is state-based, too.

It remains to prove that f is winning (i.e., f is not “too permissive”). We show this by induction over the length of a path in the run tree for P ^f. As long as along no such path, we ever reach a state from B, all nodes in the computation tree satisfy E F q. We start with the root of the computation tree of P ^f and know already that if w ₀∈B, then there is no strategy to enforce A G E F q. So we can assume that w ₀∉B. For the inductive step, take some node $\overline {w}w$ that is not in B (by the inductive hypothesis). If w∈W _e , then by the definition of B, we have that all successors of w in P ^f are also not in B. So we have that for all computation tree nodes $\overline {w}ww^{\prime }$ of P ^f with w,w ^′∈W that $\overline {w}ww^{\prime } \notin B$. If w∈W _s , then as f restricts P _f to the successor states that are not in B, the claim holds in this case as well.

In view of reducing supervisory control problems to reactive synthesis problems, we would like to reduce SSCP to RSCP. However, this reduction cannot be done directly, because SSCP asks for a maximally-permissive supervisor, whereas RSCP only asks for a strategy (since a maximally-permissive strategy may not generally exist). To avoid this problem, we exploit the result of Lemma 2 and introduce a new problem, called RSCP maxA G E F q, which is a variant of RSCP, and more precisely a variant of RSCP-CTL. In RSCP maxA G E F q, the specification is a CTL formula of the form A G E F q where q is a CTL formula without temporal operators. Lemma 2 shows that for this class of specifications, existence of a strategy implies existence of a unique maximally-permissive strategy. RSCP maxA G E F q asks precisely for this strategy, if it exists.

Definition 7 (RSCP maxA G E F q)

Given finite Kripke structure plant P and CTL formula ϕ of the form A G E F q where q is a CTL formula without temporal operators, find (if it exists, or state that there does not exist) the unique maximally-permissive state-based strategy that enforces ϕ on P.

We can generalize RSCP maxA G E F q to a more general (and ambitious) reactive synthesis control problem with maximal-permissiveness. Although we currently do not know how to solve this problem, it is useful to define it as a way of motivating future work.

Definition 8 (RSCP _max)

Given finite Kripke structure plant P and CTL ^⋆ formula ϕ, find, if there exists, a strategy which enforces ϕ on P. If so, find whether a maximally-permissive such strategy exists, and whether it is unique, and if so, compute it.

Other researchers have investigated problems related to RSCP _max, in the context of related control frameworks and general logics; see, e.g., Riedweg and Pinchinat (2004), Pinchinat and Riedweg (2005), van Hulst et al. (2014). These works show that there are problem instances where maximally permissive solutions can be computed, when they exist.

3.3 From supervisory control to reactive synthesis with plants

In this section we show how to reduce SSCP to RSCP maxA G E F q.

3.3.1 From DES plants to Kripke structure plants

Given a plant G in the form of a DES, we first construct a plant P _G in the form of a Kripke structure. Consider plant G ₁ of Fig. 3. The Kripke structure $P_{G_{1}}$ is shown in Fig. 13. States drawn as circles are system states. States drawn as rectangles are environment states.

Fig. 13

Kripke structure $P_{G_{1}}$ for DES G ₁ of Fig. 3

A system state of P _G is a state x of G. An environment state of P _G is either of the form (x,c), where c∈E _c , or (x,⊥). All successors of system states are environment states, and vice versa. From a system state x, P _G has at most |E _c |+1 possible successors, one successor of the form (x,c) for each controllable event c which is enabled at state x in G, plus an extra successor (x,⊥). Intuitively, choosing a subset of the successors of x amounts to allowing a subset of the controllable events enabled at x. If only (x,⊥) is chosen, then all controllable events are disabled and only uncontrollable events (if any) are allowed to occur at x.

From environment state (x,c), P _G has an outgoing transition to a system state x ^′ if either G has an uncontrollable transition from x to x ^′, or G has a transition labeled c from x to x ^′. That is, the only transitions enabled from (x,c) are uncontrollable transitions or the controllable transition labeled c (there can only be one controllable transition labeled c, because G is deterministic). Note that if x has no controllable transition labeled c, then (x,c) is not a successor of x by construction. Therefore, an outgoing transition is guaranteed to exist from every reachable environment state of the form (x,c) with c∈E _c .

Finally, from environment state (x,⊥), P _G has an outgoing transition to a system state x ^′ if G has an uncontrollable transition from x to x ^′. That is, only uncontrollable transitions are allowed from (x,⊥). If x has no outgoing uncontrollable transitions then a transition back to x is added to (x,⊥). In the example of Fig. 13, this is the case with states (x ₁,⊥), (x ₂,⊥), and (x ₃,⊥). These “back-transitions” achieve two goals. First, they prevent deadlocks in P _G . Second, they will allow us to prove that non-blocking strategies can always be extended to allow successors of the form (x,⊥) (Lemma 4), a property which facilitates the arguments for maximal permissiveness.

Note that apart from back-transitions, whenever there is a transition from some environment state (x,⊥) to some state x ^′, then every environment state (x,c) for some c also has a transition to x ^′. This is due to the requirement that the uncontrollable transitions are always enabled. Only the back-transitions are not duplicated; due to the fact that (x,c) is only reachable if c is an enabled action in x, deadlock-freedom is already ensured without the back-transitions.

So far we have defined the states and transitions of P _G . We also need to define its set of atomic propositions and labeling function. P _G will have a single atomic proposition, a c c. The states of P _G labeled with a c c will be system states x which are marked states in G, and environment states (x,c) or (x,⊥) where x is marked in G. In our example of Figure 13, this is the case with states x ₁ and (x ₁,⊥), drawn with double lines to represent the fact that they are labeled with a c c.

3.3.2 Stating SSCP in temporal logic

We now express the requirements of SSCP as a temporal logic formula. We will use the CTL formula

$$\phi_{nb} \;:= \;\mathsf{A}\mathsf{G} \, \mathsf{E}\mathsf{F} \, acc . $$

ϕ _{n b} states that it is always possible to reach a marked state, from any reachable state. This formula characterizes non-blockingness.

Returning to our example of Fig. 13, we observe that $P_{G_{1}}$ does not satisfy ϕ _{n b} on its own: this is because from state x ₂ there is no path reaching a state where a c c holds. The same is true for state (x ₂,⊥). Therefore, in order to enforce ϕ _{n b} , a strategy must make these states unreachable.³ Three such (state-based) strategies are shown in Fig. 14.

Fig. 14

Strategies enforcing ϕ _{n b} on $P_{G_{1}}$ of Fig. 13

The interpretation of the two right-most strategies of Fig. 14 is quite clear. f ₅ disables c ₂ at state x ₀ and c ₁ at x ₃. f ₆ disables both c ₁ and c ₂ at x ₀, and c ₁ at x ₃. Neither f ₅ nor f ₆ are maximally-permissive strategies for ϕ _{n b} . Strategy f ₄, on the other hand, is maximally-permissive.

The interpretation of f ₄ is perhaps puzzling. Interpreted as a supervisor, it appears to allow c ₁ at x ₀ (because it keeps the transition from x ₀ to (x ₀,c ₁)), and at the same time to disable all controllable events at x ₀ (because it keeps the transition from x ₀ to (x ₀,⊥)). We will not worry about this paradox, which we take to be only a matter of interpretation. The way P _G is defined, every successor of (x,⊥) is also a successor of (x,c) for any c∈E _c . As a result, (x,⊥) may be redundant, but it does not harm. On the contrary, it will allow us to prove existence of unique maximally-permissive strategies.

This intuition is formalized in Lemma 4 below.

3.3.3 The formal reduction

Let G=(X,x ₀,X _m ,E,δ) be a DES plant with E = E _c ∪E _{u c} . It is convenient to define the functions E n:X→2^E with E n(x)={e∣δ(x,e) is defined}, $\mathsf {En}_{c}:X\rightarrow 2^{E_{c}}$ with E n _c (x)=E n(x)∩E _c , and $\mathsf {En}_{u}:X\rightarrow 2^{E_{uc}}$ with E n _u (x)=E n(x)∩E _{u c} . The functions E n,E n _c ,E n _u return, respectively, the set of all events, controllable events, and uncontrollable events, enabled at state x. For instance, a state x∈X is a deadlock in G iff E n(x) = ∅.

The Kripke structure plant P _G is defined to be

$$P_{G} = (W, w_{0}, R, AP, L) $$

such that

• W = W _s ∪W _e , with W _s = X and W _e = X×(E _c ∪{⊥}).

• w ₀ = x ₀. Therefore, w ₀ is a system state.

• R = R _s ∪R _e , with

  $$\begin{array}{@{}rcl@{}} R_{s} & = & \;\;\;\{\left( x,(x,c)\right) \mid x\in X, c\in \mathsf{En}_{c}(x)\} \;\cup\; \{ \left( x,(x,\bot)\right) \mid x\in X \}\\ R_{e} & = & \;\;\; \{\left( (x,c),x^{\prime}\right) \mid x,x^{\prime}\in X, \exists e\in E_{u}\cup\{c\} : \delta(x,e) = x^{\prime} \}\\ & & \cup\; \{\left( (x,c),x\right) \mid x \in X, c \in E_{c}, c \notin \mathsf{En}_{c}(x) \}\\ & & \cup\; \{\left( (x,\bot),x^{\prime}\right) \mid x,x^{\prime}\in X, \exists u\in E_{u} : \delta(x,u) = x^{\prime} \}\\ & & \cup\; \{ \left( (x,\bot),x\right) \mid x\in X, \mathsf{En}_{u}(x) = \emptyset \} \end{array} $$

• A P={a c c}.

• $L(s) = \left \{\begin {array}{ll} \{acc\} & \text { if } s = x \text { or } s = (x,\bot ) \text { for some } x \in X_{m} \\ \{\} & \text { otherwise.} \end {array}\right .$

The following lemma guarantees that P _G does not have deadlocks, therefore, it is a valid Kripke structure plant as required in Section 3.2.1.

Lemma 3

The transition relation R of P _G defined above is total.

Proof

Let w∈W be a state of P _G . We need to find w ^′∈W such that (w,w ^′)∈R. We distinguish cases.

• Suppose w∈W _s = X. In this case, we have that (w,(w,⊥))∈R by definition of R _s .

• Suppose w∈W _e = X×(E _c ∪{⊥}).

  • Suppose w is of the form (x,c), for x∈X,c∈E _c .

    • If E n _u (x)≠∅ then there exists x ^′∈X and u∈E _{u c} such that δ(x,u) = x ^′. Then ((x,c),x ^′)∈R by definition of R _e .

    • If E n _u (x) = ∅ then

      • if δ(x,c) is defined and equals x ^′, then ((x,c),x ^′)∈R by definition of R _e ;

      • otherwise, c∉E n _c (x), therefore ((x,c),x)∈R by definition of R _e .

  • Suppose w is of the form (x,⊥), for x∈X.

    • If E n _u (x)≠∅ then there exists x ^′∈X and u∈E _u such that δ(x,u) = x ^′. Then ((x,⊥),x ^′)∈R by definition of R _e .

    • If E n _u (x) = ∅ then ((x,⊥),x)∈R by definition of R _e .

In the sequel we simplify notation for state-based strategies as follows. Whenever we are concerned with a state-based strategy f for some set of states W, we simply write f(w) for some w∈W _s to mean the value of $f(\overline {w},w)$ for any $\overline {w} \in W^{*}$. Since for state-based strategies the value of $\overline {w}$ does not make a difference, f(w) is uniquely defined.

Definition 9

Let G=(X,x ₀,X _m ,E,δ) be a DES plant and P _G =(W,w ₀,R,A P,L) be a Kripke structure built from G by the construction above. Let f be a state-based strategy for P _G . The ⊥-closure of f is defined to be the state-based strategy f ^′ that results from setting f ^′(x) = f(x)∪{(x,⊥)} for all x∈W _s .

Lemma 4

Let G=(X,x ₀ ,X _m ,E,δ) be a DES plant and P _G =(W,w ₀ ,R,AP,L) be a Kripke structure built from G by the construction above. Let f be a strategy enforcing ϕ _nb on P _G . Let f ^′ be the ⊥-closure of f. Then f ^′ also enforces ϕ _nb on P _G .

Proof

The specification ϕ _{n b} is A G E F a c c. This formula can only hold in a node of the computation tree if from every node in the computation tree, some other node marked a c c can be reached. For every state-based strategy f and x∈W _s , we have that if f ^′(x)≠f(x), then there has to exist some (x,c)∈f(x). This is because f(x) must be non-empty and if all it contains is (x,⊥) then we would have f ^′(x) = f(x). As (x,⊥)’s successors are always a subset of (x,c)’s successors, and adding paths to nodes that already satisfy A G E F a c c does not change the fact that the computation tree satisfies A G E F a c c, such a modification of the strategy does not alter the fact that it induces a computation tree that satisfies ϕ _{n b} .

The next theorem shows a one-to-one correspondence between maximally permissive strategies in a DES plant G and maximally permissive strategies in the Kripke structure P _G built from G according to the definition at the beginning of this section. Fig. 15 exemplifies the idea in the context of plant G ₁ presented earlier in Fig. 3. The figure shows the two respective strategies, one for G ₁ and one for its corresponding Krikpe structure. Every transition disabled in the strategy for G ₁ has a corresponding transition disabled in the Kripke structure (and vice versa). Recall from above that the Kripke structure has as state set W = W _s ∪W _e for W _s = X, where X is the set of the states in the DES plant. The strategies have the property that states x∈X are reachable in the DES plant if and only if they are reachable in the Kripke structure. Also, the strategy in the Kripke structure never disables transitions to states of the form (x ₀,⊥), as the outgoing edges in (x ₀,⊥) represent uncontrollable transitions in the plant. Since by the construction presented at the beginning of this section the outgoing edges of a state of the form (x,⊥) are always a subset of the edges from states of the form (x,c) for the same value of x, a maximally permissive strategy in the Kripke structure that does not deadlock in a state x thus does not need to deactivate the transition to (x,⊥).

Fig. 15

DES plant G ₁ (the same as in Figure 3), its corresponding Kripke structure, and a strategy for G ₁ that is mapped to its Kripke structure. Dashed lines represent transitions that are disabled by the strategies

Theorem 4

Let G=(X,x ₀ ,X _m ,E,δ) be a DES plant and P _G =(W,w ₀ ,R,AP,L) be a Kripke structure built from G by the construction above.

• 1. Given a non-blocking maximally-permissive state-based supervisor S:X→2 ^E for G, we can compute a maximally-permissive state-based strategy f _S enforcing A G E Facc on P_G as follows:

  $$\text{For all } w \in W_{s}, f_{S}(w) = \{(w,c) \mid c \in S(w) \cap E_{c} \} \cup \{ (w,\bot) \}. $$

• 2. Given a maximally-permissive state-based strategy f enforcing A G E Facc on P_G, we can compute a non-blocking state-based maximally-permissive supervisor S_f for G as follows:

  $$\text{For all } x \in X, S_{f}(x) = E_{\mathit{uc}} \cup \{e \in E_{c} \mid (x,e) \in f(x) \}. $$

Proof

We prove this result in three steps:

• (a) For every state-based supervisor S which is non-blocking for G, the state-based strategy f _S defined above is ⊥-closed and enforces A G E F a c c on P _G .

• (b) Starting from a ⊥-closed state-based strategy f which enforces A G E F a c c on P _G , the supervisor S _f defined above is a state-based supervisor which is non-blocking for G.

• (c) Translating from a ⊥-closed strategy f to S and back will yield the same strategy as we started with, i.e., $f_{S_{f}}=f$. Furthermore, if f is a strategy that is strictly more permissive than some strategy f ^′, then S _f is strictly more permissive than $S_{f^{\prime }}$. Likewise, if S is strictly more permissive than S ^′, then f _S is strictly more permissive than $f_{S^{\prime }}$.

Taking these facts together, we obtain that the translations above must map the (unique) maximally-permissive non-blocking supervisor S for G and the maximally-permissive strategy enforcing ϕ _{n b} on P _G onto each other. Otherwise, mapping one of the maximal solutions would yield a “more maximal solution” that is still a valid strategy/supervisor, which contradicts maximal permissiveness.

More precisely, facts (a) and (c) imply part 1 of the theorem. Indeed, let S ^∗ be the (unique) state-based maximally-permissive non-blocking supervisory for G and let $\phantom {\dot {i}\!}f^{\ast } = f_{S^{\ast }}$. By definition f ^∗ is state-based. Also, by (a), we know that f ^∗ enforces ϕ _{n b} on P _G . To prove part 1 of the theorem, it remains to show that f ^∗ is maximally-permissive. Suppose not. Then there exists strategy f which enforces ϕ _{n b} on P _G and is strictly more permissive than f ^∗. By (a), f ^∗ is ⊥-closed, therefore f must also be ⊥-closed. Let S = S _f . By (c), S must be strictly more permissive than S ^∗, which contradicts maximal permissiveness of the latter.

Similarly, facts (b) and (c) imply part 2 of the theorem. Indeed, let f ^∗ be the unique (by Lemma 2) state-based maximally-permissive strategy enforcing ϕ _{n b} on P _G . Lemma 4 and maximal permissiveness of f ^∗ ensure that f ^∗ is ⊥-closed. Let $\phantom {\dot {i}\!}S^{*} = S_{f^{*}}$. By definition S ^∗ is state-based. Also, by (b), we know that S ^∗ is non-blocking for G. It remains to show that S ^∗ is maximally-permissive. Suppose not. Then there exists non-blocking supervisor S for G which is strictly more permissive than S ^∗. Let f = f _S . By (c), f must be strictly more permissive than f ^∗, which contradicts maximal permissiveness of the latter.

It remains to perform the three steps outlined above.

Step (a): :

We prove two sub-steps. First of all, we show that for every state s that is reachable in S/G, from any state $(\overline {w},s)$ in ${P^{f}_{G}}$, we can reach an a c c-labeled state. This implies that E F a c c holds at state $(\overline {w},s)$. Then, we show that the only reachable states $(\overline {w},s)$ in ${P^{f}_{G}}$ are those that have a successor state $(\overline {w},s^{\prime })$ for which s ^′ is reachable in S/G, or s is reachable in S/G. This shows that for all reachable states in ${P^{f}_{G}}$, E F a c c holds, and thus, the computation tree of ${P^{f}_{G}}$ satisfies A G E F a c c. The fact that f is ⊥-closed is trivial as it is ⊥-closed by definition.

For the first sub-step, consider a state s∈S that is reachable in S/G. As S is a non-blocking supervisor for G, we have that there exists some sequence s ₁ e ₁ s ₂ e ₂…e _n−1 s _n in S/G with s ₁ = s, L(s _n ) = a c c, and for every i∈{1,…,n−1}, we have that s _i+1 = δ(s _i ,e _i ).

The construction of f and ${P^{f}_{G}}$ makes sure that π = s ₁(s ₁,c ₁)s ₂(s ₂,c ₂)…(s _n−1,c _n−1)s _n is a valid path in P _G for c _i = e _i whenever e _i ∈E _c , and c _i =⊥ otherwise, and for every node $(\overline {w},s)$ in ${P^{f}_{G}}$, there is a path from $(\overline {w},s)$ whose projection is π.

The second sub-step is proven by induction over a run in ${P^{f}_{G}}$. We start with state (𝜖,w ₀)=(𝜖,x ₀), for which x ₀ in S/G is reachable by definition. For the induction step, assume that the claim holds for all previous states $(\overline {w},w)$ for w∈W. If we have that w = x for some x∈X, then all possible successors in ${P^{f}_{G}}$ can only be of the form $(\overline {w}^{\prime },(x,c))$, so the claim holds here as well. If on the other hand we have that w=(x,c) for some x∈X, then either we have c=⊥, or we have c∈E _c with c∈S(x), as we defined f to only allow these actions, and thus, these are the only successors that occur in ${P^{f}_{G}}$. If c=⊥, then the next element of the run in ${P^{f}_{G}}$ can only be either $(\overline {w}^{\prime },x)$, in which case the claim holds, or $(\overline {w}^{\prime },x^{\prime })$ for some x ^′ with x ^′ = δ(x,c ^′) for some c ^′∈E _u . As by the definition of a supervisor for controlling a plant, the supervisor cannot deactivate uncontrollable actions, if x is reachable, then x ^′ is also reachable, and thus the claim holds here, too. On the other hand if c≠⊥, then the next element of the run in ${P^{f}_{G}}$ can only be either $(\overline {w}^{\prime },(x,c))$ or x ^′ with x ^′ = δ(x,c). In the first case, the claim holds again, and in the second, as c can only have been selected if c∈S(x), we need to have that the transition from x to x ^′ is possible in S/G, too, so again, the claim holds in this case.

Step (b): :

We prove two sub-steps. First of all, we show that for every state $(\overline {w},x)$ for some x∈X that is reachable in ${P^{f}_{G}}$, from state x in S _f /G, we can reach an accepting state. Then, we show that for every reachable states s in S _f /G, there is some reachable state $(\overline {w},s)$ in ${P^{f}_{G}}$. This shows that from all states that are reachable in S _f /G, there is some path to an accepting state, which implies that S _f is a valid supervisor for G.

For sub-step 1, let $(\overline {w},x)$ be some reachable state in ${P^{f}_{G}}$. As ${P^{f}_{G}}$ satisfies A G E F a c c, there has to exist some path π from $(\overline {w},x)$ to some $(\overline {w}^{\prime },x^{\prime })$ with $L((\overline {w}^{\prime },x^{\prime })) = \mathit {acc}$. Without loss of generality, let this path be loop-free (as we can always cut out loops in the path). We build from π a path from x to x ^′ in S _f /G. Whenever we move along this path from some state $(\overline {w}^{\prime \prime },x)$ to some state $(\overline {w}^{\prime \prime \prime },(x,c))$ or to $(\overline {w}^{\prime \prime \prime },(x,\bot ))$, we do not add a step in the path for S _f /G. On the other hand, whenever we move from some state $(\overline {w}^{\prime \prime },(x,c))$ or $(\overline {w}^{\prime \prime },(x,\bot ))$ to $(\overline {w}^{\prime \prime \prime },x^{\prime })$, we add x ^′ to the path to be constructed. By the definition of S _f , this is always a transition that is allowed by S _f . At the end of the path, as we have $L((\overline {w}^{\prime },x^{\prime })) = \mathit {acc}$ if and only if x ^′ is marked, our reconstructed path in S _f /G ends in a marked state.

For sub-step 2, we reconstruct a path in ${P^{f}_{G}}$ from a path π = x ₀…x _n ∈X ^ω in S _f /G. Let ρ = ρ ₀…ρ _n−1 be the actions to create the path π, i.e., we have x _i+1∈δ(x _i ,ρ _i ) for every $i \in \mathbb {N}$. We have ρ _i ∈f(x _i ) by the definition of S for every $i \in \mathbb {N}$. This allows us to construct the path π ^′=(𝜖,x ₀)(x ₀,(x ₀,c ₀))(x ₀(x ₀,c ₀),x ₁)(x ₀(x ₀,c ₀)x ₁,(x ₁,c ₁))… in ${P^{f}_{G}}$, where for every $i \in \mathbb {N}$, we have c _i =⊥ if ρ _i is an uncontrollable action, and c _i = ρ _i otherwise. As π will end in $(\overline {w},x_{n})$ for some $\overline {w}$, the sub-claim follows.

Step (c): :

The claim for step 3 consists of three sub-steps. For the first sub-step, let f be a ⊥-closed strategy, and S _f be the corresponding supervisor. We translate S _f back tlo a state-based supervisor for P _G and obtain:

$$\begin{array}{@{}rcl@{}} f_{S_{f}}(w) & = & \{(w,c) \mid c \in S_{f}(w) \cap E_{c} \} \cup \{(w,\bot)\} \\ & = & \{(w,c) \mid c \in \{ e \in E_{c} \mid (w,c) \in f(w) \} \} \cup \{(w,\bot)\} \\ & = & f(w) \end{array} $$

For the second sub-step, let f and f ^′ be state-based strategies such that for all w∈W, we have f ^′(w)⊆f(w) and for one w∈W, we have f ^′(w)⊂f(w). In this case, we have for all w ^′∈W∖{w}:

$$\begin{array}{@{}rcl@{}} S_{f^{\prime}}(w^{\prime})& = & E_{\mathit{uc}} \cup \{ e \in E_{c} \mid (w^{\prime},e) \in f^{\prime}(w^{\prime}) \} \\ & \subseteq & E_{\mathit{uc}} \cup \{ e \in E_{c} \mid (w^{\prime},e) \in f(w^{\prime}) \} \\ & = & S_{f}(w^{\prime}) \end{array} $$

Furthermore, we have:

$$\begin{array}{@{}rcl@{}} S_{f^{\prime}}(w)& = & E_{\mathit{uc}} \cup \{ e \in E_{c} \mid (w,e) \in f^{\prime}(w) \} \\ & \subset & E_{\mathit{uc}} \cup \{ e \in E_{c} \mid (w,e) \in f(w) \} \\ & = & S_{f}(w) \end{array} $$

From line two to line three in this equation, we used the fact that the elements of f ^′(w) are all of the form (w,c) for some c∈E _c ∪{⊥} (except if E n(w) = ∅, in which case f ^′(w)⊂f(w) cannot be fulfilled as we need to have f ^′(w) = f(w)=(w,⊥) then) and by assumption, we have that (w ^′,⊥)∈f ^′(w ^′), so there has to exist some c∈E n _c (w) with (w,c)∈f(w) but (w ^′,c)∉f ^′(w) for all w ^′∈W.

For the third sub-step, we apply the same idea as in sub-step two. Let S and S ^′ be state-based supervisors such that for all x∈X, we have S ^′(x)⊆S(x) and for one x∈X, we have S ^′(x)⊂S(x). Then for all x∈X∖{x}, we have:

$$\begin{array}{@{}rcl@{}} f_{S^{\prime}}(x^{\prime})& = & \{(x^{\prime},c) \mid c \in S^{\prime}(x^{\prime}) \cap E_{c} \} \cup \{(w,\bot) \} \\ & \subseteq & \{(x^{\prime},c) \mid c \in S(x^{\prime}) \cap E_{c} \} \cup \{(w,\bot) \} \\ & = & f_{S}(x^{\prime}) \end{array} $$

Furthermore, we have:

$$\begin{array}{@{}rcl@{}} f_{S^{\prime}}(x)& = & \{(x,c) \mid c \in S^{\prime}(x) \cap E_{c} \} \cup \{(w,\bot) \} \\ & \subset & \{(x,c) \mid c \in S(x) \cap E_{c} \} \cup \{(w,\bot) \} \\ & = & f_{S}(x) \end{array} $$

This result completes step three over the overall proof.

Corollary 2

SSCP can be reduced to RSCP max A G E F q with a polynomial-time reduction.

Proof

Theorem 4 establishes a one-to-one correspondence between maximally-permissive state-based non-blocking supervisors for a DES plant G and a maximally-permissive state-based strategy for A G E F a c c in a Kripke structure P _G that we construct from G. It follows that we can reduce the search for a supervisor in G as SSCP requests to searching for a strategy in P _G as RSCP maxA G E F q requests. Moreover, P _G can be constructed from G in polynomial time: the number of states of P _G is O(n⋅(m+2)) where n is the number of states of G and m is the number of controllable events.

3.4 Algorithms

3.4.1 Algorithms for supervisory control problems

The formulation and solution of BSCP-NB were first presented in the seminal papers of Ramadge and Wonham (1987), Wonham and Ramadge (1987). The “standard” algorithm for solving BSCP-NB builds a non-blocking automaton that marks the language $\mathcal {L}_{m}(S_{mpnb}/G) = L_{am}^{mpnb}$ in the notation of Section 2.1.7 from G and from a non-blocking automaton that marks the language L _{a m} . Let H be a deterministic automaton such that $\mathcal { L}(H) = \overline {L_{am}}$ and $\mathcal {L}_{m}(H) = L_{am}$. Let G have n states and H have m states. The standard algorithm for BSCP-NB builds automaton H ^mpnb such that $\mathcal {L}(H^{mpnb}) = \overline {L_{am}^{mpnb}}$ and $\mathcal { L}_{m}(H^{mpnb}) = L_{am}^{mpnb}$ by first forming the product of G with H, and then iterating over the resulting structure to delete states that violate the safety property with an uncontrollable event and/or are blocking. Iterations are necessary in general since deletion of states that violate the safety property with an uncontrollable transition may create new blocking states, and vice-versa. Convergence is guaranteed in a finite number of steps since the number of states is finite. Hence, the computational complexity of the algorithm is O(n ² m ²) in the worst case. This complexity does not include the construction of automaton H. There are special cases where the computational complexity can be reduced to O(n m) in the worst case, such as when $L_{am} = \overline {L_{am}}$ or when all cycles in G contain a marked state.

Once H ^mpnb has been obtained, it is effectively an encoding of a state-based (with respect to G×H) supervisor that achieves the maximally permissive language $L_{am}^{mpnb}$; the transitions that are defined at each state of H ^mpnb, which is a pair (x _G ,x _H ) with x _G a state of G and x _H a state of H, are the enabled controllable events and the feasible uncontrollable events.

Our transformation of BSCP-NB to SSCP in Section 3.1 is essentially an implementation of the first step of the standard algorithm (although we used an automaton A with a complete transition function therein).

The reader is referred to Cassandras and Lafortune (2008), Wonham (2015) for textbook expositions of the above material. To make this paper more self-contained, a simple algorithm for solving SSCP is given in Appendix C. This algorithm is a special case of the standard algorithm for solving BSCP-NB from Ramadge and Wonham (1987), Wonham and Ramadge (1987).

3.4.2 Algorithms for reactive synthesis problems

Algorithms for solving RSP-LTL have been provided in a number of works, e.g., in Pnueli and Rosner (1989a). Generally, these algorithms follow a similar flow, where the LTL formula ϕ is translated into some type of word automaton such as a Büchi automaton A _w , then A _w is translated into a tree automaton A _t , and finally A _t is translated into a game which is then solved algorithmically. Different methods differ by the type of automata and games that they use and how they represent them (e.g., enumeratively or symbolically). Also, in some cases some of the above steps may be missing as they are trivial. We refer the reader to Ehlers (2013) for a comprehensive overview.

Techniques for solving RSP-CTL and RSP are provided in a number of works, for instance, Kupferman and Vardi (1999), Madhusudan (2001). Madhusudan’s thesis (Madhusudan 2001) also provides a method for solving RSCP (and thus also RSCP-LTL and RSCP-CTL as special cases) by reducing it to the module-checking problem (Kupferman and Vardi 1996).

Because of the special form of the formula A G E F q and in view of the results in Section 3.3, RSCP maxA G E F q can be solved using algorithms for supervisory control problems such as SSCP or BSCP-NB. As described in Appendix C, the general idea is to start from a set of bad states (initially those that violate E F q) and iterate by labeling additional states as bad, if no strategy exists to avoid states that are already labeled bad. In the finite-state case, the algorithm ends when no more states can be added to the set of bad states, or when the initial state is added to that set. In the latter case, no winning strategy exists. The complexity of such an algorithm is polynomial in the number of states.

3.5 Reactive synthesis with plants vs. reactive synthesis without plants

In this section we discuss the links between the reactive synthesis problem with plants, RSCP, and the reactive synthesis problem without plants, RSP. Our discussion is informal, as it is beyond the scope of this paper to present detailed, formal reductions between these problems. Roughly speaking, RSP can be seen as a special case of RSCP, where the plant offers some possible input at every step. Some technical details need to be resolved, as RSP is formulated in terms of inputs and outputs whereas RSCP is formulated in terms of system and environment states. Bridging this gap should be relatively straightforward.

Conversely, RSP may appear at first sight more restrictive than it really is, as there is no notion of a plant that encodes the possible environment behavior. Yet, we can encode the plant behavior into the specification. Starting from a specification ϕ, we can modify it to some specification ϕ ^′ such that in order for the controller to satisfy ϕ ^′, it suffices that it satisfies ϕ only for those input streams that correspond to paths in a given plant. This roughly corresponds to ϕ ^′ being of the form ϕ _{p l a n t} ⇒ ϕ, where ϕ _{p l a n t} models the behavior of the plant. In this way, a strategy for controlling a plant can be obtained by chopping away the irrelevant parts of a computation tree that satisfies ϕ ^′.

The above approach may at first appear uninteresting from a practical perspective, especially when a plant is already available in the form of an automaton (or a network of automata). Indeed, for most temporal logics the reactive synthesis problem is at least exponential in the length of the formula, so keeping the size of the formula small is essential. Moreover, an exponential blow-up typically occurs when translating the formula into some form of automaton during the synthesis procedure. Therefore, encoding a plant automaton to a temporal logic specification only to translate it back to an automaton during the synthesis process may seem computationally inefficient.

However, there are methods that successfully use the approach of encoding plants as temporal logic formulas, relying on the fact that sometimes the plant can be encoded in a certain fragment of temporal logic which does not suffer from exponential blow-up during translation to automata or synthesis. This is exploited, for instance, in Kress-Gazit et al. (2007) where synthesis is used for robotics applications such as motion planning. The plant encoded in this case is the region structure of the workspace, and it is encoded in the GR(1) fragment of LTL, which admits efficient synthesis algorithms (Piterman et al. 2006). In the case of Kress-Gazit et al. (2007), the overall approach is polynomial in the number of regions.

A related approach is taken in Pinchinat and Riedweg (2005), where an alternating automaton model is used that can capture the specification formula with only linear blow-up. Then the product of this automaton and the plant is computed resulting in an alternating automaton of the same type as the automaton for the formula. Because the automaton model is essentially as powerful and concise as the formula, this boils down to the same idea as encoding the plant into the specification.

4 Conclusion

This work is an introductory treatment of the connection between the two research fields of supervisory control and reactive synthesis. Although both fields target the general problem of controller synthesis for dynamic systems, they have developed largely independently over the last three decades, often emphasizing different, yet complementary, aspects of the general controller synthesis problem. The connection established in this paper was purposefully focused on the most basic problem of supervisory control, so that non-expert readers can get a general understanding of how the gap between these two fields can be bridged. At the same time, the formal reduction described in Section 3.3 is a novel contribution. It is our hope that this paper will motivate more in-depth studies on bridging this gap and more generally advancing the state-of-the-art in controller synthesis for discrete event systems by leveraging the techniques developed in both supervisory control and reactive synthesis.

As was mentioned in the introduction, connections between supervisory control and reactive synthesis have already been established in more advanced problem domains, such as partially-observed systems, languages of infinite strings, and distributed and decentralized control settings. Yet, a number of interesting topics for future work emerge from the more elementary connection established in this paper. One such topic is extending the results in this paper to multi-tasking supervisory control (see, e.g., de Queiroz et al. (2005)), where there are several sets of marked states that must each remain reachable.

Another topic is modeling and evaluation. We have only discussed illustrative examples in this paper. Although numerous interesting case studies in synthesis do exist in the literature in both supervisory control and reactive synthesis, these have limited comparative value as they were done in one of the two frameworks, but not in both. It would be worthwhile to develop case studies that would allow a detailed comparison of these two frameworks in terms of plant and specification modeling, computational complexity of synthesis, and implementation of derived supervisor/controller.

Appendices

A Proof of theorem 1

We use the formalism defined in Section 2.1 to show that the concept of maximally permissive solution, which is a central requirement in problem BSCP-NB of Section 2.1.8, is well defined. This will provide a proof of Theorem 1 that is self-contained.

For this purpose, we must first define the disjunction of two supervisors.

Let G be a DES plant and let S ₁,S ₂ be two supervisors for G. We define S ₁∪S ₂ to be a new supervisor, denoted by S _1∪2 for G, such that S _1∪2(σ) = S ₁(σ)∪S ₂(σ) for all σ∈E ^∗. We call S _1∪2 the disjunction of S ₁ and S ₂, since S _1∪2 allows all strings that S ₁ and S ₂ respectively allow.

We now wish to characterize the controlled behavior $\mathcal {L} (S_{1\cup 2}/G)$ under the disjunction of S ₁ and S ₂. Recall that when S _i is applied to G in isolation, the definition of S _i over $E^{*} \setminus \mathcal {L}(S_{i}/G)$ is irrelevant, since these strings will never occur in the controlled system. However, in the context of disjunction, this is no longer true since the controlled behavior will in general exceed $\mathcal {L}(S_{i}/G)$ due to the actions of the other supervisor(s). In order to allow for a simple characterization of $\mathcal {L} (S_{1\cup 2}/G)$, we make the following assumption:

$$ S_{i} (\sigma) = E_{uc} \text{~for all~} \sigma \in E^{*} \setminus \mathcal{L}(S_{i}/G). $$

(3)

We refer to supervisors that satisfy this assumption as “ G-matched supervisors.”

We can think of S _i as being “out of range” when the controlled language leaves $\mathcal {L}(S_{i}/G)$. Hence, when this occurs, S _i will not enable any events, other than uncontrollable ones, as it assumes that the controlled behavior is now in the range of another supervisor. Any supervisor $S^{\prime }_{i}$, when applied in isolation to G, can be replaced by a G-matched one, S _i , that results in the same controlled behavior $\mathcal {L} (S^{\prime }_{i}/G) = \mathcal {L}(S_{i}/G)$.

It follows directly from the G-matched assumption and from the definition of disjunction that

$$ \mathcal{L} (S_{1\cup 2}/G) = \mathcal{L}(S_{1}/G) \cup \mathcal{L} (S_{2}/G) . $$

(4)

Since marking is a property of the plant, we similarly have that

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{m} (S_{1\cup 2}/G) & = & \mathcal{L}(S_{1\cup 2}/G) \cap \mathcal{L}_{m}(G) \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} & = & [ \mathcal{L}(S_{1}/G) \cup \mathcal{L} (S_{2}/G) ] \cap \mathcal{L}_{m}(G) \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} & = & [ \mathcal{L}(S_{1}/G) \cap \mathcal{L}_{m}(G) ] \cup \left[\right. \mathcal{L} (S_{2}/G)\left.\right) \cap \mathcal{L}_{m}(G)\left.\right] \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} & = & \mathcal{L}_{m}(S_{1}/G) \cup \mathcal{L}_{m}(S_{2}/G) \end{array} $$

(8)

Remark 5 (Supervisor disjunction)

It is worth noting that, without the assumption in Eq. (3), the closed-loop language under disjunction of supervisors may not be the union of their respective languages. As an example, consider again plant G ₃ of Fig. 5, with L _{a m} :={ε,c ₁}. Consider supervisors S ₁ and S ₂ where S ₁ always disables c ₁ and enables c ₂, whereas S ₂ always disables c ₂ and enables c ₁. Both S ₁ and S ₂ are non-blocking for G ₃, because all states in the closed-loop system are accepting. Moreover, both S ₁ and S ₂ are safe w.r.t. the above L _{a m} . Indeed, S ₂ always disables c ₂, while S ₁, by disabling c ₁, prevents G ₃ from reaching state x ₁, thus indirectly preventing c ₂. However, S ₁∪S ₂ is not safe, since it allows both c ₁ and c ₂ at any state.

The following result establishes a key property of supervisor disjunction.

Theorem 5

Let G be a DES plant and let $L_{am} \subseteq \mathcal {L}_{m}(G)$ be the admissible marked language. If S ₁ ,S ₂ are two non-blocking and safe supervisors that are G-matched,

then S ₁ ∪S ₂ is also a non-blocking and safe supervisor, and it is G-matched.

Proof

We have that $\overline {\mathcal {L}_{m}(S_{i}/G)} = \mathcal {L}(S_{i}/G)$ and $\mathcal {L}_{m}(S_{i}/G) \subseteq {L_{am}}$, for i=1,2.

Safety: Clearly,

$$\mathcal{L}_{m}(S_{1\cup 2}/G) = \mathcal{L}_{m}(S_{1}/G) \cup \mathcal{L}_{m}(S_{2}/G) \subseteq {L_{am}} $$

and thus S ₁∪S ₂ is a safe supervisor.

Non-blockingness: Since prefix-closure can be distributed over union (the proof of this fact is straightforward), we have that

$$\begin{array}{@{}rcl@{}} \overline{\mathcal{L}_{m}(S_{1 \cup 2}/G)} &=& \overline{\mathcal{L}_{m}(S_{1}/G) \cup \mathcal{L}_{m}(S_{2}/G)} \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} &=& \overline{\mathcal{L}_{m}(S_{1}/G)} \cup \overline{\mathcal{L}_{m}(S_{2}/G)} \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} &=& \mathcal{L}(S_{1}/G) \cup \mathcal{L}(S_{2}/G) \end{array} $$

(11)

$$\begin{array}{@{}rcl@{}} &=& \mathcal{L}(S_{1 \cup 2}/G). \end{array} $$

(12)

which proves that S ₁∪S ₂ is a non-blocking supervisor.

Finally, it is clear that S _1∪2 is G-matched as it inherits this property from the definitions of S ₁ and S ₂ outside of $\mathcal {L}(S_{1 \cup 2}/G)$.

Corollary 3

Theorem 5 holds for infinite disjunctions of supervisors.

Proof

All steps in the proof of Theorem 5 hold for an arbitrary number of disjunctions.

The hypothesis of Theorem 1 is that there exists at least one non-blocking supervisor for G that is safe w.r.t. L _{a m} . If there exists a single supervisor with these properties, then it is necessarily the unique desired S _{m p n b} , as no other safe non-blocking supervisor exists. Let us assume then that there are several safe and non-blocking supervisors. If a supervisor S is not G-matched, then we can always make it G-matched without changing $\mathcal {L}(S/G)$ or $\mathcal {L}_{m}(S/G)$. By taking the disjunction of all G-matched non-blocking supervisors for G that are safe w.r.t. L _{a m} , we obtain a unique G-matched supervisor that is also safe and non-blocking by Corollary 3; let us denote it by $S_{disj}^{G}$. Then $\mathcal {L}_{m}(S_{disj}^{G})$ contains all the sublanguages of L _{a m} that can be achieved by any safe and non-blocking supervisor. Otherwise, if the sublanguage of L _{a m} achieved by one supervisor is not contained in $\mathcal {L}_{m}(S_{disj}^{G})$, then the G-matched version of that supervisor would not have been added in the disjunction of all G-matched safe and non-blocking supervisors, a contradiction.

Once we have the unique maximally-permissive closed-loop behavior $\mathcal {L}_{m}(S_{disj}^{G})$, we take S _{m p n b} to be the unique maximally permissive supervisor that achieves it. To obtain S _{m p n b} , we simply add to $S_{disj}^{G}$ all infeasible (in G) controllable events for strings in $\mathcal {L}(S_{disj}^{G} / G)$ and all controllable events for strings in $E^{*} \setminus \mathcal {L}(S_{disj}^{G} /G)$. Since $\mathcal {L}(S_{mpnb}/G) = \mathcal {L}(S_{disj}^{G}/G)$ and $\mathcal {L}_{m}(S_{mpnb}/G) = \mathcal {L}_{m}(S_{disj}^{G}/G)$, then S _{m p n b} is non-blocking for G and safe w.r.t. L _{a m} . S _{m p n b} is not G-matched anymore, but this is of no consequence in the later developments in the paper.

This completes the proof of Theorem 1.

B Proof of theorem 2

First, we state and prove the following lemma.

Lemma 5

Let G=(X,x ₀ ,X _m ,E,δ), $L_{am}\subseteq \mathcal {L}_{m}(G)$ , and assume that L _am is $\mathcal {L}_{m}(G)$ -closed. Let A be a complete DFA such that $\mathcal {L}_{m}(A)=L_{am}$. Let S be a supervisor for G, and therefore also for G×A. Then, the following hold:

• 1. If S is non-blocking for plant G×A, then S is non-blocking for plant G.

• 2. If S is non-blocking for plant G×A, then S is safe for plant G w.r.t. L _am .

• 3. If S is non-blocking for plant G and safe for plant G w.r.t. L _am , then S is non-blocking for plant G × A.

• 4. S is safe for plant G×A w.r.t. $\mathcal {L}_{m}(G\times A)$.

Proof

• 1. To show that S is non-blocking for G, we need to show $\mathcal {L}(S/G)\subseteq \overline {\mathcal { L}_{m}(S/G)}$. Let $\sigma \in \mathcal {L}(S/G)$. We need to find σ ^′ such that $\sigma \cdot \sigma ^{\prime } \in \mathcal {L}_{m}(S/G)$. We know that $\sigma \in \mathcal {L}(S/G\times A)$ because A is complete. Also, S is non-blocking for G×A, thus $\sigma \in \overline {\mathcal {L}_{m}(S/G\times A)}$. Therefore there exists σ ^′ such that $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G\times A)$. By definition of the marked states of G×A, both G and A accept σ⋅σ ^′. Therefore, $\sigma \cdot \sigma ^{\prime } \in \mathcal {L}_{m}(S/G)$.

• 2. To show that S is safe for G w.r.t. L _{a m} , we need to show $\mathcal {L}_{m}(S/G) \subseteq L_{am}$. Let $\sigma \in \mathcal {L}_{m}(S/G)$. We need to show σ∈L _{a m} . $\sigma \in \mathcal {L}_{m}(S/G)$ implies $\sigma \in \mathcal { L}(S/G)$, and therefore $\sigma \in \mathcal {L}(S/G\times A)$ because A is complete. Consider the (unique) run of G×A on σ. We claim that this run ends on a product state that is marked for both G and A. $\sigma \in \mathcal {L}_{m}(S/G)$, therefore the product state must indeed be marked for G. We show that $\sigma \in \mathcal {L}_{m}(A)$ which implies that the product state is also marked for A. Since S is non-blocking for G×A, there exists σ ^′ such that $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G\times A)$. But this means $\sigma \cdot \sigma ^{\prime }\in \mathcal { L}_{m}(A)$, which implies $\sigma \in \overline {\mathcal {L}_{m}(A)}$. Also, $\sigma \in \mathcal {L}_{m}(S/G)$ implies $\sigma \in \mathcal {L}_{m}(G)$. Therefore, we have $\sigma \in \mathcal {L}_{m}(G)\cap \overline {\mathcal {L}_{m}(A)}$.

  Since $\mathcal {L}_{m}(A)$ (i.e., L _{a m} ) is $\mathcal {L}_{m}(G)$-closed, $\sigma \in \mathcal {L}_{m}(A)$.

• 3. To show that S is non-blocking for plant G×A, we need to show $\mathcal {L}(S/G\times A) \subseteq \overline {\mathcal {L}_{m}(S/G\times A)}$. Let $\sigma \in \mathcal {L}(S/G\times A)$. We need to find σ ^′ such that $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G\times A)$. $\sigma \in \mathcal {L}(S/G\times A)$ implies $\sigma \in \mathcal {L}(S/G)$ and $\sigma \in \mathcal {L}(A)$. Since S is non-blocking for G, there exists σ ^′ such that $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G)$. Since $\mathcal {L}_{m}(S/G)\subseteq L_{am}=\mathcal {L}_{m}(A)$, $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(A)$. $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G)$ and $\sigma \cdot \sigma ^{\prime }\in \mathcal { L}_{m}(A)$ implies $\sigma \cdot \sigma ^{\prime }\in \mathcal {L}_{m}(S/G\times A)$. Therefore $\sigma \in \overline {\mathcal {L}_{m}(S/G\times A)}$.

• 4. Trivially, since safe w.r.t. $\mathcal {L}_{m}(G \times A)$ means $\mathcal {L}_{m}(S/G \times A)\subseteq \mathcal { L}_{m}(G \times A)$, which holds for any S.

We can now present the proof of Theorem 2.

Proof

2⇒1 : We need to show that S is non-blocking for G, safe w.r.t. L _{a m} , and maximally-permissive. Non-blockingness follows from Lemma 5, part 1. Safety follows from Lemma 5, part 2.

To show that S is maximally-permissive in G, suppose there exists a non-blocking and safe w.r.t. L _{a m} supervisor S ^′ which is strictly more permissive than S. By Lemma 5, parts 3 and 4, S ^′ is non-blocking for G×A and safe for G×A w.r.t. $\mathcal {L}_{m}(G\times A)$. The fact that S ^′ is strictly more permissive than S in G also means that S ^′ is strictly more permissive than S in G×A. This contradicts the hypothesis that S is maximally-permissive in G×A.

1⇒2 : We need to show that S is non-blocking for G×A, safe for G×A w.r.t. $\mathcal { L}_{m}(G \times A)$, and maximally-permissive. Non-blockingness follows from Lemma 5, part 3. Safety follows from Lemma 5, part 4.

To show that S is maximally-permissive in G×A, suppose there exists a non-blocking supervisor S ^′ for G×A (and also trivially safe w.r.t. $\mathcal {L}_{m}(G\times A)$) which is strictly more permissive than S.

By Lemma 5, parts 1 and 2, S ^′ is non-blocking for G and safe for G w.r.t. L _{a m} . The fact that S ^′ is strictly more permissive than S in G×A also means that S ^′ is strictly more permissive than S in G. This contradicts the hypothesis that S is maximally-permissive in G.

C An algorithm for SSCP

For the sake of completeness of this paper, a simple algorithm to solve SSCP is presented below. The algorithm starts by labeling as Blocking all states that cannot reach a marked state (note that this generally requires reachability analysis). Then the algorithm iterates, repeatedly labeling more states as Blocking, until no more can be labeled. A state is labeled during this iteration, if either it has an uncontrollable successor already labeled, or all its successors are already labeled. At the end, if the initial state is labeled Blocking then no supervisor exists. Otherwise, a state-based supervisor can easily be constructed by avoiding all controllable transitions leading to Blocking states.

The above algorithm essentially computes a fixpoint of a function that takes a set of blocking states and returns those states that have an uncontrollable transition to a blocking successor or all of whose successor states are blocking. The fixpoint evaluation starts from the set of states that do not have a path to a marked state. The algorithm is furthermore an adaptation of the standard algorithm in Wonham and Ramadge (1987) for solving BSCP-NB to the special case of SSCP. Examples of the application of the standard algorithm for solving BSCP-NB can be found in Wonham (2015), Cassandras and Lafortune (2008), for instance.

As a simple example of how the algorithm operates, consider the plant G ₁ of Figure 3. After initialization, Blocking contains a single state, namely x ₂. (Note that x ₁ has no path to itself, but is not considered blocking because it is marked.) After executing the body of the repeat loop no more states are added to the set Blocking. Indeed, no state has an uncontrollable transition to x ₂, therefore the set StatesWithUncontrollablyBlockingSuccs turns out to be empty. The set NewDeadlocks also turns out to be empty because there is no state whose only successors, if any, are blocking, i.e., x ₂ (note that, again, the marked state x ₁ is exempted). Since Blocking does not change, the loop is exited after one iteration. The initial state is not blocking, therefore a supervisor exists and is defined as follows: S(x ₀)={u,c ₁}, S(x ₁) = S(x ₂)={u,c ₁,c ₂}, and S(x ₃)={c ₂}. The computed supervisor corresponds to supervisor S ₂ shown in Fig. 3.