Classification of weighted posets and digraphs admitting the extended Hamming code to be a perfect code

Abstract

In Etzion et al. (IEEE Trans Inform Theory 64(4):2398–2409, 2018), introduced metrics on $\mathbb {F}_2^n$ based on directed graphs on n vertices, and in Hyun et al. (IEEE Trans Inform Theory 65(8):4664–4672, 2019), the authors introduced weighted poset metrics on $\mathbb {F}_2^n$ which may be considered as an algebraic version of directed graph metric. They also classify weighted posets and directed graphs admitting the extended Hamming code of length 8 to be a 2-perfect code. In this paper, we will continue the classification problem further. It will be shown that every weighted poset or directed graph which admits extended Hamming code is completely determined by its structure vector. Let s be the length of the structure vector. In Sect. 3 (resp.4), we will classify structure vectors of weighted posets (resp. directed graphs) which admit the extended Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code when $s=3,4,5$ (resp. $s=3,4$). As a consequence our classification, we will classify weighted posets and directed graphs which admit the extended Hamming code of length 16 to be a 2-perfect code.

1 Introduction

Let $\mathbb {F}_2$ be the finite field of order two and $\mathbb {F}_2^n$ be the vector space of n-tuples of elements in $\mathbb {F}_2$.

Coding theory has mainly focused on the study of $\mathbb {F}_2^n$ when $\mathbb {F}_2^n$ is endowed with the Hamming metric. Since the late 1980’s several attempts have been made to generalize classical problems of the coding theory by introducing a family of new non-Hamming metrics on $\mathbb {F}_2^n$ (cf. [9, 11, 12]). These attempts led Brualdi et al. [2] to introduce the concept of poset metrics on $\mathbb {F}_2^n$ in 1995. We refer to [1, 3, 4, 6, 8, 10] for some results on poset metric spaces such as perfect codes, group of isometries, packing radius, and relation with association schemes. Recently, in [5], the authors introduced metrics on $\mathbb {F}_2^n$ based on directed graphs and they discussed basic topics of coding theory over the metric based on directed graphs. In [7], the authors extended the concept of poset metric to that of weighted poset metric. The passage from ‘poset metric’ to ‘weighted poset metric’ is not a mere generalization of concepts, but rather it is motivated by directed graph metrics. In fact, we may view weighted poset metric as an algebraic version of directed graph metric. One merit of this algebraic formulation is that it facilitates to classify directed graphs which admit a given code to be a perfect code. In [7], the authors investigated interrelations between weighted poset metric space and corresponding weighted directed graph metric space, and as an application of this interrelationship, they classify weighted posets and directed graphs which admit the extend Hamming code of length 8 to be a 2-perfect code. In the present paper, we will continue this classification problem further.

To explain our goal more clearly, we briefly introduce some terminology. We refer to [7] for detailed discussion.

1.1 Poset metrics

Recall that $\mathbb {F}_2^n$ is the vector space of binary n-tuples of elements in $\mathbb {F}_2$. The support ${\text {supp}}(x)$ of x in $\mathbb {F}_2^n$ is the set of non-zero coordinate positions. The Hamming weight $w_H(x)$ of a vector x in $\mathbb {F}_2^n$ is the size of ${\text {supp}}(x)$. Notice that there is a one to one correspondence between $\mathbb {F}^n_2$ and the set of subsets of $\{1,2,\ldots ,n\}$ defined by $x\mapsto {\text {supp}}(x)$. Throughout this paper, we identify x in $\mathbb {F}_2^n$ with its support, and so we can identify $x+y$ with $x\Delta y$, where $\Delta$ is the symmetric difference.

Throughout this paper, for a positive integer n, [n] denotes the set $\{1,2,\ldots ,n\}$, i.e $[n] \triangleq \{1,2,\ldots ,n\}$.

Let $(P,\preceq )$ be a partially ordered set (for short, poset) of size n. A subset I of P is called an order ideal if $i\in I$ and $j\preceq i$ imply that $j\in I$. For a subset A of P, $\langle {A}\rangle _P$ denotes the smallest order ideal of P containing A. The order ideal generated by $\{i\}$ is denoted $\langle {i}\rangle _P$ for short.

Without loss of generality, we may assume that P is $\{1,2,\ldots ,n\}$ and that the coordinate positions of vectors in $\mathbb {F}_2^n$ are labeled by P. The P-weight of a vector x in $\mathbb {F}_2^n$ is defined by the size of the smallest order ideal of P containing x, that is,

$$\begin{aligned} w_P(x)=\left| \langle {x}\rangle _P\right| . \end{aligned}$$

The P-distance of the elements x and y in $\mathbb {F}_2^n$ is defined by

$$\begin{aligned} d_P(x,y)=w_P(x-y). \end{aligned}$$

The metric $d_P$ on $\mathbb {F}_2^n$, which is introduced by Brualdi et al. in [2], is called a poset metric.

1.2 Weighted poset metrics

Let $(P,\preceq )$ be a partially ordered set and $\pi$ a function from P to $\mathbb {R}_{>0}$ being the set of positive real numbers. The triple $(P,\preceq , \pi )$ is called a $\pi$-weighted poset. We simply denote a weighted poset by $P_\pi$. The $P_\pi$-weight of x in $\mathbb {F}_2^n$ is defined by

$$\begin{aligned} w_{P_\pi }(x)=\sum _{i\in \langle {x}\rangle _{P}}\pi (i). \end{aligned}$$

The $P_\pi$-distance of the vectors x and y in $\mathbb {F}_2^n$ is defined by

$$\begin{aligned} d_{P_\pi }(x,y)=w_{P_\pi }(x-y). \end{aligned}$$

We have the following lemma whose proof is straightforward.

Lemma 1.1

If $P_\pi$ is a weighted poset, then $P_\pi$-distance $d_{P_\pi }$ is a metric on $\mathbb {F}_2^n$.

We call the metric $d_{P_\pi }$ on $\mathbb {F}_2^n$ a $\pi$-weighted poset metric.

1.3 Directed graph metrics

All graphs considered are directed simple graphs, that is, it has neither a loop nor a multiple edge. Let G be a directed graph (or digraph for short) consisting of a vertex set V(G) and an edge set E(G) where the (directed) edge is an ordered pair of distinct vertices. For any u and v in V(G) with $u\ne v$, we say that v is dominated by u if there is a path from u to v. For a subset S of V(G), we denote $\langle {S}\rangle _G$ the set consisting of S and the vertices which are dominated by vertices in S. The G-weight of x in $\mathbb {F}_2^n$ is defined by the size of the vertices dominated by $\{x\}$, that is,

$$\begin{aligned} w_G(x)=\left| \langle {x}\rangle _G\right| . \end{aligned}$$

The G-distance of the vectors x and y in $\mathbb {F}_2^n$ is defined by

$$\begin{aligned} d_G(x,y)=w_G(x-y). \end{aligned}$$

The metric $d_G$ on $\mathbb {F}_2^n$ which is introduced by Etzion et al. in [5] is called a digraph metric. The Hamming metric may be considered as a G-metric where G contains no edges.

1.4 Weighted poset metric and directed graph metric

In this subsection, we briefly explain how a digraph metric induces a weighted poset metric. In fact we can show that the weighted poset metric and digraph metric are ‘essentially’ equivalent. Moreover the weighted poset metric is easy to handle algebraically and this justifies the phrase ‘weighted poset metric is an algebraic version of digraph metric’. We refer to [7] for details.

Let G be a digraph with n vertices. For any u and v in V(G), we write $u\sim v$ if $u=v$ or there are paths from u to v and from v to u. One can easily check that it is an equivalence relation on V(G).

Let $G/\mathbin \sim$ be the set of equivalence classes of the relation $\sim$. Let ${\bar{v}}$ denote the equivalence class containing a vertex v. We define a relation on $G/\mathbin \sim$ by ${\bar{u}}\preceq {\bar{v}}$ if ${\bar{u}}={\bar{v}}$ or there is a path from a to b where $a\in {\bar{v}}$ and $b\in {\bar{u}}$. Recall that a poset is a directed acyclic graph and vice versa. One can easily show that this relation makes $G/\mathbin \sim$ into a poset.

We may make the poset $(G/\mathbin \sim ,\preceq )$ into a weighted poset by using a weight function ${\tilde{\pi }}: G/\mathbin \sim \rightarrow \mathbb {N}$ by ${\tilde{\pi }}({\bar{v}})=\left| {\bar{v}}\right|$. Here, for a set A, |A| denotes the size of A. The weighted poset $(G/\mathbin \sim ,\preceq , {\tilde{\pi }})$ is called the weighted poset induced by the digraph G or induced weighted poset of G. In the sequel, we simply denote it by $P_{{\tilde{\pi }}}$ instead of $(G/\mathbin \sim ,\preceq , {\tilde{\pi }})$. Notice that $P_{{\tilde{\pi }}}$ is a poset with size m where m denotes the number of equivalence classes of $G/\mathbin \sim$.

Example 1.1

In Fig. 1, the given digraph has eight vertices while the induced weighted poset has four elements which are labeled by the $P_{{\tilde{\pi }}}$-weight. Observe that ${\bar{1}}=\{1\}$, ${\bar{2}}=\{2,3,4,5\}$, ${\bar{6}}=\{6,7\}$ and ${\bar{8}}=\{8\}$.

Fig. 1

${\tilde{\pi }}({\bar{1}})={\tilde{\pi }}({\bar{8}})=1$, ${\tilde{\pi }}({\bar{2}})=4$ and ${\tilde{\pi }}({\bar{6}})=2$

1.5 Perfect codes

Let $*$ be either a weighted poset $P_\pi$ or a digraph G, and let $d_*$ be the metric on $\mathbb {F}_2^n$ based on $*$, i.e., $d_*$ is either a $d_{P_\pi }$ or a $d_G$, correspondingly. Let x be a vector in $\mathbb {F}_2^n$ and r a non-negative integer. The $*$-sphere with center x and radius r is defined as the set

$$\begin{aligned} S_*(x;r)=\{y\in \mathbb {F}_2^n\mid d_*(x,y)\le r\} \end{aligned}$$

of all vectors in $\mathbb {F}_2^n$ whose $*$-distance from x is at most r.

Let $(\mathbb {F}_2^n,d_*)$ denote the metric space on $\mathbb {F}_2^n$ endowed with the $d_*$-metric. A subset C of $(\mathbb {F}_2^n,d_*)$ is called a $*$-code of length n. We wish to define an r-error-correcting perfect (for short, r-perfect) $*$-code to be a $*$-code C of length n such that the $*$-spheres of radius r centered at the codewords of C cover the whole space $\mathbb {F}_2^n$ without overlapping. However this definition depends on the labeling of coordinate positions of a code (See, Example  3.1). So we modify the definition as follow:

Definition 1.1

Let C be a $*$-code of length n. We say that C admits an r-perfect code when there is a labeling of coordinate positions such that $*$-spheres of radius r centered at the codewords of C cover the whole space $\mathbb {F}_2^n$ without overlapping with respect to this labeling. Otherwise, we say that C does not admit an r-perfect code.

Remark 1.1

Let $\mathbb {F}_2^n$ be endowed with the Hamming metric, and C be a linear code of length n, dimension k. In this situation we say that C is an $[n,k]_H$ code or simply an [n, k] code. If the (Hamming) minimum distance of C is d, we write C is an $[n,k,d]_H$ or simply an [n, k, d] code. In our development we need to consider C as a subset of $\mathbb {F}_2^n$ endowed with the $d_*$-metric. In this situation we say that C is an $[n,k,d_*]_*$ code. In general, we have $d \le d_*$.

1.6 Size of sphere

In the weighted poset metric space, we can compute the cardinality of sphere of radius r as follows. Let $\Omega _j^\omega (i)$ be the number of order ideals of P of size i, $P_\pi$-weight $\omega$ with j maximal elements. Recall from the definition of $P_{\pi }$-weight that the number of vectors in $\mathbb {F}_2^n$ whose $P_\pi$-distance to the zero vector is exactly $\omega$ equals

$$\begin{aligned} \left\{ \begin{array}{ll} 1 &{} \text {if}~\omega =0,\\ \displaystyle \sum _{i=1}^\omega \sum _{j=1}^i2^{i-j}\Omega _j^\omega (i)&{} \text {if}~\omega >0. \end{array} \right. \end{aligned}$$

Therefore we have

$$\begin{aligned} \left| S_{P_\pi }(x;r)\right| =1+\sum _{\omega =1}^r\sum _{i=1}^\omega \sum _{j=1}^i2^{i-j}\Omega _j^\omega (i). \end{aligned}$$

(1)

We will close this introduction section with a short comment on the goal of this paper. In this paper, we consider the problem of classifying weighted posets and digraphs which admit the extend Hamming code to be a 2-perfect code. Our first goal was to classify weighted posets and digraphs which admit the extended Hamming code of length 16 to be a 2-perfect code, and our ultimate goal in this research is, of course, to classify all weighted posets and digraphs which admit the extended Hamming code of length $2^m, m \ge 2,$ to be a 2-perfect code. Keep this goal in mind, our approach for the extended Hamming code of length 16 would be as general as possible. It will be shown in Sect. 2 that a weighted poset or a digraph which admits the extended Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code is completely determined by the structure vector which will be defined at the end of Chapter 2, and we approach the problem according to the length s of the structure vector.

This paper is organized as follow: In Sect. 2, we briefly introduce basic facts which will be used in our developments. Section 3 forms a technical core of this paper. In this section, we classify all possible structure vectors of weighted posets which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code when $s=3, 4, 5$. The classification consists of two parts, namely analytic part and construction part. We first prove a necessary condition for a weighted poset to admit the extended Hamming code to be a 2-perfect code by an analytic method. Next we construct a labeling of coordinate positions of the extended Hamming code which avoid forbidden patterns for each possible structure vector. We will end Sect. 3 with the classification of weighted posets which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code. This follows easily as a corollary of our previous result together with the consideration of the case $s=6$ with structure vector (0, 0, 0, 0, 0, 0). In Sect. 4, we classify all possible structure vectors of digraphs which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code when $s=3, 4$, which gives the classification of digraphs which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code as a consequence.

2 Preliminary

In this section, we collect basic facts which will be used in our developments. We will mainly state the facts without proofs and refer to [7] for details.

Let ${\widetilde{\mathcal {H}}}_m=[n=2^m,2^m-1-m,4]$ $(m\ge 2)$ be the extended Hamming code with the usual parity check matrix $H_m$, where $H_m$ is a $(m+1)\times 2^m$ binary matrix whose first row is the all one vector of length $2^m$ and the remaining m rows of $H_m$ form a $m\times 2^m$ submatrix whose i-th column corresponds to the 2-adic representation of $i-1$.

Recall that the set of codewords of Hamming weight 4 in ${\widetilde{\mathcal {H}}}_m$ forms a Steiner system $S(3,4,2^m)$. We obtain this fact as follows: Let a and b be distinct elements in $[2^m]$ and let C be the set of codewords of Hamming weight 4 which contain $\{a, b\}$. For ${\textbf {c}} \in C$, we put ${\textbf {c}}' = {\textbf {c}} \backslash \{a,b\}$. Then $C' = \{ {\textbf {c}}': {\textbf {c}} \in C \}$ is a partition of $[2^m] \backslash \{a,b\}$.

Definition 2.1

Let a, b be distinct elements in $[2^m]$. If $\{a, b, x,y\}$ is a codeword of ${\widetilde{\mathcal {H}}}_m$, a pair (x, y) will be called a good pair with respect to a, b. In case of fixed elements a and b are clear from the context, we would call (x, y) a good pair simply.

The extended Hamming code ${\widetilde{\mathcal {H}}}_4$ is a binary code of length 16 with the parity check matrix $H_4$. Maybe one of usual way to label coordinate positions of a vector in ${\widetilde{\mathcal {H}}}_4$ would be $\{0, 1, 2, \ldots , 15 \}$. However, in order to utilize the symmetry of the matrix $H_4$, we will give a labeling of coordinate positions by

$$\begin{aligned} \{\alpha , \beta , \gamma , \delta , \alpha ', \beta ', \gamma ', \delta ', \alpha '', \beta '', \gamma '', \delta '', \alpha ''', \beta ''', \gamma ''', \delta '''\}, \end{aligned}$$

so that $H_4$ can be written as follow:

We will fix this labeling from now on. There are several advantages of this labeling: We have several typical codewords. For example, $\{\alpha , \beta , \gamma , \delta \}$, $\{\alpha ', \beta ', \gamma ', \delta '\}$, $\{\alpha , \beta , \alpha ', \beta '\}$, $\{\alpha , \gamma ', \alpha '', \gamma '''\}$, etc. are codewords of ${\widetilde{\mathcal {H}}}_4$. Moreover, if $\{x_1, x_2, x_3, x_4\}$ is a codeword, then so is $\{x_1', x_2', x_3', x_4'\}$.

The following proposition, which gives a necessary and sufficient condition for a given code to be a perfect code, was proved in [7]. Recall that we have identified a binary vector with its support.

Proposition 2.1

[7] Let $*$ be either a $\pi$-weighted poset $P_{\pi }$ or a digraph G, and C be an [n, k] binary linear $*$-code. Then C is an r-perfect $*$-code if and only if the following two conditions are satisfied:

• 1. (The sphere packing condition) $\left| S_*(0;r)\right| =2^{n-k}$,

• 2. (The partition condition) for any non-zero codeword c and any partition x and y of c, either $w_*(x)\ge r+1$ or $w_*(y)\ge r+1$,

Since we are mainly interested with weighted posets or digraphs which admit the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ to be a 2-perfect code, we apply the proposition to the extended Hamming codes to obtain the following corollary.

Corollary 2.2

[7] Let $*$ be either a $\pi$-weighted poset $P_{\pi }$ or a digraph G. The extended binary Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-packing $*$-code if and only if for any codeword c of ${\widetilde{\mathcal {H}}}_m$ with $w_*(c)=4$, and any partition x and y of c such that $w_H(x)=w_H(y)=2$, we have either $w_*(x)\ge 3$ or $w_*(y)\ge 3$, where the partition of a vector means the partition of its support.

Lemma 2.3

[7] Let $*$ be either a $\pi$-weighted poset $P_{\pi }$ or a digraph G. If the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect $*$-code, then there are no elements in $*$ whose $*$-weight is bigger than two.

We need some terminology about posets to describe our result. Let $*$ be either a $\pi$-weighted poset $P_{\pi }$ or a digraph G. For the sake of simplicity we assume that $*$ is a $\pi$-weighted poset $P_{\pi }$, and write $P_{\pi }$ by P for short. The case of $*$ is a digraph G can be treated in a similar manner by considering the induced weighted poset of G.

As usual we use a Hasse diagram to represent P graphically. To describe P literally, we introduce the following subsets of P. For an integer i, and an element a in the ground set of P, we define

$$\begin{aligned}&\Gamma ^i(P) = \{x \in P: |\langle {x}\rangle _P|= i\},\\&\Gamma _{a}=\Gamma _{a}(P) = \{x \in P: x \succ a\}. \end{aligned}$$

Let P be a weighted poset which admits the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ to be a 2-perfect code. It follows from Lemma 2.3 that every weighted poset which admits extended Hamming code to be a 2-perfect code has level at most two, and no element has weight bigger than two. Notice that x is of level i in P if and only if $x \in \Gamma ^i(P)$ for $i=1,2$. By an abuse of notation, we will call $\Gamma ^i(P)$ be the ith level set of P and an element in the set will be called a level i element or an ith level element. Let X denote the set of level one elements of weight one, and Y denote the set of level one elements of weight two. We sometimes call an element of X a root. The number of roots in the weighted poset P will play a crucial role in our development. Let s be the number of roots in P and write $X = \{r_1, r_2, \ldots , r_s\}$. The vector $(n_1, n_2, \ldots , n_s)$, where $n_i = |\Gamma _{r_i}(P)|$ is called the structure vector of the weighted poset P. It is known that the cardinality of Y (See, for example, Lemma 3.2 in the next section) is determined by that of X, and hence the structure of P could be completely determined by its structure vector.

3 Classification of weighted posets

In this section, we will classify weighted posets which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code. As it is explained in the introduction, such a weighted poset could be completely determined by its structure vector, and we are interested in the computation of all possible structure vectors. Let s denote the number of roots, i.e, s is the length of the structure vector. We divide the classification into the cases $s=3, 4, 5$. For each s, we first derive a necessary condition for the structure vectors to admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code by an analytic method. In the next, we derive a sufficient condition by constructing a labeling of coordinate positions of ${\widetilde{\mathcal {H}}}_m$ for each possible structure vector.

Let s indicate the number of roots, i.e, s is the value of $\Omega _1^1(1)$. By a slight modification of proofs in [7], we have the following lemmas:

Lemma 3.1

[7] $\left| S_{P_\pi }(0;2)\right| =1+\Omega _1^1(1)+\Omega _1^2(1)+2\Omega _1^2(2)+\Omega _2^2(2)$.

Lemma 3.2

[7] If the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect $P_\pi$-code, then $\Omega _1^2(1)=1+\frac{1}{2}\Omega _1^1(1)(\Omega _1^1(1)-3)$.

Lemma 3.3

[7] If the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect $P_\pi$-code, then $1\le \Omega _1^1(1)\le \lfloor \frac{1+ \sqrt{2^{m+3}-7}}{2} \rfloor$.

The following corollary follows immediately from Corollary 2.2.

Corollary 3.4

Let $P_{\pi }$ be a $\pi$-weighted poset. The extended binary Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect $P_{\pi }$-code if and only if for any codeword c in ${\widetilde{\mathcal {H}}}_m$ of Hamming weight 4 is not of the types in Fig. 2.

Fig. 2

Forbidden patterns for weighted posets

A codeword of these types will be called a forbidden pattern. When we need to specify the type, it will be called a forbidden pattern of type $i, 1 \le i \le 3$.

Example 3.1

Let us consider the following three pictures. Notice that $\{\alpha ,\beta ,\gamma ',\delta '\}$ is a codeword of Hamming weight 4 in ${\widetilde{\mathcal {H}}}_3$. On the one hand, in Fig. 3, $\{\alpha ,\beta ,\gamma ',\delta '\}$ is a forbidden pattern of Type 3 since the partition $\{\alpha ,\gamma '\}$, $\{\beta ,\delta '\}$ of $\{\alpha ,\beta ,\gamma ',\delta '\}$ does not satisfy the partition condition in Proposition 2.1. This illustrates that the labeling in Fig. 3 does not admit the extended Hamming code ${\widetilde{\mathcal {H}}}_3$ to be a 2-perfect code. In fact, this structure does not admit the extended Hamming code ${\widetilde{\mathcal {H}}}_3$ to be a 2-perfect code with respect to any labeling(See Theorem 3.5). On the other hand, in Fig. 4, one can check that any codeword c of Hamming weight 4 in ${\widetilde{\mathcal {H}}}_3$ does not yield a forbidden pattern. This proves that the labeling in Fig. 4 admits the extended Hamming code ${\widetilde{\mathcal {H}}}_3$ to be a 2-perfect code. However, if we change the labels on Figs. 4 and 5, it does not admit the extended Hamming code ${\widetilde{\mathcal {H}}}_3$, even though their weighted poset structures are exactly same. In Fig. 5, $\{\alpha ,\beta ,\gamma ,\delta \}$ is a codeword of Hamming weight 4 in ${\widetilde{\mathcal {H}}}_3$, but it forms a forbidden pattern of Type 2, since the partition $\{\alpha ,\gamma \}, \{\beta ,\delta \}$ of $\{\alpha ,\beta ,\gamma ,\delta \}$ does not satisfy the partition condition of Proposition 2.1.

Fig. 3

Labeling which contains a forbidden pattern of Type 3

Fig. 4

Labeling which avoids forbidden patterns

Fig. 5

Labeling which contains a forbidden pattern of Type 2

3.1 Construction from ${\widetilde{\mathcal {H}}}_k$ to ${\widetilde{\mathcal {H}}}_m$

In this subsection, we develop a method of constructing a new weighted poset structure on $[2^m]$ which avoids forbidden patterns from a given weighted poset structure on $[2^k]$ which avoids forbidden patterns. This method will play an important role in proving sufficient condition.

Definition 3.1

In a given weighted poset, the level one element of weight 1 is called a root. For a root $\alpha$, the level two elements which belong to $\Gamma _{\alpha }$ are called leaves at $\alpha$.

Let m and k be natural numbers with $k<m$, and let $H_m$ be the parity check matrix of the extended Hamming code ${\widetilde{\mathcal {H}}}_m$. We divide $H_m$ into $2^{m-k}$ submatrices $A_1, A_2, \ldots , A_{2^{m-k}}$, which we will call sections, as follow: $A_1$ denotes the submatrix of $H_m$ consists of the first $2^k$ columns, and $A_2$ denotes the submatrix of $H_m$ consists of the next $2^k$ columns, and so on. We need one more notation about vectors. Let ${\textbf {c}}$ be a vector of length $m+1$. The subvector consists of the first $m+1-k$ (resp. last k) components is called the head (resp. tail) of ${\textbf {c}}$. Then we will realize that the sections $A_1, A_2, \ldots , A_{2^{m-k}}$ have the same tail part, while they have distinct head part. We remark that to vectors ${\textbf {a}}$ and ${\textbf {b}}$ of the same length satisfy ${\textbf {a}} + {\textbf {b}} = {\textbf {0}}$ if and only if they have the same head and tail. It now follows from the definition of extended Hamming code that every codeword of Hamming weight 4 has either four columns in the same section, two columns in one section and the other two in another section, or one column in four different sections.

Let $P(=P_1)$ be a weighted poset on $[2^k]$ which avoids forbidden patterns. We will call P a basic form, and the coordinate positions belonging to other section will be called extender. The basic idea of our construction runs as follow: We start from a basic form,

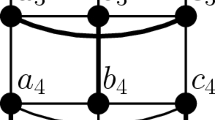
and place coordinate positions of one extender as leaf of the roots of P to form a weighted poset $P_2$ on $[2^k + 2^k]$ elements in such a way that the resulting weighted poset avoids forbidden patterns. By repeating this process $2^{m-k}-1$ times we obtain a weighted poset Q on $[2^m]$ which avoids forbidden patterns. We first illustrate our idea when $s=3$. In this case, $k=2$ and the basic form is as in Fig. 6:

Fig. 6

Basic form with $s=3$

There are two ways to add extenders to roots as in Fig. 7.

Fig. 7

Extenders of $s=3$

Recall that, when we distribute extenders to leaves on two roots say $\{\alpha , \beta \}$, we place $\{\alpha ', \beta ' \}$ as leaves on one root and the remaining two extenders as leaves on the other root. When $s>3$, basic forms will be more complicated and k becomes larger. However the basic idea remains the same.

We now return to the case of arbitrary k, and prove that the resulting weighted poset Q cannot posses a forbidden pattern. Since P and Q have the same roots, Q cannot possess a forbidden pattern of type 1 and 2. Let ${\textbf {c}}=\{a,b,c,d\}$ be a codeword $\in {\widetilde{\mathcal {H}}}_m$ of where a, b, c and d are elements in Q. Note that forbidden pattern of type 3 contain two roots. So we may assume that a and b are roots. Since ${\textbf {c}}\in {\widetilde{\mathcal {H}}}_m$, c and d are column positions of $A_j$ for some $1\le j\le i$. Notice that, from the way of distributing extenders to leaves of roots, we already avoid forbidden patterns of type 3 and this proves that ${\textbf {c}}$ is not a forbidden pattern.

3.2 The case $s=3$

From now on, we begin to classify weighted posets which admit extended hamming codes to be a 2-perfect code. We start with a few sentences of caution. The meaning of $\alpha , \beta ,\gamma ,\ldots$ from now on is different from that of $\alpha , \beta ,\gamma , \ldots$ on page 7. The $\alpha , \beta ,\gamma ,\ldots$ will denote the level one elements. We sometimes use figure $\textcircled {1}$ to denote a level one element of weight one, and $\textcircled {2}$ to denote a level one element of weight two. We will use sub-indexed notation to denote level two elements. Therefore $\alpha _i$ (respectively $\beta _j$) denotes level two elements lying above $\alpha$ (respectively $\beta$).

In this subsection, we will discuss a classification the for case of $s=3$. Then we have $(\Omega _1^1(1), \Omega _1^2(1), \Omega _1^2(2)) = (3,1,2^m-4)$. The weighted poset with the structure vector (a, b, c) may be represented as in Fig. 8.

Fig. 8

Weighted posets with $s=3$

where $a+b+c=2^m-4$. Notice that variables in this figure does not mean the labeling of coordinate positions.

Theorem 3.5

The condition that $a, b, \text{ and } c$ are even is a necessary condition for the weighted poset admits 2-perfect $P_\pi$-code.

Proof

Let $\{\alpha ,\beta ,\gamma , x \}$ be a codeword which contains $\{\alpha ,\beta ,\gamma \}$. If $x \not = \delta$, we have a forbidden pattern. This proves that $\{\alpha ,\beta ,\gamma ,\delta \}$ is a codeword in Fig. 8 above. By considering codewords which contain $\{\alpha ,\gamma ,\gamma _i\} (\text{ resp. } \{\beta ,\gamma ,\gamma _i\}), 1 \le i \le c$, we obtain the following codewords:

$$\begin{aligned} \begin{array}{cccl} \{\alpha ,\gamma ,\gamma _1,x_1\}&{}\{\alpha ,\gamma ,\gamma _2,x_2\}&{} \cdots &{}\{\alpha ,\gamma ,\gamma _c,x_c\} \\ \{\beta ,\gamma ,\gamma _1,y_1\}&{}\{\beta ,\gamma ,\gamma _2,y_2\}&{} \dots &{}\{\beta ,\gamma ,\gamma _c,y_c\} . \end{array} \end{aligned}$$

Each $x_i$ (resp. $y_i$) belongs to $\Gamma _{\beta } \cup \Gamma _{\gamma }$ (resp. $\Gamma _{\alpha } \cup \Gamma _{\gamma }$). If $x_i \in \Gamma _{\beta }$ and $y_i \in \Gamma _{\alpha }$ for some i, we obtains a forbidden pattern. Therefore we have $x_i\in \Gamma _\gamma$ or $y_i\in \Gamma _\gamma$ for each i. We claim that we may choose $x_i$ or $y_i$, namely $z_i$ for each i, so that $\{z_1 ,\ldots , z_c\} = \{\gamma _1,\ldots , \gamma _c\}$.

We first prove our claim. Assume that $x_i=x_j$ for some distinct i and j. By adding two codewords $\{\alpha ,\gamma ,\gamma _i,x_i\} \text{ and } \{\alpha ,\gamma ,\gamma _j,x_j\}$, we obtain a codeword $\{\gamma _i,\gamma _j\}$, which is a contradiction. This proves that $i\not =j$ implies that $x_i\not =x_j$ and $y_i\not =y_j$. Assume now that $x_i$ and $y_j$ are chosen and $x_i=y_j$ for some distinct i and j. Then, $\{\alpha ,\gamma ,\gamma _i,x_i\}+\{\beta ,\gamma ,\gamma _j,y_j\}=\{\alpha ,\beta ,\gamma _i,\gamma _j\}\in {\widetilde{\mathcal {H}}}_m$. Since $\{\alpha ,\gamma ,\gamma _j,x_j\}+\{\beta ,\gamma ,\gamma _i,y_i\}=\{\alpha ,\beta ,\gamma _i,\gamma _j,x_j,y_i\}\in {\widetilde{\mathcal {H}}}_m$, we have $x_j=y_i$. Note that $x_j\in \Gamma _\beta \cup \Gamma _\gamma$ and $y_i\in \Gamma _\alpha \cup \Gamma _\gamma$ so that $x_j=y_i$ only if $x_j\in \Gamma _\gamma$, and we may choose $x_j$ instead of $y_j$ in this case. Assume finally that we choose $x_i$ and $y_j$ with $x_i \not = y_j$. To complete the claim, it is enough to show that there does not exist k such that $\{x_k,y_k\}=\{x_i,y_j\}$. If $\{x_k,y_k\}=\{x_i,y_j\}$, $\{\alpha ,\gamma ,\gamma _k,x_k\}+\{\beta ,\gamma ,\gamma _k,y_k\}=\{\alpha ,\beta ,x_k,y_k\}=\{\alpha ,\beta ,x_i,y_j\}$ is a codeword of ${\widetilde{\mathcal {H}}}_m$. Therefore $\{\alpha ,\gamma ,\gamma _i,x_i\}+\{\alpha ,\beta ,x_i,y_j\}=\{\beta ,\gamma ,\gamma _i,y_j\}$ is also a codeword of ${\widetilde{\mathcal {H}}}_m$. And this would yield that $y_i=y_j$ which is a contradiction. This proves the claim.

Now next consider the summation of codewords which contain $\{\gamma ,\gamma _i,z_i\}$ where $z_i, i = 1, \ldots , c,$ are chosen in our claim:

$$\begin{aligned} \sum _{i=1}^{c}\{\alpha (\text{ or } \beta ),\gamma ,\gamma _i,z_i\}=\left\{ \begin{array}{ll} \{\alpha ,\gamma \} \text{ or } \{\beta ,\gamma \} &{}(c \text{ is } \text{ odd}) \\ \{\alpha ,\beta \} \text{ or } 0 &{} (c \text{ is } \text{ even}). \end{array} \right. \end{aligned}$$

Since the left hand side of the equation is clearly a codeword of ${\widetilde{\mathcal {H}}}_m$, c must be even. By changing roles of a, b, c we finally conclude that a, b, c are all even and this completes the proof. $\square$

Theorem 3.6

If the weighted poset structure is represented as in Fig. 8, the weighted poset admits 2-perfect $P_\pi$-code if a, b, c are all even.

Proof

Let P be a weighted poset on $[2^m]$ which avoids forbidden patterns, and let $X=\{\alpha , \beta , \gamma \}$ be the set of weight one and level one and elements in P. There should be the fourth element, say $\delta$, such that $\{\alpha , \beta , \gamma , \delta \}$ is a codeword of Hamming weight 4. To avoid forbidden patterns $\delta$ should have level one and weight two. This weighted poset can be represented as in Fig. 9.

Fig. 9

Basic form of the case $s=3$

When $m=2$, there is clearly a unique weighted poset on 4 elements avoiding forbidden patterns. On the other hand, there is only one solution for the equation $a+b+c = 2^m -4 =0$ with a, b, c are even, namely $(a,b,c)=(0,0,0)$.

We may construct two extenders whose roots are $\{\alpha , \beta ,\gamma \}$ and leaves are $\{\alpha ',\beta ',\gamma ',\delta '\}$ as in Fig. 7. By symmetry, we obtain extenders whose structure vectors are $(4,0,0),(0,4,0),(0,0,4),(2,2,0),(2,0,2)$, and (0, 2, 2).

Now let m be an arbitrary integer such that $m\ge 2$. Assume that $a+b+c = 2^m -4$ and a, b, c are even. To show there is a weighted poset P who admits 2-perfect $P_\pi$-code on $[2^m]$ with structure vector (a, b, c), it is enough to show that $(a-0,b-0,c-0)$ can be represented by sum of elements in $E=\{(4,0,0),(0,4,0),(0,0,4),(2,2,0),(2,0,2), (0,2,2)\}$.

Let $a',b'$ and $c'$ be remainders of a, b and c divided by 4 respectively. Then $a',b'$ and $c'$ are even and $a'+b'+c'$ is either 0 or 4. That is, $(a',b',c')=0$ or $(a',b',c')\in E$. Therefore, $(a,b,c)=(a',b',c')+ \frac{a-a'}{4}(4,0,0)+\frac{b-b'}{4}(0,4,0)+\frac{c-c'}{4}(0,0,4)$ implies that weighted poset avoiding forbidden patterns with structure vector (a, b, c) is constructable. $\square$

3.3 The case $s=4$

In this subsection, we will classify weighted posets admitting extended 2-perfect $P_\pi$-code for the case $s=4$. That is, $(\Omega _1^1(1), \Omega _1^2(1), \Omega _1^2(2))=(4,3,2^m-7)$ and it can be represented by a figure as in Fig. 10.

where $a+b+c+d=2^m-7$. Note that $Y=\{\omega _1,\omega _2,\omega _3\}$.

Theorem 3.7

The condition that exactly one of a, b, c and d is odd is a necessary condition for the weighted poset admits 2-perfect $P_\pi$-code.

Proof

Let $\{\alpha ,\beta ,\gamma ,x\}$ and $\{\alpha ,\beta ,\delta ,y\}$ be codewords which contain $\{\alpha ,\beta ,\gamma \}$ and $\{\alpha ,\beta ,\delta \}$ respectively. Note that $x\in \Gamma _\delta \cup Y$ and $y\in \Gamma _\gamma \cup Y$. Since $\{\alpha ,\beta ,\gamma ,x\}+\{\alpha ,\beta ,\delta ,y\}=\{\gamma ,\delta ,x,y\}\in {\widetilde{\mathcal {H}}}_m$, either $x\notin \Gamma _\delta$ or $y\notin \Gamma _{\gamma }$. This implies $x\in Y$ or $y\in Y$ and we may assume that $x\in Y$ and $x=\omega _1$. Let $\{\alpha ,\gamma ,\delta ,z\}$ be a codeword which contains $\{\alpha ,\gamma ,\delta \}$. Note that $z\in \Gamma _\beta \cup Y$ and $\{\alpha ,\beta ,\delta ,y\}+\{\alpha ,\gamma ,\delta ,z\}=\{\beta ,\gamma ,y,z\}\in {\widetilde{\mathcal {H}}}_m$. Therefore $y\in Y$ or $z\in Y$ and we may assume that $y\in Y$. Let $\{\beta ,\gamma ,\delta ,w\}$ be a codewords which contains $\{\beta ,\gamma ,\delta \}$. Then $w\in \Gamma _{\alpha }\cup Y$. Since $\{\alpha ,\gamma ,\delta ,z\}+\{\beta ,\gamma ,\delta ,w\}=\{\alpha ,\beta ,z,w\}\in {\widetilde{\mathcal {H}}}_m$, $z\in Y$ or $w\in Y$. Therefore we may assume that $z\in Y$ also. By adding $\{\alpha ,\beta ,\gamma ,x\},\{\alpha ,\beta ,\delta ,y\},\{\alpha ,\gamma ,\delta ,z\}$ and $\{\beta ,\gamma ,\delta ,w\}$ pairwise, we have x, y, z and w are distinct. So, for $|Y|=3$ and $\{x,y,z\}\subset Y$, $w\notin Y$ which implies $w\in \Gamma _{\alpha }$. This proves we may assume that $\{\beta ,\gamma ,\delta ,\alpha _1\},\{\alpha ,\beta ,\gamma ,\omega _1\},\{\alpha ,\beta ,\delta ,\omega _2\}$ and $\{\alpha ,\gamma ,\delta ,\omega _3\}$ are codewords. Now we have good pairs $(\gamma ,\omega _1)$, $(\delta ,\omega _2)$, $(\alpha _1,\omega _3)$ with respect to $\alpha$ and $\beta$.

By considering codewords which contain $\{\alpha ,\gamma ,\gamma _i\}$ and $\{\alpha ,\delta ,\delta _j\}$(resp. $\{\beta ,\gamma ,\gamma _i\}$ and $\{\beta ,\delta ,\delta _j\}$),$1\le i\le c$ and $c+1\le j\le c+d$ we obtain the following codewords:

$$\begin{aligned} \begin{array}{ccccccl} \{\alpha ,\gamma ,\gamma _1,x_1\}&{} \cdots &{}\{\alpha ,\gamma ,\gamma _c,x_c\}&{}\{\alpha ,\delta ,\delta _1,x_{c+1}\}&{}\cdots &{}\{\alpha ,\delta ,\delta _d,x_{c+d}\} \\ \{\beta ,\gamma ,\gamma _1,y_1\}&{}\cdots &{}\{\beta ,\gamma ,\gamma _c,y_c\}&{}\{\beta ,\delta ,\delta _1,y_{c+1}\}&{}\cdots &{}\{\beta ,\delta ,\delta _d,y_{c+d}\}&{}. \end{array} \end{aligned}$$

To avoid forbidden patterns, each $x_i$ (resp. $y_i$) would belong to $\Gamma _{\beta }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }\cup Y$ (resp. $\Gamma _{\alpha }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }\cup Y$). First we will prove the claim: $x_i\notin Y \text {and } y_i\notin Y$. Note that $(x_i, y_i)$ are good pairs. Therefore if $x_i=\omega _1$ or $x_i=\omega _2$ for some i, $y_i=\gamma$ or $y_i=\delta$ respectively. We can easily obtain contradiction for each cases, since $\{\beta ,\gamma ,\gamma _i,y\}$(if $1\le i \le c$) or $\{\beta , \delta ,\delta _{i-c},y_i\}$(if $c+1\le i \le c+d$) would be a forbidden pattern or have a length 2. So, $x_i\notin \{\omega _1,\omega _2\}$ and by the same argument, we also have $y_i\notin \{\omega _1,\omega _2\}$. Assume that $x_i=\omega _3$ for some i. Then $y_i =\alpha _1$. However, since $\{\beta ,\gamma ,\delta ,\alpha _1\}\in {\widetilde{\mathcal {H}}}_m$, neither $\{\beta ,\gamma ,\gamma _i,y_i\}$ nor $\{\beta ,\delta ,\delta _{i-c},y_i\}$ can be a codeword. Also if $y_i=\omega _3$ for some i, $x_i=\alpha _1\in \Gamma _{\alpha }$ and we have a contradiction. This proves $x_i\notin Y$ and $y_i\notin Y$, or $x_i\in \Gamma _{\beta }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }$ and $y_i\in \Gamma _{\alpha }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }$. If $x_i\in \Gamma _\beta$ and $y_i\in \Gamma _\alpha$ for some i, we obtain a forbidden pattern. Therefore we have $x_i\in \Gamma _\gamma \cup \Gamma _{\delta }$ or $y_i\in \Gamma _{\gamma }\cup \Gamma _{\delta }$ for each i.

Here is the second claim: we may choose $x_i$ or $y_i$, namely $z_i$ for each i, so that $\{z_1,\ldots ,z_{c+d}\}=\{\gamma _1,\ldots ,\gamma _c,\delta _1,\ldots ,\delta _d\}.$ Now we prove this claim. Assume that $x_i=x_j$ for some $i<j$. By adding two codewords $\{\alpha ,\gamma ,\gamma _i,x_i\}$ and $\{\alpha ,\gamma ,\gamma _j,x_j\}(1\le i<j \le c)$, or $\{\alpha ,\gamma ,\gamma _i,x_i\}$ and $\{\alpha ,\delta ,\delta _{j-c},x_j\}(1\le c<j\le c+d)$, or $\{\alpha ,\delta ,\delta _{i-c},x_i\}$ and $\{\alpha ,\delta ,\delta _{j-c},x_j\}(c+1\le i<j\le c+d)$, we have a contradiction. This proves that $i\not =j$ implies $x_i\not =x_j$ and $y_i\not =y_j$. For the next, assume that $x_i$ and $y_i$ are chosen and $x_i=y_j$ for some $i\not = j$. Then $\{\alpha ,\beta ,x_i,y_i\}+\{\alpha ,\beta ,x_j,y_j\}=\{x_j,y_i\}\in {\widetilde{\mathcal {H}}}_m$. Therefore $x_j=y_i$. Note that $x_i\in \Gamma _{\beta }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }$ and $y_i\in \Gamma _{\alpha }\cup \Gamma _{\gamma }\cup \Gamma _{\delta }$. So $x_j\in \Gamma _{\delta }\cup \Gamma _{\gamma }$ and we may choose $x_j$ instead of $y_j$ in this case. To complete the claim, it is enough to show that if we choose $x_i$ and $y_j$ such that $x_i\not =y_j$, there does not exist k such $\{x_k,y_k\}=\{x_i,y_j\}$. Assume that $\{x_k,y_k\}=\{x_i,y_j\}$ for some $i\not =j$ and k. Note that $\{\alpha ,\beta ,x_k,y_k\}$ is a codeword. So $\{\alpha ,\beta ,x_i,y_j\}$ should be a codeword also, which is contradiction since $\{\alpha ,\beta ,x_i,y_j\}+\{\alpha ,\beta ,x_i,y_i\}=\{y_i,y_j\}$ cannot be zero. This proves claim.

Now next consider the summation of codewords which contain $\{\gamma ,\gamma _i,z_i\}$ or $\{\delta ,\delta _{i-c},z_i\}$, where $z_i, 1\le i\le c+d$ are chosen in our last claim, namely ${\textbf {c}}$:

$$\begin{aligned}{} {\textbf {c}}=\left\{ \begin{array}{llll} \{\alpha ,\beta ,\gamma ,\delta \} &{} \text{ or } &{}\{\gamma ,\delta \} &{}(c \equiv d\equiv 1\text{(mod2) }) \\ \{\alpha ,\gamma \}&{} \text{ or } &{}\{\beta ,\gamma \} &{}(c \equiv 1, d\equiv 0 \text{(mod2) }) \\ \{\alpha ,\delta \}&{} \text{ or } &{}\{\beta ,\delta \}&{}(c\equiv 0, d\equiv 1\text{(mod2) }) \\ \{\alpha ,\beta \} &{} \text{ or } &{}0 &{} (c\equiv d\equiv 0 \text{(mod2) }). \end{array} \right. \end{aligned}$$

Since the ${\textbf {c}}\in {\widetilde{\mathcal {H}}}_m$ clearly,, c and d must be even. We may change the roles of b, c and d, without breaking the symmetry, and we finally conclude that b, c, and d are even which implies that a is odd. $\square$

Theorem 3.8

If the weighted poset structure is represented as in Fig. 10, the weighted poset admits 2-perfect $P_\pi$-code if one and only one of a, b, c is odd.

Proof

Let P be a weighted poset on $[2^m](m\ge 3)$ which avoids forbidden patterns, and let $\alpha ,\beta ,$ and $\gamma$ be level 1 elements of weight 1. There is a fourth element, namely $\delta$, such that $\{\alpha ,\beta ,\gamma ,\delta \}$ is a codeword of Hamming weight 4. To avoid forbidden patterns, $\delta$ cannot be a root. So we may assume that $X=\{\alpha ,\beta ,\gamma ,\alpha '\}$ is a set of roots. Let $\beta '$,$\gamma '$ and $\delta '$ be elements such that $\{\alpha ,\beta ,\alpha ',\beta '\}$,$\{\alpha ,\gamma ,\alpha ','\gamma '\}$,$\{\beta ,\gamma ,\alpha ',\delta '\}$ are codewords respectively. Then, to avoid forbidden patterns, $\delta \in \Gamma _{\alpha '}\cup Y$, $\beta '\in \Gamma _\gamma \cup Y$, $\gamma '\in \Gamma _\beta \cup Y$ and $\delta '\in \Gamma _\alpha \cup Y$. Assume that neither $\delta$ nor $\beta '$ is in Y. Then, $\delta \in \Gamma _{\alpha '}$ and $\beta '\in \Gamma _\gamma$. In this case, the codeword $\{\alpha ,\beta ,\gamma ,\delta \}=\{\alpha ,\beta ,\alpha ',\beta '\}=\{\gamma ,\delta ,\alpha ',\beta '\}$ be a forbidden pattern. Therefore at least one of $\delta$ and $\beta '$ should be in Y. This implies that at least three of $\delta ,\beta ',\gamma ',\delta$ are level 1 elements of weight 2. Since $|Y|=3$, one of $\delta ,\beta ',\gamma ',\delta '$ is a leaf and the others are level 1 elements of weight 2. Without loss of generality, we may assume that $\delta '\in \Gamma _\alpha$. When $m=3$, there is a unique weighted poset on 8 elements avoiding forbidden pattern, up to symmetry as in Fig. 11.

Fig. 10

Weighted posets with $s=4$

Fig. 11

Basic form of the case $s=4$

Now let $m\ge 3$ be an arbitrary integer and let a, b, c and d are integers such that $a+b+c+d=2^m-7$ and exactly one of a, b, c and d is odd. We may assume that a is an odd number. Let $a',b',c'$ and $d'$ are remainders of dividing 8 into $a-1, b, c$ and d respectively. Then $a',b',c'$ and $d'$ are even numbers and $a'+b'+c'+d'$ is multiple of 8 which is less than 32. It is obvious that $(a',b',c',d')$ can be represented by the sum of some elements in $\{(6,2,0,0),(4,4,0,0),(4,2,2,0)\}$ involving their permuted component. Note that $(a,b,c,d)=(1,0,0,0)+(a',b',c',d')+\frac{a-a'}{8}(8,0,0,0)+\frac{b-b'}{8}(0,8,0,0)+\frac{c-c'}{8}(0,0,8,0)+\frac{d-d'}{8}(0,0,0,8)$. To show that there is a weighted poset avoiding forbidden patterns with structure vector (a, b, c, d), it is enough to show that there are extenders whose structure vectors are (8, 0, 0, 0), (6, 2, 0, 0), (4, 2, 2, 0) and (2, 2, 2, 2).

In (8, 0, 0, 0), (6, 2, 0, 0), (4, 2, 2, 0) cases, it may treated similarly with $s=3$ since $\Gamma _{\alpha '}=\emptyset$, and we may construct the structure by using extenders of $s=3$. (2, 2, 2, 2) may constructed as in Fig. 12.

Fig. 12

Extenders with structure vector (2, 2, 2, 2)

So, we can obtain the result that we desired.

$\square$

3.4 The case $s=5$

If $s=5$, the structure vector of weighted posets may given by $(\Omega _1^1(1),\Omega _1^2(1),\Omega _1^2(2))=(5,6,2^m-11)$. Therefore, the least m we may consider is 4, and the number of leaves would be 5. There are seven vectors (a, b, c, d, e) where $a\ge b\ge c\ge d\ge e$ and $a+b+c+d+e=5$; (5, 0, 0, 0, 0), (4, 1, 0, 0, 0), (3, 2, 0, 0, 0), (3, 1, 1, 0, 0),(2, 2, 1, 0, 0), (2, 1, 1, 1, 0), (1, 1, 1, 1, 1). For these 7 cases, we can obtain basic forms as represented in the following weighted posets. Actually a tedious check shows that each of the poset in Fig. 13 avoids forbidden patterns.

Fig. 13

Basic forms of the case $s=5$

Now let m be an arbitrary positive integer and a, b, c, d and e be positive integers such that $a+b+c+d+e=2^m-11$. Let $a_1, b_1, c_1, d_1$ and $e_1$ be the number such that $a_1+b_1+c_1+d_1+e_1=5$ and $x-x_1(x=a,b,c,d,e)$, namely $x'$ are all even. Then, $(a,b,c,d,e)=(a_1,b_1,c_1,d_1,e_1)+(a',b',c',d',e')$ and we can easily find out that $(a',b',c',d',e')$ can be represented by the some elements in $\{(m_1,m_2,m_3,m_4,m_5):m_1+\cdots +m_5=16 \text { and } m_i\text { are even} \}$.

Now we will construct extenders with structure vector $(m_1,m_2,m_3,m_4,m_5)$, where $\sum _{i=1}^{5}m_i=16$ and $a\ge b\ge c\ge d\ge e$ are all even. If $e=0$, we may construct it by add the two extenders whose the number of leaves are 8 which is already constructed in Sect. 3.3. So, it is enough to consider the case (6, 4, 2, 2, 2) and (4, 4, 4, 2, 2). Figure 14 represents these extenders, where $\{\alpha ^1,\beta ^1,\ldots ,\delta ^4\}$ is the set of coordinates of another blocks, which may considered as a duplication of $\{\alpha ,\beta ,\ldots ,\delta ''''\}$.

Fig. 14

Extenders with $e\not =0$

From the basic forms and these extenders, we may conclude that every structure in case $s=5$ admits the extended binary Hamming code ${\widetilde{\mathcal {H}}}_m$.

Theorem 3.9

Let $P_\pi$ be a weighted poset with $(\Omega _1^1(1),\Omega _1^2(1),\Omega _1^2(2))=(5,6,2^m-11)$. Then there is a labeling for $P_\pi$ which make ${\widetilde{\mathcal {H}}}_m$ be a 2-perfect $P_\pi$-code.

3.5 A classification of weighted posets admitting ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code

Now we may classify the weighted posets which admit the extended binary Hamming code ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code. Note that the only possibilities of $(\Omega _1^1,\Omega _1^2,\Omega _2^1)$ are (1, 0, 15), (2, 0, 14), (3, 1, 12), (4, 3, 9), (5, 6, 5) and (6, 10, 0). Since we already observed for $s=1,2,3,4,5$, it is enough to consider the case $s=6$. Since ${\widetilde{\mathcal {H}}}_4$ is a code of length 16, the only possible structure vector is (0, 0, 0, 0, 0, 0), and in this case we can give a labeling which admits ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code as in Fig. 15.

Fig. 15

The weighted poset admits extended 2-perfect code ${\widetilde{\mathcal {H}}}_4$ with $s=6$

4 Classification of directed graph

In this section, we will classify the digraphs which admit the extended Hamming code to be a 2-perfect code. The theory runs similarly as that of weighted poset case. However there is a major difference between two theories, namely in the weighted poset case an element of weight two can be considered as one point in the weighted poset, while in the digraphs case an element of weight two, which is a cycle of length two in the digraphs, should be considered as two vertices in the graph. This difference yields modifications in Lemmas 3.1, 3.2 and 3.3 as follow.

Lemma 4.1

$\left| S_G(0;2)\right| =1+\Omega _1^1(1)+3\Omega _1^2(1)+2\Omega _1^2(2)+\Omega _2^2(2)$.

Lemma 4.2

If the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect G-code, then $\Omega _1^2(1)=1+\frac{1}{2}\Omega _1^1(1)(\Omega _1^1(1)-3)$.

Lemma 4.3

If the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect G-code, then $1\le \Omega _1^1(1)\le \lfloor \sqrt{2^m -1} \rfloor$.

We also need to modify Corollary 3.4 as follow

Corollary 4.4

Let G be a digraph. The extended binary hamming code ${\widetilde{\mathcal {H}}}_m$ is a 2-perfect G-code if and only if for any codeword c in ${\widetilde{\mathcal {H}}}_m$ of Hamming weight 4 is not of the types in Fig. 16.

Fig. 16

Forbidden patterns for digraphs

A codeword of these types will be called a forbidden pattern. When we need to specify the type, it will be called a forbidden pattern of type $i, 1 \le i \le 6$.

Remark 4.1

We may apply the same argument as in Sect. 3.1. We first obtain a digraph which avoids forbidden patterns, i.e., a basic form for digraphs, and get a new digraph which avoids forbidden patterns for an extended Hamming code of larger length. Note that the extenders of a weighted poset can also be used as extenders for digraphs. Therefore we may apply same process and extenders to obtain a new digraph which avoids forbidden patterns. From this remark, we may conclude that, in the proof of sufficient condition in this section, it is enough to construct appropriate basic forms.

4.1 The case $s=3$

We may represent the correspondence digraph structure as in Fig. 17 where $a+b+c=2^m-5$. Note that $Y=\{\omega ,\omega '\}$.

Fig. 17

Digraph with $s=3$

Theorem 4.5

The digraph admits 2-perfect G-code if and only if a, b, c are odd.

Proof

($\Rightarrow$)Let $\{\alpha ,\beta ,\gamma ,x\}$ be a codeword. To avoid forbidden patterns, x should be $\omega$. So $\{\alpha ,\beta ,\gamma ,\omega \}\in {\widetilde{\mathcal {H}}}_m$. Consider codewords containing $\{\alpha ,\gamma ,\gamma _i\}$ and $\{\alpha ,\omega ,\omega '\}$ (resp. $\{\beta ,\gamma ,\gamma _i\}$, and $\{\beta ,\omega ,\omega '\}$)$1\le i \le c$.

$$\begin{aligned} \begin{array}{ccccl} \{\alpha ,\gamma ,\gamma _1,x_1\}&{}\{\alpha ,\gamma ,\gamma _2,x_2\}&{} \cdots &{}\{\alpha ,\gamma ,\gamma _c,x_c\}&{}\{\alpha ,\omega ,\omega ',x_0\} \\ \{\beta ,\gamma ,\gamma _1,y_1\}&{}\{\beta ,\gamma ,\gamma _2,y_2\}&{} \dots &{}\{\beta ,\gamma ,\gamma _c,y_c\}&{}\{\beta ,\omega ,\omega ',y_0\} . \end{array} \end{aligned}$$

Each $x_i$(resp.$y_i$) belongs to $\Gamma _\beta \cup \Gamma _{\gamma }\cup \{\omega '\}$(resp. $\Gamma _{\alpha }\cup \Gamma _\gamma \cup \{\omega '\}$). Since $(x_i,y_i)$ are good pairs, we have $x_i\in \{\omega '\}\cup \Gamma _\gamma$ or $y_i\in \{\omega '\}\cup \Gamma _\gamma$ for each i. We claim that we may choose $x_i$ or $y_i$, namely $z_i$ for each i, so that $\{z_0,z_1\ldots ,z_c\}=\{\gamma _1,\ldots ,\gamma _c,\omega '\}$.

We first prove our claim. Assume that $x_i=x_j$ for some distinct $i\not =j$. If $j=0$, by adding two codewords $\{\alpha ,\gamma ,\gamma _i,x_i\}$ and $\{\alpha ,\omega ,\omega ',x_0\}$, we obtain a forbidden pattern. If neither i nor j is zero, by adding two codewords $\{\alpha ,\gamma ,\gamma _i,x_i\}$ and $\{\alpha ,\gamma ,\gamma _j,x_j\}$, we obtain $\{\gamma _i,\gamma _j\}$ which cannot be a codeword. This proves that $x_i\not =x_j$ and $y_i\not =y_j$ if $i\not =j$. Assume that $x_i$ and $y_j$ are chosen and $x_i=y_j$ for distinct i and j. Then $\{\alpha ,\beta ,x_i,y_i\}+\{\alpha ,\beta ,x_j,y_j\}=\{x_j,y_i\}\in {\widetilde{\mathcal {H}}}_m$ and $x_j=y_i$. Note that $x_i\in \Gamma _{\beta }\Gamma _\gamma \cup \{\omega '\}$ and $y_j\in \Gamma _\alpha \cup \Gamma _\gamma \cup \{\omega '\}$. So $x_j=y_i$ implies $x_j\in \Gamma _\gamma \cup \{\omega '\}$ and we may choose $x_j$ instead of $y_j$. Assume finally that we choose $x_i$ and $y_j$ with $x_i\not =y_j$. To complete the claim, it is enough to show that there does not exist k such that $\{x_k,y_k\}=\{x_i,y_j\}$. If $\{x_k,y_k\}=\{x_i,y_j\}$, we have $\{\alpha ,\beta ,x_k,y_k\}+\{\alpha ,\beta ,x_i,y_i\}=\{\alpha ,\beta ,x_i,y_j\}+\{\alpha ,\beta ,x_i,y_i\}=\{y_i,y_j\}$. Note that $\{\alpha ,\beta ,x_k,y_k\}$and $\{\alpha ,\beta ,x_i,y_i\}$ are codewords but $\{y_i,y_j\}$ is not. So, this is contradiction and the claim is proved.

Now consider the summation of codewords which contains $\{\gamma ,\gamma _i,z_i\}$ or $\{\omega ,\omega ',z_0\}$. By simple calculation, we may obtain this is $\{\alpha ,\omega \}$ or $\{\beta ,\omega \}$ if c is even, and this cannot be a codeword. So c must be odd and, by changing roles of a,b, and c, we finally conclude that a, b and c are all odd. This complete the proof.

($\Leftarrow$) If we consider the basic form of $s=3$, m should be at least 3. Let $X=\{\alpha ,\beta ,\gamma \}$ be a set of roots and let $\{\alpha ,\beta ,\gamma ,\delta \}$ be a codeword. To avoid forbidden patterns, $\delta$ should be in Y. Let $\alpha '$ be the another column of $H_m$ and assume that $\alpha '\in \Gamma _\gamma$. There should another element $\beta '$ so that $\{\alpha ,\beta ,\alpha ',\beta '\}$ be a codeword. Then, since $\{\alpha ,\beta ,\gamma ,\delta \}+\{\alpha ,\beta ,\alpha ',\beta '\}=\{\gamma ,\delta ,\alpha ',\beta '\}$ is also codeword, $\beta '\notin \Gamma _\beta \cup Y$. Therefore $\beta '\in \Gamma _\alpha$. For the elements $\gamma '$ and $\delta '$ such that $\{\alpha ,\gamma ,\alpha ',\gamma '\}$ and $\{\alpha ,\delta ,\alpha ',\delta '\}$ be codewords respectively, we may obtain $\gamma \in \Gamma _\beta$ and $\delta '\in Y$.

Now let $m=3$. Then we obtain a unique basic form as in Fig. 18.

Fig. 18

Basic form of digraph when $s=3$

Now we may apply the same extender arguments as in Sect. 3.2 to obtain the digraphs with structure vector (a, b, c) with a, b and c are odd.

$\square$

4.2 The case $s=4$

We may represent the correspondence digraph structure figure as in Fig. 19 where $a+b+c+d=2^m-10$. Note that $Y=\{\omega _1,\omega _1',\omega _2',\omega _2',\omega _3,\omega _3'\}$.

Fig. 19

Digraphs with $s=4$

Theorem 4.6

The digraph G admits 2-perfect G-code if and only if a, b, c and d are even.

Proof

($\Rightarrow$) Let $\{\alpha ,\beta ,\gamma ,x\}$ and $\{\alpha ,\gamma ,\delta ,y\}$ be codewords which contains $\{\alpha ,\beta ,\gamma \}$ and $\{\alpha ,\beta ,\delta \}$ respectively. Then $x\in \Gamma _\delta \cup Y$ and $y\in \Gamma _\beta \cup Y$. Then $\{\beta ,\delta ,x,y\}$ is a codeword, and to avoid forbidden patterns, at leas one of x and y should be in Y. So we may assume that $x=\omega _1$ in Fig. 19. Let $\{\alpha ,\beta ,\delta ,z\}$ and $\{\beta ,\gamma ,\delta ,w\}$ be codewords which contains $\{\alpha ,\beta ,\gamma \}$ and $\{\alpha ,\beta ,\delta \}$ respectively. Then, $z\in \Gamma _\gamma \cup Y$ and $y\in \Gamma _\alpha \cup Y$. To avoid forbidden patterns, it should be $z\in Y$ or $y\in Y$, since $\{\alpha , \gamma ,z,w\}\in {\widetilde{\mathcal {H}}}_m$. So we may assume that $z\in Y$. Note that sum of two codewords $\{\alpha ,\beta ,a\gamma ,x\}$ and $\{\alpha , \beta ,\delta , z\}$ gives that $\{\gamma ,\delta ,x,z\}$ is a codewords. So $z\notin \{\omega _1,\omega _1'\}$. Therefore we also may assume that $z=\omega _2$ in Fig. 4. Now we apply same argument on $\{\alpha ,\beta ,\delta ,y\}$ and $\{\beta ,\gamma ,\delta ,w\}$ and may assume that $y=\omega _3$. So, we have $\{\alpha ,\beta ,\gamma ,\omega _1\}, \{\alpha ,\beta ,\delta ,\omega _2\}, \{\alpha ,\beta ,\delta ,\omega _3\}\in {\widetilde{\mathcal {H}}}_m$.

By considering codewords which contains $\{\alpha ,\gamma ,\gamma _i\}$(resp. $\{\beta ,\gamma ,\gamma _i\}$)for $1\le i \le c$,$\{\alpha ,\delta ,\delta _i\}$(resp $\{\beta ,\delta ,\delta _i\}$)for 1$\le i\le d$, $\{\alpha ,\omega _i,\omega _i'\}$(resp. $\{\beta ,\omega _i,\omega _i'\}$)for $i=1,2,3$ or $\{\alpha ,\gamma ,\delta \}$(resp. $\{\beta ,\gamma ,\delta \}$, we obtain the following codewords:

$$\begin{aligned} \begin{array}{clcclcl} \{\alpha ,\gamma ,\gamma _1,x_1\}&{} \cdots &{}\{\alpha ,\gamma ,\gamma _c,x_c\}&{}\{\alpha ,\delta ,\delta _1,x_{c+1}\}&{}\cdots &{}\{\alpha ,\delta ,\delta _d,x_{c+d}\} \\ \{\beta ,\gamma ,\gamma _1,y_1\}&{}\cdots &{}\{\beta ,\gamma ,\gamma _c,y_c\}&{}\{\beta ,\delta ,\delta _1,y_{c+1}\}&{}\cdots &{}\{\beta ,\delta ,\delta _d,y_{c+d}\}\\ \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ccccl} \{\alpha ,\omega _1,\omega _1',x_{c+d+1}\}&{}\{\alpha ,\omega _2,\omega _2',x_{c+d+2}\}&{}\{\alpha ,\omega _3,\omega _3',x_{c+d+3}\}&{}\{\alpha ,\gamma ,\delta ,x_0\}\\ \{\beta ,\omega _1,\omega _1',y_{c+d+1}\}&{}\{\beta ,\omega _2,\omega _2',y_{c+d+2}\}&{}\{\beta ,\omega _3,\omega _3',y_{c+d+3}\}&{}\{\beta ,\gamma ,\delta ,y_0\}&{}. \end{array} \end{aligned}$$

Each $x_i$(resp. $y_i$) belongs to $\Gamma _\beta \cup \Gamma _\gamma \cup \Gamma _\delta \cup Y$(resp. $\Gamma _\alpha \cup \Gamma _\gamma \cup \Gamma _\delta \cup Y$). Since $(x_i,y_i)$ should be a good pair, either $x_i\in \Gamma _\gamma \cup \Gamma _\delta \cup Y$ or $y_i\in \Gamma _\gamma \cup \Gamma _\delta \cup Y$ for each i. We claim that we may choose $x_i$ or $y_i$, namely $z_i$ for each i, so that $\{z_0,\ldots ,z_{c+d+3}\}=\Gamma _\gamma \cup \Gamma _\delta \cup \{\omega _3,\omega _1',\omega _2',\omega _3'\}$.

We first prove our claim. Assume that $x_i=x_j$ for some distinct i and j. Then by adding the correspondence two codewords with respect to $x_i$ and $x_j$ on the above table, we may obtain a codeword of length 2 or a forbidden pattern. This is contradiction and we have $x_i\not =x_j$ and $y_i\not =y_j$ for $i\not =j$. Assume now that $x_i$ and $y_j$ are chosen and $x_i=y_j$ for some distinct i and j. Then $\{\alpha ,\beta ,x_i,y_i\}+\{\alpha ,\beta ,x_j,y_j\}=\{x_j,y_i\}\in {\widetilde{\mathcal {H}}}_m$ and it implies that $x_j=y_i$. Since $x_j\in \Gamma _\beta \cup \Gamma _\gamma \cup \Gamma _\delta \cup Y$ and $y_i\in \Gamma _\alpha \cup \Gamma _\gamma \cup \Gamma _\delta \cup Y$, we have $x_j\in \Gamma _\gamma \cup \Gamma _\delta \cup Y$. So we may choose $x_j$ instead of $y_j$ in this case. Assume that we choose $x_i$ and $y_j$ with $x_i\not =x_j$. Then we have to show that there does not exits k such that $\{x_k,y_k\}=\{x_i,y_j\}$. If there is a k such that $\{x_k,y_k\}=\{x_i,y_j\}$, it implies that $(x_i,y_j)$ is a good pair. But $(x_i,y_i)$ is a good pair and $y_j\not =y_j$, so this is a contradiction. To complete the prove of claim, it is enough to show that $x_i\notin \{\omega _1,\omega _2\}$ and $y_i\notin \{\omega _1,\omega _2\}$. If $x_i=\omega _1$(resp. $x_i=\omega _2$), $y_i=\gamma$(resp.$y_i=\delta$), since $\{\alpha ,\beta ,\gamma ,\omega _1\}$(resp.$\{\alpha ,\beta ,\delta ,\omega _2\}$). Note that both of $\gamma$ and $\delta$ are not in $\Gamma _\alpha \cup \Gamma _\delta \cup Y$. So $x\notin \{\omega _1,\omega _2\}$ and by the same reason, $y\notin \{\omega _1,\omega _2\}$ for each i. So the proof of claim is done.

Now next consider the summation of codewords which contains $\{\gamma ,\gamma _i,z_i\}$ or $\{\delta ,\delta _{i-c},z_i\}$ or $\{\omega _{i-c-d},\omega _{i-c-d},z_i\}$ or $\{\gamma ,\delta ,z_0\}$ for each i and let it be ${\textbf {c}}$. Then ${\textbf {c}}$ is,

$$\begin{aligned}{} {\textbf {c}}=\left\{ \begin{array}{llll} \{\alpha ,\beta ,\omega _1,\omega _2\} &{} \text{ or } &{}\{\omega _1,\omega _2\} &{}(c \equiv d\equiv 1\text{(mod2) }) \\ \{\alpha ,\gamma ,\omega _1,\omega _2\}&{} \text{ or } &{}\{\beta ,\gamma ,\omega _1,\omega _2\} &{}(c \equiv 1, d\equiv 0 \text{(mod2) }) \\ \{\alpha ,\delta ,\omega _1,\omega _2\}&{} \text{ or } &{}\{\beta ,\delta ,\omega _1,\omega _2\}&{}(c\equiv 0, d\equiv 1\text{(mod2) }) \\ \{\alpha ,\beta ,\gamma ,\delta ,\omega _1,\omega _2\} &{} \text{ or } &{}\{\gamma ,\delta ,\omega _1,\omega _2\} &{} (c\equiv d\equiv 0\text{(mod2) }). \end{array} \right. \end{aligned}$$

Note that $\{\alpha ,\beta ,\gamma ,\omega _1\}+\{\alpha ,\beta ,\delta ,\omega _2\}=\{\gamma ,\delta ,\omega _1,\omega _2\}$ is a codeword. Since ${\textbf {c}}$ is a codeword obviously, if c or d is odd, this is a contradiction. By changing roles of $\beta ,\gamma ,\delta$, we may obtain that b is also even. Since $a+b+c+d\equiv 0$(mod2), we finally conclude that a, b, c and d are all even and this completes the proof.

($\Leftarrow$)If $s=4$, it is clear that $m\ge 4$. In the case of $m=4$, the number of leaves is 6. Since a, b, c and d are even numbers, if we assume $a\ge b\ge c\ge d$, there are three possible vectors as a structure vectors: (6, 0, 0, 0), (4, 2, 0, 0) and (2, 2, 0, 0). For each cases, we may give a labeling to digraphs and make them avoiding forbidden patterns as in Figs. 20, 21 and 22.

Fig. 20

$(a,b,c,d)=(6,0,0,0)$

Fig. 21

$(a,b,c,d)=(4,2,0,0)$

Fig. 22

$(a,b,c,d)=(2,2,2,0)$

By using the extender, every digraph with structure vector (a, b, c, d) with a, b, c,  and d are even admits the extended Hamming code to be a 2-perfect code.

$\square$

5 Conclusion

In this section, we summarize our contributions and suggest some further problems.

In this paper, we consider the problem of classifying weighted posets and digraphs which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code. Maybe usual method to approach this problem is divide the problem according to the value of m. In this paper, we take a somewhat extraordinary method. We first showed that a weighted poset or a digraph which admits the extended Hamming code to be a 2-perfect code is completely determined by the structure vector, and we divide the problem according to the length s of the structure vector. We classify all possible structure vectors of weighted posets which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code when $s=3, 4, 5$. This result together with the consideration of the case $s=6$ with structure vector (0, 0, 0, 0, 0, 0) give the classification of weighted posets which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code. We also classify all possible structure vectors of digraphs which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_m, m \ge 2$ to be a 2-perfect code when $s=3, 4$, which gives the classification of digraphs which admit the extend Hamming code ${\widetilde{\mathcal {H}}}_4$ to be a 2-perfect code as a consequence.

Recall that, for a positive integer n, [n] denotes the set $\{1,2, \ldots , n\}$. We suggest a short list of problems for future works:

• Classification of weighted posets and digraphs on $[2^m]$ which admit the extended Hamming code ${\widetilde{\mathcal {H}}}_m$ to be a 2-perfect code for larger s.

• Establish an effective method to give an admissible labeling on basic forms.

• Classification of (weighted) poset metrics on $[\frac{3^m-1}{2} + 1]$ which admit the ternary extended Hamming code to be a 2-perfect code.

• Classification of weighted poset metrics and digraphs on [8] which admit the extended Hamming code ${\widetilde{\mathcal {H}}}_3$ to be a 3-perfect code.