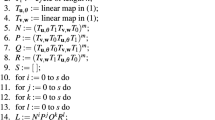1 Introduction

Since the celebrated theorem of Gleason and Prange [2], formally self-dual codes over \(\mathbb {F}_4\) with even weights, also known as Type IV codes have been studied extensively [11, Chap. 19], [12]. In [4], this notion was extended over the three rings of order four that are not a field, namely \(\mathbb Z_4\), \(\mathbb {F}_2 + u \mathbb {F}_2\), and \(\mathbb {F}_2 + v \mathbb {F}_2\). Recently, a further extension was accomplished over a non commutative non-unital ring in [1]. The concept of a self-dual code is replaced there by a quasi self-dual (QSD) code that is self-orthogonal of length n,  with \(2^n\) codewords. Type IV codes are then defined as QSD codes, whose codewords all have even Hamming weights. With every linear E-code is attached an additive \(\mathbb {F}_4\)-code obtained by forgetting the ring structure; this allows to use the additive codes package of [3] for numerical computations. Kim and Ohk [10] showed that quasi self-dual codes over that ring E can be applied to DNA codes in the sense that the GC-content concept can be described by a multiple of an element in the ring. They also improved the classification of QSD codes over E up to lengths 8. The Lee weight defined below is based on this DNA application.

In this paper, we study a special construction of QSD codes over E,  based on combinatorial matrices related to two-class association schemes, Strongly Regular Graphs (SRG), and Doubly Regular Tournaments (DRT). This is a generalization from fields to rings of the approach of [5]. We construct QSD codes and Type IV codes over E. Along the way, we improve the upper bound on the minimum distance of Type IV codes from [1] by a multiplicative factor, by an application of the classical invariant bound for the minimum distance of extremal Type IV codes over \(\mathbb {F}_4.\) Some numerical results validate our approach.

The material is arranged in the following way. Section 2 collects the notions and notations required for the rest of the paper. Section 3 studies our special construction. Section 4 develops the needed theory of combinatorial matrices from designs, SRGs and DRTs. Section 5 concludes the article.

2 Background

2.1 Association schemes

An association scheme on a set X with s classes is a partition of the cartesian product \(X\times X=\cup _{i=0}^sR_i\) with the following properties:

  1. 1.

    \(R_0=\{(x,x) \mid x\in X\}\),

  2. 2.

    \((x,y)\in R_k,\) if and only if \((y,x)\in R_k,\)

  3. 3.

    \(R_i^t=\{(y,x) \mid (x,y) \in R_i\}=R_j\) for some j,

  4. 4.

    if \((x,y)\in R_k,\) the number of \(z \in X\) such that \((x,z)\in R_i,\) and \((z,y)\in R_j,\) is an integer \(p^k_{ij}\) that depends on i, j, k but not on the special choice of x and y.

Such a scheme is called an s-class association scheme. Let \(A_k\) denote the adjacency matrix of the relations \(R_k.\) Concretely \(A_k\) is indexed by X,  and defined by

$$\begin{aligned} A_k(x,y)={\left\{ \begin{array}{ll} 1 &{}\text{ if } (x, y) \in R_k, \\ 0 &{} \text{ else. } \end{array}\right. } \end{aligned}$$

It can be shown that the adjacency matrices \(A_k\) span a commutative algebra over the complex numbers [11, Chap. 21].

If \(s=2\) two cases may occur.

  • \(A_1=A_1^T\) and \(A_2=A_2^T.\) The undirected graph \((X,R_1)\) is then strongly regular (SRG).

  • \(A_1=A_2^T.\) The directed graph \((X,R_1)\) is then a doubly regular tournament (DRT).

For future use, we denote by I the identity matrix, and by J the all-one matrix, both of order |X|.

2.2 Binary codes

Denote by wt(x) the Hamming weight of \(x \in \mathbb {F}_2^n.\) The dual of a binary linear code C is denoted by \(C^\bot \) and defined as

$$\begin{aligned} C^{\bot }=\{ y \in \mathbb {F}_2^n \mid \forall x \in C, \,( x,y)=0\} , \end{aligned}$$

where \((x,y)=\sum _{i=1}^nx_iy_i,\) denotes the standard inner product. A code C is self-orthogonal if it is included in its dual: \(C \subseteq C^{\bot }.\) Two binary codes are equivalent if there is a permutation of coordinates that maps one to the other.

2.3 Quaternary codes

An additive code of length n over \(\mathbb {F}_4\) is an additive subgroup of \(\mathbb {F}_4^n\). It is a free \(\mathbb {F}_2\) module with \(4^k\) elements for some \(k\le n\) (here 2k is an integer, but k may be half-integral). Using a generator matrix G, such a code can be represented as the \(\mathbb {F}_2\)-span of its rows. Every linear E-code C is associated with an additive \(\mathbb {F}_4\) code \(\phi (C)\) by the substitution

$$\begin{aligned} 0 \rightarrow 0,a \rightarrow \omega , b\rightarrow \omega ^2 , c\rightarrow 1, \end{aligned}$$

where \(\mathbb {F}_4=\mathbb {F}_2[\omega ].\) Note that the reverse substitution attaches to every additive \(\mathbb {F}_4\) code an additive subgroup of \(E^n,\) which may or may not be linear.

Besides the Hamming weight of a vector, we might consider its Lee weight as follows:

$$\begin{aligned} wt_L(0)=0, wt_L(a)=wt_L(b)=1, wt_L(c)=2. \end{aligned}$$

2.4 Ring theory

Consider the ring of order 4 defined by two generators a and b by the relations

$$\begin{aligned} E=\langle a,b \mid 2a=2b=0,\, a^2=a,\, b^2=b,\,ab=a,\, ba=b\rangle . \end{aligned}$$

The ring E is a non unital, non-commutative ring of order 4,  of characteristic two [1, 6]. Thus, E consists of four elements \(E=\{0,a,b,c\},\) with \(c=a+b.\) Its multiplication table is as follows.

$$\begin{aligned} \begin{array}{|c|c|c|c|c|} \hline \times &{} 0 &{} a&{} b&{} c\\ \hline 0 &{} 0&{} 0&{} 0&{} 0\\ \hline a &{} 0&{} a &{} a &{} 0 \\ \hline b&{} 0&{} b &{} b&{} 0 \\ \hline c &{} 0&{} c &{} c &{}0\\ \hline \end{array} \end{aligned}$$

From this table, we deduce that this ring is not commutative, and non-unital. It is local with maximal ideal \(J=\{0,c\},\) and residue field \(E/J=\mathbb {F}_2=\{0,1\},\) the finite field of order 2.

Denote by \(\alpha : E \rightarrow E/J=\mathbb {F}_2\), the map of reduction modulo J. Thus \(\alpha (0) = \alpha (c) = 0\), and \(\alpha (a) = \alpha (b) = 1\). This map is extended in the natural way in a map from \(E^n\) to \(\mathbb {F}_2^n\).

2.5 Codes over E

A linear E-code of length n is a one-sided E-submodule of \(E^n.\) Let C be a code of length n over E. With that code we associate two binary codes of length n : 

  1. (1)

    the residue code defined by \(res(C)=\{\alpha (y) \mid y \in C\},\)

  2. (2)

    the torsion code defined by \(tor(C)=\{x \in \mathbb {F}_2^n \mid cx \in C\}.\)

We equip \(E^n\) with the inner product (x, y) of \(x,y\in E^n\) defined by the relation

$$\begin{aligned} (x,y)=\sum _{i=1}^nx_iy_i. \end{aligned}$$

The right dual \(C^{\bot _R}\) of C is the right module defined by

$$\begin{aligned} C^{\bot _R}=\{ y \in E^n \mid \forall x \in C, \,( x,y)=0\} . \end{aligned}$$

The left dual \(C^{\bot _L}\) of C is the left module defined by

$$\begin{aligned} C^{\bot _L}=\{ y \in E^n \mid \forall x \in C, \, ( y,x)=0\} . \end{aligned}$$

An E-code C is self-orthogonal if

$$\begin{aligned} \forall x,y \in C, (x,y)=0. \end{aligned}$$

Clearly, C is self-orthogonal if and only if \(C\subseteq C^{\bot _L}.\) Likewise, C is self-orthogonal if and only if \(C\subseteq C^{\bot _R}.\) Thus, for a self-orthogonal code C,  we always have \(C\subseteq C^{\bot _L} \cap C^{\bot _R}.\) An E-code of length n is Quasi Self-Dual (QSD for short) if it is self-orthogonal and of size \(2^n.\) A QSD code is Type IV if all its codewords have even weight.

The following result went unnoticed in [1], and improves on the previously known upper bound \(d \le 2 \lfloor \frac{n+2}{4} \rfloor \) for the minimum Hamming distance d of a Type IV E-code of length n.

Theorem 1

If C is a Type IV E-code of length n, then it is formally self-dual for the Hamming weight enumerator, and its minimum distance is \(\le 2(\lfloor \frac{n}{6}\rfloor +1).\)

Proof

The first statement follows by specialization of variables in the MacWilliams relation for the joint weight enumerator of the residue and torsion code [1, Prop. 2]. The second statement follows by the standard argument used to prove the same bound for Type IV codes over \(\mathbb {F}_4\) [11, Chap. 19, (69)]. Note that the Hamming weight enumerator of a Type IV code over E belongs to the same ring of invariants as that of a Type IV code over \(\mathbb {F}_4.\) \(\square \)

Theorem 1 gives a construction of additive formally self-dual even codes over \(\mathbb {F}_4.\)

Corollary 1

If C is Type IV then \(\phi (C)\) is an additive formally self-dual even code.

Proof

The results follow by the fact that C and \(\phi (C)\) have the same Hamming weight enumerator. \(\square \)

We now study the residue and torsion code of a QSD code over E.

Theorem 2

[1] For any QSD E-linear code \(\mathcal {C}\), we have

  1. (1)

    \(res(\mathcal {C}) \subseteq {res(\mathcal {C})}^{\perp }\),

  2. (2)

    \(tor(\mathcal {C}) = {res(\mathcal {C})}^{\perp }\),

  3. (3)

    \(dim(\mathcal {C}) = dim(res(\mathcal {C})) + dim(tor(\mathcal {C}))\).

We can characterize QSD codes over E amongst linear codes over E as a function of their residue code in the following theorem.

Theorem 3

([1]) Let B be a self-orthogonal binary \(\left[ n,k_1\right] \) code, where \(0 \le k_1 \le n/2\). The code \(\mathcal {C}\) over the ring E defined by the relation

$$\begin{aligned} \mathcal {C}=aB+cB^{\perp } \end{aligned}$$

is a QSD code. Its residue code is B and its torsion code is \(B^{\perp }\). Conversely, any QSD code C can be built in that way by taking for B the residue code of C.

By Theorem 3, we know that the classification of QSD E-codes is equivalent to the classification of their residue codes. Moreover, the following result is straightforward, but useful. The easy proof is ommitted.

Theorem 4

The minimum distance d(C) of a QSD code C defined by \(\mathcal {C}=aB+cB^{\perp }\), where B is a self-orthogonal binary code, is less than or equal to \(\min \{d(B), d(B^{\perp }) \}\). If B is a self-dual binary code, then \(d(C)=d(B)\).

3 Construction

Consider the code C(M) of length 2n with a generator matrix of the form

$$\begin{aligned} G=(xI,yM), \end{aligned}$$

where \(x, y \in E,\) I is the identity matrix, and M is a binary matrix satisfying

$$\begin{aligned} MM^T=\lambda I +\mu J+\nu M \pmod {2}, \end{aligned}$$

where \(\lambda , \mu , \nu \in \mathbb {F}_2,\) and J is the all-one matrix.

Table 1 Conditions of self-orthogonal codes
Full size table

Theorem 5

The code C(M) is self-orthogonal if and only if either \(x,y\in \{0,c\}\), or \(y\in \{a,b\}\) and the three parameters \(\lambda ,\mu ,\nu \) are as in Table 1.

Proof

The code C(M) is self-orthogonal if and only if \(GG^\textrm{T}=0.\)

If \(y\in \{0,c\}\), \(GG^\textrm{T}=0\) implies \(x\in \{0,c\}\). It is trivial because the code only has a zero codeword. (In fact, it may not be a code.)

If \(y\in \{a,b\}\), then

$$\begin{aligned} \begin{aligned} GG^\textrm{T}&=x^2I+y^2MM^\textrm{T}\\&=x^2I+y(\lambda I+\mu J+\nu M)\\&=x^2I+y\lambda I+y\mu J+y\nu M. \end{aligned} \end{aligned}$$

Therefore, \(GG^\textrm{T}=0\) if and only if \(-y\nu M=x^2I+y\lambda I+y\mu J.\)

Two cases are as follows.

(1) If \(\nu =0\), then \((x^2+y\lambda )I+y\mu J=\textbf{0}\). Since \(y\in \{a,b\}\) and J is all-one matrix, \(\mu =0\). In this case, we have

  • \(\lambda =0~\text {and}~x\in \{0,c\};\)

  • \(\lambda =1~\text {and}~x=y.\)

(2) If \(\nu =1\), then \(-yM=x^2I+y\lambda I+y\mu J\). So,

$$\begin{aligned} \begin{aligned} (-yM)(-yM)^\textrm{T}&=yMM^\textrm{T},\\ [(x^2+y\lambda )I+y\mu J][(x^2+y\lambda )I+y\mu J]^\textrm{T}&=y(\lambda I+\mu J+M). \end{aligned} \end{aligned}$$

Expand and simplify this equation according to the operation over E, then

$$\begin{aligned} \begin{aligned} (x^2+y\lambda )^2I+ny\mu J&=y\lambda I+(y+x^2y+yx^2)\mu J+yM,\\ (x^2+x^2y\lambda +yx^2\lambda +y\lambda )I+ny\mu J&=y\lambda I+(y+x^2y+yx^2)\mu J-(x^2I+y\lambda I+y\mu J),\\ (x^2y+yx^2+y)\lambda I+(ny+x^2y+yx^2)\mu J&=\textbf{0}. \end{aligned} \end{aligned}$$

In this case, we have

  • \(\mu =0.\) If \(\lambda =1,\) then \(x^2y + yx^2 + y=0.\) So, if \(x\in \{0,c\}\), then \(y=0\). It is a contradiction because \(y\in \{a,b\}\). If \(x=a\), then \(ay+ya+y=a+a+a = a \ne 0\) with \(y=a\), and \(a+b+b=a \ne 0\) with \(y=b.\) Thus, \(x\ne a\). Similarly, \(x\ne b\). Therefore, \(\lambda \ne 1\) and \(\lambda = 0\). Check \(\lambda ,\mu ,\nu \), then \(x=y\) and \(M=I\) are obtained. This case is covered by the case \(\lambda =1,\mu =\nu =0\).

  • \(\mu =1.\) Then \((x^2y+yx^2+y)\lambda I+(ny+x^2y+yx^2)J=\textbf{0}.\) It is easy to check that n is even and \(\lambda =0.\) Then, we have two cases: (i) If \(x\in \{0,c\}\), then \(y\nu M=yJ\). Since \(y\in \{a,b\}\), we have \(M=J, \nu =1\). So, \(MM^\textrm{T}=J+M=J+J=\textbf{0}\). This case is covered by the case \(\lambda =\mu =\nu =0\). (ii) If \(x=y,\) then \(M=I+J\). This case is covered by the case \(\lambda =1,\mu =\nu =0\).

Thus, \(\lambda ,\mu ,\nu \in \mathbb {F}_2\) are as in Table 1. \(\square \)

The next two results give conditions for C(M) to be QSD (resp. Type IV).

Theorem 6

A self-orthogonal code C(M) is QSD if and only if \(x\in \{a,b\}\).

Proof

A self-orthogonal code C is QSD if and only if G has n linearly independent rows. If \(x\in \{a,b\}\), C is QSD because of the form of G.

If \(x\in \{0,c\}\), then we must let the determinant \(|yM|\ne 0\) to make sure there are n linearly independent rows in G. From the proof of Theorem 5, \(y\in \{a,b\}\) and \(-y\nu M=y\lambda I+y\mu J\). Then, \(\lambda =\mu =\nu =0\), and M is a binary matrix such that

$$\begin{aligned} \left\{ \begin{array}{l} |M|\ne 0,\\ MM^\textrm{T}=0. \end{array} \right. \end{aligned}$$
(1)

It is impossible for these two formulas to hold together. This completes the proof. \(\square \)

Theorem 7

A QSD code C(M) is Type IV if \(x \in \{a, b\}\) and the case \(\lambda =1\), \(\mu =v=0\) in Table 1 holds.

Proof

It is easy to check that a QSD code C(M) is Type IV if its generator matrix \(G=(xI,yM)\) consists only of rows of even weight. Note that \(x\notin \{0,c\}\) because of Theorem 6.

If \(x\in \{a,b\}\), we just prove that M has all the rows of odd weights with \(\lambda =1,\mu =\nu =0\). Now we have

$$\begin{aligned} \left\{ \begin{array}{l} MM^\textrm{T}=\lambda I+\mu J+\nu M,\\ y\nu M=(x+y\lambda )I+y\mu J. \end{array} \right. \end{aligned}$$
(2)

If \(\lambda =1,\mu =\nu =0\), then

$$\left\{ \begin{array}{l} MM^\textrm{T}=I,\\ (x+y)I=0. \end{array} \right. $$

Therefore, \(x=y\) and M has all rows of odd weights.

By the proof of Theorem 5, two cases \(\lambda =\mu =0, \nu =1\) and \(\lambda =0, \mu =1, \nu =1\) can also get Type IV codes, and these two special cases can be covered by \(\lambda =1,\mu =\nu =0\).

This completes the proof. \(\square \)

Example 8

We describe the above constructions with two examples.

  • If \(M=\begin{pmatrix}0 &{} 1 &{} 1 &{} 1\\ 1 &{} 0 &{} 1 &{}1\\ 1 &{} 1 &{} 0 &{}1\\ 1 &{} 1 &{} 1 &{}0 \end{pmatrix}\), then \(MM^T=1I+0J+0M \pmod {2}\), that is, \(\lambda =1,\mu =0,\nu =0\). It follows from Table 1 of Theorem 5 that for \(y \in \{a,b\}~\text {and}~x=y\), the matrix \(G=(xI,yM)\) generates a self-orthogonal code. In particular, this code is both QSD and Type IV with minimum distance 4.

  • If \(M=\begin{pmatrix}1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1\end{pmatrix}\), then \(MM^T=0I+0J+1M \pmod {2}\) and \(MM^T=1I+0J+0M \pmod {2}\), that is, \(\lambda =0,\mu =0,\nu =1\) or \(\lambda =1,\mu =0,\nu =0\). By Theorem 5, both of these two cases can generate self-orthogonal codes by using the matrix G. And if \(x=a \text { or } b\), then \(G=(xI, xM)\) generates a Type IV code with minimum distance 2 from Theorem 7.

We now investigate the residue and torsion codes of C(M).

From [1, Thm. 1], we write the generator matrix in the form

$$\begin{aligned} G=\left( \begin{array}{ccc} aI_{k_1}&{}X&{}Y\\ 0&{}cI_{k_2}&{}cZ \end{array} \right) . \end{aligned}$$

For \(x\ne 0\), we have the following cases depending on the values of \(x \in E.\)

  • If \(x=a\) or \(x=b\), then \(k_1=n,k_2=0,(X,Y)=yM.\) The generator matrix of the residue code is (I, M) if \(y=a,b\) and \((I,\textbf{0})\) if \(y=c.\)

  • If \(x=c\), then, \(k_1=0,k_2=n,y=c,Z=M.\) The generator matrix of the torsion code is \(G_2=(I,M)\).

The (additive) generator matrix of the corresponding additive \(\mathbb {F}_4\) code is

$$\begin{aligned} G'=\left( \begin{array}{c} \phi (aG)\\ \phi (bG) \end{array} \right) , \end{aligned}$$

where \(\phi \) is as defined in the preceding section.

Remarks:

  • If \(y=c\), then C(M) has minimum distance 1. In the examples, we shall assume that \(y=a,\) or \(y=b.\)

  • If \(x=c\), then we find that \(\phi (M)\) is a linear code over \(\mathbb {F}_4\) given by \(\phi (M) =\langle (\textbf{0},M) \rangle .\) We will avoid this case as well.

  • Now if both x, y are in \(\{a,b\},\) then we find that \(\phi (M)\) is a linear code over \(\mathbb {F}_4\) given by \(\phi (M) =\langle (I,M) \rangle .\)

4 Combinatorial matrices

4.1 Two-class association schemes

From now on, we can discuss two-class association schemes which will play an important role in M.

There are two kinds of two-class association schemes. One is a Strongly Regular Graph (SRG), where the two adjacency matrices satisfy \(A_i = A_i^T\) for \(i=1,2\). Here, \(A_2\) satisfies \(A_2 = J-I-A_1:=\overline{A_1}\). An important database of SRGs is [15].

A classical construction of a SRG is the Paley graph. It is constructed from quadratic residues in \(\mathbb {F}_q\), where \(q \equiv 1 \pmod 4\) and \(A=Q=N\). The parameters are \((q, \frac{q-1}{2}, \frac{q-3}{4}, \frac{q+1}{4})\). An example of \(q=5\) is the pentagon graph.

Another class is a Doubly Regular Tournament (DRT), which is equivalent to a skew Hadamard matrix [13]. The adjacency matrix \(A_2\) satisfies \(A_2 = J-I-A_1:=\overline{A_1}\). Note that \(A_1^T = \overline{A_1}\).

From now on, let \(A=A_1\).

Lemma 1

[5] If G is an SRG, then we have

$$\begin{aligned} AA^T = A^2 = \kappa I + \varLambda A + \mathcal {M}\overline{A}. \end{aligned}$$

If G is a DRT, then we have

$$\begin{aligned} AA^T = \kappa I + (\kappa -1-\varLambda ) A + (\kappa -\mathcal {M}) \overline{A}. \end{aligned}$$

Using the same parameters in the above lemma, both of them satisfy the equation

$$\begin{aligned} AJ=JA=\kappa J, \end{aligned}$$

and for SRGs, we have

$$\begin{aligned} A^2=\kappa I+\varLambda A+\mathcal {M}(J-I-A), \end{aligned}$$
(3)

for DRTs, we have

$$\begin{aligned} A^2=\varLambda A+\mathcal {M}(J-I-A). \end{aligned}$$
(4)

We connect these parameters to that of the matrix M of the preceding section. The trivial proof is omitted.

Proposition 1

Using the notation of Lemma 1, if M is the adjacency matrix of G with parameters \((n,\kappa ,\varLambda ,\mathcal {M})\) then

  • in the SRG case \(\lambda =\kappa -\mathcal {M}, \mu =\mathcal {M},\, \nu = \varLambda -\mathcal {M}\),

  • in the DRT case \(\lambda =\mathcal {M}, \mu =\kappa -\mathcal {M},\, \nu =\mathcal {M}- \varLambda -1\).

We can use the database of two class association schemes from Hanaki and Miyamoto’s database [8]. In particular there is a classification of DRT of sizes up to 40.

4.2 The pure and the bordered circulant codes from two-class association schemes

We can also follow the pure and the bordered construction method from [5]. Let \(Q_E(r,s,t)=rI + sA + t\overline{A}\), where \(r,s,t \in E\), where A is an adjacency matrix of a SRG or a DRT. Let \(C(Q_E(r,s,t))\) be a code of length 2n with a generator matrix of the form

$$\begin{aligned} G=(aI, Q_E(r, s, t))=(aI,rI + sA + t\overline{A}). \end{aligned}$$

This construction can be called the pure construction.

First we consider \(r=0\) and \(s,t \in \{a, b \}\). The code \(C(Q_E(0, s, t))\) of length 2n has generator matrix of the form

$$\begin{aligned} G=(aI, Q_E(0, s, t))=(aI,sA + t\overline{A}), \end{aligned}$$

where A is an adjacency matrix of a SRG or a DRT.

Theorem 9

Suppose A is an adjacency matrix of a SRG or a DRT.

  1. (1)

    If \(n = 3\), then the minimum distance of \(C(Q_E(0, s, t))\) is exactly 3.

  2. (2)

    If \(n \ge 4\), then the minimum distance of \(C(Q_E(0, s, t))\) is 4.

Proof

Due to the symmetry between A and \(\overline{A},\) we may assume \(s=a\) and \(t=b\), or \(s=t=a\). We only consider the case \(s=a\) and \(t=b\) because the other case \(s=t=a\) can be done similarly. Note that \(aG=a(aI,aA + b\overline{A})=(aI, aA+ a\overline{A})=(aI, a(A+\overline{A}))\). Since \(A+\overline{A}=J-I\), \(aG=(aI, a(J-I))\). It is easy to check that the minimum distance of the code generated by \((aI, a(J-I))\) is 3 if \(n=3\). Hence the first statement of the theorem follows. Add any two adjacent rows in aG, we can get a codeword of weight 4 if \(n \ge 4\). Hence the second statement follows. \(\square \)

Similarly, we have the following theorem.

Theorem 10

Suppose A is an adjacency matrix of a SRG or a DRT. If \(r \ne 0\), and \(s,t \in \{a, b \}\), then the following statements hold.

  1. (1)

    If \(n \ge 4\) and \(r=c\), then the minimum distance of \(C(Q_E(r, s, t))\) is exactly 4.

  2. (2)

    If r is either a or b, then the minimum distance of \(C(Q_E(r, s, t))\) is 2.

Therefore if \(n \ge 4\), it is reasonable to consider the following three constructions (i) \(C(Q_E(0, a, 0))\), (ii) \(C(Q_E(a, a, 0))\), or (iii) \(C(Q_E(c, a, 0))\), where replacing a into b gives the same result.

Note that Case (i) and Case (ii) are the same construction as C(M) with \(x=a\) and \(y=a\) in Sect. 3 by taking \(M=A\) and \(M=A+I\), respectively. Therefore, we can apply these two cases to various SRGs and DRTs.

Next we can consider the bordered construction as follows.

$$\begin{aligned} B_E(r,s,t)=\left( \begin{array}{c|ccc|c|c} a &{} 0&{} \dots &{} 0 &{} 0 &{} a ~ \dots ~ a \\ \hline 0 &{} &{} &{} &{} a &{} \\ \vdots &{} &{} aI &{} &{} \vdots &{} Q_E(r,s,t) \\ 0 &{} &{} &{} &{} a &{} \\ \end{array} \right) . \end{aligned}$$

Just like for the pure construction, we can distinguish three cases (i) \(Q_E(0, a, 0)\), (ii) \(Q_E(a, a, 0)\), or (iii) \(Q_E(c, a, 0)\).

Lemma 2

The codes in these two constructions with Case \((\textrm{i})\) and Case \((\textrm{iii})\) are the same.

Proof

In Case \((\textrm{i})\), \(Q_E(0,a,0)=aA\), and the generator matrix \(G_{(\textrm{i})}=(aI|aA)\) in pure construction. So, the code \(C_{(\textrm{i})}=\{\textbf{x}G_{(\textrm{i})}|\textbf{x}\in E^{n}\}\). In Case \((\textrm{iii})\), \(Q_E(c,a,0)=cI+aA\), and the generator matrix \(G_{(\textrm{iii})}=(aI|cI+aA)\) in pure construction. So, the code \(C_{(\textrm{iii})}=\{\textbf{x}G_{(\textrm{iii})}|\textbf{x}\in E^{n}\}\). Since

$$\begin{aligned} \begin{aligned} \textbf{x}G_{(\textrm{iii})}&=\textbf{x}(G_{(\textrm{i})}+(\textbf{0}|cI))\\&=\textbf{x}G_{(\textrm{i})}+\textbf{x}(\textbf{0}|cI)\\&=\textbf{x}G_{(\textrm{i})}, \end{aligned} \end{aligned}$$

we have \(C_{(\textrm{i})}=C_{(\textrm{iii})}\).

For the bordered construction in Case (i), we have \(C^\prime _{(\textrm{i})}=\{\textbf{y}G^\prime _{(\textrm{i})}|\textbf{y}\in E^{n+1}\},\) where

$$\begin{aligned} G^\prime _{(\textrm{i})}=\left( \begin{array}{c|ccc|c|c} a &{} 0&{} \dots &{} 0 &{} 0 &{} a ~ \dots ~ a \\ \hline 0 &{} &{} &{} &{} a &{} \\ \vdots &{} &{} aI &{} &{} \vdots &{} aA \\ 0 &{} &{} &{} &{} a &{} \\ \end{array} \right) , \end{aligned}$$

and in Case (iii), we have \(C^\prime _{(\textrm{iii})}=\{\textbf{y}G^\prime _{(\textrm{iii})}|\textbf{y}\in E^{n+1}\},\) where

$$\begin{aligned} G^\prime _{(\textrm{iii})}=\left( \begin{array}{c|ccc|c|c} a &{} 0&{} \dots &{} 0 &{} 0 &{} a ~ \dots ~ a \\ \hline 0 &{} &{} &{} &{} a &{} \\ \vdots &{} &{} aI &{} &{} \vdots &{} cI+aA \\ 0 &{} &{} &{} &{} a &{} \\ \end{array} \right) . \end{aligned}$$

Let

$$\begin{aligned} A^\prime =\left( \begin{array}{c|ccc|c|c} 0 &{} 0&{} \dots &{} 0 &{} 0 &{} 0 ~ \dots ~ 0 \\ \hline 0 &{} &{} &{} &{} 0 &{} \\ \vdots &{} &{} \textbf{0} &{} &{} \vdots &{} cI \\ 0 &{} &{} &{} &{} 0 &{} \\ \end{array} \right) , \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} \textbf{y}G^\prime _{(\textrm{iii})}&=\textbf{y}(G^\prime _{(\textrm{i})}+A^\prime )\\&=\textbf{y}G^\prime _{(\textrm{i})}+\textbf{y}A^\prime \\&=\textbf{y}G^\prime _{(\textrm{i})}. \end{aligned} \end{aligned}$$

Therefore, \(C^\prime _{(\textrm{i})}=C^\prime _{(\textrm{iii})}\). \(\square \)

Example 11

It is well known that there is a unique DRT of order 11. The pure construction with \(Q_E(0, a, 0)\) gives a QSD [22, 11, 6] code over E. The bordered construction with \(Q_E(a, a, 0)\) gives a QSD [24, 12, 8] code over E. The minimum distances of these codes are justified by Theorem 4.

Lemma 3

  1. (1)

    For SRGs we have

    $$\begin{aligned} Q_E(r,s,t)Q_E(r,s,t)^T=\omega _1I+\omega _2A+\omega _3\overline{A}, \end{aligned}$$

    where \(\omega _1=(r^2+s^2\kappa -t^2-t^2\kappa +t^2v)\), \(\omega _2=(rs+sr+s^2\varLambda -st-ts-st\varLambda -ts\varLambda +t^2\varLambda +st\kappa +ts\kappa +t^2v-2t^2\kappa )\), \(\omega _3=(rt+tr+s^2\mathcal {M}-st\mathcal {M}-ts\mathcal {M}+t^2\mathcal {M}+st\kappa +ts\kappa +t^2v)\).

  2. (2)

    For DRTs we have

    $$\begin{aligned} Q_E(r,s,t)Q_E(r,s,t)^T=\omega _1^\prime I+\omega _2^\prime A+\omega _3^\prime \overline{A}, \end{aligned}$$

    where \(\omega _1^\prime =(r^2+(s^2+t^2)\kappa )\), \(\omega _2^\prime =(rt+sr+s^2(\kappa -1-\varLambda )+t^2(\kappa -\mathcal {M})+st\varLambda +st\mathcal {M})\), \(\omega _3^\prime =(tr+rs+s^2(\kappa -\mathcal {M})+t^2(\kappa -1-\varLambda )+st\mathcal {M}+st\varLambda )\).

Proof

It is straightforward by Eqs. (3) and (4) and Lemma 1. \(\square \)

We will discuss the weight of rows of generator matrices in Case (i) and Case (ii). Then, the conditions of QSD and Type IV can be confirmed. By the form of generator matrices in pure construction and bordered construction, the code is QSD if it is self-orthogonal. The following remark gives when the code is self-orthogonal and Type IV.

Remark 1

For Cases (i) and (ii), we have the following observations.

  • Pure construction with SRGs

    For the code \(P_E(r,s,t)\) to be self-orthogonal, we need

    $$(aI| Q_E(r, s, t))(aI | Q_E(r, s, t))^T = \textbf{0}.$$

    That is, we need \(Q_E(r, s, t)Q_E(r, s, t)^T = -aI\). By Lemma 3 (1), we compute the parameters \(\kappa ,\varLambda ,\mathcal {M}\) of self-orthogonal (QSD) codes in Table 2.

    The weight of any row of \(Q_E(r,s,t)\) is related to the coefficient of I, where I is in Lemma 3 (1). So, the weight of any row of \((aI|Q_E(r,s,t))\) is

    $$\begin{aligned} 1+\alpha (r^2)+\alpha (s^2)\kappa +\alpha (t^2)(n-\kappa -1), \end{aligned}$$

    that is, \(1+\kappa \) in Case (i) and \(2+\kappa \) in Case (ii). Therefore, a QSD code is Type IV if

    $$\begin{aligned} 1+\alpha (r^2)+\alpha (s^2)\kappa +\alpha (t^2)(n-\kappa -1)=0\ (\textrm{mod}\ 2), \end{aligned}$$

    that is, \(1+\kappa =0\ (\textrm{mod}\ 2)\) in Case (i) and \(2+\kappa =0\ (\textrm{mod}\ 2)\) in Case (ii). Then we have the conditions of Type IV in Table 2.

  • Bordered construction with SRGs

    Similar to the pure construction, we need

    $$\begin{aligned} B_E(r,s,t)B_E(r,s,t)^T=\textbf{0}. \end{aligned}$$

    Then we have

    $$\begin{aligned} \begin{aligned} a(1+n)&=0\\ a(r+s\kappa +t(n-\kappa -1))&=0\\ aI+aJ+Q_E(r,s,t)Q_E(r,s,t)^T&=\textbf{0}. \end{aligned} \end{aligned}$$

    The first equation is the product of the top row with itself. The second equation is the product of the top row with any other row, and the third equation ensures that the other rows are orthogonal to each other. The results of the calculation by Lemma 3 (1) are in Table 2.

    And this code is Type IV if

    $$\begin{aligned} \begin{aligned} \alpha (a)(1+n)&=0\ (\textrm{mod}\ 2),\\ \alpha (r)+\alpha (s)\kappa +\alpha (t)(n-\kappa -1)&=0\ (\textrm{mod}\ 2). \end{aligned} \end{aligned}$$

    We also have the results in Table 2.

  • Pure and bordered construction with DRTs

    By using the same arguments as these two constructions with SRGs and Lemma 3 (2), we have the results in Table 3.

Table 2 Conditions of QSD and Type IV with SRGs
Full size table
Table 3 Conditions of QSD and Type IV with DRTs
Full size table

We computed the Hamming weight and Lee weight of some codes. These examples are from [8, 15] and MAGMA database of SRGs [3].

Theorem 12

There are QSD codes over E with the following parameters.

  1. (1)

    Based on SRGs, there are QSD codes with parameters (2n, d), where 2n is the length of the code, and d is the minimum distance:

    $$\begin{aligned} (32,8),(56,8),(70,10),(72,12),(80,12),(92,12). \end{aligned}$$
  2. (2)

    Based on DRTs, there are QSD codes with parameters (2n, d), where 2n is the length of the code, and d is the minimum distance:

    $$\begin{aligned} (22,7),(24,8),(38,8),(40,8). \end{aligned}$$

We display these results in Tables 4 and 5. The images by \(\phi \) of these codes are formally self-dual additive codes over \(\mathbb {F}_{4}\) in [7].

Table 4 Weights of some QSD codes of SRGs
Full size table
Table 5 Weights of QSD some codes of DRTs
Full size table

5 Conclusion

In this work, we have constructed QSD and Type IV codes over the ring E in the sense of [1]. The construction method is based on the adjacency matrices of two-class association schemes, in an analogue over E of [5] over finite fields. Formally self-dual additive codes over \(\mathbb {F}_4\) were introduced in [7]. This little-known class of codes deserves further exploration. In another direction, the construction methods we used can be explored over the rings H and I of the classification [6].