Speeding up similarity search under dynamic time warping by pruning unpromising alignments

Abstract

Similarity search is the core procedure for several time series mining tasks. While different distance measures can be used for this purpose, there is clear evidence that the Dynamic Time Warping (DTW) is the most suitable distance function for a wide range of application domains. Despite its quadratic complexity, research efforts have proposed a significant number of pruning methods to speed up the similarity search under DTW. However, the search may still take a considerable amount of time depending on the parameters of the search, such as the length of the query and the warping window width. The main reason is that the current techniques for speeding up the similarity search focus on avoiding the costly distance calculation between as many pairs of time series as possible. Nevertheless, the few pairs of subsequences that were not discarded by the pruning techniques can represent a significant part of the entire search time. In this work, we adapt a recently proposed algorithm to improve the internal efficiency of the DTW calculation. Our method can speed up the UCR suite, considered the current fastest tool for similarity search under DTW. More important, the longer the time needed for the search, the higher the speedup ratio achieved by our method. We demonstrate that our method performs similarly to UCR suite for small queries and narrow warping constraints. However, it performs up to five times faster for long queries and large warping windows.

1 Introduction

Following the remarkable availability of temporal data, time series mining is becoming a necessary procedure in a wide range of application domains. The estimate of a distance or similarity value between time series objects or subsequences is a common subroutine for several temporal data mining tasks. Consequently, the choice of the distance measure adopted to compare the time series may harshly affect the performance of most distance-based algorithms. The scientific community has shown that the Dynamic Time Warping (DTW) is arguably the most suitable distance measure for a wide range of applications and mining tasks, such as classification (Wang et al. 2013; Kate 2016), clustering (Begum et al. 2015), and pattern matching (Chavoshi et al. 2016).

The similarity search consists of finding the most similar subsequence of a given query in a long reference data. For some applications, it may be extended to the k-nearest neighbor search, i.e., when the user is interested in finding a group of k similar subsequences.

A straightforward implementation of DTW is quadratic regarding time and space complexities. With the speed and the amount of data collected in several applications, this makes the search under DTW impractical. However, Rakthanmanon et al. (2012) have introduced the UCR suite, a set of optimizations that make the subsequence similarity search under DTW even faster than Euclidean distance with the techniques considered state-of-the-art up to that moment. Specifically, that work mainly consists of lower-bounding and early-abandon methods to discard nearest neighbors candidates before the computation of DTW. In most cases, the UCR suite can avoid the need for a DTW distance calculation.

Regarding the problem of finding the best match of a small subsequence in a long time series, Rakthanmanon et al. (2012) claim that “for the problem of exact similarity search with arbitrary length queries, our UCR suite is close to optimal”. In fact, the authors use a large set of experiments to support this claim. However, while the UCR suite approaches the optimality in avoiding the DTW calculation, such costly operation is still required for a relatively small percentage of the time series. Even being performed only to a small fraction of the subsequences, the DTW computation still represents a significant amount of the similarity search runtime.

A simple experiment can illustrate this fact. When searching a query in an electrocardiography (ECG) dataset with approximately 30 million data points, the DTW is calculated for only $4\%$ of the total number of assessed subsequences. It demonstrates the extraordinary ability of the pruning techniques in avoiding DTW calculations. Even with this notable reduction of computations, the time for estimating the distance between the query and the assessed subsequences corresponds to approximately $60\%$ of the entire search runtime. This cost is even higher in some cases, depending on the parameters of the similarity search, such as the query length.

In this work, we propose to embed a recently introduced method into the UCR suite procedure, in order to make it even faster. Specifically, we adapt the DTW with Pruned Warping Paths (Silva and Batista 2016) to improve the internal efficiency of the DTW calculation. In this way, we can speed up the bottleneck of the similarity search under the warping distance, i.e., the comparison of pairs of time series which the pruning procedure was not capable to discard.

We demonstrate that our method is faster than the proposed by Rakthanmanon et al. (2012), considered the fastest tool for the exact similarity search under DTW. The speedup achieved by our method depends on two factors: (i) the length of the query; and (ii) the total amount of allowed warping. We demonstrate that the runtime of our method is similar to the state-of-the-art for small queries and narrow warping constraints. However, our method performs up to 5 times faster for long queries and large warping windows.

The remainder of this paper is organized as follows. Section 2 introduces the notation as well as basic concepts and definitions on time series and the DTW measure. Section 3 presents the UCR suite for similarity search. Section 4 describes the DTW with Pruned Warping Paths method and how we adapt it to the similarity search procedure. Next, Sect. 5 presents the experimental evaluation to verify the efficiency of our method. Because our method performs better on long queries and a large amount of allowed warping, Sect. 6 discusses the need for both assumptions on several application domains. Section 7 introduces how we can adapt the proposed ideas to other distance measures. Finally, Sect. 8 concludes this work.

2 Background and definitions

In this section, we define the basic concepts related to our work and introduce the notation used in the remaining of the paper. We begin by defining a time series.

Definition 1

A time series x is a set of N ordered values such that $x=(x_1, x_2, \ldots , x_N)$ and $x_i \in \mathbb {R}$. Each value $x_i$ is referred asto an observation and N is the length of the time series.

Note that, by this definition, a time series does not necessarily need to be defined in time. The only requirement is the logical order of values which needs to be respected. Furthermore, we assume that the interval between two consecutive observations can be disregarded with no loss of generality. This allows the use of the methods described in this section on sequences of real numbers used to describe shapes, spectral data, and other numerical sequences.

Given the definition of time series, we are in the position to define a subsequence.

Definition 2

A subsequence $x_{i,m}$ is a continuous subset of x of length m starting from the observation i, i.e, $x_{i,m} = (x_i, x_{i+1}, \ldots , x_{i+m-1})$, such that $i+m < N$.

The focus of this paper is the task of the subsequence similarity search,¹ defined as follows.

Definition 3

Subsequence similarity search is the procedure of finding the nearest neighbor—i.e., the most similar subsequence—of a given query time series y with length m in the long (reference) time series x with length N, such that $m \ll N$.

While describing the DTW and pruning techniques we may use the term time series for both objects under comparison, even if one of them is a subsequence of a longer time series. Also, we consider that both the query and the subsequence of the reference time series have the same length (m). We notice that the algorithms discussed in this paper may be easily adapted to the nearest neighbor algorithm in batch datasets, i.e., composed of segmented time series which represent specific events.

The most important decision for similarity search is the distance function used to match the subsequences. Despite the existence of several distance functions, there is strong evidence in the literature that Dynamic Time Warping (DTW) is the most suitable distance measure for the task of finding nearest neighbors in time series data for a multitude of application domains (Ding et al. 2008; Wang et al. 2013).

The DTW distance achieves an optimal nonlinear alignment of the observations under certain constraints. Specifically, the DTW between two time series of length n and m is the cost of the optimal (n, m)-warping path between them. Such (n, m)-warping is defined as follows.

Definition 4

An (n, m)-warping path is a sequence $p = (p_1, \ldots , p_L)$ with $p_l = (i_l, j_l) \in [1:n] \times [1:m]$ for $l \in [1:L]$ satisfying the following three constraints (Müller 2007):

• Boundary constraint: $p_1 = (1,1)$ and $p_L = (n, m)$;

• Monotonicity constraint: $i_1 \le i_2 \le \ldots \le i_L$ and $j_1 \le j_2 \le \ldots \le j_L$;

• Continuity constraint: $p_{l+1} - p_l \in \{(1,0), (0,1), (1,1)\}$ for $l \in [1:L-1]$.

Thus, an (n, m)-warping path is a mapping between elements of the time series x and y assigning the observations $x_{i_l}$ of x with $y_{j_l}$ of y. The total cost $c_p(x,y)$ of an (n, m)-warping path p between two time series x and y with respect to a cost measure c is defined by the Eq. 1.

$$\begin{aligned} c_p(x,y) = \sum _{l=1}^{L} c(x_{i_l}, y_{j_l}) \end{aligned}$$

(1)

The cost measure $c(x_{i_l}, y_{j_l})$ is usually defined by the squared Euclidean distance between the pair of observations. Therefore, every (n, m)-warping path is monotonically increasing given that $c(x_{i_l}, y_{j_l}) \ge 0$.

Finally, we define the optimal (n, m)-warping path.

Definition 5

The optimal (n, m)-warping path $p^*$ is the (n, m)-warping path having minimal cost among all possible (n, m)-warping paths, i.e., $c_{p^*}(x,y) = min\{c_p(x, y)~|~p~\text {is an }(n,m)\text {-warping path}\}$.

A dynamic programming algorithm can calculate the optimal (n, m)-warping path. Equation 2 defines the initial condition of the algorithm to estimate the DTW between two time series x and y with lengths n and m respectively.

(2)

where $i = 1 \ldots n$ and $j = 1 \ldots m$. From this, Eq. 3 defines the recurrence relation of DTW algorithm.

(3)

The DTW distance is given by the value calculated by dtw(n, m). The described algorithm iteratively fills a cost matrix, which we refer to as cumulative cost matrix or just DTW matrix from now on. Figure 1 shows an example of the DTW between two subsequences, presenting the DTW matrix and the resulting alignment.

Fig. 1

Given two time series under comparison (left), the DTW algorithm calculates a cumulative cost matrix (center) in order to find the optimal path in this matrix (highlighted in red). With such a path, it is possible to reconstruct the optimal alignment between the series (right) (Color figure online)

A space-efficient implementation of the DTW algorithm may use a two-row vector instead of the cumulative cost matrix. Such optimization is possible because the calculation of a given cell only depends on values calculated in the same and previous rows, reducing the DTW algorithm complexity to ${\mathcal {O}}(n)$ regarding space. However, reducing the ${\mathcal {O}}(n^2)$ time complexity is a more difficult matter. To the best of our knowledge, the only way to reduce its complexity is by means of approximations—which do not provide any boundaries for the approximation error—or warping windows (Sakoe and Chiba 1978; Itakura 1975).

A warping window, or constraint band, defines the maximum allowed time difference between two matched observations. From the algorithm standpoint, this technique restricts the values that need to be computed to a smaller area around the main diagonal of the matrix. In addition to providing a faster calculation, warping windows usually improves the accuracy of the similarity search and 1-NN classification (Wang et al. 2013). In this work, we consider the warping windows proposed by Sakoe and Chiba (1978).

Because DTW is a costly distance measure, several papers have proposed techniques to improve the runtime of its calculation. More specifically, most of them are indexing methods, focused on the similarity search procedure. In the next section, we discuss these algorithms and the fastest implementation of the similarity search under DTW known so far.

3 The UCR suite

Given the ubiquity of temporal data, there is a plethora of work on speeding up the subsequence similarity search of time series. However, we concentrate our attention on the work by Rakthanmanon et al. (2012), which is the first to expedite time series search to an order of trillions of observations. In this work, the authors describe some of the most important speedup methods and present novel techniques to perform the subsequence similarity search in admissible time. Also, they discuss how to use them together to create the fastest tool for exact time series similarity search under DTW available so far, the UCR Suite.

In this section, we briefly describe the techniques used to implement the UCR Suite. We refer the reader interested in more details about each method to Rakthanmanon et al. (2012). We note that DTW does not obey the triangle inequality. Therefore, indexing algorithms for metric spaces are not applicable to speeding up similarity search under this distance measure.

Given that we are interested in a single nearest neighbor of a given query, we can store the true DTW distance to the nearest subsequence up to a certain moment during the search into a variable best-so-far (bsf). The main purpose of having a bsf is to avoid the expensive DTW algorithm, discarding its calculation for subsequences that are certainly not the best match. In other words, with this value we can restrict the space of nearest neighbor candidates. Despite this approach not explicitly using indexing structures, we refer to the methods that limit the space of candidates as indexing methods or indexing techniques.

The most popular techniques to index time series are lower bound (LB) distance functions. An LB(x, y) function returns a value that is certainly lower or equal to the true DTW(x, y) distance between two time series objects x and y. If such LB is greater than the bsf, we know that x is not the nearest neighbor of y. Therefore, the subsequence x can be discarded. Despite the fact that we focus on the nearest neighbor search, this method can be trivially extended to the k-nearest neighbor search by defining the bsf as the distance to the k-th nearest subsequence so far.

An LB function needs to fulfill the following requirements to be efficient: (i) its calculation must be fast; and (ii) it needs to be tight, i.e., its value needs to be close to the true DTW. These requirements usually imply in a trade-off between tightness and time efficiency. In general, tight LB functions tend to be more expensive to calculate.

For this reason, Rakthanmanon et al. (2012) proposed to cascade LB functions. The similarity search sorts the LB functions by increasing runtime costs. If the first (and fastest) LB function fails to prune the DTW calculation, then the method tries the next one. If all LB functions fail to prune the DTW calculation, then the method computes the true DTW distance.

There exist several LB functions in the literature. However, the UCR Suite uses only three of them. The authors argue that these three functions subsume all other lower bound measures concerning the tightness-efficiency trade-off. In other words, there is always a faster-to-compute LB with, at least, a similar pruning power.

The first LB calculated in the UCR Suite is the $LB_{KimFL}$—a simplification of the $LB_{Kim}$ (Kim et al. 2001),—which is the sum of the distances between the first and the last pairs of observations of the time series. This measure is guaranteed to be an LB thanks to the boundary constraint of the DTW, specified in Definition 4.

The calculation of $LB_{KimFL}$ is extremely fast (${\mathcal {O}}(1)$); however, it prunes a small percentage of the DTW comparisons. In the cases $LB_{KimFL}$ fails to prune the distance calculation, the UCR suite uses the $LB_{Keogh}$ (Keogh and Ratanamahatana 2005) lower bound function.

Briefly, the $LB_{Keogh}$ constructs an envelope around the query, limited by the minimum and maximum values in the warping window for each observation. The lower bound measure is the squared Euclidean distance between the reference subsequence and the nearest envelope for each observation. $LB_{Keogh}$ is slower (specifically, ${\mathcal {O}}(n)$) than $LB_{KimFL}$; however, $LB_{Keogh}$ can prune a much larger number of objects.

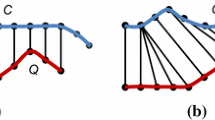
Figure 2 illustrates the previously described LB functions.

Fig. 2

The $LB_{KimFL}$ (left) estimates a lower bound as the sum of the Euclidean distances of the first and last pairs of observations. The $LB_{Keogh}$ (right) constructs an envelope around one of the time series and estimates the lower bound as the Euclidean distance from the other sequence to the nearest (lower or upper) envelope for each point outside the region encapsulated by the envelope

Finally, if the $LB_{Keogh}$ also fails in pruning the DTW calculation, it is repeated, but inverting the roles of the query and the reference subsequence with respect to the envelope. Such procedure is valid because the $LB_{Keogh}$ is asymmetric. So, its calculation using the reference subsequence to construct the envelope may result in a higher—and consequently tighter – value. In this case, the algorithm changes the value of the LB by the maximum between the two $LB_{Keogh}$ calculated and re-evaluates the pruning of the pair.

In addition to pruning by LB, an important technique to speed up the time series search is early abandoning. In several cases, it is possible to know if the distance between a pair of time series will be greater than the bsf during the computation of necessary values for the search procedure. One example is the early abandoning during the $LB_{Keogh}$ calculation. While calculating the LB, we incrementally increase its value. If at any step we find that the value of the partial LB is greater than the bsf, we can stop its calculation and skip to the next subsequence in the similarity search.

Two techniques may be used in this step to further improve the runtime of the search in addition to the LB calculation. The first one is z-normalization. The normalization procedure is necessary to improve the matching of subsequences in the presence of offset and amplitude variation Keogh et al. (2009). This procedure transforms the time series such that the mean of its observations is $\mu =0$ and the standard deviation is $\sigma =1$.

A straightforward batch algorithm to calculate the z-normalization can harm to the search runtime. Instead, the UCR suite implements it incrementally. This approach allows interspersing the z-normalization with the LB calculation. In this way, if we can early abandon the LB function, we are also abandoning the z-normalization calculation.

For this purpose, we need to look at the definitions of mean and squared standard deviation (variance). Equation 4 defines such statistics for a subsequence of the time series x starting at the p-th observation.

$$\begin{aligned} \mu = \frac{1}{m} \left( \sum _{i=p}^{m-1} x_i\right) \qquad \qquad \sigma ^2 = \frac{1}{m} \left( \sum _{i=p}^{m-1} x_i^2\right) - \mu ^2 \end{aligned}$$

(4)

Given the mean and the variance of $x_{p,m}$, these values may be reused in the calculation of the statistics referring to the subsequence $x_{p+1,m}$. This is done by subtracting the observation $x_p$ and adding $x_m$ to the summations. In the case of the standard deviation, this procedure uses the squared value from the observations. Once we keep the sum and the squared sum of the observation from a subsequence, we can update the mean and standard deviation to the next subsequence in a constant time.

The second additional method is the reordering of observations to calculate the LB. Instead of calculating the LB in the natural order (from the first to the last observation), we may sort the calculation by the absolute value of the query. This simple modification is likely to lead to the early-abandon of the LB calculation in fewer steps.

Finally, if all the previously described methods were not enough to avoid the DTW calculation, it is still possible to not calculate the whole cumulative cost matrix. Specifically, we can early abandon the DTW calculation when the minimum value obtained in a row (or column) of its cost matrix is greater than the bsf. In this case, the monotonicity property of DTW (c.f. Eq. 1) guarantees that the final value is also greater than the bsf. We can use the information of the partials calculated by the lower bound function to improve the distance early abandoning. Consider we are storing the cumulative lower bound from each point to the end of the time series. After the calculation of each row i of the DTW matrix, we can estimate a new LB of the final distance between the time series x and y given by $DTW(x_{1,i},y_{1,i}) + LB(x_{i+1,m-i},y_{i+1,m-i})$. So, if such a value is greater than the bsf, the distance computation can be abandoned. Figure 3 summarizes the similarity search techniques implemented in the UCR Suite.

Fig. 3

The UCR Suite sequentially applies different methods to avoid the costly DTW computation. The distance calculation to the current subsequence may be abandoned at any step (dashed lines). The z-normalization and the $LB_{Keogh}$ are calculated at the same time (third box), so both can be early abandoned together. DTW is calculated only if the LB and early abandon methods were not successful in pruning it. The value of the bsf is updated accordingly before the search continues to next subsequence. This process continues until the last subsequence is assessed

We performed an experiment to measure the runtime of the indexing techniques used by the UCR Suite and the time taken by the DTW calculations. For this purpose, we measured the time to search a query of length 256 in an electrocardiography time series (c.f. Sect. 5.1.3). The query was randomly selected from the data.

Fixing a relative warping window of $10\%$ of the query length, the percentage of DTW calculations was $1.42\%$ of the total number of assessed subsequences. Despite the incredibly small amount of DTW calculations, the relative time to calculate them (even with the early abandoning) corresponded to approximately $25\%$ of the runtime.

This is even more evident for longer queries or larger warping windows. For instance, using the same data with a relative warping window of $20\%$ of the query length, the number of DTW calculation was $4.06\%$ of the total number of subsequences. The time to calculate the distances took approximately $60\%$ of the whole search procedure runtime.

In this paper, we improve the UCR Suite by adapting a recently introduced algorithm, proposed to speed up DTW calculations independently of the bsf, named DTW with Pruned Warping Paths (Silva and Batista 2016). We extended our previous work incorporating the bsf to improve its performance in the similarity search. In the next section, we describe this method, as well as its adaptation to the similarity search task.

4 DTW with pruned warping paths

In this paper, we improve the UCR suite performance by augmenting it with a recently proposed method called DTW with Pruned Warping Paths—PrunedDTW—(Silva and Batista 2016). PrunedDTW was introduced as an alternative to speed up DTW calculations when the use of indexing methods is not applicable, such as applications that require the all-pairwise distance matrix within a set of time series. One example is the widely known family of hierarchical clustering  (Xu and Wunsch 2008), given that most of these algorithms require the relation among all the objects in the data set.

Although we have proposed PrunedDTW for a scenario in which current indexing techniques are not applicable, we can adapt it to similarity search. PrunedDTW is orthogonal to all lower bound functions and other indexing-based algorithms in the time series literature. In other words, the application of PrunedDTW on the similarity search is complementary to any adopted indexing techniques. While most methods to speed up the time series similarity search “compete” between them, PrunedDTW explores an entirely different strategy.

In this scenario, we propose the use of PrunedDTW when all the evidence obtained by the indexing methods was not sufficient to reject the costly dynamic programming-based distance calculation. Also, we introduce a subtle modification of PrunedDTW to use the best-so-far distance to improve its performance. Before we explain this change, we introduce the PrunedDTW algorithm.

4.1 The intuition behind PrunedDTW and its pruning strategies

Figure 4 provides a heat map of the DTW matrix for two electrocardiography time series. Note that the values around the main diagonal are relatively close to the actual DTW distance, which is approximately 2.77 in this case. In contrast, most of the values in the matrix are much higher than the real distance.

Fig. 4

DTW matrix between two electrocardiogram subsequences. The colors indicate the value obtained in each cell of the matrix (Color figure online)

The value in each cell (i, j) of this matrix represents the cost of the best alignment between the subsequences $x_{1,i}$ and $y_{1,j}$. Any alignment between x and y which contains such partial alignment has a total cost that is greater or equal to the value stored in the cell (i, j). In the case in which such cell contains a value that is greater or equal than the actual distance, the optimal partial alignment ending by matching the pair (i, j) is guaranteed to not belong to the optimal path between the whole time series under comparison. Therefore, the DTW algorithm can skip the calculations of all the alignments that contain such partial.

To use the observed fact to speed up DTW calculations, PrunedDTW works with a distance threshold to determine if a cell is amenable to pruning. For this, the original proposal uses the squared Euclidean distance (ED) as an upper bound (UB) to DTW, i.e., a value that is guaranteed to be greater or equal the actual distance. So, any cell that has a value greater than the UB can be pruned, because it is guaranteed to not belong to the optimal warping path.

Also, the algorithm uses such threshold to establish pruning strategies to decide when to start and finish the computations in each row² of the DTW matrix. Figure 5 exemplifies the pruning approach, that relies on monitoring two variables: the starting column sc and the ending column ec.

Fig. 5

Strategies adopted by PrunedDTW to prune the beginning and the end of each row of the DTW cumulative cost matrix. The variable sc (left) denotes the position of the first value lower or equal than the UB in the previous row and is used as the index to start the current iteration. On the opposite, the variable ec (right) points to the first value in the previous row that is greater than the UB. From this point, the algorithm may stop the calculation as soon as it finds a value that is greater than the UB

In the row $i+1$, the first two columns have a value greater than UB. Therefore, the variable sc is set to column 2 and the processing can safely start at column 2 in the next row. We can prune the computation of the cells containing A and B thanks to the values used by the DTW recurrence relation represented by the three arrows. Given the initialization with infinity and the large value already calculated in the cell $(i+1,0)$, the variable A will obligatorily have a value greater than UB. The same occurs to B which depends on $A > UB$ and other two cells in the previous row also greater than UB. In contrast, the cell with the value C may have a value smaller than UB since it depends on the cell $(i+1, 2) \le UB$.

The initial value of the variable sc is 0, i.e., while no values greater than UB are found, the calculation in each row will start at the first column. In the case that a warping window is used, the rows will be initiated in the column with the highest index between the column established by the pruning criteria and the one related to the warping window.

The second pruning strategy is responsible for pruning the last columns of the current row. The variable ec points to the first of a continuous sequence of values greater than UB that finishes at the end of the row. This value defines the column where we can stop the calculation of the next row.

In the presented example, row $i+1$ is processed and ec is set to $j+2$. We can stop the row $i+2$ as soon as two criteria are met: (i) the last calculated value is greater than UB and (ii) the current column index is greater or equal to ec. Suppose that A is greater than UB. In this case, criterion (ii) is not met. We can see that B may be smaller than UB since it can use $(i+1,j+1)$ which is lower or equal to UB. However, if B is greater than UB then both criteria are met, and we can stop processing the current row. This occurs because C and D can only inherit values from the matrix that are greater than UB.

For further details about the original PrunedDTW method including algorithm and detailed performance results for the problem of computing the all-pairwise distance matrix, we refer the reader to (Silva and Batista 2016). In this paper, we propose a subtle variation of PrunedDTW which can significantly improve the performance of existing similarity search indexing methods. For clarity, we refer to our proposal as SS-PrunedDTW (for Similarity Search PrunedDTW).

4.2 Embbeding PrunedDTW into the similarity search procedure

The results presented by Silva and Batista (2016) demonstrate that PrunedDTW can speed up the traditional all-pairwise DTW distance calculation from two to ten times. Such a variance is the result of the tightness of the adopted UB function—Euclidean distance. The tightness of an upper bound is related to how close its values are from the actual DTW distance, which may fluctuate between different datasets. In general, a tight UB allows PrunedDTW to prune a large number of calculations, achieving a higher speedup.

Euclidean distance is a natural and efficient UB for DTW. ED is the DTW distance obtained by the warping path defined by the main diagonal of the DTW matrix. As DTW returns an optimal path, i.e., the path that leads to the smallest distance, the DTW between two time series is always lower or equal than ED. Although ED is a reasonably tight UB for DTW, in similarity search we have access to a potentially much tighter UB, the best-so-far distance.

Note that the bsf is not an upper bound for the DTW distance between the query and the subsequence from the long time series. Instead, it is an upper limit to consider such subsequence as the (k-th) nearest neighbor of the query. Following the same principle of the distance early abandoning strategy, any partial alignment with a value greater than the bsf leads to a DTW distance greater than the distance to the current (k-th) nearest neighbor. So, the bsf is an admissible threshold for pruning in the similarity search scenario. Also, the bsf has the advantage that its value is monotonically decreasing during the search.

Regarding pruning power, bsf is usually much smaller than the ED between two time series under comparison. Then, using the bsf must imply in a higher number of skipped calculations. The bsf is usually smaller than the DTW distance between the two subsequences, and a simple observation can help us to understand why. While the DTW between two arbitrary subsequences can vary widely, the bsf is the DTW distance between the two closest time series compared until a certain point of the search process, which is independent of the current pair of subsequences.

Figure 6 visualizes the behavior of the DTW, ED, and bsf in a similarity search on a dataset of electrocardiography (c.f. Sect. 5.1.3). In this case, we stored the ED and bsf every time that we needed to calculate the DTW, i.e. when the lower bound functions were not able to prune the candidate for nearest neighbor. As we can see, the value of the bsf is usually much lower than the ED, except in the first distance calculation—when the bsf is still undefined and, then, initialized as infinite. In contrast, the ED depends only on the two time series under comparison, so its value has a significant fluctuation during the search process.

Fig. 6

Comparison of the Euclidean distance, Dynamic Time Warping, and best-so-far values during the similarity search. Specifically, this figure visualizes the distances obtained each time that the DTW was calculated in a search for a 128 observations long query and a relative warping window size of $10\%$ of the query length in an electrocardiography dataset. We highlight a moment of the search in which the current DTW is lower than the bsf, updated for the next iteration

The experiment presented in Fig. 6 indicates that the bsf is a better threshold for pruning decisions in PrunedDTW than the ED. To verify this statement, we experimented with all the datasets used in our experimental evaluation (c.f. Sect. 5). For each dataset, we established ten distinct search scenarios, varying the query and warping window lengths. One characteristic is common for every experimented scenario: after the first DTW calculation, when bsf is infinite, in $100\%$ of the subsequences not discarded by the pruning techniques, the bsf is lower than the ED between these subsequences. Specifically, the bsf is approximately 7.77 times lower than the ED in average. Besides, the bsf stores a value that is lower than the actual DTW in $94.14\%$ of these cases.

As an additional feature, just like in the distance early abandoning, we may improve PrunedDTW using partial lower bound calculations. When evaluating if a cell is liable for pruning, PrunedDTW originally considers only the value obtained by the recurrence relation of the DTW algorithm for that cell.

Alternatively, we can sum such value to the cumulative lower bound from the first observation ahead of the values comprised by the warping window to the end of the subsequences. In other words, we can use the total cost of the partial alignment summed to such lower bound partials and compare to the bsf in order to decide the pruning. For clarity, consider that cumLB[i] stores the summed contributions of $LB_{Keogh}$ from the i-th position to the end of the envelopes (c.f. Fig. 2-right). For a value stored in D[i, j], i.e., from the partial alignment ending in the i-th and j-th observations of the subsequences x and y, we guarantee that $DTW(x,y) \ge D[i,j] + cumLB[i+i+ws] \ge D[i,j]$, where ws is the absolute warping window length. Once we only have interest in a pair of subsequences x and y if $DTW(x,y) < bsf$, we need to have as result that $bsf > D[i,j] + cumLB[i+i+ws]$. For this reason, we can use the bsf and the cumulative LB as an upper bound. Specifically, if any partial alignment is such that $bsf - cumLB[i+i+ws] < D[i,j]$, we guarantee that this alignment will not lead to a distance value lower than the bsf.

We are now in a position to describe the algorithm in details. Algorithm 1 implements the SS-PrunedDTW using ${\mathcal {O}}(n)$ space. Note that, for simplicity, we omitted the early abandoning of the DTW distance calculation.

The algorithm starts by defining auxiliary variables to the pruning strategy (lines 1 to 3) and by setting the initial values of the cumulative cost matrix (lines 4 to 6).

The for loop from line 7 to 47 traverses the observations of the series x. It starts by defining the initial values of the pruning-related variables for the current iteration (lines 8 to 11).

The next for loop traverses the observations of the time series y constrained by the warping window, which length is defined by ws. In the first time that the algorithm achieves this point, it is necessary to set the first value in the cumulative cost matrix. It is done by the settings inside the condition starting in line 13 (which finishes at line 20). This condition is necessary to perform a correct initialization of such a structure.

When implemented to use linear space, the pruning of the last values in a row may cause problems with non-computed cells in the cumulative cost matrix. It occurs when the last row is pruned, and the cell which should contain the distance is currently storing a value from a previous iteration. In this case, we only need to check in which column the last row was pruned and avoid the values stored in any column ahead of it. This is done by the condition between lines 21 and 26.

Next, we calculate the value of the current cell of the DTW matrix, in line 27. Notice that we simplified this line for the sake of presentation. In an actual implementation of the algorithm, it is necessary to check if $j-1$ corresponds to a valid index. For clarity, $j-1$ may never be lower than its initial value defined in the heading of the internal for loop, i.e., $max(0,sc,i-ws)$. In this case, we use infinity instead of the partials $D[j-1]$ and $D\_prev[j-1]$.

This step of the algorithm finishes by checking whether the current row shall be pruned and if any information related to the pruning mechanism needs to be updated (lines 28 to 40). It first checks if the current value is greater or equal the bsf. In this case, it is possible to prune the end of the row, regarding only one more condition. Specifically, if the index of the current column is greater or equal the ec (line 29), then we store this index in the variable lp (line 30). Afterward, we mark the row as pruned (line 31) and prune the row calculation by skipping the next iterations on this row (line 32).

In the case that the current value is lower than the bsf, we need to update the values sc (line 36, case it was not set in this row yet) and ec_next (line 39), which is an auxiliary variable to set the ec for the next row.

After finishing the internal for loop, we first set the vector used as the previous row in the next iteration with the values of the currently calculated row (line 42). Then, we update the variables related to the pruning for the next row (lines 43 to 46). In the case that no pruning occurred at the end of the row, we set the variable lp to the index related to the last column of the warping window in the next row (line 44). In addition, we set the variable ec as ec_next (line 46).

Finally, we return the final distance value (line 51). However, we first check if the end of the last row was pruned (lines 48 to 50). In this case, we force the algorithm to return infinity (or any value indicating early abandoning of the distance calculation).

4.3 On the correctness of the SS-PrunedDTW

Consider $P = \{p_1,p_2,\ldots ,p_k\}$ the set of all k possible (n, m)-warping paths between two temporal data in which $p_o$ denotes the optimal (n, m)-warping path. By definition, any $p_i | i \ne o$ has a cost greater or equal to the cost of $p_o$. Although unlike, there may be other (n, m)-warping paths with costs equal to the optimal alignment. However, most of the paths $p_i$ do not fit this circumstance and may be disregarded.

The cell (i, j) in the cumulative cost matrix stores the cost of the optimal (i, j)-warping path, i.e., the optimal alignment between the subsequences $x_{1,i}$ and $y_{1,j}$. Recall that the cost of matching two observations is nonnegative. Thus, any (n, m)-warping path containing the (i, j)-warping path has a cost that is at least the value stored in the cell (i, j) . If this value is greater than the cost associated to $p_o$, so the (i, j)-warping path is not part of the optimal alignment between the time series under comparison.

When such observations are embedded in a similarity search scenario, the notion of which warping paths are relevant is now associated with the threshold defined by the bsf and the cumulative lower bound. Specifically, any (i, j)-warping path with a cost greater than the specified UB may be ignored. For this reason, we may say, without loss of generality, that SS-PrunedDTW is based on the same premise as the early abandoning of the distance calculation.

The correctness of the pruning strategies can be obtained by the ordering of the fulfillment of the DTW matrix. According to Eq. 3, the value of each cell is influenced by three other values:

• (I) same row, preceding column: ($i,j-1$);

• (II) preceding row, same column: ($i-1,j$);

• (III) preceding row and column: ($i-1,j-1$).

For the pruning strategy that determines the value of the starting column variable (sc), our proposal can be better understood if we observe how the cells are calculated since the column zero of the DTW matrix. Because such column is initialized with infinity, the value inherited from (I) never leads to the minimal value for the first column in the DTW matrix. This fact is likewise true for any cell that starts the calculation in a row—determined by pruning or warping constraints. Similarly, while the currently calculated value exceeds the UB, any value obtained by (I) is also greater than the distance to the ($k-th$) nearest neighbor—what only occurs due to (II) or (III). In any case, such a value could be admissibly pruned.

The analysis of the values in (II) and (III) becomes necessary from the column in which there is a value lower than the UB in the preceding row. Therefore, while the values of a row are calculated, our algorithm stores the position where this value occurs for the first time and uses this information to start the next row. In other words, our method does not prune the calculation by determining the beginning of a row in a column c if there is at least one promising value in the preceding row in any column $c' < c$. Thus, it is guaranteed that our method does not miss any promising value in (II) or (III).

The two restrictions used to define the pruning strategy of the end column in each row of the matrix guarantee the correctness of our method by the following facts. The calculation of the values in a row will never be pruned while the current value is lower than the UB, ensuring that there will be no missed promising values at the positions defined by (I). Also, we ensure that there is no loss of promising values in (II) and (III) by the fact that the algorithm monitors, with the variable ec, from which point there are no more promising values in the preceding row. A row can only be pruned if its current column is greater than ec. In other words, when calculating a value for a column c, this criterion requires that $ec \le c-1$.

5 Experimental evaluation

Given that we have presented our algorithm and proved its correctness, we evaluate the effect of SS-PrunedDTW in improving the runtime of the similarity search. For this purpose, we have modified the UCR suite and executed the same experiments using both implementations. For clarity, we refer to the proposed implementation as UCR-USP suite.

We note that we have made available the source code, as well as detailed results, in a supplementary website (Silva et al. 2016b). In our experimental evaluation, we used 6 datasets from different application domains. For each of them, we defined a long reference time series and five different queries. We do not use any knowledge from experts to define the queries. To create the queries, we randomly picked subsequences from a time series that was not used to compose the reference data. For each dataset, we selected five different queries. Also, we vary the length of the query. For this, we cropped each selected query in lengths of 128, 256, 512 and 1024. Finally, we used five different widths of the warping window: 10, 20, 30, 40, and 50% of the length of the query. So, we have experimented with 100 different search scenarios for each dataset.

For simplicity, we only evaluated the methods in single-dimensional time series. However, we note that the generalization of the applied algorithms to the multidimensional is simple. For a detailed discussion on the generalization of DTW to deal with multi-dimensional data, we refer the reader to Shokoohi-Yekta et al. (2017) and  Górecki and Łuczak (2015).

Finally, we ran all the experiments on the same computer.³ To avoid spurious time fluctuations, we guaranteed that, at any time, there was only one process—except OS processes—running on the computer.

5.1 Data

We start the description of our evaluation by briefly presenting the datasets, regarding the application domain and the length of the reference time series.

5.1.1 Physical activity monitoring

Due to the increasing availability of sensors, such as the accelerometers present in the majority of smartphones, the human activity monitoring is an application with a growing attention. In this work, we use the dataset PAMAP2 (Reiss and Stricker 2012), which contains recordings of 18 different activities performed by 9 subjects. The data have a sampling rate of 100 . In our experiments, we used the time series obtained by z-axis measurements from the accelerometer in the arm position. The reference time series has 3,657,033 observations.

Figure 7 shows how the accelerometers are arranged and an example of the collected data.

Fig. 7

The PAMAP data are collected from three different accelerometers (left), positioned according the red circles. We used the z-axis of the accelerometer in the hand position. The presented time series (right) was obtained by 2 s of walking

5.1.2 Athletic performance monitoring

Monitoring activity may also be used for professional ends. One such example is the tracking of athletes’ performance. For this, the athletes may wear sensors for recording speed, trajectory, energy and other features. In this work, we used the position in the axis attack/defense recorded by ZXY Wearable Tracking sensors⁴ in several soccer players during three matches (Pettersen et al. 2014). The data has a sampling rate of 20 Hz. The reference time series has 1,998,606 data points obtained by concatenating data from the first two matches from a single player. We randomly chose the queries from the third game.

5.1.3 Electrocardiography

Time series are a common category of data on health applications for a long time. One of such applications is the monitoring of heart activity by electrodes placed in the skin, a procedure known as electrocardiography (ECG). To evaluate our method in this type of signal, we used the MIT-BIH Arrhythmia Database (Moody and Mark 2001; Goldberger et al. 2000), a collection of 48 ECG recordings digitized at 360 samples per second. For clarity, 2 s of data (720 data points) may contain information of approximately three beats. Our reference time series for this dataset is composed of 27,950,000 values.

5.1.4 Photoplethysmography

Another application related to health care evaluated in this work is the photoplethysmography (PPG). This technique is a non-invasive alternative for monitoring the heart rate and cardiac cycle. An optical sensor placed in a peripheral portion of the patient’s body generates the data. In this work, we use PPG data collected from the fingertip (Kachuee et al. 2015). The number of observations in the reference time series is 333,570,000, with a sampling rate of 125 samples per second.

Figure 8 shows an example of the optical sensor used for the monitoring and 5 s of a PPG data.

Fig. 8

A fingertip oximeter (left) and 5 s of PPG data obtained by its use (right)

5.1.5 Freezing of gait

The last medical application employed in this work is the detection of freezing of gait (FoG), a symptom related to the Parkinson’s disease. In this work, we performed the similarity search in the Daphnet FoG data (Bachlin et al. 2010). Specifically, we used recordings of the horizontal forward acceleration of the subject’s thigh as data. This is the smallest experimented dataset, being that the reference time series contains 1,724,584 observations.

Figure 9 shows an example of the time series in the transition from a normal state to a FoG episode.

Fig. 9

This subsequence of the acceleration of a subject’s thigh shows the transition from a normal state (with high amplitude) to a freezing of gate episode (where the amplitude is clearly lower)

5.1.6 Electrical load measurements

Time series data from measuring the electrical consumption has attracted the attention of researchers because of the its wide range of applications. Some examples are the smart energy services (such as automatic demand response) and smart home and smart city solutions. The REFIT dataset (Murray et al. 2015) is composed of the electrical consumption monitoring (in Watts) of distinct appliances from 20 different households. The data are sampled such that the interval between observations is 8 s. The version of this dataset used in this work was cleaned to avoid missing data, which was substituted by the value zero. To prevent division-by-zero during the z-normalization, we have added a small amplitude noise to the original signals. In our experiments, we used the monitoring of dishwashers, composing a reference time series of 78,596,631 observations.

5.2 Results and discussion

SS-PrunedDTW is an exact algorithm that does not lead to false dismissals. Therefore, the UCR-USP suite provides the same answers as the UCR-suite or any other exact approach based on DTW. Therefore, we perform our evaluation comparing only the runtime of UCR-USP and the UCR suites. We compare the runtime of these two methods varying two parameters: query length and warping window length. We measure the warping window length by the number of observations in the warping window.

Figure 10 shows the runtime of the UCR and the UCR-USP suites for each dataset according to the query length. The results are the average time over five queries and five different lengths of warping window. However, we notice that the website that supports this paper Silva et al. (2016b) presents the results for each parameter variation.

Fig. 10

Runtime of both UCR and UCR-USP suites on the experimented datasets by varying the query length. The datasets are presented sorted by the length of the reference time series. The plotted values represent the average runtime over five different queries per query length and all the warping window rates adopted in our experiments. a FoG, b Soccer, c PAMAP, d ECG, e REFIT, f PPG

The other parameter which directly affects the results is the warping window length. Figure 11 shows the difference in runtime between the experimented suites when this parameter is varied. The reported result for each warping window is the average runtime for five queries and four query lengths.

Fig. 11

Runtime of both UCR and UCR-USP suites on the experimented datasets by varying the (relative) warping window length. The datasets are presented sorted by the length of the reference time series. The plotted values represent the average runtime over five different queries per warping window length and all the query lengths adopted in our experiments. a FoG, b Soccer, c PAMAP, d ECG, e REFIT, f PPG

The UCR-USP suite outperformed the UCR suite for most of the settings in our experiments. In the few cases in which it did not happen, the difference between the two methods is considerably small. Even more important, the UCR-USP suite only achieved similar or slightly worse performance in the cases with the smallest runtimes among our experiments, that is, for either short queries or small warping windows. Specifically, the worst case—concerning search runtime—in which our method performed slightly slower in average occurred for the dataset of PPG and with a query containing 256 observations and the warping window size of $10\%$. In this case, the search lasted 86.4 s, while the UCR suite took 86.1 s. We observe that it does not represent a notable difference in practice.

On the other hand, when searching for subsequence with 1024 observations and a relative warping window of $50\%$ in the same dataset, our method reduced the average runtime from approximately 116,100–22,250 s, i.e., the UCR-USP suite performed 5 times faster. In general, the results show that the slower the similarity search procedure, the higher the improvement provided by the UCR-USP suite.

To illustrate this fact, Fig. 12 shows the speedup ratio ordered by total time taken by the UCR suite in the ECG dataset. The speedup ratio is the runtime of the UCR suite divided by the runtime of the UCR-USP suite. In other words, a speedup ratio of 2.0 means that our method is two times faster in that experiment.

Fig. 12

Speedup ratio in the ECG dataset. There is an increasing trend according to the total time taken by the UCR suite, i.e., the speedup is inversely proportional to the runtime of the original suite. This trend is similar in all evaluated datasets. The markers represent real runtime measurements, and the dashed line presents an exponential trend line for such values

Given the presented results, we recommend the use of UCR-USP suite for all settings. However, we strengthen that its use is remarkably recommended in cases where long queries or large warping windows are required. In fact, the largest absolute warping window in which the UCR suite performed better than our proposal—in the average of different queries,—was composed of 25 observations ($10\%$ of a query with 256 data points). For all larger absolute warping windows, our method outperformed the UCR suite.

Our results on larger queries and window sizes are sound. The larger the DTW matrix is, the longer it will take calculate it. Therefore, large DTW matrices allow more opportunities for pruning and speedup for SS-PrunedDTW. We notice that several applications may require long queries and large warping windows. For this reason, we dedicate the next section to discuss such subject.

6 On the need for long queries and large warping windows

The results presented in the previous section show that the improvements in performance provided by the UCR-USP suite are more significant for long queries and large warping windows. In this section, we show that these characteristics are not only likely to appear, but required in some cases.

This scenario is particularly interesting because it defines the worst case of the similarity search under DTW. In this case, the LB-based pruning strategies tend to be less effective, i.e., the search procedure will require a higher number of DTW calculations. Also, the cost to calculate each DTW distance is also higher.

Long queries are becoming more often with newer technologies. For instance, the recent sensor technologies are more accurate and able to acquire data in higher sampling ratios. In other words, these technologies can obtain time series with a larger number of observations per second. For this reason, short subsequences can only represent a short period. As a consequence, the assessed subsequences need to be even longer than the ones used in our experimental evaluation. This topic is deeper discussed in Sect. 6.1.

At the same time, there is a multitude of applications in which a little warping window may be inadequate. For example, time series from human activities, motion, and locomotion represent people performing activities possibly in completely different paces, resulting in time series with notable differences regarding local and global scaling (Shen et al. 2017). Another example is the similarity in music applications, such as the query-by-humming (Park 2015) and music information retrieval by emotion (Deng and Leung 2015) or rhythm (Ren et al. 2016). Several other applications may require warping windows larger than the usually adopted $10\%$. Section 6.2 better explores this topic and presents a practical example.

6.1 Query length

We begin by discussing the queries length. The longest query used in our experiments has 1024 observations. However, we notice that this length is usually too small for several applications.

As an example, consider the dataset REFIT (c.f. Sect. 5.1.6), which stores the measurement of the power consumption every 8 s. So, a query of 1024 points corresponds to exact 8192 s, i.e., approximately 2 h and 15 min. If one is interested in analyzing daily consumption patterns, the adequate query should be composed of 10,800 values. Ten thousand data points are one order of magnitude longer than our longest query in the previous experiments. Moreover, some applications may use even longer data. In the example of the power consumption, one may be interested in finding weekly or even monthly patterns, for instance.

While we used the dishwasher consumption in our experiments, Fig. 13 shows two 24-h examples of electric heater consumption monitoring, which brings a more intuitive example. In this example, we used the power monitoring during the Saint Patrick’s (March 17th—early Autumn) and the Christmas (December 25th—Winter) days of the year 2014.

Fig. 13

Heater monitoring during 24 h in different seasons. Despite the similar pattern in the first 8 h of the day, the daily pattern is clearly different

Notice that both time series present a similar square shape during dawn. However, this pattern lasts for a little less than 8 h and a query of 1024 points (8 h correspond to 3600 observations) will not properly represent it.

We performed an experiment using one day long queries in this dataset, i.e., 10,800 observations. Specifically, the reference time series used in this experiment is the power consumption of the heater from only one house. All the queries come from the same kind of device but from another house. The length of the reference time series, in this case, is 6,960,008 values.

Using this dataset, the speedup achieved by the UCR-USP suite varies between 1.12 (when using the relative warping window $w=0.1$) to a slightly better rate of 1.33 (with $w=0.5$). Applying our modified suite on the dishwasher dataset with queries composed of the same number of observations, we can notice that our method may achieve better results depending on the data. For the dishwasher dataset, the speedup ratio varied from 1.42 to 3.5 using $w=0.1$ and $w=0.5$, respectively. It is important to notice that even if the speedup of 1.42 seems “humble”, it represents a decay of runtime from 97,763 to 68,679 s. In other words, in that case, the UCR-USP suite is saving 29,084 s, which represents approximately 8 h, per searched query.

Another example is the athletic performance monitoring. The sensor generates data with a sampling rate of 20 Hz. It means that a query with 1024 observations corresponds to just 51.2 s. Clearly, it is not enough data to analyze the moving pattern of any player. Figure 14 shows an example of the trajectory of a player by time series with lengths 1024, 6000 and 12,000 observations, i.e., 51.2 s, 5 min, and 10 min, respectively. For the sake of exemplification, we used the bi-dimensional trajectory time series.

Fig. 14

Examples of trajectories of an attack player monitored during 51.2 s (left), 5 min (center), and 10 min (right). Notice that in the short subsequence it is not possible to observe any playing pattern. In the subsequence regarding 5 min, it is possible to note that this player’s positioning is more concentrated in the head of the penalty area. This pattern is more clear in the last case, where it is possible to observe a wide moving pattern close to the middle-field and more concentrated in the attack

In the case of the soccer data, we analyzed the query lengths: 6000 and 12,000. For the former case, the speedup ratios varied from 1.22 (using $w=0.1$) to 3.22 (when $w=0.5$). In the case of 12,000 observations in the query,—as expected—the speedup was a bit higher, varying between 1.72 and 3.7 (using $w=0.1$ and $w=0.5$, respectively).

In both dishwasher and soccer players monitoring datasets, these experiments contribute to clarify the fact that the longer the query, the higher the speedup achieved by our method. For instance, the speedup ratio on the soccer dataset varied between 1.1 and 2.6 when we searched for 1024 observations long queries.

6.2 Warping window

The warping window is an important parameter of DTW. In some tasks, such as classification, it may cause a significant impact on the results. Empirical evidence has shown that for the UCR Time Series repository datasets (Chen et al. 2015), small window sizes are more likely to provide superior 1-NN classification accuracy (Ratanamahatana and Keogh 2005). However, the best value for this parameter is strictly data dependent. There are several datasets in which a large warping window is necessary to achieve the best accuracy results.

One example is the PAMAP data (c.f. Sect. 5.1.1). The time series in this dataset set of human activities are labeled, so we can use the class information to make some conclusions on the subsequences by our search procedure. For this purpose, we compared the class of each query to the subsequence found when using $w=0.1$ and $w=0.5$. In most cases, either both parameter values would make the correct classification, or both would make a mistake in a 1-NN classification. When the decisions are opposite to each other, the classification using $w=0.5$ is correct. Specifically, it happens in four cases—in the total of 20 combinations of query and number of observations.

The UCR Time Series repository is the largest repository of time series datasets for clustering and classification. The accuracy rates obtained by the nearest neighbor algorithm using DTW in each dataset are presented in the repository’s website in two different ways: (i) using no warping window, i.e., the relative length of the window is $100\%$ and (ii) warping-constrained DTW, in which the best value for the warping window length is learned in the training data. In some datasets, the warping window taken as optimal is larger than $10\%$ (around $15\%$ of the datasets). Even more, in several cases, the performance of DTW with no warping window is better than its constrained version.

Besides the recommendations for the 1-NN classification, there are no conclusive studies about this parameter for different algorithms or mining tasks. Silva and Batista (2016) performed an experiment on hierarchical clustering varying the warping window size in several datasets. The results show that more than a half of the best results were obtained by using warping windows larger than $10\%$ of the time series’ length, being several of them obtained using no warping window at all.

Figure 15 shows a small and intuitive example of data in which a large warping window is necessary. The time series used in this example are from the dataset REFIT (c.f. Sect. 5.1.6). It is evident, by visual inspection, that a similar cycle of the dishwasher generated two of the presented time series, but with different durations (e.g. the user chose a longer washing cycle, more suitable for greasy dishes). Nevertheless, when we cluster the time series by the single-linkage hierarchical clustering using DTW with $10\%$ of relative warping window, the best match in this simple subset is wrong. We can obtain a similar clustering using $20\%$ of warping, with changes only in the scale of the distances. When we use a larger warping window, however, the time series are correctly clustered.

Fig. 15

Single-linkage clustering obtained by using DTW with relative warping window lengths of $10\%$ (left) and $50\%$ (right). Note that the correct cluster is only obtained by using the larger warping constraint

Despite that we used a hierarchical clustering algorithm to exemplify the need for large warping window, the result presented in Fig. 15 has a direct impact on the similarity search. Consider that the objects at the bottom and the top of the figure are part of the reference time series. If we search the nearest neighbor of the object in the middle using a small window, the search will return the object at the bottom instead of the correct one (at the top).

In this dataset, the UCR-USP suite is approximately 3 times faster than the UCR suite with a warping window of $50\%$ and a query with 1024 observations (approximately 2 h and 15 min of monitoring, c.f. Sect. 6.1).

7 Pruning paths on DTW variations and other distance measures

We have stated so far the relevance of DTW on the similarity search. In fact, it is arguably the most used distance measure in time series similarity search. However, one may be interested in using another distance measure for the nonlinear alignment between time series.

In the last decades, DTW was modified in several different ways, to provide robustness to certain variances found in specific application domains. Some examples are the Derivative DTW (Keogh and Pazzani 2001), the Weighted DTW (Jeong et al. 2011), and the Prefix and Suffix Invariant DTW (Silva et al. 2016a). Also, some distance measures find a nonlinear alignment while respect the triangle inequality, i.e., they are metrics calculated by a dynamic programming algorithm similar to DTW. Some examples are the Time Warp Edit Distance (Marteau 2009) and the Move-Split-Merge (Stefan et al. 2013).

Speeding up the similarity search under different nonlinear alignment distance measures is a widely studied topic in the time series literature (Wang et al. 2013). In these cases, the procedure to avoid distance calculations may vary, depending on the distance measure. For instance, when using the distance metrics, we can apply indexing structures based on the triangle inequality to reduce the search space (Hjaltason and Samet 2003).

On the other hand, we are not aware of strategies similar to the PrunedDTW. We believe that adapting PrunedDTW to other distance measures can have a similar effect to the ones demonstrated in this work: improve the worst case of the similarity search, tackling the bottleneck of the search procedure.

Most of the distance measures for time series comparison are based on minimizing the cost of matching the observations. In these cases, the steps of PrunedDTW are fully repeated to prune unpromising alignment paths. However, the UB needs to be calculated accordingly. In general, the bsf can be used, as described in Sect. 4.

It is important to notice that some algorithms to compare time series are based on maximizing an objective function. One example of these methods is the Longest Common Subsequence (LCSS). While DTW and its variations aim to minimize the total cost of matching the observations, LCSS maximizes the length of the similar subsequence between the time series under comparison. In this case, the roles of LB and UB are inverted. To prune the LCSS calculations between pairs of subsequences, we first need to calculate a UB (Vlachos et al. 2006). Conversely, to prune unpromising partial alignments, we need to replace the UB used by PrunedDTW by an LB function. As a consequence, the comparisons used in the pruning decision step also need to be inverted. Specifically, we need to invert the operators < and >, as well as $\le$ and $\ge$.

Adapting the pruning of unpromising alignment paths for these distance measures can be subtle, and we let a deeper discussion and experimentation as part of the future work. The next section concludes this work and briefly introduces other ideas to develop in the future.

8 Conclusion

In this work, we embedded a recent advance on speeding up Dynamic Time Warping into the similarity search scenario. This approach is motivated by the fact that this algorithm can speed up the distance calculations in the cases in which the current similarity search methods perform worst. Specifically, we identified that the DTW calculations configure the bottleneck of the subsequence similarity search.

We have shown that our method can speed up the fastest tool for similarity search under DTW. Also, our method achieves the highest speed up rates for long queries and large warping windows, the worst case for the usual indexing techniques. When the queries and the warping windows are small, our method achieves similar runtime when compared to the state-of-the-art.

We notice that embedding the PrunedDTW in the similarity search procedure is not necessarily the ultimate solution to mitigate the observed bottleneck for all scenarios. For instance, if we need to perform the similarity search under sparse time series data, we may use a method specific for this case (Mueen et al. 2016). If an approximate solution is considered suitable for the problem, an algorithm that approximates DTW—such as FastDTW (Salvador and Chan 2007)—can be applied. However, PrunedDTW is exact and can be applied in any case, improving the efficiency as demonstrated by our experimental evaluation.

As a practical overview of our contribution, consider that one gets an average speedup ratio of 2, i.e., the UCR-USP Suite spends half of the time then the UCR Suite to search a set of queries. This speedup is a common achievement of our method (see, for instance, Fig. 12). It means that a laboratory of medical analysis can serve twice the number of patients per day, for example. Similarly, an industry needs to spend half the computational power for monitoring cauldrons and machines. After all, the speedup achieved by the UCR-USP Suite is directly proportional to the savings, profit or any other benefits obtained by applying it.

As future work, we intend to evaluate the use of the adapted PrunedDTW in tasks which use the nearest neighbor search as an intermediate step. Some examples are the classification (Ding et al. 2008) and clustering (Begum et al. 2015) of time series. Also, we intend to extend the proposed method to multidimensional time series (Shokoohi-Yekta et al. 2017).