1 Introduction

An option is a contract that gives its owner the due to buy or sell a defined value of a special asset at a fixed value, called the exercise value, before or on a given date, known as the maturity date. An option can be applied before maturity at any moment, called the American option, or on the maturity, called the European option. Moreover, the option that offers the right to buy defines the call option, and the option that gets the right to sell defines the put option. The pricing of an option is very important in financial derivatives to mitigate losses incurred. Therefore, we must introduce the manner to investigate the price of this option.

First of all, in 1973, three mathematicians named Black and Scholes (1973) and Merton (1973) presented a scheme to estimate the price of option named the Black-Scholes model (BSM). The merchants of an option generally buy and sell the right of an option. Because of the accuracy in options trading and the success of the strategy in anticipating options prices, it eventually adds to large growth. This financial theory was introduced by applying fractional calculus of the stochastic system’s fractal assembly. This was done by replacing the fractional Brownian movement compared to its classic type. Many phenomena in nature such as the dynamical model (Kumar et al., 2020d), the epidemic of measles (Kumar et al., 2020e), transport phenomena (Tuan et al., 2020; Kumar et al., 2020b, 2020c), tumor cells (Kumar et al., 2020b), and population model (Kumar et al., 2020a) can be modeled with the help of these fractional calculations. The only problem with this type of equation is its analytical solution. So to solve the problem of the non-locality of fractional calculus, you have to use numerical solution. In recent years, many numerical methods have been proposed to solve fractional equations (Ren & Liu, 2019; Ren, 2022; AlAhmad et al., 2021; Alia et al. 2021). Below we will summarize an important part of this work. Compact finite difference design to discrete time variable with third Chebyshev polynomials to gain full discrete in Safdari et al. (2020a), hybrid Laplace transform-finite difference method in Salama et al. (2021), the fourth kind of shifted Chebyshev that presented by Safdari et al. (2020b), an extended cubic B-spline approximation in Akram et al. (2021), Hermite wavelet by kumar in Kumar et al. (2021), spectral method based on Legendre polynomials in 2019 by singh in Singh et al. (2019a), the Fibonacci collocation method to solve two-dimensional fractional-order reaction advection sub-diffusion model by Dwivedi and Singh (2021). Moreover, numerous methods in the spectral method and homotopy perturbation method are also presented in papers (Verma et al., 2019; Singh et al., 2019b; Gao et al., 2020).

Now, this type of field, because fractional calculus is a strong instrument to illustrate the inherited and retention characteristics in mathematics, has been used with the help of modeling in financial equations and can be used in detail to model the type of European or American options (Björk & Hult, 2005; Meerschaert & Sikorskii, 2011). In this regard, many authors have developed modeling for the option, which can be referred to in the following sample. The pricing of the European call option (Wyss 2000), specific state of the bi-fractional BSM (Liang et al., 2010), describing the value of European-style derivatives (Cartea, 2013), and implementing spectral methods to develop BSM (Leonenko et al., 2013).

Let r be the risk-free interest rate, \(\sigma \) is the volatility and t is the time in the year. Then in this paper, we consider TFBSM with expressed features that u(x, t) be the value of an option, as below

$$\begin{aligned} \begin{aligned}&{}_{0}D_{t} ^{\alpha } u(x,t)-\frac{1}{2}\sigma ^{2} \frac{\partial ^{2}u(x,t)}{\partial x^{2}} -\left(r-\frac{1}{2}\sigma ^{2}\right) \frac{\partial u(x,t)}{\partial x}+ru(x,t)=f(x,t),\\&0< x< 1,~~~ 0< t \le T,~~~ 0 < \alpha \le 1, \end{aligned} \end{aligned}$$
(1)

and the boundary conditions as

$$\begin{aligned} u(0, t)=\eta _{0}(t),~~ u(1, t)=\eta _{1}(t), \end{aligned}$$
(2)

where f(x, t) and \(r>0\) are the known term. Moreover, \({}_{0}D_{t} ^{\alpha }\) is the left Caputo fractional derivative that is described as

$$\begin{aligned} {}_{0}{D}_{t}^{\alpha }u(x, t)= \frac{1}{\Gamma (n-\alpha )}\int _{0}^{t}{(t-\tau )^{n-\alpha -1}}\frac{{\partial }^{n} u(x, \tau ) }{\partial {\tau }^{n}}d\tau , ~~n-1<\alpha <n, ~~ n\in {\mathbb {N}}. \end{aligned}$$

That’s why we take a numerical approach. Of course, many numerical methods have been used to solve this problem over the years such as Legendre multiwavelet and the Chebyshev collocation method for pricing the double barrier option in Sobhani and Milev (2018) and (Mesgarani et al., 2020), respectively. Furthermore, a \(\theta \) finite-difference structure and an implicit scheme in Zhang et al. (2014) and (Song & Wang, 2013), respectively are used to price the option, In addition, in papers (Bhowmik, 2014; Chen et al., 2015; Zhang et al., 2016), other methods have been used to approximate this type of equation.

In this article, we try to act according to the following sections. We will obtain the time-discrete by using the quadratic interpolation and full scheme by the collocation method based on the third Chebyshev polynomials and investigate the convergence analysis in Sect. 2. Moreover, we will investigate the new approach by providing two numerical examples and will demonstrate the accuracy and efficiency of the method.

2 The discretization of time and space variable

In this section, we introduce and obtain the semi-discrete design as below. Considering \(u^{k}=u(x,t_{k}), {\mathfrak {p}}=\frac{\Gamma (2-\alpha )}{2}\sigma ^{2}, {\mathfrak {q}}=\Gamma (2-\alpha )(r-\frac{1}{2}\sigma ^{2}), {\mathfrak {r}}=r\Gamma (2-\alpha ), F^{k}=\Gamma (2-\alpha )f(x,t_{k})\) and \({\overline{\mathcal{S}}}_{k,j}=-{\mathcal {S}}_{k,j}\) and applying the linear design for approximating \( _{0}{D}_{t}^{\alpha }u(x,t) \) in the paper (Kumar et al., 2017), we obtain this scheme. For \( 0<\alpha \le 1 \), we get the step size \(\tau =\frac{T}{M}\) and nodes of time is \(t_{k}=k\tau ,~ k=0, 1, \ldots , M\). Then we get

$$\begin{aligned} ({\mathcal {S}}_{k,k}+{\mathfrak {r}}\tau ^{\alpha })u^{k}-{\mathfrak {p}}\tau ^{\alpha }\frac{\partial ^{2}u^{k}}{\partial x^{2}} -{\mathfrak {q}}\tau ^{\alpha }\frac{\partial u^{k}}{\partial x} =\sum _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}u^{j}+\tau ^{\alpha }F^{k}+\tau ^{\alpha }{\mathcal {R}}^{k}, \end{aligned}$$
(3)

where C is a nonnegative constant, \({\mathcal {R}}^{k}\le C{\mathcal {O}}({ \tau } ^{2-\alpha })\) and

$$\begin{aligned} {\mathcal {S}}_{k,j}= {\left\{ \begin{array}{ll} 1, &{} j=k, \\ (k-j-1)^{1-\beta }-2(k-j)^{1-\beta }+(k-j+1)^{1-\beta }, &{} 1\le j< k,\\ (k-1)^{1-\beta }-(k)^{1-\beta }, &{} j=0. \\ \end{array}\right. } \end{aligned}$$
(4)

The variational scheme can be got by omitted \({\mathcal {R}}^{k}\) in Eq. (3), as

$$\begin{aligned} {\left\{ \begin{array}{ll} ({\mathcal {S}}_{k,k}+{\mathfrak {r}}\tau ^{\alpha })U^{k}-{\mathfrak {p}}\tau ^{\alpha }\frac{\partial ^{2}U^{k}}{\partial x^{2}} -{\mathfrak {q}}\tau ^{\alpha }\frac{\partial U^{k}}{\partial x} =\sum \limits _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}U^{j}+\tau ^{\alpha }F^{k},\\ U^{0}(x)=\phi (x),~~~ 0<x<1,\\ U^{k}(0)=\eta _{0}(t_{k}),\quad U^{k}(1)=\eta _{1}(t_{k}),~~~ k=0,1,\ldots ,M, \end{array}\right. } \end{aligned}$$
(5)

where \( U^{k},~~k=0,1,\ldots ,M\) in Eq. (3) is the approximate solution.

In the present discussion, we need to consider the convergence analysis of the method. As we will see later in the final section, according to the numerical results shown, this method is unconditionally stable and the convergence order of the method is \({\mathcal {O}}({ \tau ^{2-\alpha }})\). Suppose \({\mathcal {H}}^{n}\) is the functional space that is defined as follows

$$\begin{aligned} {\mathcal {H}}^{n}_{\Omega }(\varphi )=\{\varphi \in L^{2}(\Omega ),~~ \frac{\partial ^{\alpha }\varphi }{\partial x^{\alpha }} \in L^{2}(\Omega ),~ \forall ~|\alpha |\le n \}, \end{aligned}$$

where the measurable function space in this relation is \( L^{2}(\Omega ) \) in \(\Omega \) that is square Lebesgue integrable. To prove the convergence and stability of the method, we need to convert Eq. (5) as follows. Let us assume that \( {\widehat{U}}^{j} \) is an approximate solution of Eq. (5). So by using the error function \(\varepsilon ^{k}={\widehat{U}}^{k}-U^{k}, ~k=0, 1, \ldots , M\), we get

$$\begin{aligned} (1+{\mathfrak {r}}\tau ^{\alpha })\left\langle \varepsilon ^{k},\varepsilon ^{k}\right\rangle -{\mathfrak {p}}\tau ^{\alpha }\left\langle \frac{\partial ^{2}\varepsilon ^{k}}{\partial x^{2}},\varepsilon ^{k}\right\rangle -{\mathfrak {q}}\tau ^{\alpha }\left \langle \frac{\partial \varepsilon ^{k}}{\partial x},\varepsilon ^{k}\right\rangle =\sum \limits _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\left\langle \varepsilon ^{j},\varepsilon ^{k}\right\rangle . \end{aligned}$$
(6)

Theorem 1

The generated design by Eq. (5) is unconditionally stable.

Proof

First of all, we know in Eq. (6) that \(\langle \frac{\partial \varepsilon ^{k}}{\partial x},\varepsilon ^{k}\rangle =0\) and also we have \(\langle \frac{\partial ^{2}\varepsilon ^{k}}{\partial x^{2}},\varepsilon ^{k}\rangle =-\langle \frac{\partial \varepsilon ^{k}}{\partial x},\frac{\partial \varepsilon ^{k}}{\partial x}\rangle \). As a result we get

$$\begin{aligned} (1+{\mathfrak {r}}\tau ^{\alpha })\langle \varepsilon ^{k},\varepsilon ^{k}\rangle \le \sum \limits _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\langle \varepsilon ^{j},\varepsilon ^{k}\rangle . \end{aligned}$$
(7)

Using the Cauchy–Schwarz inequality and \(1+{\mathfrak {r}}\tau ^{\alpha } \ge 1\), we get

$$\begin{aligned} \Vert \varepsilon ^{k}\Vert \le \sum \limits _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\Vert \varepsilon ^{j}\Vert . \end{aligned}$$

Now, we apply the principle of mathematical induction on k as the numerator of induction. If \(k=1\), we get

$$\begin{aligned} \Vert \varepsilon ^{1}\Vert \le {\overline{\mathcal {S}}}_{1,0}\Vert \varepsilon ^{0}\Vert . \end{aligned}$$

Regarding Lemma 5 of the paper (Safdari et al., 2020b), we can write \(-1< \mathcal {{S}}_{k,j}<0 \Longrightarrow 0<{\overline{\mathcal {S}}}_{k,j}<1,~~ j=0, 1,, 2, \ldots , k-1\). So it results

$$\begin{aligned} \Vert \varepsilon ^{1}\Vert \le \Vert \varepsilon ^{0}\Vert . \end{aligned}$$

Assume the mathematical induction is true for all \(k=1, 2, \ldots , M-1\). Now we prove it for \(k=M\). One obtains

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le \sum \limits _{j=0}^{M-1}{\overline{\mathcal {S}}}_{M,j}\Vert \varepsilon ^{j}\Vert \le {\overline{\mathcal {S}}}_{M,0}\Vert \varepsilon ^{0}\Vert + \sum \limits _{j=1}^{M-1}{\overline{\mathcal {S}}}_{M,j}\Vert \varepsilon ^{0}\Vert = ({\overline{\mathcal {S}}}_{M,0} + \sum \limits _{j=1}^{M-1}{\overline{\mathcal {S}}}_{M,j})\Vert \varepsilon ^{0}\Vert . \end{aligned}$$

Being used again with Lemma 5 of the paper (Safdari et al., 2020b) is \(-2<\mathcal {{S}}_{M,0} + \sum \limits _{j=1}^{M-1}\mathcal {{S}}_{M,j}<1\), we have

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le C\Vert \varepsilon ^{0}\Vert . \end{aligned}$$

This means that the method is stable. \(\square \)

Theorem 2

The order of convergence of the semi-discrete method (5) is \({\mathcal {O}}({ \tau ^{2-\alpha }})\).

Proof

From Eqs. (3) and (5), we define \( \xi ^k=u^k-U^k, ~~k=1, 2, \ldots , M\) and subtract Eq. (3) from Eq. (5) leading to

$$\begin{aligned} (1+{\mathfrak {r}}\tau ^{\alpha })\xi ^{k}-{\mathfrak {p}}\tau ^{\alpha }\frac{\partial ^{2}\xi ^{k}}{\partial x^{2}} -{\mathfrak {q}}\tau ^{\alpha }\frac{\partial \xi ^{k}}{\partial x} =\sum _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\xi ^{j}+\tau ^{\alpha }{\mathcal {R}}^{k}. \end{aligned}$$
(8)

Without loss of generality and using the method of proving the previous theorem, we get

$$\begin{aligned} (1+{\mathfrak {r}}\tau ^{\alpha }) \xi ^{k} \le \sum _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\xi ^{j}+\tau ^{\alpha }{\mathcal {R}}^{k}. \end{aligned}$$

It is quite evident that

$$ \begin{aligned}\Vert \xi ^{k} \Vert &\le \frac{1}{1+{\mathfrak {r}}\tau ^{\alpha }}\sum _{j=0}^{k-1}{\overline{\mathcal {S}}}_{k,j}\Vert \xi ^{j}\Vert +\frac{\tau ^{\alpha }}{1+{\mathfrak {r}}\tau ^{\alpha }} \Vert {\mathcal {R}}^{k} \Vert ,\\& \Longrightarrow \Vert \xi ^{k} \Vert \le \frac{\tau ^{\alpha }+1-1}{1+{\mathfrak {r}}\tau ^{\alpha }} \Vert {\mathcal {R}}^{k} \Vert \le \Vert {\mathcal {R}}^{k}\Vert \\ \end{aligned} $$

Because \( \frac{1}{1+{\mathfrak {r}}\tau ^{\alpha }} \le 1 \) and \(\Vert \xi ^{0}\Vert =0\). So we conclude that the convergence order is \({\mathcal {O}}({ \tau ^{2-\alpha }})\) in the case of smooth solutions in time direction. \(\square \)

Now, to get the discretization of space in Eq. (5), we use the shifted Chebyshev polynomials of the third kind (SCPTK) \({\mathcal {V}}_{i}(x), ~i=0,1,\ldots \) as

$$\begin{aligned} \begin{aligned} {\mathcal {V}}_{i}^{*}(x)&=\varvec{\Lambda }_{i}\sum _{k=0}^{i-1}\sum _{\xi =0}^{k}\Upsilon _{i, k, \xi }\times x^{k-\xi },\quad x\in [0, 1], \quad i=1, 2, \ldots , \\ \varvec{\Lambda }_{i}&=\frac{(2^{2i-2})\Gamma (i -0.5)}{i(2i-2)!},\quad \Upsilon _{i, k, \xi }=\frac{(-1)^{\xi } 2^{-k}i!\Gamma (i+k)}{k!(k-\xi )!\xi ! (i-k-1) \Gamma (k+0.5) }. \end{aligned} \end{aligned}$$

In space variable with domain [0, 1], we can apply the first \(N+1\)-terms of SCPTK as the following expansion of \( u(x,t_{j})\).

$$\begin{aligned} u(x,t_{j})=\sum _{i=0}^{N}\upsilon _{i}(t_{j}){\mathcal {V}}^{*}_{i}(x), \end{aligned}$$
(9)

where the unknown coefficients is \(\epsilon _{i}(_{j})\) that are defined as following.

$$\begin{aligned} \upsilon _{i}(t_{j})=\frac{2}{\pi }\int _{0}^{1}\sqrt{\frac{x}{1-x}}u(x,t_{j}){\mathcal {V}}^{*}_{i}(x)dx, ~~j=0,1,\ldots , M. \end{aligned}$$
(10)

Now, to approximate the space derivative of the first and second order, \(\frac{\partial ^{l}u^{M}}{\partial x^{l}}, l=1,2\), in Eq. (5), we use features of the basis SCPTK and Eq. (9) as

$$\begin{aligned} \frac{\partial ^{\xi }(u(x,t_{j}))}{\partial x^{\xi }}=\sum _{i=\xi }^{N}\sum _{k=0}^{i-\xi }\sum _{l =0}^{k}{\upsilon }_{i}(t_{j}) N_{i, k, l}^{\xi } x^{k-l},~~ \xi \in {\mathbb {N}}, \end{aligned}$$
(11)

where coefficients \(N_{i, k, l}^{\xi }\) is defined as

$$\begin{aligned} N_{i, k, l}^{\xi }=\frac{(-1)^{l }~2^{2i}~(i)!~\Gamma (i +0.5)~\Gamma (i+k+ \xi +1)~\Gamma (k-l +\xi +1)}{(2i)!~ (i-k- \xi )! ~(k+ \xi -l)! ~\Gamma (k+ \xi +1.5)~\Gamma (k-l +1)\Gamma (l+1)}\\. \end{aligned}$$

To get the linear system, we need to take the roots of SCPTK as collocation points i.e. \(\lbrace x_{s}\rbrace _{s=1}^{N+1-\xi }\) and substitute Eq. (11) in Eq. (5), we have

$$\begin{aligned}&({\mathcal {S}}_{j,j}+{\mathfrak {r}}\tau ^{\alpha })\sum _{i=0}^{N}\upsilon ^{j}_{i}{\mathcal {V}}^{*}_{i}(x_{s})-{\mathfrak {p}}\tau ^{\alpha } \sum _{i=2}^{N}\sum _{k=0}^{i-2}\sum _{l =0}^{k}\upsilon _{i}^{j}N_{i, k, l}^{2} x_{s}^{k-l } -{\mathfrak {q}}\tau ^{\alpha } \sum _{i=1}^{N}\sum _{k=0}^{i-1}\sum _{l =0}^{k}\upsilon _{i}^{j} N_{i, k, l}^{1} x_{s}^{k-l}\\ &\quad =\sum _{m=0}^{j-1}\sum _{i=0}^{N}{\overline{\mathcal {S}}}_{j,m}\upsilon _{i}^{m}{\mathcal {V}}^{*}_{i}(x_{s})+\tau ^{\alpha }F(x_{s},t_{j}),~~j=1, 2, \ldots , M,~~~~s=0, 1, \ldots , N, \end{aligned} $$
(12)

where the unknown coefficients in this system are \(\upsilon _{i}^{j}=\upsilon _{i}(t_{j})\) that must be obtained. To determine the uncharted coefficients \(\upsilon _{i}^{i}, i=0, 1, 2, \ldots \), we need two extra conditions such as the boundary conditions to turn the above relation into a linear system with \(N+1\) equations and \(N+1\) unknowns. Heed that by replacing Eq. (9) in Eq. (2), we get the boundary conditions as

$$\begin{aligned} \sum _{i=0}^{N}(-1)^{i}\upsilon _{i}^{j}=\eta _{0}(t_{j}),~~ \sum _{i=0}^{N}(2i+1)\upsilon _{i}^{j}=\eta _{1}(t_{j}),~~j=1, 2, \ldots , M. \end{aligned}$$
(13)

Moreover, we obtain the initial condition \(\upsilon _{i}^{0} \) with combining \(u(x, 0)=\phi (x)\) and Eq. (10).

3 Numerical Results

The current form of value barrier choice driven by a time-fractional BSM structure, which is one the most interesting ideas in the financial sector, has now been applied inside this part. Furthermore, using the numerical technique of TFBSM, the efficiency of the system of the proposed methodology is demonstrated. We denote the order as \( {\mathcal {C}}_{{\mathcal {O}}} \) that is calculated as follows.

$$\begin{aligned} {\mathcal {C}}_{{\mathcal {O}}}=\log _{2}\left(\frac{E_{i+1}}{E_{i}}\right), \end{aligned}$$

in which \(E_{i+1}\) and \(E_{i}\) are errors In accordance with mesh sizes 2M and M. The theoretical study is supported by the estimated findings.

Example 3.1

Consider the following problem with the homogeneous boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} {}_{0}D_{t} ^{\alpha } u(x,t)=p \frac{\partial ^{2}u(x,t)}{\partial x^{2}} +q \frac{\partial u(x,t)}{\partial x}-ru(x,t)+f(x,t),\\ u(x,0)=x^{2}(1-x),~~~ 0<x<1,\\ u(0,t)=u(1,t)=0, \end{array}\right. } \end{aligned}$$

that \(u(x, t)=(t+1)^{2}x^{2}(1-x)\) is the exact solution and the known parameters are \(\sigma =0.25, p=\frac{1}{2}{\sigma }^{2}, q=r-p, r=0.05, \alpha =0.7\) and

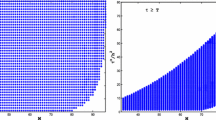
$$\begin{aligned} f(x,t)&= (\frac{2t^{2-\alpha }}{\Gamma (3-\alpha )}+\frac{2t^{1-\alpha }}{\Gamma (2-\alpha )})x^{2}(1-x)-(t+1)^{2}[p(2-6x)\\&\quad +q(2x-3x^{2})-rx^{2}(1-x)]. \end{aligned}$$

We demonstrate the error and order of this example in Table 1 at \(T=1\) with \(N=7\) that is seen the convergence order is \({\mathcal {O}}(\tau ^{2-\alpha })\) and it’s also related to the TOC (temporal order of convergence). Furthermore, as the number M increases, the error diminishes. one can deduce from the thorough findings in Table 2 that the results are remarkably similar to those of De Staelen and Hendy (2017) and Golbabai et al. (2019). Furthermore, reasonably precise findings are provided with a very small space size. When \(T=1\), we draw the absolute error and approximate solution in Fig. 1 and can deduce from this figure that the numerical method has a close accuracy.

Table 1 The error and order for Example 3.1 with \(N =7\) at \(T=1\)
Full size table
Table 2 The error and convergence order for Example 3.1 at \(T=1\)
Full size table
Fig. 1
figure 1

The error (left-side) and approximate solution (right-side)) for Example 3.1 at \(T=1\)

Full size image

Example 3.2

Take the TFBSM with nonhomogeneous boundary conditions as a second instance as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} {}_{0}D_{t} ^{\alpha } u(x,t)=p \frac{\partial ^{2}u(x,t)}{\partial x^{2}} +q \frac{\partial u(x,t)}{\partial x}-ru(x,t)+f(x,t),\\ u(x,0)=x^{3}+x^{2}+1,~~~ 0<x<1,\\ u(0,t)=(t+1)^{2},~~~ u(1,t)=3(t+1)^{2}, \end{array}\right. } \end{aligned}$$

where \(u(x, t)=(t+1)^{2}(x^{3}+x^{2}+1)\) is the exact solution and f(x, t) is got by using this solution. Moreover, the known values are \( p=1, q=r-p, r=0.5\) and \(\alpha =0.7\)

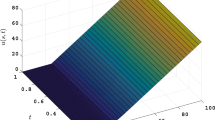
This question’s conclusions have also been reported in Tables 3, 4 and Fig. 2. Table 3 includes the new approach with compact finite difference manner (De Staelen & Hendy, 2017) and radial basis functions based on finite-difference construction (Golbabai et al., 2019) to produce successful results for the methodology. Furthermore, the order is demonstrated in Table 4 with \(N=5\) at \(T=1\) that this is supported the theoretical predictions. The numerical finding and absolute error that as seen as the approximation solution is approaching the exact solution are displayed in Fig. 2.

Table 3 The error and convergence order for Example 3.2 at \(T=1\)
Full size table
Table 4 The order, \( L_{2} \) and \(L_{\infty }\) for Example 3.2 with \(N=5\) at \(T=1\)
Full size table
Fig. 2
figure 2

The absolute error (left-side) and approximate solution (right-side) for Example 3.2 at \(T=1\) and \(N=5\)

Full size image

4 Conclusion

Rather than the construction of the integer-order derivative, the model’s fractional-order derivative’s “worldview" contributes to extremely exact and numerical approaches. For this reason, we considered the time-fractional Black-Scholes equation in this paper and presented a numerical scheme to solve that. Because for \(0 < \alpha \le 1\) the fractional derivative of Caputo and Riemann-Liouville coincide, then It is already replaced in the TFBSM. To discretize in a time sense, the authors used a linear interpolation with the accuracy order of \({\mathcal {O}}({\tau }^{2-\alpha })\). Then by using the Chebyshev collocation manner based on the third kind, we explained how to obtain a fully discrete numerical method. Moreover, the unconditional stability and the order of the temporal discrete are also stated. Two numerical examples with exact solutions are chosen to prove the resolution and convergence order of the numerical model, and the numerical result has shown the reliability of the new plan.