1 Introduction

A barrier option is referred to a particular path-dependent option whose payoff is dependent on whether the underlying price reaches a predetermined level (the barrier specified in the contract), and it can be further classified into knock-out and knock-in options, corresponding to the case where the right to exercise the option ceases and starts to exist when the barrier is touched, respectively. Barrier options are actively traded in financial markets, since they can help investors as well as companies to hedge risks while at the same time being cheaper than the corresponding vanilla ones, and thus it is very demanding for the accurate and efficient pricing of these contracts.

The history of option pricing can be dated back to 1900, when Bachelier (1900) valued stock options after assuming that the stock price process follows a Brownian motion. However, this simple assumption is obviously not appropriate since it can lead to negative stock and option prices (Merton 1973). A breakthrough was made in 1973 by Black and Scholes (1973), who assumed that the underlying price follows a geometric Brownian option and presented a closed-form pricing formula for European options. Although the Black-Scholes (B-S) model enjoys great popularity due to its simplicity and tractability, the simplified assumptions, such as the constant volatility, made in the B-S model are not appropriate and can lead to large pricing biases. Therefore, a number of modified models have been proposed, including jump-diffusion models (Merton 1976; Kou 2002), L\(\acute{e}\)vy models (Carr et al. 2002; Lin and He 2020; He and Lin 2021), and fractional B-S models (Golbabai et al. 2019; Golbabai and Nikan 2020). Among all these modifications, stochastic volatility models (Heston 1993; He and Chen 2021a, b; Lin and He 2021a, b), making the volatility another random variable, have received a lot of attention.

Unfortunately, with the addition of another stochastic source, it is impossible to preserve the analytical tractability even for European options under most of stochastic volatility models, and no closed-form pricing formula has ever been derived for barrier options under stochastic volatility models. As a result, numerical methods must be resorted to when pricing barrier options under these models. Monte Carlo simulation, as one of the most fundamental numerical approaches, is one of the possible candidates. However, this classical approach is very time consuming to obtain an accurate result for pricing continuously monitored barrier options since the barrier may be hit between the discrete computational nodes and a much smaller time step is required to reach a reasonable degree of accuracy, compared with the pricing of European options. This implies that there is a trade-off between the computational time and errors. To overcome this drawback, various simulation techniques have been introduced, including the adaptive Monte Carlo method (Dzougoutov et al. 2005), Brownian bridge method (Metwally and Atiya 2002), and the symmetrization methods (Carr and Lee 2009; Akahori and Imamura 2014). On the other hand, an alternative numerical approach to Monte Carlo simulation is the finite difference method, which also shows slow convergence when pricing barrier options under stochastic volatility models. To increase the computational efficiency for pricing barrier options under stochastic volatility models, a fourth-order smoothing scheme with improved convergence was proposed in Yousuf (2009), while Chiarella et al. (2012) developed a method of lines approach.

Although much progress has been made in numerically computing barrier option prices, these approaches are still computationally expensive, making them difficult to be implemented in practice. In contrast to numerical approaches, analytical approximation is another most common tool in derivative pricing, when closed-form solutions are not available, and this kind of approaches, if appropriately applied, can spare a lot of computational effort without losing too much accuracy. It has been applied to pricing various option contracts, such European options (Zhu and He 2016; He and Zhu 2016), barrier options (Lo et al. 2003; Funahashi and Higuchi 2018) and American options (Ju and Zhong 1999; Evans et al. 2002).

In this paper, we consider the pricing of continuously monitored barrier options under the Heston model (Heston 1993), a well-known stochastic volatility model that is widely adopted in today’s financial practice. Unlike the B-S model, where an analytical pricing formula for barrier options exists (Rubinstein and Reiner 1991), it is extremely difficult to analytically price barrier options under the Heston model, as there are two stochastic sources. To cope with this difficulty, we develop a two-step solution procedure; under the assumption that the future information of the volatility is given at the current time, we derive an analytical approximation formula for barrier options using a similar technique adopted in Lo et al. (2003), based on which the target barrier option price under the Heston model is obtained by making use of the COS method (Fang and Oosterlee 2008) as well as the density of the volatility. The efficiency and accuracy of the approximation is demonstrated through numerical experiments.

The main contribution of this paper can be summarized from two aspects. On one hand, the two-step solution process we developed splits the difficult task of pricing barrier options under the Heston stochastic volatility model into two small tasks which are relatively easier to solve. This approach is possible to be extended to deal with other complex financial derivative pricing problems. On the other hand, we present an analytical approximation formula of high efficiency and accuracy for barrier option prices under the Heston model, showing its great potential in practical applications.

The rest of the paper is organized as follows. In Sect. 2, the details on how to derive an analytical approximation formula for barrier option prices under the Heston model are illustrated. In Sect. 3, numerical examples and discussions are presented, followed by some concluding remarks in the last section.

2 Analytical Approximation of a Barrier Option

In this section, the pricing of a down and out call optionFootnote 1 is considered under the Heston model, and a two-step solution procedure is developed; upon assuming that all the information of the volatility process up to the expiry of the option contract is known at the current time, we price barrier options under the resulted time-dependent B-S model, after which the barrier option price under the Heston model is formulated using the Fourier cosine series and the density of the volatility.

2.1 A Conditional Option Price

If the underlying asset price and the volatility are denoted by \(S_t\) and \(v_t\), respectively, they are assumed to follow the Heston model under a risk neutral measure, i.e.,

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle d\ln S_t= \left(r-\frac{1}{2}v_t\right)dt+\sqrt{v_t}dC_t,&{} &{}\\ \displaystyle dv_t=k(\theta -v_t)dt+\sigma \sqrt{v_t}dB_t,&{} &{}\\ \end{array} \right. \end{aligned}$$
(2.1)

where k and \(\theta \) are the mean reversion speed and level of the volatility, respectively. \(\sigma \) is the so-called volatility of volatility, r is the risk free interest rate, \(C_t\) and \(B_t\) are two standard Brownian motions with correlation \(\rho \).

As a prior step in deriving the analytical solution, we assume that all the future information of the volatility is given, or equivalently, all the stochastic sources contained in the volatility process is deterministic. To realize this, we rewrite the dynamics in (2.1) as

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle d\ln S_t=(r-\frac{1}{2}v_t)dt+\sqrt{v_t}(\rho dB_t+\sqrt{1-\rho ^2} dW_t),&{} &{}\\ \displaystyle dv_t=k(\theta -v_t)dt+\sigma \sqrt{v_t}dB_t,&{} &{}\\ \end{array} \right. \end{aligned}$$
(2.2)

with \(W_t\) as another standard Brownian motion being independent with \(B_t\). In this case, \(B_t\) is not stochastic under our assumption, but a time-dependent value, and it can be expressed as

$$\begin{aligned} \displaystyle dB_t=\frac{dv_t-k(\theta -v_t)dt}{\sigma \sqrt{v_t}}, \end{aligned}$$

the substitution of which into (2.2) yields

$$\begin{aligned} \displaystyle d\ln S_t= \left[r-\frac{1}{2}v_t-\frac{\rho k}{\sigma }(\theta -v_t)+\frac{\rho }{\sigma }\frac{dv_t}{dt}\right]dt+\sqrt{1-\rho ^2}\sqrt{v_t}dW_t. \end{aligned}$$
(2.3)

Clearly, with the assumption that the volatility values are known in advance, the underlying price in (2.3) follows a time-dependent B-S model. If \(V(y,t|\mathscr {F}_T^B)\) represents the corresponding conditional down and out call option price, where \(y_t\) is defined as \(\displaystyle y_t=\ln S_t-\ln D\) with D as the barrier and \(\mathscr {F}_T^B\) is filtration of the Brownian motion \(B_t\) up to the expiry \(t=T\), it should follow the following PDE (partial differential equation) system according to the risk neutral pricing rule

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \frac{\partial V}{\partial t}+\frac{1}{2}(1-\rho ^2)v_t\frac{\partial ^2 V}{\partial y^2}+[r-\frac{1}{2}v_t-\frac{\rho k}{\sigma }(\theta -v_t)+ \frac{\rho }{\sigma }\frac{dv_t}{dt}]\frac{\partial V}{\partial y}-rV=0,~y>0,&{} &{} \\ V(y,T|\mathscr {F}_T^B)=\max (De^y-K,0), &{} &{} \\ V(0,t|\mathscr {F}_T^B)=0. &{} &{} \\ \end{array} \right. \end{aligned}$$

To facilitate the computation in the following, we introduce the transform of \(\tau =T-t\) and \(\displaystyle V(y,t|\mathscr {F}_T^B)=DU(y,\tau |\mathscr {F}_T^B)\) such that the above system becomes

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \frac{\partial U}{\partial \tau }=\frac{1}{2}(1-\rho ^2)v_t\frac{\partial ^2 U}{\partial y^2}+[r-\frac{1}{2}v_t-\frac{\rho k}{\sigma }(\theta -v_t)+\frac{\rho }{\sigma } \frac{dv_t}{dt}]\frac{\partial U}{\partial y}-rU,~y>0,&{} &{} \\ U(y,0|\mathscr {F}_T^B)=\max (e^y-\frac{K}{D},0), &{} &{} \\ U(0,\tau |\mathscr {F}_T^B)=0. &{} &{} \\ \end{array} \right. \end{aligned}$$
(2.4)

As System (2.4) is a heat equation with time-dependent parameters, it is natural for us to transform it into a standard heat equation. Following Lo et al. (2003), we define

$$\begin{aligned} \displaystyle&\displaystyle c_1(\tau )=\int _t^T r-\frac{1}{2}v_s-\frac{\rho k}{\sigma }(\theta -v_s) +\frac{\rho }{\sigma }\frac{dv_s}{ds}ds=\\&\quad (r-\frac{\rho k\theta }{\sigma })\tau + (\frac{\rho k}{\sigma }-\frac{1}{2})h_T+\frac{\rho }{\sigma }(v_T-v_t),\\&\displaystyle c_2(\tau )=\frac{1}{2}(1-\rho ^2)h_T, \end{aligned}$$

with

$$\begin{aligned} \displaystyle h_T=\int _t^Tv_sds, \end{aligned}$$
(2.5)

so that we make the transformation of \(\displaystyle z=y-y^*(\tau )\), where \(y^*(\tau )=-c_1(\tau )-\beta c_2(\tau )\) with \(\beta \) being an adjusted parameter to be determined later. By denoting

$$\begin{aligned} \displaystyle {\tilde{U}}(z,\tau |\mathscr {F}_T^B)=e^{r\tau }U(y,\tau |\mathscr {F}_T^B), \end{aligned}$$

the PDE system (2.4) can be converted into

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \frac{\partial {\tilde{U}}}{\partial \tau }=\frac{1}{2}(1-\rho ^2)v_t \frac{\partial ^2{\tilde{U}}}{\partial z^2}-\frac{1}{2}(1-\rho ^2)\beta v_t\frac{\partial {\tilde{U}}}{\partial z},~z>-y^*(\tau ),&{} &{} \\ {\tilde{U}}(z,0|\mathscr {F}_T^B)=\max (e^z-\frac{K}{D},0), &{} &{} \\ {\tilde{U}}(-y^*(\tau ),\tau |\mathscr {F}_T^B)=0. &{} &{} \\ \end{array} \right. \end{aligned}$$
(2.6)

The time-dependent parameters contained in the PDE of (2.6) can be eliminated if we assume \(\xi =c_2(\tau )\), and in this case (2.6) can be reformulated as

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \frac{\partial \bar{U}}{\partial \xi }=\frac{\partial ^2\bar{U}}{\partial z^2}, ~z>-y^*(\tau ), &{} &{} \\ {\tilde{U}}(z,0|\mathscr {F}_T^B)=e^{-\frac{\beta }{2}z}\max (e^z-\frac{K}{D},0), &{} &{} \\ \bar{U}(-y^*(\tau ),\xi |\mathscr {F}_T^B)=0, &{} &{} \\ \end{array} \right. \end{aligned}$$
(2.7)

with the transformation of

$$\begin{aligned} \displaystyle \bar{U}(z,\xi |\mathscr {F}_T^B)=e^{-\frac{\beta }{2}z+\frac{\beta ^2}{4}\xi } {\tilde{U}}(z,\tau |\mathscr {F}_T^B). \end{aligned}$$

Although it seems straightforward now as the PDE in (2.7) is a standard heat equation, the problem of finding \(\bar{U}(z,\xi |\mathscr {F}_T^B)\) is still not an easy task, because we now have a time-dependent barrier. To overcome this difficulty, we aim to find an appropriate \(\beta \) such that \(y^*(s)\) is always a good approximation for 0 when \(s\in [0,\tau ]\), in which case the time-dependent barrier is approximately 0. What we choose here is

$$\begin{aligned} \displaystyle \beta =-\frac{c_1(\tau )}{c_2(\tau )}, \end{aligned}$$
(2.8)

so that \(y^*(\tau )=0\). This is different from the one used in Lo et al. (2003), and it paves the way to derive the analytical formula for the down and out call option price to be presented later. By doing so, the solution to (2.7) can be approximated by the solution to the following system

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \frac{\partial \bar{U}}{\partial \xi }=\frac{\partial ^2\bar{U}}{\partial z^2},~z>0, &{} &{} \\ {\tilde{U}}(z,0|\mathscr {F}_T^B)=e^{-\frac{\beta }{2}z}\max (e^z-\frac{K}{D},0), &{} &{} \\ \bar{U}(0,\xi |\mathscr {F}_T^B)=0. &{} &{} \\ \end{array} \right. \end{aligned}$$

By utilizing the method of images and the fundamental solution, the approximation solution can be expressed as

$$\begin{aligned} \displaystyle \bar{U}(z,\xi |\mathscr {F}_T^B)=\int _0^{+\infty }\frac{1}{\sqrt{4\pi \xi }}e^ {-\frac{(z-x)^2}{4\xi }}e^{-\frac{\beta }{2}x}\max (e^x-\frac{K}{D},0)dx- \int _{-\infty }^0\frac{1}{\sqrt{4\pi \xi }}e^{-\frac{(z-x)^2}{4\xi }}e^ {\frac{\beta }{2}x}\max (e^{-x}-\frac{K}{D},0)dx, \end{aligned}$$

which can be further simplified to

$$\begin{aligned} \displaystyle&\bar{U}(z,\xi |\mathscr {F}_T^B)=e^{\frac{1}{4}(2-\beta )^2\xi +\frac{1}{2} (2-\beta )z}N \left(\frac{z+(2-\beta )\xi -\ln (\frac{K}{D})}{\sqrt{2\xi }}\right)\\&\quad -\frac{K}{D}e^ {\frac{1}{4}\beta ^2\xi -\frac{1}{2}\beta z}N \left(\frac{z-\beta \xi -\ln (\frac{K}{D})}{\sqrt{2\xi }}\right) \\- & {} e^{\frac{1}{4}(2-\beta )^2\xi -\frac{1}{2}(2-\beta )z}N \left(\frac{-z+(2-\beta )\xi - \ln (\frac{K}{D})}{\sqrt{2\xi }}\right)\nonumber \\&\quad +\frac{K}{D}e^{\frac{1}{4}\beta ^2\xi +\frac{1}{2}\beta z}N \left(\frac{-z-\beta \xi -\ln (\frac{K}{D})}{\sqrt{2\xi }}\right), \end{aligned}$$

with \(N(\cdot )\) representing the standard normal distribution function, after some algebraic calculations. Expressing in original variables, the conditional barrier option price can finally be formulated as

$$\begin{aligned} \displaystyle&V(y,t|\mathscr {F}_T^B)=De^{-r\tau +y+c_1(\tau )+c_2(\tau )}N(d_1)- Ke^{-r\tau }N(d_2)\nonumber \\- & {} De^{-r\tau +(\beta -1)[y+c_1(\tau )]+(\beta -1)^2c_2(\tau )}N(d_3)+Ke^ {-r\tau +\beta [y+c_1(\tau )]+\beta ^2c_2(\tau )}N(d_4),~~~~~~~ \end{aligned}$$
(2.9)

where

$$\begin{aligned} \displaystyle d_1= & {} \frac{y+c_1(\tau )+2c_2(\tau )-\ln (\frac{K}{D})}{\sqrt{2c_2(\tau )}},~d_2=\frac{y+c_1(\tau )-\ln (\frac{K}{D})}{\sqrt{2c_2(\tau )}},\\ d_3= & {} \frac{\ln (\frac{D}{K})-[y+c_1(\tau )+2(\beta -1)c_2(\tau )]}{\sqrt{2c_2(\tau )}},~d_4=\frac{\ln (\frac{D}{K})-[y+c_1(\tau )+2\beta c_2(\tau )]}{\sqrt{2c_2(\tau )}}. \end{aligned}$$

The formula presented in (2.9) has a similar expression as the down and out call option price under the B-S model. However, our task of pricing the down and out call option under the Heston model has not been completed, as the one we have derived is under the assumption that the values of the volatility before expiry are given at the current time, whereas we are certainly unable to predict the future information of the volatility. In the next subsection, the details on how to remove this particular assumption while still preserve the analytical tractability will be presented.

2.2 The Fourier Cosine Series Solution

This subsection is devoted to deriving the down and out call option price when both of the underlying price and the volatility are stochastic, based on the results presented in the previous subsection. In fact, the target option price, V(y, v, t), is an expectation of the condition price presented in (2.9), i.e.,

$$\begin{aligned} \displaystyle V(y,v,t)=E[V(y,t|\mathscr {F}_T^B)|\mathscr {F}_t^B], \end{aligned}$$

which seems to be an impossible task to analytically work it out, especially given the convoluted expression of \(V(y,t|\mathscr {F}_T^B)\). However, it should be noted that \(h_T\) defined in (2.5) and \(v_T\) are the only two random variables contained in the formula of \(V(y,t|\mathscr {F}_T^B)\), when the volatility is no longer deterministic. Having realized this, if we denote

$$\begin{aligned} \displaystyle M(h_T,v_T)=V(y,t|\mathscr {F}_T^B), \end{aligned}$$

the option price can be alternatively expressed as

$$\begin{aligned} \displaystyle V(y,v,t)=E[M(h_T,v_T)|v_t], \end{aligned}$$

solving which yields the desired solution. This is however not straightforward at all, as \(h_T\) and \(v_T\) are dependent on each other. To overcome this difficulty, instead of directly working on the expectation, we apply the tower rule of the expectation so that

$$\begin{aligned} \displaystyle V(y,v,t)=E\{E[M(h_T,v_T)|v_t,v_T]|v_t\}. \end{aligned}$$

This implies that the first step is to compute the inner expectation, with the terminal value of the volatility, \(v_T\), being regarded as known in advance.

If we define

$$\begin{aligned} \displaystyle V(y,v,t|v_T)=E[M(h_T,v_T)|v_t,v_T], \end{aligned}$$

the involved expectation only contains one random variable, \(h_T\), and it can certainly be represented by

$$\begin{aligned} \displaystyle V(y,v,t|v_T)=\int _0^{+\infty }M(h_T,v_T)f(h_T|v_t,v_T)dh_T, \end{aligned}$$
(2.10)

with \(f(h_T|v_t,v_T)\) being the corresponding conditional density. Of course, further steps need to be taken to derive this conditional price, as \(f(h_T|v_t,v_T)\) is not available in closed-form. We now truncate the domain of \([0,+\infty )\) into [a,b] such that the semi-infinite integral in (2.10) can be approximated by

$$\begin{aligned} \displaystyle V(y,v,t|v_T)\approx \int _a^{b}M(h_T,v_T)f(h_T|v_t,v_T)dh_T, \end{aligned}$$
(2.11)

with which we are able to seek for a solution in the form of a Fourier cosine series, using the COS method (Fang and Oosterlee 2008). In particular, the density function is firstly expanded into a Fourier cosine series as

$$\begin{aligned} \displaystyle f(h_T|v_t,v_T)=\frac{1}{2}A_0(v_t,v_T)+\sum _{k=1}^{+\infty }A_k(v_t,v_T) \cos (k\pi \frac{h_T-a}{b-a}), \end{aligned}$$
(2.12)

where the coefficients, \(A_k(v_t,v_T),k=0,1,2...\), have the expression of

$$\begin{aligned} \displaystyle A_k(v_t,v_T)=\frac{2}{b-a}\int _a^bf(h_T|v_t,v_T)\cos (k\pi \frac{h_T-a}{b-a}) dh_T,~k=0,1,2... \end{aligned}$$
(2.13)

Substituting (2.12) into (2.11) yields

$$\begin{aligned} \displaystyle V(y,v,t|v_T)=\int _a^bM(h_T,v_T)[\frac{1}{2}A_0(v_t,v_T)+\sum _{k=1}^{+\infty }A_k(v_t,v_T)\cos (k\pi \frac{h_T-a}{b-a})]dh_T.\end{aligned}$$

Interchanging the summation and the integration further leads to

$$\begin{aligned} \displaystyle V(y,v,t|v_T)=\frac{1}{2}A_0(v_t,v_T)V_0+\sum _{k=1}^{+\infty }A_k(v_t,v_T)V_k, \end{aligned}$$
(2.14)

where

$$\begin{aligned} \displaystyle V_k=\int _a^bM(h_T,v_T)\cos (k\pi \frac{h_T-a}{b-a})dh_T,~k=0,1,2,... \end{aligned}$$

Clearly, the only unknown terms involved in (2.14) are the coefficients of the Fourier cosine series, \(A_k(v_t,v_T),k=0,1,2...\), and the formula (2.14) will become analytical once they have been derived. However, the integral presented in the definition of \(A_k(v_t,v_T),k=0,1,2...\), (2.13), still requires the information of the density \(f(h_T|v_t,v_T)\), which poses an obstacle for its analytical derivation. Fortunately, making use of the relationship between the characteristic function and the density function can result in

$$\begin{aligned} \displaystyle A_k(v_t,v_T)=\frac{2}{b-a}\text {Real}[g(\frac{k\pi }{b-a}|v_t,v_T)e^{-j \frac{ka\pi }{b-a}}],~k=0,1,2,..., \end{aligned}$$

where \(g(\phi |v_t,v_T)\) is the characteristic function of \(h_T\), with a closed-form expression (Broadie and Kaya 2006) as

$$\begin{aligned} \displaystyle g(\phi |v_t,v_T)= & {} E[e^{j\phi h_T}|v_t,v_T]\\= & {} \displaystyle \frac{I_q\{\sqrt{v_tv_T}\frac{4\xi (\phi )e^{-\frac{1}{2}\xi (\phi )(T-t)}}{\sigma ^2[1-e^{-\xi (\phi )(T-t)}]}\}}{I_q\{\sqrt{v_tv_T} \frac{4ke^{-\frac{1}{2}k(T-t)}}{\sigma ^2[1-e^{-k(T-t)}]}\}}\times \frac{\xi (\phi )e^{-\frac{1}{2}[\xi (\phi )-k](T-t)}[1-e^{-k(T-t)}]}{k[1-e^{-\xi (\phi )(T-t)}]} \\\times & {} \displaystyle e^{\frac{v_T+v_t}{\sigma ^2}\{\frac{k[1+e^{-k(T-t)}]}{1-e^{-k(T-t)}}- \frac{\xi (\phi )[1+e^{-\xi (\phi )(T-t)}]}{1-e^{-\xi (\phi )(T-t)}}\}}. \end{aligned}$$

Here, \(\displaystyle q=\frac{2k\theta }{\sigma ^2}\), \(\xi (\phi )=\sqrt{k^2-2j\sigma ^2\phi }\), and \(I_q(\cdot )\) is the modified Bessel function of the first kind with order q.

Till now, the down and out call option price conditional up the information of \(v_T\) formulated in (2.14) is completely analytical, and thus the remaining task is to take the expectation of \(V(y,v,t|v_T)\) with respect to \(v_T\), i.e.,

$$\begin{aligned} \displaystyle V(y,v,t)=E[V(y,v,t|v_T)|v_t]. \end{aligned}$$

As the density function of \(v_T\) have an analytical expression as

$$\begin{aligned} \displaystyle p(v_T|v_t)=\eta e^{-\eta [v_te^{-k(T-t)}+v_T]}[\frac{v_T}{v_te^{-k(T-t)}}] ^{\frac{q}{2}}I_q[2\eta e^{-\frac{1}{2}k(T-t)}\sqrt{v_tv_T}], \end{aligned}$$

with \(\displaystyle \eta =\frac{2k}{\sigma ^2[1-e^{-k(T-t)}]}\), we can finally arrive at

$$\begin{aligned}&\displaystyle V(y,v,t)=\int _0^{+\infty }V(y,v,t|v_T)p(v_T|v_t)dv_T=\int _0^{+\infty } [\frac{1}{2}A_0(v_t,v_T)V_0\nonumber \\&\quad +\sum _{k=1}^{+\infty }A_k(v_t,v_T)V_k]p(v_T|v_t)dv_T. \end{aligned}$$
(2.15)

We have now successfully presented an analytical approximation of the down and out call option price under the Heston model in (2.15). However, once an approximation is made, it is necessary to check its accuracy to ensure its safe applications in practice. This will be discussed in the following section.

3 Numerical Examples and Discussions

In this section, the speed of convergence and the accuracy of the formula will be investigated through numerical examples. Unless otherwise stated in the following, the mean reversion speed k, the mean reversion level \(\theta \) and the volatility of volatility \(\sigma \) are assumed to take the values of 2, 0.02 and 0.1, respectively. Both of the current underlying price \(S_t\) and the strike K are 100, while the barrier level D is equal to 90. Other parameters include \(r=0.1, \rho =-0.5, v=0.01, \tau =1\). It should be noted that the truncated domain [a, b] used in the Fourier cosine series expansion should also be determined such that (2.11) is a good approximation to (2.10). In this case, the value of a should be close to 0 and it is thus allocated as 1e-4. The value of b should be large enough such that the integrand in (2.10) is approximately 0, according to which it is chosen as \(3E(v_T|v_t)T\).

Table 1 The speed of convergence
Full size table

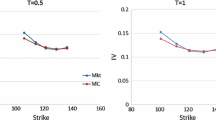
As our formula involves a series solution, its speed of convergence is an important factor that needs to be considered in practice, especially given the recent trend of algorithmic trading. As a result, Table 1 exhibits the option prices calculated with different number of terms used in the series solution. One can clearly observe that our formula actually converges very rapidly, with 15-term price already being very close to the converged one, as the maximum absolute difference (AD) between 14-term and 15-term prices is less than 0.002. The fast speed of convergence is further demonstrated by 49-term and 50-term prices, with the maximum AD between the two prices being in the order of 1e-9, and this implies that it suffices to use 50 terms in the series solution to produce the option prices. On the other hand, to figure out the accuracy of our approximation, we use the results obtained from the Monte Carlo (MC) simulation with 1,000,000 sample paths and 10,000 time steps accompanied by a 98% confidence interval as a benchmark. Obviously, our approximation using 50 terms is almost the same as the MC price when the time to expiry is very small, with the relative error (RE) between the two prices being only 0.01%. Of course, one can observe that the RE increases when the time to expiry is enlarged. However, such an increase is not very significant, and the RE is just around 2%, when the time to expiry reaches 1, which is also a clear evidence of the accuracy.

Table 2 The accuracy across different strikes and correlation
Full size table

To further show the reliableness of our approximation, we compare our approximation with the corresponding MC results for a wide range of strikes and correlations in Table 2. Overall, our formula approximates the down and out call option prices quite well, with the maximum RE between our price and MC price being less than 2.5%. In particular, an interesting phenomenon that can be observed is that our approximation becomes more accurate when the correlation between the underlying price and volatility increases, and the corresponding RE is even less than 0.25% when the correlation is equal to 0.5, no matter the option is in the money, at the money or out of money. It should also be pointed out that for different correlations, our approximation always tends to work better for out of money options than in the money ones.

4 Conclusion

In this paper, the solution procedure for deriving an analytical approximation formula for pricing barrier options under the Heston model is presented. Instead of directly working on this complicated problem, we divide the process into two steps; an approximation for the option price is obtained conditional upon all the future information of the volatility in the first step, taking expectation of which in the second step yields the desired formula, which involves a Fourier cosines series. Through numerical experiments, the newly derived formula is demonstrated to converge very rapidly and be able to produce accurate results, implying its potential for practical applications.