Forecasting Inflation Uncertainty in the United States and Euro Area

Abstract

This study forecasts a particular type of economic uncertainty (inflation uncertainty) in the United States and Euro Area over 1997–2017. By using monthly data, we compute inflation uncertainty based on three models: symmetric and asymmetric generalized autoregressive conditional heteroscedasticity models and a stochastic volatility model. While the first two provide symmetric and asymmetric measures of inflation uncertainty, respectively, the third measure offers greater flexibility when measuring uncertainty. The analysis of the out-of-sample forecasts for inflation uncertainty shows the superiority of the stochastic volatility model for forecasting the dynamics of inflation uncertainty in both the short (1 year) and medium (4 years) terms. This finding is particularly interesting, as it allows researchers to better estimate the main inflation cost, namely inflation uncertainty, as well as its effect on the real economy.

1 Introduction

Uncertainty is a situation of doubt, unpredictabilityand riskiness, which varies with regard to the market state and exogenous shocks. For example, geopolitical uncertainty becomes more volatile with the level of geopolitical tensions (e.g. in Eastern Europe and after the Arab Spring), terrorist threats, and war. In economics, uncertainty is a particularly important issue as it significantly affects different macroeconomic variables (Bloom et al. 2007; Bachmann et al. 2013; Jurado et al. 2015; Rossi and Sekhposyan 2015). Indeed, economic uncertainty constitutes a type of economic post-traumatic stress disorder for householders, investors, and the entire market. Economic uncertainty is also a source of financial instability and economic inequality. It affects consumers, investors, and householders, pushing them to question the underlying mechanisms of economic growth, unemployment, economic policy, and inflation.¹

Interestingly, economic uncertainty has recently increased because of the fragility of the financial system, increase in public and private debt, decrease in economic growth, and the renewal of secular stagnation combined with a global liquidity trap since the aftermath of the global financial crisis (2008–2009). In particular, economic policy uncertainty has been remarkable given the absence of a clear policy and institutional structure. In such a context, further doubt about the effectiveness of central banks’ tools, clarity of their policy, and transparency of their action and communication might yield inflation uncertainty (IU; Holland 1993). IU is related to uncertainty about future inflation and therefore to the action of the central bank. According to Holland (1993), IU might also arise when the policy effect takes time to work. It can reduce economic well-being via decisions on business investment and consumer saving (Holland 1993) and might imply uncertainty about other variables such as the interest rate and therefore about the real value of future payments (Golub 1994).

Different approaches have been used to estimate IU. On the one hand, IU can be estimated through surveys distributed to consumers and economists asking them to provide an acceptable range of inflation. Such surveys (e.g. Lahiri and Lui 2006), compared with the true level of inflation, can facilitate the measurement of IU. On the other hand, forecasting strategies are employed to predict inflation with large forecast errors suggesting further evidence of IU. Moreover, in the related literature, several approaches have been used to model and forecast IU. Early studies considered the standard deviation of inflation to be a proxy of IU. However, conditional variance quickly became the most popular proxy to measure IU based on the ARCH (autoregressive conditional heteroscedasticity) and GARCH (generalized ARCH) models of Engle (1982) and Bollerslev (1986), respectively to take into account further persistence in the data (Holland 1993; Ben Nasr et al. 2015).

Over the past decade, the stochastic volatility model has also been applied to model IU. For example, Berument et al. (2009) employed the stochastic volatility in mean model in line with Koopman and Hol Uspensky (2002) and Chan (2017) extended the model of Koopman and Hol Uspensky (2002) to allow for time-varying parameters of IU. Bårdsen et al. (2002) theoretically and empirically evaluated the advantages of three theoretical models and highlighted the use of standard Phillips curves for modelling IU compared with the new Keynesian Phillips curve and incomplete competition models. More recently, Bauer and Neuenkirch (2017) employed a standard new Keynesian model to forecast inflation and economic growth uncertainty.

In this study, we follow this second approach to measure IU through symmetric and asymmetric conditional variance models as well as stochastic volatility models (Poon and Granger 2003). The use of these three models offers a suitably flexible framework to account for further asymmetry as well as outliers in IU dynamics. In addition, we focus on two major regions, namely the United States and the Euro Area, in which inflation has experienced different episodes over recent decades, suggesting further evidence of IU. For example, since the subprime mortgage crisis, the US inflation rate has been volatile, falling from about 4.08% in 2007 to 0.09% in 2008, pushing policymakers to adopt unconventional monetary policy rules. As a result, US inflation increased in 2009 to 2.96%, and it has showwn several increases and decreases.² In the Euro Area, the inflation rate has shown similar behaviour. In 2007, inflation reached 3.11%, while it has remained below its target rate (2%) since 2013.³ Our findings show the superiority of the stochastic volatility model for forecasting the dynamics of IU over the short (1 year) and medium (4 years) terms. This finding is particularly interesting to better estimate the main inflation cost, namely IU, and its effect on the real economy. To our knowledge, it is the first essay to propose forecast of inflation uncertainty with the stochastic volatility model.

The remainder of this paper is structured into three sections. Section 2 presents the econometric methodology. Section 3 describes the main empirical results and the last section concludes.

2 Econometric Methodology

2.1 Measuring IU

We measure IU using three proxies: First, the GARCH model (Bollerslev 1986), to provide a symmetric and linear measure of uncertainty; second, the GJR-GARCH model (Glosten et al. 1993), to provide a measure robust to further asymmetry in the data; third, the stochastic volatility, to allow for more flexibility than the GARCH model when measuring uncertainty.

2.1.1 Linear GARCH Measure of IU

This measure relies on the ARCH and GARCH models introduced by Engle (1982) and Bollerslev (1986), respectively for which conditional volatility mainly depends on its previous tendencies. This measure is appropriate for financial data to account for the further ARCH effect and persistence; it also supplants statistical uncertainty measures based on the standard deviation.

Formally, we represent the dynamics of the inflation rate $\left( {\pi _t } \right)$ by the following ARMA (p,q) model. We define the mean equation as⁴

$$\begin{aligned} \pi _t =\alpha _0 +\mathop \sum \limits _{i=1}^P \alpha _i \pi _{t-i} +\mathop \sum \limits _{j=1}^q \beta _j \varepsilon _{t-j} +\varepsilon _t \end{aligned}$$

(1)

where $\alpha _0 ,\alpha _i \hbox { and } \beta _j$ are the parameters of the autoregressive and moving average variables $\forall i=1,\ldots ,p$, and $j=1,\ldots ,q. \varepsilon _t$ denotes the error term and $\left. {\varepsilon _t } \right| \mathcal{F}_{t-1} \sim N\left( {0,h_t } \right)$.

Here, $h_t$ denotes the conditional variance reproduced by the following GARCH(1,1) model⁵

$$\begin{aligned} h_t =\gamma _0 +\gamma _1 \varepsilon _{t-1}^2 +\gamma _2 h_{t-1}^2 \end{aligned}$$

(2)

where $\gamma _0 >0$, $\gamma _1 \ge 0$, and $\gamma _2 \ge 0$.

The above ARMA-GARCH(1,1) model can be used to generate a symmetric measure of IU. However, this measure might be restrictive as it stipulates that for two shocks with the same amplitude but a contradictory sign, IU reacts symmetrically. It is thus more realistic to expect the reaction function to vary with the shock sign, which becomes possible by extending the GARCH model to an asymmetric framework.

2.1.2 Asymmetric Measure of IU

To account for the further asymmetry in the data, we model volatility by using the GJR-GARCH(1,1) model developed by Glosten et al. (1993). Accordingly, the new variance equation becomes

$$\begin{aligned} h_t^2 =\alpha _0 +\alpha _1 \varepsilon _{t-i}^2 +\gamma _1 {\mathrm{I}}_{{\epsilon }_{\mathrm{t}-\mathrm{i}<0} } \varepsilon _{t-i}^2 +\beta _1 h_{\hbox {t}-1}^2 \quad if \varepsilon _t =z_t \sqrt{h_t} \end{aligned}$$

(3)

where $z_t$ is a standard Gaussian, and $\mathrm{I}_{{\epsilon }_{\mathrm{t}-\mathrm{i}<0} }$ is a dummy variable modelling asymmetry, as ${\mathrm{I}}_{{\epsilon }_{\mathrm{t}-\mathrm{i}<0} } =1$ if ${\epsilon }_{t-i} <0$ and ${\mathrm{I}}_{{\epsilon }_{\mathrm{t}-\mathrm{i}<0} } =0$ otherwise.

Finally, for a more flexible measure of IU that can account for further innovations related to inflation and monetary policy conduct, we also measure uncertainty by using a stochastic volatility measure.

2.1.3 Measure of IU with Stochastic Volatility

In line with Chan (2013), we propose a stochastic volatility specification with an autoregressive term between innovations to take the persistence and correlation between the innovative terms into account. In particular, we apply the stochastic volatility model that uses moving average student’s t errors.⁶ Formally we model the dynamics of inflation as follows:

$$\begin{aligned} \pi _t= & {} \mu +\tau _t \end{aligned}$$

(4)

$$\begin{aligned} \tau _t= & {} {\epsilon }_t +\psi {\epsilon }_{t-1} \end{aligned}$$

(5)

where ${\epsilon }_t \sim N\left( {0,\hbox {exp}\left( {h_t } \right) } \right) t=1,\ldots ,T$.

Further, we suppose that volatility dynamics might be captured while specifying the variance equation (that serves to compute IU) as:

$$\begin{aligned} h_t =\mu _h +\phi _h \left( {h_{t-1} -\mu _h } \right) +\zeta _t \end{aligned}$$

(6)

where $\zeta _t \sim N\left( {0,\sigma _h^2 } \right) \,t=1,\ldots ,T$. $\zeta _t$ and ${\epsilon }_t$ are independent for all leads and lags. $\left| {\phi _h } \right| <1$ is a required condition to ensure the stationarity of this process of $\left( {h_t } \right) .$ The states are initialized with $h_1 \sim N\left( {\mu _h ,\frac{\sigma _h^2 }{1-\phi _h^2 }} \right) .$

According to Chan (2013), this specification requires the following assumptions on independent prior distributions for $\mu _h$, $\phi _h$, and $\sigma _h^2$ :$\mu _h \sim N\left( {\mu _{h _0} ,V_{\mu _h } } \right)$; $\phi _h \sim N\left( {\phi _{h _0} ,V_{\phi _h } } \right) I(\left| {\phi _h } \right| <1)$; and $\sigma _h^2 \sim IG\left( {v_h ,S_h } \right)$, where $I\left[ *\right]$ is an indicator function and IG is the inverse gamma distribution.

2.2 Forecasting Strategy

To forecast IU, we employ a rolling out-of-sample strategy that forecasts IU for various horizons $\left( h \right)$. In particular, we adopt two forecasting horizons, namely 1 year (short-term horizon) and 4 years (medium-term horizon), motivated by the fact that the inflation stability objective usually spans 1–4 years. The h-step forecasts are calculated for $t=k_i ,\ldots ,T_i$, where $k_i$ is the start date of forecasting for country i and $T_i$ is the end date of the studied series for country i, where i refers to the United States and Euro Area.

To evaluate forecasting performance, we compare the forecasts of the three above uncertainty models with those of a benchmark model given by an AR(1) model. This benchmark model has the advantage of being able to reproduce volatility features such as persistence. In particular, two loss functions are used, namely mean absolute error (MAE) and mean squared error (MSE), to compare the forecasts of each model with the benchmark model. Further, as our ahead forecast horizons are higher than 1, we employ the modified version of the Diebold and Mariano tests (1995) proposed by Harvey et al. (1997), termed MDM hereafter. Indeed, the Diebold and Mariano (1995) test (DM) suffers from a correlation bias for $h > 1$ and supposes that the statistical test follows a standard normal distribution.

We consider two competing models: a candidate model $\left( {CM_J } \right)$ (noted model 1) and the benchmark model (noted model 2). The two competing forecast models of IU are defined as $IU_{t+h\left| t \right. }^{CM_j }$ and $IU_{t+h\left| t \right. }^{AR\left( 1 \right) }$ for models 1 and 2, respectively. The forecast errors are defined as $\varepsilon _{t+h\left| t \right. }^{CM_j } =IU_{t+h} -IU_{t+h\left| t \right. }^{CM_j }$ and $\varepsilon _{t+h\left| t \right. }^{AR\left( 1 \right) } =IU_{t+h} -IU_{t+h\left| t \right. }^{AR\left( 1 \right) }$, respectively. Forecasting performance is then compared based on a loss function (the squared error or absolute error) defined as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} L\left( {IU_{t+h} ,IU_{t+h\left| t \right. }^{CM_j } } \right) _i =L\left( {\varepsilon _{t+h\left| t \right. }^{CM_j } } \right) _i ;\hbox { for the CM}_{\mathrm{j}} \\ L\left( {IU_{t+h} ,IU_{t+h\left| t \right. }^{AR\left( 1 \right) } } \right) _i =L\left( {\varepsilon _{t+h\left| t \right. }^{AR\left( 1 \right) } } \right) _i ;\hbox { for the AR(1) model} \\ \\ \end{array} }} \right. \end{aligned}$$

(7)

The null hypothesis of the DM test consists of checking whether the differential $\left( {d_t } \right)$ of the loss functions of the two competing models is statistically equal to zero as follows:

$$\begin{aligned} H_0 :E\left[ {d_t^i } \right] =0,\hbox { where }d_t^i =L\left( {\varepsilon _{t+h\left| t \right. }^{AR\left( 1 \right) } } \right) _i -L\left( {\varepsilon _{t+h\left| t \right. }^{CM_j } } \right) _i \end{aligned}$$

(8)

The statistics of the DM test (supposed to be normally distributed) correspond to

$$\begin{aligned} S_i =\frac{\overline{d_i}}{\left( {\widehat{LRV}_{\sqrt{n}\bar{d}} } \right) _i ^{1/2}} \end{aligned}$$

(9)

where $\bar{d}_i =\frac{1}{n}\mathop \sum \nolimits _{t=k_i}^{T_i } d_t^i$; $\left( {\widehat{LRV}_{\sqrt{n}\bar{d}} } \right) _i$ denotes the consistent estimates of the asymptotic long-run variance of $\sqrt{n}\bar{d}$, given by $\left( {\widehat{LRV}_{\sqrt{n}\bar{d}} } \right) _i =\gamma _0 +2\mathop \sum \nolimits _{j=1}^{h-1} \gamma _j$, where $\gamma _j =cov\left( {d_t ,d_{t-j} } \right)$, and i denotes the United States and Euro Area. n is the number of observations for each region.

As the loss differential functions might be serially correlated for $h > 1$, Harvey et al.’s (1997) MDM test uses an approximately unbiased estimator of $\left( {\widehat{LRV}_{\sqrt{T}\bar{d}} } \right)$. The exact variance is defined by $\left( {LRV_{\sqrt{T}\bar{d}} } \right) _i =\gamma _0 +\frac{2}{T_i }\mathop \sum \nolimits _{j=1}^{h-1} \left( {T_i -j} \right) \gamma _j$ and the estimator used by the DM test is presented as

$$\begin{aligned} \left( {\widehat{LRV} _{\sqrt{T}\bar{d}} } \right) _i =\widehat{\gamma } _0^*+\frac{2}{T_i }\mathop \sum \limits _{j=1}^{h-1} \left( {T_i -j} \right) \widehat{\gamma }_j^*\end{aligned}$$

(10)

where $\widehat{\gamma }_j^*$ is the expected value of the sample autocovariance.⁷$T_i$ denotes the number of observations in country i.

From Harvey et al. (1997), $d_t$ has a zero mean, implying the following modified statistics for their test $(S_i^M )$:

$$\begin{aligned} (S_i^M )=\left[ {T_i +1-2h+T_i^{-1} h \left( {h-1} \right) } \right] ^{\frac{1}{2}} *S_i \end{aligned}$$

(11)

with $S_i^M \leadsto T\left( {n_i -1} \right)$.

3 Empirical Analysis

3.1 Preliminary Analysis

Our data include monthly consumer price index data for the United States and Euro Area from January 1996 to January 2017 collected from DataStream. The annual inflation rate is computed as the logarithm difference of the seasonally adjusted consumer price index, where adjusted seasonality is realized based on the CENSUS method X13.

The selection of the United States and Euro Area and the above period sample has several advantages. First, over the sample period, the Fed adopted different conventional monetary policy regimes as well as unconventional monetary policy since the aftermath of the global financial crisis (2008–2009), which could have affected inflation and therefore IU. Second, monetary policy in the Euro Area is implicitly inflation targeting; however, recently, this region has adopted unconventional monetary policy, which therefore allows us to compare the effects of the actions of the Fed and the European Central Bank. Third, the sample period not only covers different inflation episodes but also includes calm and crisis periods for which IU is likely to be time-varying and therefore interesting to forecast. Further, regarding the Euro Area the inclusion of the euro implies obvious uncertainty about this common European currency that is interesting to evaluate it.

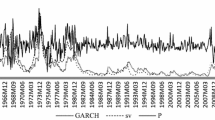
First, we check the stationarity of the US and Euro Area inflation rates by using four unit root tests: the augmented Dickey–Fuller (ADF) test, Phillips–Perron (PP) test, Ng–Perron (NgP) test, and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test. The three first tests check the null hypothesis of non-stationarity against the alternative hypothesis of stationarity. While the PP test is robust to further heteroscedasticity and autocorrelation problems in the data, the NgP test is an effective modified PP test and its application enables us to check the results of the two former unit root tests. The KPSS test is non-parametric and a test of stationarity. Table 1 shows that the inflation rate series for the United States and Euro Area is I(0). Stationarity is also confirmed by Figs. 1 and 2, which also show strong correction and even periods of deflation in the aftermath of the global financial crisis, particularly for the United States.

Table 1 Results of the Unit root tests

Fig. 1

Dynamics of the US inflation rate

Second, we compute the main descriptive statistics of the inflation rates The results in Table 2 show that on average the inflation rate is higher and more volatile in the United States than in the Euro Area with a maximum of 5.35% (4.08%) in the United States (in the Euro Area) and a minimum of − 1.93% (− 0.56%). Further, the kurtosis values exceed 3 for the United States, providing further evidence of leptokurtic excess in the data distribution against a platykurtic distribution for the Euro Area. Moreover, the US and Euro Area inflation rates are skewed to the left. This result is in line with Jarque–Bera test, rejecting the normal distribution for both inflation rate series.

Fig. 2

Dynamics of the Euro Area inflation rate

Table 2 Descriptive statistics of the inflation rate

3.2 Estimating IU

First, we propose a symmetric measure of IU. To do so, we estimate ARMA(5,5) and ARMA(1,12) models to specify the mean equation of the US and Euro Area inflation rates, respectively, while the variance equation is estimated for both regions by using a GARCH(1,1) model.⁸ This approach seems to reproduce the conditional variance for both regions correctly, as the results show no pattern for either the residuals or the squared residuals.⁹

Figures 3 and 4 report the dynamics of the estimated symmetric IU measures for the United States and Euro Area, respectively. First, IU in the United States peaks in 2009 after increasing since the end of the 1980s, while IU shows no clear trend for the Euro Area. Second, IU exhibits more short-term changes than does IU in the United States. Third, even despite the volatile IU at the end of the period, it is still lower than IU in the United States, which has risen significantly since the aftermath of the global financial crisis.

Fig. 3

US symmetric IU. Note This figure reports the graphic of the symmetric measure of inflation uncertainty

Fig. 4

Euro Area symmetric IU. Note This figure reports the graphic of the symmetric measure of inflation uncertainty

To better compare these series, we compute the main descriptive statistics of the uncertainty series for the United States and Euro Area. Table 3 shows that on average IU in the United States is more than five times higher than that in the Euro Area. It also shows the highest volatility, suggesting that economic agents’ fears about Fed policy are higher than those on the European Central Bank’s action. Further, for both uncertainty series, the normality hypothesis is rejected: the distribution seems to be skewed to the right and with a leptokurtic excess.

Table 3 Descriptive statistics of symmetric IU

Second, Figs. 5 and 6 report the main results of estimating IU by using the GJR-GARCH(1,1) model for both regions. We find strong similarities with the symmetric GARCH estimated earlier.

Fig. 5

US asymmetric IU. Note This figure reports the graphic of the asymmetric measure of inflation uncertainty

Fig. 6

Euro Area asymmetric IU. Note This figure reports the graphic of the asymmetric measure of inflation uncertainty

Table 4 presents the descriptive statistics of asymmetric IU in the United States and Euro Area. From these results, we can draw the same conclusions: asymmetric IU is higher and more volatile in the United States than in the Euro Area.

Table 4 Descriptive statistics of asymmetric IU

Finally, Figs. 7 and 8 present the IU results for the United States and Euro Area, respectively, using the stochastic volatility model. This new estimate confirms the robustness of our uncertainty estimates by capturing a similar profile for uncertainty. It increases during the Internet bubble and global financial crisis periods; however, it does show less volatility for both regions.

Fig. 7

US stochastic IU. Note This table reports the graphic of the stochastic measure of IU

Fig. 8

Euro Area stochastic IU. Note This table reports the graphic of the Stochastic measure of IU

Finally, Table 5 reports the main descriptive statistics of the uncertainty measure with stochastic volatility to better analyse its statistical properties. The United States still appears to show the highest IU on average, while the uncertainty measure has become more volatile for the Euro Area. In addition, the symmetry and normality hypotheses are rejected for both regions.

Overall, the estimates of IU using the three methodologies (symmetric GARCH, asymmetric GARCH, stochastic volatility) capture some of the important properties of uncertainty data and provide comparable results. However, to identify the model that best fits the data, we next present the results of our comparative forecasting analysis.

3.3 Forecasting Analysis of IU

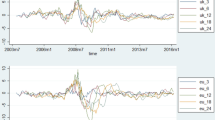
We again compute the forecasts for our three models and compare them with those of the benchmark model to understand the further persistence in IU dynamics. Figures 9 and 10 present the results for medium-term (i.e. 4 years)¹⁰ out-of-sample IU for our three candidates’ models for the United States and Euro Area, respectively. Figures a and b display the forecasting dynamics based on symmetric and asymmetric IU, respectively. In Figs. 9a, b, 10a, and b, the benchmark (blue line) only captures the linear trend of the uncertainty dynamics. However, the forecasts of symmetric and asymmetric IU (black lines) enable us to understand short-term fluctuations and tendency changes. Nevertheless, overall, the estimated models do not appear to be sufficiently suitable to forecast IU dynamics accurately. In general, the stochastic volatility model seems to supplant the benchmark model and provide better performance forecasts, particularly for the United States.

To better compare these forecasts, Tables 6 and 7 present the forecasting evaluation indicators (MAE, MSE) as well as the results of the Harvey et al. (1997) test for the medium-term horizon. The results confirm the graphical analysis. The benchmark model typically outperforms the symmetric and asymmetric models. However, the stochastic volatility model always supplants the benchmark model for the medium term. This finding suggests that the greater flexibility offered by the stochastic volatility model raises forecast uncertainty while taking into account further innovations in the data, again suggesting its superiority over the GARCH model.

Table 5 Descriptive statistics of stochastic IU

Fig. 9

US IU forecast in the medium term. a IU forecast with the symmetric GARCH model. b IU forecast with the asymmetric GARCH model. c IU forecast with the stochastic volatility model. NoteH (black line) denotes the forecast of the candidate model for IU. Forecast series (blue line) denotes the forecast of the benchmark model. The green chart refers to the realized observed IU series computed differently through the three approaches (symmetric GARCH, asymmetric GARCH, stochastic volatility model)

Fig. 10

Euro Area IU forecast in the medium term. a IU forecast with the symmetric GARCH model. b IU forecast with the asymmetric GARCH model. c IU forecast with the stochastic volatility model. NoteH (black line) denotes the forecast of the candidate model for IU. Forecast series (blue line) denotes the forecast of the benchmark model. The green chart refers to the realized observed IU series computed differently through the three approaches (symmetric GARCH, asymmetric GARCH, stochastic volatility model)

Figures 11 and 12 present the dynamics of the short-term forecasts of the three models.¹¹ In line with the medium-term analysis, there is no clear difference between the symmetric and asymmetric GARCH models compared with the benchmark model. However, Figs. 11c and 12c show the better short-term forecasting accuracy of the stochastic volatility model compared with the other two models.

Table 6 Forecasting evaluation for IU in the United States for the medium term horizon

Table 7 Forecasting evaluation for IU in the Euro Area for the medium term horizon

We also compare these forecasts in Tables 8 and 9 and report the estimated values of the statistics for the short-term forecast horizon. Our findings show that while the benchmark model better fits the data compared with the symmetric GARCH model for the United States, the latter provides a better forecasting result for the Euro Area. However, in the medium term, the stochastic volatility model appears again to be the best fitted model to forecast the dynamics of IU in the short term.

Overall, the analysis of our results shows that IU has evolved in tandem with the phases of the business cycle over time. In particular, periods of crises and economic downturns have been characterized by high IU. The analysis of our uncertainty forecasts shows the superiority of the stochastic volatility model for modelling and forecasting IU in the short and medium terms for both the United States and the Euro Area.

Fig. 11

US IU forecast in the short term. a IU forecast with the symmetric GARCH model. b IU forecast with the asymmetric GARCH model. c IU forecast with the stochastic volatility model

Fig. 12

Euro Area IU forecast in the short term. a IU forecast with the symmetric GARCH model. b IU forecast with the asymmetric GARCH model. c IU forecast with the stochastic volatility model

4 Conclusion

This study models and forecasts IU in the United States and Euro Area over 1997–2017, using three methodologies: the symmetric GARCH model, asymmetric GARCH model, and stochastic volatility model. While the two first methods provide symmetric and asymmetric measures of IU, respectively, the third measure has the advantage of offering greater flexibility in measuring uncertainty. Our out-of-sample IU forecast shows the superiority of the stochastic volatility model when forecasting IU dynamics in both the short (1 year) and the medium (4 years) terms. This finding recommends the use of the stochastic volatility model to estimate the inflation cost (IU) accurately and evaluate its effect on the real economy. Nevertheless, our conclusion might be improved by taking into account new indicators related to central banking as well as indicators used in recent unconventional monetary policy. Further, it is worth to recall that when comparing the Fed and the ECB, there are at least three main differences. First, the Fed and the ECB do not have the same mandate even if for both the fight against inflation is a priority. Second, the degree of independency is also different for the two central banks. Third, the two central banks have not adopted the conduct of the unconventional monetary policy in the same time. For all these reasons, it might appear a priori appear more relevant to focus on the modeling of inflation uncertainty in a univariate framework as we what we have done in this paper. However,it is also to expect that some common factors (e.g. the recent use of unconventional monetary rules as the Quantitative Easing, Qualitative Easing, etc.) might imply further uncertainty for inflation for both regions (Europe and the USA) and thus requires the application of a multivariate model such as VAR-GARCH model to better asses for the interaction of inflation uncertainty between these two regions. This issue might be a natural extension of the current work.

Table 8 Forecasting evaluation for IU in the United States for the short-term horizon

Table 9 Forecasting evaluation for IU in the Euro Area for the short-term horizon