Double auction mechanisms in edge computing resource allocation for blockchain networks

Abstract

Blockchain, a promising technology, has been extensively applied in numerous fields, such as network security, finance, and medical care. However, due to the low power consumption and weak computing power of the mobile environment, the application of blockchain in this environment still faces many challenges. Therefore, edge computing has been introduced to improve the computing power of mobile devices and encourage more mobile edge devices to join the blockchain network. In this paper, we propose a double auction model to address the issue of edge computing resource allocation in blockchain networks. Based on this auction model, we first propose a truthful double auction mechanism based on breakeven (TDAMB) to determine matched pairs of edge computing service providers (ECSPs) and miners. Furthermore, to improve the system efficiency, we propose a double auction mechanism based on a critical value (DAMCV). We also theoretically analyze the individual rationality, budget balance and truthfulness of the proposed mechanisms. Extensive experiments show that TDAMB and DAMCV have good effects on edge computing resource allocation in blockchain networks.

1 Introduction

Blockchain is the backbone technology of digital cryptocurrency, represented by Bitcoin [22]. On the basis of timestamps, data encryption, consensus mechanisms, economic incentives and other techniques, blockchain first solves the security problems of the trust-based centralized model. Blockchain is essentially a technology that allows any node in a P2P network to maintain and verify the transactions recorded in the ledgers and make peer-to-peer transactions without mutual trust and identity authentication. Due to the inherent advantages of blockchain technology, it has been extensively applied in network security, finance, medical care and other fields [28].

The reliability and security of blockchain rely on the consensus mechanism. The core component of the consensus mechanism adopted by permissionless blockchains represented by Bitcoin is proof-of-work (PoW) [18]. PoW requires each consensus node in the network to contribute its own computing resources to compete to calculate a specific hash value. If the correctness of the calculated target hash value is verified by the majority of other nodes, the node acquires the accounting rights to the block. Then, all transactions generated during the current period are encapsulated in the new block and linked to the main chain in accordance with the timing. At the same time, the blockchain system issues a certain amount of reward to this node, which can encourage other nodes to continue to contribute computing power. The entire process of PoW is known as mining, and the nodes that devote their computing power to calculating hash values are known as miners.

With the blossoming of blockchain, decentralized application (DAPP) based on permissionless blockchain has attracted wide attention [28]. DAPP does not rely on traditional centralized servers and adopts blockchain technology to achieve decentralized management and operation, thus possessing higher security and transparency. This is a breakthrough in relations of production, because people can quickly realize self-organized trading platforms by independently designing smart contracts without the support or permission of trusted intermediaries. On the other hand, through the Nakamoto consensus protocol based on PoW, DAPP encourages people to become consensus nodes and receive mining rewards. Unfortunately, solving the PoW puzzle requires strong computing power, which is not suitable for mobile devices with restricted resources and computing capabilities. To alleviate this bottleneck, integrating mobile edge computing (MEC) into blockchain is a feasible solution that can provide a powerful distributed network and sufficient computing resources.

Integrating MEC into blockchain has been widely studied and applied to many fields [2, 27]. For instance, the application of blockchain in the Internet of Vehicles (IoVs) can be implemented by employing edge computing. Xu et al. [26] considered roadside nodes (RSUs) in IoVs as edge computing servers. RSUs acted as computation nodes and blockchain nodes. Compared to vehicle nodes, RSUs have more computing and communication resources. Moreover, the RSUs participated in mining as miners and assisted in the information transmission of the vehicle blockchain network. The benefits of the introduction of MEC into the blockchain framework are numerous. First, edge computing technology improves the computing power of lightweight device miners in the blockchain network [1], so the rewards given to miners are also increased, which attracts more miners to join the process of mining blocks, thereby enhancing the security and robustness of the blockchain network. Second, edge computing service providers (ECSPs) can obtain many benefits by providing computing resources for miners.

Previous works [16, 34] have investigated the specific offloading process. Through wireless communication protocols such as Wi-Fi or cellular networks, mobile miners establish communication channels with edge computing servers. The mobile miners divide the nonce space into smaller segments or partitions and only work on a subset of nonces locally. Through the communication channel, they assign the remaining portions of the nonce space to the edge computing servers for computation. The edge computing servers receive the specific ranges of nonce values and perform the necessary hash computations. Once the tasks are completed, the results will be sent back to the mobile miners. By offloading, some mobile miners may have higher mining capabilities and competitive advantages, which may lead to unfairness. However, it is worth noting that the fairness of blockchain does not solely depend on the computing resources of nodes. In the PoW mechanism, the difficulty of mining is usually adjusted based on the overall computing power of the network. This means that as the total computing power in the network increases, the difficulty will correspondingly increase, making it difficult for resource rich nodes to gain unlimited advantages. This adjustment ensures fairness in mining while preventing monopoly by a few nodes. Meanwhile, blockchain systems typically reward participants based on their level of contribution. This mechanism makes participants not only rely on the computing resources, but also need to invest other resources (such as time and electricity) to obtain higher returns. This can also achieve a relatively fair reward method. Practically, to increase mining probability and increase profits, many miners have formed alliances to form mining pools [17]. Many researchers have also conducted research on ensuring the fairness of consensus mechanisms in this situation [15].

In this paper, we study the allocation of computing resources between ECSPs and miners with lightweight devices in a blockchain network. The computing resources in MEC are scarce resources, thus are very suitable for allocation through auction which can fully motivate individuals to participate in market activities [33]. Since both the mobile miners and ECSPs are multiple participants, there is internal competition between the mobile miner group and the ECSP group. Compared to traditional one-way auction mechanisms, the double auction mechanism can effectively solve internal competition between mobile miners and ECSPs as well as conflicts of interest between mobile miners and ECSPs [14]. Moreover, the pricing of the double auction is inspired by the second price sealed auction, thus can effectively protect the interests of both buyers and sellers. Therefore, the interaction between ECSPs and mobile miners can be modeled as a double auction. The computing resources of ECSPs are considered as commodities, mobile miners with task offloading requirements are considered buyers, and ECSPs are considered sellers. Therefore, we propose a double auction model between ECSPs and miners with lightweight devices and design resource allocation and pricing algorithms based on this model. The main contributions of this work are summarized as follows:

• We study the characteristics of the edge computing resource allocation problem in the blockchain scenario. We first present a hash power function and then design a resource allocation model based on a double auction to maximize the social welfare of the blockchain network.

• We design a truthful double auction mechanism based on breakeven (TDAMB). Additionally, we prove that the proposed double auction mechanism satisfies the three economic properties of individual rationality, budget balance and truthfulness. Furthermore, to improve the system efficiency, we extend TDAMB and propose a double auction mechanism based on a critical value (DAMCV); similarly, we analyze its economic properties.

• We conduct numerical simulations to evaluate the effectiveness of the proposed hash calculation function. Moreover, we conduct extensive comparative experiments between the two proposed algorithms and the previous algorithm. Finally, we verify the economic properties of the proposed algorithms.

The remainder of this paper is structured as follows. The related work is summarized in Sect. 2. The system model of edge computing resource allocation based on double auctions in blockchain networks is presented in Sect. 3. Two double auction mechanisms are discussed, and the economic properties of the proposed mechanisms are proven in Sects. 4 and 5. The performance evaluation is discussed in Sect. 6, and our conclusions and future research directions are summarized in Sect. 7.

2 Related works

Recently, several studies on edge/cloud computing resource allocation algorithms in blockchain networks have been conducted. In one of the pioneering papers, Xiong et al. [24] developed a framework for mobile blockchain, specifically considering that miners with lightweight devices can offload intensive tasks such as hash value computations to an edge computing server. Xiong et al. [25] considered the transaction model between cloud/edge computing providers and lightweight miners in a mobile blockchain network and proposed a two-stage Stackelberg game model for the edge resource management in a PoW-based blockchain network. Jing et al. [11] jointly studied resource trading and computing offload in blockchain enhanced D2D assisted mobile edge computing. They modeled the resource trading problem as a Stackelberg game, and formalized the computation offloading problem as a mixed optimization problem. Yao et al. [29] formulated the problem of cloud resource allocation and pricing between the miners and cloud provider as a Stackelberg model and proposed an efficient reinforcement learning algorithm based on multiple agents. Jiao et al. [8, 9] considered the deployment of edge/cloud computing servers to support applications based on mobile blockchain and proposed computing resource allocation mechanisms to improve the social welfare of a system based on auction theory. The system is guaranteed to be computationally efficient, individually rational, and truthful. Guo et al. [6] proposed that miners with insufficient resources could offload mining tasks such as PoW puzzle computations to nearby non-mining-devices or to edge servers and formulated the problem as double auction model and Stackelberg model via game theory. Zhang et al. [32] studied the resource allocation model in the Internet of Vehicles with public blockchain networks and proposed two truthful auction mechanisms for ECSPs and miners to optimize the social welfare of the blockchain network.

In terms of allocation algorithms and mechanisms based on double auctions, Feng et al. [5] studied the resource allocation problem of a spectrum trading market composed of spectrum holders, wireless service providers, and end users and designed a pricing algorithm based on the Vickrey–Clarke–Groves(VCG) mechanism and a uniform pricing algorithm. Chen et al. [3] proposed a multichannel spectrum resource allocation mechanism based on double auctions. This mechanism attains truthfulness while improving spectrum utilization. Jin et al. [10] focused on the interaction model between cloudlets and nearby mobile devices. The model efficiently balanced the workload from the centralized cloud and reduced the access latency of mobile devices. Faqiry et al. [4] applied the double auction mechanism to microgrid energy transactions and proposed a resource allocation algorithm that satisfies individual rationality, high efficiency and weak budget balance. Li et al. [14] designed a dynamic combinatorial double auction model that guarantees incentive compatible, individually rational and budget-balanced, as well as high performance in terms of resource utilization and social welfare. Baranwal et al. Patel et al. [19] considered how to achieve a trade-off between energy consumption and revenue in virtual resource allocation for cloud computing, formulated this goal as a joint optimization problem and transformed it into a multidimensional packing problem. Moreover, they used VCG mechanism theory to design a double auction mechanism to allocate virtual cloud computing resources. Sarenche et al. [21] combined cryptographic mechanisms with the characteristics of double auction mechanisms in smart grids. They designed a protocol based on Paillier homomorphic encryption, which ensured the security of information during the auction process.

In general, previous research has achieved good results for edge computing resource allocation algorithms in blockchain networks and resource allocation mechanisms based on double auctions. Inspired by the above works, we apply double auction mechanism to solve the edge computing resource allocation problem in blockchain networks and design two double auction mechanisms.

3 Edge computing resource allocation model in blockchain networks and mechanism design preliminaries

3.1 Double auction model design

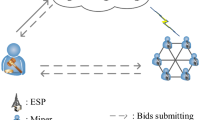
As depicted in Fig. 1, we consider a scenario of an MEC-enabled public blockchain network under the PoW consensus protocol. We select the public chain because participating in the public chain does not require permission. Mobile devices and ECSPs in the edge computing environment deploy the blockchain by running the same DAPP. In the MEC-enabled blockchain network, miners with lightweight devices intend to participate in the consensus process to gain revenue by mining blocks. Each miner has a weak local computing power and prefers to offload some of their computing tasks to the nearby edge computing servers deployed by the ECSPs. We abstract the two-sided interaction between mobile miners and ECSPs to a double auction model. We summarize the frequently used notations in Table 1.

Fig. 1

System model of an MEC-enabled blockchain network under the PoW consensus protocol

Table 1 Frequently used notations

In a market based on a double auction, there is one auctioneer, multiple buyers and multiple sellers. To ensure the fairness of the double auction, the auctioneer is set to be a third-party platform. We assume that the third-party is trustworthy. The auctioneer executes the double auction algorithm after it collects all the information of the buy-bids and sell-bids. In our double auction model, buyers are the miners with lightweight devices who bid for computing resources from the ECSPs, which are the sellers. From now on, we use the term buyers interchangeably with miners and the term sellers interchangeably with ECSPs. In our double auction model, there are N buyers and M sellers. On the buyer side, let ${\mathcal {N}} = \{1,2,\ldots ,N\}$ be the set of mobile miners. Each miner i ($i\in {\mathcal {N}}$) declares a buy-bid $\theta ^{\text {buyer}}_i= (d_i, v_i)$, where $d_i$ is her resource requirement and $v_i$ is the valuation of her resource requirement. On the seller side, let ${\mathcal {M}} = \{1,2,\ldots ,M\}$ be the set of ECSPs. Each ECSP j ($j\in {\mathcal {M}}$) declares a sell-bid $\theta ^{\text {seller}}_j= (c_j, a_j)$, where $c_j$ is his resource capacity and $a_j$ is the unit resource cost of ECSP j, which represents the minimum unit price that he is willing to charge. However, all miners and ECSPs are selfish, that is, they may manipulate their bidding information to improve their own profits. Miners may manipulate the valuations of their resource requirements. The true value of miner i’s valuation is $v_i^{\text {true}}$. The true value of ECSP j’s unit resource cost is $a_j^{\text {true}}$.

Figure 2 shows the transaction flow of the double auction mechanism between ECSPs and miners for edge computing resource allocation. First, both ECSPs and miners report their sell-bids and buy-bids to an auctioneer, respectively. Then, the auctioneer collects these bids and matches the winners among the ECSPs and miners through an allocation algorithm and calculates the payment through a pricing algorithm. Next, the auctioneer informs the ECSPs and miners of the allocation solutions, which can be represented by a matrix ${{\textbf {x}}}=\left[ \begin{matrix} x_{11} &{} x_{12} &{} \cdots &{} x_{1M} \\ x_{21} &{} x_{22} &{} \cdots &{} x_{2M} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{N1} &{} x_{N2} &{} \cdots &{} x_{NM} \\ \end{matrix} \right]$, where $x_{ij}=1$ indicates that the requirement of miner i is satisfied by ECSP j and $x_{ij}$=0 indicates that it is not. ${{{{\mathcal {M}}}}^\text {win}} \subseteq {{{\mathcal {M}}}}$ denotes the set of winning ECSPs, and ${{{{\mathcal {N}}}}^\text {win}} \subseteq {{{\mathcal {N}}}}$ denotes the set of winning miners. Then, the auctioneer requests payments from the miners and resources from the ECSPs. The ECSPs and miners then submit resources and payments to the auctioneer, respectively. Eventually, the auctioneer allocates resources to the miners and transfers payments to the ECSPs.

Fig. 2

Workflow of the double auction mechanism in the MEC-enabled blockchain network

Moreover, we assume that each miner i has a local computing power, defined as $l_i$. Therefore, miner i’s total computing capacity is:

$$\begin{aligned} d_i^{{\rm{total}}} = l_i + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} \end{aligned}$$

(1)

Therefore, miner i’s hash power, i.e., her computing power as a percentage of the entire computing power in the blockchain, can be calculated as follows:

$$\begin{aligned} {\gamma _i}(d,l,x)&= \frac{{d_i^{{\rm{total}}}}}{{\sum \limits _{i \in {{{\mathcal {N}}}}} {d_i^{{\rm{total}}}} }} \nonumber \\&= \frac{{{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} }}{{\sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )}}}\nonumber \\&= \frac{{{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} }}{{{d_{{{\mathcal {N}}}}}}} \end{aligned}$$

(2)

The hash power function is a fraction function and satisfies $\sum \limits _{i \in {{{\mathcal {N}}}}} {{\gamma _i}} = 1$, and ${d_{{{\mathcal {N}}}}} = \sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )}$ is the total computing power of the blockchain network. We use $P_i^\text {mine}$ to represent the probability that miner i successfully solves the PoW puzzle. The probability is equal to her hash power, i.e., $P_i^\text {mine} = {\gamma _i}$.

Before participating in the double auction mechanism, each miner collects unconfirmed transaction information into her own block. Let $s_i$ denote the block size of miner i. However, even if miner i succeeds in solving the PoW puzzle, she may fail to be the first one to make her block to reach consensus, i.e., her block may become an orphan block because it cannot be linked to the main chain of the blockchain. It is mainly determined by the propagation and verification time of miner i’s block, which is denoted as ${\tau _i}$. According to the statistics provided in [20], ${\tau _i}$ is a linear function of miner i’s block size $s_i$, i.e., ${\tau _i} = \xi \cdot {s_i}$, where $\xi$ is a constant reflecting the effect of $s_i$ on ${\tau _i}$. In the whole blockchain network, new blocks are generated in a Poisson process with an average rate of $\frac{1}{\lambda }$, where $\lambda$ is also called the average block time [29]. Therefore, the probability of miner i’s block becoming an orphan block is as follows:

$$P_i^{{\rm{orphan}}} = 1 - {e^{ - \frac{1}{\lambda } \cdot {\tau _i}}}$$

(3)

As mentioned, whether miner i can be the first one to make her block reach consensus depends on the probability of solving the PoW puzzle, as well as timely propagation and verification of her block. Thus, the probability that miner i’s block reaches consensus can be expressed as follows:

$${P_i}({\gamma _i}(d,l,x),{s_i}) = P_i^{{\rm{mine}}} \cdot (1 - P_i^{{\rm{orphan}}}) = {\gamma _i} \cdot {e^{ - \frac{1}{\lambda } \cdot \xi \cdot {s_i}}}$$

(4)

If miner i is the first to successfully reach consensus, she can receive a reward $R_i$. This reward of miner i is composed of a constant reward T for mining a new block, as well as a variable transaction reward $r \cdot {s_i}$, where r represents a predefined transaction fee rate [7]. Thus, miner i’s expected reward is calculated as follows:

$$\begin{aligned} R_i^{} = (T + r \cdot {s_i}) \cdot {P_i}({\gamma _i}(d,l,x),{s_i}) \end{aligned}$$

(5)

In the PoW-based blockchain network, the more miners participate, the stronger the blockchain network is, which leads to a positive network effect, that is, the stability and security of blockchain networks will be improved. In addition, the reward value given to the miners in the blockchain network will also increase. According to the statistics given in [8] and by means of curve fitting to experimental data, we define a non-negative network effect function as follows:

$$\begin{aligned} w({d_{{{\mathcal {N}}}}} ) = \frac{1-e^{-{\mu _2} \cdot {d_{{{\mathcal {N}}}}}}}{1+{\mu _1} \cdot e^{-{\mu _2} \cdot {d_{{{\mathcal {N}}}}}}} \end{aligned}$$

(6)

where ${d_{{{\mathcal {N}}}}} = \sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )}$ as mentioned is the total quantity of computing power in the blockchain network and ${\mu _1},{\mu _2} > 0$ are curve fitting parameters. This network effect function has a monotonously increasing concave shape in the feasible domain.

When participating in the double auction, each miner’s valuation in her buy-bid represents her valuation of the required computing resources. Before the auction is completed, miner i cannot know the other information, such as the other miners’ local computing resources, and the total computing capacity of the blockchain network, thus we set $w({d_{{{\mathcal {N}}}}} ) = 1$. In addition, since miner i cannot know network effects, we set $w({d_{{{\mathcal {N}}}}} ) = 1$. Meanwhile, since miner i cannot calculate her hash power, we set $P_i^\text {mine} = {\gamma _i} = 1$. Thus, miner i’s ex ante truthful valuation can be calculated as follows:

$${v_i}^{{\rm{true}}} = {R_i} \cdot {d_i} = (T + r \cdot {s_i}) \cdot {e^{ - \frac{1}{\lambda } \cdot \xi \cdot {s_i}}} \cdot {d_i}$$

(7)

After the end of the double auction, each miner is informed of the allocation results x from the auctioneer and can evaluate the network effect of the blockchain. Therefore, miner i’s ex post valuation ${v_i}^\prime$ can be expressed as follows:

$$\begin{array}{ccccc} {v_i}^\prime = & {v_i}^{{\rm{true}}} \cdot w({d_{\cal N}}) \cdot {\gamma _i}(d,l,x)\\ = & (T + r \cdot {s_i}) \cdot {e^{ - \frac{1}{\lambda } \cdot \xi \cdot {s_i}}} \cdot {d_i} \cdot \frac{{1 - {e^{ - {\mu _2} \cdot {d_{\cal N}}}}}}{{1 + {\mu _1} \cdot {e^{ - {\mu _2} \cdot {d_{\cal N}}}}}}\\ & \cdot \frac{{{l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} }}{{\sum\limits_{i \in {\cal N}} {({l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} )} }} = (T + r \cdot {s_i}) \cdot {e^{ - \frac{1}{\lambda } \cdot \xi \cdot {s_i}}}\\ \cdot & {d_i} \cdot \frac{{1 - {e^{ - {\mu _2} \cdot \sum\limits_{i \in {\cal N}} {({l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} )} }}}}{{1 + {\mu _1} \cdot {e^{ - {\mu _2} \cdot \sum\limits_{i \in {\cal N}} {({l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} )} }}}} \cdot \frac{{{l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} }}{{\sum\limits_{i \in {\cal N}} {({l_i} + {d_i} \cdot \sum\limits_{j \in {\cal M}} {{x_{ij}}} )} }} \end{array}$$

(8)

In this paper, we focus on maximizing the social welfare of the blockchain network. Ex post valuation refers to the assessment of a miner’s investment value based on her actual performance in the market [9, 32]. Thus, the social welfare is defined as the sum of miners’ ex post valuations. We formulate the double auction model as an integer programming model with the goal of maximizing the social welfare of blockchain network. The integer programming model can be formulated as follows:

$$\begin{aligned} \begin{aligned} Maximize: V&={\rm{max}} {\sum \limits _{i \in {{{\mathcal {N}}}}} {{v_i}^{\prime }} } \\&= {\rm{max}}\sum \limits _{i \in {{{\mathcal {N}}}}}\frac{{{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} }}{{\sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )} }} \\&\quad \cdot \frac{1-e^{-{\mu _2} \cdot {\sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )}}}}{1+{\mu _1} \cdot e^{-{\mu _2} \cdot {\sum \limits _{i \in {{{\mathcal {N}}}}} {( {{l_i} + {d_i} \cdot \sum \limits _{j \in {{{\mathcal {M}}}}} {{x_{ij}}} } )}}}} \cdot {v_i} \end{aligned} \end{aligned}$$

(9)

$$\begin{aligned} {\mathrm{s.t.}}:{} & {} \quad \sum \limits _{i \in {{{\mathcal {N}}}}} {d_i^{} \cdot x_{ij}^{} \le {c_j}} ,\forall j \in {{{\mathcal {M}}}} \end{aligned}$$

(10a)

$$\begin{aligned}{} & {} \quad \sum \limits _{j \in {{{\mathcal {M}}}}} {x_{ij}^{} \le 1} ,\forall i \in {{{\mathcal {N}}}} \end{aligned}$$

(10b)

$$\begin{aligned}{} & {} \quad x_{ij}^{} \in \{ 0,1\} ,\forall i \in {{{\mathcal {N}}}},\forall j \in {{{\mathcal {M}}}} \end{aligned}$$

(10c)

The objective V represents the total social welfare of the blockchain network, and our goal is to maximize it. The previously defined decision variable $x_{ij}$ indicates whether the requirement of miner i is satisfied by ECSP j. Formula (10a) is a capacity constraint that ensures that the total amount of computing resources provided by each ECSP cannot exceed his resource capacity. Formula (10b) indicates that each miner can be served by at most one ECSP. Formula (10c) indicates that the value of $x_{ij}$ is 1 or 0.

3.2 Mechanism design preliminaries

The benefit obtained by each miner or ECSP in the double auction is expressed by his or her utility. According to the above definitions, the user utilities of miners and ECSPs under the double auction model are defined as follows:

• Utility of miner. Miner i has a utility function defined as the difference between her truthful valuation and payment, which is defined as follows [13]:

  $U_i^\text {buyer} = \left\{ {\begin{array}{ll} {v_i^{\text {true}}} - p_i^\text {buyer} &{}\quad {\rm{if}}~i \in {{{{\mathcal {N}}}}^\text {win}}\\ 0 &{}\quad {\rm{otherwise}} \end{array}} \right.$

  where ${p_i^\text {buyer}}$ is the value that miner i must pay according to the payment algorithm. Each miner is committed to optimizing her utility.

• Utility of the ECSP. ECSP j has a utility function defined as the payment from miners he serves minus his truthful unit resource cost multiplied by the resource he allocates, which is defined as follows [13]:

  $U_j^\text {seller} = \left\{ {\begin{array}{ll} p_j^\text {seller}{\mathrm{- }}\sum \limits _{i \in {{{\mathcal {N}}}}} {{d_i} \cdot {x_{ij}}} \cdot {a_j^{\text {true}}} &{}\quad \text {if }j \in {{{{\mathcal {M}}}}^\text {win}}\\ 0&{}\quad {\rm{otherwise}} \end{array}} \right.$

  where ${p_j^\text {seller}}$ is the payment that ECSP j receives. Each ECSP is committed to optimizing his utility.

Individual rationality, budget balance and truthfulness are the three critical properties that guarantee the economic stability of the double auction mechanism [12]. This paper is commited to designing a double auction mechanism that satisfies these three economic properties. The desired properties are defined as follows:

Definition 1

(Individual rationality) A double auction is individually rational if no buyer (miner) and no seller (ECSP) suffer losses after participating in the auction. This means that for all miners and ECSPs winning the auction,

$$\begin{aligned} p_i^\text {buyer} \le {v_i^{\text {true}}}, \;p_j^\text {seller} \ge \sum \limits _{i \in {{{\mathcal {N}}}}} {{d_i} \cdot {x_{ij}}}\cdot {a_j^{\text {true}}},\; \forall i \in {{{\mathcal {N}}}},\; \forall j \in {{{\mathcal {M}}}} \end{aligned}$$

(11)

Definition 2

(Budget balance) A double auction is budget balanced if the auctioneer’s profit is nonnegative. The auctioneer’s profit is defined as the difference between the value received from miners and the fees paid to ECSPs:

$$\begin{aligned} \sum \limits _{j \in {{{{\mathcal {M}}}}^\text {win}}} {p_j^\text {seller}} \le \sum \limits _{i \in {{{{\mathcal {N}}}}^\text {win}}} {p_i^\text {buyer}} \end{aligned}$$

(12)

Definition 3

(Truthfulness) A double auction is truthful if no matter how other miners and ECSPs bid, no miner i or ECSP j can improve his or her own utility by bidding untruthfully.

4 A truthful double auction mechanism based on breakeven (TDAMB)

4.1 The framework of TDAMB

In this section, we propose TDAMB. The TDAMB mechanism is composed of a candidate determination part and a winner determination & pricing part. In the candidate determination part, we first build a bid density set ${ \varvec{\Theta }}= (\theta _1,\theta _2,\ldots ,\theta _N)$, where $\theta _i=\frac{v_i}{d_i}$, and then sort the bid densities of miners in ${ \varvec{\Theta }}$ in nonincreasing order. We sort the ECSPs’ unit resource costs in $\textbf{a}$ in nondecreasing order. Therefore, miners with higher bid densities and ECSPs with lower ask values are more likely to win the auction. To balance the number of winning miners and ECSPs, we eliminate the failed miners and ECSPs by breakeven, and the breakeven is determined as in [10, 23] as $a_{j_\beta }$, where $\beta =\lfloor \frac{M+1}{2}\rfloor$. Meanwhile, the bid density breakeven index for the miners is the maximum index that satisfies $k=\mathop {\arg \min }_{k \in N} \{\theta _{i_{k+1}}<a_{j_\beta }\}$. During the selection of auction winners and pricing stage, we allocate computing resources according to the bid densities of miners and the current resource capacities of ECSPs. All the winning miners pay according to the breakeven price ${a_{j_\beta }}$, and the winning ECSPs are charged according to the breakeven price.

In Algorithm 1, Lines 1–8 select the candidate miners and ECSPs. All the unit resources costs of ECSPs that are higher than $a_{j_\beta }$ are eliminated: ${\mathbf{{a}}'\leftarrow \{a_{j_1},a_{j_2},\ldots ,a_{j_{\beta -1}}\}}$. For the candidate miners, the miners whose bid densities are higher than the breakeven point are selected: ${{\varvec{\Theta }}'\leftarrow \{\theta _{i_1},\theta _{i_2},\ldots ,\theta _{i_k}\}}$. Lines 9–17 allocate resources according to the bid densities of miners and the current resource capacities of ECSPs. The winning ECSPs are charged ${a_{{j_\beta }}}$, and all winning miners must pay according to the breakeven price ${a_{{j_\beta }}}$. After resource allocation is completed, the social welfare of the blockchain network is calculated according to the resource allocation scheme (Line 18 to Line 25).

4.2 Proof of desirable properties

Theorem 1

TDAMB satisfies individual rationality.

Proof

For any miner i, according to the TDAMB algorithm, if miner i wins the auction, her bid density is not lower than the breakeven price, and the payment is $p_i^\text {buyer} = {a_{j_\beta} } \cdot {d_i} \le {\theta _i} \cdot {d_i} = {v_i}$; i.e., the miner’s payment is not higher than her bid. Therefore, miner i will not sustain a loss in the auction.

For any ECSP j, according to the TDAMB algorithm, if ECSP j wins the sell-bid, the unit resource cost is not higher than the breakeven price. Therefore, $p_j^\text {seller} = {\mathrm{(}}{c_j} - {c_j}^\prime {\mathrm{)}} \cdot {a_{j_{\beta}} } \ge {\mathrm{(}}{c_j} - {c_j}^\prime {\mathrm{)}} \cdot {a_j}$, i.e., the ECSP charges no less than his asking price. Therefore, TDAMB satisfies individual rationality. $\square$

Theorem 2

TDAMB satisfies budget balance.

Proof

According to the TDAMB algorithm, all winning miners pay according to the breakeven price ${a_{j_\beta }}$ and the winning ECSPs are charged the price ${a_{j_\beta }}$; i.e., $\sum \limits _{j \in {{{{\mathcal {M}}}}^\text {win}}} {p_j^\text {seller}} = \sum \limits _{i \in {{{{\mathcal {N}}}}^\text {win}}} {p_i^\text {buyer}}$. Therefore, TDAMB satisfies budget balance. $\square$

To prove that TDAMB is truthful, we must prove that for any miner i or ECSP j, he or she cannot improve his or her utility by submitting an untruthful declaration valuation. To accomplish this, we first prove that the winner determination process satisfies monotonicity for both miners and ECSPs, and then prove that the pricing process is bid-independent. Through the above claims, we can prove that TDAMB is truthful.

(1) Monotonic winner determination

The following two lemmas summarize the monotonicity of the winner determination process for TDAMB.

Lemma 1

If miner i declares a buy-bid $\theta ^{\text {buyer}}_i= (d_i, v_i)$ and can bid successfully, when the information submitted by other miners and ECSPs remains unchanged, by bidding $(d_i, v'_i)$ with ${v_i}^\prime \ge {v_i}$, miner i also wins the bid.

Proof

Since miner i bids successfully, the bid density is not lower than the breakeven price. When her bid increases, the bid density increases simultaneously. According to the allocation rules, miner i can still win the bid. $\square$

Lemma 2

If ECSP j declares a sell-bid $\theta ^{\text {seller}}_j= (c_j, a_j)$ and can bid successfully, when the information submitted by other ECSPs and miners remains unchanged, by bidding $(c_i, a'_j)$ with ${a_j}^\prime \le {a_j}$, ECSP j also wins the bid.

Proof

Since ECSP j bids successfully, the unit resource cost is not higher than the breakeven price. According to the allocation rules, when the sell-bid decreases, ECSP j can still win the bid. $\square$

(2) Bid-independent pricing

We show that pricing is independent of bidding for both winning miners and ECSPs.

Lemma 3

When the information submitted by other miners and ECSPs is given, if bids $v_i$ and $v'_i$ can both be made successfully, the payments of miner i are the same.

Proof

According to the TDAMB algorithm, when miner i bids successfully, the payment is related only to the breakeven price and the miner’s resource requirement. Therefore, when bids $v_i$ and $v'_i$ are both made successfully, the payments are the same. $\square$

Lemma 4

When the information submitted by other ECSPs and miners is given, if the unit resource costs $a_i$ and $a'_i$ can both be bid successfully, ECSP j is charged the same price.

Proof

According to the TDAMB algorithm, when ECSP j bids successfully, the charged price is related to only the breakeven price and the resource capacity. Therefore, the pricing is bid independent for ECSPs. $\square$

Lemma 5

TDAMB satisfies truthfulness for miners.

Proof

To prove this lemma, we must prove that no miner i can improve her utility by bidding $v_i\ne v_i^{true}$. We examine all possible cases individually, as shown in Table 2.

• CASE 1: For these two bidding strategies, miner i fails in the auction and does not need to pay, resulting in her utility being zero.

• CASE 2: This case arises only when ${v_i} < v_i^{true}$ (Lemma 1). In this case, miner i bids untruthfully and loses the auction, leading to a utility of zero. In contrast, miner i wins the auction when she bids truthfully. Theorem 1 ensures that the utility she obtains in this case is nonnegative. Therefore, the utility of a truthful bidding by miner i is not lower than that of an untruthful bidding.

• CASE 3: This case arises only when ${v_i} > v_i^{true}$ (Lemma 1). In this case, miner i wins the auction when she bids untruthfully and loses when she bids truthfully. According to the TDAMB algorithm, there must be ${\theta _i}^{true} < {a_{j_\beta}}\le {\theta _i}$. Therefore, the utility when the miner bids untruthfully is ${v_i}^{true} - {a_{j_\beta}} \cdot {d_i} < 0$, which is lower than that of a truthful bidding (zero utility).

• CASE 4: For both bids, miner i wins the auction; by Lemma 3, we know the payments are both ${a_{j_\beta}} \cdot {d_i}$, resulting in the same utility.

In summary, no miner can improve her utility by making untruthful bids (Table 2). Our proof is complete. $\square$

Table 2 Four possible results for two bidding strategies, where ✓ indicates the bidder wins and ✗ indicates she fails

Lemma 6

TDAMB satisfies truthfulness for ECSPs.

Proof

Similarly, to prove this lemma, we must prove that no ECSP j can improve his utility by bidding $a_j\ne a_j^{true}$. We also examine all the possible cases individually, as shown in Table 2.

• CASE 1: The same as the miner case.

• CASE 2: This case arises only when ${a_j} > a_j^{true}$ (Lemma 2). Theorem 1 ensures a nonnegative utility when ECSP j submits truthful bid and wins the auction. Therefore, the utility of a truthful bidding by ECSP j is not lower than that of an untruthful bidding.

• CASE 3: This case arises only when ${a_j} < a_j^{true}$ (Lemma 2). In this case, ECSP j wins the auction when he bids untruthfully and loses when he bids truthfully; according to the TDAMB algorithm, $a_j \le {a_{j_\beta}} < a _j^{true}$. Therefore, the utility when the ECSP bids untruthfully is $(c_j - {c_j}^\prime) \cdot ({a_{j_\beta}} - a _j^{true}) < 0$ (${c_j}^\prime$ is the remaining resource capacity when the allocation is complicated), which is lower than that when ECSP j bids truthfully (zero utility).

• CASE 4: For both bids, ECSP j wins the auction. According to Lemma 4, the payments are both $(c_j - {c_j}^\prime) \cdot ({a_{j_\beta}} - a _j^{true}) > 0$, leading to the same utility.

From the above, no ECSP can improve his utility by making untruthful bids. Our proof is complete. $\square$

Theorem 3

TDAMB satisfies truthfulness.

Proof

Lemmas 5 and  6 together prove that TDAMB satisfies truthfulness.$\square$

Theorem 4

The time complexity of TDAMB is polynomial.

Proof

The TDAMB algorithm mainly consists of the candidate determination part, the selection of winners and pricing part and the social welfare calculation part. In the candidate determination stage, the highest time complexity is sorting candidates and the other parts are linear (Line 1 to Line 8). We use the classic fast sorting method, thus we spend $O(N\log N)$ sorting the miners (Line 3) and $O(M\log M)$ sorting the ECSPs (Line 4). In the selection of winners and pricing stage, when traversing each candidate miner, we sort all the candidate ECSPs based on the remaining capacity and find the ECSP that meets the capacity constraint (Line 9 to Line 17). The worst-case time complexity of this process is $O(NM\log M)$. In the social welfare calculation stage, we traverse each case of $x_{ij}$, so the time complexity is O(NM). Therefore, the overall time complexity of TDAMB is $O(N\log N+NM\log M)$, which is polynomial. The time complexity of the ICAMP algorithm commonly used for comparison in the research of bidirectional auction mechanisms is $O(NM(M+\log N))$ [10]. Therefore, the TDAMB algorithm has lower time complexity and more efficient execution. $\square$

5 A double auction mechanism based on a critical value (DAMCV)

5.1 The framework of DAMCV

As many feasible pairs of miners and ECSPs are not included according to the breakeven, the system efficiency of TDAMB is limited. To enhance the system efficiency , we design a double auction mechanism based on a critical value, i.e., DAMCV, which partly relaxes the constraints on the truthfulness of ECSPs. The critical idea of DAMCV is to maintain as many feasible matches among miners and ECSPs as possible, and the pricing scheme is based on the critical value of buyers. On the basis of the definition in [30, 31], if the miner’s bid is not lower than her critical value, the miner must win the auction; otherwise, she will lose.

The candidate determination method in Algorithm 2 is similar to that of TDAMB. ECSPs and miners are first sorted according to the same rules as TDAMB, as shown in Lines 3 and 4. Next, we eliminate the failed ECSPs whose asks are higher than $\theta _{i_1}$ and miners whose bid densities are less than $a_{j_1}$, as shown in Lines 5 and 6. In the winner determination and pricing part, we allocate resources according to the bids of miners and ECSPs and the current resource capacities of ECSPs (Line 7 to Line 14). For the winning miners, Lines 15–29 use the dichotomy to find the critical values. All winning miners must pay according to their critical values, and the winning ECSPs are charged with the matching miners’ payments. After resource allocation is completed, the social welfare of the blockchain network is calculated according to the resource allocation scheme (Line 30).

5.2 Proof of desirable properties

Theorem 5

DAMCV satisfies individual rationality.

Proof

For any miner i, according to the DAMCV algorithm, if miner i wins the auction, her payment is her critical value, which is not higher than her bid. Therefore, miner i will not sustain a loss in the auction.

For any ECSP j, according to the DAMCV algorithm, if ECSP j wins the sell-bid, no charged price is less than his asking price. Therefore, DAMCV satisfies individual rationality. $\square$

Theorem 6

DAMCV satisfies budget balance.

Proof

According to the DAMCV algorithm, the payment price depends on the miners’ critical values, i.e., $\sum \limits _{j \in {{{{\mathcal {M}}}}^\text {win}}} {p_j^\text {seller}} = \sum \limits _{i \in {{{{\mathcal {N}}}}^\text {win}}} {p_i^\text {buyer}}$. Therefore, DAMCV satisfies budget balance. $\square$

Similar to TDAMB, to prove DAMCV’s truthfulness for miners, we show that for miners, the winner determination process is monotonic and the pricing process is bid-independent. Through these two claims, we prove DAMCV’s truthfulness for miners.

Lemma 7

The winner determination of DAMCV is monotonic for miners.

Proof

Since miner i bids successfully, the bid density is not lower than her critical value. When the bid increases, the bid density increases. According to the allocation rules, miner i can still win the bid. $\square$

Lemma 8

The pricing of DAMCV is bid independent for miners.

Proof

According to the DAMCV algorithm, when miner i bids successfully, the payment is related to only her critical value. Therefore, when bids $v_i$ and $v'_i$ are both made successfully, the payments are the same. $\square$

Theorem 7

DAMCV satisfies truthfulness for miners.

Proof

We prove this theorem by showing that no miner i can improve her utility by bidding $v_i\ne v_i^{true}$. We examine all possible cases individually, as shown in Table 2.

• CASE 1: For these two bidding strategies, miner i fails in the auction and she does not need to pay, leading to a utility of zero.

• CASE 2: This case arises only when ${v_i} < v_i^{true}$ (Lemma 7). In this case, miner i bids untruthfully and loses the auction, resulting in a utility of zero. In contrast, miner i wins the auction when she bids truthfully. Theorem 4 ensures that the utility she obtains in this case is nonnegative. Therefore, the utility of a truthful bidding by miner i is not lower than that of an untruthful bidding.

• CASE 3: This case arises only when ${v_i} > v_i^{true}$ (Lemma 7). In this case, miner i wins the auction when she bids untruthfully and loses when she bids truthfully. According to the DAMCV algorithm, her truthful bid is lower than her critical value, and her untruthful bid is not lower than her critical value. Therefore, the utility when the miner bids untruthfully is less than zero, which is less than that when miner i bids truthfully (zero utility).

• CASE 4: For both bids, miner i wins the auction; according to Lemma 8, the payments are both made according to her critical value, leading to the same utility.

In summary, no miner can improve her utility by making untruthful bids. Our proof is complete. $\square$

Theorem 8

The time complexity of DAMCV is polynomial.

Proof

The DAMCV algorithm consists of four parts: the candidate determination part, the selection of winners part, the pricing part and the social welfare calculation part. The candidate determination stage is similar to that of TDAMB, we spend $O(N\log N+M\log M)$ to sort the miners and ECSPs (Line 1 to Line 6). In the selection of winners stage, when traversing each candidate miner, we traverse the candidate ECSPs to find the ECSP that meets the capacity constraint (Line 7 to Line 14). The worst-case time complexity of this process is O(NM). In the pricing stage, for each $x_{ij}=1$, we use the dichotomy to find the critical values and every time we call the previous program with the time complexity of $O(N\log N+M\log M+NM)$ (Line 15 to Line 29). In the worst-case scenario, the time complexity of dichotomy is related to the maximum bid of all the miners $b_{max}$ and the accuracy $\varepsilon$. The time complexity of dichotomy is $O(\log (b_{max/}\varepsilon ))$. Thus, the time complexity of the pricing stage is $O((N\log N+M\log M+NM)\log (b_{max/}\varepsilon ))$. Therefore, we can conclude that the time complexity of DAMCV is $O((N\log N+M\log M+NM)\log (b_{max/}\varepsilon ))$, which is polynomial. $\square$

6 Experimental results and analysis

This section first conducts a real-world experiment to verify our proposed hash power function. We use the Ethereum platform because Ethereum utilizes PoW consensus mechanism and it is one of the most well-established and widely adopted blockchain platforms. Then, through multiple sets of numerical simulation experiments, we evaluate the system efficiency of our proposed TDAMB and DAMCV under different miner and ECSP scales. Finally, we verify the economic properties of the proposed algorithms.

6.1 Verification of the hash power function

We first design a DAPP based on Ethereum on the Android platform and implement it on the Alibaba Cloud Elastic Compute Service (ECS). There are three ECSPs with 8 vCPUs and 16 GB memory and three lightweight miners with 2 vCPUs and 4 GB memory in the entire blockchain network. Each ECSP provides services to one miner. The CPU utilization of the ECSPs and miners is managed by the Docker platform. To verify our presented hash power function, we fix two lightweight miners’ local computing powers (miner CPU utilization) at 50 and 100, and we fix two lightweight miners’ requests (ECSP CPU utilization) at 40 and 60. Figure 3 depicts the change in miner 3’s hash power, that is, the proportion of the number of blocks miner 3 successfully mines to the total number of blocks when she has different local computing power and resource requests. Figure 3a fixes miner 3’s local computing power to 50 and varies miner 3’s resource request. Figure 3b fixes miner 3’s resource request to 50 and varies miner 3’s local computing power. To remove the influence of randomness and ensure the correctness of the experiment, we tested 10 blockchain networks, each of which generated 100 blocks, and averaged the experimental results. As expected, the hash power defined in formula (1) fits the real results well.

Fig. 3

Comparison of real experiment results with our proposed function

6.2 Numerical results

To evaluate the effectiveness of our proposed double auction mechanisms, we introduce the existing ICAMP algorithm [10] for comparison. ICAMP is an incentive-compatible double auction algorithm. We vary the number of miners from 50 to 500 and the number of ECSPs from 10 to 100. The miners’ block sizes are uniformly distributed within (0,1000], the local computing power is uniformly distributed on the interval (0,5] and the demand is uniformly distributed on the interval (0,20]. The resource capacity of the ECSPs follows a uniform distribution within [50,100], and the unit resource cost of the ECSPs follows a uniform distribution over [10,60]. The other parameter values are the same as those in [9]. To ensure the universality of the experiment, each experimental result is the average of 100 simulations.

6.2.1 Performance under different miner scales

In this experiment, to analyze the relationship between performance and miner size, we fix the number of ECSPs at 50 and vary the number of miners from 50 to 500. The performance of our algorithms is analyzed under different miner scales in terms of social welfare, the resource utilization of ECSPs, the ratio of successful miners and ECSPs, and the total user utility of miners and ECSPs. The comparison results of the three algorithms in terms of social welfare are shown in Fig. 4. The social welfare of all algorithms increases simultaneously with the number of miners. TDAMB and DAMCV both exhibit clear superiority to ICAMP, as ICAMP allows an ECSP to serve only one miner. Additionally, DAMCV results in higher social welfare than TDAMB because TDAMB eliminates some feasible pairs of ECSPs and miners.

Fig. 4

The social welfare under different miner scales

Fig. 5

The resource utilization of ECSPs under different miner scales

Fig. 6

The ratios of successful miners and ECSPs under different miner scales

Fig. 7

The utility of served miners and ECSPs under different miner scales

Figure 5 compares the average resource utilization rates of successful ECSPs. Resource utilization is defined as (Total allocated resources / Total resource capacity of successful ECSPs). All the ratios of ICAMP are very low because ICAMP allows an ECSP to serve only one miner and the resources of the remaining ECSPs are sufficient. As the number of miners increases, the resource utilization of TDAMB and DAMCV increases and the utilization of DAMCV is typically higher than that of TDAMB. This is because more winning miners and ECSPs are selected in DAMCV, and thus more hardware resources are utilized.

Figure 6 compares the ratios of successful miners and ECSPs. As shown in Fig. 6a, as the number of miners increases, the ratios of served miners for ICAMP and DAMCV decrease because the competition becomes fiercer. The ratio of TDAMB remains approximately 0.45 because TDAMB eliminates approximately half of the miners according to the breakeven value. The ratios of the successful miners for our proposed algorithms are both typically higher than that of ICAMP. This is due to our mechanisms can select more miners. As shown in Fig. 6b, all the ratios of successful ECSPs of ICAMP are higher than those of our proposed algorithms because ICAMP allows an ECSP to serve only one miner.

Figure 7 compares the total utility of miners and ECSPs. As shown in Fig. 7a, the total utility of miners for both of our proposed algorithms is higher than that of ICAMP at all miner scales. Interestingly, the utility of miners in TDAMB increases quickly when the scale of miners is less than 300 and decreases very slowly when the scale of miners is large. This is because when the miner scale is large, each miner competes with greater intensity, and the payment of each successful miner increases; thus, the utility of each successful miner decreases. In spite of this, the total number of successful miners does not increase substantially, thus leading to a lack of increase in total utility. In Fig. 7b, we can see a comparison of the total utility of ECSPs, and the performance of our proposed algorithms is much better than that of ICAMP. This is because our algorithms can select more miners and ECSPs, and thus the total payment and utility increase. In general, as the miner scale increases, the results of ICMAP do not change much, and our proposed algorithms TDAMB and DAMCV are more superior to ICMAP.

6.2.2 Performance under different ECSP scales

In this test, we fix the number of miners at 300, and the number of ECSPs varies from 10 to 100. We also analyze the performance with respect to social welfare, the resource utilization of ECSPs, the ratio of successful miners and ECSPs, and the total utility of miners and ECSPs. Figure 8 shows that the social welfare of TDAMB and DAMCV is noticeably higher than that of ICAMP. As shown in Fig. 8, the social welfare of TDAMB and DAMCV increases sharply when the scale of ECSPs is less than 30 and decreases when the number of ECSPs is large. This is because when the number of ECSPs is small, the competition between ECSPs is not fierce. With the increase in ECSPs, more ECSPs and miners are selected as winners, and thus, social welfare increases. As shown in Fig. 9, all the ratios of ICAMP are very low, and when the number of ECSPs increases, the resource utilization of TDAMB and DAMCV decreases. This is because when the ECSP scale is large, the resources of the remaining ECSPs are sufficient. As shown in Fig. 10a, as the number of ECSPs increases, the ratios of served miners for ICAMP and DAMCV increase sharply and the ratios for TDAMB change little when the scale of the ECSPs is more than 30. This is because when the number of ECSPs increases, DAMCV can select many more miners. As shown in Fig. 10b, when the number of ECSPs increases, the ratios of served ECSPs for DAMCV decrease because the competition among ECSPs becomes fiercer. The ratio of TDAMB increases when the scale of ECSPs is less than 30 and decreases when the number of ECSPs is large, and the ratio of ICAMP shows little change. This is because when the number of ECSPs increases, the competition between ECSPs in DAMCV becomes fiercer. In Fig. 11a, DAMCV exhibits clear superiority to ICAMP and TDAMB. This is because DAMCV can serve many more miners. As shown in Fig. 11b, the utility of ECSPs in TDAMB and DAMCV increases sharply when the scale of miners is lower than 50 and decreases very slowly when the number of ECSPs is large. This is because when the scale of ECSPs is small, the competition between ECSPs is not fierce. With the increase in ECSPs, more ECSPs are selected, thus, the utilities of ECSPs increase. However, when the scale of ECSPs becomes large, the competition becomes fiercer.

Fig. 8

The social welfare under different ECSP scales

Fig. 9

The resource utilization of ECSPs under different ECSP scales

Fig. 10

The ratios of successful miners and ECSPs under different ECSP scales

Fig. 11

The utility of served miners and ECSPs under different ECSP scales

6.2.3 Economic property verification

This experiment verifies the economic properties of TDAMB and DAMCV. In Fig. 12a and b, we compare the bid density, payment density and ask for TDAMB and DAMCV with 50 ECSPs and 50 miners. Each bar in the histogram represents a successful match between ECSPs and miners. There are far more winning miners in DAMCV than that in TDAMB. For both TDAMB and DAMCV, each winning miner pays a price not higher than her bid density; at the same time, each winning ECSP is charged a price not lower than his ask. Thus, both TDAMB and DAMCV are individually rational.

Figure 13 shows the truthfulness of TDAMB and DAMCV. Figure 13a shows the situation for miner 1 in TDAMB. Her truthful buy-bid $\theta ^{\text {buyer}}_1= (10, 390)$, where 10 is her resource requirement and 390 is the truthful valuation of her resource. Thus her truthful bid density is 39. The breakeven price of the TDAMB algorithm is 34. When miner 1 wins, as she requires 10 resources and the breakeven price is 34, she needs to pay $34 \times 10=340$. According to the definition of miner utility, i.e., the utility is the difference between her truthful valuation and her payment, the utility of miner 1 is $390-340=50$. When her bid falls below 340, she will fail in the auction, leading to a utility of zero. When miner 1’s bid exceeds 340, she can always win the auction, and her utility is always 50, because if miner 1 wins, the change in her bid has no effect on the breakeven price; therefore, there will not be any change in the payment, and the utility will remain unchanged.

Figure 13b shows the situation for ECSP 1 in TDAMB. ECSP 1’s truthful sell-bid $\theta ^{\text {seller}}_1= (30, 24)$, where 30 is his resource capacity and 24 is the truthful unit resource cost of ECSP 1, which represents the minimum unit price that he is willing to charge. In the TDAMB algorithm, ECSP 1 successfully allocates 21 resources and the breakeven price is 34. When ECSP 1 wins, as the utility is the payment from miners he serves minus his truthful unit resource cost multiplied by the resource he allocates, ECSP 1’s utility is $21 \times 34-21 \times 24=210$. By constantly changing his bid, as long as his unit resource cost is lower than 34, ECSP 1 can always win the auction, and his utility remains at 210. When the unit resource cost exceeds 34, he fails in the auction, so the utility is 0.

As shown in Fig. 13c, in DAMCV, the critical value of miner 1 is 22. When miner 1’s bid density is lower than 22, i.e., her bid is lower than 220, she cannot win the auction and her utility is zero. When the miner’s bid is higher than 220, her utility remains at $390 -220=170$, because when miner 1 wins the auction, changing her bid will not change her critical value; therefore, the payment will never change, and the utility will remain unchanged.

Fig. 12

Individual rationality of TDAMB and DAMCV

Fig. 13

Truthfulness of TDAMB and DAMCV

7 Conclusion

This paper focuses on the problem of edge computing resource allocation in a blockchain network. Specifically, we propose two double auction mechanisms, TDAMB and DAMCV, to maximize the social welfare of blockchain networks. We also prove that TDAMB satisfies three economic properties–individual rationality, budget balance and truthfulness–for both miners and ECSPs, while DAMCV can achieve higher system efficiency and guarantee individual rationality, budget balance and truthfulness for miners but cannot satisfy truthfulness for ECSPs. In our experiments, we first verified the proposed hash power function with a real-world experiment on a PoW-based blockchain network. Finally, compared with the enumeration algorithms and the methods reported in existing research, our proposed auction mechanisms obtain better results in terms of social welfare, the ratio of successful miners and ECSPs, the total user utility of miners and ECSPs, the resource utilization of ECSPs, and algorithm execution time. In future work, we will study online time-varying edge computing resource allocation problems in blockchain networks to improve the practicality of double auction mechanisms. Multiple types and time-varying hardware resources are considered. The system runs in time slots and ECSPs can provide multiple types of hardware resources for a long time. Moreover, at each time slot, the capacity of each hardware resource for each ECSP is variable. Meanwhile, miners can specify the start and end times for using hardware resources. The resource requirements of each miner are also time-varying. On the other hand, we intend to incorporate security and credibility into the design of auction mechanisms. We plan to design a secure and privacy edge computing double auction mechanism based on order preserving encryption, Paillier homomorphic encryption and other algorithms. Additionally, we intend to proof the security through the random-oracle machine model.