1 Introduction

With the rapidly developing and popularizing of Internet, Peer-to-Peer (P2P) network technology has been developed speedily. The P2P network architecture in which no central server is completely different from the traditional C/S (Client/Server) model. And the basic feature is that each node of the system is P2P, i.e., each node is both a client and a server. Due to single-user computers being used as multi-user computers, P2P systems suffer from poor network security and difficulties in resource backup and recovery when large amounts of data are exchanged in [1]. Therefore, the number of nodes is an important determinant for network performance. The node evolution, scalability, efficiency of file sharing, and incentives to prevent free-riding is receiving increasing attention.

1.1 Related work

Yang et al. [2] investigated the performance of P2P file sharing systems from the perspective of service capacity. And they found that the performance of the P2P system showed excellent scalability in both transient and steady-state cases as the load increased. Silva et al. [3] focused on the P2P scalability problem, where achievable throughput models were proposed under different strategies for selecting peers and blocks computationally. From these models, new insights were gained about the behavior of P2P cluster systems, which motivated publishers and peers, so that overall performance was improved. Shi et al. [4] presented a file sharing system building on a hybrid hierarchical P2P which is a two-layer hybrid network that combines the strongpoint of DHT and flooding methods. Through experiments, it was proved that the system has high query efficiency, extensibility and relatively good stability. Kyoungsoo et al. [5] proposed a collaborative caching scheme for clustered multimedia data in mobile P2P networks based on node connectivity. In this scheme, metadata of popular multimedia data were propagated to neighboring peers for efficient data search. According to the cooperative cache policy, the query was processed in the order of local cache, metadata, affiliated cluster and adjacent cluster. Al-Janabi et al. [6,7,8] provide an overview of the main challenges and issues related to Mobile Cloud Computing. Recent work and countermeasure solutions to the challenges are presented, and finally the issue of openness and guiding future research is highlighted.

For the problem of node access failure when P2P nodes exit and join the network freely, Zheng et al. [9] proposed a pre-switching algorithm based on the backup of P2P file resources shared. The node’s access service will switch to the standby node in advance by predicting the survival time of the network node. The retrieval service blind spot caused by the service node monitoring cycle is shortened and access failures are reduced. Premakumari et al. [10] investigated a malicious peer detection system based on feed-forward back-propagation neural networks [11, 12]. Using the neural network to train and classify the extracted features, the performance of the malicious peer detection system was analysed in terms of both time delay and detection rate. Singh et al. [13] simulated user mobility by selecting two types of mobility models and quantified the failure rate of mobile nodes, lifetime of mobile nodes, available bandwidth, stability cost of per node, etc. Marozzo et al. [14] showed how to reduce energy consumption in BitTorrent using sleeping and wake-up method that allowed seeds to cycle between wake-up and sleeping modes. Experiments not only demonstrated energy savings, but also ensured excellent file sharing performance.

In a cloud P2P system, more replicas are available, the access latency is lower and the maintenance overhead is higher, and vice versa. Sun et al. [15] proposed a new online replica deduplication policy to reduce the impact on other nodes when deleting redundant replicas. A fuzzy cluster analysis approach is applied to obtain the optimal deleted replicas from the set of file replicas. Heyman et al. [16] developed a method for analyzing feedback-based traffic and congestion control protocols, which was described using a burst traffic model for network users. Singha et al. [17] presented a new incentive mechanism to strengthen cooperation in wireless environments. Using Nash equilibrium, the simulation verified the effectiveness of these mechanisms in enhancing cooperation among users. Liu et al. [18] discussed the equilibrium strategy for the mixed overlay/underlay spectrum sharing approach in cognitive radio networks, divided into visible and invisible. Based on the social optimum and spectrum revenue maximization, a pricing mechanism was derived for cognitive users. Fu et al. [19] develop a multi-server queueing model with preemption priority to analyze the stochastic behavior of different users. For maximizing the social benefits of the system [20], a revenue function is constructed and a pricing strategy is proposed that charges an appropriate trial fee for normal tasks. Zhang et al. [21] proposed a penalty strategy with differentiated service rates for the free-riding phenomenon in P2P networks, and an M/M/c queueing model is developed. Based on this model, a sleep/wake mechanism is introduced for the service side and a single asynchronous leave policy is used to reduce the energy consumption of the system.

Ge et al. [22] modeled the P2P system as a multi-class closed queueing network, where each class can be composed of a fixed cluster of nodes, and the performance of the P2P file sharing system was studied by simulating. Wang et al. [23] introduced queueing models with customer retrials and service level differentiation strategy. With a reasonable allocation of service rates and retrial of customers, the average waiting time for customers can be reduced without the need for additional service capacity. Dudin et al. [24] analyzed a queueing model consisting of two multi-server queues with finite buffers and common arrival process. According to the share of lost clients in each queue, the stationary distribution of the two queueing states was calculated. Xu et al. [25] developed an M/M/1 (the inflow process is a Poisson flow, the service time follows an exponential distribution, the system has one server for parallel service, and the system capacity is infinite) working vacation queueing model with strategies including negative customers and closed-down periods. The distributions of steady-state and waiting time were obtained by using the QBD process and matrix-geometric solution method. The optimal design for ATM network queueing was provided. Panda et al. [26] studied the economic analysis of a single-server Markov queueing system with positive customers, negative customers and multiple working vacations. The equilibrium strategies and social benefits of positive customers were obtained in visible, almost visible, invisible and almost invisible cases. The effects of model parameters and information level on the equilibrium joining behavior of positive customers were demonstrated through numerical experiments. Ma et al. [27] solved M/M/1 queueing system with multiple vacation and fault repairable by using generating function. Based on the game theory [28], utility functions were constructed. Meanwhile equilibrium strategies and social optimal strategy were analyzed. Si et al. [29] studied the feedback of requesting nodes, which are reflected in the dynamic changes of nodes, introduced the work fault repairable and impatient customer strategy. The performance of P2P network system was modeled and analyzed.

1.2 Our motivation

P2P network is a distributed application architecture that distributes tasks and workloads among peers, which is a form of networking or network formed by the P2P computing model at the application layer. In the P2P structure, most nodes have the functions of information consumer, information provider and information communication simultaneously. Each node takes on a limited number of storage and computation tasks.

As the number of nodes requesting to join the network increases, the resources contributed by nodes are abundant and therefore the quality of service improves. However, the increase in the number of service nodes with the addition of malicious nodes will lead to a higher probability of system failure. Owing to the fact that requesting nodes are not fully aware of the state of the server before entering the system (almost invisible state), i.e., they do not know the number of nodes waiting to be served in the system, but know the state of the serving nodes. Therefore, the requesting nodes will enter the system with probability, i.e., there is a gaming behavior among them.

We propose to consider the factors that lead to the instability of the system in the almost invisible scenario, including dynamic changes of service nodes, malicious nodes, etc. To save system energy, the working sleep of the service nodes, as well as the start-up and shut-down periods of the system are considered. The energy consumption, file transfers, download congestion and other problems of the P2P network is further optimized and the service pressure on the system is reduced.

1.3 Contribution

In this paper, the performance of P2P file transmission systems is analyzed in terms of the service capability. The node scheduling problem of P2P networks is studied by utilizing queueing theory. In order to save energy and guarantee the stability of the P2P system, an M/M/c (that the inflow process is a Poisson flow, the service time follows an exponential distribution, the system has c server for parallel service, and the system capacity is infinite) queueing system with start-up period, close-down period and working sleeping of service nodes is established. Considering the dynamic changes of nodes and malicious nodes in the almost invisible case, the energy consumption and download congestion are further optimized during file transmission in the P2P networks. The contributions of this paper are threefold.

  • To guarantee the stability of P2P system operation, an M/M/c queueing model is developed with the strategies of dynamic changes of servers, working sleep, start-up period and close-down period. The main purpose of this paper is to investigate how the arrival rate of the requesting nodes and the working sleep rate of the service nodes can decrease delay and increase social utility of system.

  • A three-dimensional continuous time Markov stochastic model is established, the steady-state distribution of system is derived by using matrix-geometric solution method, thereby relevant expressions of performance indicators are obtained.

  • The individual utility function and the social utility function is defined. The effects of parameter variations on the performance indicators of P2P network systems are derived through numerical analysis. Nash equilibrium and social optimization strategies are analyzed in detail. Appropriate arrival rate and working sleep rate can reduce energy consumption and enhance social utility in the P2P system.

The rest of this paper is organized as follows. In Sect. 2, the operating mechanism of the P2P system is introduced, and the relevant parameters are assumed. In Sect. 3, a three-dimensional Markov chain is constructed, and the steady-state distribution is derived. In Sect. 4, the performance indicators are evaluated by using numerical experiments and social optimal strategy are analyzed by Nash equilibrium strategy. Conclusions are introduced in Sect. 5.

2 Model description of the P2P system

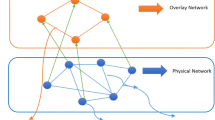
The hybrid P2P network uses server routing, which stores the directory information of each node’s network connection, and provides shared file retrieval services to all resource requesting nodes. Once the requesting node has retrieved the network connection of the service node and the directory information of the system, it can send a file request to the service node. Then the file resources are available to the requesting node through a file exchange. The system server is also responsible for refreshing the node connection information after the master node exits the network. The requesting node simply provides a query to the server, which gives a reply containing the information of the file owner, and the requesting node establishes a link directly with the file owner, i.e., the service node, to download the file. The operation mechanism of the hybrid P2P system is shown in Fig. 1.

Fig. 1
figure 1

The operation mechanism of the hybrid P2P network

Full size image

In this paper, the behavior of node is mainly considered during file transfer, after the node completes a query in a hybrid P2P network. There is a queueing problem between requesting nodes, when c service nodes need to satisfy the requests of a large number of requesting nodes around them. In an open and anonymous P2P system, arbitrary nodes are allowed to join and leave. Some malicious nodes may take the opportunity to harm the system and increase the instability of the P2P system. Therefore, the file transmission process is abstracted into service process, and the queueing model is applied to the P2P networks to analyze the dynamic changes of nodes, etc. A queueing model with malicious nodes, start-up period, close-down period, node dynamics and working sleeping is developed, which analyze the P2P network system performance in almost invisible cases. The node server scheme proposed in this paper is shown in Fig. 2. Relevant system parameters are also assumed as follows.

  1. (1)

    The arrival time of the requesting node follows the exponential distribution with parameter \(\lambda\), and the arrival time of the malicious node follows the exponential distribution with parameter \(\varepsilon\). Malicious nodes can be seen as a malfunction in the normal process operation in the system or an insecure factor outside the system that prevents system from working properly, and its main purpose is to offset the requesting node that is receiving or waiting for service. (i) If there are no requesting nodes in the system when the malicious node arrives, malicious nodes that do not themselves receive services will disappear automatically. (ii) If there is a requesting node when the malicious node arrives, the arriving malicious node one-to-one will offsets the requesting node at the end of the queue (regardless of whether the requesting node is waiting or being served), i.e., RCE (Removal of Customers in the End) offset policy.

  2. (2)

    The service time of the service node follows the exponential distribution with parameter \({\mu _{1}}\) in the official working period. Assume that there are \(n(n\le c)\) requesting nodes, \(m(m\le c)\) seeds, and the download rate is \(m{\mu _{1}}(m<n)\) or \(n{\mu _{1}}(n\le m)\). The minimum number of nodes in the online state of the system is 1 and the number of all nodes that can be utilized is c.

  3. (3)

    Nodes that served completion not only can remain in the system to serve other nodes as seeds (nodes that have a complete copy after the download is completed) with probability \(\alpha (0<\alpha <1)\), but also can leave system with probability \({\bar{\alpha }}({\bar{\alpha }}\text {=}1-\alpha )\).

  4. (4)

    At the end of the official working period of the system, if there are no requesting nodes in the system, the system will close down and the closing time D follows the exponential distribution with parameter \(\gamma\). (i) If a requesting node arrives during the close-down period, a new official work period is opened. (ii) If no requesting node arrives during the close down period, the service node starts a working sleep of random length V at the end of the close-down period, and the working sleep time V follows the exponential distribution with parameter \(\theta\). During the working sleep period, the service node serves the requesting node at a lower service rate, and the service time follows the exponential distribution with parameter \({\mu _{2}}\) \(({\mu _{2}}<{\mu _{1}})\). When a working sleep period ends, the system has a start-up delay and requesting nodes not available for service immediately, the system must go through a buffered warm-up period, which defined as a start-up period. The start-up time U follows the exponential distribution with parameter \(\beta\). The service node enters the official working period after the start-up period.

  5. (5)

    In the almost invisible case, the requesting node can query the status of the service node through the server routing, but it cannot query the number of requesting nodes waiting for the service at time t in the system. Since the requesting nodes are indistinguishable, nodes have a game, where the mixed strategy can be represented by the probability of the requesting node access to the P2P system. The objective is to determine the optimal stopping strategy for the requesting node. Therefore, according to the decision behavior of the requesting node, whose entry probability can be expressed as \(({{q}_{0}},{{q}_{1}},{{q}_{2}}),(0\le {{q}_{i}}\le 1,i=0,1,2)\), and their equilibrium mixed stopping strategy can be denoted as \(({{q}_{0}^{(e)}},{{q}_{1}^{(e)}},{{q}_{2}^{(e)}})\).

  6. (6)

    Assume that the arrival time of the requesting node and the malicious node, the working sleeping time, the start-up time, close-down time, the service time during the official working and working sleeping periods are independent mutually, The service rule is FCFS (First Come First Served).

Fig. 2
figure 2

The node server scheme proposed in this paper

Full size image

3 Modeling analysis of P2P system

3.1 State transition rate matrix

Let L(t) denote the number of requesting nodes at time t, Y(t) denote the number of service nodes at time t, J(t) denote status of the system at time t, and

  1. (1)

    \(J(t)=0\) denotes system is in working sleep period at time t,

  2. (2)

    \(J(t)=1\) denotes system is in close-down period or start-up period at time t,

  3. (3)

    \(J(t)=2\) denotes system is in official working period at time t.

Then \(\{(L(t),Y(t),J(t)),t\ge 0\}\) indicate an Markov process, which has the state space as follows:

$$\begin{aligned} \Omega =\{(i,l,j),i\ge 0,1\le l\le c,j=0,1,2\} \end{aligned}$$

where the state set \((i,1,0),(i,1,1),(i,1,2)(i,2,0),(i,2,1) (i,2,2)\cdots (i,c,0),(i,c,1),(i,c,2),\) is the level \(i (i\ge 0)\).

By arranging the states in lexicographical order, the state transition rate matrix of the system can be described.

$$\begin{aligned} \varvec{Q}=\left[ \begin{array}{*{35}{l}} {{\varvec{A}}_{0}} &{} {{\varvec{C}}_{0}} &{} {} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {{\varvec{B}}_{1}} &{} {{\varvec{A}}_{1}} &{} \varvec{C} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{B}}_{2}} &{} {{\varvec{A}}_{2}} &{} \varvec{C} &{} {} &{} {} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} \ddots &{} \ddots &{} {} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{B}}_{c-1}} &{} {{\varvec{A}}_{c-1}} &{} \varvec{C} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {} &{} \varvec{B} &{} \varvec{A} &{} \varvec{C} &{} {} \\ {} &{} {} &{} {} &{} {} &{} {} &{} \ddots &{} \ddots &{} \ddots \\ \end{array} \right] \end{aligned}$$
(1)

where \({{\varvec{A}}_{0}}\), \({{\varvec{C}}_{0}}\), \({{\varvec{B}}_{1}}\), \({{\varvec{A}}_{i}}(1\le i\le c)\), \({{\varvec{B}}_{i}}(2\le i\le c)\), \(\varvec{C}\) denote the state transition rate between corresponding levels respectively, and they are all 3c-dimensional matrices. Let \(\varvec{A}={{\varvec{A}}_{c}}\), \(\varvec{B}={{\varvec{B}}_{c}}\). For writing convenience, the following symbols are defined:

$$\begin{aligned}&{{\delta }_{i}}=-\lambda {{q}_{0}}-i{{\mu }_{2}}\alpha -\varepsilon -\theta -i{{\mu }_{2}}{\bar{\alpha }}, 1\le i\le c, \\&\quad {{\sigma }_{i}}=-\lambda {{q}_{2}}-i{{\mu }_{1}}\alpha -\varepsilon -i{{\mu }_{1}}{\bar{\alpha }}, 1\le i\le c. \\&\quad {{\varvec{A}}_{0}}=\left[ \begin{matrix} {{\varvec{A}}_{0,1}} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{A}}_{0,1}} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{A}}_{0,1}} \\ \end{matrix} \right] , \\&\quad {{\varvec{A}}_{0,1}}=\left[ \begin{matrix} -\lambda {{q}_{0}} &{} 0 &{} 0 \\ 0 &{} -\lambda {{q}_{1}} &{} 0 \\ 0 &{} \gamma &{} 0 \\ \end{matrix} \right] , \\&\quad {{\varvec{C}}_{0}}=\left[ \begin{matrix} \lambda {{q}_{0}} &{} {} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {} &{} \lambda {{q}_{1}} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {} &{} {} &{} 0 &{} {} &{} {} &{} {} &{} {} \\ {} &{} {} &{} {} &{} \ddots &{} {} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {} &{} \lambda {{q}_{0}} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {} &{} {} &{} \lambda {{q}_{1}} &{} {} \\ {} &{} {} &{} {} &{} {} &{} {} &{} {} &{} 0 \\ \end{matrix} \right] , \\&\quad {{\varvec{B}}_{1}}=\left[ \begin{matrix} {{\varvec{B}}_{1,1}} &{} {{\varvec{B}}_{1,2}} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{B}}_{1,1}} &{} {{\varvec{B}}_{1,2}} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} \ddots &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{B}}_{1,1}} &{} {{\varvec{B}}_{1,2}} \\ {} &{} {} &{} {} &{} {} &{} {{\varvec{B}}_{1,1}} \\ \end{matrix} \right] , \\&\quad {{\varvec{B}}_{1,1}}=\left[ \begin{matrix} {{\mu }_{2}}\alpha +\varepsilon &{} 0 &{} 0 \\ 0 &{} \varepsilon &{} 0 \\ 0 &{} {{\mu }_{1}}\alpha +\varepsilon &{} 0 \\ \end{matrix} \right] , \\&\quad {{\varvec{B}}_{1,2}}=\left[ \begin{matrix} {{\mu }_{2}}\alpha &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} {{\mu }_{1}}\alpha &{} 0 \\ \end{matrix} \right] . \end{aligned}$$

When \(1\le i\le c\),

$$\begin{aligned}&{{\varvec{A}}_{i}}=\left[ \begin{matrix} {{\varvec{A}}_{i,1}} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{A}}_{i,1}} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{A}}_{i,1}} \\ \end{matrix} \right] , \\&\quad {{\varvec{A}}_{i,1}}=\left[ \begin{matrix} {{\delta }_{i}} &{} \theta &{} 0 \\ {} &{} -\lambda {{q}_{1}}-\varepsilon -\beta &{} \beta \\ {} &{} {} &{} {{\sigma }_{i}} \\ \end{matrix} \right] . \end{aligned}$$

When \(2\le i\le c\),

$$\begin{aligned}&{{\varvec{B}}_{i}}=\left[ \begin{matrix} {{\varvec{B}}_{i,1}} &{} {{\varvec{B}}_{i,2}} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{B}}_{i,1}} &{} {{\varvec{B}}_{i,2}} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} \ddots &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{B}}_{i,1}} &{} {{\varvec{B}}_{i,2}} \\ {} &{} {} &{} {} &{} {} &{} {{\varvec{B}}_{i,1}} \\ \end{matrix} \right] , \\&\quad {{\varvec{B}}_{i,1}}=\left[ \begin{matrix} {{\mu }_{2}}\alpha +\varepsilon &{} 0 &{} 0 \\ 0 &{} \varepsilon &{} 0 \\ 0 &{} 0 &{} {{\mu }_{1}}\alpha +\varepsilon \\ \end{matrix} \right] , \\ {{\varvec{B}}_{i,2}}=\left[ \begin{matrix} {{\mu }_{2}}\alpha &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {{\mu }_{1}}\alpha \\ \end{matrix} \right] , \\&\quad \varvec{C}=\left[ \begin{matrix} \lambda {{q}_{0}} &{} {} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {} &{} \lambda {{q}_{1}} &{} {} &{} {} &{} {} &{} {} &{} {} \\ {} &{} {} &{} \lambda {{q}_{2}} &{} {} &{} {} &{} {} &{} {} \\ {} &{} {} &{} {} &{} \ddots &{} {} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {} &{} \lambda {{q}_{0}} &{} {} &{} {} \\ {} &{} {} &{} {} &{} {} &{} {} &{} \lambda {{q}_{1}} &{} {} \\ {} &{} {} &{} {} &{} {} &{} {} &{} {} &{} \lambda {{q}_{2}} \\ \end{matrix} \right] . \end{aligned}$$

3.2 Steady-state analysis of the system

From the structure of matrix \(\varvec{Q}\), it remains that Markov process \(\{(L(t),Y(t),J(t)),t\ge 0\}\) is a quasi-birth-and-death (QBD) process. When Markov process \(\{(L(t),Y (t),J(t)),t\ge 0\}\) is position recurrent, the steady-state distribution is defined as follows:

$$\begin{aligned}&{{\pi }_{i,l,j}}=\underset{t\rightarrow \infty }{\mathop {\lim }}\,P\text { }\!\!\{\!\!\text { }X(t)=i,Y(t)=l,J(t)=j\text { }\!\!\}\!\!\text { ,(}i,l,j\text {)}\in \Omega , \\&\quad {{\varvec{\pi }}_{i}}\text {=(}{{\pi }_{i,1,0}},{{\pi }_{i,1,1}},{{\pi }_{i,1,2}},\cdots ,{{\pi }_{i,c,0}},{{\pi }_{i,c,1}}\text {,}{{\pi }_{i,c,2}}\text {)}, i\ge 0. \end{aligned}$$

Let

$$\begin{aligned} \mathrm{{\Pi }} =({{\varvec{\pi } }_{0}},{{\varvec{\pi } }_{1}},{{\varvec{\pi } }_{2}},\cdots ) \end{aligned}$$

The sufficient and necessary conditions QBD is position recurrent is that the matrix quadratic equation

$$\begin{aligned} {{\varvec{R}}^{2}}\varvec{B}+\varvec{R}\varvec{A}+\varvec{C}=\varvec{0} \end{aligned}$$
(2)

has a minimum non-negative solution \(\varvec{R}\), and the spectral radius \(SP(\varvec{R})<1\), \(3c(c+1)\) dimensional stochastic matrix.

$$\begin{aligned} B[\varvec{R}]=\left[ \begin{array}{*{35}{l}} {{\varvec{A}}_{0}} &{} {{\varvec{C}}_{0}} &{} {} &{} {} &{} {} &{} {} \\ {{\varvec{B}}_{1}} &{} {{\varvec{A}}_{1}} &{} \varvec{C} &{} {} &{} {} &{} {} \\ {} &{} {{\varvec{B}}_{2}} &{} {{\varvec{A}}_{2}} &{} \varvec{C} &{} {} &{} {} \\ {} &{} {} &{} \ddots &{} \ddots &{} \ddots &{} {} \\ {} &{} {} &{} {} &{} {{\varvec{B}}_{c-1}} &{} {{\varvec{A}}_{c-1}} &{} \varvec{C} \\ {} &{} {} &{} {} &{} {} &{} \varvec{B} &{} \varvec{B}\varvec{R}+\varvec{A} \\ \end{array} \right] \end{aligned}$$

has left-zero vector, when QBD is position recurrent, the steady-state distribution of the system satisfies the following sets of equations:

$$\begin{aligned} \left\{ \begin{array}{*{35}{l}} ({{\varvec{\pi }_0}},{{\varvec{\pi }_1}},\cdots ,{{\varvec{\pi }_c}})B[\varvec{R}]={\varvec{0}}\text { , } \\ \displaystyle \sum \limits _{i=0}^{c-1}{{{\varvec{\pi }_i}}\varvec{e}+{{\varvec{\pi }_c}}{{({{\varvec{I}}}-\varvec{R})}^{-1}}\varvec{e}=1,} \\ {{\varvec{\pi }_i}}={{\varvec{\pi }_c}}{{\varvec{R}}^{i-c}}\text {, }i\ge c \\ \end{array} \right. \end{aligned}$$
(3)

where \({\textbf {e}}\) is a 3c-dimensional column vector in which all elements are 1. \(\varvec{I}\) is a 3c-dimensional unit matrix.

3.3 Performance indicators

In order to express an explicit expression for each performance indicator of the system, the accurate expression for the minimum non-negative solution \(\varvec{R}\) of the above matrix equation Eq.(2) needs to be formulated. But it is difficult to express explicitly since the matrices \(\varvec{A}\), \(\varvec{B}\), \(\varvec{C}\) are complicated. Therefore, the approximate solution of the minimum non-negative solution of the matrix quadratic equation Eq.(2) is obtained by the Gauss-Seidel iterative method, thus the numerical result of \({{\pi }_{i,l,j}}\) is derived. The specific algorithm is as follows (Table 1):

Table 1 Gauss-Seidel iterative algorithm
Full size table

The analysis of the above the steady-state distribution mainly utilizes the matrix-geometric solution method, the specific proof process can be referred to [30, 31].

Utilizing Little’s law, the performance indicators of the system can be derived, the specific expressions are as follows:

  1. (1)

    The average length of the requesting node is

    $$\begin{aligned} E({{L}_{s}})=\sum \limits _{i=0}^{\infty }{iP(L=i)=}\sum \limits _{i=1}^{\infty }{i\left( \sum \limits _{l=1}^{c}{\sum \limits _{j=0}^{2}{{{\pi }_{i,l,j}}}} \right) }. \end{aligned}$$
  2. (2)

    The average sojourn time of the requesting node is

    $$\begin{aligned} \begin{aligned}&E({{W}_{s}})=\frac{1}{\lambda {{q}_{0}}}\sum \limits _{i=c}^{\infty }{i}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,0}}} \right) \\&\qquad \quad \ \;\text {+}\frac{1}{\lambda {{q}_{1}}}\sum \limits _{i=c}^{\infty }{i}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,1}}} \right) \\&\qquad \quad \ \;+\frac{1}{\lambda {{q}_{2}}}\sum \limits _{i=c}^{\infty }{i}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,2}}} \right) . \\ \end{aligned} \end{aligned}$$
  3. (3)

    The average waiting length of the requesting node is

    $$\begin{aligned} \begin{aligned}&E({{L}_{q}})=\frac{1}{\lambda {{q}_{0}}}\sum \limits _{i=c+1}^{\infty }{(i-c)}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,0}}} \right) \\&\qquad \quad \ \;+\frac{1}{\lambda {{q}_{1}}}\sum \limits _{i=c+1}^{\infty }{(i-c)}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,1}}} \right) \\&\qquad \quad \ \;+\frac{1}{\lambda {{q}_{2}}}\sum \limits _{i=c+1}^{\infty }{(i-c)}\left( \sum \limits _{l=1}^{c}{{{\pi }_{i,l,2}}} \right) . \\ \end{aligned} \end{aligned}$$
  4. (4)

    The total energy consumption of the system is the total energy consumption of the nodes in the working sleep period, the start-up period, close-down period and the official working period. Assuming that \({{g}_{1}}\) is the energy consumption of nodes in the working sleep period, \({{g}_{2}}\) is the energy consumption of nodes in the start-up period and close-down period, and \({{g}_{3}}\) is the energy consumption of nodes in the official working period, the total energy consumption of the system is

    $$\begin{aligned} \begin{aligned}&{{W}_{y}}=\sum \limits _{i=0}^{\infty }{\sum \limits _{l=1}^{c}{{{g}_{1}}{{\pi }_{i.l.0}}}}+\sum \limits _{i=0}^{\infty }{\sum \limits _{l=1}^{c}{{{g}_{2}}{{\pi }_{i.l.1}}}}\\&\quad \quad \ \;+\sum \limits _{i=0}^{\infty }{\sum \limits _{l=1}^{c}{{{g}_{3}}{{\pi }_{i.l.2}}}}. \end{aligned} \end{aligned}$$
  5. (5)

    The maximum throughput of the system is the maximum number of data requests that can be accepted and served by all nodes in the system per unit time, so the maximum system throughput is

    $$\begin{aligned} \Theta \text { =}{{\mu }_{2}}\sum \limits _{i=1}^{\infty }{i\sum \limits _{l=1}^{c}{{{\pi }_{i.l.0}}}}+{{\mu }_{1}}\sum \limits _{i=1}^{\infty }{i\sum \limits _{l=1}^{c}{{{\pi }_{i.l.2}}}}. \end{aligned}$$

4 Numerical experiments on P2P systems

The numerical results of \({{\pi }_{i,l,j}}\) and the sets of equations of steady-state distribution are obtained by the Gauss-Seidel iterative method, thus the performance indicators of the P2P system can be obtained. The images of performance indicators with parameter variation are available by using MATLAB, the influence of parameter variation on performance indicators is analyzed, which can provide the theoretical basis for the scheduling strategy of the nodes in P2P system.

4.1 Impact of parameter changes on performance indicators

The performance indicators of the system are obtained based on the above analysis, and the effect of the parameters on the performance indicators is examined using numerical experiments. Assume that \(c=10\), \(\theta =0.2\), \({{\mu }_{2}}=0.3\), \(\beta =0.2\), \(\alpha =0.6\), \(\varepsilon =0.3\), \({{q}_{0}}=0.2\), \({{q}_{1}}=0.1\), \({{q}_{2}}=0.7\). Figure 3 depicts the relationship between the average length \(E({{L}_{s}})\) of the requesting node and the service rate \({{\mu }_{1}}\) of the service node in official working state and the arrival rate \(\lambda\) of the requesting node in the system. When \(\lambda\) is fixed, \(E({{L}_{s}})\) decreases with increasing service rate \({{\mu }_{1}}\). When \({{\mu }_{1}}\) is fixed, the average length \(E({{L}_{s}})\) of the requesting node increases with increasing \(\lambda\). The main reason is that the service rate \({{\mu }_{1}}\) of the service nodes is greater in official working state, the requesting nodes are serviced quickly, the average download is increased, and therefore the system will post less possible congestion, which also leads to a shorter average length of the requesting nodes. Under the service rate remains constant, when the arrival rate \(\lambda\) of the requesting nodes increases, the number of requesting nodes increases in the system and more requesting nodes are waiting to receive the service, thus the average length of the requesting nodes increases. In the case of the different arrival rates of the requesting nodes, the numerical results of the average delay and service rate of the service node in official working state are shown in Table 2.

Fig. 3
figure 3

The relationship between \(E({{L}_{s}})\) and \(\mu _{1}\), \(\lambda\)

Full size image
Table 2 The relationship between \(E({{L}_{s}})\) and \(\mu _{1}\), \(\lambda\)
Full size table

Under the assumptions of the parameters in Figs. 3 and 4 describes the relationship between the average sojourn time \(E({{W}_{s}})\) of the requesting nodes and the service rate me of the system decreases by\({{\mu }_{1}}\) of the servicing nodes in the official working period and the arrival rate \(\lambda\) of the requesting nodes. From the figure, it can be seen that when the service rate \({{\mu }_{1}}\) of the service node in official working period is fixed, the average sojourn time of the requesting node grows rapidly and then plateaus as the arrival rate \(\lambda\) of the requesting node increases continuously. When the arrival rate \(\lambda\) of the requesting node is constant, the average sojourn time of the requesting node in the system decreases as the service rate \({{\mu }_{1}}\) increases in official working period. The main reason is that when the service rate of service nodes is invariant, the increase of requesting nodes will increase the number of nodes waiting for service gradually. However, part of the requesting nodes that are served will be transformed into seeds to serve other nodes, so that the average sojourn time growth tends to be flattened gradually. When the arrival rate of requesting nodes is invariable, the file transmission of nodes increases rapidly, and the average sojourn time of requesting nodes decreases in the system as the service rate of service nodes increases in official working period. When the service rate of the service node in official working state increases by 40\(\%\), the average sojourn time of the system decreases by about 0.6–1.4\(\%\). When the arrival rate of nodes is increased by 10–30\(\%\), the average sojourn time of the system increases by 1.2–2.9\(\%\). In the case of the different service rate of the service node in official working state, the numerical results of the average sojourn time and arrival rates of the requesting nodes are shown in Table 3.

Fig. 4
figure 4

The relationship between \(E({{W}_{s}})\) and \(\mu _{1}\), \(\lambda\)

Full size image
Table 3 The relationship between \(E({{W}_{s}})\) and \(\mu _{1}\), \(\lambda\)
Full size table

Under the assumptions of the parameters in Fig. 3, assume that \({{g}_{1}}=1\), \({{g}_{2}}=0.5\), \({{g}_{3}}=2\). Figure 5 depicts the relationship between the total energy consumption \({{W}_{y}}\) of the system and the arrival rate \(\lambda\) of the requesting nodes and the service rate \({{\mu }_{1}}\) of the service nodes in official working period. When \(\lambda\) is fixed, \({{W}_{y}}\) decreases as \({{\mu }_{1}}\) increases, when \({{\mu }_{1}}\) is fixed, \({{W}_{y}}\) increases as \(\lambda\) increases. The main reason is that the service nodes consume less energy during the working sleep period than during the official working period. The least energy is consumed during the shutdown period. As the number of requesting nodes gradually increases, more and more service nodes are transferred from the working sleep period to the formal working period. As a result, the energy consumption of the system increases gradually. When the arrival rate of the requesting nodes is fixed, the service rate of the service nodes is lower and the time required for file transmission is greater. Meanwhile the average waiting time of the requesting nodes increases, which leads to total energy consumption is higher in the system. In the case of the different service rate of the service node in official working state, the numerical results of the total energy consumption of the system and arrival rates of the requesting nodes are shown in Table 4.

Fig. 5
figure 5

The relationship between \({{W}_{y}}\) and \(\mu _{1}\), \(\lambda\)

Full size image
Table 4 The relationship between \({{W}_{y}}\) and \(\mu _{1}\), \(\lambda\)
Full size table

4.2 Nash equilibrium and social optimal strategy

According to the online query mechanism of nodes, for the continuous time queueing model with randomly varying number of service nodes, the following assumptions are formulated.

  1. (1)

    r denotes the fee received by requesting nodes that have completed file transmission.

  2. (2)

    The requesting node can only observe the state of the service node, but cannot observe the the number of nodes waiting in the system, before deciding whether to enter the system, and the requesting node cannot exit midway after entering the system.

  3. (3)

    \(C_{1}\) denotes the cost of the requesting node waiting service in the system.

  4. (4)

    To achieve social optimality and inhibit the selfish behavior of nodes, reasonable access fee of requesting nodes is applied, f denotes the access fee to be paid by each node entering the system.

  5. (5)

    All nodes have the same fees standards, i.e., the same benefit function, hence the benefits of multiple nodes can be cumulative.

Therefore, the individual utility function and the social utility function are constructed, the social optimal strategy is analyzed. The individual utility function of the node is defined as:

$$\begin{aligned} {{U}_\mathrm{I}}=r-{{C}_{1}}E({{W}_{s}})-f. \end{aligned}$$

Assuming that \(c=10\), \({{\mu }_{2}}=0.5\), \({{\mu }_{1}}=1\), \(\beta =0.2\), \(\alpha =0.6\), \(\varepsilon =0.2\), \({{q}_{0}}=0.3\), \({{q}_{1}}=0.1\), \({{q}_{2}}=0.6\), \({{g}_{1}}=1\), \({{g}_{2}}=0.5\), \({{g}_{3}}=2\), \(r=10\), \({{C}_{1}}=1.8\), \({{C}_{2}}=3\), \(f=3\). Figure 6 depicts the relationship between the average individual utility \({{U}_\mathrm{I}}\) of the nodes and the arrival rate \(\lambda\) of the requesting nodes and the working sleep rate \(\theta\) of the service nodes. When \(\theta\) is fixed, \({{U}_\mathrm{I}}\) decreases as \(\lambda\) increases. When \(\lambda\) is fixed, \({{U}_\mathrm{I}}\) decreases as \(\theta\) increases. The main reason is that when the arrival rate \(\lambda\) of the requesting nodes is relatively low, the number of requesting nodes transformed into seeds is relatively less, and the average waiting time of the requesting nodes increases gradually, which resulting in individual utility reduced. As \(\lambda\) increases continuously, more and more requesting nodes are transformed into seeds, the average waiting time of requesting nodes decreases, individual utility is on a flattening upward trend gradually. When \(\lambda\) is fixed, the rate of file transmission decreases as \(\theta\) increases, which results in the average waiting time increases of the requesting node, thus the individual utility of nodes reduce in the system.

In P2P networks, majority of nodes desire to access more data resources without sharing themselves. It also means that the requesting nodes is more in the system, the average delay is the higher and the individual utility is the lower. From Fig. 6, it is shown that \({{U}_\mathrm{I}}\) exists a zero point, i.e., the equilibrium arrival rate \({{\lambda }^{e}}\) exists in the system. The above analysis shows that if we want to improve the personal utility of nodes, it is necessary to encourage the requested nodes that complete the service to be transformed into seeds,and reward the seeds for requesting the service priority next time, i.e., to increase the transformation rate of nodes appropriately. This not only improves service efficiency, but also reduces energy consumption as well as free-riding behavior. In the case of the different the working sleep rate of the service nodes, the numerical results of average individual utility of the nodes and arrival rates of the requesting nodes are shown in Table 5.

Fig. 6
figure 6

The relationship between \({{U}_\mathrm{I}}\) and \(\theta\), \(\lambda\)

Full size image
Table 5 The relationship between \({{U}_\mathrm{I}}\) and \(\theta\), \(\lambda\)
Full size table

Assume that the requesting node enters the system facing an almost invisible queueing situation, that is, the requesting node is unaware of the number of nodes waiting in the system, but is aware of the status of the service nodes. Assume that \(\Lambda\) denotes the potential arrival rate of the requesting node and \({{q}^{e}}\) denotes the response probability of the requesting node into the system under the equilibrium policy, the equilibrium policy of the requesting node is:

$$\begin{aligned} q^e=\left\{ \begin{array}{ll} \text { }0,&{} \text { when}\ r<C_1E(W)\mid _{\lambda =0}+f, \\ \dfrac{\lambda ^e}{\Lambda },&{} \text { when}\ C_1 E(W)\mid _{\lambda =0}+f\le r \\ &{}\quad \quad \quad \le C_1E(W)\mid _{\lambda =\Lambda }+f, \\ \text { }1,&{} \text { when}\ r>C_1E(W)\mid _{\lambda =\Lambda }+f \\ \end{array} \right. \end{aligned}$$

where \({{\lambda }^{e}}\) is the solution of \({{U}_\mathrm{I}}=0\).

Assume that \({{q}^{*}}\) is the optimal response probability of the requesting node when it enters the system. To evaluate the socially optimal strategy, then the social utility function \({{U}_\mathrm{S}}\) is defined as:

$$\begin{aligned} {{U}_\mathrm{S}}=\lambda (r-{{C}_{1}}E(W_{s})-f)-{{C}_{2}}{{W}_{y}}\text { }\text {.} \end{aligned}$$

The aim of social optimal is to maximize the total benefit of all nodes in the system, so when the social utility is maximized, the requesting node arrival rate is the socially optimal requesting arrival rate. Let \({{\lambda }^{*}}\) be the actual arrival rate of the requesting node under the social optimal, then

$$\begin{aligned} {{\lambda }^{*}}=\underset{0\le {{\lambda }}\le {\Lambda }}{\mathop {\arg \max }}\,(\lambda (r-{{C}_{1}}E(W_{s})-f)-{{C}_{2}}{{W}_{y}}). \end{aligned}$$

Under the assumptions of the parameters in Figs. 6 and 7 depicts the relationship between the social utility \({{U}_\mathrm{S}}\) and the arrival rate \(\lambda\) of the requesting nodes and the working sleep rate \(\theta\) of the service nodes. When \(\theta\) is fixed, \({{U}_\mathrm{S}}\) increases and then decreases as \(\lambda\) increases; when \(\lambda\) is fixed, \({{U}_\mathrm{S}}\) decreases as \(\theta\) increases. The main reason is that in the almost invisible case, with \(\lambda\) increases, the initial requesting node enters the system, the number of service nodes are abundant, the service rate of the service nodes in official working status is more quickly, and the sojourn time of the requesting node is less, so that the social utility tends to be upward. The arrival rate of requesting nodes increases continuously, which resulting in average sojourn time is longer. Thus the individual utility of requesting nodes decreases, which discourages requesting nodes from entering the system. Meanwhile, if the requesting nodes enter uncontrollably it will lead to system congestion and system energy consumption increases, which will further contribute to a gradual decrease in the social utility of the system. As the sleep rate \(\theta\) increases, the efficiency of the service decreases and the average sojourn time of the nodes increases, which also leads to a gradual decrease in the individual utility of the nodes and, therefore, the social utility also decreases in the system.

Fig. 7
figure 7

The relationship between \({{U}_\mathrm{S}}\) and \(\theta\), \(\lambda\)

Full size image
Table 6 The relationship between \({{U}_\mathrm{S}}\) and \(\theta\), \(\lambda\)
Full size table

Under the conditions of Table 6, when \(\theta =0.2\), \(\lambda \text {=}0.9\), the maximum value of social utility is derived, i.e. \(\max {{U}_\mathrm{S}}=0.5202\). In the case of the different the working sleep rate of the service nodes, the numerical results of the social utility of the system and arrival rates of the requesting nodes are shown in Table 6.

5 Conclusions

P2P networks suffer from poor security and service congestion. In this paper, we analyze a new queueing model for P2P networks based on the classical M/M/c queueing model, which combines policies such as dynamic server changes, working dormancy of service nodes, malicious nodes, start-up period and close-down period in an almost invisible manner. By constructing a three-dimensional continuous-time Markov stochastic model, the behavior of nodes during the file transition is simulated and the performance of the P2P network is analyzed. Using the QBD process and matrix-geometric solution method, the steady-state distribution of the system is derived, which in turn performance indicators are given, including the average length and sojourn time of the requesting node, energy consumption and throughput of system. Experimental results show that requesting nodes will enter the system with a certain probability to wait for service depending on the status of the serving nodes in the system, which will reduce the waste of resources and the occurrence of impatient requesting nodes. At the same time, the dynamic change of nodes will make the service efficiency of the system increase and reduce the system delay, thus improving the overall system performance. The social utility function is constructed by using Nash equilibrium and social optimal strategy, the model is analyzed in detail, and the social optimum of the P2P network is achieved through numerical experiments.