Equilibrium Joining Strategies of Positive Customers in a Markovian Queue with Negative Arrivals and Working Vacations

Abstract

We study the economic analysis of a single server Markovian queueing system with positive and negative customers and multiple working vacations. Both positive and negative customers arrive in the system according to a Poisson process. Upon arrival, positive customers acquire some system information and decide whether to join or to balk the system based on the acquired information and a linear cost-reward structure. Negative customers on arrival break the server and kill the positive customer in service. The server is immediately sent for repair, and no customers are allowed during a repair. The server takes multiple working vacations after serving all the positive waiting customers. We obtain the equilibrium strategies and social benefit of positive customers under four different information situations. Numerical experiments are presented to show the effects of model parameters and information levels on the equilibrium joining behavior of positive customers.

1 Introduction

In recent years, there is a growing interest among queueing researchers to study the effect of queue-length information on the decentralized behavior of rational customers. In such systems, strategic customers receive certain system information at their arrival instants and based on the received information and a reward-cost structure, they decide whether to join or to balk the system. Every customer tries to maximize his/her net benefit based on the reward-cost structure; that displays their desire for service and dislike for waiting. The decision of a customer is affected by the decisions made by other customers present in the system, thus, leading to a symmetric game among the present customers. Such a game-theoretic analysis in the context of a Markovian queueing system with complete information of queue-length was initiated by Naor (1969). This work was complemented by Edelson and Hilderbrand (1975). Burnetas and Economou (2007) introduced the strategic customers’ behavior in a Markovian queue with server vacations and analyzed the equilibrium joining strategies under four different information settings. Since then several researchers studied different variants of the vacation models such as working vacations (Sun and Li 2014; Li and Ba 2016; Lee 2019), Bernoulli scheduled vacation (Liu and Wang 2017; Zhang and Shi 2009; Panda et al. 2016), adaptive vacations (Sun et al. 2017), variant vacations (Panda et al. 2017), N-policy with vacations (Sun et al. 2016), etc. Extensive bibliographical references with the fundamental results in the economic analysis of various queueing systems may be found in the monographs of Hassin and Haviv (2003) and Hassin (2016).

In the past studies, the unavailability of the server is due to its self-removal (vacations). However, there are scenarios wherein forceful removal results in the server unavailability. This may be due to unexpected server breakdowns, catastrophes, and the arrival of negative customers. The strategic behavior of customers in an observable Markovian queueing system with server breakdowns and repairs was introduced by Economou and Kanta (2008). Li et al. (2014) studied the corresponding unobservable model. Several researchers further extended these works under a Markovian setting with different variants, Wang and Zhang (2011), Li et al. (2013), Sun et al. (2010), Wang and Zhang (2011), and Yu et al. (2017).

There are studies in which catastrophes or disasters occur as a result of the arrival of negative customers. This concept, called G-networks, was introduced by Gelenbe (1989) in the modeling of neural networks, in which the negative customers act as inhibitor signals. This was subsequently extended to queueing systems by Gelenbe et al. (1991); Gelenbe (1991, 1994); Artalejo, (2000). The positive customers require service and increase the queue-length, whereas negative customers do not need service. Upon arrival, negative customers remove the server (breakdown) and kill one or more positive customers in a non-empty system according to a predetermined killing strategy. The most distinctive killing mechanisms are DST (Disaster), RCH (Removal of the Customer at the Head), and RCE (Removal of the Customer at the End). In DST killing policy, a negative customer’s arrival breaks the server and kills all the positive customers in the system. This policy has interesting applications in cloud data services, where negative customers are the hackers and in computer communication systems, where the negative customer is a virus or malware. Boudali and Economou (2012, 2013) considered the equilibrium balking strategies in an M/M/1 queue subject to catastrophes (DST policy). When a catastrophe occurs, the server becomes inoperative, and all the customers in the system are forced to leave. In an RCH killing policy, a negative customer breaks the server and kills the positive customer at the head of the queue or in service. This has potential applications in the production or manufacturing industries where negative customers are faulty operations or mishandling by the operator and in telecommunication systems where negative customers are network failures that lead to lost calls. Lee (2017) considered the equilibrium behavior of customers and optimal pricing strategies of the server in an unobservable M/M/1 queue under two pricing schemes. Tian and Wang (2019) studied the strategic behavior of positive customers in an M/M/1 queue with working breakdowns under four information scenarios. Sun and Wang (2019) analyzed equilibrium and socially optimal joining strategies in an M/M/1 queue with negative customers. In the RCE killing policy, a negative customer kills the positive customer at the end of the queue; that is, the most recently joined one whether waiting in a queue or receiving service. These killing mechanisms are effective in a non-empty system.

Queueing systems with multiple vacations and negative customers are extensively used to model communication systems. One such situation is a denial of service attack (DoS), in which the legitimate users (positive customers) are unable to access system devices, information systems, or other network resources (server) due to the actions of a malicious cyber threat actor, CISA (2009). DoS attack is accomplished by flooding the targeted host or network with traffic until the target cannot respond or by sending it information that triggers a crash. For effective management of a communication system, there is a team of reliability engineers working to detect and resolve the issue in case of an attack (repair state). After a DoS attack, the system engineers repair the targeted host or restore the network to peak performance. Despite the usefulness of vacation queueing systems with negative customers in the efficient modelling of many real-life systems, few research studies are available in the economic analysis of G-queues. To the best of our knowledge, there is no work reported on the strategic behavior of positive customers in a queueing system with multiple working vacations and negative customers. In this work, we discuss the equilibrium joining strategies of positive customers in an M/M/1 queue with working vacations and negative customers under the RCH killing policy. Both positive and negative customers follow a Poisson arrival process with different arrival rates. The server renders service with two different speeds: faster service state (normal service mode) and slower service state (working vacation mode). Positive customers are served individually following a first-come first-served discipline. When all the positive customers’ services are being served with a faster speed and there are no more to be served, the server switches to a slower service state. This mechanism is useful in conserving system resources like energy saving in data centers by putting the server in standby. Upon arrival, negative customers make the server inoperative and kill the positive customer in service. The broken server is immediately sent for repair and no positive customers are allowed to join the system during the repair. We consider the system with four information cases (fully and almost observable, and fully and almost unobservable) with respect to the level of information available to positive customers before making their decisions. We analyze the positive customer’s equilibrium joining strategies in each case.

The main contributions of the work are as follows:

• We study the equilibrium joining strategies of positive customers under both observable and unobservable informational cases. We present the mean sojourn time of a positive customer when all other positive customers follow a threshold joining strategy.

• We analyze the impact of the information level on the equilibrium joining strategies. We observe that the thresholds take intermediate values between two extremes; that is, they obey the follow-the-crowd property in an almost observable system.

• We discuss the practical application of our model in a denial of service attack on web resources. This study will provide strategic customers with valuable insights regarding the reward/risk involved in following or avoiding the crowd under various information policies.

The rest of the paper is organized as follows. In Section 2, we briefly discuss the dynamics of the model and its queueing formulation. Further, the linear reward-cost structure and the decision making framework is also discussed. In Section 3, we derive the equilibrium threshold strategies for the observable cases (fully and almost observable) in which positive customers are informed about the system state before making their decisions. In Section 4, we derive the equilibrium mixed strategies in the almost and fully unobservable cases. Section 5 depicts some numerical results and discusses the findings of corresponding instances. Section 6 concludes the paper with a few challenging extensions of this research.

2 Model Description

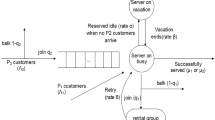
We consider a single server Markovian queueing system with infinite capacity wherein heterogeneous customers arrive according to a Poisson process. Customers are divided into two categories: positive and negative. Let λ and ϕ are the arrival rates of positive and negative customers, respectively. Positive customers are served individually by a single server following the first-come first-served discipline. The server has two modes of operation: normal service mode and working vacation mode. A working vacation is a vacation policy in which the server serves the positive customers at a lower speed during the vacation period rather than halting the service as in a classical vacation policy. The service times during the normal service (working vacation) mode are independent and exponentially distributed random variables with a rate μ (η). If the server finds no positive customers in the system after a service completion in the normal service mode, it switches to working vacation mode. Any positive customers that join the system while the server is in working vacation are served with a service rate η < μ. If there are no positive customers in the system at the end of a working vacation, the server takes another working vacation, and the process continues. Such a working vacation policy is called the multiple working vacation (MWV) policy. The working vacation times are independent and exponentially distributed with a rate 𝜃. If the working vacation mode terminates before a service completion, then that positive customer’s elapsed service is lost and its service restarts in the normal service mode. Upon arrival, a negative customer breaks down the server and removes the positive customer in service under both normal and working vacation modes. The broken server is immediately sent to repair and the repair times are exponentially distributed with rate γ. During the repair process, positive customers are not allowed to join the system and negative arrivals do no affect the server. After the server was repaired, it becomes active and remains in the idle state until the arrival of a positive customer. A negative arrival does not affect the idle server. All the random variables associated with the model are mutually independent. We may represent the above queueing system as an M/M/1/MWV queue with strategic positive customers. We list the following notations associated with the model description.

λ	potential arrival rate of positive customers
ϕ	potential arrival rate of negative customers
μ	service rate during normal service
η	service rate during working vacation
𝜃	working vacation rate
γ	repair rate of broken servers
N(t)	number of positive customers in the system at time t
ζ(t)	state of the server at time t ={ 0, server is on working vacation mode 1, server is on normal service mode 2, server is on repair mode
R	service completion reward
C	waiting cost per time unit

We consider the state of the queueing system at positive customers’ arrival instants. The system state at time t can be represented by the random variables N(t) and ζ(t), where N(t) denotes the number of positive customers in the system at time t and ζ(t) is the state of the server at the same moment. Let ζ(t) = 0, 1, and 2 represent the working vacation, normal service, and repair state of the server, respectively. The state space of the random variables N(t) and ζ(t) are $\{0,1,2,\dots , \}$ and {0,1,2}, respectively. The derivation of the system-length process {(N(t),ζ(t)), t ≥ 0} builds a continuous-time Markov chain with state space {(n,i) : n ≥ 0;i = 0,1,2}. The state transition diagram is shown in Fig. 1.

Fig. 1

State transition diagram of the original model

We discuss some basic concepts related to the game among the strategic players (positive customers). Game theory is a theoretical framework that deals with the optimal decision-making of independent and competing rational agents, called players in a strategic setting. A non-cooperative game is a competition among individual players without making any coalition or communication with other players. In a symmetric game, the players are indistinguishable; that is, the strategy sets and corresponding payoffs are the same for all players in the game. Let S be the strategy space (set of available actions) and define F(x,y) be the payoff of a player that selects a strategy x when others follow the strategy y for x,y ∈ S. A strategy x^∗ is said to be a best response against a strategy y, if F(x^∗,y) ≥ F(x,y), for every x ∈ S. An equilibrium (symmetric Nash) strategy is a best response against itself; that is, if all players agree to follow it, no one can benefit by altering it. Mathematically, a strategy x_e is an equilibrium strategy if F(x_e,x_e) ≥ F(x,x_e), for every x ∈ S. A strategy x₁ is said to weakly dominate strategy x₂ if F(x₁,y) ≥ F(x₂,y), for every y ∈ S and for at least one y the inequality is strict. A strategy x_∗ is said to be weakly dominant if it dominates all other strategies in S. The notion of a weakly dominant strategy is stronger than the notion of a Nash equilibrium; that is, every weakly dominant strategy is a Nash equilibrium, but the converse is not true.

In this non-cooperative symmetric game setting, our objective is to derive the (Nash) equilibrium strategies that are best responses against themselves; that is, no player has an incentive to deviate from such a strategy unilaterally. We assume that after a successful service completion each positive customer gets a reward of R units and on the other hand, they are charged a waiting cost of C units per time unit they spend in the system. We define the net benefit function of a positive customer as

$$ \begin{array}{@{}rcl@{}} {\varDelta} = \begin{cases} \frac{\mu}{\mu+\phi}R-C~T(\cdot),&\text{in the observable system,}\\ \frac{\mu}{\mu+\phi}R-C~W(\cdot),&\text{in the unobservable system}, \end{cases} \end{array} $$

(1)

where T(⋅) and W(⋅) represent the mean sojourn time of a positive customer who decides to join the system under the observable case and unobservable case, respectively. The service of a positive customer will complete if there is no negative arrival during his service; otherwise he will be removed from the system. Thus, the probability of service completion before a negative arrival is $\frac {\mu }{\mu +\phi }$. Based on this linear cost-reward structure and the acquired system information, positive customers make a decision only at their arrival instants to maximize their expected net benefit. One can model the system as a non-cooperative and symmetric game among positive customers. Since, we assume players (positive customers) to be indistinguishable with respect to the reward-cost structure. We are interested in the equilibrium joining behavior of positive customers. We assume that their decisions are irrevocable in the sense that retrials of balking customers and the reneging of waiting customers are not permissible. Further, zero net benefit is associated with balking customers.

3 Observable Queues with Negative Customers

In this section, we assume that upon arrival, a positive customer is well-informed of the number in the system and/or the state of the server. If arriving positive customers observe both the state of the server and the number of positive customers in the system, the model is said to be a fully observable system. If arriving positive customers observe only the number in the system, the model is said to be an almost observable system. We will discuss the fully observable and almost observable systems in the following sections.

3.1 Fully Observable Queue

Here, the positive customers already have the system-length and server status information on their arrival instants. Thus, the positive customers observe the system state (N(t),ζ(t)) before making decisions whether to join or to balk. The (Nash) equilibrium solution is a pure strategy (join or balk) of threshold type (Hassin and Haviv 1997), i.e., there exists a positive integer such that an arriving positive customer will join the system if and only if the system-length upon arrival is smaller than that value. This pure threshold strategy is a dominant one in the sense that it is the best response against any other strategies. Here, a pure threshold strategy is defined by a pair $({n_{e}^{0}}, {n_{e}^{1}})$ and the balking strategy has the form ‘while arriving at time t, observe the system state (N(t),ζ(t)); enter if $N(t)\le n_{e}^{\zeta (t)}$ and balk otherwise’, where ${n_{e}^{0}}$ and ${n_{e}^{1}}$ are the thresholds followed by the positive customer that finds the server on working vacation mode and normal service mode, respectively. As the queue builds faster in case of working vacation than the normal service, due to slower service rate, the relation among the thresholds will be ${n_{e}^{0}}\le {n_{e}^{1}}$. The maximum number of positive customers in the system under equilibrium will be ${n_{e}^{0}}+1~({n_{e}^{1}}+1)$ in working vacation (normal service) mode. We present the analysis and computation of equilibrium threshold strategies in the following theorem.

Theorem 1

In the fully observable M/M/1 queue with working vacations and negative customers, there exist thresholds

$$ \begin{array}{@{}rcl@{}} ({n_{e}^{0}},{n_{e}^{1}})=\left( \lfloor x_{e} \rfloor-1, \left\lfloor\frac{(\mu R-C)\gamma}{C(\gamma+\phi)}\right\rfloor-1 \right), \end{array} $$

(2)

where x_e is the unique root of the equation

$$\frac{R}{C}=\frac{(\mu-\eta)\left( \eta(\gamma+\phi)+\phi(\theta+\phi)\right)}{\eta\gamma\mu(\theta+\phi)}\left( 1-\left( \frac{\eta}{\eta+\theta+\phi}\right)^{x+1}\right)+\frac{\eta(\gamma+\phi)(x+1)-\mu\phi}{\eta\gamma\mu},$$

such that the strategy ‘observe (N(t),ζ(t)), join if $N(t)\le n_{e}^{\zeta (t)}$ and balk otherwise’ is a weakly dominant strategy for the positive customers.

Proof

Consider an arbitrary positive customer who observes the system state (n,i) upon arrival. Since arrivals are not allowed to join during the server’s repair state, we exclude the system states (n,2) from the decision making process. So, we only consider the case where a positive customer observes the system at states (n,0) and (n,1). Let T(n,i) be the sojourn time of a tagged positive customer that finds the system on state (n,i), i = 0,1 upon arrival. His service will start only after n waiting positive customers are served or removed and no negative arrival occurs during his service.

We can compute a tagged positive customer’s sojourn time using the first step arguments. This distinct possibilities are that the first event can be a negative arrival, a service completion, or a vacation termination. Suppose the tagged positive customer finds the system state (n,0) upon arrival. In that case, his sojourn time consists of the sojourn times in the following cases: (i) The expected time till an event occurs, $\frac {1}{\eta +\theta +\phi }$ and (ii) the expected times in the occurrence of each event. The probabilities of the first event being a WV service completion or a vacation termination or a negative arrival are $\frac {\eta }{\eta +\theta +\phi }$, $\frac {\theta }{\eta +\theta +\phi }$, and $\frac {\phi }{\eta +\theta +\phi }$, respectively. Thus, the expected sojourn time is

$$ \begin{array}{@{}rcl@{}} T(0,0)&=&\frac{1}{\eta+\theta+\phi}+\frac{\theta}{\eta+\theta+\phi}\frac{1}{\mu+\phi}\\ T(n,0)&=&\frac{1}{\eta+\theta+\phi}+\frac{\eta}{\eta+\theta+\phi} T(n-1,0)+\frac{\theta}{\eta+\theta+\phi}T(n,1)\\&&+\frac{\phi}{\eta+\theta+\phi}\left( \frac{1}{\gamma}+T(n-1,1)\right), ~n\ge 1, \end{array} $$

Using similar arguments, his expected sojourn time when he encounters the system state (n,1) is

$$ \begin{array}{@{}rcl@{}} T(0,1)&=&\frac{1}{\mu+\phi}\\ T(n,1)&=&\frac{1}{\mu+\phi}+\frac{\mu}{\mu+\phi}T(n-1,1)+\frac{\phi}{\mu+\phi}\left( \frac{1}{\gamma}+T(n-1,1)\right), ~n\ge 1. \end{array} $$

On successive iteration of T(n,0), T(n,1) and using T(0,0),T(0,1), we get

$$ \begin{array}{@{}rcl@{}} T(n,1)&=& \frac{n(\gamma+\phi)+\gamma}{\gamma(\mu+\phi)},~~n\ge 0 \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} T(n,0)&=&{{\varPsi}_{n+1}+ T(n,1)},~~n\ge 0, \end{array} $$

(4)

where ${\varPsi }_{n+1}=\frac {(\mu -\eta )\left (\eta (\gamma +\phi )+\phi (\theta +\phi )\right )}{\eta \gamma (\mu +\phi )(\theta +\phi )}\left (1-\left (\frac {\eta }{\eta +\theta +\phi }\right )^{n+1}\right )+\frac {\phi (\eta -\mu )}{\eta \gamma (\mu +\phi )}$. It can be easily checked that the mean sojourn times, T(n,i) are increasing functions of n for i = 0,1.

We assume that positive customers upon arrival are encouraged to join an empty system. It is possible if his net benefit is positive. Thus, we assume $\frac { R}{C}>\frac {\mu +\theta +\phi }{\mu (\eta +\theta +\phi )}$ in the equilibrium analysis under each information scenario. Now, the expected net benefit Δ_fo(n,i) of a tagged positive customer who decides to join the system state (n,i) can be computed from Eq. 1. Thus, a tagged positive customer who observes n positive customers in the system on arrival will join the system if Δ_fo(n,i) > 0; will balk the system if Δ_fo(n,i) < 0 and will indifferent between joining and balking if Δ_fo(n,i) = 0. Hence, the positive customer arriving at time t will join the system if and only if $N(t) \le {n_{e}^{j}}$, where $({n_{e}^{0}}, {n_{e}^{1}})$ are obtained by solving Δ_fo(n,0) = 0, Δ_fo(n,1) = 0. Solving these equations, we get the equilibrium thresholds of positive customers as ${n_{e}^{0}}=\lfloor x_{e}\rfloor -1$ and ${n_{e}^{1}}=\lfloor \frac {(\mu R-C)\gamma }{C(\gamma +\phi )}\rfloor -1$. This strategy is independent of the other positive customers’ strategies; that is, this strategy is a best response against all strategies followed by others. Therefore, the strategy is weakly dominant. □

Next, we intend to find the social benefit of positive customers under equilibrium. To compute the social benefit, we need the steady-state distribution under the equilibrium threshold strategy. If all the positive customers follow the equilibrium threshold $({n_{e}^{0}},{n_{e}^{1}})$, the state of the system can be described by the same Markov chain {(N(t),ζ(t)) : t ≥ 0} on the state space ${{\varOmega }}_{fo}=\{(n,0):~n=0,1,\dots , {n_{e}^{0}}+1\}\cup \{(n,1):~n=0,1,\dots , {n_{e}^{1}}+1\}\cup \{(n,2):~n=0,1,\dots , {n_{e}^{1}}\}$. Figure 2 illustrates the state transition diagram of the Markov chain.

Fig. 2

State transition diagram of the model when positive customers’ strategy is $({n_{e}^{0}},{n_{e}^{1}})$

The corresponding steady-state distribution π_n,i : (n,i) ∈Ω_fo can be computed by solving the following system of balance equations.

$$ \begin{array}{@{}rcl@{}} \lambda\pi_{0,1}\!&=&\!\gamma \pi_{0,2}, \end{array} $$

(5a)

$$ \begin{array}{@{}rcl@{}} (\lambda+\mu+\phi) \pi_{n,1}\!&=&\!\lambda \pi_{n-1,1} + \mu \pi_{n+1,1}+\gamma\pi_{n,2}+\theta\pi_{n,0}, {n = 1,2,\dots, {n_{e}^{0}}+1}, \end{array} $$

(5b)

$$ \begin{array}{@{}rcl@{}} (\lambda+\mu+\phi) \pi_{n,1}&=&\lambda \pi_{n-1,1}+\mu \pi_{n+1,1}+\gamma\pi_{n,2},~~{n={n_{e}^{0}}+1,\dots, {n_{e}^{1}}}, \end{array} $$

(5c)

$$ \begin{array}{@{}rcl@{}} (\mu+\phi) \pi_{{n_{e}^{1}}+1,1}&=&\lambda\pi_{{n_{e}^{1}},1}, \end{array} $$

(5d)

$$ \begin{array}{@{}rcl@{}} \lambda \pi_{0,0}&=&\mu\pi_{1,1}+\eta\pi_{1,0}, \end{array} $$

(5e)

$$ \begin{array}{@{}rcl@{}} (\lambda+\theta+\phi+\eta)\pi_{n,0}&=&\lambda\pi_{n-1,0}+\eta\pi_{n+1,0},~{n=1,2,\dots, {n_{e}^{0}}}, \end{array} $$

(5f)

$$ \begin{array}{@{}rcl@{}} (\theta+\phi+\eta)\pi_{{n_{e}^{0}}+1,0}&=&\lambda\pi_{{n_{e}^{0}},0}, \end{array} $$

(5g)

$$ \begin{array}{@{}rcl@{}} \gamma \pi_{n,2}&=&\phi\pi_{n+1,1}+\phi\pi_{n+1,0},~~{n=0,1,\dots, {n_{e}^{0}}}, \end{array} $$

(5h)

$$ \begin{array}{@{}rcl@{}} \gamma \pi_{n,2}&=&\phi \pi_{n+1,1},~~ {n={n_{e}^{0}}+1,\dots, {n_{e}^{1}}}, \end{array} $$

(5i)

The above linear system can be solved using several methods available in the literature, such as difference equation, generating function approach and iterative method. We apply the iterative method to obtain the solution in closed form, which is analytically simple as well as computationally efficient. Using the backward substitution scheme recursively on the system of equations (5e)–(5g), we get

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}&= h_{n} \pi_{{n_{e}^{0}}+1,0}, ~~~{n=0,1,\dots, {n_{e}^{0}}+1}, \end{array} $$

where the unknown coefficients h_n, are given by

$$ \begin{array}{@{}rcl@{}} h_{n}=\begin{cases} 1, & n={n_{e}^{0}}+1,\\ \frac{\theta+\phi+\eta}{\lambda}, & n={n_{e}^{0}},\\ \left( 1+\frac{\theta+\phi+\eta}{\lambda}\right)h_{n+1}-\frac{\eta}{\lambda} h_{n+2}, & n={n_{e}^{0}}-1,\dots, 0. \end{cases} \end{array} $$

(6)

Similarly, using the backward substitution scheme, the solution to the system of equations (5b)–(5d) is

$$ \begin{array}{@{}rcl@{}} \pi_{n,1}&=&t_{n} \pi_{{n_{e}^{1}}+1,1},~~{n={n_{e}^{0}},\dots, {n_{e}^{1}}+1},\\ \pi_{n,1}&=&t_{n} \pi_{{n_{e}^{1}}+1,1}+g_{n} \pi_{{n_{e}^{0}}+1,0},~~{n=0,1,\dots, {n_{e}^{0}}-1}, \end{array} $$

where the unknowns t_n and g_n are

$$ \begin{array}{@{}rcl@{}} t_{n}&=&\left( \frac{\mu+\phi}{\lambda }\right)^{{n_{e}^{1}}+1-n}, ~~{n=0,1,\dots, {n_{e}^{1}}+1}, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} g_{n}&=&\begin{cases} 0 & n={n_{e}^{0}},\\ -\left( \frac{\theta h_{{n_{e}^{0}}}+\phi h_{{n_{e}^{0}}+1}}{\lambda}\right), & n={n_{e}^{0}}-1,\\ \left( 1+\frac{\mu+\phi}{\lambda}\right) g_{n+1}-\frac{\mu+\phi}{\lambda} g_{n+2}-\left( \frac{\theta h_{n+1}+\phi h_{n+2}}{\lambda}\right), & n={n_{e}^{0}}-2,\dots, 0. \end{cases} \end{array} $$

(8)

Finally, the steady-state distribution of the number of positive customers in the system when the server is under repair is computed from Eq. 5h and Eq. 5i.

$$ \begin{array}{@{}rcl@{}} \pi_{n,2}&=&\frac{\phi}{\gamma}\left( t_{n+1}\pi_{{n_{e}^{1}}+1,1}+ (g_{n+1}+h_{n+1})\right)\pi_{{n_{e}^{0}}+1,0},~~{n=0,1,\dots, {n_{e}^{0}}},\\ \pi_{n,2}&=&\frac{\phi}{\gamma}t_{n+1}\pi_{{n_{e}^{1}}+1,1},~~ ~{n={n_{e}^{0}}+1,\dots, {n_{e}^{1}}}. \end{array} $$

Substituting the values of Eqs. 6, 7 and 8 in Eq. 5e, we get

$$ \begin{array}{@{}rcl@{}} \pi_{{n_{e}^{1}}+1,1}&=\frac{\lambda h_{0}-\eta h_{1}-\mu g_{1}}{\mu t_{1}} \pi_{{n_{e}^{0}}+1,0}= K \pi_{{n_{e}^{0}}+1,0}. \end{array} $$

Thus, the steady-state distributions are computed in terms of the only unknown $\pi _{{n_{e}^{0}}+1,0}$, which can be obtained using the normalization condition

$$ \pi_{{n_{e}^{0}}+1,0}=\left[h_{0}+g_{0}+Kt_{0}+\left( 1+\frac{\phi}{\gamma}\right) \left( \sum\limits_{n=1}^{{n_{e}^{0}}+1} h_{n}+K \sum\limits_{n=1}^{{n_{e}^{1}}+1} t_{n}+\sum\limits_{n=1}^{{n_{e}^{0}}-1} g_{n}\right)\right]^{-1}. $$

(9)

The steady-state distributions can be summarized in the following lemma.

Lemma 1

Consider a fully observable M/M/1 queue with working vacations and negative customers in which customers follow the threshold policy $({n_{e}^{0}}, {n_{e}^{1}})$. The stationary probabilities {π_n,i : (n,i) ∈Ω_fo} are given by

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}&=&h_{n} \pi_{{n_{e}^{0}}+1,0},~~n=0,1,\dots,{n_{e}^{0}}+1,\\ \pi_{n,1}&=&\begin{cases} \left( K t_{n}+g_{n}\right) \pi_{{n_{e}^{0}}+1,0},&{n=0,1,\dots, {n_{e}^{0}}-1},\\ K t_{n} \pi_{{n_{e}^{0}}+1,0},& {n={n_{e}^{0}},\dots, {n_{e}^{1}}+1}, \end{cases} \\ \pi_{n,2}&=&\begin{cases} \frac{\phi}{\gamma}\left( K t_{n+1}+g_{n+1}+h_{n+1}\right)\pi_{{n_{e}^{0}}+1,0},& {n=0,1,\dots, {n_{e}^{0}}},\\ \frac{\phi}{\gamma} K t_{n+1}\pi_{{n_{e}^{0}}+1,0},& {n={n_{e}^{0}}+1,\dots, {n_{e}^{1}}}, \end{cases} \end{array} $$

where h_n,t_n,g_n and $\pi _{{n_{e}^{0}}+1,0}$ can be obtained from Eqs. 6– 9, respectively.

The average number of positive customers in the system when the server is either on working vacation or normal service mode is given by

$$ \begin{array}{@{}rcl@{}} E(N_{r})=\sum\limits_{n=0}^{{n_{e}^{0}}+1}n\pi_{n,0}+\sum\limits_{n=0}^{{n_{e}^{1}}+1}n\pi_{n,1}. \end{array} $$

Now, the positive customers that find the system either on state $({n_{e}^{0}}+1,0)$ or $({n_{e}^{1}}+1,1)$ are not allowed to join the system and are considered lost. Thus, the probability of balking or loss probability is equal to $P_{balk} = \pi _{{n_{e}^{0}}+1,0}+\pi _{{n_{e}^{1}}+1,1}+\sum \limits _{i=0}^{{n_{e}^{1}}}\pi _{i,2}$ (due to PASTA property) and the effective arrival rate of positive customers is λ_eff = λ(1 − P_balk). If all positive customers follow the equilibrium joining threshold strategy $({n_{e}^{0}}, {n_{e}^{1}})$, then the social benefit per time unit in equilibrium is

$${\varDelta}_{s}({n_{e}^{0}}, {n_{e}^{1}})=\frac{\mu\lambda_{eff}}{\mu+\phi}R-C E(N_{r}).$$

3.2 Almost Observable Case

In this section, positive customers do not observe the state of the server on arrival, that is, they can not differentiate whether the server is on a working vacation or normal service mode before making decisions. They follow a pure threshold strategy n_e, which is computed in a way similar to the fully observable case by taking ${n_{e}^{0}} ={n_{e}^{1}}= n_{e}$ and the balking strategy has the form ‘while arriving at time t, observe only N(t); enter if N(t) ≤ n_e and balk otherwise’. The state space of the Markov chain {(N(t),ζ(t)) : t ≥ 0} is ${\varOmega }_{ao}=\{(n,i):~n=0,1,\dots , n_{e}+1;~ i=0,1\}\cup \{(n,2):~n=0,1,\dots , n_{e}\}$ and the corresponding state transition diagram is illustrated in Fig. 3.

Fig. 3

State transition diagram of the model with positive customers’ strategy n_e

The steady-state distribution {π_n,i : (n,i) ∈Ω_ao} in the almost observable queue with working vacations and negative customers can be derived by solving the following system of balance equations.

$$ \begin{array}{@{}rcl@{}} \lambda\pi_{0,1}&=&\gamma \pi_{0,2}, \end{array} $$

(10a)

$$ \begin{array}{@{}rcl@{}} (\lambda+\mu+\phi) \pi_{n,1}&=&\lambda \pi_{n-1,1}+\mu \pi_{n+1,1}+\gamma\pi_{n,2}\\ &&+\theta\pi_{n,0},~~{n=1,2,\dots, n_{e}}, \end{array} $$

(10b)

$$ \begin{array}{@{}rcl@{}} (\mu+\phi)\pi_{n_{e}+1,1}&=&\lambda\pi_{n_{e},1}+\theta\pi_{n_{e}+1,0}, \end{array} $$

(10c)

$$ \begin{array}{@{}rcl@{}} \lambda \pi_{0,0}&=&\mu\pi_{1,1}+\eta\pi_{1,0}, \end{array} $$

(10d)

$$ \begin{array}{@{}rcl@{}} (\lambda+\theta+\phi+\eta)\pi_{n,0}&=&\lambda\pi_{n-1,0}+\eta\pi_{n+1,0},~~ {n=1,2,\dots, n_{e}}, \end{array} $$

(10e)

$$ \begin{array}{@{}rcl@{}} (\theta+\phi+\eta)\pi_{n_{e}+1,0}&=&\lambda\pi_{n_{e},0}, \end{array} $$

(10f)

$$ \begin{array}{@{}rcl@{}} \gamma \pi_{n,2}&=&\phi\pi_{n+1,1}+\phi\pi_{n+1,0},~~{n=0,1,\dots, n_{e}}, \end{array} $$

(10g)

Pursuing the analysis alike to the fully observable case, we obtain the stationary distributions as

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}&=& h_{n} \pi_{n_{e}+1,0}, ~~{n=0,1,\dots, n_{e}+1},\\ \pi_{n,1}&=&\left( K t_{n}+g_{n}\right) \pi_{n_{e}+1,0}, ~~{n=0,1,\dots, n_{e}+1},\\ \pi_{n,2}&=&\frac{\phi}{\gamma}\left( K t_{n+1}+g_{n+1}+h_{n+1}\right)\pi_{n_{e}+1,0},~~ {n=0,1,\dots, n_{e}}, \end{array} $$

where $K=\frac {\lambda h_{0}-\eta h_{1}-\mu g_{1}}{\mu t_{1}}$. The h_n, t_n and g_n’s are given by

$$ \begin{array}{@{}rcl@{}} h_{n}&=&\begin{cases} 1& n=n_{e}+1\\ \frac{\theta+\phi+\eta}{\lambda}, & n=n_{e},\\ \left( 1+\frac{\theta+\phi+\eta}{\lambda}\right)h_{n+1}-\frac{\eta}{\lambda} h_{n+2}, & n=n_{e}-1,\dots, 0, \end{cases}\\ t_{n}&=&\left( \frac{\mu+\phi}{\lambda }\right)^{n_{e}+1-n}, ~~{n=0,1,\dots, n_{e}+1}, \\ g_{n}&=&\begin{cases} 0&n=n_{e}+1\\ -\frac{\theta}{\lambda}, & n=n_{e},\\ \left( 1+\frac{\mu+\phi}{\lambda}\right) g_{n+1}-\frac{\mu+\phi}{\lambda} g_{n+2}-\left( \frac{\theta h_{n+1}+\phi h_{n+2}}{\lambda}\right), & n=n_{e}-1,\dots, 0. \end{cases} \end{array} $$

Now, all the stationary distributions are expressed in terms of the only unknown $\pi _{n_{e}+1,0}$, which can be calculated using the normalization condition,

$$ \pi_{n_{e}+1,0}=\left( h_{0}+g_{0}+K t_{0}+\left( 1+\frac{\phi}{\gamma}\right) \sum\limits_{n=1}^{n_{e}+1}\left( h_{n}+K t_{n}+g_{n}\right)\right)^{-1}. $$

(11)

Let T(n) be the mean sojourn time of a tagged positive customer who observes n customers in the system upon arrival. Conditioning on the state of the server withstand by the tagged positive customer, we get

$$T(n)=T(n,0) P(\zeta=0|N=n)+T(n,1) P(\zeta=1|N=n),$$

where P(ζ = i|N = n) is the probability that the tagged positive customer gets the server at state i, given that there are n customers in the system. Applying the PASTA property, we have

$$ \begin{array}{@{}rcl@{}} P(\zeta=0|N=n)&=\frac{\pi_{n,0} }{\pi_{n,0}+\pi_{n,1}}=\frac{h_{n}}{h_{n}+K t_{n}+g_{n}}, ~~ n=0,1,\dots,n_{e}+1\\ P(\zeta=1|N=n)&=\frac{\pi_{n,1} }{\pi_{n,0}+\pi_{n,1}}=\frac{K t_{n}+g_{n}}{h_{n}+K t_{n}+g_{n}},~~ n=0,1,\dots,n_{e}+1. \end{array} $$

Substituting the values of the conditional probabilities in T(n), we get

$$ \begin{array}{@{}rcl@{}} T(n)=& \frac{n(\gamma+\phi)+\gamma}{\gamma(\mu+\phi)} +\frac{h_{n}}{h_{n}+K t_{n}+g_{n}} {{\varPsi}_{n+1}},~n=0,1, \dots, n_{e}+1. \end{array} $$

Evidently, T(n) is an increasing function of n, the number of positive customers in the system. For the tagged positive customer who finds n customers in the system and decides to join, given that all other positive customers follow a threshold strategy n_e, has expected net benefit

$$ {\varDelta}_{n_{e},ao}(n)=\frac{\mu}{\mu+\phi}R-C~ \frac{n(\gamma+\phi)+\gamma}{\gamma(\mu+\phi)} -C\frac{h_{n}~{{\varPsi}_{n+1}}}{h_{n}+K t_{n}+g_{n}},~n=0,1, \dots, n_{e}+1. $$

(12)

Thus, we have ${\varDelta }_{n_{e},ao}(n)$ is a decreasing function of n for a fixed threshold strategy n_e. Substituting n = n_e and n = n_e + 1, respectively into Eq. 12 gives

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{n_{e},ao}(n_{e})&=&\frac{\mu}{\mu+\phi}R-C~ \frac{n_{e}(\gamma+\phi)+\gamma}{\gamma(\mu+\phi)} -C\frac{\theta+\phi+\eta}{\phi+\eta+K (\mu+\phi)}{~{\varPsi}_{n_{e}+1}},\\ {\varDelta}_{n_{e},ao}(n_{e}+1)&=&\frac{\mu}{\mu+\phi}R-C~ \frac{(n_{e}+1)(\gamma+\phi)+\gamma}{\gamma(\mu+\phi)} -\frac{C}{1+K }~{{\varPsi}_{n_{e}+2}}. \end{array} $$

Now, to prove the existence of equilibrium threshold strategies and derive the corresponding thresholds, we define the functions S₁(n) and S₂(n) such that $S_{1}(n_{e})={\varDelta }_{n_{e},ao}(n_{e})$ and $S_{2}(n_{e}+1)={\varDelta }_{n_{e},ao}(n_{e}+1)$. One may examine that, S₂(n) ≤ S₁(n) for n ≥ 1. We have $S_{1}(0)=\frac {\mu }{\mu +\phi }R- CT(0)>0$, otherwise no positive customer will join an idle server. Further, $\lim \limits _{n\to \infty }S_{1}(n)=-\infty$. Hence, there exists a finite non-negative integer n_U such that $S_{1}(0),S_{1}(1),S_{1}(2),\dots ,S_{1}(n_{U})> 0$ and S₁(n_U + 1) ≤ 0. Since, S₂(n) ≤ S₁(n) for n ≥ 1, we have, S₂(n_U + 1) < S₁(n_U + 1) ≤ 0. Using the similar arguments for the sequence S₂(n), that is, S₂(0) > 0 and S₂(n_U + 1) ≤ 0, we have a finite non-negative integer n_L ≤ n_U such that $S_{2}(n_{U}+1),S_{2}(n_{U}),S_{2}(n_{U}-1),\dots ,S_{2}(n_{L}+1)\le 0$ and S₂(n_L) > 0. Hence, all pure threshold strategies ‘observe N(t), join if N(t) ≤ n_e and balk otherwise’, for $n_{e}\in \{n_{L},\dots ,n_{U}\}$, are equilibrium threshold strategies.

If n_L < n_U, then there are multiple equilibrium threshold strategies $\{n_{L},n_{L}+1,\dots ,n_{U}\}$. We have a ‘Follow-The-Crowd’ (FTC) situation when a player’s best response to a strategy x adopted by all others increases in x. In our model, the tagged positive customer who decides to join the system after observing n positive customers who followed a threshold strategy n_e has expected net benefit ${\varDelta }_{n_{e},ao}(n)$ given in Eq. 12. If the other positive customers follow the strategy n_e + 1, then his expected net benefit ${\varDelta }_{n_{e}+1,ao}(n)$ equals to ${\varDelta }_{n_{e},ao}(n)$ for all $n = 0,1, {\dots } ,n_{e}$ and ${\varDelta }_{n_{e}+1,ao}(n_{e}+1)>{\varDelta }_{n_{e},ao}(n_{e}+1)$. This is because of the relation S₁(n_e + 1) > S₂(n_e + 1). We observe that the tagged positive customer’s best response when others adopt the strategy n_e + 1 is greater than his best response when others follow the strategy n_e. Thus, the tagged positive customer’s threshold best response is increasing in the threshold policy followed by other positive customers. Therefore, the higher the threshold policy adopted by others, the higher is one’s best response; that is, he adopts others’ behavior. This characterizes an FTC situation in our model.

4 Unobservable Queues with Negative Customers

Now, we consider the unobservable queues wherein positive customers are not aware of the number in system before making their decisions whether to join or to balk. Based on the server state information, there are two scenarios: the fully unobservable and almost unobservable queues with multiple working vacations and negative arrivals.

As the decision of a positive customer depends on the strategies followed by other positive customers and the positive customers are identical, the situation is like a symmetric game among the positive customers. Two pure strategies (to join or to balk) and a mixed strategy (the probability of joining) are available to positive customers. The mixed strategy is defined by a pair (q₀,q₁) with q₀ denoting the probability of joining the queue when the server is on working vacation and q₁ is the probability of joining the queue when the server is on normal service. In both cases, the positive customers follow a mixed strategy of joining or balking the system. We analyze the strategic behavior of positive customers under both scenarios in the following sections.

4.1 Almost Unobservable Queue

Here, the positive customers do not observe the number in the system upon arrival but know the state of the server. Thus, the positive customers observe the state ζ(t) before making decisions about whether to join or to balk. They follow a mixed joining strategy to join the system, i.e., upon arrival they know ζ(t) = i and join with probability q_i, i = 0,1. Here, the equilibrium joining strategy is given by the pair $({q_{e}^{0}}, {q_{e}^{1}})$ and the balking strategy has the form ‘while arriving at time t, observe the server state ζ(t); enter with probability $q_{e}^{\zeta (t)}$ and balk otherwise’. Our objective is to derive the equilibrium mixed strategies. To do this, we first compute the stationary probability distribution of the system when all positive customers follow a mixed joining strategy (q₀,q₁). If all positive customers follow the joining strategy (q₀,q₁), the evolution of the system length process forms a continuous-time Markov chain with state space Ω_au = {(n,i) : n ≥ 0; i = 0,1,2}. The state transition diagram is depicted in Fig. 4. For the steady-state analysis under the strategy (q₀,q₁), we assume the stability condition ρ = λq₁/(μ + ϕ) < 1, otherwise the queueing system will be unstable. The stationary system length distributions can be obtained by solving the following set of balance equations.

Fig. 4

State transition diagram of the model when uninformed positive customers joining strategy (q₀,q₁)

$$ \begin{array}{@{}rcl@{}} \lambda q_{1}\pi_{0,1}&=&\gamma \pi_{0,2}, \end{array} $$

(13a)

$$ \begin{array}{@{}rcl@{}} (\lambda q_{1}+\mu+\phi) \pi_{n,1}&=&\lambda q_{1} \pi_{n-1,1}+\mu \pi_{n+1,1}+\gamma\pi_{n,2}+\theta\pi_{n,0},~~ n\ge 1, \end{array} $$

(13b)

$$ \begin{array}{@{}rcl@{}} \lambda q_{0}\pi_{0,0}&=&\mu\pi_{1,1}+\eta\pi_{1,0}, \end{array} $$

(13c)

$$ \begin{array}{@{}rcl@{}} (\lambda q_{0}+\theta+\phi+\eta)\pi_{n,0}&=&\lambda q_{0}\pi_{n-1,0}+\eta\pi_{n+1,0},~~ n\ge 1, \end{array} $$

(13d)

$$ \begin{array}{@{}rcl@{}} \gamma \pi_{n,2}&=&\phi\pi_{n+1,1}+\phi\pi_{n+1,0},~~n\ge 0 \end{array} $$

(13e)

Solving the second order linear homogeneous difference equation (13d), we obtain the representing characteristic equation,

$$ \begin{array}{@{}rcl@{}} \eta r^{2}-(\lambda q_{0}+\theta+\phi+\eta)r+\lambda q_{0}=0, \end{array} $$

(14)

which has two roots r₁ and r₂, given by

$$ \begin{array}{@{}rcl@{}} r_{1}&=\frac{(\lambda q_{0}+\theta+\phi+\eta)+ \sqrt{(\lambda q_{0}+\theta+\phi+\eta)^{2}-4\lambda q_{0} \eta}}{2 \eta}\\ r_{2}&=\frac{(\lambda q_{0}+\theta+\phi+\eta)- \sqrt{(\lambda q_{0}+\theta+\phi+\eta)^{2}-4\lambda q_{0} \eta}}{2 \eta}. \end{array} $$

Thus, the general solution of the second order difference equation (13d) becomes, $\pi _{n,0}=d_{1} {r_{1}^{n}} + d_{2} {r_{2}^{n}}$ for n ≥ 0, where d₁ and d₂ > 0 are constants. As r₁ > 1, so d₁ must be zero, because π_n,0, n ≥ 0 are probabilities, otherwise the sum of π_n,0 will be infinite. Hence,

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}= d_{2} {r_{2}^{n}},~~n\ge 0. \end{array} $$

(15)

Using Eq. 13e in Eq. 13b, then applying shift operator E defined by E^mπ_n,1 = π_n+m,1, we have

$$ \begin{array}{@{}rcl@{}} \left[(\mu+\phi) E^{2}-(\lambda q_{1}+\mu+\phi)E+\lambda q_{1}\right]\pi_{n-1,1}=-\left( \theta+\phi r_{2}\right) d_{2},~~n\ge 1. \end{array} $$

(16)

Let F(z) = (μ + ϕ)z² − (λq₁ + μ + ϕ)z + λq₁. Then by Rouche’s theorem, there exists a unique positive real number ξ < 1 such that F(ξ) = 0. Thus, the general solution of the non-homogeneous linear difference equation (16) is

$$ \begin{array}{@{}rcl@{}} \pi_{n,1}&= A \xi^{n}-\frac{\left( \theta+\phi r_{2}\right)r_{2}^{n+1}}{F(r_{2})}d_{2},~~n\ge 0, \end{array} $$

(17)

where A is an unknown to be evaluated from Eq. 13c with the help of Eqs. 15 and 17 and is given by

$$ \begin{array}{@{}rcl@{}} A&=\frac{d_{2}}{\xi}\left[ \frac{\lambda q_{0}-\eta r_{2}}{\mu} + \frac{\left( \theta+\phi r_{2}\right){r_{2}^{2}}}{F(r_{2})}\right]= B d_{2}, \end{array} $$

(18)

with $B=\frac {\lambda q_{0}-\eta r_{2}}{\mu \xi } + \frac {\left (\theta +\phi r_{2}\right ){r_{2}^{2}}}{F(r_{2})\xi }$. Now, using Eqs. 15 and 17 in Eq. 13e, we obtain

$$ \begin{array}{@{}rcl@{}} \pi_{n,2}&=\frac{d_{2}\phi}{\gamma} \left[r_{2}^{n+1}+B \xi^{n+1}- \frac{\left( \theta+\phi r_{2}\right)r_{2}^{n+2}}{F(r_{2})}\right],~~n\ge 0. \end{array} $$

(19)

We have derived all the steady-state probabilities of the number of positive customers in the system under different server states in terms of the only unknown d₂, which we can compute from the normalization condition as

$$ \begin{array}{@{}rcl@{}} d_{2}&=\left[\frac{1}{1-r_{2}}\left( 1+\frac{\phi r_{2}}{\gamma}\right) \left( 1-\frac{\left( \theta+\phi r_{2}\right)r_{2}}{F(r_{2})}\right) +\frac{B}{1-\xi} \left( 1+\frac{\phi \xi}{\gamma}\right) \right]^{-1}. \end{array} $$

The results can be summed up in the following lemma.

Lemma 2

In the almost unobservable M/M/1 queue with multiple working vacations and negative customers in which all positive customers follow a mixed balking strategy (q₀,q₁), the stationary probability distributions are

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}&=& d_{2} {r_{2}^{n}},\quad n\ge 0, \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \pi_{n,1}&=& d_{2}\left( B \xi^{n}-\frac{\left( \theta+\phi r_{2}\right)r_{2}^{n+1}}{F(r_{2})}\right), \quad n\ge 0. \end{array} $$

(21)

Let p₀ (p₁) denote the probability that the server is on working vacation (or busy) and are given by

$$ \begin{array}{@{}rcl@{}} p_{0}&=&\sum\limits_{n=0}^{\infty}\pi_{n,0}=\frac{d_{2}}{1-r_{2}}, \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} p_{1}&=&\sum\limits_{n=1}^{\infty}\pi_{n,1}=d_{2}\left( \frac{B }{1-\xi}-\frac{\left( \theta+\phi r_{2}\right)r_{2}}{F(r_{2})(1-r_{2})}\right). \end{array} $$

(23)

The average number of positive customers in the system in the almost unobservable queue can be calculated as

$$ \begin{array}{@{}rcl@{}} E(N)=\sum\limits_{n=1}^{\infty}n(\pi_{n,0}+\pi_{n,1}) =d_{2}\left[\frac{r_{2}}{(1-r_{2})^{2}}\left( 1-\frac{\left( \theta+\phi r_{2}\right)r_{2}}{F(r_{2})}\right)+\frac{B \xi}{(1-\xi)^{2}} \right]. \end{array} $$

Now, consider a tagged positive customer who finds the server on state i (i = 0,1) upon arrival. The conditional mean sojourn time of the tagged positive customer who decides to join the system with server state i, given that other positive customers follow the same mixed joining strategy (q₀,q₁) is

$$ W(i,q_{0},q_{1})=\frac{{\sum}_{n=0}^{\infty}T(n,i)~\pi_{n,i}}{\sum\limits_{n=0}^{\infty}\pi_{n,i}},\quad i=0, 1. $$

(24)

Using Eqs. 4 and 15, we obtain

$$ \begin{array}{@{}rcl@{}} W(0,q_{0},q_{1})=\frac{\gamma+\phi r_{2}}{\gamma(\mu+\phi)}\left[\frac{1}{1-r_{2}}+\frac{\mu-\eta}{\eta(1-r_{2})+\theta+\phi}\right]. \end{array} $$

Similarly, using Eqs. 3 and 17, we obtain

$$ \begin{array}{@{}rcl@{}} W(1,q_{0},q_{1})&=&\frac{1}{\mu+\phi-\lambda q_{1}} +\frac{1}{\gamma(\mu+\phi-\lambda q_{1})(1-r_{2})}\\ &&\left[\frac{(\gamma+\phi)\left( B\xi F(r_{2})(1-r_{2})-(\theta+\phi r_{2}){r_{2}^{2}}(1-\xi)\right)}{B F(r_{2})(1-r_{2})-(\theta+\phi r_{2})r_{2}(1-\xi)} -\frac{\lambda q_{1} (\gamma+\phi r_{2})}{(\mu+\phi)}\right]\\ &=&\frac{1}{\mu+\phi-\lambda q_{1}} -\frac{1}{\gamma(\mu+\phi-\lambda q_{1})(1-r_{2})}\left[\frac{\lambda q_{1} (\gamma+\phi r_{2})}{(\mu+\phi)} \right] \\ &&{}\left. -\frac{\lambda q_{1}(\gamma+\phi)\left\{ (\lambda q_{0}-\eta r_{2}) (1-r_{2})^{2}(\mu+\phi)+\mu(\theta+\phi r_{2}){r_{2}^{2}} \right\}}{(\lambda q_{0}-\eta r_{2}) (1-r_{2})^{2}(\mu+\phi)^{2}+\mu(\theta+\phi r_{2})r_{2}(\lambda q_{1}-(\mu+\phi)(1-r_{2}))}\right] \end{array} $$

From Eq. 1, the expected net benefit of a positive customer that finds the server on state i upon arrival and decides to join the system when all positive customers follow the joining strategy (q₀,q₁) is

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{au}(0,q_{0},q_{1})&=&\frac{\mu}{\mu+\phi}R-C~W(0,q_{0},q_{1}), \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{au}(1,q_{0},q_{1})&=&\frac{\mu}{\mu+\phi}R-C~W(1,q_{0},q_{1}). \end{array} $$

(26)

Consider r₂ as a function of q₀, its differentiation with respect to q₀ is

$$ \begin{array}{@{}rcl@{}} \frac{d r_{2}}{dq_{0}} &=\frac{\lambda}{2 \eta}\Big[1-\frac{ \lambda q_{0} +\theta+\phi-\eta}{\sqrt{(\lambda q_{0}+\theta+\phi+\eta)^{2}-4 \lambda q_{0} \eta}}\Big]. \end{array} $$

Therefore, r₂(q₀) is strictly increasing for q₀ ∈ [0,1]. Now Δ_au(0,q₀,q₁) is strictly decreasing for r₂ ∈ [0,r₂(1)], where

$$r_{2}(1)=\frac{(\lambda +\theta+\phi+\eta)- \sqrt{(\lambda +\theta+\phi+\eta)^{2}-4\lambda \eta}}{2 \eta},$$

and 0 < r₂(1) < 1. Thus, Δ_au(0,q₀,q₁) is strictly decreasing for q₀ ∈ [0,1]. Taking the equation Δ_au(0,q₀,q₁) = 0 with Δ_au(0,q₀,q₁) given by Eq. 25 and we solve for r₂(q₀). Suppose r_2e be the unique solution of equation for r_2e < 1 and it is given by

$$ \begin{array}{@{}rcl@{}} &r_{2e}=1+\frac{(R\mu\gamma+C\phi)(\theta+\phi)-C\mu(\gamma+\phi)}{2\mu(R\eta\gamma+C\phi)}\\ & -\frac{\sqrt{\left\{2\mu(R\eta\gamma+C\phi)+(R\mu\gamma+C\phi)(\theta+\phi)-C\mu(\gamma+\phi)\right\}^{2}-4\mu\gamma(R\eta\gamma+C\phi)(R\mu(\eta+\theta+\phi)-C(\mu+\theta+\phi))}}{2\mu(R\eta\gamma+C\phi)} \end{array} $$

The representing unique ${q_{e}^{0}}$ is obtained by substituting z = r_2e in Eq. 14. Solving this linear equation for q₀, we have

$$ \begin{array}{@{}rcl@{}} {q_{e}^{0}}=\frac{r_{2e}\left[\eta~(1-r_{2e})+\theta+\phi \right]}{\lambda (1-r_{2e})}. \end{array} $$

(27)

Solving the Eq. 26 for q₁, we get the unique solution q₁ < 1, as

$$ \begin{array}{@{}rcl@{}} &q_{1}=\frac{m_{2}(r_{2})}{2 \lambda m_{1}(r_{2})} -\frac{\sqrt{(m_{2}(r_{2}))^{2}-4 m_{1}(r_{2}) m_{3}(r_{2})}}{2 m_{1}(r_{2})}, \end{array} $$

where x₁ = (λq₀ − ηr₂)(1 − r₂)²(μ + ϕ), $y_{1}=x_{1}+\mu {r_{2}^{2}}(\theta +\phi r_{2})$, $y_{2}=\left (x_{1}-\mu r_{2}(\theta +\phi r_{2})(1-r_{2})\right )$,

$$ \begin{array}{@{}rcl@{}} {m_{1}(r_{2})}&=&\mu r_{2}(\theta+\phi r_{2})\left[r_{2}(\mu R\gamma+C\phi)-\gamma(\mu R-C)\right]\\ {m_{2}(r_{2})}&=&(\mu+\phi)\big[(\mu R\gamma+C\phi)(1-r_{2})y_{1}{{\kern-.5pt}}+{{\kern-.5pt}}\mu r_{2}(\theta+\phi r_{2})\left\{C r_{2}(\gamma{{\kern-.5pt}}+{{\kern-.5pt}}\phi){{\kern-.5pt}}-{{\kern-.5pt}}2 (\mu R-C)\gamma(1-r_{2})\right\}\big]\\ {m_{3}(r_{2})}&=&(\mu+\phi)^{2} \gamma(1-r_{2})y_{2}(\mu R-C). \end{array} $$

Consider a tagged positive customer who finds the server on working vacation mode on arrival and joins the system with probability q₀ if he earns a positive net benefit. We analyze the equilibrium joining probability ${q_{e}^{0}}$ under the following two cases:

• Case 1: $C\frac {\mu +\phi }{\mu }W(0,0,q_{1})<R\le ~C\frac {\mu +\phi }{\mu }W(0,1,q_{1})$. In this case, if all positive customers join with probability q₀ = 1, then the tagged positive customer who decides to enter has Δ_au(0,1,q₁) ≤ 0. Hence, q₀ = 1 can not be an equilibrium strategy. On the other hand, if all other positive customers join with probability q₀ = 0, then the tagged positive customer has Δ_au(0,q₀,q₁) > 0. The tagged positive customer is benefited more by joining than balking. Hence, q₀ = 0 can not be an equilibrium strategy. Therefore, a unique mixed Nash equilibrium strategy $q_{0}={q_{e}^{0}}$ exists for which positive customers are indifferent between entering and balking the queue. This unique equilibrium strategy is obtained by solving Δ_au(0,q₀,q₁) = 0 for q₀.

• Case 2: $C\frac {\mu +\phi }{\mu }W(0,1,q_{1})<R$. In this case, the best response is 1, and the tagged positive customer gets benefited by joining the system irrespective of the decisions taken by rest of the positive customers. Hence, ${q_{e}^{0}}=1$ is the only equilibrium strategy.

Next, we consider the equilibrium mixed strategies for a tagged positive customer who discovers the server on normal service mode upon arrival. From Eq. 26, the expected net benefit of the tagged positive customer is

$$ \begin{array}{@{}rcl@{}} \frac{\mu}{\mu+\phi}R-C~W(1,q_{0},q_{1}) &=\begin{cases} \frac{\mu}{\mu+\phi}R-C~W(1,{q_{e}^{0}},q_{1}) & \text{in case} ~1;\\ \frac{\mu}{\mu+\phi}R-C~W(1,1,q_{1})& \text{in case} ~2. \end{cases} \end{array} $$

To find the equilibrium joining strategy ${q_{e}^{1}}$, we analyze the following sub-cases under case 1 and case 2.

• Case 1a: $C\frac {\mu +\phi }{\mu }W(0,0,q_{1})<R\le ~C\frac {\mu +\phi }{\mu }W(0,1,q_{1})$ and $R< ~C\frac {\mu +\phi }{\mu }W(1,{q_{e}^{0}},0)$,

  $({q_{e}^{0}},{q_{e}^{1}})=\left (\frac {r_{2e}\left [\eta (1-r_{2e})+\theta +\phi \right ]}{\lambda (1-r_{2e})},0\right )$.

• Case 1b: $C\frac {\mu +\phi }{\mu }W(0,0,q_{1})<R\le ~C\frac {\mu +\phi }{\mu }W(0,1,q_{1})$ and $C\frac {\mu +\phi }{\mu }W(1,{q_{e}^{0}},0)<R\le ~C\frac {\mu +\phi }{\mu }W(1,{q_{e}^{0}},1)$,

  $({q_{e}^{0}},{q_{e}^{1}})=\left (\frac {r_{2e}\left [\eta (1-r_{2e})+\theta +\phi \right ]}{\lambda (1-r_{2e})},\frac {m_{2}(r_{2e})}{2 \lambda m_{1}(r_{2e})} -\frac {\sqrt {(m_{2}(r_{2e}))^{2}-4 m_{1}(r_{2e}) m_{3}(r_{2e})}}{2 m_{1}(r_{2e})}\right )$.

• Case 1c: $C\frac {\mu +\phi }{\mu }W(0,0,q_{1})<R\le ~C\frac {\mu +\phi }{\mu }W(0,1,q_{1})$ and $C \frac {\mu +\phi }{\mu \phi }W(1,{q_{e}^{0}},1)<R$,

  $({q_{e}^{0}},{q_{e}^{1}})=\left (\frac {r_{2e}\left [\eta (1-r_{2e})+\theta +\phi \right ]}{\lambda (1-r_{2e})},1\right )$.

• Case 2a: $C\frac {\mu +\phi }{\mu }W(0,1,q_{1})<R$ and $R < C\frac {\mu +\phi }{\mu }W(1,1,0),$

  $({q_{e}^{0}},{q_{e}^{1}})=(1,0)$.

• Case 2b: $C\frac {\mu +\phi }{\mu }W(0,1,q_{1})<R$ and $C\frac {\mu +\phi }{\mu }W(1,1,0)<R\le ~C\frac {\mu +\phi }{\mu }W(1,1,1),$

  $({q_{e}^{0}},{q_{e}^{1}})=\left (1,\frac {m_{2}(r_{2}(1))}{2 \lambda m_{1}(r_{2}(1))} -\frac {\sqrt {(m_{2}(r_{2}(1)))^{2}-4 m_{1}(r_{2}(1)) m_{3}(r_{2}(1))}}{2 m_{1}(r_{2}(1))}\right )$.

• Case 2c: $C\frac {\mu +\phi }{\mu }W(0,1,q_{1})<R$ and $C\frac {\mu +\phi }{\mu }W(1,1,1)<R,$

  $({q_{e}^{0}},{q_{e}^{1}})=(1,1)$.

The social benefit of the system when all positive customers follow the same mixed joining strategy (q₀,q₁), is

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{s}(q_{0},q_{1})&=&\lambda \frac{\mu}{\mu+\phi}(p_{0} q_{0}+p_{1} q_{1})R-C E(N)\\ &=&d_{2}\left[\frac{\lambda\mu}{\mu+\phi}R\left\{\frac{q_{0}}{1-r_{2}}+\frac{B q_{1}}{1-\xi}-\frac{q_{1}\left( \theta+\phi r_{2}\right)r_{2}}{F(r_{2})(1-r_{2})}\right\}\right.\\&&\left.-C \left\{\frac{r_{2}}{(1-r_{2})^{2}}-\frac{\left( \theta+\phi {r_{2}^{2}}\right)r_{2}}{F(r_{2})(1-r_{2})^{2}}+\frac{B \xi}{(1-\xi)^{2}} \right\}\right]. \end{array} $$

(28)

where p₀ and p₁ can be found from Eqs. 22 and 23, respectively.

4.2 Fully Unobservable Queue

In this section, positive customers do not have any information. They follow a mixed strategy of joining with probability q. The state transition diagram is illustrated in Fig. 5.

Fig. 5

State transition diagram of the model with positive customers’ strategy q

$$ \begin{array}{@{}rcl@{}} \lambda q\pi_{0,1}&=&\gamma \pi_{0,2}, \end{array} $$

(29a)

$$ \begin{array}{@{}rcl@{}} (\lambda q+\mu+\phi) \pi_{n,1}&=&\lambda q \pi_{n-1,1}+\mu \pi_{n+1,1}+\gamma\pi_{n,2}+\theta\pi_{n,0},~~ n\ge 1, \end{array} $$

(29b)

$$ \begin{array}{@{}rcl@{}} \lambda q\pi_{0,0}&=&\mu\pi_{1,1}+\eta\pi_{1,0}, \end{array} $$

(29c)

$$ \begin{array}{@{}rcl@{}} (\lambda q+\theta+\phi+\eta)\pi_{n,0}&=&\lambda q\pi_{n-1,0}+\eta\pi_{n+1,0},~~ n\ge 1, \end{array} $$

(29d)

$$ \begin{array}{@{}rcl@{}} \gamma \pi_{n,2}&=&\phi\pi_{n+1,1}+\phi\pi_{n+1,0},~~n\ge 0 \end{array} $$

(29e)

In the fully unobservable M/M/1 queue with positive customers and multiple working vacations in which all positive customers follow a strategy q, we can find the stationary state distribution by setting q₀ = q₁ = q in the almost unobservable queue.

$$ \begin{array}{@{}rcl@{}} \pi_{n,0}&=& d_{2} {r_{2}^{n}}(q),~~n\ge 0, \end{array} $$

(30)

$$ \begin{array}{@{}rcl@{}} \pi_{n,1}&=& d_{2}\left[B \xi^{n}-\frac{\left( \theta+\phi\ r_{2}(q)\right)r_{2}^{n+1}(q)}{F(r_{2}(q))}\right],~~n \ge 0, \end{array} $$

(31)

$$ \begin{array}{@{}rcl@{}} \pi_{n,2}&=&\frac{d_{2}\phi}{\gamma} \left[r_{2}^{n+1}(q)+B \xi^{n+1}- \frac{\left( \theta+\phi\ r_{2}(q)\right)r_{2}^{n+2}(q)}{F(r_{2}(q))}\right],~~n\ge 0 \end{array} $$

(32)

where r₂(q) is given by

$$ \begin{array}{@{}rcl@{}} r_{2}(q)&=\frac{(\lambda q+\theta+\phi+\eta)- \sqrt{(\lambda q+\theta+\phi+\eta)^{2}-4\lambda q \eta}}{2 \eta}. \end{array} $$

The probability π₀ that the system is on a working vacation mode, the probability π₁ that the system is on a normal service mode and π₂ that the system is on repair mode are calculated as

$$ \begin{array}{@{}rcl@{}} \pi_{0}&=&\sum\limits_{n=0}^{\infty}\pi_{n,0} =\frac{d_{2}}{1-r_{2}(q)},~~\pi_{1}=\sum\limits_{n=0}^{\infty}\pi_{n,1} =d_{2}\left[\frac{B}{1-\xi}-\frac{\left( \theta+\phi\ r_{2}(q)\right)r_{2}(q)}{F(r_{2}(q))(1-r_{2}(q))}\right],\\ \pi_{2}&=&\sum\limits_{n=0}^{\infty}\pi_{n,2}=\frac{d_{2}\phi}{\gamma}\left[ \frac{r_{2}(q)}{1-r_{2}(q)}+\frac{B \xi}{1-\xi}-\frac{\left( \theta+\phi\ r_{2}(q)\right){r_{2}^{2}}(q)}{F(r_{2}(q))(1-r_{2}(q))}\right]. \end{array} $$

The average number of the positive customers in the system

$$ \begin{array}{@{}rcl@{}} E(N)&=&\sum\limits_{n=1}^{\infty}n(\pi_{n,0}+\pi_{n,1})\\ &=&d_{2}\left[\frac{r_{2}(q)}{(1-r_{2}(q))^{2}}\left( 1-\frac{\left( \theta+\phi r_{2}(q)\right)r_{2}(q)}{F(r_{2}(q))}\right)+\frac{B \xi}{(1-\xi)^{2}}\right]. \end{array} $$

Using Little’s law, the mean sojourn time of a positive customer that decides to enter upon arrival is obtained as

$$ \begin{array}{@{}rcl@{}} W(q)=\frac{E(N)}{\lambda q}&=\frac{d_{2}}{\lambda q}\left[\frac{r_{2}(q)}{(1-r_{2}(q))^{2}}\left( 1-\frac{\left( \theta+\phi r_{2}(q)\right)r_{2}(q)}{F(r_{2}(q))}\right)+\frac{B \xi}{(1-\xi)^{2}}\right] \end{array} $$

(33)

Lemma 3

In the fully unobservable M/M/1 queue with multiple working vacations and negative customers and λ < μ, the expected mean sojourn time of a customer who decides to join the system, is strictly increasing for q ∈ [0,1].

Proof

The expected mean sojourn time can be rewritten as W(q) = g₁(q) g₂(q), where,

$$g_{1}(q){{}}={{}}\frac{r_{2}(q)}{\lambda q(1-r_{2}(q))^{2}} \quad {{}}\text{and}{{}} \quad g_{2}(q){{\kern-.5pt}}={{\kern-.5pt}} d_{2}\left( 1-\frac{\left( \theta+\phi r_{2}(q)\right)r_{2}(q)}{F(r_{2}(q))}{{\kern-.5pt}}+{{\kern-.5pt}}\frac{B \xi (1-r_{2}(q))^{2}}{r_{2}(q)(1-\xi)^{2}}\right).$$

Differentiating g₁(q) and g₂(q) with respect to q, we have

$$ \begin{array}{@{}rcl@{}} g_{1}^{\prime}(q)&=\frac{ q r_{2}^{\prime}(q)\left( 1+r_{2}(q)\right)-r_{2}(q)\left( 1-r_{2}(q)\right)}{\lambda q^{2}(1-r_{2}(q))^{3}},\\ g_{2}^{\prime}(q)&=d_{2}^{\prime}(q)g_{2}(q)+d_{2}(q)g_{2}^{\prime}(q), \end{array} $$

where $r_{2}^{\prime }(q)$ is given by

$$ \begin{array}{@{}rcl@{}} r_{2}^{\prime}(q)&=\frac{\lambda}{2 \eta}\Big[1-\frac{\lambda q+\theta+\phi-\eta}{\sqrt{(\lambda q+\theta+\phi-\eta)^{2} +4\eta(\theta+\phi)}}\Big]>0, ~q\in [0,1], \end{array} $$

Clearly, $r_{2}^{\prime }(q)>0$ for q ∈ [0,1], and 0 ≤ r₂(q) < 1. By taking λ < μ, we find that both g₁(q) and g₂(q) are strictly increasing for q ∈ [0,1], that is, $g_{1}^{\prime }(q)>0$ and $g_{2}^{\prime }(q)>0$. Therefore, we infer that W(q) is strictly increasing for q ∈ [0,1]. □

Consider a fully unobservable positive customer in a Markovian queue with multiple working vacations where arriving positive customers follow a common mixed strategy q such that the system is stable (λq < μ). Now the expected net benefit of a tagged positive customer who decides to join is

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{fu}(q)=\frac{\mu}{\mu+\phi}R-C \frac{r_{2}(q)}{\lambda q(1-r_{2}(q))^{2}} g_{2}(q), \end{array} $$

(34)

and

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{fu}(0)&=& \frac{\mu}{\mu+\phi}R~ -~ C \frac{\mu+\phi+\theta}{(\mu+\phi)(\eta+\theta+\phi)},\\ {\varDelta}_{fu}(1)&=& \frac{\mu}{\mu+\phi}R ~ - ~ \frac{C r_{2}(1)g_{2}(1)}{\lambda(1-r_{2}(1))^{2}}. \end{array} $$

Therefore, Δ_fu(q) = 0 has a unique solution $q_{e}^{*}\in (0,1)$ for

$$R\in \left( \frac{C(\mu+\phi+\theta)}{\mu(\eta+\theta+\phi)},\frac{\mu+\phi}{\mu}\frac{Cr_{2}(1)g_{2}(1)}{\lambda(1-r_{2}(1))^{2}}\right),$$

and Δ_fu(q) > 0 for each q when $R\in \left [\frac {\mu +\phi }{\mu }\frac {Cr_{2}(1)g_{2}(1)}{\lambda (1-r_{2}(1))^{2}},\infty \right ),$ that is, the tagged positive customer’s best response is 1. If $0 < R< \frac {C(\mu +\phi +\theta )}{\mu (\eta +\theta +\phi )}$, then Δ_fu(q) ≤ 0 for every q. Upon arrival of a positive customer, the best response is to balk and the unique equilibrium point is q = 0. Thus, there exists a unique Nash equilibrium strategy q_e, if the tagged positive customer takes a decision to join the system, provided R satisfies certain conditions. Hence, the Nash equilibrium strategy for the fully unobservable queue is given as follows:

$$q_{e}=\begin{cases}0 & R\in \left( 0,\frac{C(\mu+\phi+\theta)}{\mu(\eta+\theta+\phi)}\right]\\ q_{e}^{*} &R\in \left( \frac{C(\mu+\phi+\theta)}{\mu(\eta+\theta+\phi)},\frac{\mu+\phi}{\mu}\frac{Cr_{2}(1)g_{2}(1)}{\lambda(1-r_{2}(1))^{2}}\right),\\ 1 & R\in \left[\frac{\mu+\phi}{\mu}\frac{Cr_{2}(1)g_{2}(1)}{\lambda(1-r_{2}(1))^{2}},\infty\right). \end{cases}$$

Now, the social benefit per time unit when all positive customers follow the equilibrium mixed strategy q_e is Δ_s(q_e).

$$ \begin{array}{@{}rcl@{}} {\varDelta}_{s}(q_{e}) &=\lambda q_{e}\left[\frac{\mu}{\mu+\phi} R-\frac{C d_{2}}{\lambda q_{e}}\left( \frac{r_{2}(q_{e})}{(1-r_{2}(q_{e}))^{2}}\left( 1-\frac{\left( \theta+\phi r_{2}(q_{e})\right)r_{2}(q_{e})}{F(r_{2}(q_{e}))}\right)+\frac{B \xi}{(1-\xi)^{2}}\right)\right]. \end{array} $$

Remark 1

In the fully unobservable multiple working vacations queue with negative customers and λ ≥ μ, there exists a unique mixed equilibrium strategy ‘enter with probability q_e’, where q_e is given by

$$ \begin{array}{@{}rcl@{}} q_{e}=q_{e}^{*}~~\text{for }~ R\in \left( \frac{C(\mu+\phi+\theta)}{\mu(\eta+\theta+\phi)},\infty\right). \end{array} $$

(35)

5 Numerical Results and Discussions

In this section, we discuss the impact of model parameters on positive customers’ behavior through several numerical experiments. The behavior of the strategic customers under different levels of information are discussed for some variations of model parameters. The equilibrium joining strategies for the observable models and the unobservable models are presented under different situations. The role of information on the social benefit of the system is also discussed. Maple software is used to get the numerical results for the queueing systems with a variety of model parameters. In Figs. 6, 7, 8, 9, the equilibrium threshold strategies for the observable cases and in Figs. 10, 11, 12, 13, 14, 15, equilibrium joining probabilities for the unobservable cases are presented for different queueing parameters.

Fig. 6

Equilibrium threshold strategies vs. γ with λ = 3.0,μ = 4.0,ϕ = 0.3,η = 1.5,𝜃 = 0.1,R = 10,C = 1

Fig. 7

Equilibrium threshold strategies vs. η with λ = 3.0,μ = 4.0,ϕ = 0.3,𝜃 = 0.1,γ = 0.5,R = 10,C = 1

Fig. 8

Equilibrium threshold strategies vs. 𝜃 with λ = 2.0,μ = 5,ϕ = 1.0,η = 0.4,γ = 0.3,R = 10, C = 1

Fig. 9

Equilibrium threshold strategies vs. ϕ with λ = 3.0,μ = 7.0,η = 0.8,𝜃 = 1.0,γ = 0.5,R = 10,C = 1

Fig. 10

Equilibrium joining strategies vs. μ with λ = 3.0,ϕ = 0.2,η = 1.5,𝜃 = 0.1,γ = 0.3,R = 4, C = 1

Fig. 11

Equilibrium joining strategies vs. ϕ with λ = 3,μ = 3.5,η = 1.5,𝜃 = 0.1,γ = 0.4,R = 4,C = 1

Fig. 12

Equilibrium joining strategies vs. λ with μ = 3.5,ϕ = 0.2,𝜃 = 0.1,η = 1,γ = 1.5,R = 2,C = 1

Fig. 13

Equilibrium joining strategies vs. η with λ = 3.0,μ = 3.5,ϕ = 0.2,γ = 1.0,𝜃 = 0.1,R = 5, C = 1

Fig. 14

Equilibrium joining strategies vs. γ with λ = 3.0,μ = 3.5,ϕ = 0.2,η = 2.0,𝜃 = 0.1,R = 5, C = 1

Fig. 15

Equilibrium joining strategies vs. 𝜃 with λ = 3.0,μ = 3.5,ϕ = 0.2,γ = 0.15,η = 1.5,R = 5,C = 1

In the first set of experiments, we study the behavior of positive customers in the observable model. The dependence of the equilibrium joining (threshold) strategies on the system parameters is discussed. This set of experiments will help to answer the impact of negative arrivals, working vacation duration, server repair speed, and working vacation service rate on the equilibrium behavior of positive customers. The equilibrium threshold strategies are non-decreasing functions of repair rate, vacation rate, and vacation times (Figs. 6–8). If the repair rate increases, the waiting time of the positive customers’ decreases, which attracts more customers to join the system; as a result, the equilibrium threshold increases. In Figs. 7 and 8, the lesser the customers wait in the system when the server works faster during vacation or takes vacations of shorter duration, the smaller is the gap among thresholds. As the vacation rate increases, the mean vacation time decreases, which results in shorter expected sojourn times for waiting customers. Thus, the waiting time of the rest positive customers decreases substantially due to the shorter expected sojourn time during working vacation. This information about the smaller queue length attracts more customers to join the system; as a result, the threshold increases.

In Fig. 9, the thresholds decrease with frequent arrivals of negative customers. As the frequency of negative arrival increases, more positive customers (that are in service each time) are removed from the system, which results in the decrease in the threshold. We observe that the equilibrium thresholds in the almost observable model lie within the equilibrium thresholds of the fully observable model, that is, ${n_{e}^{0}}\le n_{L}\le n_{U}\le {n_{e}^{1}}$. This shows that the system congestion can be controlled by regulating the available system information.

In the second set of experiments, we consider the model under the unobservable case, where the positive customers follow a mixed equilibrium joining strategy. Customers with the server state information only do not get any benefit in case of a system with a fast server but have a visible effect when they join a slow server. Fig. 10 shows the influence of the server speed on the equilibrium joining probabilities. In Fig. 11, the effect of negative arrivals is more prominent when the server is on normal service. If more customers are removed with more negative arrivals, it reduces the waiting time of positive waiting customers; thus, their chances of getting service increases. As a result, positive customers join the system with a follow the crowd effect. When the frequency of negative arrivals increases, entirely unaware positive customers join the system with probability one. In Fig. 12, the joining probabilities have mixed variations. Positive customers finding a slower server are reluctant or less interested to join the system when their arrival rate increases. This is intuitive as the congestion in a working vacation state increases their waiting time. There is no benefit of having the server state information in a system with slower arrivals. But this has a positive effect in a system with more arrivals.

In Fig. 13, the equilibrium joining probabilities are non-decreasing functions of working vacation service rate and fully uninformed positive customers always join the system. When the repair process is faster, the server status does not have any effect on the equilibrium behavior of positive customers, where as it has a positive effect on the joining strategies for longer repair times. The effect of repair rate on the equilibrium behavior is depicted in Fig. 14. Finally, we illustrate the effect of working vacation times on the equilibrium joining strategies of positive customers in Fig. 15. When the server takes longer vacations (𝜃 ≤ 0.12), positive customers’ joining probabilities in the busy state dominates that of the working vacation state. After 𝜃 = 0.12, the dominance relation between the joining probabilities becomes the opposite. Customers are least interested to join the busy state for 𝜃 = 0.2 and beyond this more customers join the busy state with shorter vacation duration. This is because of the presence of more positive customers during the previous vacation periods. When the server has shorter vacations, positive arrivals are interested to join the vacation state expecting shorter waiting times. When more positive customers join the vacation state, it brings negative externalities on the positive customers who decide to join the busy state and these negative externalities reduce with shorter vacation duration. Thus, more positive customers are interested to join the busy state followed by shorter vacations. In the experiments, we observe that positive customers unaware of the server status, choose to ‘follow the crowd’ under equilibrium.

We observe that fully uninformed positive customers always join the system. The server status does not impact positive customers’ equilibrium behavior when the repair duration is very short. The positive customers’ waiting time decreases with the increase of the repair rate in the observable case. Thus, it pulls more customers to join the system; therefore, the equilibrium threshold increases.

6 Conclusion

In this paper, we analyzed the positive customers’ equilibrium behavior in a Markovian queueing system with working vacations and negative arrivals under four different information levels. We derived closed-form expressions of the stationary state probabilities using a recursive method. The equilibrium joining behavior and social benefit based on various parameters of the information level has been examined under the corresponding strategies. The sensitivity analysis of the equilibrium thresholds in observable cases and equilibrium joining probabilities in the unobservable cases are carried out by varying several model parameters. The effect of negative arrivals on the equilibrium behavior of positive customers under the observable and unobservable models is presented. The presented model, on the one hand, could provide strategic customers with useful insights in decision making under a variety of information policies and guide them on whether to follow or avoid the crowd. On the other hand, of the different information levels, it could provide useful information to the system manager to get the maximum benefit. The inclusion of the retrials of balking customers and the reneging of waiting customers in this problem is more challenging and is left for future exploration. This model may be extended to incorporate arbitrarily distributed service demands to a batch-arrival or a batch service queue.