Variational proof of the existence of periodic orbits in the anisotropic Kepler problem

Abstract

The anisotropic Kepler problem is a model of the motion of free electrons on an n-type semiconductor and is known to be a non-integrable Hamiltonian system. While many approximate periodic solutions have been found through numerical calculation (Sumiya et al. in Artif Life Robot 19:262–269, 2014), none have been rigorously proved to exist. In this paper, we first show that the action functional of the anisotropic Kepler problem has a minimizer under a fixed region condition with boundary conditions on a vertical half-line. Next, we identify the smallest collision trajectory that satisfies the same boundary conditions. By constructing an orbit with an action functional smaller than this collision orbit via local deformation, we show that the collision solution does not become the minimizer. This holds for any $\mu \in (0,1)$. Reversibility allows the periodic orbit to be constructed from the minimizer obtained via the action functional.

1 Introduction

The n-body problem, which has been studied since Newton discovered universal gravitation, is concerned with the motion when n mass points are gravitationally attracted to each other. Poincare showed that the three-body problem cannot be solved under various settings. Therefore, it is not possible to find a general solution of the n-body problem, but it may be possible to find a special solution, in particular, a periodic solution. One way to find such a solution is the variational method. For example, Chenciner and Montgomery famously proved the existence of the figure-eight solution to the 3-body problem with equal masses (Chenciner and Montgomery 2000). In this paper, we apply this method to the anisotropic Kepler problem (AKP).

Equations of motion of a two-dimensional potential system are defined by:

$$\begin{aligned} \ddot{x} = -\frac{\partial V}{\partial x},\quad \ddot{y} = - \frac{\partial V}{\partial y} \end{aligned}$$

(1.1)

where V(x, y) is a potential function. The potential of the AKP is represented by:

$$\begin{aligned} V(x, y) = -\frac{1}{\sqrt{x^2+\mu y^2}} \quad (\mu > 0) \end{aligned}$$

and the Lagrangian by:

$$\begin{aligned} L(x, y, {\dot{x}}, {\dot{y}}) = \frac{1}{2}({\dot{x}}^2+{\dot{y}}^2) - V(x, y). \end{aligned}$$

(1.2)

Gutzwiller introduced this problem (Gutzwiller 1991) as an equation modeling free electrons in n-type semiconductors. The AKP is non-integrable for $\mu \ne 1$ Yoshida (1987) and has a horseshoe in the range of $\mu > 9/8$ or $\mu <8/9$Devaney (1978). A number of approximate periodic solutions of the AKP have been obtained via numerical calculation, but none have been mathematically proved to exist. In this paper, we use the variational method to prove the existence of periodic orbits with certain properties in the AKP.

Our main result is the following.

Main result. For any $T>0$ and any $\mu$, there exists a periodic orbit $\varvec{q}(t)=(x(t),y(t))$ that has period 4T and satisfies the following properties in the AKP:

• ${\dot{x}}(0)={\dot{y}}(T)=0$

• $x(-t)=x(t), y(-t)=y(t), x(t+T)=-x(-t+T), y(t+T)=-y(t+T)$

• $\varvec{q} (t)$ is orthogonal to the x- and y-axis at $t = 0$ and $t= T$, respectively;

• For all $t \in (0, T)$, x(t) decreases monotonically and y(t) increases monotonically.

We organize this paper as follows. Section 2 introduces preliminaries for our proof, including reversibility and the conditions for the action functional to have the minimizer. In Sect. 3, we formulate the AKP by the variational method. Section 4 shows that the minimizer has no collision. In Sect. 5, we show the result of numerical calculation using AUTO.

2 Preliminaries

2.1 Reversibility

Consider the following ordinary differential equation:

$$\begin{aligned} \dot{\varvec{q}}=F(\varvec{q}), \quad \varvec{q} \in {\mathbb {R}}^d. \end{aligned}$$

(2.1)

Definition 2.1

(Reversibility) Let R be an involuntary linear map from ${\mathbb {R}}^d$ to ${\mathbb {R}}^d$, i.e., $R^2=E_n$. If (2.1) satisfies:

$$\begin{aligned} F(R\varvec{x})+R(F\varvec{x})=0, \end{aligned}$$

then (2.1) is said to be reversible with respect to R.

With a simple calculation, we obtain the following lemma.

Lemma 2.2

Assume that (2.1) satisfies reversibility. Then, if $\varvec{q}(t)$ is a solution of (2.1), then so is to $R\varvec{q}(-t)$.

We define

$$\begin{aligned} \textrm{Fix}(R):=\{ \varvec{q}\in {\mathbb {R}}^d\mid R\varvec{q}=\varvec{q}\}. \end{aligned}$$

Lemma 2.3

For a solution $\varvec{q}(t)$ of (2.1), $\varvec{q}(T) \in \textrm{Fix}(R)$ is satisfied if and only if $\varvec{q}(T+t)=R\varvec{q}(T-t)$.

Proof

If $\varvec{q}(T+t)=R\varvec{q}(T-t)$, then $\varvec{q}(T) \in \textrm{Fix}(R)$ by substituting $t=0$. Conversely, we assume that $\varvec{q}(T) \in \textrm{Fix}(R)$. From Lemma 2.2, if $\varvec{q}(T+t)$ is a solution, then so is to $R\varvec{q}(T-t)$. Since the initial values match from $\varvec{q}(T)=R\varvec{q}(T)$, the lemma follows owing to the uniqueness of the solution. $\square$

2.2 Minimizers of the action functional

We describe the known results of the variational problem of the Lagrangian system. Let $I = [0, T]$. Let ${\mathcal {D}}$ be a configuration space in ${\mathbb {R}}^d$. We define $A,B\in {\mathcal {D}}$ as non-empty affine spaces. Let TA and TB be linear spaces created by translating A andB so that they pass through the origin. We set:

$$\begin{aligned} {\mathcal {C}}_{A,B}=\{ \varvec{q}\in C^2(I,{\mathcal {D}}) | \varvec{q}(0)\in A, \varvec{q}(T)\in B \} . \end{aligned}$$

(2.2)

The Lagrangian is $L(\varvec{q},\dot{\varvec{q}})$, and the action functional is:

$$\begin{aligned} {\mathcal {A}}(\varvec{q}) = \int _0^T L(\varvec{q}, \varvec{{\dot{q}}}) \,\textrm{d}t . \end{aligned}$$

A solution $\varvec{q}$ that satisfies $\mathcal {A'}(\varvec{q}) =0$ is called the critical point of ${\mathcal {A}}(\varvec{q})$.

Lemma 2.4

If $\varvec{q}\in {\mathcal {C}}_{A,B,T}$ is a critical point of ${\mathcal {A}}$, then $\varvec{q}(t)$ satisfies the Euler–Lagrange equation, where $I=(t_0,t_1)$. Moreover, $\frac{\partial L}{\partial \varvec{{\dot{q}}}}(\varvec{q}(t_0),\varvec{{\dot{q}}}(t_0))$ is orthogonal to TA and $\frac{\partial L}{\partial \varvec{{\dot{q}}}}(\varvec{q}(t_1),\varvec{{\dot{q}}}(t_1))$ is orthogonal to TB. Furthermore, if $L=\frac{1}{2}|\varvec{{\dot{q}}}|^2-V(\varvec{q})$, then $\varvec{{\dot{q}}}(t_0)$ is orthogonal to TA and $\varvec{{\dot{q}}}(t_1)$ is orthogonal to TB.

We consider a Sobolev space

$$\begin{aligned} H^1(I, {\mathcal {D}})=\left\{ \varvec{q}:I\rightarrow {\mathcal {D}}| \varvec{q} \in L^2(I, {\mathcal {D}}), \frac{\textrm{d}\varvec{q}}{\textrm{d}t} \in L^2(I, {\mathcal {D}}) \right\} \end{aligned}$$

and set the norm as:

$$\begin{aligned} ||\varvec{q}||_{H^1}:=\sqrt{\int _0^T |\varvec{q}|^2+|\varvec{{\dot{q}}}|^2\, \textrm{d}t} . \end{aligned}$$

Definition 2.5

(coercive) Let $\Omega \in H^1(I, {\mathcal {D}})$. The action functional ${\mathcal {A}}|_\Omega$ is said to be coercive when it satisfies

$$\begin{aligned} {\mathcal {A}}(\varvec{q})\rightarrow \infty \quad as \quad ||\varvec{q}||_{H^1} \rightarrow \infty \quad ( \varvec{q} \in \Omega ). \end{aligned}$$

We set

$$\begin{aligned} \Omega (A,B) = \{ \varvec{q}\in H^1(I,{\mathcal {D}})|\varvec{q}(0)\in A, \varvec{q}(T)\in B \}. \end{aligned}$$

Lemma 2.6

Let $A,B\in {\mathcal {D}}$. If there exists $C_0<1$ that satisfies:

$$\begin{aligned} \varvec{a} \cdot \varvec{b} \le C_0|\varvec{a}||\varvec{b}| \end{aligned}$$

(2.3)

for any $\varvec{a}\in A$ and $\varvec{b}\in B$, then ${\mathcal {A}}|_\Omega$ is coercive.

Lemma 2.7

(Tonelli 1925) Suppose that ${\mathcal {A}}|_\Omega$ is coercive. Then, there exists a minimizer $\varvec{q}^* \in {\overline{\Omega }}$. Moreover, the minimizer $\varvec{q}^*$ satisfies $\varvec{q}^* \in {\mathcal {C}}_{A,B}$, i.e., $\varvec{q}^*$ is smooth.

3 Formulation of the AKP by the variational method

We set ${\mathcal {D}} ={\mathbb {R}}^2 - \{ (0,0) \}$ and consider the boundary condition:

$$\begin{aligned} A=\{ (x,0)\in {\mathcal {D}}|x>0 \},\quad B=\{ (0,y)\in {\mathcal {D}}|y>0\}. \end{aligned}$$

(3.1)

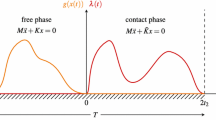
It is clear that A and B satisfy (2.3). Therefore, from Lemmas 2.6 and 2.7, there exists minimizer in ${\overline{\Omega }}(A,B)$. Moreover, from Lemma 2.4, ${\dot{\varvec{q}}}^* (0)$ is orthogonal to A and ${\dot{\varvec{q}}}^* (T)$ is orthogonal to B. The minimizer $\varvec{q^*}$ is a solution of AKP unless $\varvec{q^*}$ is a collision orbit (Fig. 1). The monotonicity will be shown later.

Fig. 1

The minimizer we aim to find

4 Estimation of collision orbit

Without loss of generality, we can limit the parameter $\mu$ in the AKP to $0<\mu <1$ by substituting 1/$\mu$ instead of $\mu$ and applying appropriate change of variables.

Now, we identify the collision orbit that minimizes the action functional. Using the polar coordinates $\varvec{q}=(r\cos \theta ,r\sin \theta )$, the action functional in the AKP is expressed by:

$$\begin{aligned} {\mathcal {A}}(\varvec{q}) =\int \frac{1}{2}({\dot{r}}^2+r^2{\dot{\theta }}^2)+\frac{1}{r\sqrt{\cos ^2 \theta +\mu \sin ^2 \theta }} . \end{aligned}$$

From this, we can see the following about the collision orbit that minimizes the action functional:

• ${\dot{\theta }}=0$ from the minimum of the kinetic energy term. In other words, the collision satisfying ${\dot{\theta }} \ne 0$ is not a minimizer because the trajectory transformed into ${\dot{\theta }}=0$ minimize action functional.

• $\theta =0$ from the minimum of the potential energy term. In other words, the collision satisfying $\theta \ne 0$ is not minimizer because the trajectory transformed into $\theta =0$ minimizes action functional.

Therefore, it suffices to show that the collision orbit that starts from positive part of the x-axis and moves to the origin along x-axis is not a minimizer. In the following, we discuss the orbit that starts from the origin and moves to the positive part of the x-axis along the x-axis because both have the same action functional and the latter is easier to handle.

4.1 Local transformation

We use the following for local evaluation of the collision orbit.

Lemma 4.1

[Sundman’s estimate, Siegel and Moser (2012)] We assume that collision trajectories $\varvec{q}_1,\ldots ,\varvec{q}_l$ in a system with a Kepler-type potential collide with c at $t=t_0$. Then:

$$\begin{aligned} \varvec{q}_k=\varvec{c}+(t-t_0)^{2/3}\varvec{a}_k+O(t-t_0)\quad (k=1,\dots ,l) . \end{aligned}$$

From Lemma 4.1, the collision orbit $\varvec{q}_{\textrm{col}}$ that starts from the origin and moves along the positive part of the x-axis is represented by:

$$\begin{aligned} \varvec{q}_{\textrm{col}} = (at^{2/3}+O(t),0), \quad a=\root 3 \of {\frac{9}{2}}. \end{aligned}$$

The main term of the action functional ${\mathcal {A}}(\varvec{q}_{\textrm{col}})$ at $t \in [0,\epsilon ]$ is:

$$\begin{aligned} \left( \frac{2}{3}a^2+\frac{3}{ a} \right) \epsilon ^{1/3}. \end{aligned}$$

We define a local transformation $\varvec{\delta }_{\epsilon }$ at $t \in [0,\epsilon ]$ as follows, where $n,m \in {\mathbb {N}}$ and free for the moment.

$$\begin{aligned} \varvec{q}_{\textrm{col}}+\varvec{\delta }_{\epsilon }(t)= \left\{ \begin{array}{ll} (a\epsilon ^{-1/3}t,c\epsilon ^m) &{} (0 \le t \le \epsilon ^n) \\ \left( a\epsilon ^{-1/3}t,c\epsilon ^m\frac{\epsilon -t}{\epsilon -\epsilon ^n} \right) &{} (\epsilon ^n \le t \le \epsilon ) \\ \varvec{q}_{\textrm{col}}(t) &{} (t > \epsilon ) \end{array} \right. . \end{aligned}$$

Fig. 2

Collision orbit that minimizes the action functional

Fig. 3

Local transformation

We can estimate the action functional at $t \in [0,\epsilon ]$ after transformation by:

$$\begin{aligned} {\mathcal {A}}(\varvec{q}_{\textrm{col}}+\varvec{\delta }_{\epsilon }) <\left( \frac{1}{2}a^2+\frac{\sqrt{2}}{a} \right) \epsilon ^{1/3} +\frac{1}{\sqrt{\mu }c}\epsilon ^{n-m} + \frac{c^2}{2}\epsilon ^{2m-1}. \end{aligned}$$

Therefore, by choosing n, m so that:

$$\begin{aligned} m\ge 2/3,\quad n\ge m+1/3, \end{aligned}$$

we obtain ${\mathcal {A}}(\varvec{q}_{\textrm{col}}) > {\mathcal {A}}(\varvec{q}_{\textrm{col}}+\varvec{\delta }_{\epsilon })$. The above remarks demonstrate that the collision orbit is not a minimizer.

4.2 Constructing a periodic solution

We discuss how to construct a periodic solution from the minimizer in the main theorem.

Lemma 4.2

We assume that $\varvec{q}=(x(t),y(t))$ is a minimizer of AKP under the boundary condition $\Omega (A,B)$. Then, x(t) and y(t) are monotone.

Proof

From (3.1), $x(0)>x(T)=0$ and it is a monotonous decrease if it is monotone. Assume that x(t) is a monotonous decrease. Then, there exist $a,b\in [0,T]$ such that $a<b$ and $x(a)<x(b)$. Then, by the mean value theorem, there exist $c\in [a,b]$ and $d\in [b,T]$ such that ${\dot{x}}(c)>0$ and ${\dot{x}}(d)<0$. From the intermediate value theorem, there exists $e\in (c,d)$ such that ${\dot{x}}(e)=0$. Therefore, we find that x(t) takes a local maximum value at $t=e$. We set

$$\begin{aligned} x^*(t)=\left\{ \begin{array}{ll} \max (x(t),x(e)) &{} \quad (t\in [0,e]) \\ x(t)&{}\quad (t\in (e,T]) \end{array} \right. . \end{aligned}$$

Since $x(t)\le x^*(t)$, we see that $|x^{\prime }(t)|\ge |x^{*\prime }(t)|$and ${\mathcal {A}}(x,y)>{\mathcal {A}}(x^*,y)$. This is contrary to the fact that x(t) is a minimizer. Similar arguments apply for the case of y. $\square$

The AKP can be represented by:

$$\begin{aligned} {\dot{x}} = p_x,&\quad {\dot{y}} = p_y, \end{aligned}$$

(4.1)

$$\begin{aligned} \dot{p_x} = -\frac{\partial V}{\partial x},&\quad \dot{p_y} = -\frac{\partial V}{\partial y}, \end{aligned}$$

(4.2)

and (4.1) has reversibility with respect to:

$$\begin{aligned} R_1 = \left( \begin{array}{cccc} -1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 \\ \end{array} \right) , R_2 = \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) . \end{aligned}$$

We assume that $\varvec{q}(t)=(x(t),y(t))$ is a solution at $t \in I$. Then, from Proposition 2.2, $\varvec{q}_1 (t)=(-x(-t),y(-t)), \varvec{q}_2 (t)=(x(-t),-y(-t))$, $\varvec{q}_3 (t)=(-x(t),-y(t))$ are also solutions, as illustrated in Fig. 4.

Fig. 4

Reversible solutions

Fig. 5

Periodic solutions

Fig. 6

Calculation results

The following lemma shows that these solutions are connected smoothly:

Lemma 4.3

${\dot{x}}(0)=0$ and ${\dot{y}}(T)=0$

Proof

From Gelfand and Fomin (2000), the variation in $t \in [0,T]$ is

$$\begin{aligned} \delta J=\int _{0}^{T} \left( L_x-\frac{\textrm{d}}{\textrm{d}t}L_{{\dot{x}}} \right) h_x(t)\textrm{d}t+\int _{0}^{T} \left( L_y-\frac{\textrm{d}}{\textrm{d}t}L_{{\dot{y}}} \right) h_y(t)\textrm{d}t+ (L_{{\dot{x}}}\delta x +L_{{\dot{y}}}\delta y) \left. \right| _{t=0}^{t=T}. \end{aligned}$$

(4.3)

where $h_x(t)$ and $h_y(t)$ are increments and $\delta x(0),\delta x(T),\delta y(0),\delta y(T)$ are the boundary coordinate increments. Since $\varvec{q}$ is a minimizer, $\delta J=0$. From the boundary conditions, $\delta x(T)=0$ and $\delta y(0)=0$. Therefore, by substituting them in (4.3), we obtain:

$$\begin{aligned} {\dot{x}}(0)\delta x(0)=0,\quad {\dot{y}}(T)\delta y(T)=0 \end{aligned}$$

for any increment. $\square$

From the above lemma, we obtain a smooth periodic solution like Fig. 5.

5 Numerical calculation

Figure 6 shows the results of numerical calculation of the periodic solution of the AKP using AUTO. The initial solution is the solution of the Kepler problem with $\mu = 1$:

$$\begin{aligned} x(t)=\left( \frac{\pi }{2} \right) ^{-\frac{2}{3}}\cos \frac{\pi t}{2}, y(t)=\left( \frac{\pi }{2} \right) ^{-\frac{2}{3}}\sin \frac{\pi t}{2}, 0\le t \le 1. \end{aligned}$$

We continue by reducing $\mu$ from 1 to 0. The boundary conditions are:

$$\begin{aligned} x(1)=y(0)={\dot{x}}(0)={\dot{y}}(0)=0. \end{aligned}$$