1 Introduction

1.1 Spectral methods

Spectral methods have been developed rapidly in the past two decades. They have been successfully applied to numerical simulations in many fields, such as heat conduction, fluid dynamics, quantum mechanics etc. These methods are powerful tools to solve differential equations. The key components of their formulation are the trial functions and the test functions. The trial functions, which are the linear combinations of suitable trial basis functions, are used to provide an approximate representation of the solution. The test functions are used to ensure that the differential equation and perhaps some boundary conditions are satisfied as closely as possible by the truncated series expansion. This is achieved by minimizing the residual function that is produced by using the truncated expansion instead of the exact solution with respect to a suitable norm (Boyd 2011; Guo et al. 2006; Shen et al. 2001; Shen and Tang 2005).

In this paper, we attempt to use the Bessel orthogonal functions as new basis functions for spectral methods. Previously, we have used the general Bessel functions for solving Blasius equation (Parand et al. 2012), but now, we aim to use the Bessel orthogonal functions as basis functions for solving the Lane–Emden type equations.

The structure of the paper is as follows: in Sect. 1.2 we describe the Lane–Emden equation, in Sect. 2, we explain the formulation of Bessel functions required for our subsequent of development and also function approximation. In Sect. 3, we summarize the application of Bessel functions method for solving Lane–Emden equations and, afterwards, we compare it with the existing methods in literature. Section 4 is devoted to the conclusion.

1.2 The Lane–Emden equation

The study of singular initial value problems modeled by second-order nonlinear ordinary differential equations (ODEs) have attracted many mathematicians and physicists. One of the equations in this category is the following Lane–Emden type equation:

$$\begin{aligned} y^{\prime \prime }(x) + \frac{\alpha }{x} y^{\prime }(x) + f(x,y(x)) = h(x), \mathtt \alpha x \ge 0 , \end{aligned}$$
(1)

with initial conditions:

$$\begin{aligned}&y(0) = A,\nonumber \\&y^{\prime }(0)= B, \end{aligned}$$
(2)

where \(\alpha , A\) and \(B\) are real constants and \(f(x,y)\) and \(h(x)\) are some given continuous real-valued functions. For special forms of \(f (x, y)\), the well-known Lane–Emden equations occur in several models of non-Newtonian fluid mechanics, mathematical physics, astrophysics, etc. For example, when \(f (x, y) = q(y)\), the Lane–Emden equations occur in modeling several phenomena in mathematical physics and astrophysics such as the theory of stellar structure, the thermal behavior of a spherical cloud of gas, isothermal gas sphere and theory of thermionic currents (Chandrasekhar 1967; Davis 1962).

Let \(P(r)\) denote the total pressure at a distance \(r\) from the center of spherical gas cloud. The total pressure is due to the usual gas pressure and a contribution from radiation:

$$\begin{aligned} P=\left( \frac{1}{3}\xi T^{4}+\frac{R T}{\upsilon }\right) , \end{aligned}$$
(3)

where \(\xi , T, R\) and \(\upsilon \) are respectively the radiation constant, the absolute temperature, the gas constant, and the specific volume, respectively (Agrawal and O’Regan 2007). Let \(M(r)\) be the mass within a sphere of radius \(r\) and \(G\) the constant of gravitation. The equilibrium equation for the configuration are:

$$\begin{aligned} \frac{d P}{d r}= - \rho \frac{G M(r)}{r^{2}},\end{aligned}$$
(4)
$$\begin{aligned} \frac{d M(r)}{d r}=4 \pi \rho r^{2}, \end{aligned}$$
(5)

where \(\rho \) is the density, at a distance \(r\), from the center of a spherical star. Eliminating \(M\) of these equations yields the following equation, which as should be noted, is an equivalent form of the Poisson equation:

$$\begin{aligned} \frac{1}{r^{2}}\frac{d}{d r}\left( \frac{r^{2}}{\rho }\frac{d P}{d r}\right) =-4\pi G \rho . \end{aligned}$$
(6)

We already know that in the case of a degenerate electron gas, the pressure and density are such that \(\rho =P^{3/5}\). Assuming that such a relation exists for other states of the star, we are led to consider a relation of the form \(P=K \rho ^{1+\frac{1}{m}}\), where \(K\) and \(m\) are constants.

We can insert this relation into Eq. (4) for the hydrostatic equilibrium condition and, from this, we can rewrite the equation as follows:

$$\begin{aligned} \left[ \frac{K(m+1)}{4\pi G}\lambda ^{\frac{1}{m}-1}\right] \frac{1}{r^{2}}\frac{d}{d r}\left( r^{2}\frac{d y}{d r}\right) =-y^{m}, \end{aligned}$$
(7)

where \(\lambda \) represents the central density of the star and \(y\) denotes the dimensionless quantity, which are both related to \(\rho \) through the following relation (Chandrasekhar 1967; Horedt 2004):

$$\begin{aligned} \rho = \lambda y^{m}(x), \end{aligned}$$
(8)

and let

$$\begin{aligned} r=ax, \end{aligned}$$
(9)
$$\begin{aligned} a=\left[ \frac{K(m+1)}{4\pi G}\lambda ^{\frac{1}{m}-1}\right] ^{\frac{1}{2}}. \end{aligned}$$
(10)

Inserting these relations into our previous relation we obtain the Lane–Emden equation (Horedt 2004):

$$\begin{aligned} \frac{1}{x^{2}}\frac{d}{dx}\left( x^{2}\frac{d y}{d x}\right) =- y^{m}, \end{aligned}$$
(11)

considering these simple relations, we will have the standard Lane–Emden equation with \(f(x,y)=y^m\)

$$\begin{aligned} y^{\prime \prime }(x)+\frac{2}{x}y^{\prime }(x)+{y^{m}(x)}=0, ~~~ x>0 . \end{aligned}$$
(12)

At this point, it is also important to introduce the boundary conditions which are based upon the following boundary conditions for hydrostatic equilibrium and normalization consideration of the newly introduced quantities \(x\) and \(y\). What follows for \(r = 0\) is

$$\begin{aligned}&r=0~~\rightarrow ~~x=0,\nonumber \\&\rho =\lambda ~~\rightarrow ~~y(0)=1. \end{aligned}$$
(13)

Consequently, an additional condition must be introduced in order to maintain the condition of Eq. (13) simultaneously

$$\begin{aligned} y^{\prime }(0)=0. \end{aligned}$$

In other words, the boundary conditions are as follows

$$\begin{aligned} y(0)=1,\quad y^{\prime }(0)=0. \end{aligned}$$
(14)

The values of \(m\) that are physically interesting lie in the interval \([0, 5]\). The main difficulty in analyzing this type of equation is the singularity occurring at \(x = 0\).

As mentioned in the literature, the solutions of the Lane–Emden equations are exact only for \(m\,=\,0, 1\) and 5 (Horedt 2004). For the other values of \(m\), the Lane–Emden equations as well as the isothermal sphere gas equation do not have exact solution, and must be solved by semi-analytical and numerical methods. Thus, we have decided to present a new and efficient technique to solve it numerically for \(m\,=\, 1.5, 2, 2.5, 3\) and 4.

Recently, many researchers have obtained approximations for Lane–Emden equations; For example, Wazwaz (2001), by using ADM, Chowdhury and Hashim (2007), Bataineh et al. (2009), Singh et al. (2009), Van Gorder (2011) by using HPM , Yildirim and Ozis (2009) and Dehghan and Shakeri (2008) by using VIM, Parand et al. (2010) by employing a Hermite functions collocation method, Boubaker and Van Gorder (2012) by using Boubaker polynomials expansion scheme and Marzban et al. (2008) by using hybrid functions.

2 Bessel functions and BFC

In this section, we describe the Bessel functions of the first kind and their main feature applied to construct the BFC (Bessel Function Collocation) method.

The Bessel functions satisfy the well-known differential equation, called Bessel’s differential equation (Watson 1967; Bell 1967):

$$\begin{aligned} x^{2}y^{\prime \prime }(x)+ x y^{\prime }(x)+(x^{2}-n^{2})y(x)=0, ~~~ x\in (-\infty , \infty ), \end{aligned}$$
(15)

for \(n\in \mathbf R \).

The Bessel functions of the first kind are solutions of (15) and are denoted by \(J_{n}(x)\):

$$\begin{aligned} J_{n}(x)=\sum _{r=0}^{\infty }\frac{(-1)^{r}}{r! \Gamma (n+r+1)}\left( \frac{x}{2}\right) ^{2r+n}, \end{aligned}$$
(16)

where, series (16) is convergent for all \( -\infty <x<\infty \), and \(\Gamma (\lambda )\) is the gamma function, defined by

$$\begin{aligned} \Gamma (\lambda )=\int \limits _{0}^{\infty }e^{-t}t^{\lambda -1} d t. \end{aligned}$$
(17)

The orthogonality relationships for the Bessel functions are different from those of most of the other common orthogonal functions in which two instances of the same functional form are applied (i.e. same order \(n\)) with differently scaled arguments.

With a variable transformation \(x = a~\xi \), the Eq. (15) can be transformed into:

$$\begin{aligned} \xi ^{2}y^{\prime \prime }(\xi )+ \xi y^{\prime }(\xi )+(a^2\xi ^{2}-n^{2})y(\xi )=0, \end{aligned}$$

This equation can be written in the following form:

$$\begin{aligned} (\xi y^{\prime }(\xi ))^{\prime }+\left( a^2\xi -\frac{n^{2}}{\xi }\right) y(\xi )=0, \end{aligned}$$

Here, we can see that this equation is a Sturm-Liouville equation with \(p(\xi )=\xi , q(\xi )=-\frac{n^{2}}{\xi }, \lambda =a^2\) and \(w(\xi )=\xi \). Satisfying appropriate boundary conditions on a finite interval such as \([0, a]\), we can have a Sturm-Liouville eigenvalue problem.

Theorem 1

Let \(\xi _{i}\) and \(\xi _{j}\) be two distinct zeroes of the Bessel function \(J_{n}(\xi a)=0\), Then:

$$\begin{aligned} \int \limits _{0}^{a} J_{n}(\xi _{i}x)J_{n}(\xi _{j}x)~x~dx=\frac{a^{2}}{2}(J_{n+1}(\xi _{i} a))^{2} \delta _{i j}, \end{aligned}$$
(18)

where \(\delta _{i j}\) is the Kronecker delta function.

Proof

The complete proof is described in Bell (1967). \(\square \)

Theorem 2

If \(f(x)\) be defined on \([0,a]\), and \(f(x)\cong \sum _{i=1}^{N}c_{i}J_{n}(\xi _{i}x)\), where \(\xi _{i}\) are roots of \(J_{n}(\xi a)=0\), then:

$$\begin{aligned} c_{i}=\frac{2 \int _{0}^{a} x f(x) J_{n}(\xi _{i} x) dx}{a^{2}[J_{n+1}(\xi _{i} a)]^{ 2}}, \end{aligned}$$
(19)

Proof

To see the complete proof, you can refer to Bell (1967). Therefore, we must find the roots of Bessel functions. \(\square \)

2.1 Computing the roots of Bessel functions

In this paper, we use the algorithm presented by Glaser et al. (2007) to obtain \(N\) roots of Bessel functions \(J_{n}(x)\). In this algorithm, we need an initial approximation \(x_{s}\) of the first root \(x_{1}\), and also the number of roots after the \(x_{1}\). This method obtains the initial root \(x_1\) from \(x_s\), and through an iterative procedure, computes \(N\) roots of \(J_{n}(x)\). This method has been proposed for the special function \(u(x)\), which is a solution of the Sturm-Liouville equation:

$$\begin{aligned} p(x) u^{\prime \prime }(x)+q(x)u^{\prime }(x)+r(x)u(x)=0, \end{aligned}$$
(20)

where \(p(x),~q(x)\) and \(r(x)\) are polynomials of degree 2. This method uses the Prüfer transform, (Prüfer 1960)

$$\begin{aligned} \theta (x)=\arctan \left( \frac{p(x) u^{\prime }(x)}{u(x)\sqrt{r(x)p(x)}} \right) , \end{aligned}$$
(21)

and

$$\begin{aligned} \frac{dx}{d\theta }=- \left( \sqrt{\frac{r}{p}}+\frac{r^{\prime } p -p^{\prime } r+2 r q}{2 r p}\frac{\sin (2\theta )}{2} \right) ^{-1}. \end{aligned}$$
(22)

In addition, in this algorithm, we use the Taylor series, Runge–Kutta method, and Newton’s method.

Now, we describe an algorithm which finds \(N\) roots of a function \(u(x)\) which satisfies the Eq. (20), recursively, by calculating each of the bigger roots from the previous one successively. Firstly, a starting value \(x_{s}\) is needed; afterwards, the algorithm will calculate the smallest root \(x_{1}\), which is larger or equal to \(x_{s}\) in two steps:

Step1: An approximation \(\widetilde{x}_{1}\) for the initial root is found by calculating \(\theta _{0}=\theta (x_{s})\) via Eq. (21) and solving the differential Eq. (22) with the initial condition \(x(\theta _{0})=x_{s}\) in the interval \(\theta \in (\theta _{0},-\frac{\pi }{2})\) via Rung–Kutta method.

Step2: Since the Newton’s method has a faster convergence rate than Rung–Kutta method, we use it to obtain a good precision for \(x_{1}\).

Now we employ the iterative algorithm (Glaser et al. 2007):

figure a

For more details about this algorithm, see (Glaser et al. 2007).

Now, by using the above notes, we can say that \(\lbrace J(\xi _{n}x)\rbrace \) denotes a system which is mutually orthogonal under (18), i.e. this system is complete in \(L_{w} ^{2}(I)\), where \(I=[0,a]\) (Guo et al. 2006). For any \(y \in L_{w} ^{2}(I) \), the following expansion holds

$$\begin{aligned} y(x)= \sum _{i=0}^{\infty }c_{i}J_{n}(\xi _{i} x), \end{aligned}$$
(23)

but, we cannot use the infinite expansion (23) in the computing system, we approximate \(u(x)\) as follows:

$$\begin{aligned} y(x) \approx y_{N}(x)= \sum _{i=0}^{N}c_{i}J_{n}(\xi _{i} x), \end{aligned}$$
(24)

3 Application of the BFC method to solve the Lane–Emden equations

In this section we apply Bessel functions collocation (BFC) method to solve some well-known Lane–Emden equations for various \(f(x,y), A, B\) and \(\alpha \).

The Bessel function \(J_{0}(x)\) is differentiable at the point \(x=0\), thus, we have no problem for satisfying the boundary conditions, though we satisfy conditions (2) by multiplying the operator (24) by \(x^{2}\) and adding it to \(A\) and \(B x\) as follows:

$$\begin{aligned} \widehat{\gamma }_{N} y(x)=A + B x +x^{2} y_{N}(x), \end{aligned}$$
(25)

where \(y_{N}(x)\) is defined in (24). Now, \(x^{2} \widehat{\gamma }_{N} y(x) =0, \widehat{\gamma }_{N} y(x)=A\) and \(\frac{d}{dx}\widehat{\gamma }_{N} y(x)= B\), when \(x\) tends to zero, so that the conditions (2) are satisfied.

To apply the collocation method, we construct the residual function by substituting \(\widehat{\gamma }_{N} y(x)\) in (24) for \(y(x)\) in Lane–Emden type Eq. (1),

$$\begin{aligned} Res(x)=\frac{d^{2}}{dx^2}\widehat{\gamma }_{N} y(x)+\frac{\alpha }{x}\frac{d}{dx}\widehat{\gamma }_{N} y(x)+f(x,\widehat{\gamma }_{N} y(x))-h(x). \end{aligned}$$
(26)

The equations for obtaining the coefficient \(\{c_{i}\}_{i=0}^{N}\) arise from equalizing \(Res(x)\) to zero on \(N+1\) collocation points:

$$\begin{aligned} Res(x_{i})=0,\quad i=0, 1, ..., N. \end{aligned}$$
(27)

In this study, we used the roots of the shifted Chebyshev function in the interval \([0,a]\), as collocation points. For more information about Chebyshev polynomials, you can see Boyd (2000).

By solving the obtained set of equations, we have the approximating function \(\widehat{\gamma }_{N} y(x)\).

3.1 Solving some Lane–Emden type equations

3.1.1 Example 1 (The standard Lane–Emden equation)

For \(f(x,y){=}y^{m}, A{=}1\) and \(B{=}0\), Eq. (1) is the standard Lane–Emden equation, which was used to model the thermal behavior of a spherical cloud of gas acting under the mutual attraction of its molecules and subject to the classical laws of thermodynamic (Shawagfeh 1993)

$$\begin{aligned} y^{\prime \prime }(x) + \frac{2}{x} y^{\prime }(x) + y^{m}(x) = 0,\quad x>0 \end{aligned}$$
(28)

with conditions

$$\begin{aligned} \nonumber y(0)=1,\\\nonumber y^{\prime }(0)=0, \end{aligned}$$

where \(m\ge 0\) is constant. For \(m=0,1\) and 5, Eq. (28) has the exact solutions, respectively:

$$\begin{aligned} y(x)=1-\frac{1}{3!}x^{2},~~~~ y(x)=\frac{\sin (x) }{x}, ~~~~y(x)=\left( 1+\frac{x^2}{3}\right) ^{-\frac{1}{2}}. \end{aligned}$$
(29)

In other cases, there is not any exact analytical solution. Therefore, we apply the BFC method to solve the standard Lane–Emden Eq. (28), for \(m=1.5, 2, 2.5, 3\) and \(4\). In this example, we construct the residual function as follows:

$$\begin{aligned} Res(x)=\frac{d^{2}}{dx^2}\widehat{\gamma }_{N} y(x)+\frac{2}{x}\frac{d}{dx}\widehat{\gamma }_{N}y(x) +(\widehat{\gamma }_{N}y(x))^{m}. \end{aligned}$$
(30)

Therefore, to obtain the coefficient \(\{c_{i}\}_{i=0}^{N}, Res(x)\) is equalized to zero at \(N+1\) collocation point. By solving this set of nonlinear algebraic equations, we can find the approximating function \(\widehat{\gamma }_{N}y(x)\).

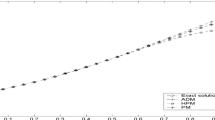
Tables 1, 2, 3 show the obtained \(y(x)\) for the standard Lane–Emden equations for \(\text{ m }= 2\), 2.5 and 3 respectively, by the proposed BFC method in this paper, and some well-known methods in other articles. These tables also show the residual function \(Res(x)\) in some points. In addition, Table 4 compares the obtained zeros of the standard Lane–Emden equations by the proposed method and values given by Horedt (2004), and Fig. 1 represents the graphs of the standard Lane–Emden equations for \(\text{ m }=1.5, 2, 2.5, 3\) and 4. Finally, Table 5 shows the Bessel coefficients for m\(=\) 2, 2.5, 3 and 4 obtained by BFC method for solving standard Lane–Emden equations. This table illustrates the convergence rate of the method.

Table 1 Obtained values of \(y(x)\) for standard Lane–Emden \(m=2\) by the present method (with \(N=30\))
Full size table
Table 2 Obtained values of \(y(x)\) for standard Lane–Emden \(m=2.5\) by the present method (with \(N=30\) )
Full size table
Table 3 Obtained values of \(y(x)\) for standard Lane–Emden \(m=3\) by present the method (with \(N=30\))
Full size table
Table 4 Obtained zeros of standard Lane–Emden equations, by the present method for several \(m\)
Full size table
Fig. 1
figure 1

The obtained graphs of solutions of Lane–Emden standard equation for \(\text{ m }=1.5, 2, 2.5, 3, 4\)

Full size image
Table 5 Representation coefficients of standard Lane–Emden equations in the present method for \(m\,=\,2,2.5,3,4\)
Full size table

3.1.2 Example 2 (The isothermal gas spheres equation)

For \(f(x,y)=e^{y}, A=0\) and \(B=0\), Eq. (1) is the isothermal gas sphere equation

$$\begin{aligned} y^{\prime \prime }(x) + \frac{2}{x} y^{\prime }(x) + e^{y(x)} = 0, ~~ x>0, \end{aligned}$$
(31)

with conditions

$$\begin{aligned}\nonumber y(0)=0,\\\nonumber y^{\prime }(0)=0. \end{aligned}$$

This model can be used to treat the isothermal gas sphere. For a thorough discussion of Eq. (31), see Davis (1962), Van Gorder (2011). This equation has been solved by some researchers, for example Wazwaz (2001) and Chowdhury and Hashim (2007) by using ADM and HPM, respectively, and Parand et al. (2010) by using Hermite collocation method.

A series solution obtained by Wazwaz (2001) by using ADM and series expansion is:

$$\begin{aligned} y(x)\simeq - \frac{1}{6}x^{2}+\frac{1}{5. 4!}x^4 - \frac{8}{21. 6!}x^{6}+\frac{122}{81. 8!}x^{8}-\frac{61.67}{495.10!}x^{10}. \end{aligned}$$
(32)

The residual function for Eq. (31) is:

$$\begin{aligned} Res(x)=\frac{d^{2}}{dx^2}\widehat{\gamma }_{N} y(x)+\frac{2}{x}\frac{d}{dx}\widehat{\gamma }_{N}y(x) +e^{\widehat{\gamma }_{N}y(x)} \end{aligned}$$
(33)

By solving the set of equations obtained from \(N+1\) equations \(Res(x)=0\) at \(N+1\) collocation points, we have the approximating function \(\widehat{\gamma }_{N} y(x)\).

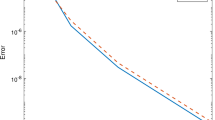
Table 6 shows the comparison of \(y(x)\) obtained by the method proposed in this paper and Parand et al. (2010), Wazwaz (2001). Also, Fig. 2a shows the graph obtained with the present method for this problem and logarithmic graphs of absolute coefficients \(|a_{i}|\) of Bessel function in the approximate solutions for this example is shown in Fig. 2. This graph illustrates that the method has an appropriate convergence rate.

Fig. 2
figure 2

Results obtained for the isothermal gas equation. (a) Graph of the approximate solution; (b) Logarithmic graph of the absolute coefficients \(|a_{i}|\) of the Bessel functions

Full size image
Table 6 The comparison of the values \(y(x)\) of Lane–Emden equation obtained by the present method with \(N\,=\,30\) and (Wazwaz 2001; Parand et al. 2010) in Example 2
Full size table

4 Conclusions

The main goal of this paper was to introduce a new orthogonal basis namely Bessel orthogonal functions to construct an approximation to the solution of non-linear Lane–Emden equation. To construct the orthogonal Bessel functions we need their roots and, to obtain them, we have used the algorithm presented by Glaser et al. (2007). The presented results show that the introduced basis for collocation spectral method is efficient and applicable. Our results have better accuracy with lesser \(N\) as compared to other results. The validity of the method is based on the assumption that it converges when increasing the number of collocation points. A comparison was made of the exact solution and the numerical solution of Horedt (2004) and the present method. It has been shown that the present work has provided an acceptable approach for solving Lane–Emden type equations. Also it was confirmed by logarithmic figures of absolute coefficients that this approach has a good convergence rate.