Introduction

Physiologic control mechanisms exist from subcellular to systemic levels and operate over multiple time scales. Continuous interplay among these different regulatory systems ensures that information is constantly exchanged across all levels of organization, even at rest, and enables an organism to adjust to an ever-changing environment and to perform a variety of activities necessary for survival. These dynamic processes, especially under healthy conditions, are evident in the complex fluctuations of physiologic output signals, such as heart rate, blood pressure, brain electrical activity, and hormone levels. In contrast, aging and pathologic systems, which have degraded control mechanisms, are likely to generate less complex outputs [1, 2]. This loss of complexity is manifest as increased randomness, (e.g., the heart rate fluctuations of a patient with atrial fibrillation), or greater periodicity (e.g., cardiopulmonary oscillations in Cheyne–Stokes syndrome with heart failure). Both classes of pathology are characterized by a “collapse of complexity,” which is associated with a breakdown of the long-range correlations, multiscale variability and time irreversibility properties of the signals observed in healthy subjects.

There is no unifying consensus definition of complexity. In information theory, complexity measures the degree of compressibility of a string of characters. Therefore, random uncorrelated strings, which are virtually incompressible, are considered the most complex [3]. In contrast, from a complex systems approach [4], which we adopt here, random uncorrelated strings of characters are among the least complex signals, and those with long-range correlations are among the most complex. Complex signals typically exhibit one (and usually) more of the following properties: (i) non-linearity––the relationships among components are not additive; therefore small perturbations can cause large effects; (ii) non-stationarity––the statistical properties of the system’s output change with time; (iii) time irreversibility or asymmetry––systems dissipate energy as they operate far-from-equilibrium and display an “arrow of time” signature; (iv) multiscale variability––systems exhibit spatio-temporal patterns over a range of scales.

The purpose of this paper is fourfold: (i) to briefly review two multiscale methods that quantify different properties of complex cardiovascular signals: multiscale entropy [5, 6] and multiscale time irreversibility (asymmetry) [7], (ii) to present a simplified version of the time irreversibility measure, (iii) to apply the two methods to the challenge of characterizing and distinguishing physiologic and surrogate time series not separable using conventional techniques, and (iv) to test models of heart rate variability previously proposed as part of an international competition.

Our underlying conceptual construct is that multiscale complexity is a marker of healthy dynamics, which have the highest functionality and adaptability, and these properties degrade with aging and disease. Multiscale entropy quantifies the information content of a signal over multiple time scales. Time irreversibility quantifies its degree of temporal asymmetry. Of note, both measures probe aspects of cardiovascular signals that are independent of traditional time and frequency domain measures such as mean, variance and Fourier spectrum, and are also independent of each other as demonstrated below. For continuous heart rate time series obtained, for example from 24 h electrocardiograms (Holter recordings), the analyzed time scales typically range from milliseconds to minutes.

Methods

Multiscale Entropy

The multiscale entropy method was developed to quantify a central aspect of complex signals, namely their multiscale variability over a range of scales. At each level of resolution, the multiscale entropy algorithm yields a value that reflects the mean rate of creation of information. The overall degree of complexity of a signal is calculated by integrating the values obtained for a pre-defined range of scales.

In practice the algorithm comprises two steps: (1) a coarse-graining procedure that allows us to look at representations of the system’s dynamics at different time scales, and (2) the quantification of the degree of irregularity of each coarse-grained time series, which can be accomplished using sample entropy (SampEn), a statistic introduced by Moorman et al. [8].

Sample entropy is the negative natural logarithm of the conditional probability that two patterns of length m, x m (i) = {x i ,…, x i  + m − 1} and x m (j) = {x j ,…, x j  + m − 1}, which are similar to each other within a tolerance r (meaning that d[x m (i), x m (j)] ≤ r, where d is a function that measures the distance between vectors), will still be considered similar to each other when points, x i + m and x j + m are added to patterns x m (i) and x m (j), respectively.

Sample entropy is a measure of irregularity. For regular signals, SampEn is very low. For uncorrelated random signals, SampEn is the highest.

Although complex signals are irregular not all irregular signals are complex. Consider, for example, a physiologic time series, which is the output of a system regulated by multiple control mechanisms, and the time series obtained by shuffling these data points. The surrogate shuffled time series is less complex than the physiologic time series. However, an entropy measure, such as SampEn, assigns a higher entropy value to the surrogate shuffled time series than to the physiologic one because the former is more random than the latter. Therefore, the use of single scale-based measures of entropy to assess complexity may lead to misleading results.

By distinction, our [5] objective is to compute entropy over multiple time scales. The underlying hypothesis is that complex systems, in particular physiologic systems controlled by regulatory mechanisms that operate on different time scales, generate time series that exhibit highly variable fluctuations at multiple levels of resolution. To quantify irregularity at different time scales we coarse-grain the original time series. Given a signal with N data points sampled at Δ Hz, the coarse-grained time series are constructed as follows. For scale 1, the coarse-grained time series is the same as the original signal. In this case the time interval between consecutive data points is 1/Δ s. For scale n (Fig. 1), we divide the data into consecutive non-overlapping blocks with n data points each and calculate the mean inside each block. The sequence of average values is the coarse-grained time series for scale n that corresponds to n/Δ s. This time series is shorter that the original one. It contains N/n data points, which should be taken into consideration when calculating the error bars for the entropy values. Of note, the choice of calculating the mean value to summarize the dynamics inside each block of data was motivated by Zhang’s work [9].

Fig. 1
figure 1

Schematic illustration of the coarse graining procedure for scales 2 and 3 used for the multiscale entropy method. (Adapted from ref. 6.)

Full size image

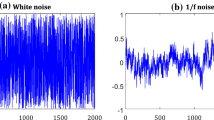
The next step is to calculate the sample entropy for each coarse-grained time series and to plot the results as a function of scale, which yields the so-called multiscale entropy curve. The multiscale entropy curve [6] for correlated fractal (1/f) noise is a straight line (the entropy is 1.8 for all scales) since at all levels of resolution new patterns of variability are revealed and, therefore, new information is created. In contrast, the multiscale entropy curve for white noise is a function that monotonically decreases with scale. This profile is characteristic of single scale signals, which at low resolution levels (higher scales) contain less information than at high resolution levels (lower scales.) Of note, the multiscale entropy does not distinguish between a given time series X = {x 1, x 2,…, x N } and that obtained by time reversing the series X′ = {x N , x N − 1,…, x 1} because the degree of irregularity/unpredictability is the same for both signals.

Multiscale Time Irreversibility

Time irreversibility (“the arrow of time”), a fundamental property of far-from-equilibrium systems, is related to the unidirectionality of the energy flow across the boundaries of the system [10]. Living beings are paradigmatic examples of systems operating far-from equilibrium. They utilize energy to evolve to and maintain ordered structural configurations, through inherently time irreversible processes. Perhaps counterintuitively, death is a state of maximum equilibrium, since there are no driving forces or consumption of energy. To the extent that all processes occurring under equilibrium conditions are time reversible, states approaching death are expected to be more time reversible than those representing far-from-equilibrium healthy physiology.

In time series analysis, time irreversibility refers to the lack of invariance of the statistical properties of a signal under the operation of time reversal [11]. Figure 2 shows the heart rate time series of a healthy young subject and of a patient with congestive heart failure, both in the forward and backward (reversed) time directions. The pathologic signal is more symmetric than the healthy one, indicating a loss of temporal irreversibility with pathology.

Fig. 2
figure 2

Heartbeat time series from a healthy subject (top panels) and patient with severe congestive heart failure (bottom panels) shown in both the forward (first and third panels) and backward time directions (second and forth panels). Note that the time series from the congestive heart failure patient “reads the same” in both forward and backward time directions, in contrast to the more asymmetric time series from the healthy subject

Full size image

A method [7] that we recently developed to quantify the degree of time irreversibility comprises three steps: a coarse-graining procedure, the computation of the degree of time irreversibility for each coarse-grained time series, and the integration of the results obtained for a pre-defined range of scales. We made the simplifying assumptions that transitions between consecutive values (an increase or decrease in heart rate) are independent and require a certain amount of ‘‘energy.’’ Based on a statistical physics approach [12] we considered that the relationship between energy E for each transition and the probability p of observing that transition was: E = p ln p. Then, we calculated the difference between the average energy for the activation (p + ln p +) and the relaxation (p − ln p −) of the heart, over a range of time scales (where p + is the probability that the value of the recorded variable increases at any time instant and p − is the probability that is decreases). Of note, the relationship between p ln p and the energy E is only valid if the transitions between states are independent. If they are not independent, we still can use the differences between p + ln p + and p − ln p − to quantify the degree of temporal asymmetry of a signal but there is no simple physical interpretation for these terms.

In this paper we present a simplified version of this algorithm that yields comparable results and is easier to implement. The simplified version is based on the observation that the number of increments (number of times x i + 1 −  x i  > 0) is equal to the number of decrements (number of times x i + 1 −  x i < 0) for a symmetric function. We use this finding for calculating the asymmetry of the original time series and for the coarse-grained time series. Consider a time series X = {x i}, 1 ≤ i ≤ N. For scale 1, we construct the time series Y 1 = {y i }, y i  = x i + 1 − x i , 1 ≤ i ≤ N − 1 Then, we calculate the difference A 1 between the percentage of increments and decrements according to

$$ A_{1} = \frac{{\sum {H[ - y_{i} ]}}- {\sum {H[y_{i} ]}}} {N - 1} $$

where H is the Heaviside function (H(a) = 0 if a < 0 and H(a) = 1 if a ≥ 0 and 1 ≤ i ≤ N − 1.) For scale j, we construct the time series Y j  = {y i }, y i  = x i  +  j  − x i , 1 ≤ i ≤ N − j. Then, we calculate the difference A j between the percentage of increments and decrements according to

$$ A_{j} = \frac{{\sum {H[ - y_{i} ]}} - {\sum {H[y_{i} ] }}} {N - j}, \, {\rm {where}} \,1 \le i \le N - j. $$

The time asymmetry (irreversibility) index is defined as ΣA j for a pre-defined range of scales.

The time irreversibility and multiscale entropy methods quantify different aspects of complex systems and are independent of each other. Consider, for example, two time series X 1, an asymmetric triangle function of period 10 (X 1 = {x i }, where x i  = 3 if i is a multiple of 10 and x i  = 0.5(1 + i) if i is not a multiple of 10, and X 2, the time series obtained from X 1 by time reversing the sequence of data points. The two time series X 1 and X 2 have the same multiscale entropy values because for all coarse-grained time scales the conditional probability that d[x m + 1(i), x m + 1(j)] ≤ r given that d[x m (i), x m (j)] ≤ r is the same that the conditional probability that d[x′ m  + 1(i), x′ m  + 1(j)] ≤ r given that d[x′ m (i), x′ m (j)] ≤ r, where x m (i) = {x i ,…, x i + m − 1} and x′ m (i) = {x i  + m − 1,…, x i }. However, X 1 and X 2 have different degrees of temporal irreversibility. For time series X 1, the degree of time irreversibility is 8/10 − 2/10 = 3/5 because, in this example, the probability that the value of x i increases is 8/10 while the probability that x i decreases is 2/10. For the temporally reversed series, the asymmetry index is −3/5.

Results

To illustrate the application of these two techniques, we apply them to a physiologic and surrogate data pair and to data from a time series modeling competition sponsored by the NIH PhysioNet Resource.

Physiologic/Surrogate Data Test

In Fig. 3 we show two time series with the same means and standard deviations and identical power spectra. One is the heart rate time series of a healthy young subject and the other is a surrogate time series generated by a computational algorithm [13] that degrades the information content of the original signal through the process of phase randomization. Although both signals have the same statistical properties as measured by conventional biostatistical methods including Fourier spectral analysis, their underlying mechanisms are very different. The surrogate time series is less complex than the physiologic time series. However, conventional time and frequency domain measures fail to fully quantify the information content of these signals, which is subtly encoded in the temporal sequence of the values. In contrast, both the multiscale entropy and time irreversibility metrics distinguish the two time series. Of interest, multiscale entropy and time irreversibility are consistently higher for the physiologic than for the surrogate time series.

Fig. 3
figure 3

Two time series with fundamentally distinct dynamics but the same mean values and standard deviations, and identical power spectra. Top panels: the heart rate time series (day time) from a young healthy subject and its Fourier power spectrum. Bottom panels: the surrogate, phase randomized series of the physiologic signal shown in the top panel and its Fourier power spectrum. The average value of entropy per scale (arbitrary units) is consistently higher for the physiologic (1.55) than for the surrogate time series (1.46). Similarly, the asymmetry index is also higher for the physiologic time series (0.37) than for the surrogate series (0.04). Thus, in contrast to traditional time and frequency measures, both the multiscale entropy and time irreversibility algorithms capture the differences between the physiologic and the surrogate time series. Furthermore the results are consistent with a degradation of complexity (nonlinearity) with the phase randomization process

Full size image

Tests on Physiologic Models of Heart Rate Variability

Models of physiologic control should account for the complex structure of physiologic time series, but in general they fail to do so. For example, in 2002, the NIH Research Resource for Complex Physiologic Signals (http://www.physionet.org), in conjunction with Computers in Cardiology (http://www.cinc.org), sponsored an international competition on cardiac interbeat interval time series modeling. This challenge had two parts. Part I called for the development of models that could generate dynamics simulating those observed in heartbeat time series from healthy subjects. Participants entering Part II were challenged to distinguish between physiologic and model-generated time series. Using only the multiscale entropy method, we were able to correctly identify the origin of 48 out of 50 synthetic time series [14]. Of note, most of the models proposed failed to account for the multiscale, fractal properties of the cardiac interbeat interval time series.

In Fig. 4, we show the time irreversibility analysis for the physiologic and synthetic time series. None of the models proposed generated time irreversible signals. Of particular interest, the time series numbered 14 and 16, which have the most marked negative time asymmetry values, were not generated by any model. Instead, they were obtained by time-reversing two physiologic series [15]. This result shows that all proposed models fail to generate time irreversible signals across a wide range of scales, a dynamical signature of real-world systems with multiscale, nonequilibrium properties. Our algorithm indicates that datasets #23 and #49 have a similar degree of asymmetry. The relatively lower asymmetry value computed for the physiologic time series (#23) could be due to unknown factors such as age, level of physical activity, drugs effects, etc. In any case, we do not expect the time irreversibility algorithm to provide absolute discrimination between different classes of time series.

Fig. 4
figure 4

Time irreversibility analysis of 50 cardiac interbeat intervals time series from the PhysioNet/CinC2002 Challenge database. Note that the physiologic time series are more time asymmetric (asymmetry index = 0.53 ± 0.16) than those generated by computational models (asymmetry index = −0.01 ± 0.06.) Time series numbered 14 and 16 (as given in http://www.physionet.org/challenge/2002/) were generated by time-reversing two physiologic time series. The time irreversibility algorithm identifies these time series. Although the absolute values of the degree of irreversibility for the time reversed signals were within the physiologic range, their sign is negative indicating that time does not run in the “correct” direction

Full size image

Discussion and Conclusions

The key finding of this presentation is that two recently developed multiscale techniques are able to extract information from cardiac interbeat interval time series not contained in traditional time and frequency domain techniques. The complementary role of conventional and newer multiscale analytical methods in cardiovascular signal analysis is a frontier area of investigation. Another technique that may be useful in this regard is multifractal analysis, which is described elsewhere [16]. Quantifying multiscale variability and time irreversibility may have important applications, including risk stratification, aging effects and assessment of therapeutic interventions and development of models of biologic control. These two measures quantify different properties of complex systems and are independent of each other. In addition they are independent of other conventional heart rate time and frequency domain measures.

Limitations

Both the multiscale entropy and time irreversibility require relatively long time series (a couple of thousand data points) and the data need to be stationary. These two requirements are often inter-related. For example, what appears to be a slow drift of the baseline, i.e., a trend without apparent physiologic meaning when we follow a process for a shorter period, may, in fact, be a dynamical pattern that is only revealed upon tracking the process over a more extended time interval.

Determining whether a “real-word” time series is stationary or not, requires the definition of a time scale of interest. In general, a process is stationary only if the characteristic scale of the dynamical structures it generates is much smaller than the recording time. For “relatively” stationary time series, the number of data points required to calculate sample entropy is of the order of a couple of hundred [4, 6]. One way of working around the nonstationarity problem is to detrend the data to eliminate those structures whose characteristic scales are not substantially much shorter (at least two orders of magnitude) than the recording length [17]. Further, defining the utility and limitations of newer multiscale complexity measures requires testing on open-access databases. Finally, we note that efforts to develop real world models of short and longer-term cardiovascular regulation need to account for the observed multiscale properties.