Continuous horizontal screw sedimentation centrifuges of the OGSh type (Russian trademark) having a horizontal cylindroconical rotor are employed in plants of chemical, oil-gas, food, and other related branches of the industry to dehydrate, concentrate and clean materials, fractionate materials by size (with solid phase fineness of 0.005-10 mm, solid phase volume concentration of 1–40%, phase density difference of more than 200 kg/m3), etc. For example, OGSh type of centrifuges are used to separate suspensions of polyvinyl chloride, ammonium nitrate, barium carbonate, etc., for classification of titanium dioxide and zirconium oxide, for dehydration of wastewater sludges, etc.

The merits of OGSh-type centrifuges are process continuity, high throughput at low specific energy consumption and small mass of the equipment, ease of servicing, low cost of sediment treatment, etc.

The demerits of OGSh-type centrifuges are poor dehydration, lack of provision for high-quality washing of the sediment, rapid wearing of the screw and rotor when abrasive materials are treated, etc.

Investigations of suspension separation process using OGSh-type centrifuges were reported in [1,2,3,4,5,6,7,8] where the following were proposed: calculation of the size of separation of the suspension solid phase, dependencies of the carry-over ratio on the centrifuge productivity and the physicomechanical parameters of the separation process, criterial modeling making use of the performance index and operating conditions of model and full-scale centrifuges, etc.

However, the physicomechanical models used for validating the analytical dependencies of the separation process are commonly based on the hypothesis of movement of an isolated particle in the suspension flow without regard for the influence of adjacent particles and the phenomenon of stratification of suspended matter concentration across the flow thickness.

Since for development of equipment (including also centrifugal with a screw device), a proper set of calculating tools of quantitative analysis is essential for predicting the suspension separation process with due regard for the conditions and characteristics of the process, the need for further in-depth scientific and technical analysis of this problem is obvious.

In this paper, we propose a more substantiated (in comparison with the analogs [1,2,3,4,5,6,7,8]) quantitative analysis of the suspension separation process in the working space of an OGSh -type centrifuge.

Formulation of the Problem

The main feature of an OGSh-type centrifuge is a built-in tubular structure (a screw) with a continuous helical surface along its longitudinal axis rotating coaxially with the main rotor (with a slightly less angular speed).

From the geometric standpoint, a distinctive feature of the equipment is a conically or cylindroconically shaped rotor with a cone angle of 10–15°, which ensures implementation of the solid sedimentation process mainly in the cylindrical section of the rotor.

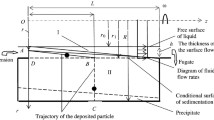
Because the suspension flow at the centrifuge feed pipe outlet is swirled by the screw blades, generally steady (almost translational) pressure-free (gravity) movement of the fluid system (FS) counter to the flow movement in the feed pipe takes place in the direction toward the rotor inlet with continuous formation (due to the action of the centrifugal force field) of a dehydrated sediment layer on the rotor shell (due to sedimentation of the solid phase). The sediment layer is moved forward by the screw to the discharge ports, where the sediment is consolidated under the action of centrifugal forces and forces from the screw, moved to the drying area, and thereafter discharged into a collector through the discharge ports (Figs. 1 and 2).

Fig. 1
figure 1

Schematic diagram of horizontal screw sedimentation centrifuge (meridional section): 1 − protective device; 2 − reducer; 3, 8 − supports; 4 − housing; 5 − screw; 6 − rotor; 7 − pipe; 9 − sediment discharge port; 10 − sediment discharge chamber; 11 – centrifugate removal chamber; 12 − drain port.

Full size image
Fig. 2
figure 2

Scheme for calculation of suspension separation process in meridional section of rotor of horizontal screw sedimentation centrifuge.

Full size image

Since the main flow near the feed pipe at the rotor inlet is practically clogged by sediment, a flow of clarified phase of the suspension directed opposite to sediment movement is initiated toward the centrifugate exit from the rotor as a result (Figs. 1 and 2).

Furthermore, the liquid flow is agitated in the working space of the centrifuge under the action of the screw in three directions, namely, longitudinal (along the rotor axis), circular (around the rotor axis), and transverse (along the radius of the equipment). Nonetheless, the centrifuge operation conditions are so chosen that the suspension separation process develops, by and large, in a laminar mode. In centrifugal suspension separation, the centrifugate contains solid particles with a size not exceeding the suspension size, and the sediment includes the whole solid phase consisting of particles, the size of which is larger than the suspension size, and of a small proportion of finer particles.

In general, from the standpoint of hydrodynamics, separation of a heterogeneous FS in the working space of the centrifuge should be treated as a kinetic process of movement under the action of centrifugal force field in a steady state of two interacting and interpermeating fluids [12].

The kinetics of a two-phase fluid flow consisting of fluids of different densities in the space between the screw and the rotor shell is complicated, but in the initial mathematical model of the sedimentation process considerable simplification is admissible in the working space of the OGSh-type centrifuge.

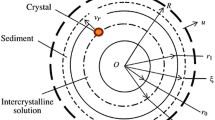
Thus, a laminar heterogeneous FS flow rotating together with the rotor with an angular speed ω (Fig. 2) and bounded by surfaces with r = R and r = r0 (where R = D/2, r0 = d/2, D is the rotor diameter, d is the screw diameter, and r is the radial coordinate) is approximately taken (with due regard for the flow kinetics) as the initial geometric model of the process of sedimentation of the solid phase in the suspension. It is also taken that a liquid−solid mixture with spherical particles (of small identical size), where the density \( {\uprho}_1^{{}^{\circ}} \) of the particle exceeds the density \( {\uprho}_2^{{}^{\circ}} \) of the liquid (the fluid mixture is uniformly premixed), is submitted to separation.

Since the main function of the OGSh-type centrifuge (equipment with a horizontal rotor) is execution of the process of centrifugal separation of suspended matter, which takes place in a direction radial to the rotor axis, in analysis of the sedimentation process it is immaterial to which side (along or opposite to the axis z ) (Fig. 2) the flow is directed.

It is assumed that the suspension flow confined by the rotor wall (radius R) and the screw axis (radius r0) moves as a semisolid body with an angular speed ω in a cylindrical system rigidly linked with the rotor with the coordinates rϑz. It is proposed that the flow is axisymmetric (∂/∂ϑ = 0; ϑ is the rotor turning angle in relative motion, not shown in Fig. 2). Here, considering the minor difference in absolute angular speeds of the rotor and the screw and, therefore, the resulting slowed down (almost translational) relative axial movement of the treated liquid continuum, the influence of inertial forces on the phases of the fluid mixture in the moving system under reference can be ignored.

The goal of the study was to ascertain and quantitatively analyze the dynamics of stratification of the volume content of the suspension phases in a direction transverse to the flow direction r as a function of physicomechanical and geometric parameters of the process of separation of the investigated FS in the rotor of a continuous horizontal screw sedimentation centrifuge (Fig. 1).

Solution of the Problem

Based on the law of mass conservation for each of the suspension phases (solid and liquid), let us use a system of flow continuity equations for improving the physicomathematical model [8] of the FS separation process:

$$ \frac{1}{r}\frac{\partial \left(r{\upalpha}_1{u}_{1r}\right)}{\partial r}+\frac{\partial \left({\upalpha}_1{u}_{1z}\right)}{\partial z}=0, $$
(1)
$$ \frac{1}{r}\frac{\partial \left(r{\upalpha}_2{u}_{2r}\right)}{\partial r}+\frac{\partial \left({\upalpha}_2{u}_{2z}\right)}{\partial z}=0, $$
(2)
$$ {\upalpha}_1+{\upalpha}_2=0, $$
(3)

where r and z are radial and axial cylindrical coordinates; α1 and α2 are volume concentration of the phases; u1r, u1z, and u2r, u2z are radial and axial components of the velocity of the particles of the solid and liquid phases, respectively (Fig. 2).

For further simplification of quantitative analysis of the problem, movement of a solid particle in a flow in axial direction is approximately taken as suspended, i.e.,

$$ {u}_{1z}\approx -{u}_{2z}. $$

Moreover, it is assumed that the movement of the FS phases in the axial direction is modeled as a piston mode of movement, i.e.,

$$ {u}_{2z}\approx -{u}_{1z}={u}_0, $$
(4)

where u0 is the flow rate,

$$ {u}_0=\frac{Q}{\uppi \left({R}^2-{r}_0^2\right)}, $$
(5)

where Q is the suspension throughput of the centrifuge, R is the rotor radius, and r0 is the screw radius.

In conditions of pressure-free (gravity) FS movement

$$ Q=\frac{s\Omega \left({R}^2-{r}_0^2\right)}{2}, $$
(6)

where s is the distance between the screw turns (conventionally, screw pitch) and Ω is the relative angular speed of the screw,

$$ \Omega ={\upomega}_1-{\upomega}_{\mathrm{s}}, $$

where ωr is the absolute angular speed of the centrifuge rotor (Fig. 2), ωs = ωr (1− 0.01k) is the absolute angular speed of the screw, and k = 1.2 [2].

With due regard for equation (4) equations (1) and (2) are transformed as

$$ \frac{\partial {\upalpha}_1}{\upalpha z}-\frac{1}{r}\frac{\partial \left(r{\upalpha}_1{u}_1\right)}{\partial r}=0, $$
(8)
$$ \frac{\partial {\upalpha}_2}{\upalpha z}-\frac{1}{r}\frac{\partial \left(r{\upalpha}_2{u}_2\right)}{\partial r}=0, $$
(9)

where u1 = u1r/u0 and u2 = u2r/u0 are the dimensionless radial components of the velocity respectively of the solid particle and the liquid referred to the velocity u0, and, in conformity with equations (1), (2), (4), and (5), u1 > 0 and u2 < 0.

Assuming that the difference between solid particle and liquid densities is minor and that the size of the particle and its transverse velocity u1 are also minor, the inertial force in relative movement along the radius r, the Coriolis force, and other less significant forces (minor in comparison with the major forces acting on the solid and liquid phases) can be ignored.

In such a case, with due regard for the pressure force, frictional force (calculated in linear approximation with respect to velocity following the Stokes law), and centrifugal force Fcf the equilibrium conditions of these force factors in relative motion in projections along the axis r, will take the form:

$$ -{\upalpha}_1\frac{\partial p}{\partial r}+{K}_{\upmu}^{\ast }{\upalpha}_1{\upalpha}_1\left({u}_1+{u}_2\right){u}_0+{\uprho}_1^{{}^{\circ}}{\upalpha}_1{\upomega}^2r=0, $$
(10)
$$ -{\upalpha}_2\frac{\partial p}{\partial r}+{K}_{\upmu}{\upalpha}_1{\upalpha}_1\left({u}_1+{u}_2\right){u}_0+{\uprho}_2^{{}^{\circ}}{\upalpha}_2{\upomega}^2r=0, $$
(11)

where \( {\uprho}_1^{{}^{\circ}} \) is the density of the first phase, \( {\uprho}_2^{{}^{\circ}} \) is the density of the second phase, p is the pressure,

$$ \upomega \approx \left({\upomega}_1+{\upomega}_{\mathrm{s}}\right)/2 $$

(see Fig. 2),

$$ {K}_{\upmu}^{\ast }=\frac{18\upmu \uppsi \left({\upalpha}_1\right)}{\updelta^2}, $$
(12)

ψ(α1) is the correction to the constrained pattern of movement of a solid particle (α1 ≠ 1),

$$ \uppsi \left({\upalpha}_1\right)={\left(1-{\upalpha}_1\right)}^{-3}, $$
(13)

δ is the diameter of the solid particle, and μ is the dynamic viscosity of the fluid [9].

Under the adopted conditions with respect to the FS treatment process parameters, the value of the coefficient Kμ can be taken in the calculations as \( {K}_{\upmu}\approx -{K}_{\upmu}^{\ast } \) with satisfactory accuracy [9]. In that case, summing up sequentially, with due account of (3), initially equations (8) and (9) and then [taking account of (12) and (13)] summing up equations (10) and (11) we get

$$ {\upalpha}_2{\upmu}_2-{\upalpha}_1{\upmu}_1=\frac{W(z)}{r}, $$
(14)

where W(z), m, is the arbitrary function of the axial coordinate z ;

$$ \frac{\partial p}{\partial r}\uprho {\upomega}^2r, $$
(15)

where ρ is the volume-averaged suspension density,

$$ \uprho ={\upalpha}_1{\uprho}_1^{{}^{\circ}}+{\upalpha}_2{\uprho}_2^{{}^{\circ}}. $$
(16)

After putting equations (15) and (16) in equation (10) we get the equation for the dimensionless rate of slipping of the phases relative to each other:

$$ {u}_{12}={u}_1+{u}_2=\frac{\uplambda r{\updelta}^2}{\uppsi \left({\upalpha}_1\right)}, $$
(17)

where

$$ \uplambda =\frac{\upomega^2\Delta \uprho}{18\upmu {u}_0},\kern3.5em \Delta \uprho ={\uprho}_1^{{}^{\circ}}-{\uprho}_2^{{}^{\circ}}>0, $$
(18)

ψ(α1) is determined by equation (13).

Based on equations (14) and (17) we get the equation

$$ {u}_1=W(z)+\frac{{\uplambda \updelta}^2{rc}_1}{\uppsi \left({\upalpha}_1\right)} $$

or, in accordance with equations (4) and (13),

$$ {u}_1=W(z)+{\uplambda \updelta}^2r{\left(1-{\upalpha}_1\right)}^4. $$
(19)

Under the conditions of sedimentation of FS components, the flows of light and heavy suspension phases are directed to opposite sides and the relationship c2u2 = − c1u1 is fulfilled approximately, so by virtue of (14), W(z) = 0 [9], because of which and in accordance with equation (19), the solid sedimentation rate is determined by the equation

$$ {u}_1={\uplambda \updelta}^2r{\left(1-{\upalpha}_1\right)}^4. $$
(20)

Upon projection onto the meridional plane rz, the differential equation for the path of a test particle has the form

$$ \frac{dr}{u_{1r}}=\frac{dz}{u_{1z}} $$

or, in accordance with (4) and (20),

$$ \frac{dr}{{\uplambda \updelta}^2r{\left(1-{\upalpha}_1\right)}^4r}=- dz. $$
(21)

Integrating equation (21) on the left with respect to r (in r to R range) and on the right with respect to z (from z to L ), where r ∈(r0, R), L is the length of the cylindrical section of the screw, we get the characteristic equation for the test particle with the diameter δ, which moves along the fixed path from the position (r, L) to the position (R, 0):

$$ \underset{r}{\overset{R}{\int }}\frac{dr}{r}{\uplambda \updelta}^2r{\left(1-{\upalpha}_1\right)}^4\underset{0}{\overset{L}{\int }} dz, $$

whence, in accordance with (18), let us determine the current critical diameter (separation size [2]) of the particle:

$$ {\updelta}_{\mathrm{cr}}=\updelta (r)=\frac{1}{{\left(1-{\upalpha}_1\right)}^2}\sqrt{\frac{18\upmu {u}_01\mathrm{n}\left(R/r\right)}{\upomega^2L\Delta \uprho}}, $$

or with due regard for equations (6) and (7)

$$ \updelta (r)=\frac{1}{{\left(1-{\upalpha}_1\right)}^2}\sqrt{\frac{9\upmu s\Omega 1\mathrm{n}\left(R/r\right)}{\uppi {\upomega}^2L\Delta \uprho}}, $$
(22)

where we took ω = (ωr + ωs)/2.

From equation ((22) it follows that inclusion in this equation of the coefficient (1− α1)−2 resulting from the effect of increased FS concentration considerably enlarges the critical diameter δcr of the test particle. This implies that the suspension separation process efficiency decreases with increase of the solid phase concentration in the FS (in keeping with the mechanical sense of critical diameter δcr).

If the solid phase in the original FS is polydispersed, the relative mass η of the settling solid, i.e., the clarification factor (CF) is calculated by the equation in [10]:

$$ \upeta =\frac{m_1(t)}{m_0}=\frac{2}{R^2-{r}_0^2}\underset{r_0}{\overset{R}{\int }}\Phi \left[\updelta (r)\right]r\ dr, $$
(23)

where m0 and m1 are the mass of the particles in the original suspension and the sediment, respectively; Φ(δ) is the mass characteristic function of particle distribution.

Numerical Experiment

The geometric and physicomechanical parameters of sugar massecuite centrifuging process in a OGSh-50 (horizontal screw sedimentation) type of centrifuge (in a design modification for separation of concentrated solution) were taken as an example for calculations: rotor radius R = 0.25 m, screw radius r0 = 0.125 m, length of cylindrical section of rotor L = 0.80 m, screw pitch s = 0.1 m, angular speed of rotor ωr = 120 rps, solid phase (sucrose) density \( {\uprho}_1^{{}^{\circ}} \) = 1560 kg/m3, fluid (intercrystalline solution) density \( {\uprho}_2^{{}^{\circ}} \) = 1350 kg/m3 (Δ = 210 kg/m3 ), dynamic viscosity of the fluid μ = 0.2 and 0.5 Pa·sec, particle size in original suspension δ ∈ 0.1 and 1.0 mm, which matches the data on the dispersity of solid and viscous massecuite of first crystallization.

In accordance with equation (6), at relative angular screw speed Ω = 0.01ωr = 1.2 rps, the suspension flow rate is

$$ Q=\frac{s\Omega \left({R}^2-{r}_0^2\right)}{2}=0.5\bullet 0.1\bullet 1.2\bullet \left({0.25}^2-{0.125}^2\right)\bullet 3600=\frac{10.1{\mathrm{m}}^3}{\mathrm{h}}. $$

In calculations by equation ((22) it was taken that (ωr + ωs)/2 = 119.4 rps.

As a mass characteristic function of solid distribution in the original suspension (by agreement) we chose

$$ \Phi \left(\updelta \right)=\left\{\begin{array}{ccc}1& \mathrm{at}& 0\le \updelta \le {\updelta}_1\\ {}\frac{\updelta_2-\updelta}{\updelta_2-{\updelta}_2}& \mathrm{at}& {\updelta}_1\le \updelta \le {\updelta}_2\\ {}0& \mathrm{at}& \updelta \ge {\updelta}_2,\end{array}\right. $$
(24)

where δ1 = 1·10−4m and δ2 = 1·10−3m.

To find the dependence of the screw machine efficiency on the operating, geometric and physicomechanical parameters of the suspension treatment process [based on CF values by (23) and the characteristic function specified by (24)] we made a quantitative model of the centrifuging process (illustrated by the curves in Fig. 3). In this regard, we numerically determined the dependence of the CF (clarification factor) η on the concentration α = α1 of the solid in the suspension using the parametric data based on the values of the screw pitch s and the dynamic viscosity μ of the liquid phase of the suspension.

Fig. 3
figure 3

Dependence of clarification factor η on solid concentration α (%), screw pitch s and dynamic viscosity μ of liquid phase of suspension (ω = 120 rps): μ = 0.2 Pa·sec: s = 0.01 m (1) and 0.02 m (2); μ = 0.5 Pa·sec: s = 0.01 m (3) and 0.02 m (4).

Full size image

As a result, we noted a natural (in physical sense) exponential decrease of CF η due to increase of suspension density (increase of solid concentration α ) and increase of other parameters (Fig. 3).

Furthermore, according to equation (6), the centrifuge throughput Q increases with increase of angular speed of the rotor Ω (a process control parameter), i.e., the separation process efficiency decreases (Fig. 3, curve 2 is below curve 1), which corresponds to the physical sense of the centrifuging process.

In addition to this (also in keeping with the physical sense of the process), the suspension separation efficiency decreases with increase of the viscosity of the liquid phase of the suspension (Fig. 3, curve 3 is below curve 1).

The results of quantitative modeling of FS (sugar massecuite) separation process in a screw centrifuge, as evident from the curves in Fig. 3, are, by and large, adequate for the physical characteristics of the centrifugal separation process.

Thus, based on scientific premises of hydrodynamics of interpermeating and interacting multiphase fluids, the kinetics of a suspension separated in the working space of an OGSh type of centrifuge is modeled by a viscous incompressible fluid flow constrained by two coaxial fast rotating cylinders.

An expression has been obtained in an analytical form to calculate the critical diameter and clarification factor of the suspension.

On the example of an OGSh-50 type of horizontal screw sedimentation centrifuge a numerical variative experiment was conducted, taking account of the main process parameters, namely, screw pitch, solid phase concentration, and dynamic viscosity of the liquid phase of the suspension, to find out the optimum centrifuge operation conditions.