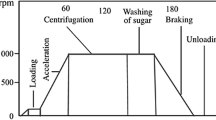
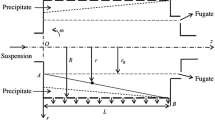
Suspension separation process in a filtering centrifuge type of equipment with periodic and continuous sediment discharge as an aggregate of phenomena of solid sedimentation, sediment formation on rotor wall, and filtration of clarified liquid was studied. A quantitative analysis was made of the liquid system separation efficiency in terms of treatment time and throughput of specific centrifugal machines as a function of solid phase concentration in the suspension, dispersity of the treated product, and filtering principles of the rotor.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Batch and continuous filtering centrifuges (BFC and CFC) are used widely in chemical, food, and other industries in the cases where the liquid phase needs to be separated from large, medium, and fine products and materials with minimal liquid content in the sediment and where the sediments needs washing.
Quantitative analysis of suspension separation process based on filtering centrifuges, which involved study of the kinetics of accumulation, washing, and dehydration of the sediment, was reported in [1,2,3,4,5,6,7,8,9,10,11]. However, these works lack the required theoretical validity of centrifugation-associated problems of removal of the liquid phase of the suspension from the rotor, estimation of the time of centrifugal treatment of the product, relationship of the separating capacity of the machine with suspension thickness, dispersity of the solid phase, etc. Also, the centrifugation process was not adequately analyzed within the framework of criterial modeling, which is important for creating innovative types of centrifugal equipment. Since designing and laboratory modeling require an appropriate mathematical apparatus to predict development of the centrifugation process with due regard for the operating conditions of the process and its characteristics, the urgency of in-depth study in this area is obvious.
In this work, we propose a method of quantitative analysis of the suspension separation process in the working space of batch and continuous filtering centrifuges, which is more substantiated compared to the known methods.
Batch filtering centrifuge. Analytical study of the separating capacity of centrifuges is based on the scientific postulate concerning critical diameter (CD) of a particle of a liquid system, i.e., concerning the size of a certain hypothetical particle moving slower than the others (in the case of a BFC) or moving along the least suitable (generally the longest) path from the point of settling of the particle in a sedimentation tank (in the case of a CFC).
If a low-concentrated suspension is separated in the rotor of a batch centrifuge with a solid (continuous) wall, then in a rotor-fitted cylindrical system of coordinates, the expression for the current critical diameter (CCD) of a particle (separation fineness) as a function of the coordinate r and the time t will have the form [7]
where
μ – dynamic viscosity of the liquid; ω – angular speed of the centrifuge rotor; Δ = ρs − ρ l > 0, ρs, ρ l − density of the solid and liquid in the suspension, respectively; R, δ – rotor radius and CCD of the particle.
In keeping with expression (1), the global critical diameter δc is
where r 0 – radius of free suspension surface.
Let Φ(δ), which is the mass characteristic function (CF) of solid phase distribution by size δ, be such that
where m 0 – mass of the solid in the original suspension; m(δ > δ′) – mass of particles of size (δ > δ′) in the same liquid system.
If the powder is monodispersed, its CF (4) will have the form
where δ0 – diameter of the powder particle.
Let, for dispersity, δc < δ0. Then, in congruence with the adopted global CD and Eq. (3), the inequality \( \ln \left(R,{r}_0\right)/ kt\le {\updelta}_0^2 \) is satisfied, whence, within the confines of the adopted formulation of the problem, we get an estimate of the complete suspension clarification time T:
where k is determined by formula (2).
For calculation (hypothetically taking the rotor of the machine as continuous), we chose, as an example, the process of separation of massecuite of the first product in an FPN-1251 T-01 sugar plant centrifuge. The centrifuge and massecuite parameters are: R = 0.625, r 0 = 0.41, H = 1 m, ω = 150 rad/sec, ρ l = 1450 kg/m3, ρs = 1560kg/m3, and μ = 0.5 Pa·sec [4, 12].
Taking δ0 = 5 ⋅ 10−4 min in expression (5), in keeping with the chosen process implementation conditions and formula (6), we obtained
If, on the other hand, a thickened polydispersed suspension is treated in a BFC with a perforated rotor, for estimating the treatment time, it is essential to take account of removal of the liquid from the working space of the machine and sediment accumulation on the filtering base of the rotor as well as the constrained nature of sedimentation of the suspended matter in the liquid system. Because of the complexity of physicomathematical modeling of the kinetics of such a process, we shall make simplifying assumptions with due account of the typical aspects of the studied phenomenon.
Thus, with a minor error the initial suspension layer with r 0 ≤ r < R can be replaced by a layer with ζ ≤ r < R and the settling solid layer with r 1 ≤ r < R, by a layer with ξ ≤ r < R, where ζ < ξ. Then, we get the model of momentary motion of an annular liquid layer with ζ ≤ r < ξ, which rotates with an angular speed ω as a quasi-solid body together with a cylinder of radius ξ (with a solid wall), where
V – suspension volume; H – rotor height;
c – volume concentration of the solid phase of the suspension; σ – sediment porosity; c ≠ 0 and σ ≠ 1 (Fig.1).
Here, in the projection onto the radius r, the absolute speed V r of a particle is roughly calculated as the sum of the relative speed v r and the transport speed u of the particle arising from filtration of the liquid, i.e.,
where strictly particle sedimentation rate
the correction factor for suspension thickness [13]
δ – particle diameter.
According to Darcy law (if we ignore the sediment resistance, which is minor compared to the sifter (filter) resistance [4]), the liquid filtration rate is calculated by the equation [2]
where k 0 – penetrability coefficient of the sifter surface, and ν = μ/ρ – kinematic viscosity coefficient of the liquid.
In such a case, in conformity with Eqs. (7)–(9), the characteristic equation for CCD δ * = δ has the form
where δ = δ(r, t, c) – particle diameter that changes over time t from r = r(ζ ≤ r < ξ) to r = ξ; ξ = (R − h)− reduced inner radius of the sediment layer; h = (R − r 1)/[2(1 − σ)]; and r 1 – sediment accumulation surface radius specified by Eq. (9), which depends on the concentration c (Fig. 1).
The parameter δ = δ* in Eq. (13) is determined as
In keeping with the chosen object of study (FPN-1251 T-01 centrifuge, massecuite as suspension, sucrose crystals as solid phase, and intercrystalline solution (syrup) as liquid phase), in addition to the adopted machine parameter values, also adopted are: volume particles concentration c = 0.3 and 0.5, sediment porosity σ = 0.4, and sifter penetrability k 0 = 2 ⋅ 10−10 m2 [4].
For the chosen equipment, the reduced radius values calculated by Eqs. (7)–(9) were: on the free massecuite surface ζ = 0.517 m along the inner radius of the sediment surface ξ(c = 0.3) = 0.578 m and ξ(c = 0.5) = 0.545 m. Since in accordance with Eq. (12) the filtration rate was u = 0.0073 m/sec, the average solid sedimentation time T = V(1 − c)/2πRHu ≈ 15 sec, where V = 0.7 m3 is the rotor holding capacity and c = 0.4 is the volume solid phase concentration in the suspension. The separation time is limited to 8 sec based on calculation.
The calculations were based on the CCD–centrifugation time relationships (13) and (14) in the range of change in real BFC parameter values (Fig. 2).
The dependence of global CD δc of particles on centrifugation process parameters (at fixed values of other parameters), which conforms to the physical concept of the problem, was disclosed by visual analysis of the plots shown in Fig. 2. In this context, increase in suspension thickness slows down settling of the suspended matter and concurrently facilitates sediment accumulation (particle settling path decreases), and these characteristics are expressed in the plots. In fact, in the initial treatment stage, at a lower liquid system concentration c, the calculated CD value of a particle is slightly lower than the corresponding particle CD value at higher concentrations, which occurs in the case of suspended matter sedimentation in a diluted suspension. Then, in the treatment process, because of shortening of the sedimentation path (due to increase in sediment layer thickness), the habit of the plots changes. As per calculation, with increase in solid concentration the particle CD value becomes less than at reduced concentration and so (in keeping with the concept of CD) the concentrated suspension separation process accelerates.
The kinetics of sediment accumulation over time t was analyzed quantitatively based on the suspension clarification coefficient η (%) [7]
The function Φ(δ) was taken in the form (by agreement)
where δ1 = 0.5 ⋅ 10−3 m and δ2 = 1.5 ⋅ 10−3 m are the minimum and maximum diameters of a sucrose crystal.
By analogy with Eq. (15), the clarification coefficient was calculated by the equation
where ζ and ξ are determined by Eqs. (7) and (8) and δ, by Eq. (14).
The coefficient of clarification η over the centrifugation time was calculated by Eqs. (14), (16), and (17) in the range of variation of a real BFC over the time 0 < t ≤ 8 sec (Fig. 3). From the shape of the curves, it is obvious that at fixed values of the process parameters the coefficient η increases exponentially (together with increase in the value of the process control parameter t, being the time) and decreases with increase in solid phase concentration c (due to increase in suspension thickness).
Also, analysis of the plots shows (Fig. 3) that, according to all calculation variants, at least 80% of the solid phase settles by the end of the treatment time (8 sec), and thereafter, until the instant of time T = 15 sec. occurs only dehydration of the sediment, which agrees with observations and results of other theoretical studies.
Continuous filtering centrifuge. Quantitative analysis of suspension separation process in CFC is difficult because this process develops in the working space of a complex cylindroconical type of equipment under conditions of considerable thickness of the treated liquid system, solid particle size variation, etc. So, in [2, 5,6,7,8], where the suspension process in CFC was studied, several hypotheses simplifying formulation and solution of the referred complex problem were adopted in calculations of the kinetics of accumulation, washing, and dehydration of the sediment. However, such factors of the process as dispersity of the suspended matter, hindrance to solid particle sedimentation from a liquid, kinetics of sediment accumulation, etc., were not studied in these works.
For practical purposes, it is desirable to get an expression for the parameters of control of this process based on dimensionless and criterial quantities, which make it possible to reduce the number of parameters and to adapt laboratory study results to full-scale prototypes of the centrifugal equipment. So, the problem was studied within the framework of criterial modeling.
Having studied the sedimentation process in a liquid + solid heterogeneous system in a centrifuge rotor with continuous sediment discharge, we assume that suspension separation in a CFC rotor is a kinetic liquid system treatment process in the centrifugal force field of two interacting and interpermeating media in a channel bounded by adjoined walls of a cylinder and a cone.
To simplify the problem, let us validate the geometric parameters of the cylinder that models the CFC rotor. The liquid flow in the CFC rotor having a working space of a cylindroconical shape with a conicity semiangle α ≈ 30° is taken as an axisymmetric thin-layered flow (in real situations, the ratio of the average liquid layer thickness h av to its length L in the order of magnitudes is h av/L ≈ 1%) inside a cylinder with a reduced radius R (Fig. 4). It is assumed that the liquid flow mode is laminar and voluntary (gravitational).
Then, if R l and R u are the radii of the lower and upper sections of the conical part of the rotor, then we shall roughly take the semi-average value of the radii of the lower and upper sections of the conical part of the rotor as the radius R of the cylinder that models this part of the rotor:
and as the radius r 0 (not shown in Fig.4) of the free flow surface we shall take
where R is determined by Eq. (18), and h is the average flow thickness.
If the suspension, having passed through the filter, moves over the sifter surface transversely, within the framework of the adopted schematization of the studied problem, the flow velocity u z = w 0 in the axial direction was taken as the semi-average value of the liquid flow velocities at the channel inlet and outlet:
where Q is the suspension flow throughput of the centrifuge; R and h are obtained by Eqs. (18) and (19).
In turn, considering that the sediment layer thickness is small, we shall ignore the influence of the sediment layer on the filtering capacity of the centrifuge and so the rate u = u r of liquid filtration through the sifter surface of the rotor can be calculated by Eq. (12).
In conformity with the proposed formalized model of the problem, we shall analyze the kinetics of a hypothetical particle of a specified size in a liquid flow, which rotates together with the cylinder and models the suspension flow in the working space of the CFC.
Since in the solid phase sedimentation process the force factors acting on the particle are oriented essentially along the radius and the particle moves along the axis z as being suspended with a speed w 0 (Eq. 20), the particle equilibrium conditions in the rotor-linked coordinates system rz (Fig. 5) projected along the axes r and z, will roughly have, in accordance with the D’Alembert principle, the following form [7]:
where k is determined by Eq. (2), v r , by Eq. (10); u r = u is the liquid transfer rate along the radius; δ is the particle diameter; and r is the current particle radius.
Further, by analogy with Eqs. (12)–(14), we get
where
In conformity with the proposed calculating equation based on Eq. (23) and the technical parameters of the FPI-1001K-01 industrial centrifuge [4], a numerical experiment was conducted to analyze the efficiency of the centrifugal suspension separation process; massecuite from the sugar plant III was chosen as a model of the liquid system. Process parameters were: massecuite throughput of the machine Q m = 8 tons/h; radius of the lower section of the conical part of the rotor R l = 0.167 m and of the upper part R u = 0.5 m; reduced radius of the cylinder R = 0.333 m; rotor length L = L c = 0.5 m; flow thickness averaged over the rotor length h = 5 mm [4]; radius of free flow surface r 0 = 328 m; and angular rotor speed ω = 220 rad/sec. Massecuite parameters were: volume crystal concentration c = 0.3, 0. 4, and 0.5; density of sucrose ρ1 = 1560 and of syrup ρ = 1450 kg/m3; dynamic viscosity of syrup μ = 5 Pa·sec; and sifter surface penetrability coefficient/ k 0 = 2·10–10 m2 [4, 12, 15].
Massecuite volume flow rate Q (m3/sec) was calculated by the equation Q = Q m /{[(1 − c)ρ + cρ1] ⋅ 3.6}, whence (assuming c = 0.4, Q m = 8 tons/h) we got Q = 1.466·10–3 m3/sec. As a result, in conformity with Eq. (20), the axial liquid flow velocity at the channel inlet was found to be w z0 = 0.142 m/sec. Due to discharge of the liquid phase through the sifter along the channel length, in the calculations the average axial liquid velocity (as in piston mode) was taken to be w 0 = w z0/2 = 0.071 m/sec, so the test particle residence time in the rotor was T = L/w 0 = 7.1 sec.
We chose R, ω, and ρ, being cylinder radius, angular rotor speed, and syrup density, respectively, in a dimensionless form as the characteristic parameters of the process. Then, the calculating equation (23) is expressed via the following criterial complexes: Taylor number (first) Ta = (ωR 2/v)2, which is the specific value of the centrifugal force relative to the viscous force; Reynolds number Re = w 0 R/ν, which is the specific value of the inertial force in axial direction relative to viscous forces, and also via the simplexes: ξ = L/R, which is the specific value of the length of the cylinder relative to its radius; χ = ρ1/ρ, which is the ratio of the sucrose and syrup densities (effective density); κ = k 0/R 2, which is the specific value of the coefficient k 0 of penetrability of the sifter surface in fractions of the cross-sectional area of the cylinder (specific penetrability).
The clarification coefficient in dimensionless quantities
where
\( \overline{\updelta}=\updelta /R \) is the dimensionless particle diameter.
Equations (23) and (24) are foundations for quantitative modeling of the suspension separation process in a CFC rotor.
Based on the chosen operating parameter values for the FPI-1001K-01 centrifuge, the following values of the dimensionless parameters were obtained: Ta = 5.02 ⋅ 107, Re = 6.82, ξ = 1.5, χ = 1.08, and κ = 1.8 ⋅ 10−9. So, after performing numerical operations, the following values were taken: Ta = 5 ⋅ 107 and 6 ⋅ 107; Re = 7–14 (this range corresponds also to laminar liquid flow).
In the calculations, we chose Eq. (16) as CF, δ1 = 0.1 mm, and δ2 = 0.5 mm [12]. The results of the calculations based on the cited parameters and solution of Eq. (23) with respect to global particle CD are plotted in Fig. 6.
Analysis of the data in Fig. 6 revealed that the dependence of the global particle CD δc on the centrifugation process parameters is consistent with the physical concept of the problem (at specified values of other parameters): increase in δc (which corresponds to worsening of suspension separation conditions) with increase in solid phase concentration c and the control parameter Re (i.e., when the suspension flow rate increases); decrease in δc with increase in Taylor number, which indicates acceleration of the suspension separation process (Fig. 6, curves 1, 3 and 2, 4).
In turn, for the adopted characteristic equation, visualization of the data (Fig. 7) also confirms matching of the calculated data with the physical concept of the centrifugation process: clarification coefficient η decreases with increase of concentration c (i.e., suspension separation process efficiency decreases with increase of suspended matter thickness (density) in the suspension) and of the control parameter Re. The coefficient η increases (i.e., sharpness of suspension separation increases) with increase of Taylor number (with increase of motive force of the process), which indicates improvement in suspension separation conditions (Fig. 7, curves 1, 3 and 2, 4).
Furthermore, it is evident from the habit of the curves (Fig. 7) that for the operating parameters of the machine Ta = = 5·107 and 6·107 and solid concentration c ≤ 0.5 in the control parameter range Re = 7–9.5, which is the clarification coefficient η ≈ 100%, i.e., according to calculation, complete solid phase sedimentation is achieved on the sifter (filter) surface of the machine when FPI-10001K-01 industrial centrifuge is used under fixed conditions.
References
A. N. Planovskii, V. M. Ramm, and S. Z Kagan, Chemical Engineering Processes and Apparatuses, Goskhimizdat, Moscow (1962).
V. I. Sokolov, Modern Industrial Centrifuges, Mashinostroenie, Moscow (1967).
V. M. Luk”yanenko and A.V. Tarantsev, Industrial Centrifuges, Khimiya, Moscow (1974).
B. N. Tereshin, Industrial Centrifuges in Sugar Industry, Pishchev. Prom., Moscow (1975).
D. E. Shkoropad, Centrifuges for Chemical Plants, Mashinostroenie, Moscow (1975).
E. V. Semenov and V. A. Karamzin, “Separation of a suspension in the rotor of a filtering sedimentation centrifuge,” Teor. Osn. Khim. Tekhnol., 41, No. 2, 183–190 (2007).
E. V. Semenov and A. A. Slavyanskii, Modeling of Crystallization and Centrifugation Processes, SPUTNIK+, Moscow (2015).
M. Sambuichi and F. M. Tiller, “Theory of batchwise centrifugal filtration,” AIChE J., 33, No. 1, 109–120 (1987).
M. Sambuichi, H. Nakakura, and K. Osasa, “Comparison of batchwise centrifugal and constant-pressure filtration,” J. Chem. Eng. Japan, 21, No. 4, 418–223 (1988).
R. J. Wakeman and T. S. Tarleton, Filtration, Elsevier Science, Oxford–New York–Tokyo (1999).
F. Ruslim, “Modified lab-scale beaker centrifuge as a tool for investigation on filter cake washing processes,” Aufbereit.-Technik, 47, No. 11, 20–31 (2006).
I. S. Gulyi, V. M. Lysysanskii, L. P. Reva, et al., Physicochemical Processes of Sugar Production, Agropromizdat, Moscow (1987).
R. I. Nigmatulin, Fundamentals of Mechanics of Multiphase Mixtures, Pt. II, Nauka, Moscow (1987).
E. V. Semenov, “Particle settling in liquid centrifuges,” Teor. Osn. Khim. Tekhnol., 38, No. 4, 446–450 (2004).
A. R. Sapronov, Sugar Production Technology, KolosS, Moscow (1999).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Khimicheskoe i Neftegazovoe Mashinostroenie, No. 5, pp. 7–12, May, 2017.
Rights and permissions
About this article
Cite this article
Semenov, E.V., Slavyanskii, A.A. Distinctive Features of Suspension Separation Process in Filtering Centrifuge Rotors. Chem Petrol Eng 53, 288–296 (2017). https://doi.org/10.1007/s10556-017-0336-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10556-017-0336-4