Polymer flooding has been successfully used as an enhanced oil recovery (EOR) method [1–3].

It was previously assumed that the mechanism for enhanced oil recovery with polymer flooding involves reducing the mobility ratio and increasing the macro sweep efficiency. However, recently it was observed that polymer solutions can significantly improve the micro sweep efficiency because of viscoelastic flow in a porous medium, which is significantly different from Newtonian flow [4–6].

A number of papers have been devoted to the influence of the viscoelastic properties of polymer solutions on oil displacement efficiency. Xia et al. [7] compared the displacement efficiency for a viscoelastic polymer solution with the displacement efficiency for a glycerin solution of the same viscosity. It is shown that polymer solutions are characterized by greater displacement efficiency. Yue et al. [8], based on results of a study of the flow characteristics of a polymer solution in dead-end pores, showed that the flow rate can be improved by increasing the viscosity of the polymer solution. The residual oil thus becomes recoverable oil [8]. However, the micro sweep efficiency is not only affected by the elasticity but also by the viscosity and flow velocity. In this paper, we have constructed a mathematical model of polymer solution flow in dead-end pores, and we have analyzed the factors influencing the micro sweep efficiency.

Governing equations. We considered the flow as two-dimensional isothermal steady flow. The model includes a continuity equation, a momentum conservation equation, and a constitutive equation (equation of state). The governing equations are dimensionless [9–11].

Continuity equation:

$$ \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0 $$
(1)

where u, v are the velocity components in the x and y directions respectively.

Momentum conservation equation:

$$ \mathrm{R}\mathrm{e}\left[\frac{\partial }{\partial x}(uu)+\frac{\partial }{\partial y}(uv)\right]=\frac{\partial \rho }{\partial x}+\frac{\partial {T}^{xx}}{\partial x}+\frac{\partial {T}^{xy}}{\partial y} $$
(2)
$$ \mathrm{R}\mathrm{e}\left[\frac{\partial }{\partial x}(vv)+\frac{\partial }{\partial y}(vu)\right]=\frac{\partial \rho }{\partial y}+\frac{\partial {T}^{xx}}{\partial x}+\frac{\partial {T}^{yy}}{\partial y} $$
(3)

Where T xx, T xy, T yy are the stresses in the corresponding directions; Re = ρUL/μ; U is the characteristic velocity (the average velocity at the inlet); ρ is the density of the polymer solution, kg/m3; μ is the viscosity of the polymer solution, Pa·s; L is the characteristic length.

The rheological behavior of polymer solutions is determined mainly by the primary normal stress difference. The upper-convected Maxwell (UCM) equation corresponds to this property:

$$ {A}_1{\tau}^{xx}+\mathrm{We}\left(\mu \frac{\partial {\tau}^{xx}}{\partial x}+v\frac{\partial {\tau}^{xx}}{\partial y}\right)=2B{\tau}^{xy}+{F}_1 $$
(4)
$$ {A}_2{\tau}^{xy}+\mathrm{We}\left(\mu \frac{\partial {\tau}^{xy}}{\partial x}+v\frac{\partial {\tau}^{xy}}{\partial y}\right)=C{\tau}^{xx}+B{\tau}^{yy}+{F}_2 $$
(5)
$$ {A}_3{\tau}^{yy}+\mathrm{We}\left(\mu \frac{\partial {\tau}^{yy}}{\partial x}+v\frac{\partial {\tau}^{yy}}{\partial y}\right)=C{\tau}^{xy}+{F}_3 $$
(6)

where

$$ \begin{array}{l}{A}_1=1-2\mathbf{We}\frac{\partial u}{\partial x};\kern0.5em {A}_2=1;\kern0.5em {A}_3=1-2\mathbf{We}\frac{\partial v}{\partial y};\kern0.5em B=\mathbf{We}\frac{\partial u}{\partial y};\kern0.5em C=\mathbf{We}\frac{\partial v}{\partial x}\hfill \\ {}\kern5em {F}_1=2\frac{\partial u}{\partial x}\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2\right]\hfill \\ {}\kern4em {F}_2=\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2\right]\hfill \\ {}\kern5em {F}_3=2\frac{\partial v}{\partial y}\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^2\right]\hfill \end{array} $$

In the equations given above, τ is the stress in the corresponding direction; We = λU/L; λ is the relaxation time of the polymer solution, in seconds. The parameters L, U, T are dimensionless.

Numerical solution is made difficult due to the lack of a pressure equation. The term containing pressure does not have to be solved in velocity – stream function variables; the continuity equation can be solved automatically. The stream function and vorticity are defined by the equations:

$$ u=\frac{\partial \psi }{\partial y};\kern0.62em v=\frac{\partial \psi }{\partial y} $$
(7)
$$ \omega =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} $$
(8)

where ω is the vorticity; ψ is the stream function.

These expressions were substituted into Eq. (3):

$$ \omega =-{\nabla}^2\psi $$
(9)
$$ \begin{array}{l}\kern7em .\frac{\partial^2\omega }{\partial {y}^2}+\frac{\partial^2\omega }{\partial {x}^2}+\mathrm{R}\mathrm{e}\left(\frac{\partial \psi }{\partial x}\frac{\partial \omega }{\partial y}-\frac{\partial \psi }{\partial y}\frac{\partial \omega }{\partial x}\right)=\hfill \\ {}=\frac{\partial^2{T}^{xx}}{\partial x\partial y}+\frac{\partial^2{T}^{xy}}{\partial {y}^2}-\frac{\partial^2{T}^{xy}}{\partial {x}^2}-\frac{\partial^2{T}^{yy}}{\partial x\partial y}+\frac{\partial^3y}{\partial {x}^3}-\frac{\partial^3u}{\partial {x}^2\partial y}+\frac{\partial^3v}{\partial x\partial {y}^2}-\frac{\partial^3u}{\partial {y}^3}\hfill \end{array} $$
(10)

Boundary conditions. For the dead-end model, the inlet conditions are: u = 6(y – y 2), v = 0. The boundary conditions when parallel to the x axis are: u = 0, v = 0. The boundary conditions when parallel to the y axis are: u = 0, v = 0. The outlet conditions correspond to the Neumann boundary condition. The velocity gradient at the outlet is equal to zero, and so u NI  = u NI − 1.

Numerical simulation. A nonuniform grid was used for going to the difference equations from (4)-(6), (9), and (10). The stream function equation was solved by a central finite difference method. The left-hand and right-hand sides of the vorticity equation were transformed by a first-order upwind difference scheme and a central difference scheme. When A m  ≤ 0(m = 1, 2, 3), we use a downwind difference scheme; when A m  ≥ 0, we use an upwind difference scheme.

$$ \frac{\psi_{j+1,k}-2{\psi}_{j,k}+{\psi}_{j-1,k}}{H_x^2}+\frac{\psi_{j+1,k}-2{\psi}_{j,k}+{\psi}_{j-1,k}}{H_y^2}=-{\omega}_{j,k} $$
(11)
$$ \begin{array}{l}{k}_0{\omega}_{j,k}+{k}_1{\omega}_{j-1,k}+{k}_3{\omega}_{j,k+1}+{k}_4{\omega}_{j,k-1}=\frac{1}{4{H}_x{H}_y}\left({S}_{j+1,k+1}^{xx}+{S}_{j-1,k+1}^{xx}+{S}_{j+1,k-1}^{xx}+{S}_{j-1,k-1}^{xx}\right)=\hfill \\ {}\kern4em =\frac{1}{H_y^2}\left({S}_{j,k+1}^{xy}-2{S}_{j,k}^{xy}+{S}_{j,k-1}^{xy}\right)-\frac{1}{H_x^2}\left({S}_{j+1,k}^{xy}-2{S}_{j,k}^{xy}+{S}_{j-1,k}^{xy}\right)\hfill \end{array} $$
(12)

where H x and H y are the mesh spacing in the x and y directions; for S, see (14).

$$ \begin{array}{l}{k}_0=-\frac{2}{H_x^2}-\frac{2}{H_y^2}-2{\left(\left|{f}_1\right|+\left|{f}_2\right|\right)}_{;\kern0.5em }{k}_2=\frac{1}{H_x^2}+\left|{f}_2\right|-{f_2}_{;\kern0.5em }\kern0.5em {k}_4=\frac{1}{H_y^2}+\left|{f}_1\right|-{f}_1\hfill \\ {}\kern11em {f}_1=\frac{b_1}{2{H}_y}{}_{;}f_2=\frac{b_2}{2{H}_x}\hfill \\ {}\kern5em {b}_1=\mathbf{R}\mathbf{e}\frac{\psi_{j+1,k}-{\psi}_{j-1,k}}{2{H}_x};\kern0.5em {b}_2=-\mathbf{R}\mathbf{e}\frac{\psi_{j,k+1}-{\psi}_{j,k-1}}{2{H}_y}\hfill \\ {}\kern2em {k}_0^{A_1}{T}_{j,k}^{xx}-{k}_1^{A_1}{T}_{j+1,k}^{xx}-{k}_2^{A_1}\left|{T}_{j-1,k}^{xx}-{k}_3^{A_1}{T}_{j,k+1}^{xx}-{k}_4^{A_1}{T}_{j,k-1}^{xx}\right.=\left(2{B}_{j,k}{T}_{j,k}^{xy}+{F}_{1j,k}\right)\mathbf{s}\mathbf{g}\mathbf{n}\left({A}_1\right)\hfill \\ {}{k}_0^{A_2}{T}_{j,k}^{xy}-{k}_1^{A_2}{T}_{j+1,k}^{xy}-{k}_2^{A_2}{T}_{j-1,k}^{xy}-{k}_3^{A_2}{T}_{j,k+1}^{xy}-{k}_4^{A_2}{T}_{j,k-1}^{xy}=\left({C}_{j,k}{T}_{j,k}^{xx}+{B}_{j,k}{T}_{j,k}^{xy}+{F}_{2j,k}\right)\mathbf{s}\mathbf{g}\mathbf{n}\left({A}_2\right)\hfill \\ {}\kern2em {k}_0^{A_3}{T}_{j,k}^{yy}-{k}_1^{A_3}{T}_{j+1,k}^{yy}-{k}_2^{A_3}{T}_{j-1,k}^{yy}-{k}_3^{A_3}{T}_{j,k+1}^{yy}-{k}_4^{A_3}{T}_{j,k-1}^{yy}=\left(2{C}_{j,k}{T}_{j,k}^{xy}+{F}_{3j,k}\right)\mathbf{s}\mathbf{g}\mathbf{n}\left({A}_3\right)\hfill \end{array} $$
(13)

In Eq. (13),

$$ {k}_1=\left|{B}_1^{A_m}\right|-{B}_1^{A_m};\kern0.5em {k}_2=\left|{B}_1^{A_m}\right|+{B}_1^{A_m};\kern0.5em {k}_3=\left|{B}_2^{A_m}\right|-{B}_2^{A_m};\kern0.5em {k}_4=\left|{B}_2^{A_m}\right|+{B}_2^{A_m} $$

The coefficients A, B, C, and F are calculated by a central difference scheme.

The additional stress tensor due to non-Newtonian flow is expressed by the equation:

$$ \left.\begin{array}{l}{S}_{j,k}^{xx}={T}_{j,k}^{xx}-{F}_{1j,k}\hfill \\ {}{S}_{j,k}^{xy}={T}_{j,k}^{xy}-{F}_{2j,k}\hfill \\ {}{S}_{j,k}^{yy}={T}_{j,k}^{yy}-{F}_{3j,k}\hfill \end{array}\right\} $$
(14)

The nonlinear equations were solved by relaxation methods. The inner iteration of the linear differential equations was solved by the Gauss – Seidel iteration method. The external iteration, concluding with the equations and boundary conditions, was solved by the under-relaxation method.

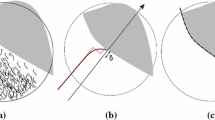
Analysis of hydrodynamic characteristics. The stream functions, the velocity, and the stress were calculated according to the simulation model described above. We compared the velocity contours for the different conditions (Fig. 1). As we see, the sweep area, bounded by the 0.05 line, increases as the Weber number (We) increases, i.e., as the elasticity of the polymer solution increases. We also see that the velocity contour changes only very slightly as the Reynolds number (Re) changes.

Fig. 1
figure 1

Velocity contours: a) We = 0, Re = 5·10–5; b) We = 0.3, Re = 5·10–5; c) We = 0, Re = 0.1; d) We = 0.3, Re = 0.1.

Full size image

Factors influencing micro sweep efficiency. The micro sweep efficiency was calculated based on the velocity contour:

$$ \eta =\frac{A_1}{A_1+{A}_2}100\% $$

In this equation, A 1 and A 2 are defined as shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram for determining the micro sweep efficiency.

Full size image

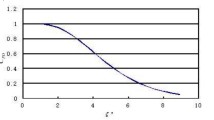
The elasticity of the polymer solutions was determined from the relaxation time. A longer relaxation time means higher elasticity of the solution. In the dimensionless calculations, the Weber number is proportional to the relaxation time, i.e., a higher We means higher elasticity. Figure 3 shows the results of calculating the micro sweep efficiency for the same values of the Reynolds number (10-5) but different values of the Weber number. As we see, the micro sweep efficiency increases as the Weber number increases for We above 0.15.

Fig. 3
figure 3

Micro sweep efficiency vs. elasticity of the polymer solution.

Full size image

The dimensionless quantity Re is inversely proportional to viscosity. Figure 4 shows the change in the micro sweep efficiency as the Reynolds number is varied. As we see, the micro sweep efficiency increases as the Reynolds number increases, i.e., as the viscosity decreases. With a decrease in the viscosity of the solution, the resistance to flow decreases and so the micro sweep efficiency increases for dead-end pores. From Fig. 4, we also see that the micro sweep efficiency does not depend much on viscosity for the low Reynolds number values characteristic under reservoir conditions.

Fig. 4
figure 4

Micro sweep efficiency vs. Reynolds number and Weber number (see numbers on curves).

Full size image

The dimensionless quantity Re is directly proportional to the flow velocity of the polymer solution. From Fig. 4, we see that the micro sweep efficiency increases with the Reynolds number and consequently with the flow velocity. However, under reservoir conditions, the Reynolds number varies in the range from 10-5 to 1. In this range, the Re value has practically no effect on the micro sweep efficiency.

Therefore the elasticity of the polymer solution is the major factor influencing micro sweep efficiency.