1 Introduction

One of the hallmarks of porous media is the relatively large value of the specific area, i.e., the surface-to-volume ratio, therefore making interfacial phenomena of great importance in the study of mass and momentum transport. This is particularly true for the flow of polymer molecules that are relatively large (up to \(100\,\text {nm}\)) and can interact with the solid surface in a variety of ways. In general, repulsion (Agarwal et al. 1994) and attraction (Gennes 1981) mechanisms can have significant impacts on momentum transport in porous media. For instance, sorption mechanisms associated with electrostatic forces often lead to a cushion of polymer molecules that can strongly affect the macroscale flow (see Brochard and Gennes (1992)) for a description of different regimes). On the other hand, repulsion mechanisms—originating from a variety of phenomena such as steric hindrance (Joanny et al. 1979), electrostatic repulsion (Uematsu 2015), or migration of polymer molecules away from high-shear regions (Cuenca and Bodiguel 2013)—can lead to a depletion layer close to the solid/liquid interface ((see Auvray (1981)) and the very good reviews from Barnes (1995) or Sochi (2011) for more details). The concentration of polymer is then lower in the depletion layer than in the bulk, leading to a lower viscosity in the vicinity of the wall. Consequently, this layer acts as a lubricating film, over which the polymer molecules slip. The properties of this depletion layer depend on parameters such as pH (Sorbie and Huang 1992), polymer concentration, or even the flexibility of the molecules (Gennes 1981; Ausserre et al. 1986). For diluted solutions, the depletion layer thickness, which we call \(\delta \) in the remainder of this paper, is often estimated using the gyration radius for flexible molecules and using the length of the molecules for rigid polymers.

How does this depletion layer affect the flow on larger scales? To describe the macroscale flow, a modified version of the isotropic Darcy’s law (Gogarty 1967) is often used,

$$\begin{aligned} \mathbf {U}=-\frac{k_{0}}{\mu _{\text {app}}}\left( \nabla P-\rho \mathbf {g}\right) , \end{aligned}$$
(1)

with \(\mathbf {U}\) the superficial average velocity, \(k_{0}\) the intrinsic permeability (associated with the flow of a Newtonian fluid which does not induce a depletion layer or any other particular phenomena), \(\nabla P\) the gradient of the intrinsic average pressure, \(\rho \mathbf {g}\) the gravitational force and \(\mu _{\text {app}}\) the apparent viscosity. The effects of slip at the pore scale are usually included in this apparent viscosity, which decreases as slip increases. The apparent viscosity drop has been observed experimentally with rigid or flexible polymer molecules over a wide range of porous media (Fletcher et al. 1991; Aubert and Tirrell 1982; Agarwal et al. 1994).

However, the physics of polymer flow in porous media is very rich and complex (De Gennes 1979) so that this apparent viscosity also includes a variety of other important, often even predominant, phenomena. These include non-Newtonian rheology, retention mechanisms (Huh et al. 1990), thermochemical or mechanical degradation of polymer chains (Gao 2013; Maerker 1975) or inaccessible pore volume (Lund 1992). Due to the combined effects of these phenomena, \(\mu _{\text {app}}\) includes rock geometrical and structural effects and may be very different from the bulk viscosity \(\mu _{\text {bulk}}\), with apparent thinning or thickening effects. These effects can be extremely complex, a striking example of this being elastic turbulence at low Reynolds numbers, resulting in apparent thickening for the flow of rigid and flexible polymer molecules through porous media (Amundarain et al. 2009; González et al. 2005; Groisman and Steinberg 2000).

We focus in this work on the link between slip at the pore scale and the apparent viscosity at the Darcy scale. We consider the bulk fluid rheology as Newtonian and overlook all the other complex features of polymer flows, including non-Newtonian effects in the rheology. The rationale for doing so is twofold. Firstly, there are many situations in which interfacial effects are predominant in the control of the flow. One of the practical cases where this occurs is enhanced oil recovery (EOR), where polymer solutions are often injected into oil-bearing reservoirs (Morel et al. 2008). The idea of the technology is to benefit from an increase in the bulk fluid viscosity in the reservoir compared to just water, which increases sweep efficiency by a number of mechanisms including a reduction of hydrodynamic instabilities (Sorbie 1991). In field applications, a significant portion of the reservoir is composed of regions with relatively small velocities where the polymer solution essentially behaves as a Newtonian fluid. In the Newtonian regime, core-flood experiments further show that the flow of polymer solutions through typical sandstones yields an apparent viscosity drop that can reach 20% (Fletcher et al. 1991; Chauveteau 1982), which is consistent with a predominance of slip. Furthermore, different effects are known to reduce the non-Newtonian effects under typical reservoir conditions, such as mechanical degradation or the presence of salt ions (these are further discussed in Sect. 2). Therefore, there is a clear engineering and practical interest in determining the impact of slip on the macroscopic flow assuming a Newtonian rheology.

The second reason for using a Newtonian rheology is on a more fundamental level. The approach using an apparent viscosity is mostly empirical and, as we have discussed before, it is used successfully as a black box to describe a variety of phenomena at the pore scale. However, there is little fundamental understanding of the relative contributions of these phenomena in different configurations. To make progress in this direction, we believe that it is necessary to evaluate the influence of each effect separately, so that we can understand better the physics of multiscale polymer flows in porous media. For example, we recently studied the Newtonian to non-Newtonian transition without slip effects using a digital rock physics approach (Zami-Pierre et al. 2016). This fundamental understanding of the physics may ultimately lead to better models of polymer flows that accurately combine the different effects, with potential applications in many engineering problems such as EOR. Therefore, we need to propose a tool to evaluate simply the impact of the depletion layer.

How can we study the depletion layer phenomenon and the associated slip effect? To do so, different tools are available. Molecular dynamics approaches, often with simple molecules, are useful to understand the fundamental physics at the molecular level (Rouse 1953; Joshi et al. 2000; Sochi 2011). However, simulations cannot yet be performed on sufficiently large volumes to model flow in porous media, especially in the case of polymer solutions. Therefore, mesoscale models are usually adopted (see Fig. 1a, b). The so-called two-fluid model proposed by Chauveteau (1982), whereby the concentration of polymer and the viscosity are piecewise constant (see the red dotted curve in Fig. 1b), is probably the simplest way to represent the depletion layer (other models use continuous and linear (Sorbie and Huang 1991) or nonlinear (Aubert and Tirrell 1982) concentration fields, see the black curve in Fig. 1b). In the two-fluid model, the viscosity is \(\mu _{\text {layer}}\) inside the depletion layer of thickness \(\delta \) and \(\mu _{\text {bulk}}\) outside, with \(\mu _{\text {bulk}}>\mu _{\text {layer}}\).

Fig. 1
figure 1

Different scales for different models: a molecular-scale description, b mesoscale where the curves describe the concentration field that decreases near the wall (according to a continuous or discontinuous model) and c pore scale at which an effective condition can be used

Full size image

How can this two-fluid model be used to calculate the apparent viscosity of a polymer solution flowing through a porous medium? One way to proceed is to exploit the simplicity of the two-fluid model to obtain an analytic solution for the flow through a single capillary and then go on to apply the obtained analytic solution to represent more complex structures in order to predict the apparent viscosity (Sorbie 1990; Fletcher et al. 1991; Omari et al. 1989; Chauveteau 1982). To do so, a characteristic length must be defined and used instead of the radius of the capillary. For complex structures, the choice of this characteristic length is not obvious. More generally, in porous media sciences, the definition of a single characteristic length is a frequent issue. In this case, according to the choice that is made, the prediction of the apparent viscosity might be inaccurate. For instance, in the article from Chauveteau (1982), the apparent viscosity prediction is accurate in beads packing, where the capillary analogy is relevant, and fails in natural rocks like sandstones.

Another method would be to use computational fluid dynamics (CFD) to solve the Stokes equations at the pore scale in complex porous structures. However, this approach requires a large number of mesh elements to capture gradients in the thin depletion layer and, in most cases, it is not computationally tractable. A way to overcome this issue is to further simplify the representation and use a slip boundary condition at the solid/liquid interface (see Fig. 1b–c). The slip coefficient can be obtained from the solution in a capillary tube and then applied to more complex pore-scale structures. The idea is that computations where only the slip length is estimated using the capillary tube model may be more accurate than models where the whole porous medium is treated as a capillary tube. This is because it deals with the realistic pore-scale structure instead of simplifying it and there is no requirement of characteristic length estimation. However, there is no strong theoretical basis for estimating differences in accuracy, and therefore, the validity of such an effective condition must be tested.

In this paper, we revisit the use of a pore-scale slip effective condition to model a wall repulsion mechanism. The derivation of this pore-scale effective condition is detailed in Sect. 3, and the slip length that we obtain is directly related to parameters of the depletion layer. In order to validate the expression of the slip length, we compare the apparent viscosity (see Eq. 1) obtained from several core-flood experiments from the literature (Chauveteau 1982; Sorbie and Huang 1991) and CFD calculations that we perform on associated geometries; see Sect. 4. We show that our model provides an estimation of the apparent viscosity within an accuracy of about \(10\%\) in most cases. The main contribution of this paper is to show that this computational approach is a simple way to estimate the contribution of the depletion layer to the macroscale flow. This method also lays the foundation for further improvements, such as accounting for a non-Newtonian rheology that could be easily implemented in the numerical model.

2 The Newtonian Framework in EOR

In this section, we go beyond the qualitative discussion of the Introduction and further justify the Newtonian framework in which this study is set for EOR applications.

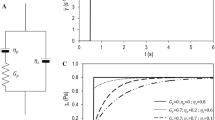
The bulk rheology of a polymer solution, as measured for example by a rheometer, exhibits non-Newtonian effects. For most polymer fluids, the solution has a Newtonian behavior in the limit of low shear rates, i.e., \(\mu _{\text {bulk}}=\mu _{0}\) (except yield stress fluids that are not considered in this study), and, in most cases, a shear-thinning behavior under moderate shear rates (for \(\dot{\gamma }>\dot{\gamma }_{\text {c}}\) , \(\mu _{\text {bulk}}\propto \dot{\gamma }^{n-1}\), see Fig. 2). Various laws exist to describe the shear-thinning rheology. The viscosity usually drops according to a power-law (Bird et al. 1977), as is the case for xanthan or partially hydrolyzed polyacrylamide (HPAM) polymers, which are commonly used in EOR (Sorbie 1991). As discussed in the Introduction, under higher shear rates elastic turbulence may occur for HPAM or xanthan, yielding an apparent shear-thickening. This effect is not represented in Fig. 2.

In a porous medium, there exists a complex coupling between this bulk rheology and the multiscale geometry of the porous structure. Despite this apparent complexity, it is well accepted (Chauveteau 1982; Morais et al. 2009) that there is a critical value of the Darcy velocity, or equivalently the pressure gradient, that controls the transition from a Newtonian to a non-Newtonian regime at the macroscale. Below this critical velocity, the flow behaves in a Newtonian manner. Fundamental aspects of this transition are discussed in Zami-Pierre et al. (2016). In EOR modeling, this is often considered via an apparent viscosity \(\mu _{\text {app}}\) (the limitations of this approach are discussed in the Introduction) that is treated as a function of an equivalent shear rate \(\dot{\gamma }_{\text {eq}}\) that is usually calculated as

$$\begin{aligned} \dot{\gamma }_{\text {eq}}=\alpha \frac{4\left\| \mathbf {U}\right\| / \epsilon }{R_{\text {eq}}}, \end{aligned}$$
(2)

with \(\alpha \) an empirical parameter that characterizes the impact of the medium structure and

$$\begin{aligned} R_{\text {eq}}=\sqrt{\frac{8k_{0}}{\epsilon }}, \end{aligned}$$
(3)

with \(\epsilon \) the porosity (Chauveteau 1984). The definition of the equivalent radius \(R_{\text {eq}}\), sometimes called the “pore throat radius”, results from an analogy with the flow through a capillary tube. In this paper, we will also use the length \(R_{\text {eq}}\) as a characteristic length of the medium, in order to evaluate the impact of the depletion layer of thickness \(\delta \). This definition of \(\dot{\gamma }_{\text {eq}}\) is derived from models based on a tube (\(\alpha =1\) corresponding to the expression of the maximum shear rate in a capillary tube) and a similar expression is used in petroleum engineering simulators (UTCHEM 2000). In these simulators, the flow is also considered Newtonian for \(\dot{\gamma }_{\text {eq}}\lesssim \dot{\gamma }_{\text {c}}\). Figure 2 represents a simplified view of the bulk and apparent viscosities dependence upon the shear rate for a xanthan solution. In an ideal situation where all the phenomena described in the Introduction are not occurring, the apparent viscosity drop in the Newtonian regime, \(\varDelta \mu _{\text {app}}\) in Fig. 2, is only induced by the depletion layer.

Fig. 2
figure 2

Simplified representation of the viscosity dependence upon the shear rate [the viscosity is calculated with a Bird–Carreau model (Bird and Carreau 1968)] for a xanthan polymer solution. For HPAM, the apparent shear-thinning is often not observed, as elastic effects rapidly become predominant in the non-Newtonian regime (Seright et al. 2008). In a porous medium, the apparent viscosity (\(\mu _{\text {app}}\) in Eq. 1) is plotted versus an apparent shear rate \(\dot{\gamma }_{\text {eq}}\) (Chauveteau 1984). The apparent and bulk viscosities are represented with the same slope in the non-Newtonian regime. This might not always be the case in practical situations (Sorbie 1991) where different slopes have been observed. The parameter \(\alpha \) in Eq. 2 is used to superpose the apparent and bulk viscosity curves in the non-Newtonian regime. This leads to a shift in the transition from the Newtonian to the non-Newtonian regime between the bulk and apparent viscosities. For example, \(\alpha \) is about 2 for beads packings (Zitha et al. 1995) and rises up to 10 for sandstones (Fletcher et al. 1991)

Full size image

We now ask the question of whether the situation \(\dot{\gamma }_{\text {eq}}\lesssim \dot{\gamma }_{\text {c}}\) actually occurs in EOR? For the xanthan polymer, \(\dot{\gamma }_{\text {c}}\) values are typically in the range 1–10 \(\text {s}^{-1}\) for concentrations used in EOR (Sorbie and Huang 1991; Omari et al. 1989; Sorbie 1991). This range of \(\dot{\gamma }_{\text {c}}\) must be compared to the values of \(\dot{\gamma }_{\text {eq}}\) associated with the flow through reservoirs. To estimate \(\dot{\gamma }_{\text {eq}}\), we perform a simple order of magnitude estimation. Let us consider two wells at a distance of about \(500\,\text {m}\) [in off-shore fields the well spacing may even reach \(1500\,\text {m}\) (Morel et al. 2008)]. The thickness of the reservoir is supposed to be \(10\,\text {m}\) and the injection flow rate is about \(20\,\text {m}^{3}\,\text {h}^{-1}\) (Morel et al. 2008). By mass flux conservation, the velocity deep into the reservoir, i.e., halfway between the two wells, can be estimated to about \(3\,\text {cm}\,\text {day}^{-1}\). Using typical values of the permeability (1 Darcy), porosity (0.20), and \(\alpha \) (2.5 Morel et al. (2015)), Eq. 2 yields an order of magnitude for \(\dot{\gamma }_{\text {eq}}\) of \(0.5\,\text {s}^{-1}\). This value is consistent with real oil fields applications (Morel et al. 2015). This suggests that, in a significant part of the reservoir, the flow is primarily Newtonian.

Moreover, several other effects may limit the impact of non-Newtonian rheology. For instance, in some regions of the reservoir, low polymer concentrations may exist (due for instance to a transient regime), which may also limit non-Newtonian effects (Skauge et al. 2015). Concerning HPAM, the strong degradation that polymer molecules undergo when they penetrate the reservoir results in a breakage of the chains, hence lowering the non-Newtonian effects in the bulk rheology of the fluid (Stavland et al. 2010). Finally, the salt hardness and concentration may affect the rheological properties of the solution if the polymer is charged (which is the case for HPAM) (Sorbie 1991). As shown by Seright (2011), the salt concentration in the injected polymer slug can lead to Newtonian-like behavior deep into the reservoir. Under these circumstances, the flow is likely Newtonian in a significant portion of the reservoir.

From the order of magnitude calculation of \(\dot{\gamma }_{\text {eq}}\) combined with these remarks, we conclude that setting the study under the Newtonian flow framework is both fundamentally important and relevant for petroleum engineering applications.

3 The Slip Boundary Condition

The goal of this section is to revisit an effective condition at the pore scale that is derived from the two-fluid model (Blake 1990; Cohen and Metzner 1985). To this end, we will study a model for the flow in a single capillary tube. First, let us consider the flow of a Newtonian fluid through a tube of radius R and length L oriented along \(\mathbf {e}_{z}\). In this tube, the viscosity is described as

$$\begin{aligned} \mu \left( r\right) ={\left\{ \begin{array}{ll} \mu _{\text {layer}} &{} \text {if }R-\delta \le r\le R,\\ \mu _{0} &{} \text {if }0\le r\le R-\delta , \end{array}\right. } \end{aligned}$$
(4)

where \(\mu _{0}\) and \(\mu _{\text {layer}}\) are constant. From Eq. 4, it is assumed that the depleted layer thickness is uniform in the porous medium. In addition, a no-slip condition is imposed at the solid surface. Under these circumstances, as demonstrated by Chauveteau (1982), the filtration velocity of the two-fluid model \(U_{2\text {f}}\) is given by

$$\begin{aligned} U_{2\text {f}}=\frac{R^{2}\varDelta P}{8\mu _{\text {app}}L},\text { with }\mu _{\text {app}}=\frac{\mu _{0}}{1+\left( \varrho -1\right) \left[ 1-\left( 1-\frac{\delta }{R}\right) ^{4}\right] }, \end{aligned}$$
(5)

where \(\varrho \) is the ratio \(\mu _{0}/\mu _{\text {layer}}\) and \(\varDelta P\) is the pressure drop (\(\varDelta P>0\)). The absence of a depletion layer, \(\delta =0\), is a limiting case that leads back to the no-slip case (\(\mu _{\text {app}}=\mu _{0}\) in Eq. 5).

The goal now is to upscale the two-fluid model (Fig. 1b) into an equivalent one-fluid model along with an effective boundary condition (Fig. 1c). The choice for this boundary condition is a Navier slip, which has been widely used in different geometries (Navier 1823; Lasseux et al. 2014). The slip length, which may be considered constant (Brochard and Gennes 1992) or shear rate dependent (Hatzikiriakos and Dealy 1991; Kalyon 2005), is the only control parameter of the boundary condition. To connect this slip length to the mesoscale representation, i.e., the two-fluid model, we compare the flow of a two-fluid model through a single tube and the flow of a one-fluid model with a Navier slip boundary condition. Let us now consider an equivalent fluid with uniform viscosity, \(\mu _{0}\), and a slip boundary condition in the form

$$\begin{aligned} u_{\text {wall}}=-\ell \left. \frac{d\,u}{d\,r}\right| _{\text {wall}}, \end{aligned}$$
(6)

where \(\ell \) is the slip length. The analytic solution of the velocity profile is the sum of the classical Poiseuille flow and a velocity offset. It reads

$$\begin{aligned} u\left( r\right) =u_{\text {wall}}+\frac{R^{2}\varDelta P}{4\mu _{0}L}\left( 1-\left( \frac{r}{R}\right) ^{2}\right) . \end{aligned}$$
(7)

As already calculated by Churaev et al. (1984), the mean velocity over the cross section of the tube in the one-fluid model \(U_{1\text {f}}\) is then

$$\begin{aligned} U_{1\text {f}}= & {} \frac{R^{2}\varDelta P}{8\mu _{0}L}\left( 1+\frac{4\ell }{R}\right) . \end{aligned}$$
(8)

We now seek \(\ell \) so that the average velocity is the same for the one- and two-fluid models in Eqs. 5 and 8. After some simple algebra, \(U_{1\text {f}}=U_{2\text {f}}\) yields

$$\begin{aligned} \ell =\frac{R}{4}\left( \varrho -1\right) \left[ 1-\left( 1-\frac{\delta }{R}\right) ^{4}\right] . \end{aligned}$$
(9)

A key step now consists in assuming that the thickness of the depletion layer is much smaller than the tube radius, which is correct if the pores are much larger than the polymer molecules. This assumption, \(\delta \ll R\), is widely used in the development of mesoscale models and is often verified in practical situations, where R may be estimated for a porous medium by the equivalent radius \(R_{\text {eq}}\) (see Eq. 3). As explained earlier, in this study, we do not recognize \(R_{\text {eq}}\) as a precise geometrical length, but rather as an order of magnitude estimate of a typical pore size. With the assumption \(\delta \ll R\), we can use a Taylor series expansion in Eq. 9 to obtain

$$\begin{aligned} \ell =\delta \left( \varrho -1\right) \left( 1+\mathcal {O}\left( \frac{\delta }{R}\right) \right) \simeq \delta \left( \varrho -1\right) . \end{aligned}$$
(10)

We also recover the limiting case \(\delta =0\) that yields a no-slip condition. Many studies assume further that \(\varrho \gg 1\), so that the slip length reduces to \(\ell =\delta \varrho \) (Cuenca and Bodiguel 2013). However, if incorrect, this simplification could greatly overestimate the slip length, so that we do not use it here. The formulation \(\ell =\delta \left( \rho -1\right) \) is not novel. This formulation has actually already been derived, using either molecular kinetic theory as demonstrated by Tolstoi (1952) [the original paper is in Russian, a translation can be found in Blake (1990)] or, in a similar manner to what we did here, using a creeping flow through a tube (Cohen and Metzner 1985). This expression has also been directly used in the literature (Ma and Graham 2005; Priezjev and Troian 2004; Cuenca and Bodiguel 2013).

With this expression, how do we link \(\ell \) to an apparent viscosity? At this point, considering that \(\delta \) and \(\varrho \) are known, two options are available to predict the apparent viscosity drop for a given sandstone. The first option consists in using the formulation of Chauveteau (1982) (Eq. 5), replacing R by a characteristic length of the porous medium. The major drawback of this approach is that the choice of this characteristic length is somewhat arbitrary. We could choose, by analogy with a capillary tube, the value \(\sqrt{8k_{0}/\epsilon }\), but we might as well choose a geometrical chord length or any other similar metric. We draw the reader’s attention to the fact that, in the paper from Chauveteau (1982), the characteristic length that replaces R in Eq. 5 is calculated such as the apparent viscosity prediction matches the experimental measurements. While for beads packings, \(\sqrt{8k_{0}/\epsilon }\) works quite well to predict \(\mu _{\text {app}}\); for more complex media (such as the Fontainebleau sandstone), the use of this length predicts very poorly the apparent viscosity. This approach is hence limited to simple porous media where the capillary analogy holds.

The second option consists in performing numerical simulations on the image of the sandstone with a Navier slip condition at the interface, where the slip length is defined by Eq. 10. Since the slip length expression is independent from the tube radius, this approach is free of any characteristic length estimation. Despite the fact that both approaches have a similar origin, i.e., assimilating the porous medium to a capillary tube and using a slip length derived from the simple flow in a tube, it is absolutely not obvious that they will lead to the same apparent viscosity prediction. In particular, the slip approach captures the complex geometry of the porous medium, whereas the approach based on a capillary simplifies it. Moreover, the effective slip condition lends itself very well to future improvements. Among them, we could modify the slip length and use a non-uniform expression in the porous medium. In a tube, since the shear rate does not vary along \(\mathbf {e}_{\text {z}}\), considering a uniform slip length is indeed relevant. However, in a real porous medium, under locally high shear rates, polymer molecules may align along the wall with the orientation of the flow field, therefore potentially decreasing the parameter \(\delta \) (Auvray 1981; Sorbie and Huang 1991). In the same manner, the non-Newtonian effects might modify the parameter \(\varrho \) (Omari et al. 1989). These are possible mechanisms that could be taken into account using an effective description of the depletion layer.

To the best of our knowledge, the accuracy of the Navier slip as an effective condition to represent the depletion layer has never been evaluated for numerical applications. Besides, an effective slip condition is commonly used for a variety of interface phenomena to represent the macroscale effects. For instance, microfluidic experiments have shown that red blood cells tend to create a cell-depleted layer near the wall, that also induces an apparent slip effect (Fåhræus and Lindqvist 1931; Sherwood et al. 2012). Gas flow through porous media under low Knudsen number might also be accurately characterized with an effective slip condition (Lasseux et al. 2014). From a fundamental and general point of view, it is hence important to test the validity of such a boundary condition regarding the depletion layer effect.

4 Accuracy of the Effective Model

Here, we assess the accuracy of our model by comparing CFD results to core-flood experimental data obtained from the literature, where the fluid injected into the core is a polymer solution and the apparent viscosity drop has been measured. In this section, parameters related to experimental data are denoted with the superscript XP, while the corresponding parameters related to numerical results are denoted with the superscript CFD.

4.1 Experimental Data from the Literature

Among all the data sets available, we chose to limit our comparison to xanthan flow in beads packings in the studies of Chauveteau (1982) and Sorbie and Huang (1991). We chose beads packings because the complexity of the porous structure is described by a limited number of parameters (primarily, beads size and porosity), therefore allowing us to easily reproduce geometrical features of the system in CFD simulations. For more complex structures, such as Berea, Clashach, or Bentheimer sandstones (Fletcher et al. 1991; Chauveteau 1984), used in experiments where apparent viscosities have actually been measured, we lack information regarding the geometry of these particular structures, which may be fundamental in evaluating the macroscale effect of the depletion layer. We also chose xanthan mainly because the polymer molecules are semi-rigid, as opposed to HPAM molecules for example that are flexible. Flexible molecules yield more complicated physical phenomena [such as entanglement or elasticity as shown by Groisman and Steinberg (2000)]. Obviously, our simple slip model would not be able to capture such complicated effects. In addition, for the selected studies, the sorption of xanthan molecules to the wall was negligible so that the repulsion mechanism dominates and the two-fluid model is relevant.

Finally, we chose the works of Chauveteau (1982) and Sorbie and Huang (1991) because Chauveteau (1982) uses the same polymer solution and changes the characteristics of the porous medium while Sorbie and Huang (1991) always use the same porous medium but with different solutions. Hence, comparison with Chauveteau (1982) allows us to test the robustness of the slip model with respect to the distribution of pore sizes, in particular in the limit where \(R_{\text {eq}}=\mathcal {O}\left( \delta \right) \), whereas comparison with Sorbie and Huang (1991) allows us to evaluate the impact of the depletion layer.

For all the configurations considered, we report in Table 1 the main experimental parameters, i.e., the porous medium characteristics (the minimum \(D_{\text {min}}^{\text {XP}}\) and maximum \(D_{\text {max}}^{\text {XP}}\) beads diameters, the intrinsic permeability \(k_{0}^{\text {XP}}\) which is measured for the flow of the solvent, i.e., without a depletion layer, and porosity \(\epsilon \)), the properties of the depletion layer (\(\delta \) and \(\varrho \)) and the measured apparent viscosity, \(\mu _{\text {app}}^{\text {XP}}\). We note that different methods exist to estimate the thickness of the depletion layer, \(\delta \), and the viscosity ratio, \(\varrho \). To be consistent, for all experimental data sets, we use \(\delta =0.7b\) (where b is the molecular length, valid approximation at low shear rates for rigid molecules (Chauveteau 1984)), and \(\mu _{\text {layer}}\) as to calculate \(\varrho =\mu _{0}/\mu _{\text {layer}}\) [proposed by Chauveteau (1982)]. In the paper from Sorbie and Huang (1991), the polymer concentration is different for all the experimental configurations, implying that \(\varrho \) varies, but the molecular length is always the same, meaning that \(\delta \) remains constant. The slip length associated with each configuration is also calculated according to Eq. 10.

In Table 1, we also report the experimental apparent viscosity drop, . As expected, we observe with the cases from Sorbie and Huang (1991) that the apparent viscosity drop increases with the slip length. On the other hand, in the cases from Chauveteau (1982), the slip length is fixed and \(k_{0}^{\text {XP}}\), or the experimental equivalent radius \(R_{\text {eq}}^{\text {XP}}=\sqrt{8k_{0}^{\text {XP}}/\epsilon }\), varies. We observe that small values of \(k_{0}^{\text {XP}},\) or \(R_{\text {eq}}^{\text {XP}}\), correspond to large values of \(\varDelta \mu _{\text {app}}^{\text {XP}}\). This is because, for a fixed average velocity, the shear rates close to the wall will be larger for the smallest values of \(R_{\text {eq}}^{\text {XP}}\), hence inducing a higher slip velocity.

Table 1 Description of the experimental parameters used in Chauveteau (1982) and Sorbie and Huang (1991). In Chauveteau (1982) (C cases) the depletion layer characteristics are identical, whereas in Sorbie and Huang (1991) (S cases) the porous medium used is the same for all experiments. The experimental apparent viscosity drop is calculated as . All lengths in \(\mu \text {m}\), intrinsic permeability \(k_{0}^{\text {XP}}\) in \(\mu \text {m}^{2}\) and viscosity in cP
Full size table

4.2 CFD Simulations

For CFD simulations, we approximate the flow in the beads packings using face-centered cubic (FCC) packings. In the standard FCC, the porosity is about 0.26 and the beads are in contact. The beads diameter of the generated FCC is denoted by \(D^{\text {CFD}}\). To generate a geometry close to the packings used in the experiments, we first shrank the beads, which are not in contact anymore (see Fig. 3a), until we match the porosity (\(\epsilon ^{\text {XP}}=\epsilon ^{\text {CFD}}=\epsilon \)). Then, we scaled the beads diameter so that (see Tables 1, 2), while preserving the correct porosity.

Fig. 3
figure 3

a Typical porous structure used in the CFD simulations and b grid convergence study, with the error \(E\left( k_{0}\right) \) plotted against the normalized number of cells \(N/N_{\text {max}}\). The final meshes are chosen for an acceptable relative error of about \(0.5\%\)

Full size image

We could have used other methods to produce more realistic beads packings, e.g., generating the packings randomly (Adams and Matheson 1972) or imaging an actual packing via X-ray microtomography. Compared to the experiments, we would have probably obtained a more realistic geometry than the FCC packings (in terms of disorder or tortuosity). However, the aim here is to keep the procedure as simple as possible in order to evaluate whether a Navier slip condition captures the characteristics of the macroscopic flow. Moreover, slip is known to strongly depend on the distribution of pore sizes. For instance, if the slip length is too small compared to the typical geometrical length, the slip effect becomes negligible. Therefore, we expect that to correctly estimate the slip effect, matching the pore size may be more important than matching the spatial organization of the beads or the permeability.

In the liquid phase, denoted by subscript \(\beta \), the flow is described by the incompressible Stokes equations

$$\begin{aligned} \nabla \cdot \left[ \mu _{0}\left( \nabla \mathbf {v_{\beta }}+\left( \nabla \mathbf {v_{\beta }}\right) ^{\mathsf {T}}\right) \right] -\nabla p_{\beta }+\mathbf {f}=0, \end{aligned}$$
(11)

along with \(\nabla \cdot \mathbf {v_{\mathrm {\beta }}}=0\), where \(\mathbf {f}\) is a source term, playing the role of \(-(\nabla P-\rho {\mathbf {g}})\) in Eq. 1. For the solid/liquid interface, which we note \(A_{\beta \sigma }\) (\(\sigma \) is the solid), we use the Navier (1823) slip boundary condition,

$$\begin{aligned} \mathbf {v_{\mathrm {\beta }}}=-\ell \,\left[ \mathbf {n}\cdot \left( \nabla \mathbf {v_{\beta }}+\left( \nabla \mathbf {v_{\beta }}\right) ^{\mathsf {T}}\right) \right] \cdot \left( \mathsf {I-\mathbf {nn}}\right) , \end{aligned}$$
(12)

where \(\mathbf {n}\) is the unit normal vector to the surface directed from \(\beta \) to \(\sigma \). For the external boundaries, periodic conditions are applied to both the velocity and pressure.

These equations are solved using the finite volume toolbox OpenFOAM (Weller et al. 1998) via a SIMPLE algorithm originally developed by Patankar (1980). Since the grids are collocated (pressure and velocity are calculated at the same point), a Rhie–Chow type interpolation (Rhie and Chow 1983) is employed during the pressure correction steps in OpenFOAM, by estimating the pressure gradient on the cell faces with the pressure values of the neighboring cell centers. This Rhie-Chow method prevents the solution from becoming unstable, by enforcing the pressure/velocity coupling in the course of the SIMPLE algorithm [see a detailed description in Nordlund et al. (2016)].

Table 2 Description of the numerical cases investigated and the associated results. The relative difference is \(E\left( \mu \right) =\frac{\mu _{\text {app}}^{\text {CFD}}-\mu _{\text {app}}^{\text {XP}}}{\mu _{\text {app}}^{\text {XP}}}\). All lengths in \(\mu \text {m}\), intrinsic permeability \(k_{0}^{\text {CFD}}\) in \(\mu \text {m}^{2}\) and viscosity in cP
Full size table

To assess numerical convergence, several unstructured hex-dominant meshes (from coarse to fine) were generated, and the accuracy of the associated solutions is evaluated using a convergence error estimate of the no-slip permeability \(k_{0}^{\text {CFD}}\),

$$\begin{aligned} E\left( k_{0}\right) =\frac{k_{0}^{\text {CFD}}-k_{0\text {finest}}^{\text {CFD}}}{k_{0\text {finest}}^{\text {CFD}}}, \end{aligned}$$
(13)

where \(k_{0\text {finest}}^{\text {CFD}}\) corresponds to the finest calculation of the intrinsic permeability. The number of cells in the finest grid is denoted as \(N_{\text {max}}\) and is about 26 millions. Figure 3b shows the error estimate decreasing with the number of cells. The final chosen grids for our CFD simulations contain about 3 million cells.

Using the final chosen grids, we calculated for each case of Table 2 the intrinsic permeability tensor \(\mathsf {K_{0}^{\text {CFD}}}\), defined with a no-slip boundary condition at \(A_{\beta \sigma }\). Since the medium is isotropic and the momentum transport operator is linear (Eq. 11), the permeability tensor can be written as \(\mathsf {K_{0}}=k_{0}^{\text {CFD}}\mathsf {I}\). In the CFD simulations, we impose the source term \(\mathbf {f}\) along the spatial direction \(\mathbf {e}_{z}\), \(\mathbf {f}=f\mathbf {e}_{z}\), yielding an average velocity \(\mathbf {U}=U\mathbf {e}_{z}\). The apparent permeability is then simply calculated with Eq. 1 as .

4.3 Results and Discussion

Numerical simulations with and without slip are used to estimate the apparent viscosity \(\mu _{\text {app}}^{\text {CFD}}\) and perform a comparison with its experimental value \(\mu _{\text {app}}^{\text {XP}}\). We calculate the relative difference

$$\begin{aligned} E\left( \mu \right) =\frac{\mu _{\text {app}}^{\text {CFD}}-\mu _{\text {app}}^{\text {XP}}}{\mu _{\text {app}}^{\text {XP}}}. \end{aligned}$$
(14)
Fig. 4
figure 4

Comparison of experimental and numerical results via the dimensionless viscosity \(E\left( \mu \right) =\frac{\mu _{\text {app}}^{\text {CFD}}-\mu _{\text {app}}^{\text {XP}}}{\mu _{\text {app}}^{\text {XP}}}\). The averaged value of \(E\left( \mu \right) \) is about \(-4.4\%\) for Chauveteau (1982) and \(3.5\%\) for Sorbie and Huang (1991)

Full size image

Results are summarized in Table 2 and \(E\left( \mu \right) \) is plotted in Fig. 4. Since our porous medium is idealized in the CFD simulations, we further introduce uncertainties to facilitate the comparison with experiments:

  • First, in the FCC packings, the beads are perfectly ordered which is not the case in the experiments. In order to evaluate the uncertainty induced by this, we randomly shifted the position of the beads, authorizing contact between beads, and simulated the flow through these geometries. We find that the influence of disorder is rather small (less than \(1\%\) change in the apparent viscosity).

  • Second, there is a distribution of beads sizes in the experiments (unknown since only a range is reported in the papers) that is not captured by the FCC structures. To estimate the uncertainty associated with the distribution of sizes, we simulated the flow through FCC packings with beads size \(D^{\text {CFD}}\) corresponding to \(D_{\text {min}}^{\text {XP}}\) and \(D_{\text {max}}^{\text {XP}}\) reported in the papers. We find that the influence of the beads size on \(\mu _{\text {app}}^{\text {CFD}}\) can be significant, with differences up to \(12\%\).

Figure 4 shows that, for the mean values, CFD simulations in FCC packings provide an accurate estimation of the apparent viscosity, with an error below \(10\%\) for most cases. We also emphasize that, even though the estimation of the apparent viscosity is accurate, the permeability prediction is less accurate. We observe indeed that the ratio of permeability between CFD and experiments varies between 0.75 and 1.20 for the study of Chauveteau (1982) and is about 2 for the paper from Sorbie and Huang (1991). We note that in the paper from Sorbie and Huang (1991), the accuracy of the intrinsic permeability measurement is lower than in the paper from Chauveteau (1982).

The question then arises: What would have been the apparent viscosity prediction if we had chosen \(D^{\text {CFD}}\) such as \(k_{0}^{\text {CFD}}=k_{0}^{\text {XP}}\)? We tested this configuration and found that the predictions were always in the range of the error bars plotted in Fig. 4 (except for medium C1, where the error is extremely small anyway). For instance, for the media in Sorbie and Huang (1991), tuning \(D^{\text {CFD}}\) so that the experimental and numerical permeabilities are matched actually leads to \(D^{\text {CFD}}\simeq D_{\text {min}}^{\text {XP}}\), which corresponds to the lowest part of the error bar. While this choice improves the prediction for some media, it also makes it worse for other media. The arbitrary choice of \(D^{\text {CFD}}\) such as \(k_{0}^{\text {CFD}}=k_{0}^{\text {XP}}\) is thus not better than . For the reason explained above, we prefer to compare porous media that have the same geometrical characteristic length rather than the same permeability.

Interestingly, the only case for which the error is over \(10\%\) corresponds to a configuration where \(R_{\text {eq}}^{\text {CFD}}\) is small and for which we have the largest uncertainty. For the results of Chauveteau (1982), Fig. 4 also shows that the accuracy of the model is the poorest for media C6 and C7 and tends to increase with \(R_{\text {eq}}^{\text {CFD}}\). While the assumption \(\delta \ll R_{\text {eq}}^{\text {CFD}}\) is necessary to obtain the expression of the slip length, the ratio gets close to unity for media C6 and C7 (see Table 2). We hypothesize that this is the cause of the observed inaccuracies. When the polymer size is close to the size of the pores (\(R_{\text {eq}}^{\text {CFD}}=\mathcal {O}\left( \delta \right) \)), the physics involved might indeed be very different, and a pore-scale description of the polymer solution as a continuum could be irrelevant. On the other hand, in the configurations from Sorbie and Huang (1991), \(R_{\text {eq}}^{\text {CFD}}\) is fixed and the assumption \(\delta \ll R_{\text {eq}}^{\text {CFD}}\) is always verified. Hence, we can focus on the dependence of \(E\left( \mu \right) \) on the slip length. We observe no clear trend of \(E\left( \mu \right) \) with respect to \(\ell \). We conclude that the accuracy of the model is not sensitive to the slip length.

Finally, it is important to keep in mind the following. Firstly, other phenomena may occur that are not described by our model, such as the retention of polymer molecules (Huh et al. 1990), or microgels (Chauveteau and Kohler 1984). Moreover, when the flow regime is high enough, non-Newtonian effects should be taken into account. This would result in \(E\left( \mu \right) \) being a function of the average velocity. Secondly, the effective condition is based on the two-fluid model that is a relatively crude description of the depletion layer (because of the discontinuous concentration field). Finally, experimental uncertainties were not clearly quantified in the studies of Chauveteau (1982) and Sorbie and Huang (1991). Despite this, values of \(E\left( \mu \right) \) are below 10% in most cases, and we conclude that our approach for calculating the slip length provides a good first-order estimation of the apparent viscosity.

5 Summary and Conclusions

Polymer molecules can arrange and interact with the solid/liquid interface in a variety of ways. At the molecular scale, one of these rearrangements is a repulsion mechanism of polymer molecules from the wall, creating a depletion layer acting as a lubricating film. At the macroscale, this effect can be described using an apparent viscosity in Darcy’s law that is lower than the bulk viscosity. There are several practical situations where this interfacial effect is predominant in the macroscale flow behavior, such as polymer injection for EOR. Therefore, it is important to have available a rapid and simple tool to quantify the relative contribution of the depletion layer with respect to other phenomena associated to polymer.

In this paper, we have investigated the accuracy of an effective slip condition in capturing the apparent viscosity drop. We first revisited the formulation \(\ell =\delta \left( \varrho -1\right) \), where \(\delta \) is the thickness of the depletion layer and \(\varrho \) the ratio of viscosity between the bulk fluid and the depletion layer. We then assessed the accuracy of this effective condition by comparing viscosity drops obtained in core-flood experiments in Chauveteau (1982) and Sorbie and Huang (1991) to CFD calculations in model geometries. We found that in most cases the effective condition predicts the apparent viscosity with an error below \(10\%\). This method only requires the parameters \(\delta \), \(\varrho \) and an image of the porous medium. Therefore, this simple expression of the slip length in the Navier boundary condition may be used as a quick way to evaluate the macroscale apparent viscosity drop.

Several subsequent investigations may follow from the proposed numerical methodology. For instance, we validated the proposed methodology with beads packing, where the complexity of the porous structure is moderate compared to natural media, such as sandstones. However, the main advantage of the effective condition approach is that it deals with the actual pore-scale structure instead of simplifying it. Therefore, if the geometry of the medium is available, we assume that the effective slip condition would yield a similar accuracy when applied to natural porous media. However, this is a conjecture, and it requires further investigations.

A step further would also be to assess the impact of non-Newtonian effects on the Navier slip length and the impact of this effective slip on the macroscale transition between Newtonian and non-Newtonian regimes (Zami-Pierre et al. 2016). In addition, an advantage of the slip formulation, as opposed to the two-fluid model, is its ability to deal with a non-uniform depletion layer. For instance, the viscosity ratio \(\varrho \) may be treated as a function of the local concentration field or profile (Ausserre et al. 1986; Chauveteau 1982) in future work. Likewise, as suggested by Sorbie and Huang (1991), \(\delta \) may vary with the local wall shear rate.