Geostrophic Drag Law in Conventionally Neutral Atmospheric Boundary Layer: Simplified Parametrization and Numerical Validation

Abstract

This study investigates the parameterization of the geostrophic drag law (GDL) for conventionally neutral atmospheric boundary layers (CNBLs). Utilizing large eddy simulations, we confirm that in CNBLs capped by a potential temperature inversion, the boundary-layer height scales as $u_*/\sqrt{N f}$, where $u_*$ represents the friction velocity, N the free-atmosphere Brunt–Väisälä frequency, and f the Coriolis parameter. Additionally, we confirm that the wind gradients normalized by the Brunt–Väisälä frequency have universal profiles above the surface layer. Leveraging these physical insights, we derived analytical expressions for the GDL coefficients A and B, correcting the earlier form of Zilitinkevich and Esau (Q J R Meteorol Soc 131:1863–1892, 2005). These expressions for A and B have been validated numerically, ensuring their accuracy in representing the geostrophic drag coefficient $u_*/G$ (G is the geostrophic wind speed) and the cross-isobaric angle. This work extends the range for which the GDL has been validated up to $u_*/G =[0.019, 0.047]$. This further supports the application of GDL to CNBLs over a broader range of $u_*/G$, which is useful for meteorological applications such as wind energy.

1 Introduction

The atmospheric boundary layer (ABL) is the lower part of the troposphere where most human activity and biological processes occur (Katul et al. 2011). The flow dynamics in the ABL are influenced by the Earth’s surface, Coriolis force, and thermal stratification (Monin 1970). When the potential temperature flux on the surface is approximately negligible and the flow develops against a stable background stratification, the ABL is considered conventionally neutral (CNBL, Zilitinkevich and Esau 2002). CNBLs are commonly observed, for example, over sea, above large lakes, and over land during the transition period after sunset or on cloudy days with powerful winds (Allaerts and Meyers 2017; Liu and Stevens 2022)

For simplicity, we neglect the effects of baroclinicity, clouds, subsidence, and nonstationarity and focus on the Northern Hemisphere, where the Coriolis parameter $f>0$. Then, it follows from dimensional analysis that the dynamics in CNBLs are governed by two independent dimensionless parameters, e.g. the Rossby number $Ro=u_*/(f z_0)$ and the Zilitinkevich number $Zi=N/f$ (Esau 2004), where $u_*$ is the friction velocity, $z_0$ is the roughness length, and N is the free-atmosphere Brunt–Väisälä frequency. Note that the ratio N/f is sometimes called the inverse Prandtl ratio (Dritschel and McKiver 2015) and is closely related to the square root of the slope Burger number (Shapiro and Fedorovich 2008). In this study, the coordinate system is oriented such that the streamwise direction is parallel to the wind direction at the surface, and the spanwise direction is orthogonal to the streamwise and vertical directions. Thus, the geostrophic drag law (GDL) for CNBLs can be written as (e.g. Zilitinkevich and Esau 2005; Liu et al. 2021a),

$$\begin{aligned} A(Zi)= & {} \ln Ro - \frac{\kappa U_g}{u_*}, \end{aligned}$$

(1a)

$$\begin{aligned} B(Zi)= & {} - \frac{\kappa V_g}{u_*}, \end{aligned}$$

(1b)

where $\kappa = 0.4$ is the von Kármán constant, A and B are the GDL coefficients,¹ and $(U_g, V_g)$ are the streamwise and spanwise components of the geostrophic wind. If the expressions of A and B are already known, the geostrophic drag coefficient $u_*/G$, where $G=(U_g^2+V_g^2)^{1/2}$ is the geostrophic wind speed, and the cross-isobaric angle $\alpha _0 = \arctan \, (|V_g/U_g|)$ can be determined from Eq. (1).

In general, the GDL coefficients A and B can be parameterized through two approaches. One is by first parameterizing the eddy viscosity (Ellison 1955; Krishna 1980; Kadantsev et al. 2021), and the other is by first parameterizing the mean wind velocity (Zilitinkevich 1989a, b; Zilitinkevich et al. 1998; Narasimhan et al. 2024). Then, an asymptotic matching technique is used to determine the final expressions of the GDL coefficients A and B. For example, Ellison (1955) derived analytical expressions for A and B by solving the Ekman equations under the assumption of a linear eddy viscosity profile throughout the boundary layer. Zilitinkevich (1989b, 1989a) used log-polynomial approximations for the wind and temperature profiles in combination with the requirement that these are asymptotically consistent with the well-established Monin–Obukhov surface-layer flux-profile relationships to obtain the GDL and heat transfer laws for stable ABLs. Zilitinkevich et al. (1998) extended the ideas of Zilitinkevich (1989a, 1989b) to account for the effect of static stability in the free flow above the ABL. They expressed the GDL coefficients A and B with composite stability parameters, which are constructed through the interpolation between the Ekman length scale $L_f=u_*/f$ (Ekman 1905), the external static-stability length scale $L_n=u_*/N$ (Kitaigorodskii and Joffre 1988), and the Obukhov length scale $L_s = -u_*^3/(\kappa \beta q_s)$ (Obukhov 1946) with $q_s$ denoting the surface heat flux and $\beta =g/\theta _0$ the buoyancy parameter. Here, g is the gravity acceleration and $\theta _0$ is the reference potential temperature. Later, Zilitinkevich and Esau (2005) proposed the general expressions of the coefficients A and B for stable ABLs and CNBLs,

$$\begin{aligned} A= & {} -a m_A + \ln \, (a_0 + m_A) - \ln \left( \frac{f h}{u_*} \right) , \end{aligned}$$

(2a)

$$\begin{aligned} B= & {} \frac{f h}{u_*} (b_0 + b m_B^2). \end{aligned}$$

(2b)

Here $(a, a_0, b, b_0)$ are empirical constants, and $(m_A, m_B)$ are the composite stratification parameters for the coefficients (A, B), respectively,

$$\begin{aligned} \frac{m_A^2}{h^2}= & {} \frac{1}{L_s^2} + \frac{c_{na}^2 }{L_n^2} + \frac{c_{fa}^2 }{L_f^2}, \end{aligned}$$

(3a)

$$\begin{aligned} \frac{m_B^2}{h^2}= & {} \frac{1}{L_s^2} + \frac{c_{nb}^2 }{L_n^2} + \frac{c_{fb}^2 }{L_f^2}, \end{aligned}$$

(3b)

where $(c_{fa},c_{fb}, c_{na},c_{nb})$ are empirical constants.

To obtain analytic expressions for A and B, the boundary-layer height h in Eqs. (2) and (3) has to be parameterized. In general, two ABL-depth scales were proposed for the ABL dominated by the static stability aloft: one is $h \propto u_*/\sqrt{Nf}$ (Pollard et al. 1973), and the other is $h \propto u_*/N$ (Kitaigorodskii and Joffre 1988). Using energy considerations, Zilitinkevich and Mironov (1996) developed a simple equation for the equilibrium height of the stable ABLs, and gave a comprehensive discussion of the CNBL-depth scales. In particular, they advocated the scale $u_*/N=L_n$, where the ABL depth ceases to depend on the Coriolis parameter if the static stability is sufficiently strong. Note that this scaling has also been demonstrated by Pedersen et al. (2014) using large eddy simulations (LES). Using momentum considerations, Zilitinkevich et al. (2002) advocated the scale $u_*/\sqrt{ Nf }$, where the ABL depth depends on the Coriolis parameter regardless of the strength of static stability. Mironov and Fedorovich (2010) revisited this problem and obtained a more general power-law formulation for the CNBL depth, viz., $h/L_n \propto (N/f)^\delta$, where $\delta$ is the exponent. With $\delta =0$ and $\delta =1/2$, the formulations by Kitaigorodskii and Joffre (1988) and by Pollard et al. (1973), respectively, are recovered. However, as convincingly argued by Mironov and Fedorovich (2010), $\delta$ can assume any value in the range $0\le \delta < 1$. Importantly, $\delta$ cannot be determined by dimensional analysis. An exact solution to the problem in question is needed, which is still an active research topic. For example, Zilitinkevich et al. (2007, 2012) usually parameterized the boundary-layer height h as:

$$\begin{aligned} \frac{L_f^2}{h^2} = \frac{1}{c_r^2} + \frac{Zi}{c_n^2} + \frac{\mu }{c_s^2}, \end{aligned}$$

(4)

where $(c_r, c_n, c_s)$ are empirical constants and $\mu =L_f/L_s$ is the Kazanski-Monin parameter (Kazanski and Monin 1961). Note that for CNBLs Eq. (4) has been well validated against simulations (Liu et al. 2021a) and field measurement data (Uttal et al. 2002; Zilitinkevich and Esau 2009).

The A and B coefficients from the GDL play a critical role in estimating available wind resources at higher altitudes through vertical extrapolation (Gryning et al. 2007; Kelly and Gryning 2010; Kelly and Troen 2016) or at different sites through horizontal extrapolation (Troen and Petersen 1989; Kelly and Jørgensen 2017), and in predicting the turbulent flows over wind farms (Li et al. 2022) and canopies. Liu et al. (2021a) numerically revisited the analytical expressions of A and B for CNBLs proposed by Zilitinkevich and Esau (2005). As they found significant deviations between the simulation results and the original parameterization of the GDL, the authors updated the empirical constants involved in Eqs. (2)-(4). In their simulations, only the free atmospheric lapse rate and latitude were varied, and thus only a limited range of the geostrophic drag coefficient was covered. Liu et al. (2021b) performed simulations by varying the lapse rate and roughness length, but they considered only six cases and didn’t investigate the GDL. To further evaluate the validity of the GDL, systematic simulations that cover a wide range of atmospheric parameters are required, which we provide in this study.

The GDL parameterization of Eqs. (2)–(4) has a relatively complicated form, which includes ten empirical constants for CNBLs. This poses significant challenges in determining the values of these empirical constants. For example, Liu et al. (2021a) had to empirically determine the values for a and b such that the asymptotic behavior of A and B is well captured in the high Zi limit, and the correction constants $a_0$ and $b_0$ are set such that A and B also capture the low Zi limit well. Although this approach sometimes works, it is difficult to adapt to other flow configurations, such as wind farms or canopy flows, as it requires a lot of data and is technically challenging. As a compromise, Li et al. (2022) had to resort to numerically fitting the GDL coefficients instead of analytically updating the GDL to wind farm flows. Therefore, it is necessary to further investigate the GDL for CNBLs theoretically.

The organization of the paper is as follows. In Sect. 2 we derive analytical expressions of A and B. In Sect. 3 we discuss the numerical method and LES setup for CNBLs, which covers a much wider range of $u_*/G$ than considered previously. In Sect. 4 we validate the derived expressions of A and B with the simulation data. In Sect. 5 we compare the geostrophic drag coefficient and the cross-isobaric angle obtained from the simulations and theoretical predictions. We conclude with a summary of the main findings in Sect. 6.

2 Theoretical Model

2.1 Parametrization of the Boundary-Layer Height

In this study, we use the boundary layer height parametrization proposed by Pollard et al. (1973). We adopt this parametrization as it is derived from momentum considerations, which also form the basis of the GDL derivation. Therefore, we parameterize the boundary-layer depth as:

$$\begin{aligned} \frac{h}{L_n} = c_n \sqrt{Zi}, \end{aligned}$$

(5)

where the constant $c_n=2^{3/4}$ is determined theoretically by Pollard et al. (1973). Note that Eq. (5) is an asymptotic case of Eq. (4) since the middle term of Eq. (4) becomes the dominant one for $Zi \gg 1$.

2.2 Analytical Expression of A

We first determine the expression of A. In the surface layer, the mean streamwise velocity U can be written as:

$$\begin{aligned} \frac{\kappa U}{u_*} = \ln \left( \frac{z}{z_0} \right) . \end{aligned}$$

(6)

Above the surface layer, Zilitinkevich and Esau (2005) assumed the streamwise velocity gradient scales as N,

$$\begin{aligned} \frac{1}{N} \frac{\text {d} U}{\text {d} z} = \frac{1}{\kappa } f_u(\xi ), \quad \xi =\frac{z}{h}, \end{aligned}$$

(7)

where $f_u$ is presumed to be independent of Ro and Zi. We remark that Liu and Stevens (2022) derived an analytical expression of U that is valid in the entire boundary layer, which indicates that $f_u$ is independent of Ro. However, the independence of $f_u$ from Zi is only valid asymptotically when $Zi\gg 1$. Despite this, we continue to use Eq. (7) to derive the analytical expression for A, evaluating its performance for $Zi \gg 1$.

Integrating Eq. (7) from a height z to the top of the boundary layer, we find:

$$\begin{aligned} \frac{\kappa }{u_*} [U_g - U(z)] = \frac{ h}{L_n} \int _\xi ^1 f_{u} \mathrm d \xi '. \end{aligned}$$

(8)

We further assume the mean streamwise velocity given by Eqs. (6) and (8) matches at some height $\xi =L_n/(c_1 h)$, where $c_1$ is an empirical constant. Thus, by substituting Eq. (6) into Eq. (8), there is:

$$\begin{aligned} \frac{\kappa U_g}{u_*} = \ln \left( \frac{L_n}{c_1 z_0} \right) + \frac{ h }{L_n} \int _{ \frac{L_n}{c_1 h} }^1 f_{u} \mathrm d \xi '. \end{aligned}$$

(9)

Finally, substituting Eqs. (1a) and (5) into Eq. (9) and noting that $L_f/L_n=Zi$, we obtain:

$$\begin{aligned} A = \ln \, (c_1 Zi) - a_1 \sqrt{Zi}, \end{aligned}$$

(10)

where $a_1 = c_n \int _{ \frac{1}{c_1 c_n \sqrt{Zi}} }^1 f_{u} \text {d} \xi '$. Although $a_1$ may depend slightly on Zi, we assume it to be constant for simplicity. Note that this assumption implies that $U_g/(hN)$ retains a Zi-dependence.

We remark that, Eq. (10) is the same as the first expression of Eq. (39) in Zilitinkevich and Esau (2005), which is an asymptotic expression corresponding to $Zi \gg 1$. Due to its relatively simple form, the performance of Eq. (10) at both moderate and high values of Zi is evaluated below. In addition, by substituting Eq. (5) into Eq. (2a), we get $A = \ln \, (c_{na} Zi) - a c_{na} c_n \sqrt{Zi}$ in the limit $Zi \gg 1$, which is the same as Eq. (10) when $c_{na}=c_1$ and $a c_{na} c_n =a_1$. This indicates that the introduction of the correction constant $a_0$ is not necessary for CNBLs.

2.3 Analytical Expression of B

To determine the analytical expression of B, we recall that:

$$\begin{aligned} \frac{\textrm{d} \tau _y}{\textrm{d} z} = f (U-U_g), \end{aligned}$$

(11)

where $\tau _y$ is the spanwise component of the total shear stress tensor. First, we focus on the surface layer. Then, by substituting Eq. (6) into Eq. (11) and combining the result with Eq. (1a) there is:

$$\begin{aligned} \frac{\kappa }{f u_*} \frac{\textrm{d} \tau _y}{\textrm{d} z} = A + \ln \left( \frac{z}{L_f} \right) . \end{aligned}$$

(12)

The bottom boundary condition of Eq. (12) is $\tau _y(0)=0$. Integrating Eq. (12) from 0 to z, one can obtain:

$$\begin{aligned} \frac{\kappa \tau _y}{f u_*} = \left[ A-1 + \ln \left( \frac{z}{L_f} \right) \right] z. \end{aligned}$$

(13)

In the surface layer the eddy viscosity approach is valid, such that:

$$\begin{aligned} \tau _y = K_m \frac{\textrm{d} V}{\textrm{d} z}, \quad K_m = \kappa u_* z, \end{aligned}$$

(14)

where V is the spanwise velocity. By combining Eqs. (13) and (14), there is:

$$\begin{aligned} \frac{\kappa ^2 }{f } \frac{\textrm{d} V}{\textrm{d} z} = A-1 + \ln \left( \frac{z}{L_f} \right) . \end{aligned}$$

(15)

The bottom boundary condition of Eq. (15) is $V(0)=0$. Then, by integrating Eq. (15) from 0 to z one can determine the mean spanwise velocity V in the surface layer as:

$$\begin{aligned} \frac{\kappa ^2 V}{f} = \left[ A-2 + \ln \left( \frac{z}{L_f} \right) \right] z. \end{aligned}$$

(16)

Next, similar to the derivation of A, we also assume the spanwise velocity gradient scales as N,

$$\begin{aligned} \frac{1}{N} \frac{\textrm{d} V}{\textrm{d} z} = - \frac{1}{\kappa } f_v(\xi ), \end{aligned}$$

(17)

where $f_v$ is independent of Ro and Zi. Integrating Eq. (17) from a height z to the top of the boundary layer, there is:

$$\begin{aligned} \frac{\kappa }{u_*} (V_g - V) = - \frac{h}{L_n} \int _\xi ^1 f_v \mathrm d \xi '. \end{aligned}$$

(18)

We further assume the mean spanwise velocity given by Eqs. (16) and (18) matches at the height $\xi =L_n/(c_2 h)$, where $c_2$ is an empirical constant. Thus, by substituting Eq. (16) into Eq. (18), we find:

$$\begin{aligned} \frac{\kappa V_g}{u_*} = \frac{L_n}{\kappa c_2 L_f} \left[ A-2 + \ln \left( \frac{L_n}{c_2 L_f} \right) \right] - \frac{ h }{L_n} \int _{ \frac{L_n}{c_2 h} }^1 f_{v} \text {d} \xi '. \end{aligned}$$

(19)

Finally, substituting Eqs. (1b), (5) and (10) into Eq. (19) and noting that $L_f/L_n=Zi$, we find:

$$\begin{aligned} B = \frac{2 + \ln \, (c_2/c_1)}{\kappa c_2 Zi} + \frac{ a_1 }{\kappa c_2 \sqrt{Zi}} + b_1 \sqrt{Zi}, \end{aligned}$$

(20)

where $b_1 = c_n \int _{ \frac{1}{c_2 c_n \sqrt{Zi}} }^1 f_{v} \mathrm d \xi '$. Similar to $a_1$, we assume $b_1$ to be constant.

We remark that, Eq. (20) is different from the second expression of Eq. (39) in Zilitinkevich and Esau (2005). In the derivation of Zilitinkevich and Esau (2005) the spanwisve velocity is not continuous across different layers. As a result, their expression includes only the final term of Eq. (20), while the first two terms are omitted. As shown below, the prediction of Zilitinkevich and Esau (2005) with only the final term of Eq. (20) leads to significant deviations at moderate values of Zi. On the other hand, by substituting Eq. (5) into Eq. (2b), we find that $B = {b_0 c_n}/{ \sqrt{Zi} } + b c_{nb}^2 c_n^3 \sqrt{Zi}$ in the limit $Zi \gg 1$. Meanwhile, in the limit $Zi \gg 1$ the 1/Zi term in Eq. (20) will be smallest and thus Eq. (20) can be approximated as $B=a_1 / (\kappa c_2 \sqrt{Zi}) + b_1 \sqrt{Zi}$. Clearly, these two expressions are the same when $b_0 c_n = a_1 / (\kappa c_2)$ and $b c_{nb}^2 c_n^3 = b_1$. This indicates that the introduction of the correction constant $b_0$ in Eq. (2b) is to improve the prediction of B using Eq. (2b) at moderate values of Zi.

3 Large-Eddy Simulation

Using state-of-the-art LES, Liu et al. (2021a) simulated the CNBL flow over an infinite flat surface with homogeneous roughness. These simulations are used to determine the empirical constants in the original GDL parameterization of Zilitinkevich and Esau (2005). However, in that study only the free atmospheric lapse rate and the latitude were varied, and thus only a very narrow range of the geostrophic drag coefficient $(u_*/G)$ was covered. To evaluate the validity of the GDL in practical applications, extended simulations that cover a wide range of atmospheric parameters are required. Therefore, we perform 19 new LES in which we vary the free-atmosphere lapse rate $(\varGamma )$, the latitude $(\phi )$, the geostrophic wind speed (G), and the roughness length $(z_0)$. This extends the range of $u_*/G$ in simulations from [0.019, 0.026] up to [0.019, 0.047], which covers about half of commonly observed values in atmospheric measurements (Hess and Garratt 2002a, b; van der Laan et al. 2020).

The code used to solving the flow field is the same as that adopted by Liu et al. (2021a), which originates from the work by Albertson (1996), and later contributions by Bou-Zeid et al. (2005), Calaf et al. (2010), and many others. The grid points are uniformly distributed, and the computational planes for horizontal and vertical velocities are staggered in the vertical direction. A second-order finite difference method is used in the vertical direction, while a pseudo-spectral discretization with periodic boundary conditions is employed in the horizontal directions. Time integration is performed using the second-order Adams-Bashforth method (Canuto et al. 1988). The projection method is used to ensure the divergence-free condition of the velocity field (Chorin 1968). At the top boundary the vertical velocity, the sub-grid scale shear stress and potential temperature flux are enforced to zero, while the potential temperature gradient is imposed by a constant value. In the top 25% of the domain a Rayleigh damping layer is used to reduce the effects of gravity waves (Klemp and Lilly 1978). At the bottom boundary, we employ a wall model based on the Monin-Obukhov similarity theory for both the velocity and potential temperature fields (Moeng 1984; Stoll and Porté-Agel 2008).

Similar to Liu et al. (2021a), the computational domain size is $2\pi \, \textrm{km} \times 2\pi \, \textrm{km} \times 2\, \textrm{km}$ in streamwise, spanwise, and vertical directions, respectively, and the corresponding grid points are $288\times 288\times 281$. Pedersen et al. (2014) demonstrated that for CNBLs convergence is obtained in much coarser meshes than required for stable boundary layer simulations. In our previous work (Liu et al. 2021a, b) we studied grid convergence and obtained similar conclusions, showing that the employed grid resolution used here is sufficient. The horizontal domain size is at least six times larger than the boundary layer height such that long streamwise structures are captured appropriately for all cases. The initial potential temperature profile is $\theta (z) = \theta _0 + \varGamma z$, where $\theta _0 = 300$ K and $\varGamma = 0.001\sim 0.009$ K $\hbox {m}^{-1}$. The initial velocity profile is set as the geostrophic wind $G=6\sim 20$ m $\hbox {s}^{-1}$. The latitude is $\phi =10\sim 50^\circ$ and the roughness length is $z_0=0.0007\sim 0.32$ m. To reduce the impact of inertial oscillations, we run the simulations for a long duration with respect to the Coriolis parameter. As shown in Liu et al. (2021a), friction velocity and cross-isobaric angle show very limited oscillations when the dimensionless time $ft>9$, which is consistent with the conclusion of Pedersen et al. (2014) that the mean momentum equations reach a steady state balance after $ft>6$. Furthermore, we note that in Liu et al. (2021a) we averaged over a time span $\varDelta (ft) =1$, while in Liu et al. (2021b) we averaged over $\varDelta (ft)= 2\pi$. The comparison of these data in Figs. 4 and 5 below demonstrates that the inertial oscillations has been significantly damped. Therefore, statistics are collected over the interval $ft \in [9, 10]$, where the boundary layer has reached a quasi-stationary state. A summary of these simulations is given in Table 1, where $G=( U_g^2+V_g^2 )^{1/2}$ is the geostrophic wind speed, $\alpha _0= \arctan \, (|V_g/U_g|)$ is the cross-isobaric angle (i.e. the total wind angle change across the boundary layer), and h is the boundary layer height.

It is worth noting that the boundary layer height can be defined based on the vertical profiles of total turbulent stress, wind speed, potential temperature flux, or potential temperature (Abkar and Porté-Agel 2013; Allaerts and Meyers 2015; Kelly et al. 2019). For example, one of the commonly accepted definitions of the boundary layer height is $h_{0.05}$, which is defined as the height where the total turbulent stress is 5% of its wall value. In this study, we also define the boundary layer height h based on the vertical profile of total turbulent stress. However, since the total shear stress follows a power law with exponent 3/2 (Nieuwstadt 1984), a more appropriate definition of the boundary-layer height is $h=h_{0.05}/(1-0.05^{2/3})$, which is the height where the total turbulent stress first reduces to zero (van Dop and Axelsen 2007; Liu et al. 2021b).

Table 1 The table summarizes the present simulations

4 Model Validation

4.1 The Boundary-Layer Height and Wind Gradients

Figure 1 compares the dimensionless boundary-layer height $h/L_n$ obtained from atmospheric measurements (Uttal et al. 2002), numerical simulations (Zilitinkevich et al. 2007; Liu et al. 2021a), and theoretical predictions. The good agreement confirms that the boundary-layer height h is indeed parameterized well by Eq. (5). Since $Zi=N/f$ and $L_n=u_*/N$, Eq. (5) also indicates that $h/(u_*/\sqrt{Nf}) = c_n$, i.e. the boundary-layer height h scales as $u_*/\sqrt{Nf}$. This result is in agreement with Pedersen et al. (2014), who demonstrated that the scaling of the boundary layer height with Zi remains constant over time after reaching the statistically stationary state ($ft>6$).

Fig. 1

The dimensionless boundary-layer height $h/L_n$ versus the Zilitinkevich number Zi. Solid line: theoretical curve by Eq. (5) with $c_n=2^{3/4}$; diamonds: simulation data of Table 1; circles: simulation data of Liu et al. (2021a); triangles: simulation data of Zilitinkevich et al. (2007); squares: atmospheric data of Uttal et al. (2002)

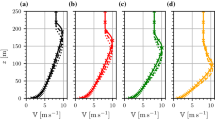
Figure 2 shows the profiles of normalized vertical gradient of (a) streamwise velocity $(1/N) (\text {d} U/\text {d} z)$ and (b) spanwise velocity $(1/N) (\text {d} V/\text {d} z)$ in CNBLs for large values of Zi. The good collapse of all symbols indicates that the wind gradients indeed scale as N for $Zi \gg 1$. Note that the asymptotic independence of $f_u$ on Zi is valid $\xi \gtrsim 0.2$ due to the term proportinal to $1/\xi$ involved in $f_u$ (see Fig. 2a). In contrast, the asymptotic independence of $f_v$ on Zi is nearly valid in the whole boundary layer (see Fig. 2b).

Fig. 2

The profiles of normalized vertical gradient of a streamwise velocity $(1/N) (\text {d} U/\text {d} z)$ and b spanwise velocity $(1/N) (\text {d} V/\text {d} z)$ in CNBLs. For case information see Table 1

4.2 The Coefficients A and B

Figure 3 shows the comparison of the GDL coefficients A and B obtained from the simulations (symbols, see Table 1 and Liu et al. (2021a)), the theoretical predictions of (a) Eq. (10) and (b) Eq. (20) (solid line), and the theoretical prediction of Zilitinkevich and Esau (2005), i.e. the final term in Eq. (20) (dashed line). The empirical constants $a_1=0.12, b_1=0.29, c_1=0.24, c_2=0.054$ are determined from the simulation data of Liu et al. (2021a) using a least-squares fitting procedure (e.g. the MATLAB fminsearch function). To evaluate the goodness of the fit, we introduce the mean absolute percentage error (MAPE),

$$\begin{aligned} \text {MAPE}\, (X) = 100 \frac{1}{n} \sum _{i=1}^n \left| \frac{ X_i^{\textrm{LES}} - X_i^{\textrm{fit}} }{ X_i^{\textrm{LES}} } \right| , \quad X=A, B, \end{aligned}$$

(21)

where i is the case number, $n=24$ is the total number of the simulations performed by Liu et al. (2021a), and the superscripts “LES” and “fit” denote the values of X obtained by LES and the fitting procedure. We find that $\textrm{MAPE}\, (A) = 3.9$ and $\textrm{MAPE}\, (B) = 1.3$, indicating the goodness of the fit. Overall, the present theoretical predictions capture the simulation results of Liu et al. (2021a) and the present study very well. This confirms the validity of the simplified analytical expressions of A and B given by Eqs. (10) and (20), which have much less empirical constants than Eq. (2) proposed by Zilitinkevich and Esau (2005). Note that Fig. 3b also shows clearly that their prediction significantly underestimates the values of B at moderate values of $Zi \lesssim 300$.

Fig. 3

The GDL coefficients a A and b B versus the Zilitinkevich number Zi. Solid line: theoretical curve of (a) Eq. (10) and (b) Eq. (20) with $a_1=0.12, b_1=0.29, c_1=0.24, c_2=0.054$ determined using a least-squares fitting procedure with the simulation data of Liu et al. (2021a); dashed line: theoretical curve of Zilitinkevich and Esau (2005), i.e. Equation (20) with only the final term; diamonds: present simulations of Table 1; circles: previous simulations of Liu et al. (2021a)

5 Geostrophic Drag Coefficient and Cross-Isobaric Angle

Figure 4 compares (a) the geostrophic drag coefficient $u_*/G$ and (b) the cross-isobaric angle $\alpha _0=\arctan \, (|V_g/U_g|)$ obtained from the present simulations of Table 1 and the previous simulations of Liu et al. (2021a, 2021b) with that from the GDL given by Eq. (1), where the GDL coefficients A and B are parameterized by Eqs. (10) and (20), respectively. Note that the empirical constants $(a_1, b_1, c_1, c_2)$ involved in Eqs. (10) and (20) are determined merely based on the simulation data of Liu et al. (2021a), where $u_*/G$ covers only a narrow range of $u_*/G \in [0.019, 0.026]$. The figure shows that the agreement between the simplified parametrization and all the numerical data with a wide range of $u_*/G \in [0.019, 0.047]$ is very good. In particular, Fig. 4a shows that the range of $u_*/G$ of the simulations of Liu et al. (2021a) is between 0.019 and 0.026, while that of the present simulations of Table 1 is between 0.028 and 0.047. These simulations together cover about half of the values of $u_*/G$ commonly observed in atmospheric measurements (Hess and Garratt 2002a, b), and the good agreement between the theoretical predictions and simulations of Liu et al. (2021b) and the present study confirms the validity of the GDL for CNBLs in the high geostrophic drag coefficient regime. Figure 4b shows that the cross-isobaric angle varies between $10^\circ$ and $40^\circ$, where all LES data collapse to the theoretical curve. This good agreement is expected as $\alpha _0=\arcsin \, [(B u_*)/(\kappa G)]$ and B (Fig. 3b) and $u_*/G$ (Fig. 4a) have already been predicted accurately.

Fig. 4

The comparison of a the geostrophic drag coefficient $u_*/G$ and b the cross-isobaric angle $\alpha _0 = \arctan \, |V_g/U_g|$ obtained from various simulation data and the GDL of Eq. (1) with A and B parameterized by Eqs. (10) and (20). Diamonds: present simulations of Table 1; circles: previous simulations of Liu et al. (2021a); triangles: previous simulations of Liu et al. (2021b). Note that the empirical constants involved in Eqs. (10) and (20) are determined only from the simulation data of Liu et al. (2021a) with a limited range of $u_*/G$

Fig. 5

The (a) geostrophic drag coefficient $u_*/G$ and (b) cross-isobaric angle $\alpha _0 = \arctan \, (|V_g/U_g|)$ versus the Rossby number Ro for the cases with the Zilitinkevich number $Zi=89$. Solid line: theoretical predictions of Eq. (1) with A and B parameterized by Eqs. (10) and (20); diamonds: present simulations of Table 1; triangles: previous simulations of Liu et al. (2021b). Note that the empirical constants involved in Eqs. (10) and (20) are determined only from the simulation data of Liu et al. (2021a) with a limited range of $u_*/G$

Figure 5 shows (a) the geostrophic drag coefficient $u_*/G$ and (b) the cross-isobaric angle $\alpha _0 = \arctan \, (|V_g/U_g|)$ versus the Rossby number $Ro=u_*/(fz_0)$. The solid line is the theoretical predictions of Eq. (1) with A and B parameterized by Eqs. (10) and (20), the diamonds are the simulations of Table 1, and the triangles are the simulation of Liu et al. (2021b). The figure focuses on cases with a fixed Zilitinkevich number ($Zi=89$), which is a typical value observed in atmospheric measurements (see Fig. 1). In particular, the figure focuses on cases with the lapse rate $\varGamma =0.003$ K $\hbox {m}^{-1}$ and the latitude $\phi =50^\circ$. The figure shows that the geostrophic drag coefficient $u_*/G$ and the cross-isobaric angle $\alpha _0$ decrease as the Rossby number Ro increases, by either increasing the geostrophic wind speed G or decreasing the roughness length $z_0$ (Table 1). The collapse of all symbols to a single curve, which can be accurately predicted by the GDL of Eq. (1), clearly demonstrates the validity of the simplified parametrization. Note that the empirical constants involved in Eqs. (10) and (20) are determined only from the simulation data of Liu et al. (2021a) with a limited range of $u_*/G$. Therefore, Fig. 5 also indicates that the GDL is very useful in predicting the geostrophic drag coefficient and cross-isobaric angle in the relevant meteorological regime (Hess and Garratt 2002a, b).

6 Conclusions

We investigated theoretically and numerically the GDL for CNBLs. First, we derived the analytical expressions of A and B based on two assumptions. That is, the eddy viscosity approach $K_m=\kappa u_* z$ is valid in the surface layer, and the wind gradients normalized by the free-atmosphere Brunt–Väisälä frequency N have universal profiles above the surface layer. The validity of the first assumption is self-evident, while our physical arguments and simulation data support the second assumption for the cases with strong stability (i.e. $Zi\gg 1$). The resultant expressions of A and B are very simple, which involve only four empirical constants, i.e. $(a_1, b_1, c_1, c_2)$. The values of these empirical constants are determined using a least-squares fitting procedure with the simulation data of Liu et al. (2021a) with a limited range of $u_*/G$.

To demonstrate the validity of the GDL over a wider range of the geostrophic drag coefficient $(u_*/G=[0.019, 0.047])$ than considered previously (Liu et al. 2021a), we performed 19 simulation cases in which we simultaneously vary the free-atmosphere lapse rate, the latitude, the geostrophic wind, and the roughness length. The validity of the GDL over an extended range of $u_*/G$ is thus confirmed by the nearly perfect collapse of the GDL coefficients A and B obtained from carefully performed LES to a single curve when plotted against the Zilitinkevich number Zi. In addition, we show through LES that the GDL with the simplified parameterization of A and B derived in the limit $Zi \gg 1$ accurately captures the geostrophic drag coefficient and the cross-isobaric angle for both the moderate and high values of Zi considered by Liu et al. (2021a, 2021b) and the present study.

Our findings are relevant for meteorological applications such as wind energy. For example, Li et al. (2022) showed that the GDL also applies for flows over extended wind farms, but the A and B values are different from that over flat terrains. Based on this finding, the authors proposed an analytical model of fully developed wind farms in CNBLs, and found that the theoretically predicted wind farm power output agrees well with the numerical simulations. Updating the parametrization of A and B in the original GDL by Zilitinkevich and Esau (2005) is challenging as it involves updating numerous empirical constants. Therefore, Li et al. (2022) had to numerically fit A and B coefficients rather than directly updating the GDL coefficients. While this approach is practical, it limits theoretical exploration and analysis. The GDL parametrization we provide offers more flexibility and applicability for a variety of flow scenarios, including wind farms and canopy flows. This adaptability may facilitate further theoretical exploration and analysis of such situations where the GDL can be applied.