The generalized HSS method with a flexible shift-parameter for non-Hermitian positive definite linear systems

Abstract

Based on the Hermitian and skew-Hermitian splitting (HSS), we come up with a generalized HSS iteration method with a flexible shift-parameter for solving the non-Hermitian positive definite system of linear equations. This iteration method utilizes the optimization technique to obtain the optimal value of the flexible shift-parameter at iteration process. Both theory and experiment have shown that the new strategy is efficient.

1 Introduction

In this study we focus on solving the large sparse non-Hermitian and positive definite system of linear equations

$$\begin{aligned} Ax=b, \end{aligned}$$

(1.1)

where $A \in \mathbb {C}^{n\times n}$ is nonsingular and $x,b\in \mathbb {C}^n$. Based on the Hermitian/skew-Hermitian (HS) splitting [25]

$$\begin{aligned} A=H+S \end{aligned}$$

of the coefficient matrix A, where

$$\begin{aligned} H=\frac{1}{2}(A+A^*), \ S=\frac{1}{2}(A-A^*), \quad A^{*} \ \hbox {is the conjugate transpose of } A, \end{aligned}$$

Bai et al. [9] first proposed the efficient Hermitian and skew-Hermitian splitting (HSS) iteration method with a fixed shift-parameter in 2003 for solving the system (1.1). The method was designed as follows: Given an initial guess $x_0\in {\mathbb {C}^n}$, for $k=0,1,2,\ldots$ until the sequence of iterates $\{x_k\}_{k=0}^\infty \subset {\mathbb {C}^n}$ converges, compute the next iterate $x_{k+1}$ according to the following formulation:

$$\begin{aligned} \left\{ \begin{array}{ll} (\alpha I+ H)x_{k+\frac{1}{2}}=(\alpha I-S)x_k+b,\\ (\alpha I+S)x_{k+1}=(\alpha I-H)x_{k+\frac{1}{2}}+b, \end{array} \right. \end{aligned}$$

(1.2)

where I is the identity matrix and $\alpha$ is a fixed shift-parameter (a given positive constant).

Note that the HSS iteration (1.2) may also be considered as a splitting iteration induced from the splitting of the matrix A as follows,

$$\begin{aligned} A=M(\alpha )-N(\alpha ), \end{aligned}$$

where

$$\begin{aligned} M(\alpha )=\frac{1}{2\alpha }(\alpha I+H)(\alpha I+S)\quad \text {and} \quad N(\alpha )=\frac{1}{2\alpha }(\alpha I-H)(\alpha I-S). \end{aligned}$$

(1.3)

It was proved in [9] that the HSS iteration method converges unconditionally to the unique solution of the linear system (1.1), and the upper bound of the convergence rate of the method is about the same as that of the conjugate gradient method applied to a linear system of the coefficient matrix H. The optimal shift-parameter [9] is estimated as

$$\begin{aligned} \alpha _{\mathrm{opt}}=\text {arg} \min _{\alpha }\left\{ \max _{\lambda _{\text {min}}\le \lambda \le \lambda _{\text {max}}}\left| \frac{\alpha -\lambda }{\alpha +\lambda }\right| \right\} =\sqrt{\lambda _{\text {min}}\lambda _{\text {max}}}, \end{aligned}$$

where $\lambda _{\text {min}}$ and $\lambda _{\text {max}}$ are the minimum and the maximum eigenvalues of the matrix H, respectively.

Because of its outstanding performance and elegant mathematical properties, the HSS iteration method obtains widespread attention. For instance, it is extended to solve non-Hermitian positive semi-definite matrices [7, 11], the saddle point problems [2, 4, 6, 23], complex symmetric linear systems [5, 16] and so on. Many modifications and generalizations of the HSS iteration method can be found in [1, 10, 12, 18–21] and the references therein. On the other hand, some effective algorithms use the HSS iteration as a preconditioner or use the preconditioning variants of the HSS iteration, which often work out excellent results; see [13–15] and their references.

However, we have noticed that the shift-parameter $\alpha$ is a constant throughout the iteration process in all discussed above, which reduces the effectiveness of the methods from one point of view.

For the Hermitian positive definite linear system, Pearcy [22] has designed the device of changing iteration shift-parameters on the half-steps

$$\begin{aligned} \left\{ \begin{array}{ll} x_{k+{\frac{1}{2}}}=-\left( V_1+\alpha _{k+\frac{1}{2}}D\right) ^{-1} \left[ (V_2-\alpha _{k+\frac{1}{2}} D)x_{k}-b\right] ,\\ x_{k+1}= -(V_2+\alpha _{k+1} D)^{-1}\left[ (V_1-\alpha _{k+1}D)x_{k+\frac{1}{2}}-b\right] , \end{array} \right. \end{aligned}$$

where D is a positive definite normalizing matrix, $V_1, V_2$ are Hermitian positive definite matrices such that $A=V_1+V_2$, $\alpha _{\frac{1}{2}}\ge \alpha _{1}\ge \alpha _{1+\frac{1}{2}}\ge \cdots \ge \alpha _{t-\frac{1}{2}}\ge \alpha _{t}$, and $\alpha _{k}=\alpha _{k(\text {mod}\;t)}$ for $k>t$. But the convergence of this alternating direction implicit (ADI) iteration method depends on the positive definiteness of the splitting matrices $V_1$ and $V_2$. Furthermore, for the case $V_1V_2=V_2V_1$ and $D=I$, Douglas [17] showed that ADI was always convergent and the problem of choosing an optimal parameter sequence [24] has also been solved for this case. Unfortunately, the problems of practical interest are usually with $V_1V_2\ne V_2V_1$. So we propose the generalized HSS iteration method with a flexible shift-parameter. Moreover, motivated by the optimization models [26], shift-parameters $\alpha _k,k=1,2,\ldots$ are constructed by the minimization of residuals.

The remained of the paper is organized as follows. In Sect. 2, we describe the proposed iteration method. In Sect. 3, we use some numerical experiments to show the effectiveness of the new iteration method. Finally, we end the paper with a conclusion in Sect. 4.

2 The generalized HSS method with a flexible shift-parameter

In this section, we present a generalized HSS method to solve the system of linear equations (1.1) and it is stated as follows.

Method 2.1

(The generalized HSS method with a flexible shift-parameter) Let $x_{0}\in {\mathbb {C}^n}$ be an arbitrary initial guess and $\varepsilon > 0$ be a given tolerance. The splitting matrices $M(\alpha )$ and $N(\alpha )$ are defined by (1.3). For $k=0,1,2,\ldots$ until the sequence of iterates $\{x_{k}\}_{k=0}^ \infty \subset {\mathbb {C}^n}$ converges, compute the next iteration $x_{k+1}$ according to the following procedure.

• (1) Compute $r_{k}=b-Ax_{k}$.

• (2) Solve the following system of linear equations:

  $$\begin{aligned} \left\{ \begin{array}{ll} (\alpha _{k+1} I +H)x_{k+{\frac{1}{2}}}=(\alpha _{k+1} I-S)x_{k}+b,\\ (\alpha _{k+1} I +S)x_{k+1}=(\alpha _{k+1} I-H)x_{k+\frac{1}{2}}+b,\\ \end{array} \right. \end{aligned}$$

  (2.1)

  where $\alpha _{k+1}$ is the solution of the following optimization problem

  $$\begin{aligned} \min _{\alpha } r_{k+1}^{*}\left( \alpha I-H\right) ^{-2}r_{k+1}, \end{aligned}$$

  (2.2)

  here, $r_{k+1}=N(\alpha )M(\alpha )^{-1}r_k$.

• (3) If $\Vert r_{k+1}\Vert _2 \le \varepsilon$, stop; otherwise, $k\Leftarrow k+1$ and go to (1).

If $\alpha =\alpha _1=\alpha _2=\cdots$ in (2.1), Method 2.1 reduces to the HSS iteration method with a fixed shift-parameter. So we only consider the situation that the shift-parameters $\alpha _k$, $k=1,2,\ldots$ are not all equal, which is said the generalized HSS method with a flexible shift-parameter.

In matrix-vector form, the scheme (2.1) can be equivalently written as

$$\begin{aligned} x_{k+1}=T_{\alpha _{k+1}}x_k+G_{\alpha _{k+1}}b,\quad k=0,1,2,\ldots , \end{aligned}$$

where

$$\begin{aligned} T_{\alpha _{k+1} }=(\alpha _{k+1} I+ S)^{-1}(\alpha _{k+1} I-H)(\alpha _{k+1} I+H)^{-1}(\alpha _{k+1} I-S) \end{aligned}$$

(2.3)

and

$$\begin{aligned} G_{ \alpha _{k+1} }=2\alpha _{k+1}(\alpha _{k+1} I+ S)^{-1}(\alpha _{k+1} I+ H)^{-1}. \end{aligned}$$

Evidently, we can express $x_{k+1}$ as

$$\begin{aligned} x_{k+1}=Q_{k+1}x_0+c_{k+1}, \quad k=0,1,2,\ldots , \end{aligned}$$

where

$$\begin{aligned} Q_{k+1}=T_{\alpha _{k+1}}T_{\alpha _{k}}\cdots T_{\alpha _1} \end{aligned}$$

(2.4)

and

$$\begin{aligned} c_{k+1}=\left( G_{\alpha _{k+1}}+T_{\alpha _{k+1}}G_{\alpha _{k}} +T_{\alpha _{k+1}}T_{\alpha _{k}}G_{\alpha _{k-1}}+\cdots +T_{\alpha _{k+1}} T_{\alpha _{k}}\cdots T_{\alpha _2} G_{\alpha _1} \right) b. \end{aligned}$$

Lemma 2.1

Let $x_{k}$ be generated by Method 2.1, $M(\alpha )$ and $N(\alpha )$ be given by (1.3). Then at the (k+1)-st step it holds that

$$\begin{aligned} \left\| (\alpha I-H)^{-1}r_{k+1}\right\| ^2_2=r_k^{*}(\alpha I+H)^{-2}r_k, \end{aligned}$$

(2.5)

where $\alpha$ is obtained by the optimization model (2.2). Furthermore,

$$\begin{aligned} \frac{d}{d \alpha }\left( \left\| (\alpha I-H)^{-1}r_{k+1}\right\| ^2_2\right) =-2r_k^{*}(\alpha I+H)^{-3}r_k. \end{aligned}$$

(2.6)

Proof

Let $\varPhi (\alpha )=(\alpha I-S)(\alpha I+S)^{-1}$, we see that $\varPhi (\alpha )^{*}\varPhi (\alpha )=I$, which means that $\varPhi (\alpha )$ is a unitary matrix. Since

$$\begin{aligned} (\alpha I-H)^{-1}N(\alpha )M(\alpha )^{-1}=(\alpha I-S)(\alpha I+S)^{-1}(\alpha I+H)^{-1}=\varPhi (\alpha )(\alpha I+H)^{-1}, \end{aligned}$$

we have

$$\begin{aligned} \left\| (\alpha I-H)^{-1}r_{k+1}\right\| ^2_2= & {} \left( (\alpha I-H)^{-1} N(\alpha )M(\alpha )^{-1}r_k,(\alpha I-H)^{-1}N(\alpha )M(\alpha )^{-1}r_k\right) \\= & {} \left( \varPhi (\alpha )(\alpha I+H)^{-1}r_{k},\varPhi (\alpha )(\alpha I+H)^{-1}r_{k}\right) \\= & {} r_k^{*}(\alpha I+H)^{-2}r_k. \end{aligned}$$

Note that

$$\begin{aligned} \frac{d\left( (\alpha I+H)^{-1}\right) }{d\alpha }=-(\alpha I+H)^{-1}\frac{d\left( \alpha I+H\right) }{d\alpha }(\alpha I+H)^{-1} \quad \text {and} \quad \frac{d\left( \alpha I+H \right) }{d\alpha }=I. \end{aligned}$$

Then,

$$\begin{aligned}&\frac{d}{d\alpha }\left( \left\| (\alpha I-H)^{-1}r_{k+1}\right\| ^2_2\right) \\&\quad =r_k^{*}\frac{d\left( (\alpha I+H)^{-1}\right) }{d\alpha }(\alpha I+H)^{-1}r_k+r_k^{*}(\alpha I+H)^{-1}\frac{d\left( (\alpha I+H)^{-1}\right) }{d\alpha }r_k\\&\quad =-2r_k^{*}(\alpha I+H)^{-3}r_k. \end{aligned}$$

$\square$

Theorem 2.1

Let A be a non-Hermitian positive definite matrix. Then the iteration sequence $\left\{ x_k\right\}$ generated by Method 2.1 converges to the unique solution $x_*$ of the system of linear equations (1.1). Furthermore, if A is a normal matrix, then the 2-norm of the error vector $e_k=x_k-x_*$ is strictly decreasing, i.e., $\Vert e_{k+1}\Vert _2<\Vert e_{k}\Vert _2$, $k=0,1,2,\ldots$.

Proof

Let $e_k=x_k-x_{*}$ be the error at the kth step of Method 2.1. If $\alpha _{k+1}$ is obtained by the minimization model (2.2), then for any $\alpha _k>0$ it holds that

$$\begin{aligned} r_{k+1}^{*}(\alpha _{k+1} I-H)^{-2} r_{k+1} =r_{k}^{*}(\alpha _{k+1} I+H)^{-2}r_{k} \le r_{k}^{*}(\alpha _{k} I+H)^{-2}r_{k}. \end{aligned}$$

(2.7)

From (2.7), we have

$$\begin{aligned} \left\| (\alpha _{k+1} I-H)^{-1}r_{k+1}\right\| _2\le & {} \left\| (\alpha _k I+H)^{-1}r_{k}\right\| _2 \\= & {} \left\| (\alpha _k I+H)^{-1}(\alpha _k I-H)(\alpha _k I-H)^{-1}r_{k}\right\| _2\\\le & {} \left\| (\alpha _k I+H)^{-1}(\alpha _k I-H)\right\| _2 \left\| (\alpha _{k} I-H)^{-1}r_{k}\right\| _2\\= & {} \max _{\lambda _i \in \lambda (H)} \left| \ \frac{\alpha _k-\lambda _i}{\alpha _k+\lambda _{i}}\right| \left\| (\alpha _{k} I-H)^{-1}r_{k}\right\| _2. \end{aligned}$$

It is noted that there exists a positive number $\gamma$ such that for any $\alpha _k>0$ the inequality $\max _{\lambda _i \in \lambda (H)} \left| \ \frac{\alpha _k-\lambda _i}{\alpha _k+\lambda _{i}}\right| \le 1-\gamma$ is valid. Thus we have

$$\begin{aligned} \left\| (\alpha _{k+1}I-H)^{-1}r_{k+1}\right\| _2\le & {} (1-\gamma )\left\| (\alpha _{k} I-H)^{-1}r_{k}\right\| _2 \le \cdots \\\le & {} (1-\gamma )^{k+1}\left\| (\alpha _0 I-H)^{-1}r_{0}\right\| _2. \end{aligned}$$

Moreover,

$$\begin{aligned} \lim _{k\rightarrow \infty }(\alpha _{k+1}I-H)^{-1}r_{k+1}=0. \end{aligned}$$

For any $\alpha >0$, the matrix $(\alpha I-H)^{-1}$ is of full rank. Hence, we have $\lim \limits _{k\rightarrow \infty }r_{k+1}=0$.

On the other hand, if A is a normal matrix, we get

$$\begin{aligned} HS=SH. \end{aligned}$$

Thus, $T(\alpha )=(\alpha I+ S)^{-1}(\alpha I-S)(\alpha I-H)(\alpha I+H)^{-1}$ is also a normal matrix, which implies that

$$\begin{aligned} \Vert T(\alpha )\Vert _2=\rho (T(\alpha )). \end{aligned}$$

Therefore, for the iteration matrix $Q_{k+1}$ in (2.4), it holds that

$$\begin{aligned} \Vert Q_{k+1}\Vert _2\le & {} \Vert T_{\alpha _{k+1}}\Vert _2\Vert T_{\alpha _{k}}\Vert _2\cdots \Vert T_{\alpha _1}\Vert _2= \rho \left( T_{\alpha _{k+1}}\right) \rho \left( T_{\alpha _{k}}\right) \cdots \rho \left( T_{\alpha _1}\right) <1. \end{aligned}$$

Moreover,

$$\begin{aligned} \Vert Q_{k+1}\Vert _2 =\Vert T_{\alpha _{k+1}}Q_{k}\Vert _2<\Vert Q_{k}\Vert _2<1. \end{aligned}$$

So,

$$\begin{aligned} \Vert e_{k+1}\Vert _2=\Vert Q_{k+1}e_0\Vert _2=\Vert T_{\alpha _{k+1}}Q_{k}e_0\Vert _2<\Vert Q_{k}e_0\Vert _2 =\Vert e_{k}\Vert _2. \end{aligned}$$

$\square$

It is worthy to note that the solution of the minimization model (2.2) is equivalent to compute the root of $\frac{d}{d \alpha }\left( \Vert (\alpha I-H)^{-1}r_{k+1}\Vert ^2_2\right) =0$ in Theorem 2.1. However, the computational formula (2.6) is only of theoretical meaning and it is far away from actual applications, since the computational cost of the matrix $(\alpha I+H)^{-3}$ is expensive. Instead, we approximate the root of $f(\alpha )=\Vert (\alpha I-H)^{-1}r_{k+1}\Vert ^2_2=0$ by the Newton method. An alternative procedure might be to approximate the value of $f(\alpha )=\Vert (\alpha I+H)^{-1}r_{k}\Vert ^2_2=0$ by (2.5). Hence, Method 2.1 could be rewritten into a practical form stated in Method 2.2.

Method 2.2

(The practical generalized HSS method with a flexible shift-parameter) Let $x_{0}\in {\mathbb {C}^n}$ be an arbitrary initial guess and $\varepsilon > 0$ be a given precision. The splitting matrices $M(\alpha )$ and $N(\alpha )$ are defined by (1.3). For $k=0,1,2,\ldots$ until the sequence of iterates $\{x_{k}\}_{k=0}^ \infty \subset {\mathbb {C}^n}$ converges, compute the next iteration $x_{k+1}$ according to the following procedure.

• (1) Compute $r_{k}=b-Ax_{k}$.

• (2) Solve the systems of linear equations:

  $$\begin{aligned} \left\{ \begin{array}{ll} (\alpha _{k+1} I +H)x_{k+{\frac{1}{2}}}=(\alpha _{k+1} I-S)x_{k}+b,\\ (\alpha _{k+1} I +S)x_{k+1}=(\alpha _{k+1} I-H)x_{k+\frac{1}{2}}+b,\\ \end{array} \right. \end{aligned}$$

  where $\alpha _{k+1}$ is the root of the equation

  $$\begin{aligned} f(\alpha )=\Vert (\alpha I+H)^{-1}r_{k}\Vert ^2_2=0. \end{aligned}$$

• (3) If $\Vert r_{k+1}\Vert _2 \le \varepsilon$, stop; otherwise, $k\Leftarrow k+1$ and go to (1).

Remark 2.1

For the sake of saving computational cost, we can perform a new update on the shift-parameter $\alpha$ for every p iteration steps.

3 Numerical experiments

In this section, we provide numerical results to illustrate the effectiveness of Methods 2.1 and 2.2 in terms of the iteration steps (denoted as IT), the elapsed computing times in seconds (denoted as CPU), and the relative residual error (denoted as RES) defined by

$$\begin{aligned} \hbox {RES}=\frac{\Vert b-Ax_{k}\Vert _2}{\Vert b-Ax_{0}\Vert _2}. \end{aligned}$$

All tests are started from the vector $x_{0}=0$, and terminated when the current iteration satisfies RES$\le 10^{-6}$. In addition, the numerical experiments are performed in MATLAB (version R2013a) on PC in double precision, which is 2.40 GHz central processing unit [Intel(R) Core(TM)i7-4500 CPU] with 8G memory and Microsoft Window 8 operating system. In actual computation, the $\alpha _k$ is updated for every 5 iteration steps.

Example 3.1

[8] Consider the two-dimensional convection-diffusion equation

$$\begin{aligned} -(u_{xx}+u_{yy})+\beta (u_x+u_y)=g(x,y), \end{aligned}$$

on the unit square $(0,1)\times (0,1)$ with constant coefficient $\beta$ and subject to Dirichlet-type boundary condition. By applying the five-point centered finite difference discretization, we get the system of linear equations (1.1) with the coefficient matrix

$$\begin{aligned} A=T\otimes I+I\otimes T, \end{aligned}$$

where $h=\frac{1}{m+1}$ is the equidistant step-size (In this test, $m=32$.), $\otimes$ denotes the Kronecker product, and T is a tridiagonal matrix given by

$$\begin{aligned} T=\hbox {tridiag}(-1-R_e,2,-1+R_e), \end{aligned}$$

where

$$\begin{aligned} R_e=\frac{\beta h}{2} \end{aligned}$$

(3.1)

is the mesh Reynolds number. Moreover, the right-hand side vector b is taken to be $b=Ax_*$ with $x_*=(1,1,\ldots ,1)^T\in \mathbb {R}^n$ being the exact solution.

Here and in the sequel, BGN-HSS means the HSS method by Bai et al. [9], and H-HSS means the new practical methods by Huang [19]. Correspondingly, Methods 2.1 and 2.2 are termed briefly as $\hbox {MWZ}_1$-HSS, and $\hbox {MWZ}_2$-HSS, respectively.

Table 1 Iteration Step, CPU Time, and RES of BGN-HSS, H-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.1

In Table 1, we give the iteration numbers, the CPU times and the RES values of BGN-HSS, H-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.1 with respect to different choices of the problem parameter $\beta$.

From Table 1, it can be seen that for different $\beta$ the numbers of iteration steps of $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods are less than those of BGN-HSS and H-HSS methods at almost the same CPU times. The case $\beta =50$ and $\beta =5000$ of these observations can be further illustrated by the iteration pictures plotted in Fig. 1. Clearly, $\hbox {MWZ}_2$-HSS method outperforms both BGN-HSS and H-HSS methods.

Fig. 1

Relative residual versus iteration step for the BGN-HSS, H-HSS and $\hbox {MWZ}_2$-HSS methods with $m=32$

Example 3.2

[8] We solve the linear system $Ax = b$, where A is a 2-by-2 block matrix as follows:

$$\begin{aligned} A=\begin{pmatrix} B &{} E \\ -E^T &{} 0.5I \\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} B=\begin{pmatrix} I\otimes T_H +T_H\otimes I&{} 0 \\ 0 &{} I\otimes T_H +T_H\otimes I \\ \end{pmatrix}\in \mathbb {R}^{2m^2\times 2m^2}, \ E=\begin{pmatrix} I\otimes F \\ F\otimes I \\ \end{pmatrix}\in \mathbb {R}^{2m^2\times m^2}, \end{aligned}$$

with

$$\begin{aligned} T_H=\begin{pmatrix} 2 &{} -1 &{} &{} \\ -1 &{} 2 &{} \ddots &{} \\ &{} \ddots &{} \ddots &{} -1 \\ &{} &{} -1 &{} 2 \\ \end{pmatrix} \in \mathbb {R}^{m\times m},\;\; F=\delta h\cdot \begin{pmatrix} 1 &{} &{} &{} \\ -1 &{} 1 &{} &{} \\ &{} \ddots &{} \ddots &{} \\ &{} &{} -1 &{} 1 \\ \end{pmatrix}\in \mathbb {R}^{m\times m}, \end{aligned}$$

and $h=\frac{1}{m+1}$ being the discretization mesh-size.

In this example, the total number of variables is $3m^2$, and the right-hand side vector b is taken to be $b=Ax_*$ with $x_*=(1,1,\ldots ,1)^T\in \mathbb {R}^n$ being the exact solution.

In Table 2, we provide the iteration numbers, the CPU times and the RES values of BGN-HSS, H-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.2 with respect to different choices of the problem parameter $\delta$ as well as the problem size m. Clearly, the iteration steps of $\hbox {MWZ}_2$-HSS method is much less than those of H-HSS and BGN-HSS methods. For the case $\delta =1000$, when the problem size m becomes large the iteration steps of $\hbox {MWZ}_2$-HSS method unchange but those of BGN-HSS and H-HSS methods are increasing. As for the computing time, the situation is almost the same except for $\hbox {MWZ}_1$-HSS method.

Table 2 Iteration Step, CPU Time, and RES of BGN-HSS, H-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.2

Furthermore, we use the following singular linear system to further examine the effectiveness of $\hbox {MWZ}_2$-HSS method. Note that H-HSS method fails for this example. The generalized HSS method proposed by Li et al. [20] (as the above manner, denoted as LLP-GHSS) could be applied for comparison.

Example 3.3

[3] Consider the two-dimensional variable-coefficient second-order differential equation satisfying the periodic boundary condition given as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} -\frac{\partial }{\partial x}\left( c(x,y)\frac{\partial u}{\partial x} \right) -\frac{\partial }{\partial y}\left( c(x,y)\frac{\partial u}{\partial y} \right) + \gamma \left( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}\right) =f(x,y), &{}(x,y)\in (0,1)\times (0,1), \\ u(x,0)=u(x,1), &{}x\in (0,1), \\ u(0,y)=u(1,y), &{}y\in (0,1). \end{array} \right. \end{aligned}$$

(3.2)

The right-hand side vector is taken to be $b=Ax_*$ with $x_*=(1,2,\ldots ,n)^T$ being the exact solution.

Table 3 Iteration Step, CPU Time, and RES of BGN-HSS, H-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.3

Fig. 2

Relative residual versus iteration number for the BGN-HSS, LLP-HSS and $\hbox {MWZ}_2$-HSS iteration methods with respect to the different n

When $c(x,y)\equiv 1$, the differential equation (3.2) is discretized by using the same approach as Example 3.1, with the equidistant stepsize $h=\frac{1}{m}$ and $n=m^2$. So we can get the real linear system with the singular and positive semi-definite n-by-n coefficient matrix

$$\begin{aligned} A=\begin{pmatrix} \vartriangle &{} -(1-R_e)I &{} 0 &{} \cdots &{} 0 &{} -(1+R_e)I \\ -(1+R_e)I &{} \vartriangle &{} -(1-R_e)I &{} \cdots &{} 0 &{} 0 \\ 0 &{} -(1+R_e)I &{} \vartriangle &{} \cdots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} \vartriangle &{} -(1-R_e)I \\ -(1-R_e)I &{} 0 &{} 0 &{} \cdots &{} -(1+R_e)I &{} \vartriangle \\ \end{pmatrix}\in \mathbb {R}^{n\times n}, \end{aligned}$$

where $\vartriangle \in \mathbb {R}^{m\times m}$ is given by

$$\begin{aligned} \begin{pmatrix} 4 &{} -1+R_e &{} 0 &{} \cdots &{} 0 &{} -1-R_e \\ -1-R_e &{} 4 &{} -1+R_e &{} \cdots &{} 0 &{} 0 \\ 0 &{} -1-R_e &{} 4 &{} \cdots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 4 &{} -1+R_e \\ -1+R_e &{} 0 &{} 0 &{} \cdots &{} -1-R_e &{} 4 \\ \end{pmatrix}, \end{aligned}$$

and $R_e$ is defined by (3.1).

In Table 3, we list the numbers of iteration steps, the CPU times and the RES values of BGN-HSS, LLP-HSS, $\hbox {MWZ}_1$-HSS and $\hbox {MWZ}_2$-HSS methods for Example 3.3 with respect to different choices of the problem parameter $\beta$ as well as the problem size m.

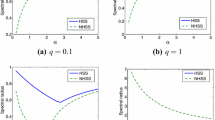
From Table 3, we see that $\hbox {MWZ}_1$-HSS method is not sensitive to the shift-parameter $\alpha _{k+1}$. In this table, all methods can get a satisfactory approximation for solving this singular linear system. Evidently, the number of iteration steps tends to a constant when $\beta$ becomes large. Table 3 shows that $\hbox {MWZ}_2$-HSS method requires less iteration steps and computing times than BGN-HSS and LLP-GHSS methods. It is also noted that $\hbox {MWZ}_2$-HSS method needs to compute the updated optimal shift-parameter for every 5 iteration steps, while BGN-HSS and LLP-GHSS methods do not require this additional computation. In Fig. 2, we further show the numerical advantages of $\hbox {MWZ}_2$-HSS method over the other three methods for different values of $\beta$ and n.

4 Conclusion

In this paper, we propose a generalized HSS iteration method for solving the non-Hermitian positive definite system of linear equations. The numerical experiments show that the proposed $\hbox {MWZ}_2$-HSS method is superior to the methods given in [9, 19, 20]. Even though the coefficient matrix is singular and non-Hermitian positive semi-definite, the new iteration method can gain almost the same excellent properties as the HSS method.