Energy-based seismic design for self-centering concrete frames

Abstract

Conventional concrete frames are designed to dissipate the earthquake energy through inelastic deformation of the structural elements. It leads to hefty repairment costs and prolonged down time after earthquakes. Self-centering concrete frames (SCCF) have been introduced to minimize the unrecoverable structural damages and post-earthquake repairment costs. SCCF exhibits predictable yield mechanism and self-centering capacity. This paper presents an energy-based seismic design (EBSD) procedure for SCCFs. Based on a proposed damage model, hysteretic energy demand, E_H, is introduced as a key design parameter. The desired damage state and structural deformations can be considered in design process. EBSD allows designers to select various performance objectives at different seismic intensities. A prototype building is designed using the proposed EBSD procedure. The performance of SCCF designed using EBSD is compared with the same prototype structure designed using direct displacement-based design method (DDBD). The results show that SCCF has high performance with low residual drift. The performance of the EBSD designed SCCF exhibits more controlled damage compared with the DDBD designed SCCF.

1 Introduction

It has been observed in recent earthquakes that conventional systems can be designed to avoid collapse from strong earthquake shaking through inelastic deformations in structural members. Such yield mechanism results in hefty repairment costs and prolonged down time. To improve the structural performance and post-earthquake repairability, self-centering structures and components have been conceived. Critical components equipped with post-tensioned (PT) tendons and energy-dissipation devices have been proposed to enhance the structural performance of existing structures. (Barbagallo et al. 2020; Wang et al. 2020, 2021; Cai et al. 2021; Xue et al. 2021; Wu et al. 2021;). Meanwhile, self-centering moment frame structures have been developed (Priestley et al. 1993; Cheok et al. 1994; EL-Sheikh et al. 1999; El-Sheikh et al. 2000; Korkmaz et al. 2005) to upgrade aseismic performance of conventional frames. These systems exhibit excellent performance, where the structures can be functional immediately or shortly after strong earthquake shaking. The self-centering concrete frame (SCCF) originally proposed by Priestley and Tao (1993) is one such system. SCCF uses PT tendons and yielding components at the beam-column connections to dissipate earthquake energy and provide the self-centering mechanism. SCCF is commonly designed using the direct displacement-based design (DDBD) method (Priestley et al. 2002). DDBD focuses on the use of maximum deformation as the main design parameter to satisfy the strength and deformation requirements. Unlike conventional concrete frames, SCCF is more sensitive to the cumulative effect and residual deformation (Zhou et al. 2020a). Hence, it is more rational to utilize an energy-based design approach for SCCF structures.

Energy-balance concept was first introduced by Housner in the first world conference on earthquake engineering (Housner et al. 1959). The input energy from earthquakes, E_I, is mainly dissipated through damping energy, E_D, and hysteresis energy, E_H. While the remaining energy is stored in the system as kinetic energy E_K and elastic strain energy E_s. Equation (1). shows the energy-balance concept (Uang et al. 1990).

$$E_{{\text{I}}} {\text{ = }}E_{{\text{D}}} {\text{ + }}E_{{\text{H}}} {\text{ + }}E_{{\text{K}}} {\text{ + }}E_{{\text{S}}}$$

(1)

Many researchers have proposed energy-based design methods for different structural systems. Akiyama (1985) illustrated a systematic design procedure based on the energy-balance concept, and it has been implemented in a technological standard for earthquake-resistant calculation method in Japan since 2005 (2005). Fajfar et al. (1996) proposed the N2 method and modified Park-Ang model for the design and performance evaluation for conventional concrete frames. Akbas et al. (2001) conducted statistical analyses to study energy input and dissipation. Since the study was performed based on small sample set and a linear distribution of energy dissipation along structural heights was adopted, energy features could not be evaluated precisely. Chou et al. (2003) studied the distribution of E_H via multi-pushover analyses (MPA) method and proposed an energy-based design approach. It has been proved that the seismic energy is not only related to structural features, but also ground motion characteristics, including peak values, frequency and duration (Zhou et al. 2019a). Since the MPA method is a static methodology for structure analyses, it cannot accurately capture the real structural behaviors and responses under seismic actions. Thus, the applicability of MPA still remains to be discussed. Meanwhile, Yang et al. (2018; 2020) proposed an equivalent energy design procedure, which allows designers to select various performance objectives for different seismic intensities. It enables structures achieve desired strength and deformation without iterations in the design procedure.

Since the energy-based design procedure specific to self-centering concrete frame structures is still limited, an energy-based design method to routinely design SCCFs is needed. Several specific subjects, including the energy spectra, the damage evaluation and the energy distribution within SCCFs have been investigated in previous researches (Zhou et al. 2020a, b; Song et al. 2021). In this paper, a newly conceived energy-based seismic design (EBSD) procedure for SCCF structures is presented. Based on the proposed damage model, the hysteretic energy demand E_H is introduced as a key design parameter for SCCFs. The proposed design procedure considers not only the deformation and energy demands of SCCFs, but also the desired damage states, which would limit the damage development in the well-designed structures. In addition, it allows designers to select various performance objectives for different seismic intensities satisfying with multiple performance levels.

2 Energy-based seismic design procedure

The first step of the proposed EBSD is to determine the E_I and E_H for the whole structure from the design energy spectra. The second step of EBSD is to quantify the hysteretic energy demand for the critical components E_Hi. Then, E_Hi is converted as a key design index. The last step of EBSD is to select the critical design parameters, including the maximum deformation θ_m, the recoverable deformation θ_r, the ultimate deformation θ_u and damage index DI, to achieve multi-performance objectives.

2.1 Energy-dissipation mechanism for SCCF

Figure 1 shows the yield mechanism of SCCF with typical beam-column joints, known as hybrid joints (Cheok et al. 1993; ACI 2003). The hybrid joint has: (a) equal moment strength for top and bottom energy-dissipating mild steels; (b) unbonded PT tendons that connected the beams to the columns through the centroid of the beam. NIST program (Cheok et al. 1993) showed that a well-designed hybrid joint has sufficient strength, stiffness and energy-dissipation capacities, while exhibiting great self-centering behaviors under cyclic loads. The nonlinearity occurred in mild steels can dissipate seismic energy to protect critical components from sever damages. This leads to stable and controllable damage development.

Fig. 1

Yielding mechanism of SCCF

2.2 Quantification of E _H

The quantification of energy demands includes determining E_H and its distribution within structures. Normally, the energy demand for different systems can be derived from input energy spectra and hysteretic energy spectra (Zhou et al. 2019a, b). It has been demonstrated that both the ground motion types and structural features have great effects on E_I (Decanini et al. 1998; Chou et al. 2000; Cruz et al. 2000), while the hysteretic model should be considered in determining E_H (Zhou et al. 2019b). Therefore, the applicability of existing energy spectra needs to be considered in the quantification of E_I and E_H for SCCFs. Meanwhile, for implementing the design method into component level, quantification of the energy demands for critical components E_Hi are needed after determining E_H for the whole system.

2.2.1 Energy spectra

Zhou et al. (2020b) proposed a practical design energy spectrum for self-centering systems. The proposed energy spectra are applicable to different site class stipulated in the Chinese code (2016) and can consider the influences of ground motion types and structural characteristics.

Equivalent velocity, Ve, as shown in Eq. (2), is adopted as the input energy per unit mass of structures (Zhou et al. 2020b):

$$Ve = \sqrt {\frac{{2E_{{\text{I}}} }}{m}}$$

(2)

where m represents the mass of the system.

Figure 2 shows the flag-shaped hysteretic model adopted in the study to model seismic responses of self-centering systems (Zhou et al. 2020b). M_y and θ_y represent the yield strength and deformation, respectively. K represents the initial stiffness, α represents the post-yield stiffness ratio, η represents the ratio of the yield strength. θ_u represents the maximum deformation. The ductility factor μ, which defined as θ_u/θ_y, was adopted to define the nonlinear behaviors of systems and to construct the constant-ductility spectra.

Fig. 2

Flag-shaped hysteretic model

In order to predict Ve of different systems, a benchmark model with η = 0.4, ξ = 0.02, μ = 2 and α = 0.2 is adopted in the study, where ξ is the damping ratio. Design spectrum of the benchmark model is denoted as Ve_benchmark. The design spectrum of target systems with different η, ξ, μ and α can be constructed based on Ve_benchmark. The proposed design spectra are divided into three portions as a function of the vibration period. Figure 3 illustrates the construction of design spectrum for the benchmark model (Zhou et al. 2020b).

Fig. 3

Construction of design spectra for Ve_benchmark

Where Ve_{benchmark, max} is the peak value of the design spectrum; T₁, T₂ are characteristic periods related to ground motion types; γ is the fitting parameter.

It has been demonstrated that input energy spectra closely relate to ground motion features (Zhou et al. 2019a; Zhou et al. 2020b). According to the Chinese code (2016), ground motions are divided into 12 types according to site types (I ~ IV) and design groups (1 ~ 3). Site types are classified based on the shear wave velocity of soil, while design groups are defined by characteristic period. Detailed information can be obtained from the code (2016). Figure 4 illustrates Ve_benchmark corresponding to different site types and design groups constructed according to Fig. 3 (Zhou et al. 2020b).

Fig. 4

Design spectra for Ve_benchmark

Figure 5 illustrates the design input energy spectrum for self-centering systems with different structural features and seismic intensities. It is constructed based on the Ve_benchmark presented in Figs. 3 and 4. τ, ρ, φ and λ are the corresponding correction factors related to structural features. detailed information of τ, ρ, φ and λ can be derived from the reference (Zhou et al. 2020b). Results showed that the proposed procedure can reasonably predict the input energy for self-centering systems (Zhou et al. 2020b). E_I of the system can be derived from Eq. (2).

Fig. 5

Design Ve spectrum

As for E_H, Zhou et al. (2020b) proposed E_H/E_I spectra to determine the hysteretic energy demand E_H for self-centering systems. Equation (3) gives the method to calculate the target E_H / E_I spectrum. The results show that the proposed E_H / E_I spectrum can give a reliable estimation of E_H / E_I for self-centering systems. E_H of the target system can be derived from the E_H / E_I spectrum. Detailed information can be obtained from the reference.

$$\left( {E_{{\text{H}}} /E_{{\text{I}}} } \right)_{{\xi ,\mu ,\eta }} = 0.35I_{1} \cdot I_{2} \cdot I_{3}$$

(3a)

$$I_{1} = 5.75 \cdot \xi ^{{0.28}} \cdot \eta ^{{1.06 + 0.17 \cdot \ln \left( {\xi - 0.0087} \right)}}$$

(3b)

$$I_{2} = \left( {0.014 + 0.08\eta } \right) \cdot \xi ^{{ - 0.56 - 0.52 \cdot 0.23^{\eta } }}$$

(3c)

$$I_{3} = A + B \cdot T + C \cdot T^{2}$$

(3d)

$$A = 0.35 + 0.52 \cdot \mu - 0.06 \cdot \mu ^{2}$$

(3e)

$$B = - 0.11 \cdot \ln \left( {\mu - 1.19} \right)$$

(3f)

$$C = 0.02 - 0.04 \cdot 0.80^{\mu }$$

(3g)

2.2.2 Distribution of E _H in structures

Many theoretical and numerical studies have been conducted to quantify energy distribution in conventional systems (Bojorquez et al. 2008; Lopez-Barraza et al. 2016; Du et al. 2019; Tu et al. 2018). Song et al. (2021) evaluated the distribution of E_H in self-centering frame structures with various structural features and heights. Empirical equations were established to quantify the hysteretic energy demands for hybrid joints, as shown in Eq. (4) and Table 1.

$$\begin{aligned} E_{{{\text{Hi}},joint}} /E_{{{\text{H,joint\_all}}}} &= (A_{{11}} + A_{{12}} \cdot PGA)\frac{{H_{i} }}{H} + (A_{{21}} + A_{{22}} \cdot PGA)(\frac{{H_{i} }}{H})^{2} \hfill \\ &\quad + (A_{{31}} + A_{{32}} \cdot PGA)(\frac{{H_{i} }}{H})^{3} + (A_{{41}} + A_{{42}} \cdot PGA)(\frac{{H_{i} }}{H})^{4} \hfill \\ \end{aligned}$$

(4)

where E_{Hi, joint} is the hysteretic energy demand of hybrid joints at the i-th floor; E_{H, joint_all} is the energy demand of all hybrid joints; H_i/H is the height of each floor normalized by the total height of the structure; n is the total number of the floor. Meanwhile, the results showed that self-centering parameter λ has non-negligible effects on E_{Hi, joint} when PGA ≤ 0.2 g, especially E_{Hi, joint} of the top floor, denoted as E_{Hn, joint}. A modified method was suggested to estimate E_{Hn, joint} / E_{H, joint_all} considering λ, as shown in Eq. (5) and Table 2. It has been demonstrated that the proposed approaches can be adopted to quantify the distribution of E_H within SCCFs appropriately (Song et al. 2021).

$$E_{{{\text{Hn}},joint}} /E_{{{\text{H,joint\_all}}}} = (A_{{11}} + A_{{12}} \cdot PGA) + (A_{{21}} + A_{{22}} \cdot PGA) \cdot \lambda$$

(5)

Table 1 Fitting results for distribution of E_H

Table 2 Fitting results for E_{Hn, joint} / E_{H, joint_all}

It should be noted that NZS3101:2006 (2006) uses self-centering parameter λ to consider relations between the self-centering property and the energy-dissipation capacity. It is defined as the ratio of resisting moment attributed from PT tendons M_PT to that of mild steels M_S, as:

$$\lambda {\text{ = }}\frac{{M_{{{\text{PT}}}} }}{{M_{{\text{s}}} }} \ge 1.0$$

(6)

Normally, λ = 1 ~ 2 is adopted as a key index to design the basic relation between self-centering and energy-dissipation capacities for SCCFs (Pampanin et al. 2010). However, as discussed in Sect. 2.2.1 and Fig. 3, η is defined as the ratio of the yield strength to represent the energy-dissipation capacity in the proposed energy spectra, which can be obtained from Eq. (7a) (Pampanin et al. 2010). In order to switch λ and η in design procedures, the relation of λ with η can be given based on Eq. (6) and Eq. (7a) as:

$$\eta = \frac{{2M_{{\text{S}}} }}{{M_{{\text{S}}} {\text{ + }}M_{{{\text{PT}}}} }}$$

(7a)

$$\eta = \frac{2}{{\lambda {\text{ + }}1}}$$

(7b)

2.3 Conversion of the hysteretic energy demand as a design parameter

In order to consider the effect of the hysteretic energy demand on the structural performance and the damage development, it needs to be converted as a design parameter in EBSD. Zhou et al. (2020a) proposed a damage model composing of structural deformations and the hysteretic energy demand of hybrid joints E_Hjoint to quantify the damage development in hybrid joints, as shown in Eq. (8).

$${\text{DI}}_{{\theta _{{\text{c}}} }} = \frac{{\theta _{{\text{m}}} - \theta _{{\text{r}}} }}{{\theta _{{\text{u}}} - \theta _{{\text{r}}} }}{\text{ = }}\frac{{\theta _{{\text{c}}} }}{{\theta _{{\text{u}}} - \theta _{{\text{r}}} }}$$

(8a)

$${\text{DI}}_{{E_{{\text{H}}} }} = \beta \frac{{E_{{{\text{Hjoint}}}} }}{{M_{{\text{y}}} \theta _{{\text{u}}} }}$$

(8b)

$${\text{DI}} = {\text{DI}}_{{\theta _{{\text{c}}} }} + {\text{DI}}_{{E_{{\text{H}}} }}$$

(8c)

where E_Hjoint represents the hysteretic energy demand of hybrid joints under cyclic loads; θ_m and θ_r are the maximum and recoverable deformation, respectively; θ_u represents the ultimate deformation under monotonic loads; M_y represents the design moment for hybrid joints, which generally corresponds to the state when PT tendons yield; β represents a non-negative factor related to energy-dissipation capacity; θ_c = θ_m—θ_r represents the residual deformation of the structure. Equation (9) can be used to quantify θ_u for hybrid joints (El-Sheikh et al.2000).

$$\theta _{u} = \frac{{\varepsilon _{{cc}} }}{c} \cdot L_{{cr}}$$

(9a)

$$L_{{cr}} {\text{ = min}}\left\{ {2c\beta ^{\prime},b^{\prime\prime}} \right\}$$

(9b)

where ε_cc represents the ultimate strain of the confined concrete; c represents the compression height of the beam; L_cr represents the length of the plastic hinge developed along the beam; β′ is the coefficient corresponding to the concrete compression height; and b″ is the width of the confined concrete.

Equation (8) can be re-written as:

$$M_{{\text{y}}} = \frac{{\beta E_{{{\text{Hjoint}}}} }}{{{\text{(DI}} - \frac{{\theta _{{\text{c}}} }}{{\theta _{{\text{u}}} - \theta _{{\text{r}}} }})\theta _{{\text{u}}} }}$$

(10)

It can be seen that Eq. (10) converts E_Hjoint as a design parameter by relating M_y with E_Hjoint and the deformation responses. Meanwhile, the structural damage state under certain seismic intensities can also be considered by selecting desired damage index DI.

As discussed in the reference (Zhou et al. 2020a), β closely relates to structural features and has great effects on the damage evaluation. Zhou et al. (2020a) proposed Eq. (11) to determine β for hybrid joints.

$$\beta = 0.0742(1.444\rho _{\nu } - 0.935)(0.736 + 0.171\lambda )(0.026f_{{\text{c}}} - 0.213)$$

(11)

where ρ_v represents the stirrup reinforcement ratio at beam ends, f_c represents the concrete strength.

2.4 Determination of critical design parameters

To achieve multi-performance objectives, DI, θ_m, θ_r, and θ_c in Eq. (10) need to be quantified corresponding to different requirements. Zhou et al. (2020a) investigated the damage development and suggested damage intervals for hybrid joints, as shown in Table 3. Compared with damage intervals presented by Park–Ang for conventional concrete structures (Park et al. 1985), the damage limits corresponding to different damage states are extended, implying the superiorities in the performance improvement and damage control of self-centering systems (Zhou et al. 2020a). Meanwhile, it has been demonstrated that well-designed hybrid joints can limit structural damages within the joint and prevent other critical components from severe damages.

Table 3 Damage intervals for hybrid joints

According to Eq. (10), smaller DI indicates less damages in the hybrid joints, which results in bigger M_y. Designers are free to choose a DI for desired damage states under target seismic intensity.

The damage development and behaviors of 29 hybrid joints under cyclic loads were analyzed to investigate deformation indexes (Zhou et al. 2020a). The results showed that θ_c under minor damage states were all less than 0.1%, while θ_m corresponding to a minor earthquake was suggested based on the Chinese building code (2016) (Zhou et al. 2020a). According to the study, θ_c = 0.2% was adopted for DBE to ensure the minor damage state and structural integrity (Zhou et al. 2020a). Meanwhile, ACI T1.2–03 recommend θ_m = 3.5% to ensure the stability of force transferring under MCE (ACI 2003). In addition, to satisfy with the repairable performance objective for MCE, θ_c = 0.4% was adopted to control the damage developed in structures. Zhou et al. (2020a) suggested the damage-based deformation indexes for hybrid joints, as listed in Table 4, where DBE represents the design-based earthquake, MCE represents the maximum considered earthquake. Detailed information can be derived from the reference (Zhou et al. 2020a).

Although θ_m, θ_c are suggested in Table 4, designers can select other values for various performance objectives based on reliable analyses.

Table 4 Performance-based deformation indexes

2.5 Determination of design rotations for hybrid joints

Story drift θ_i is normally adopted as the design index, which is different from rotations of hybrid joints θ_n. In this case, θ_n need to be converted from story drifts θ_i in the design procedure. The method elaborated in PRESSS Design Handbook (2010) is adopted in this paper to obtain rotations for hybrid joints.

A normalized nonlinear mode deformation δ_i is adopted to elaborate the deformed shape at the peak displacement response (Pampanin et al. 2010). For frames higher than four floors, an inelastic mode deformation is defined by Priestley et al. (2002), as shown in Eq. (12).

$$\delta _{{\text{i}}} = \frac{4}{3}\left(\frac{{H_{i} }}{{H_{n} }}\right)\left(1 - \frac{{H_{i} }}{{4 \cdot H_{n} }}\right)$$

(12)

The target displacement at the i-th floor can be given as:

$$\Delta _{{\text{i}}} = \delta _{{\text{i}}} \left(\frac{{\Delta _{{\text{c}}} }}{{\delta _{{\text{c}}} }}\right)$$

(13)

where δ_c is the normalized displacement of the first floor obtained from Eq. (12); Δ_c is the displacement of the first floor.

According to the design handbook (2010), the story drift θ_i can be divided as the sum of the yielding drift θ_y and the beam rotation θ_p. Priestley has noted that for frames utilizing unbonded post-tensioned tendons (Priestley 2002), θ_y can be obtained as:

$$\theta _{{\text{y}}} = 0.0004(\frac{{L_{{\text{b}}} }}{{h_{{\text{b}}} }})$$

(14)

where L_b and h_b are the length and height of beams.

Therefore, the rotation of the hybrid joint θ_n can be derived from the following equation (Pampanin et al. 2010):

$$\theta _{{\text{p}}} = \theta _{{\text{i}}} - \theta _{{\text{y}}}$$

(15a)

$$\theta _{{\text{n}}} = \frac{{\theta _{{\text{p}}} }}{{1 - \frac{{h_{{\text{c}}} }}{{L_{{\text{b}}} }}}}$$

(15b)

where h_c is the height of column sections.

Figure 6 presents the flow chart of the EBSD procedure for SCCF proposed in this paper. The procedure has three steps: determination of design parameters, capacity design for critical components and evaluation of structural performance. It allows designers to select different performance objectives based on desired damage states and deformation responses at target seismic intensities.

Fig. 6

Flow chart for EBSD

3 Application of EBSD

To demonstrate the applicability of EBSD, the concrete building presented in the PRESSS Design Handbook (2010) is adopted as the prototype building. A five-story SCCF and an eight-story SCCF are designed using both the EBSD and DDBD procedures under different hazard levels. Seismic performances of the design examples are compared by nonlinear dynamic analyses.

3.1 Prototype building

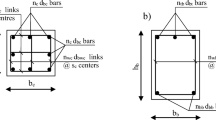
The prototype building is assumed to be located in areas where the Site Class is classified as II according to the Chinese building code (2016). The characteristic period T_g = 0.4 s. Figure 7a shows the plan view of the prototype building. The building includes two types of seismic force resisting systems: SCCF in the East–West direction and self-centering shear walls in the North–South direction. In this paper, only the SCCF in the East–West direction is designed and examined. The elevation view of the frame is presented in Fig. 7b. Dimensions of beams and columns are 400 mm × 650 mm and 700 mm × 700 mm for both EBSD and DDBD designed structures.

Fig. 7

Geometry of the prototype building

In order to validate the applicability of the proposed design procedure, different hazard levels are adopted for different design examples. The five-story SCCF is designed assuming the seismic fortification intensity equaling to 7 degree according to the Chinese building code (2016), while that of the eight-story SCCF is 8 degree. It should be noted that all material and dimension information are the same for both the five-story and eight-story design examples.

Table 5 lists the material properties of the prototype building. They are adopted for both EBSD and DDBD designed structures.

Table 5 Material properties

In this paper, the inter-story drift limit is selected as 2% for both design examples in EBSD and DDBD design procedures. λ is chosen as 2 to ensure a full re-centering capacity for the system. Design deformations of two SCCFs are given in Tables 6 and 7. They are adopted in both the EBSD and DDBD procedures. Design rotations of hybrid joints θ_n at each floor are summarized in Tables 6 and 7. Δ_i is calculated according to Eq. (12) and Eq. (13). θ_n is calculated based on Eq. (14) and Eq. (15).

Table 6 Design rotation for hybrid joints in the five-story structure

Table 7 Design rotation for hybrid joints in the eight-story structure

3.2 Structure design

3.2.1 Determination of design parameters

According to Sect. 2 and Fig. 1, the design energy spectrum needs to be determined first. As discussed in Sect. 2.2, the ductility factor μ is adopted for defining nonlinear behaviors of systems and constructing constant-ductility spectra. Priestley (1999) noted that for jointed precast systems, superior ductility can be guaranteed compared with traditional concrete systems. An allowable limit of μ = 6 can be selected for frame structures. For both design examples, θ_y = 0.51% and θ_u = 3.4% can be calculated according to Eq. (14), Eq. (15) and Eq. (9). The resultant μ = 6.67. Hence, μ = 6 is adopted to construct energy spectra for both design examples in this case. According to Eq. (7), η = 0.67.

Based on the calculated structural features and the proposed design energy spectra shown in Fig. 5 and Eq. (3), key parameters of the target energy spectra for both the examples are summarized in Table 8. Design energy spectra can be obtained according to procedures elaborated in Sect. 2.2.1. Figure 8 present the design energy spectra for both the five-story and eight-story SCCFs.

Table 8 Target design energy spectra

Fig. 8

Design energy spectra

Table 9 lists the main energy indexes of the two design examples.

Table 9 Energy indexes

As discussed in Sect. 2.2, results of E_{Hi, joint} / E_{H, joint_all} for both the five-story and eight-story design examples are listed in Tables 10 and 11. In this paper, the maximum of E_{Hi, joint}/E_{H, joint_all} is adopted for hybrid joints at each floor to conservatively design the structure. Thus E_{Hi, joint}/E_{H, joint_all} = 0.261 and E_{Hi, joint}/E_{H, joint_all} = 0.171 are adopted for the two design examples, respectively. It has been demonstrated that for self-centering frames, the energy demand can be equally distributed among hybrid joints at the same floor (Song et al. 2021). Since there are a total of eight joints per floor, the energy demand is about 1/8 of all joints at the same floor. Thus, the energy demand of each hybrid joint is E_Hjoint = 72 KN·m in the five-story SCCF, while E_Hjoint = 109 KN·m in the eight-story SCCF.

Table 10 E_{Hi, joint} / E_{H, joint_all} for the five-story SCCF

Table 11 E_{Hi, joint} / E_{H, joint_all} for the eight-story SCCF

According to Tables 3 and 4, DI = 0.5 and θ_c = 0.4% are selected to limit the damage development for the repairable requirement after seismic actions in both design examples. The recoverable deformation θ_r = 0.834%.

3.2.2 Capacity design for critical components

Based on Eq. (10), the design moment of hybrid joints can be calculated. Table 12 lists design moments of both design examples using EBSD and DDBD procedures (Priestley 2002).

Table 12 Design moments for hybrid joints

Reinforcement design for hybrid joints is performed according to NZS3101 Appendix B (2006). Detailed reinforcement information for all design examples is presented in Table 13.

Table 13 Detailed information of reinforcement for hybrid joints

M_hybrid—θ responses for a typical hybrid joint can be derived from that contributed by PT tendons M_PT and mild steels M_S. Four performance points, including decompression, MS yield, PT yield and ultimate limit, can be calculated based on reinforcement properties listed in Table 13. The procedure elaborated in the PRESSS Design Handbook (2010) is adopted to calculate corresponding M_hybrid, M_PT and M_S. Table 14 and Fig. 9 summarize the moment-rotation co-ordinates of the EBSD and DDBD designed hybrid joints for the two design examples. It can be seen from the table that the EBSD designed structures require higher design moments than that of the DDBD designed structures. Since the cumulative effect is considered in the EBSD, bigger design strength shall be needed in the EBSD designed structures to limit damages developed in structures.

Table 14 Moment-rotation co-ordinates for hybrid joints

Fig. 9

Moment-rotation co-ordinates for hybrid joints

4 Evaluation of seismic performance

4.1 Numerical modeling

Figure 10 shows the modeling of the hybrid joint developed in OpenSees (2000). The hybrid model was developed using zero-length spring element. ElasticMultilinear material in OpenSees was selected to simulate M_PT—θ responses. Steel02 material is adopted to model M_S—θ responses. The hysteretic behavior of hybrid joints can be obtained by combining two materials with parallel command.

Fig. 10

Numerical model for hybrid joints in OpenSees

A displacement-based fiber element is used to model the column. The length of the element, where the plastic hinge formed during earthquakes L_cr, can be calculated according to Eq. (9). Behaviors of mild steels are modeled by Steel02 with CorotTruss elements. Since mild steels are debonded for a length through the lower part of columns, rigid links are used to model relative relations between columns and mild steels. Rayleigh damping model is utilized based on 5% of critical damping ratio to the first and third modes of models. Table 15 shows the first three modal period of the EBSD and DDBD designed structures.

Table 15 Modal period of structures

The columns and beams are capacity designed to remain elastic, while all the nonlinearities are concentrated at the joint zones and at the base of columns at the first floor. Therefore, only nonlinearities of the joints and column based are modeled, while beams and columns are constructed with elastic elements. Post-processing has been performed to guarantee these elements remain elastic after seismic actions.

The experimental data of M-P-Z4 and O-P-Z4 specimens obtained from the NIST program (Cheok et al. 1993) are adopted to validate the modeling approaches discussed above. Four mild steels were installed in M-P-Z4 specimen, while O-P-Z4 specimen had six mild steels. Detailed information of specimens can be obtained from the reference (Cheok et al. 1993). Figures 11 and 12 present the moment—rotation curves of the tested hybrid joints from the experimental data and numerical results. It shows that the strength, stiffness and the flag-shaped hysteretic behavior of hybrid joints with different mild steels under cyclic loads can be modeled well using the proposed numerical model.

Fig. 11

Comparison of the numerical result with the test data of M-P-Z4

Fig. 12

Comparison of the numerical result with the test data of O-P-Z4

4.2 Ground motions

Table 16 shows the summary of the 22 set far-field ground motions adopted in this study (FEMA 2009). Each set has 2 ground motion records in different directions. Thus, a total of 44 ground motion records were used in analyses.

Table 16 Detailed information of selected ground motions

4.3 Structural performance

To compare structural responses DI, θ_c, and θ_m with the design targets, nonlinear dynamic analyses are conducted on both the EBSD designed structures with 44 ground motions. According to the Chinese building code (2016), ground motions are scaled as PGA = 220 gal for the five-story SCCF and 400 gal for the eight-story SCCF, respectively. The results of DI, θ_c, and θ_m of all hybrid joints are listed in Table 17.

Table 17 Analytical results

In the design procedure, DI = 0.5 was selected to limit the damage development for the repairable requirement after seismic actions. For the five-story SCCF, DI from all seismic actions is less than 0.5 except for three specific ground motion records, which satisfies with the repairable limit defined in Table 3. Meanwhile, damages developed in the eight-story SCCF surpass the repairable limit under only four ground motions. The mean values of DI under 44 seismic actions are 0.306 and 0.415, respectively. They are both smaller than the design target. Since the maximum of E_{Hi, joint}/E_{H, joint} was adopted in this paper to conservatively design the structure, the actual energy demand of each floor is less than the design value. As shown in Eq. (8), DI decreases with smaller ∫dE, which leads to the numerical results less than design expectation. Nevertheless, according to Table 3, DI = 0.306 and 0.415 represent the moderate damage state, implying good agreement with the desired damage development. Meanwhile, θ_c and θ_m well match the target objectives determined during the EBSD design process. According to the standard deviations listed in Table 17, the discrepancy of quantified damages in hybrid joints is relatively bigger than that of deformation indexes. It indicates that damages developed in structures not only relate to structural features, but also ground motion characteristics. Damages formed in structures might vary greatly under different seismic actions.

Figure 13 presents statistical results of E_{Hi, joint}/E_{H, joint} under 44 scaled ground motions for the EBSD designed five-story and eight-story SCCFs. It can be seen that the mean values of E_{Hi, joint} / E_{H, joint} are in good agreement with the predicted energy distribution listed in Tables 10 and 11. It indicates that the proposed method can reasonably quantify the distribution of energy demand in self-centering frame structures. On the other hand, great discrepancy in the energy distribution under different seismic actions can be observed according to statistical results (STD, MEAN + STD and MEAN–STD). It implies that the energy factor depends on both the structure features and earthquake characteristics.

Fig. 13

Comparison of energy dissipation

Seismic fragility analyses are conducted on both examples designed using the EBSD and DDBD procedures. Figure 14 shows fragility curves of two designed structures corresponding to three limit states, including Immediate Occupancy (IO), Life Safety (LS) and Collapse Prevention (CP). These limit states are defined with the maximum deformation in accordance with minor earthquakes, DBE and MCE given in Table 4. It can be seen that for the same S_a(T₁, 5%), DDBD has higher probability of exceedance than EBSD on all three states considered in both design examples. This means that DDBD designed structures are likely to have more damages than the EBSD designed structures. Similarly, the differences of 50% exceedance probability between EBSD and DDBD designed five-story structure for IO, LS and CP are 0.12 g, 0.13 g, and 0.14 g, respectively for the five-story SCCF, while that of the eight-story structure are 0.9 g, 0.11 g and 0.14 g. This shows DDBD designed structures are more vulnerable. Since structural damages gradually develop and accumulate with bigger earthquakes, cumulative damages will have more significant effects on structural performance. Therefore, the EBSD designed structures exhibit better aseismic capacity, which results from the hysteretic energy considered in EBSD.

Fig. 14

Comparison of fragility curves

5 Conclusions

To improve structural performance and optimize post-earthquake repairable capacity, self-centering frame structures have been developed. These systems exhibit excellent aseismic performance and resilient capacities, whereas existing design procedures cannot consider the effects of cumulative damages. This paper presents an energy-based seismic design (EBSD) procedure for self-centering concrete frame structures. Based on a proposed damage model, hysteretic energy demand E_H is introduced as a key design parameter to consider the effects of cumulative damages on structures. In addition, the damage state and structural deformation under the target earthquake intensity can be assigned. EBSD allows designers to select performance objectives for different seismic intensities corresponding to different structural performance targets. The detailed derivation of EBSD is illustrated in the paper. To demonstrate the applicability of EBSD, two SCCFs with different heights and hazard levels are designed and analyzed by nonlinear dynamic analyses. The results show that the EBSD designed structures exhibit better performance and more controlled damage than the DDBD. Meanwhile, the damage state and deformation responses well match the objectives determined during the EBSD design process. The results show that the well-designed structures satisfy with the repairable performance objective, which indicates significant source savings and downtime reduction for the structure after earthquakes.