1 Introduction

Dynamic response of soil-foundation-structure systems has been the aim of numerous studies in the last four decades. Two basic methods and various alternates exist for the analysis of the soil-foundation-structure interaction (SFSI) phenomenon. In the direct method, the entire soil-foundation-structure system is analyzed in a single step, usually by a finite element model. The direct method accepts material and geometrical nonlinearity, but three-dimensional nonlinear dynamic analyses are still very expensive in computational terms, and have inherent problems in satisfying the radiation condition of the wave field towards infinity. To overcome the spatial limitations of the unbounded soil medium, special absorbing boundaries (Lysmer and Kuhlemeyer 1969; Chongbin and Valliappan 1993) are used in the finite element model, in order to restore the conditions of the unbounded medium. However, such models for SFSI problems usually result in large equation systems that require extensive computational resources (Yerli et al. 2003). The substructure method, on the other hand, is widely used in practice, as it is relatively easy to gain physical insight. Many numerical tools exist for the analysis of each subdomain, depending on the complexity of the model, and ranging from simple equivalent mass-spring-dashpot systems (Veletsos and Meek 1974; Bielak 1975) to more complex finite element or boundary element models (Karabalis 2004; Pitilakis and Clouteau 2010).

In the substructure approach, the problem is typically decomposed into two subtasks, namely kinematic and inertial interaction, the solution of which provides the effective excitation and the response of the superstructure respectively. Solving the inertial interaction problem requires determining the dynamic impedance functions (i.e. stiffness and damping) of the foundation, which constitutes the single most important subtask in such analyses. Detailed reviews of the subject can be found in Gazetas (1991), Pais and Kausel (1988) and Mylonakis et al. (2006). Once the dynamic impedance functions of the foundation are known, the response of the superstructure can be readily estimated from standard dynamics of structures analyses (Chopra 2011). In the framework of performance-based assessment, correct calculation of dynamic stiffness and damping of the foundation is crucial for the estimation of seismic demand parameters, as well as for the structural capacity.

Impedances proposed in literature concern mainly rigid foundations. For practical engineering purposes (i.e. reinforced concrete structures) this assumption is valid and compliance of the foundation itself is typically neglected. According to Gazetas (1983), the main parameter that modifies the response of flexible foundations, with respect to the case of rigid foundations, is the decrease of the static foundation-soil system stiffness in the former case. For flexible foundations, complicated analytical solutions indicate that for low frequency vibrations the variation of foundation-soil stiffness is not significantly affected by footing compliance (Iguchi and Luco 1981; Gucunski and Peek 1993b; Liou and Huang 1994; Chen and Hou 2009). As a result, the value of dynamic foundation-soil stiffness can be considered to be equal to the one for static, small-strain conditions, accounting for foundation flexibility.

Historical masonry structures are often characterized by massive masonry foundation systems combined with significant mass and elaborate structural systems. The supporting walls of the structure are extended to a certain depth in the soil, followed by a widening in the wall section, forming the foundation system. Dynamic response of such complex systems is likely to be influenced by SFSI, especially for monuments not founded on rigid rock. In addition, such flexible foundation systems can only transfer negligible tensile stress and no bending moment. Consequently, flexible brittle foundations cannot undergo significant rocking movement, which should be properly taken into consideration in the assessment of the overall structural response. So far, from practical engineering point of view, very few means exist to take into account foundation flexibility in soil-foundation interaction (SFI) analyses.

In the framework of European project PERPETUATE (Performance-based approach to earthquake protection of cultural heritage in European and Mediterranean countries) (Lagomarsino et al. 2010), we propose dynamic linear stiffness values for flexible masonry foundations, called hereafter “foundations”, to account for foundation flexibility in SFI analyses, for practical use in a performance-based design framework. These values of soil-foundation stiffness (“spring values” for practical applications) refer to low-frequency vibration, where, as mentioned above, dynamic response is approximately equal to static. We present a simplified, yet efficient procedure to take into account foundation flexibility in SFI analysis, in order to produce linear dynamic springs for structural numerical software to estimate seismic response. These flexible foundation-soil stiffness values were used in the TREMURI software (Lagomarsino et al. 2013; Cattari et al. 2014) to estimate the response of historical masonry monuments by static analyses. The pertinence of the proposed dynamic linear stiffness values is assessed by application to the Arsenal De Milly masonry monument in Rhodes, Greece, where response is evaluated and compared with and without the flexible foundation-soil system. Departing from historical masonry structures, the proposed methodology can be applied as a first assessment of importance of flexible foundation systems on the superstructure response.

2 Foundation-soil stiffness

The dynamic impedance S of a rigid foundation along any degree-of-freedom can be expressed in the familiar complex form as:

$$\begin{aligned} {{\varvec{S}}}={{\varvec{K}}}+ i\,\omega \,{{\varvec{C}}} \end{aligned}$$
(1)

where the real part K stands for dynamic stiffness and is represented by a spring. The imaginary part \((\omega {{\varvec{C}}})\) is referred to as loss stiffness, \(\omega \) being the cyclic excitation frequency; C is represented by a dashpot coefficient accounting for the combined effect of radiation and material damping in the soil medium. Radiation damping corresponds to energy dissipation due to waves emanating from the soil-foundation interface in perfectly elastic soil. The second part (hysteretic damping) is associated with energy loss due to hysteretic action in the soil material. Equation (1) can be cast in the alternative form (Gazetas 1983):

$$\begin{aligned} {{\varvec{S}}}={{\varvec{K}}}\left[ {{\varvec{k}}}(\alpha _{0},\,\nu )+i\,\alpha _{0}\, {{\varvec{c}}}\,\left( {\alpha _{0},\,\nu }\right) \right] \,\left( {1+2\,i\,\xi }\right) \end{aligned}$$
(2)

where now dynamic stiffness is expressed in terms of a static part, \(K\), times a dynamic modifier, k; the radiation dashpot coefficient is similarly expressed in terms of static stiffness and the product of a dimensionless frequency, \(\alpha _{0} (= \omega r/V_{s}\), where \(r =\) characteristic foundation dimension and \(V_{s} =\) shear wave velocity of soil profile) times a dynamic modifier, c. In the above equation, \(\xi \) denotes the hysteretic material damping ratio, \(\nu \) the Poisson’s ratio and \(i =\) the imaginary unit. Linearity is implicit in Eq. (2). In this study only stiffness of the foundation-soil is of interest, to be introduced in finite element software for calculation of dynamic system response.

Foundation impedance is an integral force acting from the soil to the basement in response to certain motion of the soil-basement contact surface. For a rigid basement, this motion in every point of the surface is fully described by a six by six impedance matrix for each frequency. For a flexible foundation, the motion of the contact surface is no longer rigid, as it depends on the distributed loads applied to the foundation-soil interface. Different types of loading (e.g. concentrated load applied in the centroid of the foundation, or uniformly distributes load) will result in different response forces. In this study, an assumption of uniformly distributed load on the soil-foundation interface is made (Pitilakis and Karatzetzou 2012).

In case of historic masonry structures, the supporting walls are typically extended in the soil, down to a depth of a few meters, as seen in Kallioudakis et al. (2011), forming the structure’s foundation system. Moreover, the materials that form the foundation are usually deteriorated due to weathering and aging effects (Kržan et al. 2012, 2014). Naturally, initial masonry material properties, such as stiffness and strength, have to be modified in order to account for the aforementioned effects. In modern codes for masonry structures, the initial value of masonry’s Young’s modulus of elasticity is reduced by 50 %, as conventionally proposed in the Italian Code for Structural Design 2008 (NTC 2008) and in Eurocode 8 (CEN 2005). However, the large number of existing monumental foundations makes it difficult to consider a more specific value for the foundation elastic modulus. In addition, uncertainties concerning masonry material properties of existing monuments are important, whereas there are not enough laboratory tests and field measurements to validate the aforementioned assumption.

Regarding stiffness of flexible foundations, as said by Iguchi and Luco (1981) and Gucunski and Peek (1993a) it can be assumed that for values of \(\alpha _{0}\) lower than 1, dynamic stiffness of the foundation-soil system is approximately equal to the initial small-strain stiffness, the so-called static stiffness \(\hbox {K}_{\mathrm{static}}\). Moreover, in SFI analysis, for the prevailing resonant frequency of the soil \(f_{0}\) (let it be single layer profile, thus \(f_{0}=Vs/4H\), with \(H =\) thickness of the layer), \(\alpha _{0}\) depends solely on the foundation size and the soil layer thickness. Results show that for typical monuments, \(\alpha _{0}\) varies between 0 and 1.

3 Proposed methodology

The proposed calculation of stiffness of monumental flexible masonry foundations can be decomposed in four discrete steps, which are explained below.

In the first step, dimensionless frequency \(\alpha _{0}\) is determined for the foundation-soil system for the configuration and the degree-of-freedom of interest.

Following the estimation of \(\alpha _{0}\) and provided that it does not exceed the value of 1, in the second step the small-strain “static” foundation-soil system stiffness \(K_{static}\) can be readily calculated by closed-form analytical solutions proposed in literature, accounting for linear (Gazetas 1991; Mylonakis et al. 2006) or equivalent-linear soil behavior (Pitilakis et al. 2013). For practical purposes, \(K_{static}\) is calculated for any degree-of-freedom of interest (translational or rotational).

In the third step, the initial masonry foundation wall modulus of elasticity \(E_{w,init}\) has to be estimated from building material properties. The initial value of \(E_{w,init}\) has to be properly reduced to \(E_{w}\) in order to account for aging, weathering or other deterioration effects. As noted above, reduction by 50 % is reasonable for most masonry monuments. The elastic modulus of the soil \(\hbox {E}_{\mathrm{s}}\) may be calculated by standard equations (Bowles 2001).

In the final step, the reduction of stiffness of the monumental flexible masonry wall foundation can be calculated by the proposed diagrams in this paper, with respect to the ratio of \(E_{w} / E_{s}\), for the degree-of-freedom of interest (translational or rotational).

4 Numerical modeling

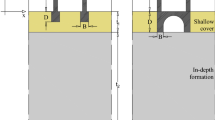
Static two-dimensional plane-strain analyses of soil-foundation models are performed to calculate the stiffness of the flexible foundation-soil system. For the analyses, the general purpose finite element code ABAQUS (ABAQUS 2012) is utilized. Equivalent springs are estimated from reaction forces for unit displacement and rotation, for translational and rotational modes respectively, at the geometrical center of the assumed foundation plane, as this is where usually the finite element model or the macroelement of the superstructure (i.e. the supporting masonry wall) ends (Fig. 1). Surface and embedded foundations resting on a homogeneous halfspace soil profile are considered for the analyses. We performed analyses for different foundation geometries and for different soil and foundation properties covering a wide range of monumental masonry foundations.

Fig. 1
figure 1

Schematic representation of the soil-foundation system for the horizontal translational degree-of-freedom for the horizontal and embedded foundation types considered in the analyses

Full size image

In the numerical simulation of the foundation, 4-node quadratic plane-strain elements are used for the translational degrees-of-freedom, while beam elements are used for the rotational motion. In both cases, the soil is modeled with plane-strain elements. The foundation is rigidly connected to the soil. Linear elastic behavior is assumed for both soil and foundation media. The height of the soil mesh was chosen to vary between 1.5 and 30 times the masonry foundation width \(B\), as for static analysis the created stress bulbs in the soil do not exceed two to three times the foundation width (Gazetas 1983). The width of the soil mesh was four times its height, in order to avoid spurious wave reflections at the boundaries. In all analyses, the resulting displacement field was zero at (or close to) the boundaries, to make sure that boundary effects were avoided.

Concerning the estimation of the resisting force at the foundation geometrical center, for simplicity reasons and by taking into account that a masonry foundation wall may be considered stiff enough in its transversal dimension, we assumed uniform distribution of the load on the foundation-soil interface. The schematic representation of the system for the horizontal degree-of-freedom for both surface and embedded foundations is shown in Fig. 1.

Foundation type and geometry were carefully chosen from existing monuments extracted from the database of the PERPETUATE project (Pitilakis et al. 2011). Representative rectangular foundations of varying dimensions (height \(h\) and width \(B\)) were chosen for the analyses (Table 1). A question that was raised on how we estimate the actual dimensions of the monumental foundations. For embedded foundations, i.e. where the supporting masonry wall extends in the soil, the geometry of the foundation can be naturally assumed as the portion of the wall below the ground surface. On the other hand, for surface (or almost surface) foundations of monuments, one can assume that the lower part of the masonry wall acts as the foundation system. As seen from Table 1, the slenderness ratio \(h/b\) (height-over-half-width), where \(b=B/2\) is the half-width (Fig. 1) of the masonry of the masonry foundation, varies between 0.1 and 8, covering a wide range of foundation geometries. This wide range of foundation slenderness ratios is needed in order to capture both the in-plane and the out-of-plane response of the foundation wall.

Table 1 Dimensions of foundation’s systems
Full size table

Material properties for the masonry wall foundation have been chosen from reference values proposed in the Italian Code for Structural Design (NTC 2008) as a function of different masonry types and from the PERPETUATE database that concerns existing monuments (Pitilakis et al. 2011). Table 2 shows the elastic moduli of the masonry foundation wall and the soil properties. The elastic modulus value of the masonry foundation wall is reduced by 50 % from the initial value, in order to take into consideration the current condition of the masonry materials (cracked, deterioration due to environmental and aging effects, differential settlements etc). The soil properties that were used in these analyses correspond to four different typical soil classes according to Eurocode 8 soil classification scheme (CEN 2004).

Table 2 Masonry elastic modulus (initial), reduced elastic modulus by 50 % \((\hbox {E}_{\mathrm{w}})\), soil shear wave velocity \((V_{s})\) and soil elasticity modulus \(\hbox {E}_{\mathrm{s}}\) according to the soil type
Full size table

For every one (out of twelve, see Table 1) geometrical case of masonry foundation, analyses were performed for all seven masonry elastic modulus values and for all soil types. As a consequence, the resulting stiffness values for surface or embedded foundations for each vibration mode are the outcome of more than 330 finite element parametric analyses.

5 Stiffness of rigid foundations

The idea of the proposed methodology is to evaluate the stiffness of the flexible masonry foundation by properly reducing the stiffness for the geometrically equal rigid foundation, \(K_{j,rigid},\,j = h,\,v,\,r\) for the horizontal, vertical and rocking mode respectively; reduction depends on the foundation wall-to-soil Young’s modulus ratio \(E_{w}/E_{s}\). The later is considered an adequate normalization describing relative stiffness between the masonry foundation and the surrounding soil. As explained above, given that the dimensionless frequency \(\alpha _{0}\) is lower than 1, the dynamic stiffness of a foundation section can be approximated adequately by the “static stiffness”, the latter being the stiffness of the foundation-soil system under small-strain (static) loading. The advantage of this approach is that numerous well accepted analytical and numerical solutions exist for the calculation of the static stiffness \(K_{static}\) of rigid foundation, mainly for linear (Gazetas 1991; Mylonakis et al. 2006), but also for equivalent-linear soil behavior (Pitilakis et al. 2013). Knowing the static stiffness for the rigid foundation, we propose a reduction factor to account for masonry foundation flexibility in SFI analyses.

In order to validate our approach, we calculated numerically the static stiffness assuming rigid foundation and we compared with the available analytical solutions. We performed a set of static elastic finite element analyses that simulate the response of a rigid strip foundation laying on a homogeneous soil stratum over rigid bedrock, for the horizontal and vertical mode of vibration and for all geometry cases presented in Table 1. The finite element model was calibrated based on the static stiffness resulting from analytical solutions, so that the reaction force (to unit displacement) in the numerical model does not vary much from the analytical response.

Comparison of the analytical solution for strip foundations (Gazetas 1983) and of the reaction force from the finite element model is shown in Fig. 2, for surface foundation under horizontal (Fig. 2a) and vertical (Fig. 2b) displacement. In these plots, normalized stiffness is plotted for twelve different foundation geometries. We noticed that for horizontal translation, differences between the numerical and the analytical solution are negligible, whereas for vertical translation they tend to increase with increasing slenderness ratio \(h/b\). More interestingly, discrepancy between numerical and analytical values increases with increasing foundation slenderness ratio \(h/b\). In any case, the difference does not exceed a reasonable value of 28 %. This inconsistency could be attributed to the fact that in the numerical model, reaction force is calculated at the geometrical center of the foundation plan, while analytical solutions produce the reaction on the soil-foundation interface, ignoring foundation height (or slenderness).

Fig. 2
figure 2

Normalized static stiffness of the surface soil-foundation system for various height-over-half-width values of the foundation, a for horizontal and b for vertical foundation displacement. The numerical results are compared with the analytical solution from Gazetas (1983)

Full size image

For the rocking vibration, the foundation was modeled with a rigid beam, instead of 4-node quadratic plane-strain elements, because the latter cannot account for rotation. Effects of slenderness of the foundation are more pronounced in this case, and the computed values of static rocking stiffness present higher scatter compared to analytical solutions (Gazetas 1983), especially for foundation shapes with higher slenderness ratio \(h/b\). This inconsistency for slender foundations was expected, as it is rather difficult to simulate accurately the rocking response of a massless foundation by numerical means. Estimation of rocking stiffness is notably easier and more straightforward using analytical solutions, as the height of the foundation is irrelevant. In addition, as mentioned before, flexible masonry foundations cannot transfer bending moment to the soil, and therefore cannot support rocking vibration. To this end, comparison between numerical and analytical solution for rocking is not presented herein, and rotational response in the next section should be viewed under these considerations.

For embedded strip foundations resting on a soil layer overlaying rigid bedrock, no analytical solutions exist, at least to our knowledge, and therefore no safe conclusions can be drawn on the adequacy of the numerical solution.

Based on the aforementioned good convergence between the analytical and numerical estimate of the static stiffness of rigid foundations, we normalized the calculated static stiffness of flexible foundations \(K_{flex}\) to the stiffness of rigid foundations \(K_{rigid}\), calculated by a finite element model for a wide range of masonry foundation wall Young’s modulus \(E_{w}\).

6 Stiffness of flexible foundations

The reduction of stiffness for flexible masonry wall foundations is calculated as the ratio of the stiffness of the rigid masonry wall foundation \((K_{flex} / K_{rigid})\), with respect to the foundation wall-to-soil Young’s modulus \((E_{w}/E_{s})\). Stiffness reduction from rigid case has been calculated for surface and embedded foundations, for horizontal, vertical and rocking vibration modes and for different foundation geometries, as elaborated in previous sections.

Figure 3a shows the stiffness reduction of surface flexible foundation in the horizontal vibration mode. The reduction from the rigid foundation stiffness is very large for very low ratios of \(E_{w}/E_{s}\) (lower than 2), while \(K_{h,flex} / K_{h,rigid}\) increases with increasing \(E_{w}/E_{s}\). For ratios \(E_{w}/E_{s}\) larger than 18, \(K_{h,flex}\) tends to increase at constant rate. From Fig. 3a it is also clear that geometry of the assumed foundation is critical for the calculation of stiffness. For slenderness ratios \(h/b\) lower than 1, reduction from stiffness of rigid foundation is lower than it is for slenderness ratio \(h/b\) between 1 and 4. For \(h/b<1\) the stiffness for very flexible foundation-soil systems (large \(E_{w}/E_{s})\) is on average at 70 % of the rigid one, while ideally it will reach the value of rigid case for very large ratios of \(E_{w}/E_{s}\). For \(h/b>4\), stiffness reduces drastically from the rigid foundation for any \(E_{w}/E_{s}\), with the mean value is \(<\)20 % of the rigid case stiffness. For \(h/b\) between 1 and 4, the mean curve (and its standard deviation) is found between the two curves for \(h/b<1\) and \(h/b>4\). For each one of the three \(h/b\) groups of curves, standard deviation does not exceed 5 %.

Fig. 3
figure 3

Stiffness reduction of flexible foundation \((K_{flex})\) from rigid foundation \((K_{rigid})\) with respect to wall-to-soil elasticity moduli \((E_{w}/E_{s})\), for surface foundations and horizontal (a), vertical (b) and rocking (c) modes of vibration. Each dot represents a single numerical analysis of soil-foundation model. Thick lines represent average values and thin lines their standard deviation

Full size image

Numerical modeling does not allow for \(K_{h,flex}\) to reach \(K_{h,rigid}\) for large \(E_{w}/E_{s}\), as for flexible foundations a single node (at the centroid of the finite element foundation model) is constrained, while movement of all nodes in the rigid foundation model is constrained in all directions except the one of interest. For example, in the vertical mode horizontal and rotation motion of foundation nodes is constrained in order to assure rigid block vibration. This difference in the level of constrains eventually leads to different upper bound of stiffness for the flexible foundation with respect to the rigid one. Nevertheless, such a modeling was necessary in the light of the numerical simulation of the response of rigid foundations.

For the vertical vibration mode (Fig. 3b), two groups of curves are formed based on the slenderness ratio \(h/b\), notably when the latter is greater or \(<\)1. In this case, and contrary to the horizontal mode, for \(h/b<1\) values we observe higher reduction compared to the rigid foundation stiffness. For higher slenderness ratios \((h/b>1)\) the reduction from rigid case is still important but not as important as for lower \(h/b\) ratio. Apparently, the finite element model is able to capture salient effects of a rigid foundation submerging into a softer medium, like the soil, and particularly the lateral expansion of the soil in the vicinity of the foundation. Lower \(h/b\) values imply larger area of foundation in contact with the soil, compared to its height, and consequently larger stiffness reduction. Again, for every group of \(h/b\) geometries, standard deviation does not exceed 6 %.

Finally, Fig. 3c presents the stiffness reduction for the rocking mode of vibration. The scatter now is very significant, certainly attributed to the importance of foundation shape and geometry (slenderness ratio). Again two groups of curves are proposed, for \(h/b\) ratio greater and lower than 1. In the first case, the mean reduction can reach 80 % of the rigid stiffness, while in the second case (\(h/b\) lower than 1) flexible foundation stiffness does not exceed on average the 20 % of the rigid case. It is also observed that for slenderness \(h/b\) higher than 1, the computed mean value has a very large standard deviation (approximately 18 %), which is explained by the fact that the reaction moment to unit rotation greatly depends on the shape and the slenderness of the foundation. Because of the large scatter, reduction factors for the rocking stiffness should be used with caution.

For embedded foundations, the ratio of flexible-to-rigid stiffness for the foundation \((K_{flex}/K_{rigid})\) is shown in Fig. 4. For the horizontal mode (Fig. 4a), very low discrepancy due to foundation geometry is noted. Stiffness reduction is uniform for all slenderness ratios \((1<h/b<8)\), with the average value of \(K_{h,flex}\) reaching 75 % of \(K_{h,rigid}\) for very soft soil profiles (large \(E_{w}/E_{s}\)). Standard deviation for horizontal stiffness is on average around 5 %.

Fig. 4
figure 4

Stiffness reduction of flexible foundation \((K_{flex})\) from rigid foundation \((K_{rigid})\) with respect to wall-to-soil elasticity moduli \((E_{w}/E_{s})\), for embedded foundations and a horizontal b vertical and c rocking modes of vibration. Each dot represents a single numerical analysis of soil-foundation model. Thick lines represent average values and thin lines their standard deviation

Full size image

For the vertical mode, stiffness of embedded flexible foundations (Fig. 4b) is very similar to the one for surface foundations (Fig. 3b). Either for \(h/b<1\), or for \(h/b>1\), standard deviation from the mean value is lower than 10 %, almost equal to the one for surface foundation under vertical unitary displacement (Fig. 3b). This resemblance with surface foundation response is expected, as embedding of foundation affects mostly the horizontal stiffness of the foundation-soil system, rather than the vertical.

Regarding the rocking mode (Fig. 4c), no safe conclusion can be drawn on the stiffness reduction of flexible foundation, in the same way as for surface foundations (Fig. 3c). Stiffness ratios \(K_{flex}/K_{rigid}\) can be roughly divided into two groups, with respect to the slenderness \(h/b\) ratio. However, standard deviation is 16 % of the average for \(h/b>1\) and 6 % of the average value for \(h/b<1\). Slender foundations tend to present larger discrepancy on the rocking response. Specifically for very slender wall foundations \((h/b\gg 1)\), rocking stiffness of flexible foundations seems to decrease only for very stiff soil profiles, for \(E_{w}/E_{s} <2\). For medium to softer soil profiles, the stiffness tends to approach the rigid foundation values.

For similar reasons with surface foundations, the upper bound of the stiffness of embedded flexible foundations is always less than the rigid one, due to different numerical modeling as mentioned above.

7 Application on Arsenal De Milly

In this section we apply the proposed methodology for estimation of dynamic stiffness of flexible masonry wall foundation systems to the monument of Arsenal De Milly in Rhodes, Greece. The aim is to highlight, through the proposed procedure, that SFI together with flexibility of masonry foundation influence the outcome of the seismic assessment of historical structures. A comparative analysis of different modelling strategies and some more information on the building are provided in Cattari et al. (2013).

7.1 Description of Arsenal De Milly

Arsenal De Milly (Fig. 5) is located at the northeast corner of the medieval fortifications of Rhodes island in Greece. It is a one storey rectangular building (\(10.20\,\hbox {m} \times 23.88\,\hbox {m}\) in planar view) covered by pointed vaulted ceiling, supported at one side on the fortified wall. Arsenal De Milly was built in the middle of the fifteenth century during the era of Grand Magister De Milly and its first use was armory or arsenal. This monument has been subjected to many interventions during the past and it has been restored recently.

Fig. 5
figure 5

The Arsenal de Milly a at its current state (after the restoration), b main façade and c plan view (courtesy of the Foundation for the Financial Administration and Realization of Archaeological Projects, FFARAP)

Full size image

7.2 Modeling

Based on the results obtained from laboratory tests (Papayanni et al. 2004), microtremor measurements (Negulescu et al. 2014) and previous studies (Pitilakis et al. 2002), structural identification of the building has been achieved and the building could be accurately modeled using continuum constitutive laws model. Table 3 shows the well-known elastic mechanical properties and the masonry’s strength parameters adopted in the models. Due to the fact that the defensive wall is a three-leaf masonry, we considered in the analyses for the defensive wall a reduced elastic modulus \(E_{w}=\hbox {900\,MPa}\), as the half of the initial value \(E_{w,init}=\hbox {1,800\,MPa}\).

Table 3 Masonry’s properties
Full size table

The numerical model was constructed in the finite element code OpenSees (McKenna et al. 2007). Eight-node brick elements with 3 degrees-of-freedom at each node were used. This is a continuous model with homogeneous material properties. The non-linear response is distributed to the whole structure by using Drucker–Prager plasticity law (Drucker and Prager 1952). The Drucker–Prager yield criterion is defined in OpenSees by the following parameters: the bulk modulus \(k\) and the shear modulus \(G\) that are functions of the elastic modulus considered, the yield stress \(\sigma _{Y}\) and the frictional strength parameter \(\rho \). The Drucker–Prager strength parameters, frictional strength parameter \(\rho \) and yield stress \(\sigma _{Y}\) could be related to the Mohr–Coulomb friction angle \(\varphi \) and cohesive intercept \(c\) by evaluating the yield surfaces in a deviatoric plane as described by Chen and Saleeb (1994). This relation is based on the shear strength criterion as it is expressed in Eq. (3), where the shear strength with no compression is \(f_{vk0}=c=\hbox {0.2\,MPa}\), the frictional coefficient is \(\mu =tan\varphi \) and \(\sigma _{n}\) is the compressive stress. The values used for the Drucker–Prager strength parameters are shown in Table 4. The bulk modulus \(k_{eff}\) and the shear modulus \(G_{eff}\) refer to the defensive wall.

$$\begin{aligned} f_{vk} =f_{vk0} +\mu \cdot \sigma _{n} \end{aligned}$$
(3)
Table 4 Drucker–Prager plasticity law parameters for the foundation soil
Full size table

Two different models were analysed. The first model is fixed at its base (FIXED) while the second one considers SFSI using stiffness values estimated for flexible masonry wall foundation. Rocking stiffness is not considered, since brick elements used in the finite element model do not allow rotation. For the evaluation of the horizontal and vertical stiffness values assuming rigid foundation, we used equations proposed by Gazetas (1983) (horizontal) and Mylonakis et al. (2006) (vertical) respectively. Figure 6 shows the three-dimensional fixed-base model of the Arsenal De Milly, together with the planar view of the nodes at the level of foundation.

Fig. 6
figure 6

Numerical model of Arsenal De Milly a 3D view, b planar view at the foundation level

Full size image

At the foundation level, the nodes have the stiffness corresponding to the flexible masonry wall foundation and the surrounding soil. Stiffness values at each node are calculated with the proposed methodology described above. The north wall, which is connected directly to the massive fortification wall, is considered fixed at its base, since the fortification wall is founded directly in limestone.

At a first step, the dimensionless frequency \(\upalpha _{0}\) is calculated for each one of the frequencies of interest, and more specifically for the resonant frequency of the soil, of the fixed-base structure and of the flexible-base structure. For the south wall (Fig. 5c), \(\alpha _{0soil} = 0.42, \,\alpha _{0fixed}=0.91\) and \(\alpha _{0sfsi}=0.86\) respectively. In a similar way, for the east/west walls, \(\alpha _{0soil} = 0.18,\,\alpha _{0fixed}=0.40\) and \(\alpha _{0sfsi}=0.37\) respectively. In all cases, \(\alpha _{0}\) is \(<\)1, and therefore the static stiffness is calculated for rigid foundation. Then, based on the ratio \(E_{w}/E_{s}\,(E_{w}\) from Table 3 and \(E_{s}\) from Table 4), the flexible stiffness \(K_{flex}\) is calculated from Figs. 4a and 4b, for all degrees-of-freedom of interest (two translational and one vertical). The average values of stiffness for the rigid and the flexible foundation are summarized in Table 5.

Table 5 Stiffness (in GN/m) for rigid and flexible foundation systems
Full size table

8 Results

Modal and pushover analyses are performed for both fixed-base and flexible-base models. Table 6 shows the computed structural periods for the first five modes and Fig. 7 the pushover curves of the examined models.

Table 6 Structural periods (in seconds) for the first 5 modes, for the fixed-base structure (fixed) and for the actual structure founded on a flexible wall foundation (sfsi)
Full size table
Fig. 7
figure 7

Pushover curves in two directions a East–west and b North–south for the examined models

Full size image

Foundation flexibility and SFI inevitably increase the compliance of the system. There is no significant difference between the results that stem from the average normalized stiffness value for the embedded flexible wall foundation and the ones from the plus and minus one standard deviation. The push-over curves in Fig. 7 show that the maximum strength of both fixed- and flexible-base models is approximately equal. However, the maximum displacement and, consequently, the ductility of the flexible-base model are considerably increased compared to the fixed-base one, especially in the NS direction, i.e. along the flexible side of the structure, where the out-of-plane response is predominant.

9 Conclusions

A methodology is proposed for assessment of earthquake response of monuments with non-rigid foundations, including SFI. We provide diagrams, resulting from numerical investigation of typical soil-foundation systems, which correlate foundation stiffness reduction, due to masonry flexibility, with the relative masonry foundation wall-to-soil modulus of elasticity. Stiffness of flexible masonry foundations is provided for surface and embedded foundations, for translational and rocking modes of vibration. Key parameter in the stiffness reduction is the initial assumption on the geometry of the foundation, notably the “participating” height and width of the masonry wall that can be considered as the foundation of the monument. Overall, geometry is more important for the rocking mode, rather than for the translational ones.

We conclude that flexible-foundation stiffness reduces more from the rigid case for embedded foundations in the vertical mode, the reduction being more important for short squatty foundations (low slenderness ratio). On the other hand, horizontal foundation stiffness seems to reduce more in case of surface flexible foundations, and more specifically for tall slender foundations (large slenderness ratio). Discrepancy due to geometry does not permit safe conclusions to be drawn on stiffness reduction in the rocking mode. For very slender wall foundations, rocking stiffness of flexible embedded foundations seems to decrease only for very stiff soil profiles. For medium to softer soil profiles, rocking stiffness of embedded foundations tends to approach the rigid case values.

The proposed procedure is sought to be used in conjunction with the finite element method, in order to perform more accurate seismic performance assessment of historical masonry structures. Thereby, the proposed methodology is applied to the monument of Arsenal De Milly in Rhodes, Greece. It is shown that accounting for masonry foundation flexibility in SFSI increases the maximum displacement exhibited by the structure.