The Influence of Soil-Foundation-Structure Interaction on the Seismic Performance of Masonry Buildings

Abstract

Most of the damage and of the casualties induced even by the most recent strong-motion earthquakes which stroke Central and Southern Italy can be attributed to the extreme seismic vulnerability of the ordinary residential buildings. Both in small villages and in mid-size towns, these latter are mainly constituted by two- to four-story masonry structures built without anti-seismic criteria, with direct foundations corresponding to an in-depth extension of the loadbearing walls or to an underground level. For such structures, especially when founded on soft soils, soil-foundation-structure interaction can significantly affect the seismic performance; on the other hand, its influence must be handled with methods which should be as simple and straightforward as possible, in order to be cost-effective and accessible by practitioners. The contribution wishes to summarize the studies carried out in the last years at University of Napoli Federico II, based on parametric numerical analyses on complete soil-foundation-structure models reproducing the most recurrent building configurations combined with different subsoil conditions. The analyses provided calibration criteria for: i) predicting the elongation of the fundamental period of the structure, ii) defining and optimizing fragility functions for different damage mechanisms accounting for soil-foundation-structure interaction. The effectiveness of these simplified tools was validated against well-documented case studies at the scale of single instrumented buildings or of extended areas, with building properties and subsoil conditions comparable to those adopted in the parametric analyses.

1 Introduction

According to the World Bank [1], the number of natural disasters in the last years has increased both in magnitude and frequency. Certainly, earthquakes are among the natural events with the greatest impact on the world economy and on the loss of lives. Such evidence makes the seismic protection of the built heritage to be urgent, in order to limit damages and consequent human and economic losses.

The seismic risk in Europe is maximum in the South-East Mediterranean countries, due to both the significant seismic hazard, as shown by the European Seismic Hazard Map [2] in Fig. 1a, and the high structural vulnerability [3], as remarked after the most recent earthquakes (see Fig. 1b) that struck Italy [4, 5] or Greece [6].

Fig. 1.

(a) SHARE seismic hazard map of peak ground acceleration with a probability of exceedance equal to 10% in 50 years [2] and percentage of URM buildings in some European countries [3], (b) masonry buildings damaged by out-of-plane mechanisms in recent seismic events.

The high vulnerability is due to the fact that most of the existing structures are made of unreinforced masonry (URM) (see Fig. 1a) [3, 7] and were built before the emanation of seismic codes. The consequent lack of structural elements to withstand horizontal actions makes the load-bearing walls to be subjected to significant out-of-plane (OOP) lateral actions, frequently resulting in local collapse mechanisms.

Moreover, numerous URM buildings are founded on shallow soft covers which amplify the seismic motion and affect the structural response through soil-foundation-structure interaction (SFSI) mechanisms [8]. Amplification of the seismic waves propagating through a soft soil deposit may be further affected by the kinematic interaction between the embedded masonry foundation and the surrounding soil, which modifies the foundation input motion with respect to the free-field conditions. Simultaneously, the structure transfers to its base inertial forces and moments which induce foundation swaying and rocking motions. These latter affect the structural response in terms of displacements and accelerations, as well as by increasing the period, $T^*$, and damping, $\xi^*$, due to the additional energy dissipated by wave radiation and soil hysteresis.

Nevertheless, few research studies have investigated the effects of SFSI on the seismic response of URM structures, like as towers [9,10,11,12,13], fortresses [14, 15], masonry bridges [16] and school buildings [17]. Even fewer are the cases in which fragility curves were computed accounting for SFSI effects [18, 19].

All the above-mentioned studies were developed for specific case studies or very peculiar structures, rather than ordinary residential buildings which this paper focuses on. Thus, after a synthetic overview of a hierarchy of approaches available for the analysis of SFSI (Sect. 2), this study was addressed to the following main objectives:

• (i) to evaluate the effects of soil deformability on the dynamic response of typical URM residential buildings (Sect. 3), by updating traditional simplified approaches according to the results of advanced numerical analyses (Sect. 4);

• (ii) to account for SFSI effects in order to define fragility curves relevant to the OOP damage mechanisms of masonry walls (Sect. 5).

The main methodological advances developed with reference to objectives (i) and (ii) were assessed and validated through applications to well-documented case studies at territorial scale.

2 Approaches for the SFSI Analysis: An Overview

Figure 2 shows a hierarchy of models with different degrees of refinement for soil and structure adopted in the literature, to account for SFSI in seismic performance assessments. The structural models can be sorted according to an increasing complexity level as follows:

Fig. 2.

SFS models with different complexity levels related to the structure and soil: SDOF oscillator, MDOF system, continuum structural model on springs and dashpots (a, b, c), and on continuum soil model (d, e, f).

• a single-degree-of-freedom (SDOF) oscillator with mass m, flexural stiffness k, and damping ratio $\xi ,$ which is characterized by a single vibration mode and, consequently, by a single natural period (Fig. 2a and Fig. 2d);

• a multi-degree-of-freedom (MDOF) system with n lumped masses m_i, stiffness matrix K, and damping matrix C, which is characterized by n vibration modes (Fig. 2b and Fig. 2e);

• a continuum model with mass density $\rho$, shear modulus G, Poisson’s ratio $\nu$, and a given shape and size, which is characterized by infinite vibration modes and can be discretized by a numerical technique, such as the finite element method or finite difference method (Fig. 2c and Fig. 2f).

On the other hand, the presence of the soil can be simulated through:

• a combination of springs and dashpots with stiffness K_ij and damping coefficients C_ij, related to each translational and rotational component of the foundation motion (Fig. 2a-b-c);

• a continuum model with mass density $\rho$, shear modulus G, Poisson’s ratio $\nu$, characterized by suitable in-depth and lateral extensions as well as by reflecting or absorbing boundaries (Fig. 2d-e-f).

In the simplest approaches, the spring stiffness and the constant of the dashpots simulating the soil compliance to the foundation motion are calibrated through the impedance functions [20]. They are the sum of a real part representing the dynamic stiffness and an imaginary part accounting for the damping:

$$ \bar{K}_{ij} = k_{ij} \left( {a_0 } \right)K_{ij} + {\rm i}\,\omega c_{ij} \,\left( {a_0 } \right)C_{ij} $$

(1)

In Eq. (1):

• i is the imaginary unit;

• the subscripts i, j indicate that $\bar{K}_{ij}$ links the component i of the vector of the loads transmitted by the foundation into the soil to the component j of the displacement vector;

• the low-frequency stiffness, K_ij, and the dashpot coefficient, C_ij, depend on the soil shear modulus, G, and Poisson’s ratio, ν, as well as on a characteristic dimension of the foundation, r;

• the dynamic coefficients, k_ij(a₀) and c_ij(a₀), depend on the vibration frequency, ω, the characteristic dimension of the foundation, r, and the soil shear wave velocity, V_S, through the dimensionless frequency factor, $a_0 \, = \,\omega r/V_S .$

Unless experimentally measured from records on existing structures during free and forced vibration tests [21, 22], the impedances are typically calibrated through analytical expressions referred to rigid massless foundations, more or less embedded in the soil. The latter is generally assumed to be an elastic homogeneous half-space [20, 23], an elastic stratum placed on a half-space (e.g. [20]) or a layered soil profile (e.g. [24]).

As usual in soil dynamics, the variation of the impedance under moderate to strong motions due to non-linear and dissipative soil behavior can be taken into account through the equivalent-linear approach [25]. This is the main limitation of the impedance functions, which can be overcome through macro-element approaches, reproducing the overall soil-foundation behavior through a single constitutive relationship, capable of describing the non-linear behavior until failure [26, 27].

The simple oscillator with compliant base (Fig. 2a) is the system more extensively adopted as a reference to derive simplified approaches to calculate the SFS dynamic response parameters ($T^* ,\xi^*$) since the pioneering work by Veletsos and Meek [28] to the most recent analytical developments [29] and adaptations to non-trivial soil-foundation-structure systems (e.g. [30] and [31]).

In terms of analytical procedures, the study of interaction effects through each of the models reported in Fig. 2 can be classified as:

• uncoupled approaches, in which the system is analyzed by decoupling the ‘kinematic’ from the ‘inertial’ interaction with the so-called “substructure method”;

• coupled approaches, in which all the effects of the interaction can be evaluated simultaneously, performing dynamic analyses on a model including soil, foundation and structure.

In the first kind of procedures, a dynamic analysis is performed on a subsoil model including the foundation stiffness but neglecting the structural mass. The resulting ‘foundation input motion’ (FIM) is used as dynamic load at the base of a complementary structural model, in which the soil-foundation system is replaced by a set of springs and dashpots. If the foundation is shallow, the kinematic interaction is negligible, hence the FIM is almost coincident with the ‘free field motion’ derived from a conventional seismic response analysis. This approach is typically applied to the models shown in Fig. 2a, b, c.

Conversely, the coupled procedures jointly analyze the structure and the soil, with this latter modeled as a continuum (see Fig. 2 d, e, f). In such cases, a rigorous calibration of all the parameters involved in the simulation is necessary; otherwise, the results may not be the most realistic. On the other hand, in the uncoupled approach, an accurate definition of equivalent properties is required to consider material nonlinearity and the actual geometry of the single elements of the SFS system (i.e. structure with distributed mass, embedded and/or flexible foundation, soil inhomogeneity and/or irregular morphology).

Some of these aspects represent a significant limitation in seismic performance assessment of URM structures, usually characterized by bearing wall embedments or underground stories which cannot be assumed rigid, due to the material nature and deterioration caused by aging. It follows that the more refined coupled procedures should be in principle adopted for most URM structures, but the corresponding experimental and analytical effort can be justified only for high-value historical buildings. For ordinary residential structures, however, numerical simulations in which the SFS system is regarded as a coupled model can support the calibration and validation of simpler and more sustainable approaches, as shown in the following sections.

3 Soil – Foundation – Structure Systems Analyzed

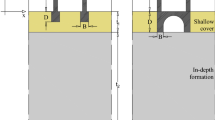
The reference soil-foundation-structure models analyzed in this study are summarized in Fig. 3 [30]. The structural geometry reproduces the transverse section of a masonry building for residential use with single-span floors (Fig. 3a). The width, b, and inter-story height are constant and respectively equal to 8 m and 4 m; the total height, h, varies considering 2, 3 and 4 above-ground stories, which correspond to aspect ratios h/b equal to 1, 1.5 and 2. Such structural configuration is recurrent in constructions located in the Euro-Mediterranean region [32, 33].

Fig. 3.

(a) SFS model; profiles of shear wave velocity for (b) homogeneous and (c) layered soil.

The structure consists of two load-bearing masonry walls connected each other by mixed steel-tile floor systems, pinned to the walls and composed of steel I-beams, clay tiles and poor filling material. The pitched roof is made of timber elements. The thickness of the walls reduces along the building height, leading to a fairly homogeneous distribution of vertical stresses from the ground floor to the top. As typical for masonry residential buildings [33], the lowly embedded foundations were assumed to be made of the same material of the above-ground structure, with a width, B, and a depth, D, equal to 2.0 m and 2.5 m, respectively.

The building schemes were settled on:

• four homogeneous subsoil models, with lithology and properties representative of the Eurocode-conforming ground types A, B, C and D [34];

• three-layered subsoil profiles, D-B, D-C and C-B, constituted by a shallow cover with a thickness t₁ = 5 m overlying a main formation as thick as t₂ = 25 m.

A stiff bedrock pertaining to ground type A was systematically assumed at a depth of 30 m. The stiffness and strength parameters of the subsoil model belonging to the class D were assumed as either constant (homogeneous profile, D_ho) or variable with depth (heterogeneous profile, D_he). The profiles of shear wave velocity, V_S, for each model are shown in Fig. 3b–c.

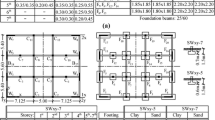
Table 1 and Table 2 summarize the material properties adopted in the linear and nonlinear analyses, respectively. Soil and masonry were modeled as a continuum with mass density, $\rho$, bulk modulus, K, shear modulus, G, and Poisson’s ratio, $\nu$. Floors and roof were modeled as equivalent beam elements made of a homogenized material.

Table 1. Material properties adopted for linear analyses.

Table 2. Material properties adopted for nonlinear analyses.

The soil density and Poisson’s ratio were realistically assumed as respectively increasing and decreasing with V_S, and representative of soft rock (A), gravel (B), dense sand (C) and loose sand (D). The properties of the tuff stone masonry (TSM) considered for the linear analyses were defined from the experimental results collected by [35].

In nonlinear analyses, a limit shear strength was introduced for soil types C and D through a Mohr-Coulomb criterion with a friction angle, $\phi ,$ equal to 35° for the former, and a Tresca criterion for the latter, which this time was assumed as a fine-grained soil characterized by an undrained strength, c_u. The homogeneous and heterogeneous soil profiles, D_ho and D_he, were defined as representative, respectively, of a lightly overconsolidated and a normally consolidated clay with a plasticity index IP = 30% for the homogeneous (D_ho) and IP = 20% for the heterogeneous (D_he) profile. The variations with depth of shear stiffness at small strains and undrained strength in the heterogeneous soil profile follow the model adopted by Capatti et al. [36]. Due to the light overconsolidation, for soil type D_ho the undrained strength was set constant with depth and higher than that of the heterogeneous soil profile.

For both soft soil profiles, a pre-failure hysteretic behavior was modelled. The strain-dependent variation of normalized shear modulus, G/G₀, and of the damping ratio, D, was described for the soil type C by the standard curves reported by Seed and Idriss [37], while for soil profiles D by those suggested by Vucetic and Dobry [38] for the relevant plasticity indexes. The standard curves were implemented in the numerical model by fitting them through ‘sigmoidal’ functions.

The energy dissipation at very small strains, for nonlinear analyses, was simulated through a Rayleigh approach, with a minimum damping ratio, D₀, equal to 2% and 5%, for soil and structure, respectively. The control frequency was calibrated on the fundamental frequency of the input motion joint to that of the free-field soil or the fixed-base structure, as detailed by Piro [39].

Finally, in nonlinear analyses two different types of structural material were considered, namely, rubble stone masonry (RSM) and clay brick masonry (CBM). The masonry was modeled as an equivalent homogeneous material adopting an elastic-perfectly plastic constitutive model with the Mohr-Coulomb failure criterion, to limit the computational work. The elastic parameters listed in Table 2 were set equal to the median values reported by the Italian Building Code Commentary [40] for existing masonry buildings. The value of the friction angle, $\phi$, was set based on the friction coefficient, depending on the ratio between the compression stress, $\sigma$₀, at the base of the above-ground structure under the static load and the uniaxial compression strength, $\sigma$_c, equal to the value reported by [40]. The cohesion, c, was back-calculated from $\phi$ and $\sigma$_c on the basis of the Mohr-Coulomb criterion. A tensile cut-off, $\sigma$_t, equal to 0.1$\sigma$_c was also implemented in the model.

Table 3 summarizes all the combinations of soil and structure models with the corresponding analyses represented by different color shadings. It should be underlined that, while the linear analyses were focused on the masonry type characterized by average mechanical properties (TSM) and extended to all subsoil profiles considered, the nonlinear simulations were addressed to assessing the SFSI effects by comparing each other the extreme combinations (i.e. softest vs. stiffest soils, as well as most vs. less deformable masonry types).

Table 3. Summary of the dynamic analyses performed (linear: light blue, nonlinear: red).

4 Prediction of the Fundamental Frequency of the SFS System

4.1 Coupled Approach

The SFS systems described in Sect. 3 were analyzed as continuum coupled models (see Fig. 2f) by means of the 2D finite difference code FLAC ver. 7.0 [41]. As an example, Fig. 4 shows the model adopted for the SFS systems on a homogeneous soil profile. The subsoil domain is 50 m wide, 30 m deep and includes the top of the bedrock through a finite layer with a thickness of 10 m.

Fig. 4.

2D finite difference mesh for a homogeneous soil profile.

The infinite extension of bedrock in depth was simulated by dashpots attached to the bottom nodes and oriented along the normal and shear directions. To minimize the model size, free-field boundary conditions were imposed to the vertical sides of the soil volume, simulating an ideal horizontally layered soil profile connected to the main-grid domain through viscous dashpots. The soil was discretized into a mesh of quadrilateral elements, the size of which was defined to satisfy the criterion by [42] for accurately reproducing the shear wave propagation up to a frequency of 25 Hz. In the proximity of the structure, the size of the quadrilateral elements was reduced in order to approximate the dimensions (length and height) of a single masonry brick. Floor and roof systems were modeled through one-dimensional (1D) beam elements with 1 m-wide homogenized cross-section and with pinned connections to load-bearing walls. The input motions were applied as a shear stress time-history at the bottom of the bedrock layer.

The fundamental frequency of each model was firstly computed at strain levels well below structural and geotechnical failure states. Thus, a linear visco-elastic behavior of the materials was assumed, with the properties listed in Table 1 and a very low Rayleigh damping ratio equal to 0.1%. The latter was properly minimized in order to isolate the effect of the radiation damping.

Being impossible to perform modal analyses through FLAC software, the procedure developed by [12] was used to detect the fundamental frequency of each SFS system. The base of the model was subjected to a low-amplitude random input motion with a frequency content ranging between 1 and 25 Hz and a duration of 10 s, after which the free vibration of the SFS system was numerically monitored over 20 s.

The fundamental frequency, $f^*$, of each SFS system was back-figured from the peaks of the Fourier spectra of the displacement time histories recorded during the free vibration at the control points shown in Fig. 4. The plots in Fig. 5a-b show the dynamic response (in terms of displacement amplitudes, U_i, normalized with respect to the roof maximum value, U_TOPmax) of two-story (h/b = 1) and four-story (h/b = 2) structures, respectively, laying on homogeneous soil A and layered soil D-B. The SFS fundamental frequency $f^*$ is highlighted by spectral peaks at all elevations, whereas dashed lines indicate the free-field soil natural frequencies, denoted as f_soil. The fundamental frequency of the fixed-base (FB) structural model, f₀, was assumed to be coincident with that of the SFS system characterized by homogeneous soil type A (upper plots).

Fig. 5.

Frequency response at different structural elevations for (a) two-story (h/b = 1) and (b) four-story (h/b = 2) SFS systems on rock outcrop and layered soil D-B.

A non-negligible reduction of the fundamental frequency of the shortest structure (h/b = 1) on the layered soil D-B is observed with respect to the fixed-base value, i.e. 4.18 Hz vs 5.01 Hz. Conversely, the frequency of the tallest structure (Fig. 5b) was found to be much less affected by the soil deformability ($f^*$ from 2.02 Hz to 1.94 Hz), highlighting that the dynamic response of the masonry building is increasingly influenced by SFSI with the increase of the structure-soil stiffness ratio [13, 30].

4.2 Simplified Approaches

Veletsos and Meek [28] firstly proposed a closed-form solution to evaluate the fundamental frequency, $f^*$, of a SFS system (Fig. 6a) based on the ideal scheme of a compliant-base SDOF as that drawn in Fig. 6b.

Fig. 6.

Definition of replacement oscillator for SFS system: (a) typical transverse cross-section of a URM building; (b) compliant-base SDOF system; (c) replacement oscillator.

The dynamic response of the compliant-base SDOF is in turn assumed as equivalent to that of the ‘replacement oscillator’ (Fig. 6c), i. e. a fixed-base SDOF with the same frequency, $f^*$, and damping ratio, $\xi^*$. The total flexibility of this latter to dynamic loadings can be taken as the sum of the flexibilities of each SFS component, as follows:

$$ \frac{1}{k^* (f^* )} = \frac{1}{k} + \frac{1}{k_u (f^* )K_u } + \frac{h^2 }{{k_\theta (f^* )K_\theta }} $$

(2)

The second and the third denominators on the right side of Eq. 2 are the real parts of the translational and the rotational impedances equivalent to those of the building foundation. By replacing Eq. 2 in the well-known expression of the fundamental frequency of the SDOF, that of the SFS system can be easily calculated as:

$$ f^* = \frac{1}{2\pi }\sqrt {\frac{k^* }{m}} $$

(3)

The same authors proposed a set of curves representing the dependence of $f^*$ normalized with respect to the fixed base frequency, $f^* /f_0$, on the soil-structure relative stiffness, $\sigma$, defined as:

$$ \sigma = \frac{V_S }{{f_0 \,h}} $$

(4)

The latter parameter is hard to define for URM buildings with irregular geometry above and under the ground level, as well as with flexible foundations placed on layered soil. To overcome such limitation, Piro et al. [30] proposed to calculate $\sigma$ based on an equivalent shear wave velocity, V_S,eq, resulting from the weighted contributions - through appropriately calibrated coefficients - of the stiffness and the mass of the SFS components falling in the volume underlying the building significantly affected by the inertial interaction mechanism (see Fig. 7b). For a given aspect ratio, h/b, the equivalent stiffness ratio, $\sigma_{eq} \, = \,V_{S,eq} /hf_0$, leads to the corresponding value of the frequency reduction factor, $f^* /f_0$ , by referring to the same curves suggested by Veletsos and Meek [28], as shown in Fig. 7c.

Fig. 7.

Approach for the estimation of the frequency reduction factor, $f^* /f_0$: (a) typical transverse cross-section of a URM building; (b) soil volume affected by inertial interaction mechanism; (c) frequency reduction factor, $f^* /f_0$, versus equivalent soil-structure stiffness ratio, $\sigma_{eq}$.

As an example, Fig. 8 compares the frequency reduction induced by the soil compliance predicted by the traditional formulation of σ [28] (hollow circles) and by $\sigma_{eq}$ [30] (full circles) for the SFS systems characterized by h/b = 1 and h/b = 2 on the layered soil profile D-B (see Fig. 5). It is apparent that the traditional formulation leads to a higher reduction of the fundamental frequency because σ is calibrated on the V_S value of the upper softer layer. Moreover, it can be checked that the frequency reduction factors, (f^*/f₀)_num, shown by the horizontal dashed lines, resulting from the numerical analyses as the ratios between those reported in the lower and upper plots in Fig. 5, are in a perfect agreement with those predicted through the procedure based on σ_eq.

Fig. 8.

Comparison between the predictions through the approaches by Veletsos and Meek [28] and Piro et al. [30] for two and four-story SFS systems on layered soil profile D-B.

4.3 Urban-Scale Application to the City of Matera

The simplified approach above described was applied to seven buildings located in the historical city of Matera, located in Southern Italy and well-known for its peculiar ‘Sassi’ caves. The two main geological formations (Fig. 9a–b) are the Altamura limestone and Gravina calcarenite which outcrop in the North-West and South-East areas of the urban center. The latter is covered by the Sub-Apennine clays, with thickness varying from a few meters, near the Sassi area, to 40–50 m inwards. Down-hole and seismic refraction tests revealed a shear wave velocity increasing with depth from 146 m/s to 450 m/s in the Sub-Apennine clays and ranging between 394 m/s and 1185 m/s in the Gravina calcarenite depending on its degree of cementation, while it is almost constant (around 950 m/s) in the Altamura limestone.

Fig. 9.

(a) Geological map and (b) section with the location of analyzed buildings; (c) reference schemes of structure and subsoil for the application of the approach by Piro et al. [30].

Figure 9c reports the cross-sections of seven soil-foundation-structure systems analyzed through the simplified approaches based on the replacement oscillator to estimate the fundamental frequency. The soil stratigraphy and the shear wave velocity profiles were inferred from available investigations. In lack of direct measurements, the unit weight was set equal to typical values of 17.50 kN/m³, 19.50 kN/m³ and 27.50 kN/m³ respectively for the clay, calcarenite and limestone formations.

The geometries of the selected buildings (height, width and number of stories) were obtained from the survey by Gallipoli et al. [43], while empirical correlations were applied to estimate the thickness of the bearing walls, made of calcarenite.

An enlargement of 0.15 m at each side of the bearing wall was considered to determine the foundation width, while the embedment was set equal to 1.5 m. In lack of specific survey, the properties of walls with irregular texture provided by the Italian Building Code Commentary [40] were assigned to the masonry, referring to the most recurrent typology in the historical center.

The fundamental frequency of all the seven buildings was measured through Horizontal/Vertical Spectral Ratios (HVSR) of white noise records during the CLARA project [44]. Even though the number of stories is the same for the buildings 1-2-5 in Fig. 9c, the measured value, $f^*_{exp}$, reduces with the thickness of the clay layer, highlighting a first evidence of the effects of subsoil conditions and of SFS interaction.

Such influence is confirmed by the application of the simplified approaches to estimate $f^*$ , the results of which are compared to $f_0$ in Table 4. The latter was estimated through a correlation between the experimental frequency and the height of masonry buildings directly founded on calcarenite outcrops, obtained by Gallipoli et al. [43].

Table 4. Comparison between experimental and analytical frequencies calculated with the traditional and proposed approaches.

On average, the traditional formulation overestimates the frequency reduction, while a significantly better agreement was found between the proposed procedure and the experimental data, as shown by the low values of the percentage error ${\upvarepsilon }$, computed as:

$$ \varepsilon = \left( {\frac{{f_{\exp }^* - f^* }}{{f_{\exp }^* }}} \right) \times 100 $$

(5)

Note that the only exceptions are represented by buildings 5 and 7, which is likely to be due to their hollow geometrical plan.

5 Nonlinear Performance of SFS Systems

5.1 Reference Input Motions

The influence of SFS interaction on the activation of limit states for both out-of-plane mechanisms of masonry walls and plastic straining in the soil-foundation system was investigated using nonlinear time history analyses.

The so-called ‘cloud method’ [45] was adopted by selecting a set of 15 reference input motions from the SIMBAD database [46]. The 15 ground motions were selected according to the following criteria [45]:

• to consider a wide range of spectral accelerations, i.e. $S_a (T^* )$  = 0.01 g–3.00 g;

• to avoid records of the same seismic events;

• to select ground motions recorded on stiff outcropping formations, being site effects properly accounted for in the coupled SFS analysis.

In detail, twelve ground motions were recorded on soils classified as type A, whereas the others were recorded on type B with equivalent shear wave velocity, V_S30, higher than 500 m/s. Each input motion was applied to the base of the 16 coupled SFS models subjected to nonlinear time history analyses, i.e. those corresponding to the red-hatched cells in Table 3.

The high variability of the selected input motions is shown in Fig. 10a through the scatter plot of peak ground acceleration (PGA) versus moment magnitude (M_W) and epicentral distance (R). As a matter of fact, the acceleration spectra reported in Fig. 10b are characterized by a significant variation of spectral shapes and amplitudes, these latter by an order of magnitude. The green dashed-dotted lines correspond to the soil fundamental periods, with reference to a linear free-field seismic response. The red and black dashed lines identify the ranges of fundamental periods numerically evaluated for brick and rubble masonry buildings, respectively, relevant to the structural models with either h/b = 1 or h/b = 2 laying on different subsoil profiles (see Table 3).

Fig. 10.

(a) PGA–M_W–R distribution and (b) acceleration response spectra of the selected input motions.

5.2 Performance Assessment of SFS Components

Soil amplification in free-field conditions was firstly investigated in terms of spectral ratios, S_a,s/S_a,b, between surface and bedrock motions. Response spectra were obtained from acceleration time histories predicted at the foundation level (z = −2.5 m) and at a distance of 20 m from the structural model axis, which was assumed to be representative of free-field conditions (see Fig. 4). The comparison between spectral ratios computed at the foundation level for the soil profiles D_ho and D_he is shown in Fig. 11 for the ground motions #1, 8 and 14, which were respectively characterized by PGA values equal to 1.15 g, 0.40 g and 0.06 g. Just like in Fig. 10b, the vertical dashed and dashed-dotted lines in Fig. 11 correspond to structural and soil periods, respectively.

Fig. 11.

Seismic response in terms of spectral ratios between free-field motion at the foundation level (S_a,s) and bedrock motion (S_a,b) for homogeneous and heterogeneous D soil profiles.

Under the strongest motion #1, significant reductions of PGA and spectral amplitudes (resulting in S_a,s/S_a,b < 1) can be observed in the period range of the two-story buildings (h/b = 1) located on both soft soil profiles. Conversely, the spectral amplitudes of the weakest motion #14 are found to be amplified (resulting in S_a,s/S_a,b > 1), especially in the case of heterogeneous soil profile. On the other hand, in the period range of four-story buildings (h/b = 2), spectral amplitudes of all the three records are amplified, with the fundamental period of the tallest CBM structure so close to that of the soils to induce double resonance.

The maximum settlement (w) and tilting rotation (θ) were assumed as engineering demand parameters, EDPs, for the assessment of foundation performance, as illustrated in Fig. 12. Time histories of the settlements (w₁ and w₂) of the opposite corners of each footing were recorded during the analysis and θ was calculated as their difference ($w_{1} -w_{2}$ ) divided by the foundation width (B).

Fig. 12.

Definition of (a) MIDR and (b) foundation settlement (w) and rotation (θ).

Figure 13 shows the values of the engineering demand parameters computed for clay brick masonry buildings with h/b = 1 (left column) and h/b = 2 (right column) founded on soil types D_ho and D_he (red and blue circles, respectively), plotted versus PGA at the bedrock. The lower stiffness of the heterogeneous soil profile close to the surface leads to higher foundation settlements (Fig. 13a–b) than those resulting for the homogeneous soil profile. The values of w calculated for structures with h/b = 2 are visibly larger than those associated with h/b = 1, due to more pronounced rocking induced in the foundation soil by the heavier and taller four-story buildings. In any case, the values of w predicted under even the highest PGA values are significantly below the conventional threshold levels adopted in engineering practice for loadbearing masonry walls, which are typically around 2.5 cm [47].

Fig. 13.

Scatter plots of the maximum settlement (w), maximum rotation (θ) and maximum inter-story drift ratio (MIDR) versus PGA, produced by the selected input motions for two-story (a, c, e) and four-story (b, d, f) clay brick masonry structures.

Figure 13c–d show that the values of θ predicted for the homogeneous soil are again lower than those relevant to the heterogeneous profile, but the differences are significantly smaller than those observed on settlements. In all cases, even the maximum θ-values are below the typical thresholds of 0.2% (i.e. 1/500) for infills and 0.5% (i.e. 1/200) for loadbearing walls [48] adopted in engineering practice.

The engineering demand parameter representative of the structural out-of-plane response was the maximum inter-story drift ratio, MIDR, i.e. the peak relative displacement at the j-th floor divided by the inter-story height (h_j):

$$ MIDR = \max \left( {\frac{{u_{str,j + 1} - u_{str,j} }}{h_j }} \right)_{j = 1,N} $$

(6)

where u_str,j and u_str,j+1 are the horizontal displacements at the j-th and j-th + 1 floors, respectively. The values of u_str were obtained as the total displacements minus the rigid base motions corresponding to the foundation rotation and translation.

Figure 13e–f show the MIDR values resulting from the nonlinear analyses on fixed-base (black circles) and compliant-base (red and blue circles) SFS models. The MIDR resulting from compliant-base models on both soft soil profiles are similar to each other, with the highest values pertaining to the tall structures on homogeneous soil profiles subjected to high PGA levels. Moreover, MIDR values are in some cases comparable to those predicted by the fixed-base models, implying less significant SFSI effects.

The data points are compared to three different damage level thresholds (DLs):

• DL1: formation of tensile cracks at the toe of the wall, due to the attainment of tensile strength of masonry;

• DL2: activation of the rocking mechanism;

• DL3: near-collapse limit state due to overturning.

The latter two were referred to the ultimate limit state in which the wall collapse is caused by overturning under out-of-plane motion, which takes place when the inter-story drift ratio is equal to [49]:

$$ IDR_u = \frac{s}{2h} $$

(7)

being s the masonry wall thickness. In the case of rubble stone masonry, IDR_u is reduced by 35% [50] in order to account for nonlinear effects an d possible loss of masonry integrity. In the present study, values of 0.25IDR_u The comparison between the structural demand (MIDR) and the capacity (damage thresholds) show that the vulnerability of the four-story structures is greater than that of the two-story buildings. This is not only due to the increase of MIDR with the building slenderness, but also to the lower inter-story drift ratio capacity related to the reduced masonry thickness at the highest floors. Such a difference is enhanced in case of compliant base models, due to the proximity of the soil and structural fundamental periods, inducing double resonance (see Fig. 11). Both effects make only the taller structural models to overcome the thresholds associated with the most severe DLs.

5.3 Fragility Curves

Once defined the MIDR as EDP for the structural performance, the probability P of overcoming one of the above described damage thresholds, DL_i, for a given seismic intensity measure, IM, of the input motion, was estimated as follows:

$$ P\left[ {MIDR > MIDR_i |IM} \right] = \Phi \left( {\frac{{\ln (IM/\eta_{DLi} )}}{{\beta_{DL} }}} \right) $$

(8)

where Φ is the cumulative normal distribution function, while η_DLi and β_DL are the median and standard deviation of the lognormal distribution of the IM value causing the attainment of MIDR_i. The ‘cloud method’ [45] assumes a linear relationship between MIDR and IM in the log-log scale, so that η_DLi was estimated as the abscissa of the intersection between the i-th damage threshold and the linear regression model that fits the (MIDR, IM) data points resulting from the analyses.

Among the several peak, spectral and integral synthetic parameters of the input motion which can be correlated to the seismic damage, in this study only three were selected as intensity measures which can reasonably satisfy the requirements of efficiency, sufficiency and hazard computability. They are the peak ground acceleration, PGA, and velocity, PGV, and the Housner intensity, I_H, i.e. the integral of spectral velocity S_v(T):

$$ I_H = \int_{T_1 }^{T_2 } {S_v (T)dT} $$

(9)

evaluated in the period range [T₁, T₂] equal to [0.1 s, 2.0 s].

As an example, Fig. 14 shows the correlations of the MIDR with PGA, I_H and PGV for the clay brick masonry buildings founded on subsoil profiles A (black circles), D_ho (red circles) and D_he (blue circles). The median values η_DL1, η_DL2 and η_DL3 are highlighted in Fig. 14b for the tallest structure on soil type A and IM = PGA.

Fig. 14.

EDP–IM relationships for fixed- and compliant-base models of clay brick masonry buildings with (a) h/b = 1 and (b) h/b = 2.

The plots in Fig. 14a reveal that the rate of increase of MIDR with each one of the selected IMs is almost independent of the soil model for the shortest structure. The same rate significantly reduces in case of the tallest structure on soft soil D_ho and D_he with respect to that founded on soil type A. In other words, while the performance of slender masonry buildings on soft soils results more significantly affected by soil-foundation-structure interaction, their vulnerability appears less sensitive to an increase of the seismic loading. This is likely due to a higher amount of energy dissipated through foundation damping associated to rocking motion [39].

The efficiency of the selected IMs was checked by comparing them in terms of standard deviation ($\sigma$_EDP|IM) and coefficient of determination (R²) of the regression model. The best-fit lines computed for all SFS models returned $\sigma$_EDP|IM ranging between 0.27 and 0.79, and R² varying between 0.38 and 0.94. The ranking of IMs according to decreasing values of $\sigma$_EDP|IM and increasing values of R² revealed that PGV is the most efficient parameter, followed by I_H and PGA. This outcome points out that the commonly adopted PGA is not the best option for predicting structural damage of masonry buildings accounting for SFS interaction.

Figure 15 compares the fragility curves at each DL for two-story (dark lines) and four-story (light lines) clay brick masonry buildings, as computed for the most efficient IMs (i.e. I_H and PGV).

Fig. 15.

Fragility functions for clay brick masonry structures in terms of (a) I_H and (b) PGV.

The fragility functions for fixed-base models (solid lines) are always shifted towards higher IM levels with respect to those associated with compliant base models, implying that neglecting site effects and soil-foundation-structure interaction on soft soils leads to a significant underestimation of the probability of damage.

The heterogeneity in soft soil profiles (dotted lines) reduces the structural fragility, except for the shortest structure at DL1. As a matter of fact, settlements and rotations of the foundation on the heterogeneous soil are larger than in case of homogeneous profile (see Fig. 13), leading to a higher dissipation of seismic energy and a consequent reduction of the MIDR (see the log–log plots in Fig. 14). For example, if the activation of the rocking mechanism of a two-story structure is considered (h/b = 1, DL2), the median value of PGV is reduced from 81 cm/s to 49 cm/s (i.e. by almost 50%) in the case of homogenous soft soil and to 59 cm/s in the case of heterogeneous profile (Fig. 15b).

Whatever the soil conditions, the significant shift to the left of the thin curves (h/b = 2) with respect to the thick ones (h/b = 1) once again shows the higher vulnerability of the slender structures with respect to OOP damage mechanisms of the masonry walls.

The histograms in Fig. 16 summarize, for each damage level, the reduction factor, R_F, of the 16^th, 50^th and 84^th percentiles of the IMs relevant to RSM and CBM buildings founded on soft soils, with respect to fixed-base conditions. For a given percentile x, such a reduction factor is defined as follows:

$$ R_F = \frac{{IM_{xD} }}{{IM_{xA} }} $$

(10)

Fig. 16.

Reduction factors R_F for 16^th, 50^th and 84^th percentiles of I_H and PGV in case of (a) rubble stone and (b) clay brick masonry structures with h/b = 1 (upper plots) and h/b = 2 (lower plots)

Similarly to the factor proposed by Petridis and Pitilakis [51], R_F quantifies the combined influence of site amplification and SFSI on the OOP seismic vulnerability of masonry structures, by measuring the distance between the fragility functions. A R_F value lower or higher than unity implies that the combination of seismic amplification and SFSI is detrimental or beneficial, respectively.

It can be noted that:

• in most cases, R_F is significantly lower than unity, i.e. both site amplification and SFSI lead to detrimental effects on the OOP behavior of the structure;

• for two-story structures, R_F increases with the stiffness of the masonry type (upper plots); the opposite occurs for the four-story structures (lower plots) because the proximity between the soil and structural fundamental periods (see Fig. 11) leads to double resonance phenomena (except for DL3 and heterogeneous soil profile);

• for a given masonry type, at the lower damage levels R_F on average decreases (i.e. the detrimental effects of soil deformability are more significant) with the building height;

• at any DL, the distance between the functions relevant to fixed- and compliant-base structures – on average – decreases for D_ho and increases for D_he, with the exception of the stiffer clay brick structures, for which the effects of soil inhomogeneity with depth are less detrimental on the OOP fragility at higher damage levels.

5.4 Urban-Scale Application to the Village of Onna

Aisa et al. [52] reported a damage analysis of Onna, a hamlet close to L’Aquila city (Central Italy), in the middle of the Aterno river valley, which was severely damaged by a M_W 6.1 earthquake on the 6^th of April 2009 (Fig. 17a). The structural typology most widespread in the village corresponds to two- or three-storey buildings with rubble stone loadbearing masonry walls and mixed steel-tile floor systems. Hence, they were considered as pertaining to vulnerability class B (Fig. 17b) according to the European Macroseismic Scale EMS-98 [53], i. e. masonry structures with irregular texture and efficient connections or with regular texture and inefficient connections. The same authors also observed that masonry disgregation and OOP mechanisms were the most common failure modes (as exemplified by the picture in Fig. 1b). The above factors suggested to consider this case history in order to validate the fragility curves developed in this study.

Fig. 17.

(a) Shakemap representative of the M_W 6.1 seismic event on 6^th April 2009 (http://shakemap.ingv.it/shake4/viewLeaflet.html?eventid=1895389); (b) distribution of vulnerability classes according to EMS-98 [53] with location of geophysical surveys; (c) shear wave velocity profiles.

Figure 17a shows the shakemap in terms of macroseismic intensity and PGA contours of the mainshock, as reported by National Institute of Geophysics and Volcanology. In lack of any record of the seismic motion in the village area, in order to infer the intensity measures characterizing the site during the mainshock, the bedrock motion at Onna was assimilated to that recorded by the closest seismic station, AQG. The assumption is reasonable because both the seismic station and the village fall within the surface projection of the fault plane. In such conditions and up to a Joyner and Boore source-to-site distance equal to 4 km, ground motion prediction equations are flat (e.g. Bindi et al. [54]), hence there is no need to scale the recorded signal.

Since the weathered and fractured rock underlying the AQG station is far from being a stiff rock outcrop, the horizontal components of the recorded motion were deconvoluted to the bedrock by Evangelista et al.[55], then projected along the fault parallel (FP) and fault normal (FN) directions. PGA resulted equal to 0.31 g along both directions, while I_H was equal to 91.7 cm and 83.7 cm along FP and FN, respectively, due to the impulsive and directivity effects influencing the velocity spectrum.

Such values were used to predict the damage through the fragility curves of the SFS systems. To this aim, the shear wave velocity profiles measured in the alluvial coarse-grained deposit for the seismic microzonation emergency study [56] were firstly examined. Three geophysical surveys, i.e. two refraction microtremors tests (ReMi1 and ReMi2 in Fig. 17b) and a MASW test (see purple, blue and light blue circles) were performed. Figure 17c reports the comparison between the measured shear wave velocity profiles and that adopted in this study for ground type C (see Sect. 3), which represents the most suitable soil category for the site of Onna.

Figure 18a shows the comparison between the fragility curves computed in this study for the same kind of masonry buildings (rubble stone, h/b = 1) founded on homogeneous soil types A, C and D, in terms of PGA (as the most commonly used IM) and one of optimal IM for this case, i.e. Housner Intensity computed between 0.1 s and 2.0 s.

Fig. 18.

(a) SFS fragility functions for rubble stone masonry buildings with h/b = 1 founded on ground types A, C, D; (b) territorial damage distribution at Onna for vulnerability class B; (c) comparison between statistical distributions of observed and predicted damage.

Since the RSM short buildings had a fundamental frequency close to that of the C soil profile (2.50 Hz), it can be observed, for DL1, that the fragility functions for soil type C (dotted lines) are shifted further towards lower IM levels with respect to those related to the D soil profile (dashed lines), leading to higher probability of damage. On the other hand, at high levels of I_H the probability of exceeding DL2 and DL3 in ground type C appears reduced. The vertical arrows in Fig. 18a show the values in terms of PGA and I_H which correspond to the reference bedrock motion inferred at Onna.

Figure 18b shows the territorial distribution of the observed damage as classified by [53] for vulnerability class B, by referring to the EMS-98 scale, which identifies the following six damage levels:

• D0: no damage;

• D1: development of few cracks in several walls;

• D2: significant cracks in many walls and collapse of plaster;

• D3: development of extensive and extended crack in many walls;

• D4: significative collapse of walls, or partial structural collapse of roofs;

• D5: destruction of the structure.

In order to compare such damage levels with the thresholds defined in the fragility study (see Sect. 5.3), D1 and D2 were considered equivalent to DL1 and DL2, respectively, while D3 and D4 were merged and assimilated to DL3.

The histograms in Fig. 18c show the comparison between the statistical distributions of observed vs. predicted damage, the latter derived by computing the difference between the probabilities of exceeding DL_i and DL_i+1. It can be observed that the use of either PGA or PGV as IM can lead to significant overestimation of damage at DL2, while the opposite occurs for DL3 or higher. Instead, a much better agreement with the observed distribution was found at all damage levels using the spectral intensity I_H as intensity measure.

6 Conclusions and Perspectives

This paper was dedicated to report the main methodological outcomes of a long-term comprehensive study, which was developed by the authors with the purpose of calibrating up-to-date straightforward tools to account for soil-foundation-structure interaction in assessing the seismic safety of the most widespread typologies of residential masonry buildings in the most hazardous countries in the Mediterranean area. Although not exhaustive of all the possible geometries, material properties and damage mechanisms, the parametric studies sampled a range of representative combinations extended enough to highlight the role of several factors on the dynamic response and seismic damage, such as the building slenderness, the soil-structure stiffness ratio and the degree of inhomogeneity in the subsoil profile.

The procedure enabling to predict the elongation of the fundamental period of a ‘replacement oscillator’ was proved to be effectively extended to SFS systems for which some critical factors may be overlooked by assuming simplified hypotheses. The case study of Matera provided a significant validation test based on several measurements of the soil-building fundamental frequency; however, the proposed method deserves further improvements to account for irregular structural geometries. Once soil non-linearity and overall system damping are appropriately considered, the method might be fruitfully adopted for an evaluation of the seismic inertial loads acting on structures and foundations, by using free-field response spectra derived from seismic response analyses, at both local and territorial scale.

On the other hand, the formulation of fragility curves for typical soil-foundation-structure systems as a function of synthetic intensity measures of the reference bedrock motion can ideally support the simulation of damage scenarios at a territorial scale, by a ‘convolution’ of shakemaps through site and building classification databases. The consistency between the statistical distributions of damage predicted and observed in the village of Onna seems an encouraging example of application for a representative case study. Nevertheless, the procedure deserves to be assessed also against alternative approaches, e.g. by expressing the probability of damage as a function of the ground motion including site amplification, and validated versus case studies where on-site seismic records and more detailed inventories of the damage mechanisms are available.