Coordination of multiple AGVs: a quadratic optimization method

Abstract

This paper presents an optimization strategy to coordinate a fleet of Automated Guided Vehicles (AGVs) traveling on ad-hoc pre-defined roadmaps. Specifically, the objective is to maximize traffic throughput of AGVs navigating in an automated warehouse by minimizing the time AGVs spend negotiating complex traffic patterns to avoid collisions with other AGVs. In this work, the coordination problem is posed as a Quadratic Program where the optimization is performed in a centralized manner. The proposed method is validated by means of simulations and experiments for different industrial warehouse scenarios. The performance of the proposed strategy is then compared with a recently proposed decentralized coordination strategy that relies on local negotiations for shared resources. The results show that the proposed coordination strategy successfully maximizes vehicle throughput and significantly minimizes the time vehicles spend negotiating traffic under different scenarios.

1 Introduction

Automated warehouses are becoming an increasingly popular solution for end-of-line logistics due to improved efficiency and flexibility (Sabattini et al. 2013). In order to meet the increasing delivery throughput requirements, warehouses are employing more and more Automated Guided Vehicles (AGVs) such that it is now common to find hundreds of AGVs in a single warehouse. It is therefore not surprising that multi-vehicle planning and coordination is receiving even more attention by the robotics community in the last years, especially in the context of AGVs for industrial applications.

Existing work addressing the multi-vehicle planning and coordination problem for AGVs in industrial applications includes (Zhang and Mehrjerdi 2013; Hoshino and Seki 2013; Pecora et al. 2012; Olmi et al. 2011; Secchi et al. 2015) and references therein. Recently, a hierarchical strategy for the coordination of a fleet of AGVs in an automated warehouse was proposed in Digani et al. (2014b), Digani et al. (2015b). The hierarchical strategy first partitions the robots’ environment into sectors. The sequence of sectors each AGV has to cross to reach its destination is computed using a Model Predictive Control (MPC) based centralized planner in order to maximize the performance of the entire fleet. Within each sector, a decentralized strategy is used to coordinate the AGVs to provide a simple and scalable traffic strategy. Each time an AGV enters a new sector, the central unit determines the traffic level in each sector by counting the number of AGVs it contains. Using the $A^*$ (LaValle 2006) algorithm, the sequence of sectors the AGV needs to track is recomputed based on the current traffic condition. The introduction of such a simple traffic measure, namely counting the number of AGVs within each sector, has significantly increased the performance of the traffic manager, see Digani et al. (2015b) for more details and Sabattini et al. (2015) for an industrial benchmark. The decentralized coordination within each sector is performed by means of a negotiation strategy among the AGVs based on a priority scheme. A shared resource, i.e., a road segment, is allocated to the winner of each negotiation round, while the loser of the negotiation round must wait until the shared resource becomes free. It is worth noting that this negotiation mechanism inevitably leads the AGVs to spend most of their time waiting. Thus a drawback of these previous approaches is that vehicles crossing a sector end up spending most of their time waiting for negotiations. Thus the amount of time spent locally, namely inside each sector, dominates the overall performance of the fleet.

This paper aims at overcoming this major drawback by minimizing the number of interactions among AGVs. The idea is to minimize the amount of time vehicles spend negotiating complex traffic patterns within each sector as they avoid collisions with one another while navigating through the workspace. In this work, we propose a strategy that completely avoids negotiations by partitioning the indoor environment into several sectors. Within each sector, a local coordination strategy that maximizes the AGV throughput through the sector is formulated as a centralized optimization problem. The contribution of the paper lies in a complete formulation of the coordination problem as a quadratic optimization problem (QP), where the crossing time for the vehicles, i.e., the time it takes for the vehicles to enter and leave a given sector, is minimized with respect to the vehicle velocities. Furthermore, an exhaustive experimental validation is provided, in real scenarios extracted from real automated warehouses with AGV systems. The paper extends the idea in Digani et al. (2015a) and exploits the framework presented in Digani et al. (2014b), Digani et al. (2015b). Some preliminary results in which a draft version of the method is applied to a virtual environment can be found in Digani et al. (2015a).

1.1 Related work

Coordination of groups of autonomous vehicles is a relevant topic in multi-robot systems that has been widely addressed in the literature (LaValle 2006). In general, existing approaches can be divided into two main categories: centralized versus decentralized. Decentralized approaches (see for instance Yang et al. 2008; Zhang and Mehrjerdi 2013) are known to scale well with the number of robots. Namely, decentralized approaches directly address the complexity of large-scale multi-robot coordination problems. In these methods, each robot autonomously determines its routes, resolving conflicts with other robots by collecting information from them (Habib et al. 2013; Jager and Nebel 2001; Zheng et al. 2013). Decentralized techniques are generally faster than centralized ones, but they present several drawbacks. While existing works, such as Fanti et al. (2015), Manca et al. (2011), provide deadlock-free strategies, decentralized approaches can fail to find valid paths for all robots and feasible solutions may be far from optimal. As such, decentralized strategies may not be suitable for many industrial applications where efficiency is paramount.

With centralized strategies, a single decision maker determines the entire path plan for all the robots. The main advantage of centralized approaches is their ability to find optimal solutions (LaValle and Hutchinson 1998). For this reason, fleets of AGVs in industrial applications are generally coordinated by a centralized supervisor (the control center) which manages all the information coming form the Warehouse Management System (WMS) and from the environment. The control center handles the coordination of the fleet, solving a multi-robot path planning problem (see e.g Olmi et al. 2008; Hoshino and Seki 2013). Recently, existing works have proposed dynamic strategies to coordinate a fleet of robots where the central coordinator dynamically re-computes the paths using local information (Secchi et al. 2015; Pecora et al. 2012). However, in most cases the dimension of the multi-robot configuration space may be very high and require considerable computational resources to obtain a solution.

A multi-layer structure world representation can reduce the multi-robot path planning search space. As explained in Park et al. (2012), the approach constructs a hierarchical map which can abstract the traversable areas using an adequate number of nodes and edges in a graph. The path is obtained by searching through the graphs of the various layers. Other popular solutions to reduce the search space rely on a roadmap approach (Kavraki et al. 1996; Makarem and Gillet 2012; Hui 2010), where local interaction rules or local strategies for conflict resolution are often included (Pallottino et al. 2007; Reveliotis and Roszkowska 2011). Recently, in Digani et al. (2014b), Digani et al. (2015b) a hierarchical strategy was proposed that exploits the benefits of both centralized and decentralized approaches for the coordination of an AGV fleet. Based on this approach, a dynamic traffic model was derived in Digani et al. (2016). While centralized approaches are known to scale poorly with respect to the number of agents, they are often preferred in many industrial applications because of their solution optimality guarantees which provide performance assurances. The reliance on centralized approaches is also further backed by the ever decreasing cost of fast high-end computing and the potential loss in revenue caused by deadlocks.

Lastly, path planning strategies can also be performed by employing prioritized schemes. Namely, the paths are sequentially computed based on the priorities of the robots in order to avoid conflicts (Cap et al. 2015; van den Berg and Overmars 2005). These approaches have been shown to be effective in practice, but they are incomplete, i.e., there are solvable problem instances that the algorithms fail and thus provide no guarantees of success: completeness guarantees can be provided by appropriately structuring the operational environment (van den Berg and Overmars 2005). Other approaches include fixed-path coordination which aims at coordinating robots on a predefined set of paths to avoid collision (LaValle 2006). This work falls in this last category, where the vehicles are constrained to move on a predefined roadmap.

Irrespective of the approach, existing work has shown the impact of uncertainties on the overall system performance of large-scale multi-agent systems. Specifically, Mather et al. (2010), Mather and Hsieh (2010) have shown how uncertainties inherent in any systems deployed in a realistic setting can detrimentally impact the overall system performance. These uncertainties may arise from sensor/actuation noise, model parameters, and local vehicle-to-vehicle interactions can lead to ensemble effects that are difficult to diagnose without an appropriate macroscopic view of the system. In Mather et al. (2010), Mather and Hsieh (2010) showed how these detrimental impacts can be mitigated by minimizing the local vehicle-to-vehicle interactions within a given system. As such, this work focuses on maximizing traffic throughput in specific regions of the workspace and thus minimizing the local vehicle-to-vehicle interactions that can lead to detrimental ensemble effects.

Coordination along a roadmap in a specific region can be achieved using different approaches (Alami et al. 1998). In particular, complete and optimal solutions have been developed (see e.g. Peng and Akella 2005; Siméon et al. 2002; Olmi et al. 2011), but are known to be very computationally expensive. The method proposed in this work provides a solution that is only locally optimal, but is shown to have very low computational requirements.

1.2 Organization

The paper is organized as follows: the problem formulation and key assumptions to the approach are stated in Sect. 2. Section 3 describes the optimization problem and the formulation of the problem as a quadratic program. Section 4 shows the implementation of the proposed method and Sect. 5 presents simulation and experimental results. Finally Sect. 6 summarizes key results and Sect. 7 concludes with some discussions for future works.

2 Problem definition

We consider the problem of coordinating a fleet of ${\bar{N}}$ AGVs in an automatic warehouse. In modern AGV systems, the vehicles are constrained to move on a predefined (virtual) roadmap $\mathcal {R}$. The roadmap is partitioned into a collection of segments $\mathcal {P} = \lbrace p_1, \ldots , p_W \rbrace$. The tasks the AGVs have to accomplish correspond to picking some goods in a location of the roadmap and delivering it to another location. Thus, each time a task is assigned to AGV i, the path $\pi _i$ the vehicle has to follow is computed. A path is simply a sequence of adjacent segments, i.e., $\pi _i=\left\{ p_i^1,\ldots , p_i^{M_i}\right\}$.

Each vehicle is modeled as a circle with the center on the path it is following and radius $\nicefrac {\delta }{2}$, where $\delta >0$ is chosen in order to obtain a circle sufficiently big to enclose the biggest AGV traveling along the roadmap.¹ For each segment $p\in \mathcal {P}$, we denote with $\mathcal {V}(p)$ the portion of space occupied by a vehicle moving along p, i.e., the trace of the vehicle along that segment. Two AGVs traveling on two segments that are too close to each other may collide. Formally, two segments $p_i,p_j\in \mathcal {P}$ are colliding segments if $\mathcal {V}(p_i) \cap \mathcal {V}(p_j) \ne \emptyset$. Consequently, given a segment $p\in \mathcal {P}$, the Collision Segment Set of p (CSS(p)) of p is given by:

$$\begin{aligned} { CSS}(p) = \lbrace \rho \in \mathcal {P}, \rho \ne p \text{ s.t. } \mathcal {V}(p)\cap \mathcal {V}(\rho )\ne \emptyset \rbrace \end{aligned}$$

(1)

As shown in Digani et al. (2014a), Beinschob et al. (2017), it is possible to automatically build a roadmap and a partition of the warehouse into a finite set of sectors $S=\lbrace S_1,\ldots ,S_Q \rbrace$ such that each sector contains at most an intersection area, i.e., a portion of the roadmpap where the AGVs need to coordinate their motion in order to avoid collisions. In this paper we will consider a constant partitioning of the environment. In Sabattini et al. (2016) an algorithm for the dynamic partitioning of the warehouse has been proposed.

Consider the sector $S_\sigma$, where $\sigma \in \{1, \ldots , Q\}$. The set of segments contained in $S_\sigma$ is given by $\mathcal {P}_\sigma =\bigcup _{i=1}^{{\bar{N}}}(\pi _i\cap S_\sigma )$. The intersection area (that can be empty) of $S_\sigma$ is given by

$$\begin{aligned} \mathcal {A}_\sigma =\bigcup _{p\in \mathcal {P}_\sigma }{} { CSS}(p) \end{aligned}$$

(2)

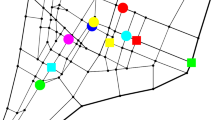
An example of the partitioning of a real workspace is shown in Figs. 1 and 2 highlights segments and paths within a sector.

Fig. 1

Roadmap and sectors in a real environment: black areas are obstacles, red lines represents sectors’ borders and red dots are the centres of the sectors (Color figure online)

Fig. 2

Definitions of path and segment for a sector

Given a set of ${\bar{N}}$ tasks to complete and, consequently, ${\bar{N}}$ paths the AGVS have to track, the following metrics are used for evaluating the performance of the AGV system.

• Completion Time the time needed by one AGV for tracking its assigned path

• AGV-Time the time necessary for tracking all the paths, i.e., the sum of all the completion times

The sector partitioning can be exploited to deal with the complexity of the AGV coordination problem. This can be accomplished using hierarchical approaches where the coordination problem is solved within each sector and the planning problem is solved between sectors. For example, in Digani et al. (2015b), the traffic manager works on two layers. The first layer performs a high level finite-horizon centralized planning that computes the sequence of sectors each AGV has to cross to reach its destination using the $A^*$ algorithm on the sectors. The second layer represents a low level decentralized coordination strategy for safe navigation inside each sector. Thus, coordination is only required within each sector, and in particular within at most one intersection area, where the number of interactions among the agents is given by the number of local negotiations among them. A shared resource, i.e., a segment, is then allocated to the winner of each negotiation round, while the losers of the negotiation round must wait until the shared resource becomes free. It is worth noting that the results of these negotiations are not known a priori and that they depend on the paths and on possible priorities of the AGVs. Thus, the system is not deterministic and the traffic control and management is not trivial. In particular, the negotiation process affects the total time a vehicle spends traversing a given sector.

The goal of this paper is to propose a novel coordination strategy for AGVs crossing an intersection area. The proposed methodology aims at determining for each AGV the best speed it should travel along its path in order to minimize the total crossing time while avoiding conflicts (i.e., possible collisions) with other vehicles. This will allow rid the system of non deterministic negotiations or of other heuristics for shared resource allocations.

Coordination happens in sectors, which contain at most one intersection area. Thus, the problem of coordinating ${\bar{N}}$ AGVs moving on $\mathcal {R}$ can be recast into the problem of coordinating $N\le {\bar{N}}$ AGVs moving inside a generic sector. Improving the coordination performance inside a sector will lead to an improvment of the coordination performance of the overall fleet on the roadmap.

Formally, we aim at solving the following problem

Problem 1

Given a group of $N\le {\bar{N}}$ AGVs crossing a sector on paths $\{\pi _1, \ldots , \pi _N\}$, define the velocity profile of each AGV in order to minimize the AGV-Time necessary for completing the tasks while avoiding conflicts among the AGVs.

Figure 3 shows a simple example of the problem where three AGVs have to follow the assigned paths while avoiding collisions. Each AGV starts in an initial position along its path and has to reach its own final position.

Fig. 3

Multi AGV coordination problem in an intersection area of a sector

We will make the following assumptions:

• A1 No external obstacles (e.g. people, manual forklifts) can be found on the roadmap.

• A2 The velocity along a segment is constant

• A3 The velocity of each AGV is bounded:

  $$\begin{aligned} 0<V_{{ min}}<\nu<V_{{ max}}<\infty \end{aligned}$$

  (3)

  where $\nu$ represents the velocity of an AGV and $V_{{ min}}$ and $V_{{ max}}$ are the lower and upper velocity bounds respectively.²

• A4 Each segment can be occupied by at most one AGV

• A5 Each AGV has a different pair of initial and final positions

We would like to remark that these assumptions do not introduce significant limitations to the applicability of the proposed strategy. In particular, Assumption A1 is generally verified, during normal operations, since human operators and manual forklifts are not allowed to occupy areas traveled by AGVs: their presence on the AGVs’ path is handled by safety systems.

Assumption A2 is imposed for the sake of simplicity of explanation: while it would be possible to extend the proposed approach considering acceleration and deceleration along each segment, we prefer to keep the explanation simple, and consider only the average velocity. Conversely, Assumption A3 is trivially verified for any real AGV.

Assumption A4 is generally imposed in any AGV system used for industrial logistics, for safety and coordination reasons: in fact, it helps in guaranteeing collision avoidance, and it simplifies the coordination problem.

Finally, Assumption A5 is, in general, trivially verified, thanks to the redundancy of roadmaps typically utilized in industrial environments.

3 Modeling and optimization problem

In this section we show how to model the AGV coordination problem (Problem 1) as a QP problem. The output is a set of velocities that guarantees a safe minimum distance between all agents and that minimizes the total time the AGVs need to accomplish the tasks.

Let $\pi _i=\left\{ p_i^1, \ldots , p_i^{M_i}\right\}$, $i=1, \ldots , N$, be the path the i-th AGV has to track inside the sector. Let $d_i^k$ and $v_i^k$ be the length of $p_i^k$ and the velocity of the AGV i along segment $p_i^k$ respectively. Since, according to Assumption A2, $v_i^k$ is constant, the completion time for AGV i to track $\pi _i$ is given by:

$$\begin{aligned} \varDelta t_i = \sum _{k=1}^{M_i} \dfrac{d_i^k}{v_i^k} \end{aligned}$$

(4)

and the AGV-Time is given by

$$\begin{aligned} \varDelta T = \sum _{i=1}^{N} \sum _{k=1}^{M_i} \varDelta t_i = \sum _{i=1}^{N} \sum _{k=1}^{M_i} \dfrac{d_i^k}{v_i^k}. \end{aligned}$$

(5)

Let ${\bar{M}}=M_1 + \cdots + M_N$ be the total number of segments to be crossed by N AGVs and let $\mathbf {v}\in \mathbb {R}^{{\bar{M}}}$ and $\mathbf {d}\in \mathbb {R}^{{\bar{M}}}$ be defined as

$$\begin{aligned} \mathbf v= & {} \left( v_1^1, \ldots , v_1^{M_1}, \ldots , v_N^{M_N} \right) ^T \end{aligned}$$

(6)

$$\begin{aligned} \mathbf d= & {} \left( d_1^1, \ldots , d_1^{M_1}, \ldots , d_N^{M_N} \right) ^T \end{aligned}$$

(7)

Moreover, let $v_i\in \mathbb {R}$ and $d_i\in \mathbb {R}$, $i=1, \ldots , {\bar{M}}$, denote the i-th component of $\mathbf {v}$ and $\mathbf {d}$, respectively.

Minimizing the AGV-Time corresponds to finding a set of velocities each AGV has to track the segments of its paths with. Formally

$$\begin{aligned} {\mathop {{{\mathrm{argmin}}}}\limits _{\mathbf {v}}} \varDelta T={\mathop {{{\mathrm{argmin}}}}\limits _{\mathbf {v}}}\sum _{i=1}^{N} \sum _{k=1}^{M_i} \dfrac{d_i^k}{v_i^k} \end{aligned}$$

(8)

We introduce now a new vector of optimization variables $\phi \in \mathbb {R}^{{\bar{M}}}$ defined as follows:

$$\begin{aligned} \phi = \left( \dfrac{1}{v_1^1}, \ldots , \dfrac{1}{v_1^{M_1}}, \ldots , \dfrac{1}{v_N^{M_N}} \right) ^T \end{aligned}$$

(9)

Moreover, let $\phi _i\in \mathbb {R}$, $i=1, \ldots , {\bar{M}}$, denote the i-th component of $\phi$. Clearly, finding optimal the value of $\phi$ leads to directly defining the corresponding optimal value of $\mathbf v$.

The functional to minimize is the weighted sum of terms depending only on one of the variables $\phi _i$ to optimized, and the weights are represented by the elements of vector $\mathbf {d}$. Hence, solving (8) can be written as the problem of minimizing the following linear objective function:

$$\begin{aligned} f(\phi ) = - \sum _{i=1}^{\bar{M}}d_i \phi _i. \end{aligned}$$

(10)

We consider two constraints for the optimization problem. The first is related to the boundedness of the velocities and the second is the maintenance of a safe distance between the AGVs. Considering (3), we have that each component of $\phi$ is bounded as:

$$\begin{aligned} \varPhi _{{ min}} \le \phi _i \le \varPhi _{{ max}},\quad \forall i = 1, \ldots , \bar{M} \end{aligned}$$

(11)

which can be represented as a linear constraint with respect to $\phi$. According to (3), $\varPhi _{{ min}} = \nicefrac {1}{V_{{ max}}}$ and $\varPhi _{{ max}} = \nicefrac {1}{V_{{ min}}}$.

As remarked in Sect. 2, each AGV is modeled as a circle with radius $\nicefrac {\delta }{2}$. Let the center of the circle representing the i-th AGV be denoted by $\mathcal {X}_i(t)=[x_i(t),y_i(t)]^T$, where $[x_i(t),y_i(t)]^T$ is the cartesian position of the vehicle. Collision avoidance is guaranteed by ensuring that the relative distance $\gamma _{i,j}$ between any two AGVs is greater than $\delta$, i.e.:

$$\begin{aligned} \gamma _{i,j} (t)&= ||\mathcal {X}_i(t) - \mathcal {X}_j(t)||\nonumber \\&= \sqrt{ (x_i(t) - x_j(t))^2 +(y_i(t) - y_j(t))^2 }> \delta \nonumber \\&\qquad i\ne j \in \{1, \ldots , N \} \end{aligned}$$

(12)

This is a non convex constraint that needs to be imposed for all the pairs of AGVs all over their paths. The non convexity of (12) makes the optimization problem too complex to be solved continuously for each sector, especially if the number of AGVs is quite big. Luckily, the constraint in (12) can be reformulated as a quadratic constraint, which leads to a computationally efficient solution.

Let each path $\pi _i$ be parameterized by a curvilinear abscissa $s_i\in [0,d_i]$, where $d_i=\sum _{k=1}^{M_i}d_i^k$, and indicate, with a slight abuse of notation, with $\pi _i(s_i)$ the cartesian position (x, y) on path $\pi _i$ corresponding to the value of the curvilinear abscissa $s_i$. We denote with:

$$\begin{aligned} \varDelta X_{i,j} = \left\{ s_i\,| \,\exists s_j \,\, \text{ such } \text{ that } \,||\pi _i(s_i) - \pi _j(s_j)|| \le \delta \right\} . \end{aligned}$$

(13)

the portion of the of path $\pi _i$ where a collision between AGV i and AGV j can happen on path i. It is worth noting that the collision regions can be computed totally off-line since they are based solely on geometric information regarding the roadmap and the size of the vehicles.

Let $s_{ij}^{{ min}}$ and $s_{ij}^{{ max}}$ be the values of the curvilinear abscissa corresponding to the beginning of the segment that contains ${ min}\varDelta X_{ij}$ and the end of the segment that contains ${ max}\varDelta X_{ij}$. Thus, the portion $[s_{ij}^{{ min}},s_{ij}^{{ max}}]$ represents the smallest subset of segments of $\pi _i$ containing the collision region $\varDelta X_{i,j}$.

In order to keep the notation simple, we will hereafter consider that $\varDelta X_{ij}$ is a single connected sub-interval of $[0, d_i]$. While this may not be true when considering the paths along the whole roadmap, this is always true in practice when considering a single intersection area in a sector. All the results of the paper can be straightforwardly generalized to the case in which $\varDelta X_{i,j}$ is a disconnected subset. In particular, this can be achieved, for instance, splitting the paths into sub-paths that contain at most a connected component of $\varDelta X_{i,j}$, and then apply the results that will be derived in the sequel to each pair of intersecting sub-paths.

Furthermore, let $\omega _{i,j}^{{ min}}$ and $\omega _{i,j}^{{ max}}$ be the time instants at which AGV i reaches $\pi _i\left( s_{ij}^{{ min}}\right)$ and $\pi _i\left( s_{ij}^{{ max}}\right)$ respectively. Thus, AGV i can collide with AGV j in the time interval $\varOmega _{i,j}=\left[ \omega _{i,j}^{{ min}}, \omega _{i,j}^{{ max}}\right]$. Similarly, it is possible to define the portion of the path $\pi _j$ where a collision between AGV j and AGV i can happen on $\pi _j$ and, consequently, the time interval $\varOmega _{j,i}$ where a collision between AGV j and AGV i can happen. Collision avoidance between the AGV i and AGV j is verified only if:

$$\begin{aligned} \varOmega _{i,j} \cap \varOmega _{j,i} = \emptyset . \end{aligned}$$

(14)

Figure 4 pictorially depicts the described problem: with an abuse of notation, the vertical axis represents both the parameter $s_i$ and $s_j$. The condition (14) implies that the set $\varOmega _{i,j},\varOmega _{j,i}$, denoted by the red and blue line segments on the time axis in Fig. 4, are disjoint.

Fig. 4

Coordination space in the case of two agents: the lines represent the velocities of the AGVs

It is possible to reformulate (14) using the midpoints of the sets $\varOmega _{i,j},\varOmega _{j,i}$. In particular the distance between two mid-points has to be grater than the sum of the distances between the mid-point and one extreme point of both the sets. Formally, we define

$$\begin{aligned} \alpha _{i,j}= & {} \omega _{i,j}^{{ max}} + \omega _{i,j}^{{ min}} \\ \beta _{i,j}= & {} \omega _{i,j}^{{ max}} - \omega _{i,j}^{{ min}} \end{aligned}$$

The condition described by (14) can then be formalized as follows:

$$\begin{aligned} \left| \dfrac{\alpha _{i,j}}{2} - \dfrac{\alpha _{j,i}}{2}\right| > \dfrac{\beta _{i,j}}{2} + \dfrac{\beta _{j,i}}{2} \end{aligned}$$

(15)

which simplifies to

$$\begin{aligned} | \alpha _{i,j} - \alpha _{j,i} | > \beta _{i,j} + \beta _{j,i} \end{aligned}$$

(16)

and squaring (16), the constraint becomes quadratic:

$$\begin{aligned} (\alpha _{i,j} - \alpha _{j,i})^2 > \left( \beta _{i,j} + \beta _{j,i}\right) ^2. \end{aligned}$$

(17)

Let us now introduce the following Proposition which will show that (17) is quadratic with respect to $\phi$. This will be instrumental in the formulation of the problem as a QP.

Proposition 1

The constraint in (17) can be represented in the following form

$$\begin{aligned} \left( \phi _i^T, \phi _j^T\right) ^T\varLambda _{ij}\left( \phi _i^T, \phi _j^T\right) >0 \end{aligned}$$

for an appropriately defined matrix $\varLambda _{ij}$.

Proof

Let $\left\{ p_i^{m_i}, \ldots p_i^{m_i+n_i}\right\}$ and $\left\{ p_j^{m_j}, \ldots p_j^{m_j+n_j}\right\}$, where $m_i,m_j,n_i,n_j\ge 1$, $m_i+n_i\le M_i$ and $m_j+n_j\le M_j$, be the set of segments containing $\varDelta X_{ij}$ and $\varDelta X_{ji}$ respectively. Considering that the velocity of the AGVs is constant on each segment, we can write:

$$\begin{aligned} \alpha _{i,j}=\sum _{k=1}^{m_i+n_i}\frac{d_i^k}{v_i^k}+\sum _{k=1}^{m_i-1} \frac{d_i^k}{v_i^k}=\sum _{k=1}^{m_i+n_i}a_{ik}\frac{1}{v_i^k} \end{aligned}$$

(18)

where

$$\begin{aligned} a_{ik}=\left\{ \begin{array}{ll} 2d_i^k&{}\text{ if }\quad k<m_i \\ d_i^k &{}\text{ if }\quad k\ge m_i \\ \end{array} \right. \end{aligned}$$

(19)

Similarly,

$$\begin{aligned} \alpha _{j,i}=\sum _{k=1}^{m_j+n_j}a_{jk}\frac{1}{v_j^k} \end{aligned}$$

(20)

where

$$\begin{aligned} a_{jk}=\left\{ \begin{array}{ll} 2d_j^k&{}\text{ if }\quad k<m_j \\ d_j^k &{}\text{ if }\quad k\ge m_j \\ \end{array} \right. \end{aligned}$$

(21)

It is convenient to write (18) and (20) in matrix form as:

$$\begin{aligned} \alpha _{i,j}= & {} \mathbf {1}_{(m_i+n_i)}^TA_i\phi _i\nonumber \\ \alpha _{j,i}= & {} \mathbf {1}_{(m_j+n_j)}^TA_j\phi _j \end{aligned}$$

(22)

where $\mathbf {1}_\rho$ indicates a vector of ones of dimension $\rho$. Furthermore,

$$\begin{aligned} A_i={ diag}(a_{i1}, \ldots , a_{i(m_i+n_i)}) \end{aligned}$$

and

$$\begin{aligned} \phi _i=\left( \frac{1}{v_i^1},\ldots ,\frac{1}{v_i^{(m_i+n_i)}}\right) ^T \end{aligned}$$

The quantities $A_j$ and $\phi _j$ are defined analogously. Thus, we can write

$$\begin{aligned} (\alpha _{i,j}-\alpha _{j,i})^2= & {} \left( 1_{(m_i+n_i)}^TA_i\phi _i-1_{(m_j+n_j)}^TA_j\phi _j\right) ^T\nonumber \\&\times \left( 1_{(m_i+n_i)}^TA_i\phi _i-1_{(m_j+n_j)}^TA_j\phi _j\right) \end{aligned}$$

(23)

By straightforward computations we can write:

$$\begin{aligned} (\alpha _{i,j}-\alpha _{j,i})^2=\phi _{ij}^TM_{ij}\phi _{ij} \end{aligned}$$

(24)

where $\phi _{ij}=\left( \phi _i^T, \phi _j^T \right) ^T$ and

$$\begin{aligned} M_{ij}=\begin{pmatrix} A_i\mathbf {1}_{m_i+n_i}\mathbf {1}_{m_i+n_i}^TA_i &{} -A_i\mathbf {1}_{(m_i+n_i)}\mathbf {1}_{(m_j+n_j)}^TA_j \\ -A_j\mathbf {1}_{(m_j+n_j)}\mathbf {1}_{(m_i+n_i)}^TA_i &{} A_j\mathbf {1}_{m_j+n_j}\mathbf {1}_{m_j+n_j}^TA_j \end{pmatrix} \end{aligned}$$

(25)

Similarly, we can write:

$$\begin{aligned} \beta _{i,j}=\sum _{k=1}^{m_i+n_i}\frac{d_i^k}{v_i^k}-\sum _{k=1}^{m_i-1} \frac{d_i^k}{v_i^k}=\sum _{k=1}^{m_i+n_i}b_{ik}\frac{1}{v_i^k} \end{aligned}$$

(26)

where

$$\begin{aligned} b_{ik}=\left\{ \begin{array}{ll} 0 &{} \text{ if }\quad k<m_i \\ d_i^k &{} \text{ if }\quad k\ge m_i \\ \end{array} \right. \end{aligned}$$

(27)

and

$$\begin{aligned} \beta _{j,i}=\sum _{k=1}^{m_j+n_j}b_{jk}\frac{1}{v_j^k} \end{aligned}$$

(28)

where

$$\begin{aligned} b_{jk}=\left\{ \begin{array}{ll} 0 &{} \text{ if }\quad k<m_j \\ d_j^k &{} \text{ if }\quad k\ge m_j \\ \end{array} \right. \end{aligned}$$

(29)

Thus, using a vector notation as for obtaining (25), we can write:

$$\begin{aligned} (b_{i,j}+b_{j_i})^2=\phi _{ij}^TN_{ij}\phi _{ij} \end{aligned}$$

(30)

with

$$\begin{aligned} N_{ij}= \begin{pmatrix} B_i\mathbf {1}_{m_i+n_i}\mathbf {1}_{m_i+n_i}^TB_i &{} B_i\mathbf {1}_{(m_i+n_i)}\mathbf {1}_{(m_j+n_j)}^TB_j \\ B_j\mathbf {1}_{(m_j+n_j)}\mathbf {1}_{(m_i+n_i)}^TB_i &{} B_j\mathbf {1}_{m_j+n_j}\mathbf {1}_{m_j+n_j}^TB_j \end{pmatrix}\nonumber \\ \end{aligned}$$

(31)

where $B_i={ diag}(b_{i1}, \ldots , b_{i(m_i+n_i)})$ and $B_j={ diag}(b_{j1},\ldots , b_{j(m_j+n_j)})$.

Thus, we can rewrite (17) as:

$$\begin{aligned} \phi _{ij}^T(M_{ij}-N_{ij})\phi _{ij}>0 \end{aligned}$$

(32)

Define now matrix $\varLambda _{ij} \in \mathbb {R}^{ \left( m_i+n_i+m_j+n_j\right) \times \left( m_i+n_i + m_j+n_j\right) }$ as follows:

$$\begin{aligned} \varLambda _{ij} = M_{ij} - N_{ij} \end{aligned}$$

(33)

The inequality in (32) can then be rewritten as follows:

$$\begin{aligned} \phi _{ij}^T\varLambda _{ij}\phi _{ij}>0 \end{aligned}$$

(34)

Since $\phi _{ij}=\left( \phi _i^T, \phi _j^T\right) ^T$, then the statement is proven. $\square$

3.1 Quadratic constraints linear programming

The coordination within a single sector is modeled as an optimization problem using a linear objective function, and a set of quadratic constraints with linear constraints on the boundary.

For this purpose, consider the inequality in (34). Matrix $\varLambda _{ij}$ can be partitioned as follows:

$$\begin{aligned} \varLambda _{ij} = \left( \begin{array}{cc} \varLambda _{ij}^{ii}&{} \varLambda _{ij}^{ij} \\ \varLambda _{ij}^{ji}&{} \varLambda _{ij}^{jj} \end{array} \right) \end{aligned}$$

(35)

where $\varLambda _{ij}^{ii} \in \mathbb {R}^{\left( m_i+n_i\right) \times \left( m_i+n_i\right) }$, $\varLambda _{ij}^{jj} \in \mathbb {R}^{\left( m_j+n_j\right) \times \left( m_j+n_j\right) }$, and $\varLambda _{ij}^{ij}={\varLambda _{ij}^{ji}}^T \in \mathbb {R}^{\left( m_i+n_i\right) \times \left( m_j+n_j\right) }$.

The optimization problem is then given by:

$$\begin{aligned} \text{ minimize }&\,\, \,\, f(\phi ) \end{aligned}$$

(36a)

$$\begin{aligned} \text{ subject } \text{ to }&\,\, \,\, A \phi \le b \end{aligned}$$

(36b)

$$\begin{aligned} \text{ and }&\,\, \,\, \phi ^T H_{ij} \phi \le 0\quad \forall i,j = 1,\ldots , \bar{M},\quad \text{ with }\quad j > i \end{aligned}$$

(36c)

Matrix $A \in \mathbb {R}^{2 \bar{M} \times \bar{M}}$ and vector $b \in \mathbb {R}^{2 \bar{M}}$ in the linear constraint (36b) encode the bounds on the elements of $\phi$ defined in (11).

The quadratic constraint (36c) represents the collision avoidance constraint, according to Proposition 1: matrix $H_{ij} \in \mathbb {R}^{ \bar{M} \times \bar{M}}$ represents the inequality (32). It is defined as a block matrix, whose block $\left( h,k\right)$ is given by

$$\begin{aligned} H_{ij}^{hk} = \left\{ \begin{array}{ll} \varLambda _{ij}^{ii} &{}\text {if}\quad h=i, k=i\\ \varLambda _{ij}^{jj} &{}\text {if}\quad h=j, k=j\\ \varLambda _{ij}^{ij} &{}\text {if}\quad h=i, k=j\\ \varLambda _{ij}^{ji} &{}\text {if}\quad h=j, k=i\\ \mathbb {O} &{}\text {otherwise} \end{array}\right. \end{aligned}$$

(37)

where $\mathbb {O}$ is a zero matrix of appropriate dimension.

4 Implementation

The proposed method aims at coordinating a fleet of agents on a map composed by several sectors. For this reason, each sector is provided with a dedicated process which manages the optimization routine in order to implement the proposed methodology. The optimization algorithm runs independently in each sector whenever a new agent enters or leaves the intersection area.

Some variations are introduced in order to implement the methodology among several sectors and thus among several intersections. The methodology proposed in the previous sections is based on the assumption that all the vehicles are at the initial position of their paths in the sector. The optimization algorithm runs whenever a new agent enters or leaves the intersection area. Thus, in general, at each computation of the algorithm a vehicle i can be at any position along its path, not necessary the initial position (where $s_i= 0$).

Fig. 5

Different intersections used during the simulations. a Intersection 1, b intersection 2, c intersection 3, d intersection 4

Fig. 6

Real map used in the simulations. a Real map, b sectors

Algorithm 1 shows the actual implemented method where $\mathcal {Q}_{{ new}}(\mathcal {A}_q)$ represents the current list of vehicles contained the intersection area $\mathcal {A}_q$, and $\mathcal {Q}_{{ old}}(\mathcal {A}_q)$ represents list of vehicles at the previous iteration of the algorithm. The starting position of each vehicle along its path, namely the current position at the instant of iteration of the algorithm, is collected in the vector $init(\mathcal {A}_q)$. Finally $\mathbf v$ is the vector of the optimized velocities, obtained by the solution $\phi$ of the optimization problem. Algorithm 1 is performed at each sample time $\tau$.

Algorithm 2 describes the single implemented controller for the i-th vehicle. It is worth noting that each AGV is controlled in a decentralized manner. Thus, each AGV entering a new intersection area $\mathcal {A}_q$ updates its position on the vector ${ init}(\mathcal {A}_q)$ in order to get the correct and optimized velocity vector

$$\begin{aligned} \mathbf v (i) = \left[ v_i^1, \ldots , v_i^{M_i} \right] . \end{aligned}$$

The i-th AGV stays in the queue $\mathcal {Q}_{{ old}}(\mathcal {A}_q)$ and $\mathcal {Q}_{{ new}}(\mathcal {A}_q)$ until it leaves the intersection area.

5 Validation

The proposed optimized coordination is validated by means of comparison with the coordination strategy first presented in Digani et al. (2014b) which relies on local negotiations. Hereafter we refer to the current proposed methodology as the Optimized Strategy, and to the other one as Negotiated Strategy. A decoupled optimal priority scheme (Bennewitz et al. 2001) is applied to the Negotiated Strategy in order to obtain a better comparison.

The simulations are performed on different single intersections extracted form the roadmap of real warehouses, as shown in Fig. 5. Subsequently experimental tests are performed on a complete real environment. Figure 6a shows a simple real environment composed by four rectangular obstacles and nine sectors. A roadmap is built for that environment using the algorithm described in Digani et al. (2014a).

5.1 Simulations

The topological complexity of the roadmaps is different in each scenario which depends on the number of possible paths, the number of possible interactions, and physical size of the environment. Repeated tests have been conducted under the following conditions:

• 4 topology of intersection

• number of AGVs $\in [2,11]$,

• the simulation stops when the intersection area is cleared,

• the priorities (Digani et al. 2014b) for the Negotiated Strategy are optimized each time,

• the same paths assigned to the AGVs are considered for the comparison, and

• the paths are assigned randomly.

Ten simulation runs were performed for each configuration.

To compare, we consider the time needed for all AGVs to clear the sector or the maximum of the crossing time ($t_{{ clearing}}$). We also considered the worst waiting time ($t_{{ wait}}$), the average waiting time ($\bar{t}_{{ wait}}$), and the computational time needed to obtain a solution ($t_{{ calc}}$). The waiting time is the time that the AGVs have to wait in the same position, with zero velocity, when yielding to other robots with higher priorities at an intersection in the roadmap. The worst waiting time is the maximum waiting time for all the AGVs in the sector. The computational time is the actual time to compute a solution to the centralized optimization problem. The worst waiting time and the average waiting time are computed for the Negotiated Strategy, while the computational time is computed for the Optimized Strategy.

The simulations were performed in Matlab with the standard optimization solver. The results are summarized in Fig. 7.

Fig. 7

Average of the clearing time versus number of AGVs in the different single intersections on 10 runs. a Negotiated strategy, b Optimized strategy

5.2 Experiments

The proposed approach has been implemented on a real indoor environment. The experimental environment and the implemented roadmap are shown in Fig. 8. The roadmap is divided into several sectors as shown in Fig. 6a.

Fig. 8

Real environment used for the experimental validation

The robots are differential-drive robots equipped with an onboard processor and odometry, an RGB-D sensor, and wifi networking capabilities. Localization for the vehicles is provided by an external motion capture system. Figure 9 shows the implementation architecture of the system. The core of the system, namely the Optimized Coordination, is implemented in the Matlab workspace. Then each robot is controlled by means of an independent ROS (Robot Operating System Quigley et al. 2009) module which manages the tracking of the trajectories of the roadmap.

Fig. 9

Implementation and architecture of the system

Fig. 10

Total time versus number of agents in the complete map with standard deviation

The experiments aim at validating the proposed optimized coordination method in a real scenario. As such a mixed-reality approach was employed where additional simulated robots are deployed with the real ones in order to increase the number of the fleet and thus the number of inter-robot interactions. The validation has been conducted under the following experimental set-up:

• 5 real robots

• 3 to 15 simulated robots

• tasks randomly assigned both to real and simulated robots

A representative instance of the performed experiments is shown in the accompanying video.

Table 1 Statistical validity of the comparison

Fig. 11

Waiting time versus clearing time for the Negotiated strategy. Data presented for intersection 4

The main difference compared to the single intersection simulation is that the coordination of the fleet is based on the hierarchical control architecture presented in Digani et al. (2014b). The proposed method (Optimized Strategy) is still compared to the Negotiated Strategy with respect to the time needed for all AGVs to reach their final destination, that is $t_{{ total}}$. Figure 10 shows the trend of the $t_{{ total}}$ with respect the number of AGVs on both of the strategies.

The data was also evaluated in terms of significance. Table 1 shows the statistical evaluation where $h=1$ indicates a rejection of the null hypothesis at the 5% significance level and $h=0$ indicates a failure to reject the null hypothesis at the 5% significance level.

Fig. 12

Computational time for the optimized strategy with respect to the number of AGVs

Fig. 13

Clearing time versus number of agents in the intersection 3 with standard deviation

6 Discussion

The simulations for a single intersection show that the average clearing time (or the maximum crossing time) is always smaller using the Optimized Strategy compared to the Negotiated Strategy. The results clearly show the proposed methodology performs better than the previous one. Figure 11 shows the relationship between the waiting time and the time a vehicle is actually moving (i.e., the time in which its velocity is non-zero) in the sector for the Negotiated Strategy. Overall, the time a vehicle spends waiting or idling is considerable when the Negotiated Strategy is used. In particular, the results show that the average waiting time is almost 50% of the total time a vehicle spends within the sector and the worst waiting time is up to 90% of the total time. One can conclude that under the Negotiated Strategy the time an AGV spends at an intersection is mostly spent on waiting for its turn to cross. It is important to note that by construction the waiting time for each vehicle under the Optimized Strategy is always null. Here, coordination is achieved by managing the relative velocities of the agents to ensure collision avoidance while constraining the velocities to be always higher than zero.

In light of the average per vehicle waiting time resulting from the Negotiated Strategy, the computational time of the Optimized Strategy is essentially negligible (see Fig. 12). The optimization algorithm does not suffer from a high computational burden despite being implemented in a centralized manner. This claim is supported by the fact that the strategy is designed to work with specific roadmaps and thus always tuned to the worst case scenario (Fig. 5d). Furthermore, the required computation burden still stays low when the number of segments increases. The Optimized Strategy is concerned only with the number of vehicles since the collision regions are computed totally offline. Figure 13 shows a comparison between the scalability of the Negotiated Strategy, which is almost linear, and the Optimized Strategy. We note that in the Optimized Strategy the maximum crossing time does not linearly increase with the number of agents but rather its trend is piecewise linear. This suggests that the Optimized Strategy can potentially be further exploited when the system is complex. This is further supported by the fact that the waiting time for the Negotiated Strategy is two orders of magnitude higher than the computational time for the Optimized Strategy.

For the complete scenario and for the real experiments, the results were very similar to the previous simulation. In particular $t_{{ total}}$ in the Optimized Strategy is always less then in the Negotiated Strategy. In addition, on a complete and real map the Optimized Strategy works better in term of total time. It is worth noting that the coordination and the performances within a sector are, in general, independent of the other sectors. Thus the complete behavior of the proposed methodology on the full map is approximately a linear combination of the local behavior within each sector.

Lastly, Fig. 10 shows the difference between the total time between the two strategies increases as the number of AGVs increases. As more vehicles are added to the workspace, the bigger the difference between the total time of the two strategies. While the complexity of the scenario affects the total time, the Optimized Strategy consistently performs better in the presence of more agents. The experiments also show that the proposed method works well under realistic conditions, where noise and disturbances normally arise (e.g. localization, delay, etc.).

7 Conclusion

An optimized coordination strategy which aims at minimizing the time a fleet of AGVs takes to traverse different sectors has been proposed. The typical applicable scenario of such a strategy is an indoor environment for industrial applications like automated warehouses. The coordination problem among the vehicles is modeled as an optimization problem and a procedure was used to transform a non-linear and non-convex optimization problem into an equivalent quadratic program. Coordination is then achieved by efficiently solving the optimization problem in a centralized fashion within each sector of the warehouse and a set of optimal velocities is assigned to each vehicle.

Several simulations and real experiments validate the theoretical assertions and confirm the existence of solutions to the optimization problem. The method was compared to a decentralized negotiated strategy presented in a previous work. The negotiated strategy allowed AGVs to traverse through a desired sector in the environment while avoiding collisions with other AGVs in the same sector by assigning different priorities to each AGV. The experimental set-up provided a realistic validation scenario where real robots together with virtual ones move on the roadmap. Simulation and experimental results show that the proposed optimized strategy significantly outperforms the decentralized negotiated strategy.

In this paper, the problem of coordinating the motion of the AGVs on the higher layer was not considered, focusing on the coordination within each sector. While the coordination within each sector can be performed independently, the overall performance of the AGV fleet may depend on the interplay between inter-sector and intra-sector coordination and is a direction for future work. Nevertheless, the proposed strategy can be used to compliment any existing coordination strategy to further improve the overall system performance by smoothing out potential traffic congestions in high volume sectors that may arise from any system uncertainties that are difficult to model.

The method proposed in this paper aims at minimizing the sum of the travel times for all the AGVs. Future work will aim at considering different cost functions, comparing the obtained solutions in different scenarios.