Goal state driven trajectory optimization

Abstract

Many applications demand a dynamical system to reach a goal state under kinematic and dynamic (i.e., kinodynamic) constraints. Moreover, industrial robots perform such motions over and over again and therefore demand efficiency, i.e., optimal motion. In many applications, the initial state may not be constrained and can be taken as an additional variable for optimization. The semi-stochastic kinodynamic planning (SKIP) algorithm presented in this paper is a novel method for trajectory optimization of a fully actuated dynamic system to reach a goal state under kinodynamic constraints. The basic principle of the algorithm is the parameterization of the motion trajectory to a vector in a high-dimensional space. The kinematic and dynamic constraints are formulated in terms of time and the trajectory parameters vector. That is, the constraints define a time-varying domain in the high dimensional parameters space. We propose a semi stochastic technique that finds a feasible set of parameters satisfying the constraints within the time interval dedicated to task completion. The algorithm chooses the optimal solution based on a given cost function. Statistical analysis shows the probability to find a solution if one exists. For simulations, we found a time-optimal trajectory for a 6R manipulator to hit a disk in a desired state.

1 Introduction

For the robotic system to accomplish its designated tasks, it must be able to generate a feasible motion. Usually, the motion is along a trajectory from an initial state (generalization vector of the position and velocity) to a desired goal state under kinematic and dynamic constraints, denoted in short as kinodynamic constraints. Examples for such motions are robotic arm manipulation tasks (Kim et al. 2013), motion of autonomous vehicles (Heo and Chung 2013), and UAV’s (Motonaka et al. 2013). Feasible motions are those that obey the mechanical and environmental constraints of the system, i.e., satisfy the kinodynamic constraints (Donald et al. 1993; Pham et al. 2013). Mechanical constraints are physical limitations of the system such as joints limits or maximum and minimum bounds of the joints’ velocities and torques. Environmental constraints are generally static or dynamic obstacles in the workspace of the system that limit its motion in some states. To acquire a feasible motion of the dynamic system, a planning algorithm is required to generate a trajectory that allows motion satisfying all constraints.

An unconstrained robot may perform motion with excessively high velocities and torques to reach a desired state. However, when obvious limitations on actuators’ position, velocity and torques are applied, and additional workspace obstacles are present, a feasible collision-free trajectory must be found. Moreover, in industrial processes, achieving efficient manufacturing is essential for maximizing the productivity (Verscheure et al. 2009). An industrial robot will perform a routine trajectory over and over again. Therefore, an optimal motion that minimizes, for example, time, energy, torques/forces, path length, or velocities, must be applied. Hence, we seek an optimal collision-free trajectory that satisfies the kinodynamic constraints.

A general trajectory optimization for a given task requires start and goal states. The start state is usually the current pose of the robot while the goal state is defined by the desired task. In many applications, the goal state is the parameter that matters. For example, throwing an object from a desired position and velocity, hitting an object in a specific force, regrasping an object, soft catching a free-flying object, etc. When a specific initial state is not a necessary constraint as in the examples above, the optimal trajectory problem has additional free parameters for optimization. Thus, the number of possible solutions will increase and the acquisition of better ones is possible. Therefore, in this work we propose to apply a trajectory-optimization algorithm that also optimizes the initial state of the robot. This planning problem is given the term: the Goal State driven Trajectory Optimization Problem (GSTOP).

We propose to divide the planning into two parts: plan a trajectory to the goal while optimizing the initial state as well, and plan an administrative path to that initial state from the current pose of the robot. The main trajectory will satisfy the kinodynamic constraints and will be optimized. On the contrary, the planning of the administrative path can rely solely on kinematic constraints. A prominent real-life example of this approach can be taken from the world of baseball where a batter tries to hit a thrown ball. The batter will take an administrative motion to position the bat above his shoulder. Then, he will execute a somewhat optimal trajectory for the bat to hit the ball flying toward him. It would not make sense nor be optimal for the batter to start the hitting motion from an arbitrary pose. Another example is in-hand regrasping motions where a robotic arm releases the object and catches it in a different relative pose (Sintov and Shapiro 2017). The choice of the release pose is essential for a successful completion of the task and should thus be optimized. Thus, the motion is no longer constrained by the initial pose and the administrative path enables the choice of the right starting state. We also note that this approach could be used to improve the performance of any kinodynamic system with an existing trajectory previously found for some initial state (excluding pick-and-place operations where the initial state cannot be changed). Thus, by throwing away the initial state and replanning with the proposed approach, one could find a new and better initial state that reduces the operational cost. In this paper we disregard the planning of the administrative path where many planners exist and focus on the GSTOP.

We present a novel algorithm termed Semi-Stochastic KInodynamic Planning (SKIP) as a method for finding an optimal solution for the motion planning problem taking the kinodynamic constraints into account. Applications of the algorithm for object throwing and regrasping have been presented by the authors in Sintov and Shapiro (2015) and Sintov and Shapiro (2017), respectively. However, in this paper we present a general and extended algorithm for any dynamic system. We focus on finding a feasible and optimal trajectory in some finite time while only the goal state is given. We propose a different parameterization of any trajectory for a dynamical system. In addition, as opposed to the previous work, here we also consider equality constraints. The proposed method can generally optimize both initial pose and velocity. We note however that for practical applications, the administrative path should be simple and move the robot to complete stop at the required initial pose. Therefore, without loss of generality, we only focus on the optimization of the initial pose and set the velocity to zero.

The key component of the algorithm is parameterizing an analytic trajectory function with redundant parameters to serve along with the goal time as free parameters for the optimization. We formulate the kinodynamic constraints of the problem in the free parameters space. The formulated set of constraints defines the Time-Varying Constraint (TVC) problem and an easy-to-use numerical method is proposed. The numerical method is a semi-stochastic algorithm, and a statistical analysis is presented to calculate the probability to find a solution if one exists. In general, similar to other sampling-based approaches, we show that the probability to find a solution if one exists, approaches one as the number of generated random points increases to infinity. The statistical analysis provides an automatic parameter selection for determining certain parameters for the algorithm. An important advantage of this method is the ability to calculate the probability to find a solution based on the allowed computational run-time.

The paper is organized as follows. Related work is presented in Sect. 2. Section 3 defines the motion planning problem with its constraints. In Sect. 4 some preliminary background notions are presented. In Sect. 5 we formulate the kinodynamic constraints in a specific manner based on mechanical limitations and the control method. The formulated constraints define the TVC problem, which is solved in Sect. 6. Section 7 performs statistical and complexity analysis of the algorithm. In Sect. 8 we present simulations of a 6R manipulator motion while avoiding dynamic obstacles to show the feasibility of the algorithm. Conclusions and future work are presented in Sect. 9.

2 Related work

The motion planning problem under kinodynamic constraints has been under extensive research in the past three decades. During that time, it has been shown that a complete algorithm for only the kinematic planning problem is sufficiently difficult in terms of computational costs (Schwartz and Sharir 1983; Brooks and Lozano-Perez 1983; Canny 1988; Reif 1979). Therefore, it is hard to implement them in practical applications. Some work applied some assumptions to reduce complexity; in Van der Stappen et al. (1998) the algorithm assumes low density obstacles and therefore lower complexity bounds exist, or in Van der Stappen et al. (1993) the assumption is that the robot is relatively small compared to the obstacles.

Finding an optimal trajectory under kinodynamic constraints has two main approaches: trajectory optimization and optimal control. Distinction between the two is well defined in Rao (2009). While in optimal control we desire an input function to acquire an optimal trajectory, in trajectory optimization we seek for static parameters that define the optimal trajectory. Although optimal control is a well-established method for finding an optimal trajectory, its capabilities to handle obstacle avoidance is rather inadequate (Zucker et al. 2013). Moreover, the solution of an optimal control demands an initial state of the system, which invalidates its usage for GSTOP. In addition, the work presented in this paper is closer to trajectory optimization and therefore, we focus on related work in that field. Khatib (1986) first introduced artificial potential fields for finding a collision-free trajectory. Rimon and Koditschek (1992) later extended the method with navigation functions free of local minima. One of the recent and prominent methods is the CHOMP (Ratliff et al. 2009; Zucker et al. 2013) and its variants (Dragan et al. 2011; Kalakrishnan et al. 2011; Byravan et al. 2014; Park et al. 2012). CHOMP is a functional gradient descent method that continuously refines the trajectory toward collision freeness. More prominent methods are the TrajOpt (Schulman et al. 2013) and the shooting-method (Keller 1976). An extended survey on trajectory optimization methods can be found in Rao (2014).

In the motivation to find more practical algorithms, probabilistic sampling methods have become common. They provide easy to implement methods with relatively low complexity, good results, and efficiency planning in high-dimensional configuration spaces. Moreover, they do not require an analytical representation of the obstacles. The most common probabilistic methods are the Probabilistic Roadmaps (PRM) and the Rapidly-exploring Random Trees (RRT). PRM (Kavraki et al. 1996; Hsu et al. 2002; Song and Amato 2001; Clark 2005; Denny et al. 2013) is a kinematic planning method that generates random states in the state space and constructs a graph by connecting the random states with collision-free trajectories. RRT was first introduced in Lavalle (1998) and LaValle and Kuffner (1999) as a randomized approach for kinodynamic planning. It incrementally builds a search tree in the state space while integrating the control inputs to ensure that the kinodynamic constraints are satisfied. Some other extensions of the RRT are the CL-RRT (Luders et al. 2010), and TB-RRT (Sintov and Shapiro 2014). One of the drawbacks of PRM and RRT algorithms is that they provide an arbitrary solution rather than an optimal one. Karaman and Frazzoli introduced the PRM* and RRT* (Karaman and Frazzoli 2011), which use the notion of PRM and RRT, respectively, but ensures an optimal solution with probability one as the number of random points approaches infinity. However, both extended methods can be applied to systems where motion between any two states can be made on a straight line. Hence, differential constraints of the system cannot be applied. The work in Webb and van den Berg (2013) extended the RRT* for systems with linear differential constraints, this by optimally connecting any pair of states in the tree. All of the above mentioned methods demand an initial state for the motion. Hence, they cannot be applied for the GSTOP discussed in this paper.

3 Problem formulation

In this section we define the dynamic motion planning problem including the constraints and assumptions.

3.1 Given system and environment

Let $\mathcal {Q}\subseteq \mathbb {R}^n$ be the configuration space of a fully actuated dynamic system with n degrees of freedom and let $\mathcal {U}\subseteq \mathbb {R}^n$ be its set of all possible force/torque inputs. Moreover, let $\varUpsilon \subset \mathbb {R}_{\ge 0}$ be the time space of the problem. The equations of motion of the dynamic system are given

$$\begin{aligned} M(\phi )\ddot{\phi }+C(\phi ,\dot{\phi })\dot{\phi }+G(\phi )=\mathbf {u}, \end{aligned}$$

(1)

where $\phi (t)\in \mathcal {Q}$ is the configuration of the system at time $t\in \varUpsilon$, M is an $n\times n$ inertia matrix, C is an $n\times n$ matrix of centrifugal and Coriolis acceleration terms, G is an $n\times 1$ vector of gravitational effects, and $\mathbf {u}(t)\in \mathcal {U}$ is a vector of control input forces and torques to the actuated degrees of freedom (DOF) at time $t\in \varUpsilon$.

Let $\mathcal {Q}_{res}\subset {Q}$ be a restricted subspace of the configuration space defined by physical limitations of the system’s DOF, e.g., joint mechanical limitations in a robotic arm. In addition, the environment of the system comprises dynamic obstacles. Formally, the obstacle region is a restricted time-varying subset denoted by $\mathcal {QT}_{obs}\subset \mathcal {Q}\times \varUpsilon$. Therefore, we define a projection map from such space to the configuration space as follows.

Definition 1

Let the map $\varPi _t:\mathcal {Q}\times \varUpsilon \rightarrow \mathcal {Q}$ be a projection map of the time-varying configuration space to the configuration space at time t.

With this system and its environment we can now define the bounding constraints.

3.2 Constraints

The motion of the dynamic system is limited under the following constraints:

• 1. The dynamic system is constrained to be in the allowed configuration space $\mathcal {Q}_{free}^{t}=\mathcal {Q}\setminus (\mathcal {Q}_{res}\cup \mathcal {Q}_{obs}^{t})$ at all times t, where $\mathcal {Q}_{free}^t$ is the allowed configuration $\mathcal {Q}_{free}\subseteq \mathcal {Q}$ at time t and $Q_{obs}^{t}=\varPi _t\circ \mathcal {QT}_{obs}$.

• 2. The allowed control inputs are defined by the abilities of the actuators and given by $\mathcal {U}_{al}\subseteq \mathcal {U}$.

• 3. Let $\mathcal {V}\subseteq \mathbb {R}^n$ denote the set of all maximal and minimal velocity bounds of the DOF. The allowed DOF velocities are defined by the abilities of the actuators and given by $\mathcal {V}_{al}\subseteq \mathcal {V}$.

• 4. Let $L_s:\mathcal {Q}\rightarrow \mathcal {S}$, where $\mathcal {S}\subseteq \mathbb {R}^e$ and $e\le n$, be a map from the configuration space to an e-dimensional sub-space in $\mathcal {Q}$. We constrain a trajectory $\phi (t)\in \mathcal {Q}$ to be on the sub-space such that

  $$\begin{aligned} L_s(\phi (t))\in \mathcal {S}\subset \mathcal {Q} \end{aligned}$$

  (2)

  for all $t\in [0,t_g]$. This is a formulation of an equality constraint and examples for such could be: maintaining a coffee cup upright or sliding a manipulator’s end-effector on a surface. Limitations on $L_s(\cdot )$ will be set further on.

A trajectory $\mathbf {\phi }(t)\in \mathcal {Q}$ is said to be a feasible trajectory in $t\in [0,t_g]$ if it satisfies the above constraints at that time frame.

3.3 Optimality criterion

Let $H:\mathcal {Q}\times \mathcal {U}\times {\varUpsilon } \rightarrow \mathbb {R}_{\ge 0}$ be a scalar cost functional that maps a trajectory to a non-negative cost. An optimal trajectory is the one that minimizes the given cost-functional $H(\phi (t),\mathbf {u}(t),t_g)$ where $t_g$ is the time when the system reaches the goal state. Examples of possible cost functions to minimize could reflect: the operation time, actuator’s torques/forces, energy consumption, the negative of the proximity from the boundaries of the kinodynamic constraints, etc.

3.4 Motion planning problem

The motion planning problem under kinodynamic constraints is defined as follows. Given the desired goal state $\mathbf {q}(t_g)=[\phi (t_g)~\dot{\phi }(t_g)]^T$ of the system and the cost function $H(\phi ,\mathbf {u},t_g)$, compute the optimal trajectory $\phi ^*(t)\in \mathcal {Q}_{free}$, $\dot{\phi }^*(t)\in \mathcal {V}_{al}$ for the dynamic system to reach the goal state at some finite time $t_g\in [0,T]$ where $T\in \varUpsilon$. The open-loop control input $\mathbf {u}^*(t)\in \mathcal {U}_{al}$ for $t\in [0,t_g]$ would also be provided to form an optimal trajectory. The required initial state of the motion would be the result of $\phi ^*(0)$.

3.5 Assumptions

The assumptions for this work are as follows:

• 1. We assume full knowledge of the system’s dynamics.

• 2. The trajectories of the dynamic obstacles are fully known.

• 3. The goal position is in $\mathcal {Q}_{free}$ and its desired velocity is in $\mathcal {V}_{al}$.

• 4. For practical applications, as stated in the introduction, the trajectory’s initial velocity is considered zero. This assumption can be easily released as will be discussed in Sect. 4.2.

4 Preliminaries

In this section we present some notions that are used in the proposed algorithm.

4.1 Configuration and task spaces

This paper uses the notion of the configuration space (C-space) to parameterize the general coordinates of the dynamical system. Moreover, we use the notion of the Task Space (T-space) to parameterize some coordinates of the system that are essential to the designated work task.

Let $\mathcal {T}\subseteq \mathbb {R}^m$ be the T-space of the dynamic system given in Eq. (1), where m is dimension of the T-space, and let $\mathbf {p}(t)\in \mathcal {T}$ be some task of the system at time t. For example, a task of a robotic manipulator is the end-effector’s position and orientation. Moreover, let $\mathcal {T}_{free}$ denote the allowed T-space corresponding to the allowed C-space $\mathcal {Q}_{free}$. Transformation from the C-space to T-space is performed using the direct kinematics of the system. Therefore, we define a transformation map $L_M:\mathbb {R}^n\rightarrow \mathbb {R}^m$ based on the direct kinematics of the system. That is,

$$\begin{aligned} \mathcal {T}=L_M\circ \mathcal {Q}. \end{aligned}$$

(3)

An arbitrary configuration $\phi (t)\in \mathcal {Q}_{free}$ is mapped to a task $\mathbf {p}(t)\in \mathcal {T}_{free}$ according to

$$\begin{aligned} \mathbf {p}(t)=L_M(\phi (t)). \end{aligned}$$

(4)

Mapping of a velocity in the C-space to velocity in the T-space is given by

$$\begin{aligned} \dot{\mathbf {p}}(t)=J\dot{\phi }(t), \end{aligned}$$

(5)

where $J=J(\phi (t))=\frac{d{\mathbf {p}}}{d{\phi }}$ is the Jacobian matrix of the system. Same could be done to the task acceleration

$$\begin{aligned} \ddot{\mathbf {p}}(t)=J\ddot{\phi }(t)+\dot{J}\dot{\phi }(t). \end{aligned}$$

(6)

In this paper, the planning is performed in the T-space for generality and demonstration of using both C-space and T-space. However, without loss of generality, the planning could also be performed in the C-space with no reference to the T-space.

4.2 Trajectory parameterization

We propose a parameterization formulation for a trajectory to reach the goal state. First we define an optional candidate trajectory that could complete the task.

Definition 2

A trajectory function $\mathbf {s}(t)\in \mathcal {T}$ is a candidate trajectory if it is twice differentiable and satisfies some h boundary constraints.

That is, in our motion planning problem, a trajectory $\mathbf {s}(t)$ is a candidate trajectory if it satisfies the following $h=3m$ boundary constraints that impose the initial velocity (according to Assumption 4) and final state:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\mathbf {s}}(0)=\mathbf {0} \\ \mathbf {s}(t_g)=L_M(\phi (t_g)). \\ \dot{\mathbf {s}}(t_g)=J\dot{\phi }(t_g)\\ \end{array}\right. } \end{aligned}$$

(7)

Note that, although out of the scope of this paper, if one desires to constrain an initial position as well, then m more boundary constraints are added for $\mathbf {s}(0)$. Similarly, if we wish to have a non-zero initial velocity (to remove Assumption 4), the first constraint in (7) should be removed and the velocity parameters must be added to the parameterization vector described next.

The following definition describes a candidate trajectory function that is constrained by the problems boundary constraints and has redundant parameters to optimize.

Definition 3

A candidate trajectory function $\mathbf {s}(t)=f_s(t,\mathbf {w})\in \mathcal {T}$, where $\mathbf {w}=[w_1~\cdots ~w_{m\cdot k}]^T\in \mathbb {R}^{m\cdot k}$ and has h boundary constraints, is redundant if ${m\cdot k}>h$ for $k\in \mathbb {R}^+$.

The parameters in $\mathbf {w}$ are coefficients of the trajectory function $\mathbf {s}(t)$ that can be taken as, for example, coefficients of a polynomial function or of a Fourier series. The three constraints in (7) impose the values for $w_i$, $i=1,\ldots ,h$ and leave $d=m\cdot k-h$ free parameters for the function to be optimized. Moreover, the goal time $t_g$ can also be chosen as a free parameter if no time constraint is imposed. Therefore, the redundant parameters are denoted as $\sigma =[w_{h+1}~\cdots ~w_{m\cdot k}~t_g]^T\in \varOmega$, where $\varOmega \subseteq \mathbb {R}^d\times \varUpsilon$. If the goal time $t_g$ is fixed and known, it should not be included in the parameters vector $\sigma$. The parameterization vector $\sigma$ is therefore, the set of free parameters of $\mathbf {s}(t)$ that are not constrained by (7). As such,the boundary constraints are imposed on function $\mathbf {s}(t)=f_s(t,\sigma )$ while providing a desired number of free parameters in $\sigma$ for motion planning and optimization. The following is an example of the parameterization.

Example 1

Consider a one-dimensional system with the following boundary constraints: $\dot{s}(0)=0$, $s(t_g)=s_g$, and $\dot{s}(t_g)=v_g$. The trajectory can be chosen as an 7-dimensional polynomial function of the form:

$$\begin{aligned} s(t)=\sum _{n=0}^7 a_n t^n. \end{aligned}$$

(8)

Therefore, the constraints can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} a_0=0 \\ \sum _{n=0}^7 a_n t_g^n=s_g \\ \sum _{n=1}^7 n a_n t_g^{n-1}=v_g \\ \end{array}\right. }. \end{aligned}$$

(9)

Thus, $a_0$ and two more parameters, say $a_1$ and $a_2$, are defined in terms of the remaining parameters, $a_3,\ldots ,a_7$ and the goal time $t_g$. Hence, the parameterization vector is defined by these six free parameters to be

$$\begin{aligned} \sigma =[a_3,a_4,a_5,a_6,a_7,t_g]^T. \end{aligned}$$

(10)

$s(t)=f_s(t,\sigma )$ is now a function of the values in $\sigma$ and the goal time. The trajectory in the configuration space can be expressed as

$$\begin{aligned} \phi (t)=L_M^{-1}(s(t)),~~ \dot{\phi }(t)=J^{-1}\dot{s}(t). \end{aligned}$$

(11)

These expressions can now be used to reformulate the constraints as described in Sect. 5. $\square$

4.3 Open-loop control input

Given a desired task trajectory $\mathbf {p}(t)=f_p(t,\sigma )$ defined by $\sigma$, an expression of the desired open-loop control force/torque is required. Using Eqs. (4)–(6), the expression for $\phi (t)$, $\dot{\phi }(t)$ and $\ddot{\phi }(t)$ in terms of $\sigma$ are given by

$$\begin{aligned} \phi (t,\sigma )= & {} L_M^{-1}\left( f_p(t,\sigma )\right) , \end{aligned}$$

(12)

$$\begin{aligned} \dot{\phi }(t,\sigma )= & {} J^{-1}\left( \dot{f}_p(t,\sigma )\right) \end{aligned}$$

(13)

and

$$\begin{aligned} \ddot{\phi }(t,\sigma )=J^{-1}\left( \ddot{f}_p(t,\sigma )-\dot{J}\dot{\phi }(t)\right) , \end{aligned}$$

(14)

where $J=J(\phi (t,\sigma ))=J(L_m^{-1}f_p(t,\sigma ))$. We assume the existence of $L_m^{-1}(\cdot )$ and $J^{-1}(\cdot )$ due to the fully actuated system in (1). Substituting (12)–(14) in (1) yields an expression for $\mathbf {u}(t)\in \mathcal {U}$:

$$\begin{aligned} \mathbf {u}(t)=\varTheta (t,\sigma ) \text { or } \varTheta (t,\sigma )-\mathbf {u}(t)=0, \end{aligned}$$

(15)

where $\varTheta (t,\sigma )=M\ddot{\phi }(t,\sigma )+C\dot{\phi }(t,\sigma )+G.$ One may see $\varTheta (t,\sigma )=0$ as a time-varying d-dimensional hyper-surface in $\varOmega$ expressing the dynamics of the system. To track a trajectory $\phi (t)$ parameterized by $\sigma$, the hyper-surface must contain $\sigma$ for all times $t\in [0,t_g]$. Therefore, in expression (15) we have the open-loop control input $\mathbf {u}(t)$ which is used to force the hyper-surface to contain $\sigma$ throughout the motion. Hence, satisfying condition (15) is required to follow the desired trajectory. Another way to look at (15) is as an inverse dynamics (Spong et al. 2006) expression in terms of t and $\sigma$. We choose the open-loop control input, i.e., force/torque $\mathbf {u}(t),$ such that the constraint is satisfied.

We have acquired expressions for the task response which depend on the choice of the free parameter $\sigma$ of the problem. Therefore, we seek to find a choice of $\sigma$ that will provide an optimal trajectory under the kinodynamic constraints.

5 Constraints formulation

In this section we formulate the constraints of the system’s motion in terms of the free parameters of the problem. We formulate C-space constraints that define $\mathcal {Q}_{free}$, other constraints in the T-space, and finally velocity and torque constraints imposed by the limitations of the system. In the following section, we denote the ith component of a vector with index i in the subscript, e.g., $(\cdot )_i$.

As mentioned in Sect. 3.2, it is possible that not all the C-space $\mathcal {Q}$ is accessible. Therefore, we can formulate the free space $\mathcal {Q}_{free}$ explicitly as a set of $z_1$ constraints $\varPhi \in \mathbb {R}^{z_1}$

$$\begin{aligned} \varPhi _i(\phi (t))\le 0,~\forall i=1,\ldots ,z_1. \end{aligned}$$

(16)

The set of constraints is composed of limitations of the actuator’s range and forbidden regions due to obstacles. The set of constraints in Eq. (16) could also be written in terms of the task using (12) as

$$\begin{aligned} \varPhi _i\left( L_M^{-1}(f_p(t,\sigma ))\right) \le 0,~\forall i=1,\ldots ,z_1. \end{aligned}$$

(17)

Note that if some obstacles cannot be described explicitly, conventional sampling-based collision checking can also be applied in the algorithm straight forward. Other constraints in the T-space could be formulated as $g_c\in \mathbb {R}^{z_2}$ by

$$\begin{aligned} g_{c_i}(\mathbf {p}(t))=g_{c_i}\left( f_p(t,\sigma )\right) \le 0,~\forall i=1,\ldots ,z_2. \end{aligned}$$

(18)

The set of allowed velocities $\mathcal {V}_{al}$ in C-space is the actuator’s velocities within defined bounds for each joint i

$$\begin{aligned} \omega _{{min}_i}\le \dot{\phi _{i}}(t)\le \omega _{{max}_i},~\forall i=1,\ldots ,n. \end{aligned}$$

(19)

Using (13), the velocity constraints of (19) in terms of t and $\sigma$ are equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( J^{-1}\frac{\partial f_p(t,\sigma )}{\partial t}\right) _i-\omega _{{max}_i}\le 0 \\ -\left( J^{-1}\frac{\partial f_p(t,\sigma )}{\partial t}\right) _i+\omega _{{min}_i}\le 0 \\ \end{array}\right. },~\forall i=1,\ldots ,n, \end{aligned}$$

(20)

if both are satisfied.

The same could be done to constrain the necessary forces/torques such that $\mathbf {u}(t)\in \mathcal {U}_{al}$. Explicitly we can set upper and lower bounds to the open-loop control input required to track the trajectory such that

$$\begin{aligned} {u}_{{min}_i}\le {u}_i(t)\le {u}_{{max}_i},~\forall i=1,\ldots ,n. \end{aligned}$$

(21)

Therefore, in terms of t and $\sigma$ and according to (15), the force/torque constraints are written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \varTheta _i(t,\sigma )-{u}_{{max}_i}\le 0 \\ -\varTheta _i(t,\sigma )+{u}_{{min}_i}\le 0 \\ \end{array}\right. },~\forall i=1,\ldots ,n \end{aligned}$$

(22)

and are equivalent to (21) if both are satisfied. The set of inequalities given in (17), (18), (20), (22) could be written as

$$\begin{aligned} \varPsi _i(t,\sigma )\le 0,~i=1,\ldots ,z, \end{aligned}$$

(23)

where $\varPsi (t,\sigma )$ is a set of z functions:

$$\begin{aligned} \varPsi (t,\sigma )= \left( \begin{array}{c} \varPhi \left( L_M^{-1}(f_p(t,\sigma )) \right) \\ g_c\left( f_p(t,\sigma )\right) \\ J^{-1}\frac{\partial f_p(t,\sigma )}{\partial t}-\omega _{max} \\ -J^{-1}\frac{\partial f_p(t,\sigma )}{\partial t}+\omega _{min} \\ \varTheta (t,\sigma )-\mathbf {u}_{max} \\ -\varTheta (t,\sigma )+\mathbf {u}_{min} \\ \end{array} \right) _{z\times 1} \end{aligned}$$

(24)

and $z=z_1+z_2+4n$.

Equation (23) expresses the inequality constraints of the problem. Further, we must formulate the equality constraints presented in (2) in terms of $\sigma$. Explicitly, a trajectory $\phi (t)$ is constrained to be on the sub-space $\mathcal {S}$ for all times $t\in [0,t_g]$, if it satisfies an equality constraint of the form $\mathbf {h}_e(\phi (t))=0$. Using (12) we can acquire the constraint

$$\begin{aligned} \mathbf {h}_e(t,\sigma )=0. \end{aligned}$$

(25)

Equality constraint (25) is a time-varying surface in $\varOmega$. However, the aim is to find a single $\sigma$ which is on the surface at all times. Therefore, we impose limitations on function $\mathbf {h}_e(t,\sigma )$ such that $\mathbf {h}_e\in C^l$ is continuously differentiable l times, where $l<\infty$ and there exist a time-invariant region $\bar{\mathbf {h}}_e$ in $\mathbf {h}_e$ obtained by explicitly solving the set of equations

$$\begin{aligned} \mathbf {h}_e^{(j)}(t,\sigma )=0 \end{aligned}$$

(26)

where $\mathbf {h}_e^{(j)}$ is the jth time derivative of $\mathbf {h}_e$ for $j=1,\ldots ,l$. Therefore, the new time-invariant equality constraint will be

$$\begin{aligned} \bar{\mathbf {h}}_e(\sigma )=0. \end{aligned}$$

(27)

We define $\mathcal {H}\subset \varOmega$ as the subset containing the points which satisfy (27). If no equality constraints exist, then $\mathcal {H}=\varOmega$. If formulation (27) could not be obtained by solving (26), it means that a time-invariant region does not exist in h. Therefore, a single $\sigma$ satisfying (25) could not be obtained and there is no solution to the desired trajectory optimization problem.

The inequalities in (23) define the feasible region of the dynamic system in terms of time and the desired trajectory parameter $\sigma$. That is, we obtained a set of analytical constraints that defines a time-varying region in $\varOmega$. The next section presents the time-varying constraint problem and the search algorithm to find an optimal trajectory satisfying the constraints.

6 Feasibility search algorithm

In this section we define the trajectory feasibility problem and present an algorithm for solving it.

6.1 Time-varying constraint (TVC) problem

In the previous section we obtained a set of inequalities depending on t and the parameters vector $\sigma$. Recall that the components in $\sigma$ are independent of the time. Therefore, we would like to find an optimal vector $\sigma ^*\in \varOmega$ that satisfies the constraints from initial to goal time and minimizes some cost function. Such an optimal vector will sufficiently define the motion of the system under the kinodynamic constraints. Let $\varSigma \subset \varOmega$ be a user defined allowed region for $\sigma$. The range of set $\varSigma$ is chosen in a pre-processing step where the user simulates sets of points in $\varOmega$ with different ranges. The user then chooses the range that best fits the workspace of the robot. The range for the time parameter in $\varSigma$ is chosen according to the allowed time frame for the motion. Next, we define the notion of a feasible set.

Definition 4

A set $\varOmega _f\subset \varOmega$ is a feasible set in $t\in [t_1,t_2]$ if $\varOmega _f\subseteq \varSigma$ and each $\sigma \in \varOmega _f$ satisfies inequality (23) and equality (27) for all time $t\in [t_1,t_2]$.

We now define a feasible vector.

Definition 5

A vector of trajectory parameters $\sigma \in \varOmega$ is said to be feasible in $t\in [t_1,t_2]$ if $\sigma \in \varOmega _f$.

The above two definitions conclude that a vector is feasible if

$$\begin{aligned}&\sigma =\{ \sigma \in \varOmega _f|\sigma \in \varSigma ,\varPsi _i(t,\sigma )\le 0,\bar{\mathbf {h}}_e(\sigma )=0,\nonumber \\&\quad \forall t\in [t_1(\sigma ),t_2(\sigma )] \} \end{aligned}$$

(28)

for all $i=1,\ldots ,z$. Notice that the time interval is written in general $[t_1(\sigma ),t_2(\sigma )]$ and is a function of $\sigma$. This is due to the definition of the free parameters vector $\sigma$, which could include parameters that define the operation time. Therefore, the choice of $\sigma$ determines the boundary time. We now face the problem of finding the feasibility set $\varOmega _{f}\subseteq \varSigma$ where for all vectors within it, inequality (23) is maintained at all times. Formally, the problem is as follows.

Problem 1

Given the set of constraints in (23) and the set $\varSigma$, find the feasibility set $\varOmega _{f}\subseteq \varSigma$.

Solving the above problem provides the feasible set $\varOmega _f$ from which the optimal solution is to be chosen. Hence, we define the following minimization problem.

Problem 2

Find the vector $\sigma ^*\in \varOmega _f$ where $\varOmega _f\subseteq \varSigma$ such that

$$\begin{aligned} \begin{aligned}&\sigma ^* = \underset{\sigma }{\arg \min }&H(\sigma ) \\&\text {subject to}&\sigma ^*\in \varOmega _f \\ \end{aligned} \end{aligned}$$

(29)

where $H(\sigma )$ is some cost function to minimize.

Fig. 1

The TVC problem where $t_1<t_a<t_b<t_2$

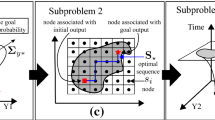
In other words, the above general problem is finding an optimal vector $\sigma ^*$ that is feasible and minimizes some cost function $H(\sigma )$. Figure 1 illustrates the two problems. The position and volume of $\varPsi (t,\sigma )$ in $\varOmega$ varies in time and therefore, the solution of the problem is in a domain formed by projecting the constraints for time $t_1$ to $t_2$ on space $\varOmega$. The intersection formed by these projections, if one exists, is the feasibility domain that the optimal solution $\sigma ^*$ should be chosen from.

The above problem seeks a feasibility set over a period of time. It is important to note that we seek a feasibility set if such exists. In the next subsection we present an algorithm for finding the feasibility set and choosing an optimal solution from it. The probability to find a solution if one exists is also presented.

6.2 Feasibility search algorithm

A search algorithm is now presented to find the set $\varOmega _f$ of feasible vectors. The domain formed by the set of constraints in inequality (23) is non-linear, non-convex, and not continuous. Therefore, an analytical solution of the reachable set is only possible in rare and simple instances. We present a numerical search algorithm to find a set of vectors satisfying the above constraints. Further, we can choose one vector from the set that best minimizes the cost function. We begin by presenting a simple definition for normalizing the time interval.

Lemma 1

A vector $\sigma$ is feasible in $t\in [t_1,t_2]$ if the constraint $\varPsi _i(\lambda t_1+(1-\lambda )t_2,\sigma )\le 0$ is satisfied for all $0\le \lambda \le 1$ and for all $i=1,\ldots ,z$.

Proof

For each time instant $t\in [t_1,t_2]$ there exists $\lambda$ such that $t=\lambda t_1+(1-\lambda )t_2$ and $0\le \lambda \le 1$. Therefore, if a vector $\sigma$ satisfies $\varPsi _i(t,\sigma )\le 0$ for all $i=1,\ldots ,z$ and $t_1\le t\le t_2$, it must also satisfy $\varPsi _i(\lambda t_1+(1-\lambda )t_2,\sigma )\le 0$ for all $i=1,\ldots ,z$ and $0\le \lambda \le 1$. $\square$

Lemma 1 is utilized as a criterion for determining whether a vector $\sigma$ is feasible. Numerically, for $\sigma$ we check the constraint for time $t=\lambda t_1+(1-\lambda )t_2$ with $\lambda = \{0,\varDelta \lambda _1, \varDelta \lambda _1+\varDelta \lambda _2,\ldots ,1\}$. The value of the step $\varDelta \lambda _j$ will be further defined. Figure 2 illustrates an abstraction of the feasibility problem and the line in time defined by Lemma 1. Without loss of generality, from this point we will address the problem with the time frame $[t_1,t_2] = [0,t_g]$.

Fig. 2

Vector $\sigma$ satisfying Lemma 1

The basis of the algorithm’s operation is selecting a set of N random points within $\varSigma$ and checking each for its feasibility. The feasibility search algorithm is presented as the $\texttt {Feasibility\_Search}(\cdot )$ function in Algorithm 1. The algorithm’s input is the allowed set $\varSigma$ chosen the user, equality set $\mathcal {H}$ and the set of constraints of Eq. (23). The first step of the algorithm is to determine the number of random points N such that the probability to find a solution is more than a user defined probability $1-P_{max}$. The calculation of N based on the choice of $P_{max}$ will be presented later in the algorithm’s analysis. The next step is to sample N random points $\mathcal {P}=\{\sigma _1,\ldots ,\sigma _N\}$ uniformly distributed in $\varSigma$. The allowed region formed by $\varSigma$ is a hyper-rectangle in $\varOmega$ and therefore we sample points in each axis of $\varOmega$ within the boundaries defined by $\varSigma$. Such sampling provides a Poisson distribution over the volume of $\varSigma$. However, due to the equality constraint (27), we sample points in $\varSigma \cap \mathcal {H}$. That is, we sample points that are in $\varSigma$ and satisfy (27). Thus, imposing the equality constraint on the desired trajectory.

The next step is going over all the N points in $\mathcal {P}$ and filtering out those that are not feasible. The final time $t_{g_i}(\sigma _i)$ is determined for each point $\sigma _i$ checked. We check if the constraints are satisfied for time $t=\lambda t_{g_i}$ where $\lambda = \{0,\varDelta \lambda _1,\varDelta \lambda _1+\varDelta \lambda _2,\ldots ,1\}$. Those that do not satisfy the constraints are eliminated and the filtered set $\mathcal {P}$ with size $M\le N$ is outputted.

Scanning the constraint $\varPsi (\lambda t_{g_i},\sigma _i)$ for $\lambda =\{0,\varDelta \lambda ,2\varDelta \lambda ,\ldots ,1\}$ where $\varDelta \lambda$ is a constant value is rather risky. The value of $\varPsi$ might ascend over 0 and descend below again within the discretized step size. An example of such is shown in Fig. 3 where with step size above 0.03 failure of the constraints might not be discovered. Moreover, too small step sizes could be unnecessary and the price would include very high complexity. Therefore, we present a simple adaptive step size algorithm to fine tune the time steps and diagnose or rule out such scenarios.

Fig. 3

The maximum constraint value along time with change of the step size $\varDelta \lambda$

Definition 6

The constraint value of a feasible point $\sigma _i$ at time $\lambda t_{g_i}$ is defined to be

$$\begin{aligned} \tilde{\varPsi }_{i,\lambda }=\max _j\left\{ \varPsi _j(\lambda t_{g_i},\sigma _i) \right\} , \end{aligned}$$

(30)

where $\varPsi _j$ is the jth component of the constraint vector $\varPsi$.

That is, the constraint value is the shortest distance at time $\lambda t_{g_i}$ from point $\sigma _i$ to the boundary of the closest constraint. Notice that we refer to a distance with a positive value, but the value of $\tilde{\varPsi }_{i,\lambda }$ is maintained negative for an indication that $\sigma _i$ is a feasible point. Assume that the change rate of the constraint value with regards to $\lambda$ is bounded by

$$\begin{aligned} \frac{\varDelta \tilde{\varPsi }_{i,\lambda }}{\varDelta \lambda }\le S_{max},~\forall ~0\le \lambda \le 1. \end{aligned}$$

(31)

That is, the maximum slope of the constraint value $\tilde{\varPsi }_{i,\lambda }$ is $S_{max}$. Under this assumption we can say that if at time $\lambda t_{g_i}$ the constraints are satisfied, $\tilde{\varPsi }_{i,\lambda }<0$, then the minimum time for the constraint to reach 0 is $(\lambda +\varDelta \lambda _{min})t_{g_i}$ where $\varDelta \lambda _{min}=-\frac{\tilde{\varPsi }_{i,\lambda }}{S_{max}}$. Therefore, as we get closer to a boundary of a constraint, we decrease $\varDelta \lambda$ such that reaching above the zero line in that time frame is not possible. Figure 4 illustrates the selection of $\varDelta \lambda$ as it gets smaller when approaching the zero line and larger when receding. However, in this adaptive approach, even though $\tilde{\varPsi }_{i,\lambda }$ passes the zero line, the algorithm will never do so as it will continue to decrease $\varDelta \lambda$. Therefore, we bound such that the algorithm will stop checking the current $\sigma _i$ (and remove it) if $\tilde{\varPsi }_{i,\lambda }<\epsilon _b<0$, where $\epsilon _b$ is a value that will be defined further in the algorithm’s analysis. This also serves as a safety distance, assuring the solution is far enough from the constraints boundary. To calculate $S_{max}$ we differentiate the constraint vector by $\lambda$ to acquire its slope $\frac{\partial {\varPsi }(\lambda t_g,\sigma )}{\partial {\lambda }}$, where $t_g$ is the maximum possible goal time based on the allowed time interval given in $\varSigma$. $S_{max}$ is the maximum slope of all components over all time and can be computed by the following maximization problem

$$\begin{aligned} \begin{aligned}&S_{max} = \underset{\lambda ,\sigma ,j}{\text {max}}&S_j(\lambda t_g,\sigma ) \\&\text {subject to}&0\le \lambda \le 1 \\&\sigma \in \varSigma \\ \end{aligned} \end{aligned}$$

(32)

where $S_j$ is the jth component of the constraints derivative $S(\lambda t_g,\sigma )=\frac{\partial {\varPsi }(\lambda t_g,\sigma )}{\partial {\lambda }}$. This could be computed analytically using Kuhn–Tucker conditions (Kuhn and Tucker 1950) or numerically. The adaptive step size function $Adaptive\_Check(\cdot )$ is presented in Algorithm 2.

Fig. 4

Adaptive step size algorithm

The adaptive step size with the maximum slope $S_{max}$ provides efficient sweep of the generated points by reducing the number of checks for each point in $\mathcal {P}$. However, for high-dimensional systems such adaptive search by its own can take a long time. Therefore, we propose a filtering process in which we start with a fraction $0\le \delta _S\le 1$ of $S_{max}$. That is, in the first iteration of the $\texttt {Adaptive\_Check}(\cdot )$ function, the maximum allowed slope will be $\delta _S\cdot S_{max}$. Vectors which are diagnosed to be non-feasible with maximum slope of $\delta _S\cdot S_{max}$ will surely be non-feasible with the full maximum slope $S_{max}$. Therefore we can eliminate them with less checks. In the next iterations $\delta _S$ is increased and so on, until the last iteration where $\delta _S=1$. In this process, with small $\delta _S$ in the beginning, large time steps would be taken to reduce runtime avoiding excessive calculations. For each iteration we take the fraction as $\delta _S=i\cdot \varDelta S$ where $\varDelta S$ is the step size, $i=1,\ldots ,b$ and $b\varDelta S=1$. Hence, the following problem is the determination of the step size $\varDelta S$. Small $\varDelta S$ can cause excessive iterations which could cause the opposite and increase the runtime. Experiments on the algorithms runtime on several systems have revealed a typical behavior as shown in Fig. 5. The optimal step size should be $\varDelta S=\frac{1}{3}$ which decreases the runtime by an average of 50%.

In high-dimensional systems, computation of the dynamic system (Eq. (15)) takes a large percentage of the runtime. Therefore, in addition to filtering-out non-feasible solutions using $\delta _S$, we can separate the torque constraint check from the other constraints. In that way, only candidate trajectories which passed the kinematic constraints will be checked for the torque constrains. Experiments have shown a $90\%$ runtime reduction compared to a non-separated constraint check.

Fig. 5

Typical runtime with respect to change of $\varDelta S$

6.3 Optimal solution

The final step of the algorithm is selecting the optimal solution among the set of feasible points $\varOmega _f=\{\sigma _1,\ldots ,\sigma _M\}$ found in Algorithm 1 and perform local fine-tuning optimization. Given the cost function $H(\sigma )$, the optimal solution $\sigma ^*$ is found according to Algorithm 3. In this algorithm, first a simple naive search is performed on the feasibility set $\varOmega _f$ to find a feasible point $\sigma _k$ that best minimizes $H(\sigma )$ (Line 1). Recall that the trajectory is an analytical function and therefore, in most cases, the derivative of $H(\sigma )$ can be acquired. Thus, we can utilize a Gradient Descent (GD) method (Cauchy 1847) to refine the solution and find a local minimum in the neighborhood of $\sigma _k$. The GD method is an iterative algorithm with an update law (Line 5) of the form

$$\begin{aligned} \sigma ^{(i+1)}=\sigma ^{(i)}-\gamma \nabla H(\sigma ^{(i)}) \end{aligned}$$

(33)

where $\gamma >0$ is chosen using exact or backtracking line search (Boyd and Vandenberghe 2004). In each iteration the constraints is checked. Notice that the $\texttt {Adaptive\_Check}$ function prevents the solution from approaching the constraint boundary with distance less than $\epsilon _b$. The iterations are terminated if the new point breaks the constraints or if the convergence condition is satisfied (Line 10 of Algorithm 3). Figure 6 presents two examples of local refinement of the optimal solution; one was stopped by the constraint while the other managed to reach the local minimum. The convergence condition checks if the norm of the current descent is smaller than a predefined tolerance $\epsilon _d$, that is, we have reached a local minimum with $\epsilon _d$ accuracy. The last point of the iteration is the optimal solution and is returned by the algorithm.

Fig. 6

Two examples of the optimal solution refinement; one (left) descended to the local minimum while the other (right) was stopped by the constraint boundary

6.4 Overall algorithm

The full SKIP algorithm is presented in Algorithm 4. The algorithm receives input of the system’s constraints in the form of inequalities (23), the desired probability $P_{max}$ (will be presented in the next section), and the convergence tolerances $\epsilon _b$ and $\epsilon _d$. If Algorithm 1 returns an empty set, the algorithm reports a failed search. Else, its final output is, according to (12), the desired optimal trajectory

$$\begin{aligned} \phi ^*(t)=L_M^{-1}(\mathbf {f_p(t,\sigma ^*)}), \end{aligned}$$

(34)

The optimal open-loop control signals could also be obtained according to (15) and are

$$\begin{aligned} \mathbf {u}^*(t) = \varTheta (t,\sigma ^*). \end{aligned}$$

(35)

Once a trajectory is found, trajectory tracking methods such as inverse-dynamics and PD control (Spong et al. 2006) can be applied straightforward.

7 Analysis

In this section a statistical and complexity analysis is performed for the proposed SKIP algorithm.

7.1 Statistical analysis

A statistical analysis is performed in this subsection to calculate the probability to find a solution if it exists. First, we define an operator that measures the volume of a set.

Definition 7

Let a map $\mathcal {L}_V:\varGamma \rightarrow \mathbb {R}_{>0}$ such that $\varGamma \subset \mathbb {R}^d$. The value of $\mathcal {L}_V\circ \varGamma$ is the hyper-volume measure of $\varGamma$ according to the Lebesgue measure (Lebesgue and May 1966).

Fig. 7

Two-dimensional example of $\varSigma$ and $\varOmega _f$ in $\varOmega$

Let us assume $\varOmega _f$ is known and let $0\le \rho \le 1$ be the relative portion of $\varSigma$ that is feasible; that is, the ratio between the hyper-volumes of $\varOmega _f$ and $\varSigma$:

$$\begin{aligned} \rho =\frac{\mathcal {L}_V\circ \varOmega _f}{\mathcal {L}_V\circ \varSigma }. \end{aligned}$$

(36)

For simplification and practical usage, we will refer to $\varSigma$ as a hyper-rectangle in $\varOmega$ (Fig. 7). Let $X_j$ be a random variable that takes the value 1 if $\sigma _j\in \varSigma$ falls within $\varOmega _f$ and 0 if not. Thus, $X_{j}$ is defined

$$\begin{aligned} X_j={\left\{ \begin{array}{ll} 1, &{} \sigma _j\in \varOmega _f \\ 0, &{} \sigma _j\notin \varOmega _f \\ \end{array}\right. }. \end{aligned}$$

(37)

Because $X_j$ can take only two values $\{0,1\}$ and the probability of a random $\sigma _j\in \varSigma$ to fall in $\varOmega _f$ is $\rho$, then $X_j\sim Bernoulli(\rho )$. Therefore, the probability for a random point $\sigma _j$ to have a compatible random variable $X_{j}=y$ is

$$\begin{aligned} P(X_j=y)=\rho ^y(1-\rho )^{1-y}~for~y\in \{0,1\}. \end{aligned}$$

(38)

If a set of N points $\mathcal {P}=\{\sigma _1,\ldots ,\sigma _N\}\in \varSigma$ are independent, identically distributed random variables, and their compatible random variables $X_i$, $i=1,\ldots ,N$ are all Bernoulli distributed with success probability $\rho$, then the sum of the random variables is

$$\begin{aligned} Y=\sum X_i\sim Binomial(N,\rho ). \end{aligned}$$

(39)

Therefore, the probability to have k points in $\varOmega _f$ for N random points ($k=0,1,\ldots ,N$) is

$$\begin{aligned} P(Y=k)=\left( \begin{array}{c} N \\ k \\ \end{array} \right) \rho ^k(1-\rho )^{N-k} \end{aligned}$$

(40)

where $\left( \begin{array}{c} N \\ k \\ \end{array} \right)$ is the binomial coefficient representing the number of combinations distributing k successes in N random points. The Poisson distribution can be used as an approximation of the Binomial distribution if the number of random points N goes to infinity ($N\rightarrow \infty$) and the Bernoulli probability is sufficiently small ($\rho \rightarrow 0$). Therefore, $Y\sim Poisson(\overline{\lambda })$ where $\overline{\lambda }=N\rho$. That is,

$$\begin{aligned} P(Y=k)\simeq \frac{\overline{\lambda }^k}{k!}e^{-\overline{\lambda }}. \end{aligned}$$

(41)

We determine that if a solution exists, the highest allowed probability that the solution will not be found ($k=0$) out of N random points is defined to be

$$\begin{aligned} P(Y=0|\rho )=e^{-N\rho }. \end{aligned}$$

(42)

In the next Theorem we show the probability to find a solution in $\varSigma$ if one exists.

Theorem 1

The probability to find a solution in $\varSigma$, if one exists, approaches 1 as the number of generated random points approaches infinity.

Proof

The probability not to find a solution in $\varSigma$ is given in (42). Therefore, the probability to find a solution is

$$\begin{aligned} P_s(N)=P(Y>0|\rho )=1-e^{-N\rho }. \end{aligned}$$

(43)

If we increase N to infinity, then $e^{-N\rho }$ and the limit for the probability is

$$\begin{aligned} \lim _{N\rightarrow \infty }P_s(N)=1. \end{aligned}$$

(44)

That is, as N approaches infinity, the probability to find a solution in $\varSigma$ approaches 1. $\square$

However, taking infinite number of points is not feasible. Hence, we provide a formula for finding the number of random points to be taken given the highest allowed probability $P_{max}$ not to find a solution. Based on (42), the number N of random points in $\varSigma$ must be chosen such that

$$\begin{aligned} e^{-N\rho }\le P_{max}. \end{aligned}$$

(45)

This condition states that given $\rho$, the number of random points to be chosen such that if a solution exists, the probability not to find it is lower than $P_{max}$. That is, the probability to find a solution is higher than $1-P_{max}$.

The last issue that must be addressed is how to determine $\rho$ such that (45) could be used to calculate N given $P_{max}$. The determination of $\rho$ is a resolution of how close we allow the desired parameters vector to be from the constraints boundaries. That is, how small do we allow the feasibility set to be in order to be considered to exist. If the volume of the feasibility set $\varOmega _f$ is very small, the points within it must be very close to the constraints boundary. This is an undesired situation. Such a case must be bounded so that if $\varOmega _f$ is too small, we would determine that a solution does not exist. For that matter, we propose a heuristic approach of approximating a characteristic measure of the constraints. We define a characteristic measure that is the average minimum distance from the center of the feasible region to the constraints boundaries over time. The centroid of the subspace formed by the constraints in (23) at time $\lambda _it_g$ is calculated by

$$\begin{aligned} \sigma _{b_i} = \underset{\sigma }{arg\min } \left\{ \sum _{j=1}^z ~a_{j,i}\varPsi _j(\lambda _i t_g,\sigma ) \right\} , \end{aligned}$$

(46)

$\varPsi _j$ is the jth component of the constraint vector $\varPsi$, $\lambda _i=0,\overline{\varDelta \lambda },..,\beta \overline{\varDelta \lambda }$, where $\beta =1/\overline{\varDelta \lambda }$, and $t_g$ is the last component of vector $\sigma$. Because each constraint in $\varPsi$ has a different gradient, which affects the distance-value ratio, it is multiplied by its relative weight $a_{j,i}$ given by

$$\begin{aligned} a_{j,i}=\frac{\sum _{k=1}^{z,k\ne j}\varPsi _k(\lambda _i t_g,\sigma )}{\sum _{k=1}^{z}\varPsi _k(\lambda _i t_g,\sigma )}. \end{aligned}$$

(47)

Hence, the average distance over time (with step size $\overline{\varDelta \lambda }t_g$) is given by

$$\begin{aligned} r = \frac{1}{\beta }\sum _{i=1}^\beta \left( \frac{1}{z}\sum _{j=1}^z \varPsi _j(\lambda _i t_g,\sigma _{b_i})\right) \end{aligned}$$

(48)

and is a characteristic measure of the constraint’s size. Heuristically, the average is computed in $\beta$ time steps and increasing $\beta$ will increase the accuracy. Then, the minimum allowed volume $\varOmega _{min}$ is defined as

$$\begin{aligned} \mathcal {L}_V\circ \varOmega _{min} = (\alpha r)^d, \end{aligned}$$

(49)

where $0<\alpha \le 1$ is the allowed fraction of r and is user-defined. That is, we define a hyper-cube with edge length $\alpha r$ and compute its volume to be the minimal allowed one. Thus, $\rho$ is chosen as $\rho _{min}=(\mathcal {L}_V\circ \varOmega _{min})/(\mathcal {L}_V\circ \varSigma )$ and the minimal number of random points N for a given $P_{max}$ can be calculated according to (45) by

$$\begin{aligned} N\ge -\frac{1}{\rho }\log (P_{max}). \end{aligned}$$

(50)

Moreover, the value of $\epsilon _b$ defined in Sect. 6.2 to be the minimum allowed distance from the constraint boundary is chosen using the characteristic measure calculated in (48) to be $\epsilon _b=\alpha r$.

In the following Theorem we conclude the probability to find a solution if such exists.

Theorem 2

If a solution for the time-varying problem exists in $\varSigma$ and N satisfies (50), the probability for the algorithm to find a solution is at least $1-P_{max}$.

Proof

The probability not to find a solution if one exists is given in (42). If the algorithm selects N random points in the allowed set $\varSigma$ such that (50) is satisfied with given probability $P_{max}$ and a minimum allowed volume ratio $\rho _{min}$, then substituting it in (42) yields

$$\begin{aligned} P(Y=0|\rho _{min})=P_{max}, \end{aligned}$$

(51)

which is the probability not to find a solution. Hence, the probability to find a solution is $1-P_{max}$. $\square$

The choice of N is done ensuring finding a solution if such exists above a known probability $1-P_{max}$. It should be noted that the local optimization performed in Algorithm 3 does not affect the probability to find a solution because it is performed only if a solution is found.

The following corollary extends Theorem 2 to calculate the probability to find a solution given a maximal calculation runtime $T_c$ and assuming the time for computing one point is known to be $\tau _c$.

Corollary 1

Given a desired calculation time $T_c$ and the computer cycle time $\tau _c$ to calculate one point, the probability to find a solution if one exists is

$$\begin{aligned} P_s=1-e^{-\frac{T_c}{\tau _c}\rho }. \end{aligned}$$

(52)

Proof

The maximal number of random points that can be generated is $N_c=\left\lfloor \frac{T_c}{\tau _c}\right\rfloor$. Therefore, given $\rho$ and according to (42), the probability not to find a solution is

$$\begin{aligned} P(Y=0|\rho )=e^{-N_c\rho }=e^{-\frac{T_c}{\tau _c}\rho }. \end{aligned}$$

(53)

Therefore, the probability to find a solution is $1-e^{-\frac{T_c}{\tau _c}\rho }$. $\square$

It is important to note that this analysis addresses the probability of finding a solution if one exists. It does not, however, prove that the result is indeed optimal. As like other sampling-based optimal planners (Karaman and Frazzoli 2011), optimality will be achieved if the planner is allowed to run long enough.

7.2 Complexity

The complexity of the proposed algorithm is presented next.

Theorem 3

The upper bound time complexity of the proposed algorithm is in the order of $O(\xi N)$.

Proof

We generate N random points in $\varSigma$ and therefore, the N points are to be checked for feasibility. Given the maximum constraint slope $S_{max}$ and the maximum allowed boundary constraint distance $\epsilon _b$. In the worst case, the constraint value $\tilde{\varPsi }_{i,\lambda }$ approximately equals $\epsilon _b$ for all $0\le \lambda \le 1$. Moreover, in the worst case, during the $\delta _S$ iterations, no points will be filtered-out but in the last iteration. Therefore, each time step size will be $\varDelta \lambda =\frac{\epsilon _b}{S_{max}}$ and the number of time steps each $\sigma _i$ will be checked for satisfying the constraints is $\xi =b\frac{1}{\varDelta \lambda }=b\frac{S_{max}}{\epsilon _b}$. Hereafter, N random points will be checked, in the worst case, $\xi$ times. Thus, the upper bound time complexity of the algorithm is in the order of $O(\xi N)$. $\square$

8 Simulations

In this section we demonstrate the algorithm’s operation. We present a trajectory planning and optimization for a 6R manipulator for hitting a disk in a desired goal state. Here, we demonstrate planning for a high-dimensional system with no initial state, i.e., the initial state is left for planning. The algorithm was implemented in Matlab¹ on an Intel-Core i7-2620M 2.7 GHz laptop computer with 8 GB of RAM. The simulation videos can be seen on-line in resource 1.

The manipulator’s dynamics is given by (1), where its physical properties are given in Table 1; $m_i$, $I_i$, $L_i$, and $l_i$ are the mass, moment of inertia, length, and center of mass position (relative to the links joint) of link i, respectively. The joints’ angles are $\phi (t)=[\varphi _1~\varphi _2~\varphi _3~\varphi _4~\varphi _5~\varphi _6]^T$ and the end-effectors task is $\mathbf {p}(t)=L_M(\phi (t))=[p_x(t)~p_y(t)~p_z(t) \varphi (t)~\theta (t)~\psi (t)]^T$, where $\varphi ,\theta ,\psi$ are the roll, pitch, and yaw, respectively.

Table 1 Kinematic and dynamic properties of the manipulator used in the simulations

Fig. 8

The 6R simulation setup

The aim of the planning is to slide a cylinder, held by the end-effector, on an horizontal table. The cylinder must avoid static and dynamic obstacles, and hit a disk at a required position and velocity:

$$\begin{aligned} \mathbf {p}(t_g) = \left( \begin{array}{c} -0.54\,[{\text {m}}] \\ 0\,[{\text {m}}] \\ 0\,[{\text {m}}] \\ 0\,[{\text {rad}}] \\ \pi /2\,[{\text {rad}}] \\ 0\,[{\text {rad}}] \end{array} \right) ,\;\; \dot{\mathbf {p}}(t_g)=\left( \begin{array}{c} -1\,[{\text {m/s}}] \\ 0\,[{\text {m/s}}]\\ z_t\,[{\text {m/s}}]\\ 0\,[{\text {rad/s}}]\\ 0\,[{\text {rad/s}}]\\ 0\,[{\text {rad/s}}]\\ \end{array} \right) , \end{aligned}$$

(54)

where $z_t$ is the desired end-effector’s height in order to maintain the grasped cylinder on the table. The setup for the simulation is seen in Fig. 8. The desired trajectory function $\mathbf {s}(t)\in \mathcal {T}$, where

$$\begin{aligned} \mathbf {s}(t)=(s_x(t)~s_y(t)~s_\theta (t))^T, \end{aligned}$$

(55)

is given in the T-space by a g-order polynomial vector as

$$\begin{aligned} \mathbf {s}(t) = \sum _{i=0}^g \mathbf {m_i}t^i, \end{aligned}$$

(56)

where $\mathbf {m_i}=[a_i~b_i~c_i~d_i~e_i~f_i]^T,~i=0,\ldots ,g$ are the coefficients of the polynoms. The desired goal state (54) and zero initial velocity impose the values for $\mathbf {m_1}=\dot{\mathbf {p}}(0)=\mathbf {0}$, $\mathbf {m_2}$, and $\mathbf {m_3}$. Hence, the parameters’ vector is defined by the remaining coefficients and the goal time such that

$$\begin{aligned} \sigma = \begin{bmatrix} \mathbf {m_0}^T&\mathbf {m_4}^T&\cdots&\mathbf {m_g}^T&t_g \\ \end{bmatrix}^T, \end{aligned}$$

(57)

and the desired trajectory is defined by $\sigma$ such that $\mathbf {s}(t)=\mathbf {s}(t,\sigma )$. The static and dynamic obstacles are constraints in the form of

$$\begin{aligned} r_o^2-(s_x(t)-x_b(t))^2-(s_y(t)-y_b(t))^2\le 0, \end{aligned}$$

(58)

where $r_o$ is the sum of the cylinder and obstacle radii, $x_b(t)$ and $y_b(t)$ are obstacles’ center coordinate. Note that for static obstacles, the center coordinates are constant in time. We use the desired trajectory (56) and the kinematic and dynamic model of the arm. By that, the obstacle constraints of (58), and the angle, angular velocity, and torque bounds shown in Table 2, are formed as (23) in terms of time and $\sigma$.

Table 2 Angle, angular velocity and torque bounds of the manipulation used in the simulations

Fig. 9

The 6R manipulator’s trajectory avoiding the obstacles and hitting the disk. The red obstacles are dynamic with a cyclic trajectory while the blue obstacles are static

In addition to the inequality constraints above, we have some equality constraints. First, because the end-effector’s motion is on a 2D plane parallel to the table, its height is constrained such that $s_z(t,\sigma )=z_t$. Moreover, we constrain the end-effector to be perpendicular to the table, that is, have constant pitch such that $\theta (t,\sigma )=\pi /2$. In more complex problems we would have to generate the random points on the constraints. However, these two equality constraints impose some values in $\sigma$, in particular, $c_0=z_t,~c_i=0$, which are the coefficients for the $s_z(t)$ polynom, and $e_0=\pi /2$ and $e_i=0$, which are the coefficients of the pitch polynom $\theta (t)$, for $i=1,\ldots ,g$. These values could be maintained in $\sigma$ or could be removed by reducing the dimension of $\sigma$, either way would not change runtime.

We have formed kinodynamic constraints as a function of $\sigma$ and t in the form of Eqs. (23) and (24). Moreover, we have embedded the equality constraints in the structure of $\sigma$. Next, we set the parameters for the adaptive search. The desired trajectory polynomials $\mathbf {s}(t,\sigma )$ are chosen to be in the order of $g=20$ and therefore the dimension of the parameter set is $\varOmega \subseteq \mathbb {R}^{108}\times \varUpsilon$. This value was chosen by means of trial and error to have enough free parameters for optimization but small enough not to negatively affect the performance. In the preprocessing step we chose $\varSigma$ such that the free trajectory parameters are in the range of $a_i,b_i,d_i,f_i=[-10,10]\times 10^{-12},~i=0,4,\ldots ,g-1$, $a_g,b_g=[-0.7,0.7]$, $d_g,f_g=[0,2\pi ]$ and the goal time interval to be $t_g=[0.5,3.5]$. These values were set based on preliminary analysis showing the range of values for feasible polynomials. This step is currently manual and future work should consider ways for choosing the right values. Therefore, the set $\varSigma$ is a 109-dimensional hyper-rectangle in $\varOmega$. Numeric calculation of $\rho$ with user selection of $\alpha =0.18$ (18% of the average distance) yields the relative portion $\rho =0.0021$. After choosing the maximum probability $P_{max}=0.05$ not to find a solution, the minimum number of random points needed is $N=1426$ [Eq. (45)]. Therefore, by generating the N points in $\varSigma$, the probability to find a solution if one exists is 95%.

With generating N random points in $\varSigma$ and using $S_{max}$ calculated to be 3.28, the algorithm outputted 12 feasible solutions after 4.01 min. Choosing a minimum time cost function

$$\begin{aligned} H(\sigma )=\min \{t_g\}, \end{aligned}$$

(59)

an optimal trajectory solution is outputted. Snapshots of the optimal motion are illustrated in Fig. 9. The end-effector navigates the grasped cylinder between the obstacles to hit the disk. The joints angle, angular velocity, and torque response of the optimal trajectory are shown in Figs. 10, 11 and 12, respectively. As could be seen, they are within the bounds defined by the kinodynamic constraints. The task response of the end-effector is presented in Fig. 13. The goal state is reached after 1.17 s while maintaining the height and pitch constraints. The results were repeatable in all attempted trials. The outputted trajectory now provides the optimal trajectory over all possible start states. In addition, for this particular start state, the trajectory is the optimal one.

Fig. 10

The 6R joint angles within the allowed bounds

Fig. 11

The 6R joint angular velocities within the allowed bounds

Fig. 12

The 6R joint torques within the allowed bounds

Fig. 13

The 6R end-effector task taken to the desired goal state

The computation runtime is due to the $6\times 6$ matrices computation of the dynamic model in (15). Removing the torque constraint (21) yields runtime of 24.17 s, that is, 89.93% less. In this simulation we have used $\varDelta S=1/3$ and separated between the constraint checks as discussed in Sect. 6.2. Without these methods, the runtime would excessively be 1.45 h.

Fig. 14

A three degrees of freedom manipulator moving through dynamic obstacles from start (left) to goal (right) configurations

Fig. 15

The joints angles response for the 3R manipulator solved with the SKIP and RRT* algorithms (Color figure online)

We wish also to demonstrate the optimality of the SKIP solution compared to the known RRT* algorithm (Karaman and Frazzoli 2011). We tested both algorithm on the planar three degrees of freedom manipulator seen in Fig. 14 moving through dynamic obstacles and with a minimal time cost function. For that matter, an initial configuration was set and not optimized for SKIP. The joint angles, angular velocity and torque limits were set to $\pm \,150^{\circ }$, $\pm \,70$ RPM and $\pm \,2$ Nm, respectively. For the SKIP implementation, the desired trajectory function in the task space was chosen to be a 5th order polynomial. $N=1061$ random points were generated with 98% probability of finding a solution. A time optimal solution with goal time of $t_g=0.77~{\text {s}}$ was found after runtime of 0.28 s. The RRT* algorithm was implemented as in Webb and van den Berg (2013) with state-time representation (Sintov and Shapiro 2014) for dynamic obstacles avoidance. The RRT* ran for 20,000 iterations generating a trajectory with $t_g=0.756~{\text {s}}$. The angle response of both algorithms can be seen in Fig. 15. The SKIP output is near optimal since it is confined to a polynomial trajectory. That is, the SKIP algorithm found an optimal solution under the restrictions of a polynomial trajectory.

9 Conclusions

We present an algorithm for goal state driven trajectory optimization taking into account the kinodynamic constraints of the system. The trajectory is parameterized to a high-dimensional parameter space based on the goal state and the trajectory function. The algorithm uses the formalized constraints in the parameter space to find a feasible set of solutions. The set is found by generating random points within the allowed region of the free parameters and checking each one for feasibility. The feasibility analysis was done with an adaptive step size algorithm, decreasing the step size if the point approaches the constraint boundary. Moreover, an optimal solution is chosen from the set of feasible solutions and a gradient descent approach is used to refine the solution to the near by local optimum. The probability to find a solution was shown to approach one if the number of random points increases to infinity. Moreover, the statistical analysis enabled an automatic parameter selection for the algorithm to find a solution in a given probability or runtime.

It was shown that the algorithm has the worst case time complexity in the order of $O(\xi N)$. It should be noticed that the algorithm plans the motion off-line prior to the motion. To reduce the runtime, the computation could be done with less strict parameters to see if solutions could be found more quickly. Future work will involve runtime reduction and application for online planning.

Currently, the allowed region $\varSigma$ is user defined by pre-processing simulations. Future work will deal with the definition of the allowed region $\varSigma$. That is, finding optimal boundaries of the set $\varSigma$ while decreasing the number of random points to be generated and of the runtime.