Balancing of humanoid robot using contact force/moment control by task-oriented whole body control framework

Abstract

Balancing control of humanoid robots is of great importance since it is a necessary functionality not only for maintaining a certain position without falling, but also for walking and running. For position controlled robots, the for-ce/torque sensors at each foot are utilized to measure the contact forces and moments, and these values are used to compute the joint angles to be commanded for balancing. The proposed approach in this paper is to maintain balance of torque-controlled robots by controlling contact force and moment using whole-body control framework with hierarchical structure. The control of contact force and moment is achieved by exploiting the full dynamics of the robot and the null-space motion in this control framework. This control approach enables compliant balancing behavior. In addition, in the case of double support phase, required contact force and moment are controlled using the redundancy in the contact force and moment space. These algorithms are implemented on a humanoid legged robot and the experimental results demonstrate the effectiveness of them.

1 Introduction

Balancing is one of the most important and fundamental functionalities for bipedal robots. Contact between feet and ground has a critical role of exchanging force and moment between the robot and ground, especially because the bipedal robot does not have any fixed base. These contact forces and moments are necessary to control the motion of the robot. On the other hand, if the robot cannot maintain the balance with current contact states, one of the feet needs to be located into a different place to prevent the robot from falling down.

In this paper, we focus on the problem of maintaining current contact state. Most balancing algorithms control contact forces and moments to be within the contact conditions on frictions and zero moment point (ZMP) (Vukobratovic and Borovac 2004). To implement these algorithms on position controlled robots, inverse kinematics (IK) are used to find out what joint angles to be commanded to achieve certain center of mass (COM) position of the robot, and body posture. Huang et al. (2000) proposed a real-time joint trajectory modification method to control ZMP for balance. Kajita et al. (2001) implemented balancing by controlling torque of ankle joint using servo motor. Sugihara and Nakamura (2002) modified COM trajectory through COM Jacobian. Kajita et al. (2010) reduced modification of predetermined trajectory by using body posture and contact foot controller. These approaches on position controlled robots heavily depend on the force/torque sensors, and the contact forces and moments are indirectly controlled through the configuration of the robot.

On the other hand, the methods based on joint torque control have been focused on accomplishing direct control of contact forces and moments by commanding the required contact forces and moments to generate desired COM motion for maintaining balance. The method proposed by Hyon (2009) described ground applied force (GAF) required for COM motion, and contact force/moment control by distributing required contact force to be applied on contact points. Ott et al. (2011) proposed a similar method with that of Hyon (2009), which calculates contact force distribution by optimization using frictional grasping method. Stephens and Atkeson (2010) proposed dynamic balance force controller reflecting effects from motion generated by model-based controller including multi-body dynamics. Lee and Goswami (2012) supplemented additional effects of angular momentum to the COM dynamics. The results from these methods demonstrated the effectiveness of balancing through direct contact force control in simulations or experiments. In these approaches, however, the whole-body motion of the robot, other than COM, is not accounted for because only COM dynamics is used for contact force control.

Control frameworks utilizing the full-body inverse dynamics have the advantage of accounting for the whole-body motion and force of the robot. Whole-body control framework for human-like robot is proposed by Khatib et al. (2004), and the framework for floating base system with considering contact constraints is studied by Park and Khatib (2006). The framework is demonstrated through simulation that it can be used effectively in various multi-contact situations. Studies by Park (2008) and Sentis et al. (2010) showed that control of task with maintaining balance simultaneously is possible through controlling contact force/moment in null-space. Righetti et al. (2011) simplified calculations of operational space control approach based on contact constrained inverse dynamics, applying orthogonal projection method to solve inverse dynamics. Also they showed that contact force distribution is possible by applying optimization, which minimizes tangential forces on contact points (Righetti et al. 2013), to the framework developed in their previous work (Righetti et al. 2011). Herzog et al. (2014) showed that it is possible to add existing balancing algorithm (Lee and Goswami 2012) to hierarchical inverse dynamics controller. Similarly, Del Prete (2013) proposed task space inverse dynamics controller for floating base robot. Saab et al. (2013) developed a generic framework which maintains tasks, constraints, and contact conditions by hierarchical method, and obtained the solution which always satisfies contact conditions.

In this paper, a controller for balancing is developed with using the control of contact force and moment through the task-oriented whole-body control framework (Park and Khatib 2006). In this proposed approach, the contact force and moment are controlled to remain within the boundary for stability through the null-space of specific tasks of the robot while the robot is operating. The specific task would be the one that is critical for the robot, for example, the vertical motion of COM. The whole-body dynamics is utilized in the computation of the contact force/moment from the commanding joint torques, and vice versa. Balancing methods proposed by Hyon (2009), Ott et al. (2011), Stephens and Atkeson (2010), and Lee and Goswami (2012) control the COM for balancing, using simplified dynamics considering relation between the COM and contact points to calculate proper desired force on the COM. In those approaches the COM is always controlled for balancing, while the COM is not explicitly controlled for balancing of the robot in our proposed approach. The COM motion is affected by the control of contact force/moment only when this control is needed for balancing. Therefore, more tasks can be controlled when the control of contact force/moment is not activated.

In addition, contact force/moment re-distribution is proposed in the case when there is redundancy in the contact force space such as double support phase. This is, in fact, performed simultaneously with the aforementioned balancing approach. It would not create any additional motion of the robot. This contact force/moment distribution can be often necessary to maintain individual contacts. Del Prete (2013) did not consider contact force/moment distribution problem and Righetti et al. (2013) take into account contact force/moment when solving inverse dynamics to minimize tangential forces. Minimizing tangential forces can increase probability to maintain contacts. However, it cannot always satisfy contact conditions. Our proposed balancing process provides possible solutions for contact force/moment distribution satisfying contact constraints. Taking advantages of the task-oriented whole-body control framework, all algorithms can be composed in a single control framework and various tasks can be added if the robot has enough degrees of freedom. The developed algorithms are implemented on a torque-controlled humanoid legged robot with 12-DOF. This is one of the first experimental results on a physical legged robot using the operational-space-based whole-body control framework proposed in Park and Khatib (2006) and Sentis et al. (2010).

Fig. 1

Overview of the proposed balance algorithm using whole-body control framework

This paper is organized as follows. The next Sect. 2 explains the overview of the proposed algorithm using the task-oriented whole-body control framework. Review of the whole-body control framework is provided in Sect.  3. The contact conditions to check contact state using expected contact force/moment are explained in Sect. 4. In Sect. 5, the control method for balancing is developed by contact force/moment control using null-space. Contact force/moment distribution algorithm during double support contact is explained in Sect. 6. Experimental results of the algorithm with 12-DOF humanoid legged robot are presented in Sect. 7. Finally, conclusion about the work is in Sect. 8.

2 Overview of balancing algorithm using whole-body control algorithm

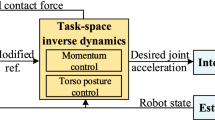
Overview of the proposed balancing algorithm is shown in Fig. 1. First, the task-oriented whole-body control framework computes the desired joint torques to be commanded, given the desired tasks of the robot. The contact force/moment can be calculated from the desired joint torques and the dynamics of the robot, given contact condition of the robot. That is, we can compute or estimate the contact force/moment that are to be produced if we command the desired joint torques to the robot, before these torques are commanded to the robot. When these estimated contact force/moment do not satisfy contact conditions to maintain the current contact state, the desired contact force/moment are calculated to meet the contact conditions for balance by changing the actual commanding torques to the robot.

To compute the additional torque for achieving these desired contact force/moment, control using the null-space of high-priority task will be used. The torque for contact force/moment control in the null-space can be combined with the pre-designed task torque. The specific high-priority tasks can be selected as the ones that are not to be disturbed by this additional torque for the control of contact force/moment. Therefore, the generated motion by this null-space control can change some of the tasks of the robot, other than the high-priority tasks. In the case of the excessive motion or torque from the null-space control, the control strategy needs to be modified such that the high-priority task is altered or the contact state is to be changed such as changing foot step plan.

On the other hand, when there are more than 6-DOF contact between the robot and environment such as double support (12-DOF), there can be redundancy in the contact force/moment space. That is, the contact force and moment can be modified using this redundancy without changing the motion of the robot. This redundancy of contact force/moment is also actively used for maintaining contact conditions for balance.

3 Whole-body control framework: review

The dynamic equations for the robot with k joints, which have rigid body contact with environment, can be described as follow,

$$\begin{aligned} A(q)\ddot{q} + b(q,\dot{q}) + g(q) + J_{c}^{T}f_{c} = {\varGamma } , \end{aligned}$$

(1)

where q is the $n \times 1$ vector of joint angles and ${\varGamma }$ is the $n \times 1$ vector of joint torque. The matrix A(q) is the $n \times n$ inertia matrix, $b(q,\dot{q})$ is the $n \times 1$ vector of Coriolis/centrifugal forces and g(q) is the $n \times 1$ gravity vector. Here, $n=k+6$ since the floating base robot includes 6-DOF of rigid body motion. The matrix $J_{c}$ is the contact Jacobian which describes the Jacobian for the contact positions and orientations and $f_{c}$ is the vector of contact forces and moments.

3.1 Contact constrained dynamics

The contact Jacobian $J_{c}$ is defined as

$$\begin{aligned} {\dot{x}}_{c} = J_{c} \dot{q}. \end{aligned}$$

(2)

The dynamics of the robot (1) can be projected into contact space with the contact Jacobian. The projected dynamics can be described as

$$\begin{aligned} {\varLambda }_{c} \ddot{x}_{c} + \mu _{c} + p_{c} +f_{c} = \bar{J}_{c}^{T}{\varGamma }, \end{aligned}$$

(3)

where

$$\begin{aligned}&{\varLambda }_{c} = (J_{c} A^{-1} J_{c}^T)^{-1} \end{aligned}$$

(4)

$$\begin{aligned}&\mu _{c} = {\varLambda }_{c}\{J_{c}A^{-1}b(q,\dot{q})-\dot{J_{c}}\dot{q}\} \end{aligned}$$

(5)

$$\begin{aligned}&p_{c} = {\varLambda }_{c}J_{c}A^{-1}g(q) \end{aligned}$$

(6)

$$\begin{aligned}&\bar{J}_{c}^{T} = {\varLambda }_{c} J_{c} A^{-1}. \end{aligned}$$

(7)

The matrix ${\varLambda }_{c}$ is the inertia matrix at the contact space, $\mu _{c}$ is the vector of Coriolis/centrifugal forces at the contact space, $p_c$ is the vector of gravity forces at the contact space and $\bar{J_{c}}$ is the dynamically consistent inverse of $J_{c}$.

If the contacts are stationary and rigid, we can assume ${\ddot{x}}_{c} = 0$ and ${\dot{x}}_{c} = 0$. Then, Eq. (3) becomes

$$\begin{aligned} f_{c}=\bar{J_{c}^{T}}{\varGamma } - \mu _{c} - p_{c}. \end{aligned}$$

(8)

Equation (8) can be substituted to Eq. (1) to get contact constrained dynamics in the joint space.

$$\begin{aligned} A(q) \ddot{q} + b(q,\dot{q}) + g(q) -h_{c}(q,\dot{q}) = N_{c}^{T}{\varGamma }, \end{aligned}$$

(9)

where

$$\begin{aligned}&h_{c} = J_{c}^T (\mu _{c} + p_{c}) \end{aligned}$$

(10)

$$\begin{aligned}&N_{c}^T = I-J_{c}^{T}\bar{J}_{c}^{T} . \end{aligned}$$

(11)

3.2 Contact constrained dynamics of the operational space coordinate

With the given operational space coordinate, x, the corresponding Jacobian is defined as

$$\begin{aligned} \dot{x} = J \dot{q}. \end{aligned}$$

(12)

The constrained dynamics equation of the operational space can be obtained by pre-multiplying Eq. (9) by $\bar{J}^T$.

$$\begin{aligned} {\varLambda }(q) \ddot{x} + \mu (q,\dot{q}) + p(q) = F, \end{aligned}$$

(13)

where

$$\begin{aligned}&{\varLambda }(q) = (J A^{-1} N_{c}^{T} J^T )^{-1} \end{aligned}$$

(14)

$$\begin{aligned}&\bar{J}^T = {\varLambda } J A^{-1} N_{c}^{T} \end{aligned}$$

(15)

$$\begin{aligned}&\mu (q,\dot{q}) = \bar{J}^T b(q,\dot{q}) - {\varLambda } \dot{J} \dot{q} + {\varLambda } J A^{-1} J_{c}^T {\varLambda }_{c}\dot{J}_{c} \dot{q} \end{aligned}$$

(16)

$$\begin{aligned}&p(q) = \bar{J}^T g(q), \end{aligned}$$

(17)

where ${\varLambda }(q)$ is the inertia matrix at the operational space, $\mu (q,\dot{q})$ is the vector of the Coriolis and centrifugal forces at the operational space, p(q) is the vector of the gravity forces at the operational space, and F is the vector of forces and moment in operational space.

3.3 Control framewrok solving inverse dynamics

To compose a control torque only at real actuated joints, the $k \times n$ selection matrix S can be used as

$$\begin{aligned} {\varGamma } = {S^T{\varGamma }_{a}}, \end{aligned}$$

(18)

where ${\varGamma }_{a}$ is the $k \times 1$ vector of control torque for actuated joints. In the case that the floating base body motion is described in the first six joints,

$$\begin{aligned} {S} = [0_{k \times 6} \quad I_{k \times k}]. \end{aligned}$$

(19)

Using the selection matrix to exclude the un-actuated joints,

$$\begin{aligned} F=\bar{J}^{T}{S^{T}}{{\varGamma }_{a}} \end{aligned}$$

(20)

To solve the equation when there are redundancy, we will minimize joint acceleration energy (Bruyninckx and Khatib 2000). The acceleration energy can be described as

$$\begin{aligned} E_{a} = \frac{1}{2}{{\varGamma }_{a}^{T}}W{{\varGamma }_{a}}, \end{aligned}$$

(21)

where

$$\begin{aligned} W= & {} {SN_{c}}A^{-1}N_{c}^{T}{S^{T}} \nonumber \\= & {} SA^{-1}N_{c}^{T}S^{T}. \end{aligned}$$

(22)

Define ${\widetilde{J}^T}$ as one of the generalized inverses which minimizes $E_{a}$.

$$\begin{aligned} {\widetilde{J}^{T}} = \overline{\bar{J}^T{S^T}}. \end{aligned}$$

(23)

Then the commanding torque can be described as

$$\begin{aligned} {{\varGamma }_{a}}= & {} {\widetilde{J}^{T}} F \nonumber \\= & {} {\widetilde{J}^T} {\varLambda } \{ f^* + \mu + p \}, \end{aligned}$$

(24)

where $f^*$ is desired acceleration of the x. For PD control,

$$\begin{aligned} f^{*} = k_{p}(x_{d}-x)+k_{d}(\dot{x}_{d} - \dot{x}), \end{aligned}$$

(25)

where $x_d$ is the vector of the desired position, the term $\dot{x}_{d}$ is the vector of the desired velocity, and the values $k_p$ and $k_d$ are the proportional and derivative gain, respectively.

3.4 Null-space control

The null-space projection matrix is described as

$$\begin{aligned} {\widetilde{N}^{T}}=I-{\widetilde{J}^{T}} \overline{{\widetilde{J}^{T}}}, \end{aligned}$$

(26)

where

$$\begin{aligned} \overline{{\widetilde{J}^{T}}} = {\bar{J}}^{T}{S^{T}}. \end{aligned}$$

(27)

Then the null-space control torque is ${\widetilde{N}^{T}}{{\varGamma }_{a,0}}$, where ${{\varGamma }_{a,0}}$ is an arbitrary control torque. The overall command torque can be composed with

$$\begin{aligned} {{\varGamma }_{a}} = {\widetilde{J}^{T}}F + {\widetilde{N}^{T}}{{\varGamma }_{a,0}}. \end{aligned}$$

(28)

4 Contact conditions

In this work, the contact state is assumed as 6-DOF plane contact. To maintain the contact, the following conditions must be satisfied for each plane contact.

$$\begin{aligned}&F_{z}<0, \end{aligned}$$

(29)

$$\begin{aligned}&|(F_{x}^{2} + F_{y}^{2})^{0.5}| < \mu _{s} |F_{z}|, \end{aligned}$$

(30)

$$\begin{aligned}&|M_{z}| < \mu _{s} |F_{z}|, \end{aligned}$$

(31)

$$\begin{aligned}&|M_{x}|<|F_{z}|\frac{l_{y}}{2}, \end{aligned}$$

(32)

$$\begin{aligned}&|M_{y}|<|F_{z}|\frac{l_{x}}{2} , \end{aligned}$$

(33)

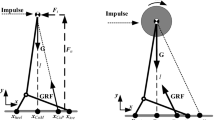
where $F_{x}$ and $F_{y}$ are tangential forces in the contact plane, and $F_{z}$ is normal force of the contact plane. $M_{x}$, $M_{y}$, and $M_{z}$ are moments about x, y, and z axis, respectively. Axis of each direction is defined in the local frame of each contact plane as seen in Fig. 2. $\mu _{s}$ is static friction coefficient, and $l_{x}$ and $l_{y}$ are length and width in the x and y direction if the shape of contact plane is rectangular. These contact conditions must be met to maintain the current contact. Therefore, these conditions are to be checked with the estimated or expected contact force/moment from the desired control torque for the given tasks of the robot.

Fig. 2

Coordinate and frames to describe contact conditions

The contact forces and moments can be computed before robot control. With the commanding control torque from Eq. (24), the expected contact forces and moments are obtained by

$$\begin{aligned} F_{c} = \bar{J}_{c}^T{S^{T}{\varGamma }_{a}} - \mu _{c} - p_{c}. \end{aligned}$$

(34)

The contact Jacobian $J_{c}$ for the plane contact can be described with 6-DOF position and orientation for each contact foot. For the single support with plane contact, the contact force/moment vector is composed as $F_{c} = [F_{x} \ F_{y} \ F_{z} \ M_{x} M_{y} \ M_{z}]^{T}$. For the double support with two plane contacts, the contact force vector can be described as $F_{c} = [F^T_{c,r} \ F^T_{c,l}]^{T}$, where $F_{c,r}$ and $F_{c,l}$ are contact force/moment vector of the right foot and the left foot, respectively.

On the other hand, when there are multiple contacts such as double support, the overall balance of the whole robot can be determined by using resultant contact force and moment of the both feet at the arbitrary frame O. The frame O is set to be located at the center of two feet and the direction y of the frame is parallel to the line which passes through the centers of two feet. The resultant contact force/moment can be described as

$$\begin{aligned} ^{O}F_{c}= & {} ^{O}KF_{c} \nonumber \\= & {} \begin{bmatrix} ^{O}R_{r}&\,\,\ 0_{3\times 3}&\,\,\ ^{O}R_{l}&\,\,\ 0_{3\times 3}\\ ^{O}R_{r} {^{O} \widehat{P}_{r}}&\,\,\ {^{O}R_{r}}&\,\,\ {^{O}R_{l} {^{O} \widehat{P}_{l}}}&\,\,\ ^{O}R_{l} \end{bmatrix} \begin{bmatrix} F_{c,r}\\ F_{c,l} \end{bmatrix}, \end{aligned}$$

(35)

where $^{O}R_{r}$ and $^{O}R_{l}$ are $3 \times 3$ orientation matrices of right foot and left foot with respect to the reference frame O, $0_{3\times 3}$ is $3\times 3$ zero matrix, ${^{O} \widehat{P}_{r}}$ is skew symmetric matrix of the vector $^{O}P_{r} = [x_{r} \ y_{r} \ z_{r}]^{T}$ from frame O to the right foot and ${^{O} \widehat{P}_{l}}$ is skew symmetric matrix of the vector $^{O}P_{l} = [x_{l} \ y_{l} \ z_{l}]^{T}$ from frame O to the left foot. For single support, $^{O}F_{c} = F_{c}$. The skew symmetric matrix with given vector $P = [x \ y \ z]^{T}$,

$$\begin{aligned} \widehat{P} = \begin{bmatrix} 0&\,\,\ -z&\,\,\ y\\ z&\,\,\ 0&\,\,\ -x\\ -y&\,\,\ x&\,\,\ 0 \end{bmatrix}. \end{aligned}$$

(36)

The balance of the humanoid robot can be checked if the resultant force/moment $^{O}F_{c}$ meets contact conditions in addition to the individual contact condition on each contact.

In most cases of double support, the contact plane or polygon is not a rectangular shape. We set the square boundary inside of the boundary composed of foot edges as shown in Fig. 3, and this boundary with green square in Fig. 3 is treated as acceptable region for the center of pressure from the resultant force/moment $^{O}F_{c}$. The rest of the regions inside of the boundary composed of edges of two feet is considered as safety margin area.

Fig. 3

Contact boundary for double support phase

If the computed resultant contact force/moment do not satisfy the contact conditions, the resultant contact force/moment have to be modified to meet the condition. In this work, we discuss the control of the resultant contact force/moment for balancing in Sect. 5 and distribution of the contact force/moment for each foot will be considered in the Sect. 6.

5 Contact force/moment control for balancing by null-space control

In this section, the control method using the null-space torque to meet the balance condition on the resultant contact force/moment is discussed. That is, the center of pressure from $^{O}F_{c}$ in (35) needs to remain in the acceptable region in Fig. 3. Increasing vertical force $F_z$ is one way to meet the condition, but this will create the acceleration of COM in the z-direction. This motion may not be always preferable because it can reach its boundary quickly with straightening the knee joint.

Instead, our proposed algorithm controls the contact forc-e/moment except $F_{z}$. The condition for $M_{x}$ and $M_{y}$ can be re-described as

$$\begin{aligned}&-\frac{l_{x}}{2} < r_{x} < \frac{l_{x}}{2} , \end{aligned}$$

(37)

$$\begin{aligned}&-\frac{l_{y}}{2} < r_{y}<\frac{l_{y}}{2}. \end{aligned}$$

(38)

where $r_{x} = -{^{O}M_{y}}/{^{O}F_{z}}$ and $r_{y} = {^{O}M_{x}}/{^{O}F_{z}}$ which express the position of the center of pressure in Frame O. When this position $r_{x}$ or $r_{y}$ is out of the boundary, it has to be moved to the nearest boundary point to meet the moment conditions. A new reference frame $O_{d}$ can be set at the desired position at the boundary (Fig. 3). In this frame $O_{d}$, the desired resultant contact moment $^{O}M_{x,d}$ and $^{O}M_{y,d}$ have to be zero.

For the contact force/moment control, the following control structure is used:

$$\begin{aligned} {{\varGamma }_{a}} = {\widetilde{J}_{t}^{T}}F + {\widetilde{N}_{h}^{T}}{{\varGamma }_{a,c}}, \end{aligned}$$

(39)

where ${\widetilde{J}_{t}^{T}}$ is the Jacobian composed with task Jacobian for all the tasks, ${\widetilde{N}_{h}^{T}}$ is the null-space projection matrix composed with high priority task Jacobian, and ${{\varGamma }_{a,c}}$ is torque to control contact force/moment in the null-space. It has to be noted that ${\widetilde{N}_{h}}$ is not the null-space projection matrix for the task Jacobian ${\widetilde{J}_{t}}$ but the null-space projection matrix for the specific high priority task.

For example, later in the experiment, the task Jacobian includes the COM position and the orientation of the pelvis. However, the null-space projection matrix ${\widetilde{N}_{h}}$ is defined only for the vertical direction of the COM position.

$$\begin{aligned} {\widetilde{N}_{h}^{T}}=I-{\widetilde{J}_{com,z}^{T}\overline{\widetilde{J}_{com,z}^{T}}}, \end{aligned}$$

(40)

where $J_{com,z}$ is $1 \times n$ Jacobian for height of the COM.

This is not a nominal decomposition of task and null-space control because the null-space control interferes with some of the tasks. However, this strategy is effective in balance control, because the null-space control does not affect a critical high priority task but modifies the other tasks during balancing. Then, when the balancing in the null-space control is de-activated, all the tasks are back to be controlled. For example, the robot has 12-DOF for motion during single support phase. If the position of COM, orientation of upper-body, and position/orientation of the swing foot are controlled, which is total 12-DOF, there is no redundancy. The control of the resultant contact moment around x and y axes is not always required. However, when the resultant contact moment around x and y axes are to be controlled for balancing, these control will conflict with the motion control of the robot because there is no redundancy. In this paper, it is proposed that the resultant contact moment around x and y axes are to be precisely controlled by composing the null-space projection matrix accounting for only COM z direction control. The motion tasks other than COM z direction will be compromised when the resultant contact moment around x and y axes are controlled.

The control torque in the null-space ${{\varGamma }_{a,c}}$ can be calculated as

$$\begin{aligned} {{\varGamma }_{a,c}} = {^{O_d}\widetilde{J}^{T}} \begin{bmatrix} -^{O_d}M_{x}\\ -^{O_d}M_{y} \end{bmatrix}, \end{aligned}$$

(41)

where $^{O_d} M_{x}$ and $^{O_d} M_{x}$ are contact moment about x and y axis in the reference frame $O_{d}$. $^{O_d}\widetilde{J}^{T}$ is the Jacobian to control resultant contact moment in frame $O_{d}$ which is defined with using the dynamically-consistent inverse to minimize $E_{a}$.

$$\begin{aligned} {^{O_d}\widetilde{J}^{T}}= & {} \overline{ \{ S_{c} \, ^{O_d} K \bar{J}_{c}^{T} {S^{T}}, {\widetilde{N}^{T}} \} } \end{aligned}$$

(42)

where $S_{c}$ is $2\times 6$ selection matrix to choose $^{O_d} M_{x}$ and $^{O_d} M_{y}$ and in this case it can be composed as

$$\begin{aligned} S_{c} = \begin{bmatrix} 0_{2\times 3}&I_{2\times 2}&0_{2\times 1},\\ \end{bmatrix}, \end{aligned}$$

(43)

The matrix $^{O_d}K$ is used to describe 6-DOF contact force/moment in the frame $O_d$. For the double support, $^{O_d}K$ can be defined as

$$\begin{aligned} ^{Od}K = \begin{bmatrix} ^{O_d}R_{r}&\,\,\ 0_{3\times 3}&\,\,\ ^{O_d}R_{l}&\,\,\ 0_{3\times 3}\\ ^{O_d}R_{r}{^{O_d} \widehat{P}_{r}}&\,\,\ ^{O_d}R_{r}&\,\,\ ^{O_d}R_{l} {^{O_d} \widehat{P}_{l}}&\,\,\ ^{O_d}R_{l} \end{bmatrix}, \end{aligned}$$

(44)

for the single support with right foot

$$\begin{aligned} ^{O_d}K = \begin{bmatrix} ^{O_d}R_{r}&\,\,\ 0\\ ^{O_d}R_{r} {^{O_d} \widehat{P}_{r}}&\,\,\ ^{O_d}R_{r} \end{bmatrix}, \end{aligned}$$

(45)

and for the single support with left foot

$$\begin{aligned} ^{O_d}K = \begin{bmatrix} ^{O_d}R_{l}&\,\,\ 0\\ ^{O_d}R_{l} {^{O_d} \widehat{P}_{l}}&\,\,\ ^{O_d}R_{l} \end{bmatrix}, \end{aligned}$$

(46)

where $^{O_d}R_{r}$ and $^{O_d}R_{l}$ are the orientation matrices of right and left foot to the reference frame $O_{d}$, respectively. $^{O_d}P_{r}$ and $^{O_d}P_{l}$ are the skew symmetric matrices of the vector from reference frame $O_{d}$ to right foot and left foot, respectively.

6 Contact force/moment distribution for double support

Without appropriate contact force/moment distribution, the robot can lose its contact at the double support phase since the generalized inverse in Eq. (23) minimizes only the acceleration energy $E_{a}$. So we need to re-distribute the contact force/moment to each contact foot considering the contact conditions.

6.1 Contact force/moment control using contact redundancy

Park (2006) proposed to control contact force/moment by using contact null-space when a robot is in multi-contact situation. Using this approach, contact force/moment can be controlled without disturbing the tasks. When the W matrix in Eq. (22) is rank-deficient, the system has more than 6 motion constraints. Therefore, it is possible to modify commanding torques using redundancy while generating the same motion. The torque space can be described by singular value decomposition (SVD) of the matrix W.

$$\begin{aligned} W = U{\varSigma } V^{T}, \end{aligned}$$

(47)

where U is unitary matrix, ${\varSigma }$ is diagonal matrix with singular values and $V^T$ is conjugate matrix of unitary matrix V. U is equal to V since the matrix W is symmetric.

$$\begin{aligned} W= & {} V{\varSigma } V^{T} \end{aligned}$$

(48)

$$\begin{aligned}= & {} \begin{bmatrix} V_{1}&V_{2} \end{bmatrix} \begin{bmatrix} \sigma _{1}&\,\,\ 0\\ 0&\,\,\ 0\\ \end{bmatrix} \begin{bmatrix} V_{1}^{T} \\ V_{2}^{T} \end{bmatrix} . \end{aligned}$$

(49)

The torque in the vector space spanned by the column vectors of $V_{2}$ will not change the acceleration energy and will not produce any acceleration in the task space. Therefore, the torques in the $V_{2}$ vector space can be used to modify contact force/moment without disturbing the task control. The contact force/moment can be expressed as

$$\begin{aligned} F_{c,d} = \bar{J}_{c}^{T}{S^{T}}V_{2}\alpha . \end{aligned}$$

(50)

Then $\alpha$ can be derived by using dynamically-consistent inverse which minimizes $E_{a}$.

$$\begin{aligned} \alpha = \overline{\bar{J}_{c}^{T}{S^{T}}} F_{c,d}, \end{aligned}$$

(51)

where $F_{c,d}$ is the vector of desired contact force/moment generated by additional torque ${{\varGamma }_{a,n}}$ in the contact null-space. We can say that $V_{2}\alpha$ as the torque vector for contact force control in contact null-space.

$$\begin{aligned} {{\varGamma }_{a,n}} = V_{2}\alpha . \end{aligned}$$

(52)

Then, this torque can be added to the torque in Eq. (39).

$$\begin{aligned} {{\varGamma }_{a}} = {\widetilde{J}_{t}^{T}}F + {\widetilde{N}_{h}^{T}}{{\varGamma }_{a,c}} + {{\varGamma }_{a,n}}, \end{aligned}$$

(53)

where the first term in the right hand side is the task torque, the second term is the torque for balancing to meet the overall the contact condition, and the last term is the torque for contact force/moment re-distribution when there is redundancy in the contact force/moment space.

6.2 Contact force/moment distribution for double support

Many balance control for biped robots include algorithms for appropriate contact force/moment distribution. That is, we need to determine $F_{c,d}$ in Eq. (50) to meet the contact conditions on each foot in Sect. 4 during double support. Hyon (2009) distributed the contact forces using pseudo inverse to minimize the norm of total contact forces, and Kajita et al. (2010) distributed the contact force/moment by selecting distribution ratio which is determined by simple heuristics. QP-based distribution methods for contact force and moment are developed in Park et al. (2007), Stephens and Atkeson (2010), Ott et al. (2011), Lee and Goswami (2012), Righetti et al. (2013) and Saab et al. (2013). Quadratic optimization solves the contact force/moment distribution problem considering contact conditions, however it requires irregular and high computational costs that might disturb real time control. In this paper, we used an analytic way of contact force/moment re-distribution based on simple assumptions, and the method is described in the Sect. 1. Appendix.

Fig. 4

Dynamic robotic system (DYROS) humanoid leg. a Snapshot of the robot. b Joint position of the robot and length of each link. The joints from Joint 1 to 6 are hip yaw, hip roll, hip pitch, knee pitch, ankle pitch, and ankle roll for each leg

In the case when the contact state changes, for example, from double support to single support, this contact force/moment re-distribution algorithm can also be applied so that the contact force/moment on the lifting foot can be controlled to be zero before lifting. This can be realized by the proposed method in Sect. 1. Appendix, where the weighting factor between the vertical forces on two feet can be used for this purpose. The experimental result of this algorithm is presented in the section for experiment.

7 Experimental results

Experiments were conducted on the 12-DOF DYROS humanoid legged robot (Schwartz et al. 2014) as seen in Fig. 4. The actuators of the DYROS Humanoid leg are torque controlled electric motors and those are directly connected with gear. Low gear ratio of 1:50 is used for all the joints so that the joints are back-drivable. For torque control of the joint, it is assumed that input current to the motor is linearly proportional with output torque. The relation can be described as

$$\begin{aligned} \tau = Hk_{T}i_{m}, \end{aligned}$$

(54)

where $\tau$ is generated joint torque, H is gear ratio, $k_{T}$ is torque constant, and $i_{m}$ is input current to the motor. Torque constant for each motor is set as the value in the data sheet of the product. Input current is controlled using the digital servo driver, Elmo gold solo whistle. Note that joint torque sensor is not used, so joint torque feedback control is not implemented. The height of the robot is 1.425 (m) and its total weight is 54.63 (kg). It has 6-DOF F/T sensor on each foot which are used only for measurement in this paper, and inertial measurement unit (IMU) is installed in the upper body. EtherCAT is used for communication and 500 Hz control loop is used on a PC with Intel I7–630 m processor and 4 Gbyte DDR3 RAM. Computation of robot dynamics and control algorithm is implemented through the software, RoboticsLab from SimLab Inc.

7.1 Contact force/moment distribution on two-feet standing during gravity compensation

The performance of gravity compensation and contact force re-distribution algorithm are demonstrated when the robot is on two-feet standing during gravity compensation. The ground was flat surface and there was no slope. During the gravity compensation, the robot becomes compliant and does not resist to external forces as seen in Fig. 5 while maintaining the foot contact. In this experiment, there is only gravity compensation but no other control tasks, so that the effect of contact force/moment re-distribution can be clearly observed. The desired contact force/moment are determined with following the distribution rules in the Sect. 1. Appendix. The experimental results of the desired and measured contact force/moment are plotted in Fig. 6. The contact force/moment are controlled to be re-distributed by using torques in the null-space of the contact force and moment as described in Sect. 6. The contact force and moment on each foot did not track the desired values exactly. This is because the values from the force/torque sensor are not used for feedback control while there are always modeling errors on the robot dynamics and contact model between foot and ground.

Fig. 5

Snapshots of the robot during gravity compensation. The posture of the robot can be easily changed by external force applied by a person while maintaining foot contact

Fig. 6

Contact force/moment control during gravity compensation. Computed contact force/moment for each foot and measured force/moment by F/T sensor during gravity compensation are plotted. The desired force $F_{x}$, $F_{y}$ and $M_{z}$ for right foot (blue dash line) are all zero so they are overlapped with black dash line (Color figure online)

Fig. 7

COM motion when the contact force/moment change by contact force/moment control in Fig. 6

The COM motion is plotted in Fig. 7 to show that there was approximately no motion on the robot during this contact force/moment control. Just small motion about $0.001 \sim 0.003$ (m) appeared when the contact force/moment had a relatively large change at approximately 7–11 and 19–23 (s), respectively.

7.2 Balancing during double support phase

The proposed balancing algorithm using null-space control is implemented during double support. During the experiment, disturbance was applied to the robot to test the algorithm. The COM position and orientation of the upper-body were controlled to keep initial values in the operational space. The external force was provided to the robot by human using a stick as shown in Fig. 8. The F/T sensor was attached to the right side of the robot upper body to measure the applied external force during this experiment. The PD-control is used in the Eq. (25). The proportional gain was set to $k_{p} = 225$, the derivative gain was chosen as $k_{d}=10$, and the desired velocity was set to zero. The contact ground was flat and there was no slope.

Fig. 8

Snapshot of balancing experiment during double support. Force is applied to the F/T sensor which is attached at the right side of robot. The balancing algorithm with contact force/moment control recovers the position while maintaining the foot contact stability

Fig. 9

Result after external force applied in the lateral direction during the double support in Fig. 8. a Motion of the COM after external force is applied. The yellow area shows the time when the balancing algorithm runs. Y-direction indicates the lateral direction. b Magnitude of applied external force measured by F/T sensor (Color figure online)

The COM position during the experiment of balancing algorithm is plotted in Fig. 9a. The external force started to be applied at about 0.35 s to lateral direction (y-direction). The maximum position error in the lateral direction was approximately 0.035 m and the balancing algorithm operated during 0.418–1.312 s. The magnitude of the applied force is shown in Fig. 9b. The maximum value of the applied force was approximately 188.91 N.

Comparison of contact conditions for the expected resultant force/moment at Frame O is shown in Fig. 10. The center of pressure of the resultant force and moment must meet the conditions in Eqs. (37) and (38). The right terms of the conditions are plotted as the red lines of limit value in Fig. 10, and the left terms are plotted as the blue lines. In this experiment, $l_{x}/2$ and $l_{y}/2$ were 0.13 and 0.07 m, respectively. The computed values are always smaller than the limit. During 0.418–1.312 s computed $|^{O}M_{x}|/|^{O}F_{z}|$ is the same as the limit value since balancing algorithm operated at the time. The measured value on $|^{O}M_{x}|/|^{O}F_{z}|$ shortly went outside of the boundary when there was a disturbance. However, the robot did not fall down because of the safety margin in this case. When external force is large enough to make the center of pressure go out of the real contact plane, the robot will fall down by losing its contact.

Fig. 10

Contact condition and resultant contact force/moment at frame O for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data, and red dashed line is limitation value. a Plot shows contact condition $l_{y}/2>|^{O}M_{x}|/|^{O}F_{z}|$. b Plot shows contact condition $l_{x}/2>|^{O}M_{y}|/|^{O}F_{z}|$ (Color figure online)

For balancing of the robot, the contact conditions for each foot also have to be satisfied. Figures 11 and 12 show the plots of contact conditions for each foot with computed contact force/moment and F/T sensor measurement data. The size of each foot was 0.3 m long and 0.15 m wide. Safety margin is adapted to the foot to assume $l_{x}/2 = 0.12$ m and $l_{y}/2 = 0.05$ m. Static friction coefficient $\mu _{s}$ was assumed as 0.9. The computed values in Eqs. (32) and (33) always satisfied the conditions. However, the value for condition (32) from F/T sensor of right foot sometimes went out of the limit when the external force was applied to the robot. This is because the robot dynamics model does not consider external force and there was no sensor feedback control. Other expected values are similar with those from F/T sensor. As seen in Figs. 11c and 12c, computed contact moment around x-axis for each foot is zero during the experiment because the contact force/moment re-distribution is applied to minimize the magnitude of the moment around x-axis for each foot.

Fig. 11

Contact condition and contact force/moment of right foot at local frame of the foot for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data, and red dashed line is limitation value. a Plot shows contact condition $\mu _{s}>(F_{x}^{2} + F_{y}^{2})^{0.5}/|F_{z}|$. b Plot shows contact condition $\mu _{s}>|M_{z}|/|F_{z}|$. c Plot shows contact condition $l_{y}/2>|M_{x}|/|F_{z}|$. d Plot shows contact condition $l_{x}/2>|M_{y}|/|F_{z}|$ (Color figure online)

Fig. 12

Contact condition and contact force/moment of left foot at local frame of the foot for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data and red dashed line is limitation value. a Plot shows contact condition $\mu _{s}>(F_{x}^{2} + F_{y}^{2})^{0.5}/|F_{z}|$. b Plot shows contact condition $\mu _{s}>|M_{z}|/|F_{z}|$. c Plot shows contact condition $l_{y}/2>|M_{x}|/|F_{z}|$. d Plot shows contact condition $l_{x}/2>|M_{y}|/|F_{z}|$ (Color figure online)

7.3 Balancing during single support

The COM position, orientation of the upper-body, position of left foot, and orientation of the left foot were controlled to recover initial values in the operational space while maintaining single contact with the right foot sole. The contact ground was flat surface without slope. The external force was applied to the robot on the right side of the body as the same way as in the experiment in Sect. 7.2. This force was measured by F/T sensor. The snapshot of the experiment is shown in Fig. 13 and the experimental results of the COM position, the left foot position, and the magnitude of the applied external force are plotted in Fig. 14a–c, respectively. The position of the robot starts to move at approximately 0.29 s due to the external force. At approximately 0.44 s, the left foot starts to move due to the balancing algorithm. Since the tasks were modified or affected by the null-space control except the height of the COM, the foot position also moved due to the control of contact force/moment. The maximum value of the external force was 96.39 N, the maximum error of the COM position in the y-direction was about 0.0106 m, and the maximum error of the foot position in the y-direction was about 0.015 m. Smaller external force was applied than that of double support case because the contact plane was smaller.

Fig. 13

Snapshot of balancing experiment during single support. Force is applied to the F/T sensor which is attached at the right side of robot. The balancing algorithm with contact force/moment control recovers the position while maintaining the foot contact stability

Fig. 14

Result after external force of lateral direction applied at the single support in Fig. 13. a Motion of the COM after external force is applied. The yellow area shows when the balancing algorithm operated. y-direction indicates the lateral direction. b Motion of the left foot after external force is applied. The yellow area shows when the balancing algorithm operated. c Magnitude of applied external force measured by F/T sensor (Color figure online)

The conditions (30), (31), (32) and (33) are compared with the computed and measured contact force/moment on the supporting foot in Fig. 15. We assumed static friction coefficient $\mu _{s}= 0.9$ and safety margin was adapted to the foot to assume $l_{x}/2 = 0.12$ m and $l_{y}/2 = 0.06$ m. The computed values always satisfied the contact conditions, and the measured contact moment $M_{x}$ was not within the contact condition due to the effect of the external force, which is similar to experimental results in Sect. 7.2.

Fig. 15

Contact condition and contact force/moment of the right foot at local frame of the foot for balancing during single support phase. Blue line is that value calculated by expected contact force/moment, black line is F/T sensor data, and red dashed line is limitation value. a Plot shows contact condition $\mu _{s}>(F_{x}^{2} + F_{y}^{2})^{0.5}/|F_{z}|$. b Plot shows contact condition $\mu _{s}>|M_{z}|/|F_{z}|$. c Plot shows contact condition $l_{y}/2>|M_{x}|/|F_{z}|$. d Plot shows contact condition $l_{x}/2>|M_{y}|/|F_{z}|$ (Color figure online)

7.4 Contact force/moment distribution for contact transition

When the contact state of the robot changes from double support to single support, the contact Jacobian $J_c$ also changes to include from 12 contact force/moment to 6 contact forc-e/moment. This can cause discontinuity in contact force/moment and thus commanding joint torques. To remove this discontinuity, the contact force/moment on the lifting foot can be controlled to be zero before actually lifting. This can be implemented by the contact force/moment re-distribution in Sect. 6.2.

Fig. 16

Commanding torques for every pitch joint of right foot during the experiment. Blue line shows the results with contact distribution algorithm to continuously remove contact force/moment at the contact transition foot and black line shows the results without any contact transition algorithm. a Hip pitch joint. b Knee pitch joint. c Ankle pitch joint (Color figure online)

In this experiment, X and Y position of the COM were controlled to be near the center of right foot before the contact transition experiment for lifting the left foot so that the desired contact force/moment of the left foot can be controlled to be zero using contact force distribution without falling. The contact ground was flat and there was no slope. There was no external force during this experiment. The COM position and upper-body orientation were controlled to maintain initial values in operational space during double support. Additionally, left foot position and orientation were controlled to keep initial values in operational space during single support. The experiments of contact transition were conducted with and without contact force/moment control to show the efficiency of the contact force re-distribution at the contact transition.

The contact force/moment of the contact transition foot is changed to zero with using contact force distribution algorithm during 0.5–1.0 s in Figs. 16 and 17. Contact Jacobian was composed with Jacobian of both feet during 0.0–1.0 s, and only right foot Jacobian was used for the composition of contact Jacobian during 1.0–2.0 s. Figure 16a shows the experimental result that the discontinuity of the commanding torque in every pitch joint of right leg has been removed when it is compared to the other experimental results which do not eliminate contact force/moment before contact state transition. The magnitudes of the desired torque for each experiment are different because each experiment was conducted not in the perfectly same configuration of the robot. In Fig. 17, the experimental results of the vertical motion (z-direction) of the left foot are compared when the contact transition algorithm is applied or not. Unexpected foot position movement appears due to the discontinuous torque commands when the contact state abruptly changes. By eliminating the contact force/moment before contact transition, unexpected foot motion was reduced. These results demonstrate the necessity of contact transition algorithm and efficiency of the contact force distribution algorithm.

Fig. 17

The vertical direction motion of foot when contact state changes from two feet to one foot contact. Blue line shows the results with contact distribution algorithm to continuously remove contact force/moment at the contact transition foot and black line shows the results without any contact transition algorithm (Color figure online)

7.5 Stepping on unknown surface

In this experiment balancing algorithm is demonstrated in continuous motion control including contact transition and unknown contact environment. Snapshots of the experiment are shown in Fig. 18 and the control results are expressed in Fig. 19. The COM position and orientation of the upper body were controlled at double support. At single support, the position of the left foot and orientation of the left foot were controlled in addition to the tasks during the double support phase. The tasks were controlled during 30 s. Double support phase was at 0–5 and 26–30 s, and single support phase was at 5–26 s. At the first double support, the robot was controlled to move the COM to the center of the right foot for 2 s. Then, the contact transition algorithm in Sect. 7.4 was performed to prepare for the lift of the left foot, and the left foot was controlled in the vertical direction to move 0.12 m higher than the position of the supporting foot for 2 s. An object of which height was about 0.09 m and irregular surface with soft material was placed under the left foot before the foot controlled to move down to the ground. Slope of the object was approximately parallel to the ground. Then, at 23 s the left foot was controlled to move in the vertical direction down near to the object assuming that we approximately know the height of the object. The contact transition algorithm was performed to change the contact from single to double support at 26 s. Finally, the COM was controlled to move 0.1 m away from right foot in the y-direction for 2 s. As mentioned earlier, contact transition algorithm ran to eliminate the contact force/moment of left foot at 4.5–5 s and to generate smooth contact force/moment on the left foot at 26–26.5 s.

Fig. 18

Experiment of stepping on unknown surface

Fig. 19

Control result of the robot motion in Fig. 18. a Control result of the COM in the Y-direction which indicates the lateral direction. The yellow area shows the time when the balancing algorithm runs. b Control result of the left foot in the Z-direction which indicates the vertical direction (Color figure online)

Fig. 20

State of the left foot contact with object of unknown surface. a Position of the left foot in vertical direction. b Measured contact force and computed contact force of the left foot in vertical direction

Fig. 21

Rotation angle error about x-axis of the upper body during tasks in Fig. 18. a At the first double support phase. b At the second double support phase with balancing algorithm which is shown as yellow area (Color figure online)

Initial contact point was lower than expected, and the surface of the object was irregular and composed of soft surface, the contact position in the vertical direction of the left foot was moved as seen in Fig. 20a. This was unexpected motion for contact foot since control framework assumes stationary and rigid contact. The left foot moved downward due to the soft surface of the contact object as seen in Fig. 20 when the magnitude of the contact force on left foot in the vertical direction increases.

The balancing algorithm was executed during 28.22–28.54 s since the desired motion during the time required large contact moment. The balancing algorithm affected the tasks other than the high-priority task, the COM z-position in this experiment, and the effect can be shown in Fig. 21. Especially, the rotation motion around x-axis of upper body was generated due to the null-space control for balancing. Figure 21a can be compared with Fig. 21b to clearly see the effect in the second double support phase since balancing algorithm was not much executed at the first double support phase.

Fig. 22

Contact condition and resultant contact/force moment at frame O for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data, and red dashed line is limitation value. a Plot shows contact condition $l_{y}/2>|^{O}M_{x}|/|^{O}F_{z}|$. b Plot shows contact condition $l_{x}/2>|^{O}M_{y}|/|^{O}F_{z}|$ (Color figure online)

Fig. 23

Contact condition and contact force/moment of right foot at local frame of the foot for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data, and red dashed line is limitation value. a Plot shows contact condition $\mu _{s}>(F_{x}^{2} + F_{y}^{2})^{0.5}/|F_{z}|$. b Plot shows contact condition $\mu _{s}>|M_{z}|/|F_{z}|$. c Plot shows contact condition $l_{y}/2>|M_{x}|/|F_{z}|$. d Plot shows contact condition $l_{x}/2>|M_{y}|/|F_{z}|$ (Color figure online)

Fig. 24

Contact condition and contact force/moment of left foot at local frame of the foot for balancing during the double support phase. Blue line is the value calculated by expected contact force/moment, black line is F/T sensor data and red dashed line is limitation value. a Plot shows contact condition $\mu _{s}>(F_{x}^{2} + F_{y}^{2})^{0.5}/|F_{z}|$. b Plot shows contact condition $\mu _{s}>|M_{z}|/|F_{z}|$. c Plot shows contact condition $l_{y}/2>|M_{x}|/|F_{z}|$. d Plot shows contact condition $l_{x}/2>|M_{y}|/|F_{z}|$ (Color figure online)

Figure 22 shows the contact conditions for resultant force /moment. Figures 23 and 24 show the contact conditions for each foot with computed and measured contact force /moment. The measured data for left foot during 5–26 s are zero since the left foot was not in a contact at that time. Computed contact force/moment always satisfy the conditions. The condition for $M_{y}$ at the left foot violates the condition shortly at a 26–26.8 s although there were no external force during the time. This is because the left foot had unknown contact at the beginning of the double support and the object under the left foot had compliance, which was not accounted for in the controller.

8 Conclusion

Balancing of a humanoid legged robot is presented in this paper. The contact force/moment control is used for the balance of the torque controlled robot through the task-oriented whole-body control framework. This control approach enables the compliant balancing behavior due to the advantage of using the full dynamics of the robot and direct torque command to the joint.

The experimental results demonstrated the successful implementation of compliant motion with gravity compensation, balancing on one foot and two feet standing, and compliant contact transition between one foot and two feet standing. It is noted that the computed contact force and moment were comparable to the measured contact force and moment. The proposed control framework successfully performed these tasks even without using force/torque sensor information in the control, because the computed and measured contact force/moment are close enough for the dynamic model of the robot to be used for control. On the other hand, it is believed that the performance of the robot could be further improved if the values from the force/torque sensor were used for control. Therefore, the use of F/T sensor information for the feedback control of contact force/moment is one of our future work. More interesting compliant and dynamic behavior are expected to be performed using the proposed control framework.

Appendix: Proportional distribution of contact force/moment

The resultant contact force/moment $^{O}F_{c}$ in frame O can be recalculated with Eq. (34) using commanding torque. The vector $^{O}F_{c}$ is known value and the contact force/moment of each foot can be calculated by the Eq. (35). This equation can be described as

$$\begin{aligned} ^{O}F_{x}= & {} ^{O}F_{x,r} + ^{O}F_{x,l}, \end{aligned}$$

(55)

$$\begin{aligned} ^{O}F_{y}= & {} ^{O}F_{y,r} + ^{O}F_{y,l}, \end{aligned}$$

(56)

$$\begin{aligned} ^{O}F_{z}= & {} ^{O}F_{z,r} + ^{O}F_{z,l}, \end{aligned}$$

(57)

$$\begin{aligned} ^{O}M_{x}= & {} ^{O}M_{x,r} + ^{O}M_{x,l} - \left( z_{r} \, ^{O}F_{y,r}+z_{l} \, ^{O}F_{y,l}\right) \nonumber \\&+ \left( y_{r} \, ^{O}F_{z,r}+y_{l} \, ^{O}F_{z,l}\right) , \end{aligned}$$

(58)

$$\begin{aligned} ^{O}M_{y}= & {} ^{O}M_{y,r} + ^{O}M_{y,l} + \left( z_{r} \, ^{O}F_{x,r}+z_{l} \, ^{O}F_{x,l}\right) \nonumber \\&\, -\left( x_{r} \, ^{O}F_{z,r}+x_{l} \, ^{O}F_{z,l}\right) , \end{aligned}$$

(59)

$$\begin{aligned} ^{O}M_{z}= & {} ^{O}M_{z,r} + ^{O}M_{z,l} + \left( x_{r} \, ^{O}F_{y,r}+x_{l} \, ^{O}F_{y,l}\right) \nonumber \\&\, -\left( y_{r} \, ^{O}F_{x,r}+y_{l} \, ^{O}F_{x,l}\right) , \end{aligned}$$

(60)

where $^{O}F_{x,r}$, $^{O}F_{y,r}$, $^{O}F_{z,r}$, $^{O}M_{x,r}$, $^{O}M_{y,r}$, $^{O}M_{z,r}$ are contact force/moment of the right foot at frame O and $^{O}F_{x,l}$, $^{O}F_{y,l}$, $^{O}F_{z,l}$, $^{O}M_{x,l}$, $M_{y,l}^{O}$, $^{O}M_{z,l}$ are contact force/moment of the left foot at frame O. To re-distribute these contact force/moment to each foot, assume every force/moment terms are divided in same ratio $\eta$ as

$$\begin{aligned} \eta =\frac{^{O}F_{z,r}}{^{O}F_{z}}. \end{aligned}$$

(61)

The coefficient $\eta$ has the value between zero and one, since $^{O}F_{z} < ^{O}F_{z,r} < 0$. Now we can rewrite the Eqs. (55–60) as,

$$\begin{aligned}&{}^{O}F_{x,r}= \eta ^{O}F_{x},\quad ^{O}F_{x,l}=(1-\eta ) ^{O}F_{x}, \end{aligned}$$

(62)

$$\begin{aligned}&{}^{O}F_{y,r}= \eta ^{O}F_{y},\quad ^{O}F_{y,l}=(1-\eta ) ^{O}F_{y}, \end{aligned}$$

(63)

$$\begin{aligned}&{}^{O}F_{z,r}= \eta ^{O}F_{z}, \quad ^{O}F_{z,l}=(1-\eta ) ^{O}F_{z}, \end{aligned}$$

(64)

$$\begin{aligned}&{}^{O}M_{x,r} = \eta \left( ^{O}M_{x,r} + ^{O}M_{x,l}\right) , \nonumber \\&{}^{O}M_{x,l} = (1-\eta ) \left( ^{O}M_{x,r} + ^{O}M_{x,l}\right) , \end{aligned}$$

(65)

$$\begin{aligned}&{}^{O}M_{y,r} = \eta \left( ^{O}M_{y,r} + ^{O}M_{y,l}\right) , \nonumber \\&{}^{O}M_{y,l}= (1-\eta ) \left( ^{O}M_{y,r} + ^{O}M_{y,l}\right) , \end{aligned}$$

(66)

$$\begin{aligned}&{}^{O}M_{z,r} = \eta \left( ^{O}M_{z,r} + ^{O}M_{z,l}\right) , \nonumber \\&{}^{O}M_{z,l}=(1-\eta ) \left( ^{O}M_{z,r} + ^{O}M_{z,l}\right) . \end{aligned}$$

(67)

This assumption can be applied since every contact condition in Eqs. (30–33) are proportional to the normal force $F_{z}$. So when the resultant contact force/moment $^{O}F_{c}$ satisfies the contact conditions, distributed contact forc-e/moment can also satisfy the conditions for each.

The contact force can always maintain contact satisfying the conditions (29), (30), when $\eta$ has the value between 0 and 1 because forces are independent with moments. On the other hand, contact moments are related with forces at each foot. So the contact condition for moments (31–33) can be violated depending on $\eta$. The Eq. (58) can be described as the relation between $^{O}M_{x,r}$ and $\eta$ by substituting Eqs. (56–64).

$$\begin{aligned} ^{O}M_{x,r}= & {} \left\{ (z_{r}- z_{l}) \, ^{O}F_{y} - (y_{r} - y_{l}) \, ^{O}F_{z} \right\} \eta ^{2} \nonumber \\&+ \left( ^{O}M_{x} + z_{l} \, ^{O}F_{y} - y_{l} \, ^{O}F_{z}\right) \eta , \end{aligned}$$

(68)

and contact condition (58) can be expressed as

$$\begin{aligned} |^{O}M_{x,r}| < |^{O}F_{z}\eta | \frac{l_{y}}{2}, \end{aligned}$$

(69)

Substitute Eq. (68) to the condition (69) to find the boundary of the $\eta$.

$$\begin{aligned} a^{2}\eta ^{2} + 2ab\eta + \left( b^{2}-c^{2}\right) < 0, \end{aligned}$$

(70)

where

$$\begin{aligned}&a = (z_{r}- z_{l}) \, ^{O}F_{y} - (y_{r} - y_{l}) \, ^{O}F_{z}, \end{aligned}$$

(71)

$$\begin{aligned}&b = ^{O}M_{x} + z_{l} \, ^{O}F_{y} - y_{l} \, ^{O}F_{z}, \end{aligned}$$

(72)

$$\begin{aligned}&c = \frac{l_{y}}{2} \, ^{O}F_{z}. \end{aligned}$$

(73)

Boundary of $\eta$ about condition for $M_{y}^{O}$ Eq. (33) can be achieved by the same process using Eqs. (55), (57), (58), (62) and (64). The structure of the equation is the same as that of Eq. (70) and the following terms are different as

$$\begin{aligned}&a = -(z_{r}- z_{l}) \, ^{O}F_{x} + (x_{r} - x_{l}) \, ^{O}F_{z}, \end{aligned}$$

(74)

$$\begin{aligned}&b = ^{O}M_{y} - z_{l} \, ^{O}F_{x} + x_{l} \, ^{O}F_{z}, \end{aligned}$$

(75)

$$\begin{aligned}&c = \frac{l_{x}}{2} \, ^{O}F_{z}. \end{aligned}$$

(76)

Boundary of $\eta$ about condition for $M_{z}^{O}$ (31) also can be calculated by the same process by Eqs. (55), (56), (60), (62) and (63). The structure of the equation is the same as Eq. (70) and the following terms are different as

$$\begin{aligned}&a = - (x_{r}- x_{l}) \, ^{O}F_{y} + (y_{r} - y_{l}) \, ^{O}F_{x}, \end{aligned}$$

(77)

$$\begin{aligned}&b = ^{O}M_{z} - x_{l} \, ^{O}F_{y} + y_{l} \, ^{O}F_{x}, \end{aligned}$$

(78)

$$\begin{aligned}&c = \mu _{s} \, ^{O}F_{z}. \end{aligned}$$

(79)

Boundary of feasible $\eta$ can be determined by Eq. (70) about conditions for $^{O}M_{x,r}$, $^{O}M_{y,r}$ and $^{O}M_{z,r}$. In this research we minimize the magnitude of $M_{x,r}$ and $M_{x,l}$ because the foot width $l_{y}$ is relatively small than the length of the foot $l_{x}$ and static friction coefficient $\mu _s$. Coefficient $\eta$ to make $M_{x,r}= 0$ can be determined in Eq. (68). If the calculated $\eta$ is out of boundary, then nearest value of the boundary can be selected as $\eta$. Finally, distribution of the contact force/moment can be determined by $\eta$ in Eqs. (62–67).