Optimization of the ground reaction force for the humanoid robot balance control

Abstract

This paper proposes an effective framework to control humanoid-ground physical interaction for balance. The key concept is to control both humanoid robot linear and angular momenta, which are computed by the whole body kinematics. We firstly determine the ground reaction force (GRF) according to the momenta and then distribute the GRF to the two feet. After determining the foot GRFs, we calculate the joint torques to realize the foot GRFs. Herein, we present an effective method to set the appropriate foot GRFs and transform these forces into full-body joint torques. It operates as a force control process. The joint redundancy is solved by optimizations and constraints. Besides, we modify the classical contact model for the legged robot system. The modified contact model can provide the scientifical ground reaction force. We test the controller using our full-sized humanoid robot emulational platform, including compliant balance and squatting, which demonstrates the effectiveness of the method.

1 Introduction

Humanoid robots are designed for serving humans in a large variety of tasks. To achieve an elegant and effective performance, the robot needs to adapt to variations of environments, such as shaky ground [1]. Therefore, the humanoid robot’s balance in uncontrollable situations is a problem that must be solved before the humanoid robot is stepping out from the laboratory to the complex external environment.

The need for a balancing system arises from the requirement that the humanoid be capable of performing on a similar level as that of humans. Until recently, a lot of balance control techniques have attempted to maintain balance by controlling only the linear motion of a humanoid. For instance, Hyon proposed a method to calculate the joint torques to control the location of the robot’s center of mass (CoM) [2]. When the CoM leaves the target position, a net GRF is determined by a simple CoM state feedback law to bring the CoM back to the target position. In fact, the rotational motion of the robot around the CoM plays an essential role in the balance. For example, when a human is walking or running, his hands and feet often move in opposite directions to each other to ensure that the angular momentum of the torso is stable. The importance of angular momentum in humanoid was firstly reported by Raibert, who is one of the founders of Boston Dynamics, in 1986, when he still was the director of MIT Leg Lab [3]. However, it went unnoticed for a long time. In 2004, Popovic performed a physiological experiment on human walking and found that the neural center of the human body intentionally regulated the angular momentum of human to maintain near-zero value while walking, which suggested that angular momentum may play a significant role in human behavior [4, 5]. Subsequently, different balance control strategies based on momentum have been proposed. Komura et al. [6] presented a simplified model named the angular momentum pendulum model, which augments the well-known linear pendulum model [1] with an additional capability of possessing centroidal angular momentum. Uemura et al. [7]. designed a switching rule of standing or stepping according to the angular momentum around ankle. Orin et al. [8] put forward the concept of spatial momentum, divided the momenta into linear and angular momenta, and proposed the centroid momentum matrix. Macchietto et al. [9] also divided robot momenta into linear and angular momenta and employed the centroid momentum matrix to determine the joint accelerations for balance. Besides, Twan et al. [10] elaborated a momentum-based control framework for the humanoid robot “Atlas”. They computed the joint acceleration vector with the limitations of GRF lying on a quadratic program. Hence, controlling the motion of the robot from the view of the momentum has become popular in recent years.

According to the basic D’Alembert’s principle, the resultants of all external forces and moments are equal to the change rates of the momenta. Hence, for a force control task, it can be translated into a momentum control issue. In such a task, two levels are distinct within the control process: (i) designing the humanoid-ground interaction force, and (ii) generating the joint torques to realize the interaction force. Although the external forces and moments have a one-to-one relation with the momentum change rates, the actual operation for the task is complicated and is worth discussing. One of the issues that should be solved is how to handle redundant degrees of freedom (DoF).

For determining the GRFs applied to the feet, Hyon et al. [2] presented a method to minimize the sum of the squared norm of forces at some contact points on the boundary of each foot while satisfying the desired net GRFs. Years later, they applied the method to unknown rough terrain and nonhorizontal ground [11]. Besides, they succeeded to control a hydraulic humanoid robot maintaining balance under the interference of external force [12]. Sentis et al. [13] used a virtual-linkage model to precisely determine GRFs in a more general setting of multi-contact interaction (net GRF) between the humanoid robot and the environment. However, the determination of net GRF increases the complexity of the system, and it also may generate a large ankle torque to keep the foot from sliding and turning. Herein, we control the foot GRFs and center of pressure (CoP) by directly controlling the ankle torques for avoiding the feet sliding and turning.

It is also important to ascertain the relationship between GRFs and joint torques properly. Starting from the early work of Vukobratovic et al. [14], they have developed the relationship between the action point of GRF, i.e., ZMP, and joint motion. Kajita et al. [15] introduced a method using the pseudo-inverse of the inertia matrix to generate the whole body motion based on the linear and angular momentum. Jamisola Jr et al. [16] used the relative Jacobian matrix to control standing dual arms robot. Similarly, Ramamoorthy et al. [17] also computed joint torques by statics equivalence between joint torques and GRF. The statics equivalence is widely used for force interaction control of manipulators. It should be pointed out that replacing dynamics with statics only works in a non-high velocity situation. Lee et al. [18] defined the balance control objectives in terms of CoM and CoP, and adopted the centroidal momentum matrix to determine the joint accelerations, followed by calculating the joint torques using inverse dynamics. Determining the joint torques using centroidal momentum can also be seen in [19, 20]. However, the centroidal momentum differentiation matrix is quite complicated due to the high redundancy of the humanoid robot.

In this paper, we firstly specify the desired GRF according to the momentum states. Due to some constraints, such as the CoPs cannot run outside the feet’s support domain, i.e., the feet cannot flip or slide, and GRFs need to be naturally unilateral, the desired GRFs are not always reliable. Then, we obtain the admissible GRF under each foot sole to achieve the desired GRF as close as possible. Herein, we neglect the weight of the feet and assume that the forces and torques applied to the ankles are equivalent to the GRFs. In such a process, we can directly determine admissible foot GRFs without using conventional and complicated net GRF of the robot. In the next step, we establish a dynamic equivalent relationship between joint torques and GRFs such that we computed necessary joint torques to create admissible GRFs to maintain balance. For model reality, we also present a contact model which can be applied to the shanking and moving ground. We highlight our work with various demonstrations of humanoid balance maintenance and squatting.

The main contributions and novelties of this paper are listed as follows:

• 1. A scientific method is proposed to determine the physically available foot GRFs for balance.

• 2. Dynamic mapping of GRFs to joint torques with constraints is established.

• 3. An effective and reliable ground contact model is developed, and it includes the main relevant contact phenomena that will affect the dynamic behavior of the robotic system.

2 The momentum-based balance controller of the humanoid robot

2.1 Centroidal dynamics of a humanoid robot

The CoM is the valid location of the robot’s total mass and the point where the resultant gravity force acts. Hence, it takes a unique role in a humanoid robot in its dynamics. A humanoid robot can be simplified as a tree-structure topology with N + 1 links and N joints. Each link has 6° of freedom, corresponding precisely to the 6 dimensions of momentum.

Here, we adopt a humanoid robot model developed by ourselves. The height of the humanoid robot is 1.34 m, and its mass is about 40 kg. It has a total of 23 DoFs. Moreover, the freedom degree distribution of the robot is: 2 for each shoulder, 2 for each elbow, 3 for the waist, 3 for each hip, 1 for each knee, and 2 for each ankle. It is designed to have similar geometrical and dynamical parameters to those of a teenager, who is about 14 years old. Figure 1 and Table 1 gather the simplified structure and physical parameters of the biped. All the links motion states can be obtained by kinematics referring to the ground coordinate system ${{\Sigma }}$ _G.

Fig. 1

Kinematic modelling

Table 1 Physical parameters of the humanoid robot

The homogeneous transformation matrix of each link CoM concerning the ground coordinate system is [1]:

$${\varvec{{\rm T}}}_{j} = \left[ {\begin{array}{*{20}c} {{\varvec{R}}_{j} } &\quad {{\varvec{c}}_{j} } \\ {0{{ 0 0}}} &\quad 1 \\ \end{array} } \right]$$

(1)

where R_j ∈ R^3×3 and c_j ∈ R^3×1 are the rotation matrix and the position vector of the j-th link, respectively. We also can obtain the relationship between the velocity (v_j,$\bf{\omega }$ _j) of the CoM of the j-th link and the velocity vector ${{\dot{q}}}$ by kinematics:

$$\left[ {\begin{array}{*{20}c} {{\varvec{v}}_{j} } \\ {{\varvec{\omega }}_{j} } \\ \end{array} } \right] = {\varvec{J}}_{j} {{\dot{\varvec{q}}}}$$

(2)

where J_j is the Jacobian matrix of the j-th link. The total momentum of the robot composed of N connecting links is:

$${\varvec{P}} = \left[ \begin{gathered} {\varvec{L}} \hfill \\ {\varvec{A}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \sum\limits_{{j = 1}}^{N} {m_{j} {\varvec{v}}_{j} } \hfill \\ \sum\limits_{{j = 1}}^{N} {{\varvec{I}}_{j}^{{cm}} {\varvec{\omega }}_{j} } \hfill \\ \end{gathered} \right]$$

(3)

where m_j is the mass of the j-th link, and I_j^cm is a 3 × 3 j-th link rotational inertia matrix about the CoM of the robot:

$${\varvec{I}}_{j}^{{cm}} = {\varvec{R}}_{j} {\bar{\varvec{I}}}_{j} {\varvec{R}}_{j}^{T} + m_{j} {\varvec{S}}({\varvec{c}}_{G} - {\varvec{c}}_{j} ){\varvec{S}}^{T} ({\varvec{c}}_{G} - {\varvec{c}}_{j} )$$

(4)

where ${{\bar{I}}}$ _j represents the inertia tensor of the j-th link for its local coordinate system, ${{c}}_{{{G}}}$ = $\mathop \sum \nolimits_{{j = 1}}^{N} m_{j} c_{j} /m_{{{{tot}}}}$ is the CoM of the robot, m_tot is the total mass of the robot, and the quantity S(p) is the skew-symmetric matrix that satisfies S(p)$\bf{\omega }$ = p × $\bf{\omega }$ for any 3D vector $\bf{\omega }$.

Substituting (2) into (3), the robot’s total momentum can be obtained as follows:

$${\varvec{P}} = {\varvec{I}}({\varvec{q}}){\varvec{J}}({\varvec{q}}){\dot{\varvec{q}}}$$

(5)

where the Jacobian matrix J(q) ∈ R^6N×N is the combination of the Jacobian matrix of each link:

$${\varvec{J}} = \left[ {{\varvec{J}}_{1}^{T} ,{\varvec{J}}_{2}^{T} , \cdots {\varvec{J}}_{j}^{T} , \cdots {\varvec{J}}_{N}^{T} } \right]^{T},$$

(6)

and I(q) is the 6 × 6 N inertia matrix:

$${\varvec{I}} = \left[ {\begin{array}{*{20}c} {{\varvec{M}}_{1} } &\quad {\varvec{0}} &\quad {{\varvec{M}}_{2} } &\quad {\varvec{0}} &\quad \cdots & {{\varvec{M}}_{N} } &\quad {\varvec{0}} \\ {\varvec{0}} &\quad {{\varvec{I}}_{1}^{{cm}} } &\quad {\varvec{0}} &\quad {{\varvec{I}}_{2}^{{cm}} } &\quad \cdots &\quad {\varvec{0}} & \quad{{\varvec{I}}_{1}^{{cm}} } \\ \end{array} } \right]$$

(7)

where M_j is a 3 × 3 mass diagonal matrix. Rin et al. [8] defined the system momentum matrix N = IJ. The system momentum matrix is the product of the inertia matrix and the system Jacobian matrix, and its dimension is 6 × N. Therefore, we can rewrite (5) as follows:

$${\varvec{P}} = {{\varvec{N}}\dot{\varvec{q}}}.$$

(8)

2.2 Balance control of the robot based on centroidal momentum

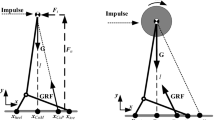
Regarding the robot as a whole mass, as shown in Fig. 2, all the external forces can be turned into a force and a moment, or equivalently, the linear and angular momentum change rates, $\dot{L}$ and $\dot{A}$, at the CoM [8].

Fig. 2

Centroidal dynamics of the humanoid robot

Here, we can define a PD controller based on the CoM and momentum states so that it realizes the desired position and velocity of the CoM:

$$\left\{ \begin{array}{l} {\dot{\varvec{L}}}_{d} = {\varvec{K}}_{{p1}} ({\varvec{c}}_{{c,d}} - {\varvec{c}}_{G} ) + {\varvec{K}}_{{d1}} ({\dot{\varvec{c}}}_{{c,d}} - {\dot{\varvec{c}}}_{G} ) \hfill \\ {\dot{\varvec{A}}}_{d} = {\varvec{K}}_{{p2}} ({\varvec{A}}_{{c,d}} - {\varvec{A}}) + {\varvec{K}}_{{d2}} ({\dot{\varvec{A}}}_{{c,d}} - {\dot{\varvec{A}}}) \hfill \\ \end{array} \right.$$

(9)

where c_c,d and ${{\dot{c}}}$ _c,d are the desired CoM location and velocity, respectively, and A_c,d and $~{{\dot{A}}}$ _c,d are desired CoM momentum states.

2.2.1 Determination of the GRFs

The feet of the robot occupy a small part of the robot’s overall mass, so the mass of the robot’s feet can be ignored. In this view, the GRF can be regarded as the force and moment applied to the ankles as shown in Fig. 3. The advantage is that we can control the angular momentum change rate of the robot by determining the positions, forces, and torques of the feet. Also, it can be easy to ensure the CoP in the interior of the foot’s support polygon by controlling the ankle torque. And the momentum change rates can be expressed as follows:

$$\begin{gathered} {\dot{\varvec{L}}} = {\varvec{f}}_{r} + {\varvec{f}}_{l}, \hfill \\ {\dot{\varvec{A}}} = {\dot{\varvec{A}}}_{f} + {\dot{\varvec{A}}}_{\tau }, \hfill \\ {\dot{\varvec{A}}}_{f} = ({\varvec{c}}_{r} - {\varvec{c}}_{G} ) \times {\varvec{f}}_{r} + ({\varvec{c}}_{l} - {\varvec{c}}_{G} ) \times {\varvec{f}}_{l}, \hfill \\ {\dot{\varvec{A}}}_{\tau } = {\varvec{\tau }}_{r} + {\varvec{\tau }}_{l} \hfill \\ \end{gathered}$$

(10)

where f_r and f_l are the GRFs acting on the right and left foot, respectively, c_r and c_l represent the positions of the ankles, and $\tau _{r}$ and $\tau _{l}$ are the torques of the right and left ankles.

Fig. 3

Translation of the GRFs to the ankles

To ensure stationary contacts, the CoP at each foot needs to be within the foot’s support polygon. Therefore the moment $\tau _{{l,r}}$ = [$\tau _{{l,r\_x}} ,~\tau _{{l,r\_y}} ,~\tau _{{l,r\_z}}$]^T generated by the GRF and applied to the ankle can be expressed as follows:

$${\varvec{\tau }}_{{l,r}} = \left( {{\varvec{c}}_{{l,r}} - {\varvec{c}}_{{l,r\_CoP}} } \right) \times {\varvec{f}}_{{l,r}}$$

(11)

where c_{l,r_CoP} is the CoP of the left or right foot.

Except for gravity, the change of the momentum is caused by a combination of GRFs at the left and right foot. After determining $\dot{L}$ and $\dot{A}$, we need to distribute the GRF to the left and right foot. The allocation rule can be accomplished by the optimization criteria as follows:

$$\begin{gathered} \min \left\| {{\dot{\varvec{L}}}_{d} - {\dot{\varvec{L}}}({\varvec{f}}_{r} ,{\varvec{f}}_{l} )} \right\|^{2} + w_{k} \left\| {{\dot{\varvec{A}}}_{d} - {\dot{\varvec{A}}}({\varvec{f}}_{r} ,{\varvec{f}}_{l} )} \right\|^{2} + w_{f} \left( {\left\| {{\varvec{f}}_{r} } \right\|^{2} + \left\| {{\varvec{f}}_{l} } \right\|^{2} } \right), \hfill \\ s.t.{{ }}{\varvec{F}}_{{l,r\_n}} \ge 0\,\,{{ and }}\,\,\arctan \frac{{\left| {{\varvec{F}}_{{l,r\_t}} } \right|}}{{{\varvec{F}}_{{l,r\_n}} }} \le u_{s} \hfill \\ \end{gathered}$$

(12)

where ${{\dot{L}}}$(f_r, f_l) and ${{\dot{A}}}$(f_r, f_l) are described in (10), and ${{\dot{A}}}$(f_r, f_l) is only related to the GRFs at left and right foot, which equals ${{\dot{A}}}$ _f in (10). F_{l,r_n} and F_{l,r_t} are the normal support force and tangential friction force, respectively. Note that, once either left or right foot lifts off the ground, the GRF only applies to the standing support leg.

The reason why we did not add the ankle torque item in (12) is that it would be difficult to get a real-time optimal solution due to the nonlinearity of cross-product terms in ankle torque item [18]. Moreover, the benefit of ignoring the ankle torque item is to minimize the ankle torques as possible such that it would be easier to assure the CoPs within the foot’s support polygon and avoid foot slipping.

2.2.2 Determination of foot CoPs and desired ankle torques

Actually, the foot GRFs are difficult to satisfy both the desired linear and angular momentum change rates. The difference value $\dot{A}_{{d,\tau }}$ = $\dot{A}$_d− $\dot{A}$_f, needs to be generated by ankle torques. Furthermore, ankle torques should have upper and lower bound after determining the GRFs to avoid flipping. The CoP of each sole can be solved by an optimization problem as follows:

$$\begin{gathered} \min \left\| {{\dot{\varvec{A}}}_{{d,\tau }} - \left( {{\varvec{\tau }}_{l} ({\varvec{c}}_{{l\_CoP}} ) + {\varvec{\tau }}_{r} ({\varvec{c}}_{{r\_CoP}} )} \right)} \right\|^{2} \hfill \\ s.t.\quad {\varvec{r}}_{{l,r\_CoP}} \in \left[ {{\varvec{l}}_{{heel}} ,{\varvec{l}}_{{toe}} } \right] \hfill \\ \end{gathered}$$

(13)

where ${{\tau }}_{{{l}}}$(c_{l_CoP}) and ${{\tau }}_{{{r}}}$(c_{r_CoP}) are described in (11). Note that: there is no yaw degree of freedom at the ankle, $\bf{\tau }$ _{l,r_y} is offset by the hip. Then the desired ankle torques can be determined by substituting the optimized GRFs in (12) and the optimized CoPs in (13) into (11).

2.2.3 Determination of joint torques

In Sect. 2.1, the spatial centroidal momentum P = [L^T A^T]^T is expressed. And the relationship between spatial centroidal momentum and generalized joint velocities is expressed: P = N${{\dot{q}}}$. In [8, 9, 18], they took a derivative of spatial centroidal momentum ${{\dot{P}}}$ = N ${{\ddot{q}}}$ + ${{\dot{N}\dot{q}}}$, and replaced ${{\dot{P}}}$ referring to [${{\dot{L}}}$ T ${{\dot{A}}}$ T]T in (9). And then they obtained the joint accelerations which satisfied the constraint J ${{\ddot{q}}}$ + ${{\dot{J}\dot{q}}}$ = 0. Finally, it is easy to compute the torques by performing inverse dynamics. Unfortunately, the robot is a multibody mechanism. Thus, the spatial centroidal momentum differential equation is quite complicated such that it would be difficult to real-time compute the joint accelerations. Besides, in the floating dynamics, there are no actuating rotation joints equipped at the CoM (or the base) to control the robot’s attitude angle. The simple substitution of GRFs and joint accelerations makes it possible to appear the robot attitude torques, which is physically impossible to achieve. We develop a different approach, with computing joint torques directly instead of the centroidal momentum differential equation.

Let ${{c}}_{{{G}}}$ = [x_c, y_c, z_c]^T ∈ R³ be the position vector of the CoM in the world coordinate frame. Let ${{\Omega }}$ = [${{\theta }}_{{{x}}}$,$~{{\theta }}_{{{y}}}$,$~{{\theta }}_{{{z}}}$]^T ∈ R³ be the attitude of the robot. Thus, the generalized coordinates are described with the vector x = [${{c}}_{{{G}}}^{{{T}}}$, ${{~\Omega }}^{{{T}}}$, qT] T, and the dynamic model of the floating-base robot is established as follows:

$${\varvec{D}}({\varvec{x}}){\varvec{\ddot{x}}} + {\varvec{C}}({\varvec{x}},{\dot{\varvec{x}}}){\dot{\varvec{x}}} + {\varvec{G}}({\varvec{x}}) = {\varvec{B\tau }} + {\varvec{J}}({\varvec{x}})^{T} {\varvec{F}},$$

(14)

With the constraint equations to define the contact between the stance feet and ground:

$${\varvec{J}}({\varvec{x}}){\dot{\varvec{x}}} = 0, {\dot{\varvec{J}}}({\varvec{x}}){\dot{\varvec{x}}}{{ + }}{\varvec{J}}({\varvec{x}}){\varvec{\ddot{x}}} = 0$$

(15)

where D(x) ∈ R^(n+6)×(n+6) is a positive definitive inertia matrix, C(x,${{\dot{x}}}$) ∈ R^(n+6)×(n+6) contains the centrifugal and Coriolis matrix, G(x) ∈ Rⁿ⁺⁶ is the gravity term, B is the constant transformation matrix, ${{\tau }}$ represents joint torques,${{~J(x)}}$ ∈ R^m×(n+6) is the Jacobian constraint matrix associated with the contact, and vector F ∈ R^m is the contact force, i.e., GRFs and moment applied at the left and right foot soles. Note that ${{J(x)}}$ is the composition matrix of the left and right foot sole Jacobian matrices. m = 6 or 12 depending on the robot with single support or double support.

Since there is an unknown joint angular acceleration term ${{\ddot{x}}}$ in (14), the joint torques cannot be calculated directly with the contact force F. Considering that the inertia matrix is generally symmetric positive definite, that is, a generally invertible matrix, we multiply JD⁻¹ from the left-hand side of (14):

$${\varvec{J\ddot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{C\dot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{G}} = {\varvec{JD}}^{{ - 1}} {\varvec{B\tau }} + {\varvec{JD}}^{{ - 1}} {\varvec{J}}^{T} {\varvec{F}},$$

(16)

$${\varvec{JD}}^{{ - 1}} {\varvec{B\tau }} = {\varvec{J\ddot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{C\dot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{G}} - {\varvec{JD}}^{{ - 1}} {\varvec{J}}^{T} {\varvec{F}}.$$

(17)

Substituting the contact constraints mentioned in (15) into the above equation, we can get:

$$\begin{gathered} \underline{{{\varvec{JD}}^{{ - 1}} {\varvec{B}}}} {\varvec{\tau }} = \underline{{ - {\dot{\varvec{J}\dot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{C\dot{x}}} + {\varvec{JD}}^{{ - 1}} {\varvec{G}} - {\varvec{JD}}^{{ - 1}} {\varvec{J}}^{T} {\varvec{F}}}} \hfill \\ {{ }}{\varvec{H}}{{ }}{\varvec{W}} \hfill \\ \end{gathered},$$

(18)

$${\varvec{H\tau }} = {\varvec{W}}.$$

(19)

${\dot{\varvec{J}}}$ is only related to joint angles and angular velocities, and the sensors can obtain the current states of the joints. There is another advantage that the equation directly contains contact constraint.

Besides, to keep the upper body as upright as possible, the desired moment applied at the torso can be derived using a standard PD control with the extent to the robot falls:

$$\begin{gathered} {\varvec{\tau }}_{{l\_h}} - {\varvec{\tau }}_{{r\_h}} = \underline{{{\varvec{K}}_{{p3}} {\varvec{q}}_{{torso}} + {\varvec{K}}_{{d3}} {\dot{\varvec{q}}}_{{torso}} }} \hfill \\ {{ }}{\varvec{\tau }}_{{dh}} \hfill \\ \end{gathered}$$

(20)

$${\varvec{T\tau }} = {\varvec{\tau }}_{{dh}}$$

(21)

where ${{\tau }}_{{{{l\_h}}}}$ ∈ R³ and ${{\tau }}_{{{{r\_h}}}}$ ∈ R³ are left and right hip torques, respectively, K_p3 and K_d3 are 3 × 3 diagonal matrices and represent the parameters of the proportional and differential term, q_torso ∈ R³ is the inclination of the torso in the world coordinate frame, and T ∈ R^3×n is the hip actuation transformation matrix.

Based on known joint states, the relationship between joint torques and contact forces is established. Furthermore, the desired torso moment to keep upright is determined. Hence, we can express the objective function as follow:

$$\begin{gathered} {\varvec{\tau }}_{a} = \min \left\| {{\varvec{H\tau }} - {\varvec{W}}_{a} } \right\|^{2} + {\varvec{w}}_{{torso}} \left\| {{\varvec{T\tau }} - {\varvec{\tau }}_{{dh}} } \right\|^{2} + {\varvec{w}}_{\tau } \left\| {\varvec{\tau }} \right\|^{2}, \hfill \\ st.\,\,{{ }}{\varvec{q}}_{{\min }} \le {\varvec{q}}{{ + }}{\dot{\varvec{q}}}\vartriangle t + \frac{1}{2}{\varvec{\ddot{q}}}({\varvec{\tau }})\vartriangle t^{2} \le {\varvec{q}}_{{\max }} \hfill \\ \end{gathered}$$

(22)

where $\Delta t$ is the control period of the system, q_min and q_max are the upper and lower limits of the robot joint motion, respectively, and ${{\ddot{q}(\tau )}}$ is expressed in the Appendix in detail.

To avoid numerical errors, we add a kinematic feedback control term. After obtaining the joint torques, the joint accelerations can be expressed:

$$\begin{gathered} {\varvec{\ddot{x}}}_{a} = {\varvec{D}}^{{ - 1}} ({\varvec{{\rm B}\tau }}_{a} + {\varvec{J}}^{T} {\varvec{F}}_{a} - {\varvec{C\dot{x}}} - {\varvec{G}}), \hfill \\ {\varvec{\ddot{q}}}_{a} = {\varvec{E\ddot{x}}}_{a} \hfill \\ \end{gathered}$$

(23)

where ${{\ddot{q}}}$_a are the all joint admissible accelerations expect those of the floating freedoms, E is the transformation matrix for selecting the joint accelerations, and the theoretical contact force F_a is:

$${\varvec{F}}_{a} = ({\varvec{JD}}^{{ - 1}} {\varvec{J}}^{T} )^{{ - 1}} [ - {\dot{\varvec{J}\dot{x}}} + {\varvec{JD}}^{{ - 1}} ({\varvec{C\dot{x}}} + {\varvec{G}} - {\varvec{B\tau }}_{a} )].$$

(24)

Note that, if J is a square matrix and reversible, (23) can be simplified by substituting (24) into (23):

$${\varvec{\ddot{x}}}_{a} = - {\varvec{J}}^{{ - 1}} {\dot{\varvec{J}\dot{x}}}.$$

(25)

Equation (25) is consistent with the constraint equation. If the joint accelerations could be obtained by (25), then joint torques can be computed by performing inverse dynamics, and the joint torques can be acquired directly. Unfortunately, the Jacobian matrix is usually not irrevertible. Moreover, joint accelerations obtained from the contact constraints can only keep the foot from sliding. The robot is still highly likely to fall down without sliding. Finally, the commanded joint torques are obtainable as:

$${\varvec{\tau }}{{ = }}{\varvec{\tau }}_{d} + {\varvec{\tau }}_{k}$$

(26)

where $\tau _{d}$ is computed by performing dynamics, and $\tau _{k}$ is determined by adding feedback terms:

$${\varvec{\tau }}_{k} = {\varvec{K}}_{p} \left( {{\varvec{q}}_{d} - {\varvec{q}}} \right) + {\varvec{K}}_{i} \int {\left( {{\varvec{q}}_{d} - {\varvec{q}}} \right)dt} + {\varvec{K}}_{d} \left( {{\dot{\varvec{q}}}_{d} - {\dot{\varvec{q}}}} \right)$$

(27)

where K_p, K_i, and K_d are proportional, integral, and differential gain, respectively. The desired position and velocity are both obtained by time integration of ${{\ddot{q}}}_{{{d}}}$.

3 Summary

The overall control procedure can be summarized as follows.

• (P1) Calculate all forward kinematics to obtain the positions and velocities of each part of the robot.

• (P2) Compute the momentum of the CoM by (1–8).

• (P3) Set the desired GRF and moment by (9).

• (P4) Ignore the weight of the feet and regard that the force is applied to the ankle as the GRF.

• (P5) Calculate the admissible GRFs, CoPs, and ankle torques by (10–13).

• (P6) Transform the admissible GRFs to joint torque commands for the active joints by (14–27).

4 Ground contact model

To demonstrate the implementation of the control scheme described in Sect. 2, we need to model the ground and GRF that will be applied to the feet of the biped robot. In this Section, we will introduce a general ground contact model for the biped robot.

4.1 The normal force

We regard the contact surface as a series of contact points. And each contact point consists of a combination of nonlinear spring and damper element in the normal direction such that the relationship between the viscoelastic deformation and the resulting force can be derived. The nonlinear spring and damper, known as the Hunt-Crossley model [21], is expressed as:

$$f_{y} = k_{y} \left| {\Delta y} \right|^{a} {{ + }}c_{y} \left| {\Delta y} \right|^{a} \Delta \dot{y}$$

(28)

where k_y is the stiffness coefficient, a can be determined by the geometry of the contact surfaces, c_y represents the damping factor, and $\Delta y$ is the insertion depth of the foot contact point.

Furthermore, the Hunt-Crossley model seems to be physically meaningful: the energy loss caused by the contact bodies’ damping which dissipates energy in the form of heat and larger depth means closer contact of the body surface which leads to larger stiffness and damping factor. However, it should be noted that it may generate downward normal forces as long as the velocity away from contact is fast enough. It does not obey the nature of the contact. Once the two contact bodies start to separate, the contact force cannot be the pulling force to prevent them from leaving. Here, we propose a modified normal support force which is expressed as:

$$f_{y} = \left\{ \begin{array}{ll} k_{y} \left| {\Delta y} \right|^{\rho } & \Delta y \le 0\; \&\; \Delta \dot{y} \ge 0 \hfill \\ k_{y} \left| {\Delta y} \right|^{\rho } + c_{y} \left| {\Delta y} \right|^{\kappa } \Delta \dot{y}& \Delta y \le 0\;\&\; \Delta \dot{y} < 0 \hfill \\ 0 & \Delta y > 0 \hfill \\ \end{array} \right.$$

(29)

where $\rho$ and $\kappa$ describe the influences of penetration depth on the stiffness and damping coefficients. The prime aim we piecewise calculate the normal force function is to simulate unilateral surface constraint between the two contact bodies. And the parameters of the normal contact model are shown in Table 2.

Table 2 Parameters of the ground contact model

Note that: if the constant step size is adopted in the simulation, the contact force starts being applied at the first time step after the bodies come into contact. As a result, a large contact force may be generated at the beginning of the simulation due to the high stiffness. Hence, to avoid the artificial initial energy, a variable step solver is suggested or the penetration depth at the time the contact is first detected is used as a reference position to calculate a relaxed penetration depth estimate y_r as follows:

$$\Delta y_{r} = y - y_{{r,0}}$$

(30)

where y is the current normal position of the contact point, y_r,0 =  − 1/2gt² is the penetration depth at the instant the impact is detected, and t represents the single time step.

4.2 Tangential friction force

Unlike the normal force which can be derived using scalar equations, the surface friction force is a vectorial quantity by nature. Canudas de Wit et al. [22] introduced a bristle friction force model. The tangential friction also can be modelled as a linear or nonlinear spring-damper system based on a bristle friction model. However, it is only appropriate for non-sliding or low-velocity condition. In the case of high velocity, it always performs to pull the contact point back to the initial contact position. To make the simulation closer to reality and consistent with the observation by Coulomb, whereby the tangential friction increases linearly with the normal load, we adopt the Stick–Slip friction model [23], as shown in Fig. 4.

Fig. 4

The relationship between friction coefficient and sliding speed

The friction force is the product of frictional coefficient and normal force, where the coefficient of friction is a function of the relative velocity at the point of contact. The explicit tangential friction model in the x-direction is:

$$f_{x} = \left\{ \begin{array}{ll} - {{u_{s} } \mathord{\left/ {\vphantom {{u_{s} } {v_{{{{th}}}} }}} \right. \kern-\nulldelimiterspace} {v_{{{{th}}}} }}\Delta \dot{x}f_{y} & \Delta y \le 0\; \&\; \left| {\Delta \dot{x}} \right| \le v_{{{{th}}}} \hfill \\ - \left( {u_{s} {sgn} (\Delta \dot{x}) - \Delta \dot{x}\frac{{\left( {u_{s} - u_{k} } \right)}}{{0.5v_{{{{th}}}} }}} \right)f_{y} & \Delta y \le 0\;\&\; v_{{{{th}}}} \le \left| {\Delta \dot{x}} \right| \le 1.5v_{{{{th}}}} \hfill \\ - u_{d} {sgn} (\Delta \dot{x})f_{y} {{ }}\Delta y \le 0\;\&\; \left| {\Delta \dot{x}} \right| \ge v_{s} \hfill \\ 0& \Delta y > 0 \hfill \\ \end{array} \right.$$

(31)

where u_s = 0.7 and u_k = 0.5 are static friction coefficient and kinetic friction coefficient, respectively, and v_th = 5 × 10^–4 represents the threshold velocity. All the parameters are determined by a parametric analysis. The tangential force can be expressed by its two components in x and z directions. Similarly, the friction in the z-direction has the same form as the one in x-direction.

4.3 Nonhorizontal and nonstationary ground

In reality, the contact conditions are complicated. Hence, we progressively extend the contact model to more general shapes. Here, we mainly discuss the nonhorizontal and nonstationary field to simulate the slope, earthquake, etc.

4.3.1 Determination of whether touching the surface and the last landing point

Obviously, the penetration depth and velocity in the contact model must be relative to the last contact point. In the horizontal surface, we determine whether the two bodies are in touching by ∆y < 0. Nevertheless, the judgment condition is not rigorous in the nonhorizontal slope. The intuitive method to judge whether the contact point touches the surface is to see wthether the contact point is below the surface or not. Here, for ease of understanding and calculation, we mainly discuss the contact condition that one of the contact surfaces is flat. We rotate and translate the contact points under each sole and the land to the initial horizontal position:

$${\varvec{p}}_{{f2}} = {\varvec{R}}(\theta _{x} ,\theta _{y} ,\theta _{z} )^{{ - 1}} \left( {{\varvec{p}}_{f} - {\varvec{t}} - {\varvec{p}}_{c} } \right) + {\varvec{p}}_{c}$$

(32)

where p_f2 = [x_f2, y_f2, z_f2]^T is the corresponding location of the contact point when the slope rotates to horizontal. R represents the rotation matrix of l₂ to l₁, and ${{\theta }}_{{{x}}}$, ${{\theta }}_{{{y}}}$, and ${{\theta }}_{{{z}}}$ are the rotation angles of the slope. t = [t_x, t_y, t_z]^T is the translation quantity of the slope. p_c = [r_x, r_y, r_z]^T is the center of rotation. Indeed, we can assume that the initial height of the horizontal ground is 0 such that we only need to judge y_f2. After rotating and translating, the criteria for determining whether to contact the land is the same as before. Note that, when ∆y > 0, it means that the two bodies do not touch each other. Once ∆y is less than 0 again, recording the current location p_s = [x_s, y_s, z_s] ^T, the original contact point needs to be updated. It is crucially important in the contact simulation.

4.3.2 Determination of the offset of deformation

After determining the original contact point p_s, the offset of deformation ∆d = [∆x, ∆y, ∆z]^T should be determined to compute the contact force. It should be noted that the original contact point is no longer the location where it was recorded before in the world frame if the land is moving or shaking. The current location p ${{'}}$ _s = [$x_{s}^{'}$,$~y_{s}^{'}$,$~z_{s}^{'}$]^T of the original contact point also needs to be updated:

$${\varvec{p^{\prime}}}_{s} = {\varvec{R}}({\varvec{\theta ^{\prime}}})\left( {{\varvec{p}}_{s} - {\varvec{p^{\prime}}}_{c} } \right) + {\varvec{p^{\prime}}}_{c} + {\varvec{t^{\prime}}}$$

(33)

where θ' = [$\theta _{x}^{'}$, $\theta _{y}^{'}$, $\theta _{z}^{'}$] and t = [$t_{x}^{'} ,~t_{y}^{'} ,~t_{z}^{'}$]^T represent the angle of rotation and quantity of translation after touching, respectively. Clearly, (33) is the inverse operation of (32). So, we can obtain the offset of deformation ∆d:

$$\Delta {\varvec{d}} = {\varvec{p}}_{f} - {\varvec{p^{\prime}}}_{s}.$$

(34)

It should be pointed out that ∆d is the offset of deformation in the world frame, which needs to be translated to the surface local coordinate system:

$$\Delta {\varvec{d^{\prime}}} = {\varvec{T}}_{a} \Delta {\varvec{d}}$$

(35)

where the transformation matrix T_a is:

$${\varvec{T}}_{a} = \left[ {\begin{array}{*{20}c} {c_{x} c_{y} c_{z} - s_{x} s_{z} } &\quad {c_{x} s_{z} + c_{y} c_{z} s_{x} } &\quad {c_{z} s_{y} } \\ { - c_{z} s_{x} - c_{x} c_{y} s_{z} } &\quad {c_{x} c_{z} - c_{y} s_{x} s_{z} } &\quad { - s_{y} s_{z} } \\ { - c_{x} s_{y} } &\quad { - s_{x} s_{y} } &\quad {c_{y} } \\ \end{array} } \right]$$

(36)

where s_x, c_x, s_y, c_y, s_z, and c_z are the sine and cosine values about the three axes, respectively. Similarly, we obtain the relative velocity ∆$\dot{d}$ ' = [∆$x_{s}^{'}$, ∆$~y_{s}^{'}$, ∆$~z_{s}^{'}$]^T:

$$\Delta {\dot{\varvec{d}^{\prime}}} = {\varvec{T}}_{a} \Delta {\varvec{v}}$$

(37)

where $\Delta v$ is the relative velocity in the world frame:

$$\Delta {\varvec{v}} = {\dot{\varvec{p}}}_{f} - {\dot{\varvec{p^{\prime}}}}_{s} = {\dot{\varvec{p}}}_{f} - {\dot{\varvec{R}}}({\varvec{\theta ^{\prime}}})\left( {{\varvec{p}}_{s} - {\varvec{p^{\prime}}}_{c} } \right) - {\dot{\varvec{t^{\prime}}}}$$

(38)

where $\dot{p}_{s}^{'}$ = [∆$x_{s}^{'}$, ∆$~y_{s}^{'}$, ∆$~z_{s}^{'}$]^T is the velocity of the contact point by sensors in the world frame. After obtaining the offset of deformation ∆d' and the relative velocity ∆$\dot{d}$', the contact force is computed using (12) and (15). Physical quantities, such as location and velocity of the contact point, are obtained by tensors, and the contact force all refer to the world frame. In this approach, it is easy to integrate the contact model under a common framework. In some simulation software, the rotation motion is described by the quaternion. Here we only need to convert the quaternion into the rotation matrix, the mentioned shaking and translation principles are still applicable.

5 Experiments

Herein, we only actuate the joints that produce necessary motions on the legs and fix other joints. Different scenes are defined for verifying the feasibility and effectiveness of the ground contact model and balance controller. There is a total of fifty contact points under each toe and heel. And all the simulations are begun at the double support. Moreover, the environment such as the directions, magnitudes, and the locations of perturbations and types of the ground are unknown to the controller. Besides, only the joint angles, joint velocities, joint torques, and GRF at each sole can be measured by sensors (Fig. 5).

Fig. 5

For any nonhorizontal and nonstationary slopes l, they can be converted from horizontal one l₂ by translation and rotation. The center of rotation is located at p_c. p_s1 is the interim point translated from landing point p_s and rotated by [$\theta _{x}$, $\theta _{y}$, $\theta _{z}$] to get p_s2. Similarly, p_f, p_f1, and p_f2 are the contact point locations of the robot before and after translation or rotation, respectively

5.1 Maintaining balance on the stationary horizontal beam

Firstly, we test the robot while standing on a stable horizontal beam. Figure 6 shows a series of results when the robot encounters an instantaneous perturbation in the sagittal plane. The external force (150 N) is applied at 0.1 s, locates at the CoM and lasts 0.1 s. The desired position of CoM is where the robot would be standing upright, and the desired linear and angular momenta are set to zero.

Fig. 6

Push recovery in the sagittal plane

The gravity of the robot is equivalent to a step response for the ground contact model. Thus, the foot support shows saltation at the beginning of the simulation. Caused by this, momentum and CoP locations also change significantly. After 0.02 s, the robot tends to be stable. Under the constant external force, the linear and angular momenta increase approximately linearly until the force disturbance vanishes (0.2 s). Figure 6a shows that the CoM location is continuing to offset from 0.2 s to nearly 0.31 s, however, the offset velocity is decreasing obviously. Meanwhile, both the linear and angular momenta decline and change the direction. Our controller distributes the support force to each foot. And the resultant support force nearly equals the gravity due to no dramatical change in the height of the robot. Hence, the support forces shown in Fig. 6e are approximately mirror pattern. Figure 6d shows that the actual angular momentum change rate is nearly identical to its desired value. They actually are slightly different because of the optimization as well as the errors carried by the ground contact model. The CoPs in the forward direction under the left and right soles are always kept in the safe support region (− 0.07–0.13 m).

5.2 Balance on moving and shaking ground

To simulate the robot standing on a ship or a public transport, the second experiment is subjected to maintain balance on the floating ground. In this case, we specify the motions of moving and shaking as a sinusoidal signal. The magnitude of the moving sinusoidal signal is 0.1 m and frequency is 5 Hz. For shaking motion, the magnitude and frequency are 5° and 5 Hz, respectively. The ground movements start at 0 s. Besides, all the momenta exhibited here are referring to the moving or shaking ground, i.e., the momenta are zero as long as the robot is relatively stationary to the ground although the ground is moving or shaking. The target centroidal positions and momenta are the same as those in Sect. 4.1.

Under the sinusoidal signal, the overall trajectories of CoM, momenta, and GRFs exhibit patterns very similar to the sinusoidal signal. In the coronal plane, the range of the CoP location is larger during the double support compared with that in the sagittal plane. Hence, the actual angular momentum change rate is roughly the same as the desired value (Fig. 7e). Figure 7f shows that the path of the left foot support force is a mirror image of that of the right foot, and the resultant force of them is roughly equal to the gravity of the robot. Theoretically, as long as the robot is moving at the same velocity as the ground, it does not fall. Hence, our controller chooses the ground frame when calculating the momenta. Figure 7f shows the support forces of the left and right feet rise and fall alternately, and it drives the actual angular momentum change rate to follow the desired one (Fig. 7d).

Fig. 7

Maintaining balance on moving and shaking ground

5.3 Squatting down

Simulation results of balanced squatting with the linear and angular momenta controlled are shown in Fig. 8. The desired horizontal position of CoM is the center of the supporting convex hull, and the target height of the CoM is 0.418 m. Note that we do not add the extra desired torso moments in (22) due to the phenomenon that the human’s torso does not stay upright during squatting down. Figure 9 shows a series of snapshots illustrating that the robot is squatting.

Fig. 8

Balance squatting task

Fig. 9

Animation of a balanced squatting

Similarly, the trajectories of the CoM, linear momentum, and angular momentum in Fig. 8a–c show that they all come to the desired values smoothly. The actual angular momentum change rate roughly has a similar path as the desired one. The support forces under each foot are highly identical. Besides, the support decreases first and then increases, which is also in line with the theoretical change of the support during the robot squatting down process. Figure 8f presents the actual CoP in the x-direction under each foot. Similarly, the CoP trajectories of the two feet are also highly consistent. There are saltations near 2 s in both Fig. 8d and 8f caused by ending of squatting down. And the total support equals gravity while the robot is motionless.

6 Conclusions and discussion

In this paper, we present our motivation for controlling humanoid robots in terms of their suitability to anthropogenic environments. The controller distributes the GRFs under the left and right feet according to the linear and angular momenta and computes the joint torques to generate the GRFs. To obtain high-fidelity simulation, we develop a ground contact model which includes all contact and impact phenomena. Our controller involves three optimization problems, and all of them are solved effectively by the least-square algorithm. Finally, we show the performance of the balance controller by several simulation experiments. The results confirm that the controller can deal with different types of ground and perturbation.

Our work mainly follows a series of centroid dynamics research [8]. We propose a practical approach to establish the dynamic equivalence relation between GRFs and joint torques. We hope that this paper not only introduces a humanoid-ground interaction force control method but also serves as an excellent example for readers who decide to build a new robotics simulation physical environment instead of some commercial robot simulation software. Also, the dynamic mapping between joint space and operational system space has a value worthy of reference for the researchers who plan the GRF to obtain the desired motion.

We have proposed an overall humanoid-ground contact framework, and it is clear that the framework can have a much wider application. In the near future, we will test the humanoid grasping tasks. Furthermore, according to our knowledge, the nature of the arm movement is not fully understood. Bassel et al. [24] explored the arm swing effects on walking bipedal gaits. Numerical results showed that passive movement of a biped due to the dynamics of the locomotor system has higher values of the sthenic criterion than that of actuated shoulders. Inspired by them, our future work will determine whether the optimal movement of the arms for balance is passive or not and verify the effect of arms on keeping balance.

Appendix

In double support phase, extract m = rank(J) linearly independent rows from J, and partition the generalized coordinates into m dependent variables, $\dot{q}$_a and n + 6-m primary variables, $\dot{q}$_b:

$${\varvec{x}} = {\varvec{K}}\left[ {\begin{array}{*{20}c} {{\varvec{x}}_{a} } \\ {{\varvec{x}}_{b} } \\ \end{array} } \right],{\dot{\varvec{x}}} = {\varvec{K}}\left[ {\begin{array}{*{20}c} {{\dot{\varvec{x}}}_{a} } \\ {{\dot{\varvec{x}}}_{b} } \\ \end{array} } \right]$$

(39)

where K represents an (n + 6) ${{ \times }}$ (n + 6) permutation matrix with the determinant of 1. The constraint can be written in terms of these variables:

$$\left[ {{\varvec{J}}_{a} ,{\varvec{J}}_{b} } \right]\left[ \begin{gathered} {\dot{\varvec{x}}}_{a} \hfill \\ {\dot{\varvec{x}}}_{b} \hfill \\ \end{gathered} \right] = \bf{0}$$

(40)

where J_a is an m ${{ \times }}$ m matrix formed by extracting m independent rows and columns from J and J_b is m ${{ \times }}$ (n − m). As J_a is always invertible, q_b can be expressed in terms of:

$${\dot{\varvec{x}}}_{a} = - {\varvec{J}}_{a}^{{ - 1}} {\varvec{J}}_{b} {\dot{\varvec{x}}}_{b}.$$

(41)

Hence, the joint angular velocities and the joint angular accelerations can be expressed as:

$${\dot{\varvec{x}}} = {\varvec{K}}\left[ \begin{gathered} {\dot{\varvec{x}}}_{a} \hfill \\ {\dot{\varvec{x}}}_{b} \hfill \\ \end{gathered} \right] = {\varvec{K}}\left[ \begin{gathered} {{ }} - {\varvec{J}}_{a}^{{ - 1}} {\varvec{J}}_{b}, \hfill \\ {\varvec{I}}_{{(n + 6 - m) \times (n + 6 - m)}} \hfill \\ \end{gathered} \right]{\dot{\varvec{x}}}_{b} = {\varvec{N\dot{x}}}_{b},$$

(42)

$${\varvec{\ddot{x}}} = {\varvec{N\ddot{x}}}_{b} + {\dot{\varvec{N}\dot{x}}}_{b}.$$

(43)

Substituting (39) and (48) into (14), the dynamics of the humanoid robot can be described as:

$${\tilde{\varvec{{\rm I}}}}({\varvec{x}}_{b} )({\varvec{N\ddot{x}}}_{b} + {\dot{\varvec{N}\dot{x}}}_{b} ) + {\varvec{\tilde{C}}}({\varvec{x}}_{b} ,{\dot{\varvec{x}}}_{b} ){\varvec{N\dot{x}}}_{b} + {\varvec{\tilde{G}}}({\varvec{x}}_{b} ) = {\varvec{B\tau }} + {\varvec{J}}^{T} {\varvec{F}}.$$

(44)

Now we multiply (44) by N^T from the left-hand side and obtain:

$${\varvec{N}}^{T} {\tilde{\varvec{{\rm I}}}}({\varvec{x}}_{b} ){\varvec{N\ddot{x}}}_{b} + {\varvec{N}}^{T} \left( {{\tilde{\varvec{{\rm I}}}}({\varvec{x}}_{b} ){\dot{\varvec{N}}} + {\varvec{\tilde{C}}}({\varvec{x}}_{b} ,{\dot{\varvec{x}}}_{b} ){\varvec{N}}} \right){\dot{\varvec{x}}}_{b} + {\varvec{N}}^{T} {\varvec{\tilde{G}}}({\varvec{x}}_{b} ) = {\varvec{N}}^{T} {\varvec{B\tau }} + {\varvec{N}}^{T} {\varvec{J}}^{T} {\varvec{F}}.$$

(45)

Here, we can notice that JN = 0:

$${\bf{JN}} = {{\bf JA}}\left[ \begin{array}{l} - {{\bf J}}_a^{ - 1}{{{\bf J}}_b}\\ {{{\bf I}}_{(n + 6 - m) \times (n + 6 - m)}} \end{array} \right] = \left[ {{{{\bf J}}_a},{{{\bf J}}_b}} \right]\left[ \begin{array}{l} - {{\bf J}}_a^{ - 1}{{{\bf J}}_b}\\{{\bf{I}}_{(n + 6 - m) \times (n + 6 - m)}}\end{array} \right] = - {{\bf{J}}_a}{\bf{J}}_a^{ - 1}{{\bf{J}}_b} + {{\bf{J}}_b} = 2{0}.$$

(46)

Thus, the reduced form of the dynamical model in the double support phase is given as:

$${\varvec{I}}_{b} ({\varvec{x}}_{b} ){\varvec{\ddot{x}}}_{b} + {\varvec{C}}_{b} ({\varvec{x}}_{b} ,{\dot{\varvec{x}}}_{b} ){\dot{\varvec{x}}}_{b} + {\varvec{G}}_{b} ({\varvec{x}}_{b} ) = {\varvec{B}}_{b} {\varvec{\tau }}$$

(47)

where

$${{\bf{I}}_b} = {{\bf{N}}^T}{{\tilde {\bf I}N}},{\rm{ }}{{\bf{C}}_b} = {{\bf{N}}^T}\left( {{{\tilde {\bf I}\dot N}} + {{\tilde {\bf CN}}}} \right),{\rm{ }}{{\bf{G}}_b} = {{\bf{N}}^T}{{\tilde {\bf G}}},{\rm{ }}{{\bf{B}}_b} = {{\bf{N}}^T}{\bf{B}}.$$

(48)

As a result, given the current state and the joint torques, the unique angular acceleration can be obtained:

$${\varvec{\ddot{x}}}_{b} = {\varvec{I}}_{b}^{{ - 1}} \left( {{\varvec{B}}_{b} {\varvec{\tau }} - {\varvec{C}}_{b} {\dot{\varvec{x}}}_{b} - {\varvec{G}}_{b} } \right).$$

(49)