1 Introduction

The subject that is attracting several researchers, in modern cosmology, is the accelerated expansion of the universe (Riess et al. 1998; Perlmutter et al. 1999). It has been said that this is caused by an exotic negative pressure which is known as dark energy (DE). Several DE models have been proposed to explain this phenomenon which even today remains as mystery. The cosmological constant is supposed to account for this DE. But it has some serious problems. Hence two approaches have been suggested to describe this mysterious concept. One method is to construct DE model and study their significance in relation to this cosmic inflation. Another way is to modify Einstein’s theory of gravitation and to construct DE models with a special reference to the observations of modern cosmology which throws a better light to explain this scenario.

For this purpose, there have been several modifications of Einstein’s theory of gravitation by modifying the Einstein-Hilbert action of general relativity and introducing Scalar Fields (SFs) into Einstein theory. Introduction of SFs leads to the well known quintessence models which help to explain the accelerated expansion of the universe. Thus the modified theories of gravitation are \(f(R)\) and \(f(R,T)\) theories (Nojiri and Odintsov 2003; Harko et al. 2011) and scalar-tensor theories proposed by Brans and Dicke (1961) and Saez and Ballester (1986). Anisotropic DE models in the above modified theories of gravitation were investigated by numerous researchers (Copeland et al. 2006; Nojiri et al. 2005; Kiran et al. 2014; Reddy et al. 2014; Aditya et al. 2016; Rao et al. 2018; Aditya and Reddy 2018a, 2019).

Here we are interested in the interacting scalar meson fields. Scalar meson fields are of two types—zero mass SFs and massive SFs. Zero mass SFs describe long range interactions while massive SFs represent short range interaction. In fact, this physical significance of SFs leads to immense study of SFs. Also, SFs are very important since they represent matter fields with spin less quanta and describe gravitational fields. In the literature, there are several investigations of cosmological models in the presence of mass less and massive SFs coupled with different physical sources. Here we are mainly concerned with models in the presence of massive scalar fields. Some note worthy models are obtained by Naidu (2018), Aditya and Reddy (2018a) and Reddy and Ramesh (2019) in the presence of massive SFs.

In an attempt to unify gravity and electromagnetic fields several modifications of Riemannian geometry have been proposed. Significant among them is Lyra (1951) geometry. In this geometry a gauge function has been introduced into the structureless manifold so that displacement field arises naturally. The energy conservation is not valid in this theory. The displacement field, in this theory plays the same role as the cosmological constant in general relativity. Several cosmological models in this particular theory have been discussed extensively. The following are relevant and significant to our investigation: Singh and Rani (2015) have discussed Bianchi type-\(\mathit{III}\) cosmological models into coupled perfect fluid and attractive massive scalar field as physical source in Lyra geometry. Very recently, Reddy et al. (2019) investigated Bianchi type-\(\mathit{III}\) DE cosmological model in the presence of massive scalar field in this geometry.

In order to discuss the early stages of evolution of the universe, immediately after big bang, higher dimensional cosmology plays a vital role. Subsequently, the universe has undergone compactification and we have the present four dimensional universe. Witten (1984) and Appelquist et al. (1987) are some of the authors who have studied higher dimensional cosmology. In particular, in Kaluza-Klein (Kaluza 1921; Klein 1926) five dimensional geometry the extra dimension is used to couple the gravity and electromagnetism. Hence, Kaluza-Klein models gain importance. Kaluza-Klein cosmological models have been discussed by several authors in modified theories of gravity (Reddy and Lakshmi 2014; Sahoo et al. 2016; Santhi et al. 2016a; Naidu et al. 2018a; Reddy and Aditya 2018; Aditya and Reddy 2018b).

The above discussion motivates us to investigate Kaluza-Klein cosmological model in the presence of anisotropic DE fluid coupled with an attractive massive scalar field. The plan of this paper is the following: In Sect. 2, the Kaluza-Klein model and the field equations in the presence of anisotropic DE fluid and massive scalar field are derived. Section 3 presents the solution of the field equations and the model. Section 4 is devoted to compute all the dynamical parameters and to present physical discussion. In Sect. 5 the results are summarized with conclusions.

2 Basic field equations

Here we derive the basic field equations with the help of the Kaluza-Klein (KK) metric which is defined as

$$ ds^{2} = dt^{2} - A^{2} \bigl(dx^{2} + dy^{2} + dz^{2}\bigr) - B^{2} d\psi ^{2} $$
(1)

where \(A\), \(B \) are functions of cosmic time \(t\) and fifth coordinate \(\psi \) is space-like. Unlike Wesson (1983), here, the spatial curvature has been taken as zero (Gron 1988).

We consider the field equations in the normal gauge in Lyra manifold as

$$ R_{ij}-\frac{1}{2}g_{ij}R + \frac{3}{2}\biggl(d_{i}d_{j}- \frac{1}{2}g_{ij}d _{k}d^{k}\biggr)= -T_{ij} $$
(2)

where \(d_{i}\) is the displacement vector field of the manifold (function of time \(t\)) defines as

$$ d_{i}=\bigl[\beta (t),0,0,0\bigr] $$
(3)

here we assume gravitational units so that \(8\pi G = c = 1\). The other symbols have their usual meaning. \(T_{ij}\) is the energy-momentum tensor given by

$$ T_{ij}=T^{de}_{ij}+T^{s}_{ij} $$
(4)

where \(T^{de}_{ij}\) is the energy-momentum of DE given by

$$ T^{de}_{ij}=(\rho _{\varLambda }+ p_{\varLambda }) u_{i} u_{j} - p_{\varLambda }g_{ij}, \quad u_{i}u^{i}=1 $$
(5)

which can also be written as

$$ T^{de}_{ij}=\operatorname{diag}[\rho _{\varLambda },- p_{\varLambda },- p_{\varLambda },- p _{\varLambda }]. $$
(6)

We assume the anisotropic distribution of DE to ensure the present acceleration of Universe. Hence the energy-momentum tensor \(T^{de} _{ij}\) can be parameterized as

$$\begin{aligned} T^{de}_{ij} =&[1,-w_{x},-w_{y},-w_{z},-w_{\psi }] \rho _{\varLambda } \\ =&\bigl[1,-w_{\varLambda },-(w_{\varLambda }+\alpha ),-(w_{\varLambda }+ \gamma ),-(w _{\varLambda }+\delta )\bigr]\rho _{\varLambda } \end{aligned}$$
(7)

where \(\omega _{x}=\omega _{\varLambda }\), \(\omega _{y}=\omega _{\varLambda }+ \alpha \), \(\omega _{z}=\omega _{\varLambda }+\gamma \) and \(\omega _{\psi }= \omega _{\varLambda }+\delta \) are the directional equations of equation of state (EoS) parameters on \(x\), \(y\), \(z\) and \(\psi \) axes respectively. Here, \(\alpha \), \(\gamma \) and \(\delta \) are the deviations from \(\omega _{\varLambda }\) on \(y\), \(z\) and \(\psi \) axes respectively. \(p_{\varLambda }\) and \(\rho _{\varLambda }\) being the energy density and pressure of DE fluid, \(w_{\varLambda }= \frac{p_{\varLambda }}{\rho _{\varLambda }}\) is the EoS parameter of DE.

Also

$$ T^{(s)}_{ij} = \phi _{,i} \phi _{,j} - \frac{1}{2}\bigl(\phi _{,k} \phi ^{\prime \,k} - M^{2} \phi ^{2} \bigr) $$
(8)

where \(\phi \) is the massive scalar field, \(M\) is the mass of the scalar field (SF). This scalar field satisfies the Klein-Gordon equation, which is given by

$$ g^{ij} \phi _{;ij} + M^{2} \phi = 0. $$
(9)

With the use of Eqs. (3)–(9), the Lyra manifold field equations (2) for the KK metric (1), explicitly, can be derived as (we use co-moving coordinates)

$$\begin{aligned}& 3 \biggl(\frac{\dot{A}^{2}}{A} + \frac{\dot{A}\dot{B}}{AB} \biggr) - \rho _{\varLambda }- \frac{\dot{\phi }^{2}}{2} - \frac{M^{2} \phi ^{2}}{2} - \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(10)
$$\begin{aligned}& 2\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}}+2 \frac{\dot{A}\dot{B}}{AB}+\frac{\ddot{B}}{B}+w_{\varLambda }\rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2} \\& \quad-\frac{M^{2} \phi ^{2}}{2}+ \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(11)
$$\begin{aligned}& 2\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}}+2 \frac{\dot{A}\dot{B}}{AB}+\frac{\ddot{B}}{B}+(w_{\varLambda }+\alpha ) \rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2} \\& \quad-\frac{M^{2} \phi ^{2}}{2}+ \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(12)
$$\begin{aligned}& 2\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}}+2 \frac{\dot{A}\dot{B}}{AB}+\frac{\ddot{B}}{B}+(w_{\varLambda }+\gamma ) \rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2} \\& \quad-\frac{M^{2} \phi ^{2}}{2}+ \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(13)
$$\begin{aligned}& 3 \biggl(\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}} \biggr)+(w_{ \varLambda }+\delta ) \rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2}- \frac{M ^{2} \phi ^{2}}{2}+\frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(14)
$$\begin{aligned}& \ddot{\phi } +\dot{\phi } \biggl(3\frac{\dot{A}}{A} + \frac{\dot{B}}{B} \biggr) + M^{2} \phi = 0. \end{aligned}$$
(15)

Here an overhead dot indicates differentiation with respect to time \(t \).

The following cosmological parameters are useful to solve our field equations:

Spatial volume (\(V\)), average scale factor (\(a(t)\)), mean Hubble parameter (\(H\)) and scalar expansion (\(\theta \)) are given by

$$\begin{aligned}& V = a^{3}(t) = A^{3}B \end{aligned}$$
(16)
$$\begin{aligned}& H = \frac{\dot{a}}{a} = \frac{1}{4} \biggl(3\frac{\dot{A}}{A} +\frac{ \dot{B}}{B} \biggr) \end{aligned}$$
(17)
$$\begin{aligned}& \theta = 4 H = \biggl(3\frac{\dot{A}}{A} + \frac{\dot{B}}{B} \biggr). \end{aligned}$$
(18)

Shear scalar \(\sigma ^{2}\), average anisotropy parameter (\(\Delta \)) and deceleration parameter (DP) \(q\) are given by

$$\begin{aligned}& \sigma ^{2} = \frac{1}{2} \sigma ^{ij} \sigma _{ij} = \frac{1}{2} \biggl(\sum _{i=1}^{4} H_{i}^{2}-\frac{1}{3} \theta^{2} \biggr) \end{aligned}$$
(19)
$$\begin{aligned}& \Delta = \frac{1}{4} \sum _{i=1}^{4} \biggl(\frac{H_{i} - H}{H} \biggr) ^{2} \end{aligned}$$
(20)
$$\begin{aligned}& q = -1 + \frac{d}{dt} \biggl( \frac{1}{H} \biggr). \end{aligned}$$
(21)

The nature of expansion of the model can be explained using the DP. For positive value of DP, the model decelerates in the standard way. If DP vanishes then the model expands with constant rate. For \(-1\leq q<0\), we get accelerated expansion of the universe. The model exhibits an exponential expansion for \(q=-1\) and super exponential expansion for \(q<-1\).

3 Kaluza-Klein DE model

Here, we solve the field equations (10)–(15) and present Kaluza-Klein DE model within the framework of Lyra manifold in the presence of massive scalar field.

From Eqs. (11) and (12) we have

$$ \alpha = 0. $$
(22)

From Eqs. (12) and (13) we obtain

$$ \alpha = \gamma $$
(23)

consequently from Eqs. (22) and (23), we obtain

$$ \alpha = \gamma = 0. $$
(24)

This is because of the fact that the universe is isotropic in \(x\), \(y\) and \(z\) directions and hence the deviations from EoS of DE vanished.

Using Eq. (24) in Eqs. (10)–(15) reduce to the following independent equations

$$\begin{aligned}& 3 \biggl(\frac{\dot{A}^{2}}{A} + \frac{\dot{A}\dot{B}}{AB} \biggr) - \rho _{\varLambda }- \frac{\dot{\phi }^{2}}{2} - \frac{M^{2} \phi ^{2}}{2} - \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(25)
$$\begin{aligned}& 2\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}}+2 \frac{\dot{A}\dot{B}}{AB}+\frac{\ddot{B}}{B}+w_{\varLambda }\rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2} \\& \quad-\frac{M^{2} \phi ^{2}}{2}+ \frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(26)
$$\begin{aligned}& 3 \biggl(\frac{\ddot{A}}{A}+\frac{\dot{A}^{2}}{A^{2}} \biggr)+(w_{ \varLambda }+\delta ) \rho _{\varLambda }+\frac{\dot{\phi }^{2}}{2}- \frac{M ^{2} \phi ^{2}}{2}+\frac{3}{4}\beta ^{2} = 0 \end{aligned}$$
(27)
$$\begin{aligned}& \ddot{\phi } +\dot{\phi } \biggl(3 \frac{\dot{A}}{A} + \frac{\dot{B}}{B} \biggr) + M^{2} \phi = 0. \end{aligned}$$
(28)

Now Eqs. (25)–(28) are a system of four independent differential equations in seven unknowns (\(A, B, \phi , \rho _{\varLambda }, w_{\varLambda }, \delta \) and \(\beta \)). Hence, we are free to choose three more mathematical or physical conditions to find a deterministic model. We choose the following conditions:

  1. (i)

    We use the fact that expansion scalar \(\theta \) is proportional to shear scalar \(\sigma ^{2}\), so that we have (Collins et al. 1980) a relation between the metric potentials as follows:

    $$\begin{aligned} A = B^{n} \end{aligned}$$
    (29)

    where \(n\) is a positive constant which retains the anisotropy of the space-time. The motivation behind considering this relation is explained by Thorne (1967). Observations from the velocity-red-shift relation for extragalactic sources suggest that Hubble expansion of the universe is isotropic at present within \(\approx 30\) per cent (Kantowski and Sachs 1966; Kristian and Sachs 1966). In particular, the studies of red-shift survey place the limit as

    $$ \frac{\sigma }{H}\leq 0.3, $$
    (30)

    in the neighborhood of our present day Galaxy. Collins et al. (1980) have shown that the normal congruence to the homogeneous expansion satisfies the condition \(\frac{\sigma }{H}\) is constant.

  2. (ii)

    In recent years, it is quite natural to use a power-law relation between scalar field \(\phi \) and average scale factor \(a(t)\) of the form (Johri and Sudharsan 1989; Johri and Desikan 1994)

    $$\begin{aligned} \phi \propto \bigl[a(t)\bigr]^{m} \end{aligned}$$
    (31)

    where \(m\) is a power index. Several researchers have studied different aspects of this form of scalar field \(\phi \) (Rao et al. 2015; Santhi et al. 2016b; Aditya and Reddy 2018b). In view of the physical importance of above relation, here we assume the following assumption to reduce the mathematical complexity of the system

    $$ \frac{\dot{\phi }}{\phi }=-(3n+1)\frac{\dot{B}}{B}. $$
    (32)

    This is a consequence of Eq. (31). This relation (32) has been already taken by many authors and have constructed cosmological models using this relation. Singh (2005), Singh and Rani (2015), Aditya and Reddy (2018a, 2019) and Naidu et al. (2019) have studied Bianchi type cosmological models with massive scalar fields using the above relation (32).

  3. (iii)

    In addition to the above, we have taken a power law relation between \(\beta (t)\), the displacement vector field and average scale factor \(a(t)\) given by

    $$ \beta (t) = \beta _{0} \bigl[a(t) \bigr]^{k} $$
    (33)

    where \(\beta _{0}\neq 0\) and \(k\) are positive constants.

Now from Eqs. (28)–(32) we get

$$ \phi = \exp \biggl(\phi _{0} t - \frac{M^{2} t^{2}}{2} + \phi _{1} \biggr) $$
(34)

where \(\phi _{0}\) and \(\phi _{1}\) are constants of integration.

Equations (32) and (33) together yield

$$ \begin{aligned} &A = \exp \biggl(\frac{n(M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1})}{2(3n+1)} \biggr), \\ &B = \exp \biggl(\frac{M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1}}{2(3n+1)} \biggr). \end{aligned} $$
(35)

Using Eq. (35) in Eq. (1), the Kaluza-Klein model in the presence of massive scalar field is given by

$$\begin{aligned} ds^{2} =& dt^{2} - \exp \biggl(\frac{n(M^{2} t^{2} - 2\phi _{0} t - 2 \phi _{1})}{3n+1} \biggr) \\ &{}\times\bigl(dx^{2} + dy^{2} + dz^{2}\bigr) \\ &{}- \exp \biggl(\frac{M ^{2} t^{2} - 2\phi _{0} t - 2\phi _{1}}{3n+1} \biggr) d\psi ^{2} \end{aligned}$$
(36)

and the massive scalar field in the model is given by Eq. (34).

4 Dynamical parameters of the model

Dynamical or cosmological parameters (16)–(21) have a significant role in the discussion of the cosmological models of the universe. Hence we evaluate them and present here

$$\begin{aligned}& V = \exp \biggl(\frac{M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1}}{2} \biggr) \end{aligned}$$
(37)
$$\begin{aligned}& H = \biggl(\frac{M^{2} t - \phi _{0}}{3} \biggr) \end{aligned}$$
(38)
$$\begin{aligned}& \theta = M^{2} t - \phi _{0} \end{aligned}$$
(39)
$$\begin{aligned}& \sigma ^{2} = \frac{1}{2} \biggl(\frac{M^{2} t - \phi _{0}}{3n+1} \biggr) ^{2} (n-1)^{2} \end{aligned}$$
(40)
$$\begin{aligned}& \Delta = \frac{9 n^{2} - 12 n +7}{4 (3n+1)^{2}} \end{aligned}$$
(41)
$$\begin{aligned}& q = - \biggl(1 + \frac{3 M^{2}}{(M^{2} t - \phi _{0})^{2}} \biggr). \end{aligned}$$
(42)

Now from Eqs. (16), (34) and (35) we get

$$ \beta (t) = \beta _{0} \exp \biggl( \frac{k(M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1})}{6} \biggr). $$
(43)

Now from Eqs. (25)–(27), (33), (35) and (43) we obtain energy density \(\rho _{\varLambda }\), EoS parameter \(\omega _{\varLambda }\) of DE and skewness parameter \(\delta \) as

$$\begin{aligned}& \rho _{\varLambda }= \frac{n (4n+1)}{(3n+1)^{2}} \bigl(M^{2} t - \phi _{0} \bigr)^{2} \\& \phantom{\rho _{\varLambda }=} - \biggl[\frac{(M^{2} t - \phi _{0})^{2} + M^{2}}{2} \biggr] \exp \bigl(2 \phi _{0} t - M^{2} t^{2}+ 2\phi _{1} \bigr) \\& \phantom{\rho _{\varLambda }=} - \frac{3}{4}\beta _{0}^{2} \exp \biggl( \frac{k(M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1})}{6} \biggr). \end{aligned}$$
(44)
$$\begin{aligned}& w_{\varLambda } =-\frac{1}{\rho _{\varLambda }} \biggl\{ \frac{2n (n+1)(M ^{2} t - \phi _{0})^{2}}{(3n+1)^{2}} + \frac{n M^{2}}{3n+1} \\& \phantom{w_{\varLambda } =}+ \biggl[\frac{(M ^{2} t - \phi _{0})^{2} - M^{2}}{2} \biggr]\exp \bigl(2\phi _{0} t - M ^{2} t^{2} + 2\phi _{1} \bigr) \\& \phantom{w_{\varLambda } =}+ \frac{3}{4}\beta _{0}^{2} \exp \biggl( \frac{k(M^{2} t^{2} - 2\phi _{0} t - 2\phi _{1})}{6} \biggr) \biggr\} \end{aligned}$$
(45)
$$\begin{aligned}& \delta =\frac{n (1-3n)}{\rho _{\varLambda }(3n+1)^{2}} \bigl[M^{2}- \bigl(M^{2} t - \phi _{0}\bigr)^{2} \bigr], \end{aligned}$$
(46)

where \(\rho _{\varLambda }\) is given by Eq. (44).

Several DE models have been formulated for analyzing the DE phenomenon in the accelerated expansion of the universe. Hence there is a need to distinguish these DE models so that one can decide which DE model provides good explanation for the present status of the universe. Because of the fact that various DE models give almost the same present values of the deceleration and Hubble parameters. Hence, these parameters can not differentiate the DE models completely. For this reason, Sahni et al. (2003) have introduced two new dimensionless parameters known as statefinders defined as follows:

$$ r = \frac{\dddot{a}}{aH^{3}}, \qquad s= \frac{r-1}{3 (q-\frac{1}{2} )}. $$

For our model the above parameters are obtained as

$$\begin{aligned}& r = 1 + \frac{27M^{2}}{(M^{2} t - \phi _{0})^{2}} \end{aligned}$$
(47)
$$\begin{aligned}& s= \frac{-6M^{2}}{(M^{2} t - \phi _{0})^{2} + M^{2}}. \end{aligned}$$
(48)

For \((r, s) = (1, 0), (1, 1)\) we obtain \(\varLambda CDM\) and \(CDM\) limits, respectively. However, \(s>0\) and \(r<1\) shows the DE regions such as phantom and quintessence-like, \(s<0\) and \(r>1\) indicate the Chaplygin gas. Recently, many authors have investigated the statefinders analysis with different geometries (Jawad 2014; Singh and Kumar 2016; Santhi et al. 2017; Naidu et al. 2018b; Sharma and Pradhan 2019).

5 Physical discussion

Here, we have obtained Kaluza-Klein DE universe (Eq. (36)) in the presence of attractive massive scalar field in the framework of Lyra manifold. It can be seen that the volume of our model is non-zero at \(t=0\), i.e., the model is free from the initial singularity. It is clear from Eq. (25) that the volume of the model is exponential function, hence the model exhibits an exponential expansion from a finite volume as \(t\) increases. Also, it is observed that the physical parameters \(H, \theta , \sigma ^{2}\) are finite at \(t=0\) and they tend to infinity as \(t\rightarrow \infty \). We observed that the anisotropy parameter \(\Delta \) is independent of the time \(t\). Hence the universe is uniform and spatially homogeneous. In Fig. 1, we have plotted the behavior of displacement vector \(\beta \) versus redshift \(z\) for different values of \(\phi _{0}\). It can be seen form Fig. 1 that \(\beta \) is a decreasing and positive function. The function \(\beta (t)\) decreases with increase in \(\phi _{0}\).

Fig. 1
figure 1

Plot of \(\beta (t)\) versus redshift \(z\) for \(M=1.5\), \(k=0.18\), \(\phi _{1}=10\), \(n=0.9\) and \(\beta _{0}=0.01\)

Full size image

In order to study the behavior of physical parameters we have plotted them in terms of cosmological redshift \(z\). We used the relation between the redshift \(z\) and the average scale factor \(a(t)\) as \(1+z=\frac{a _{0}}{a}\). We consider the present value of average scale factor \(a_{0}\) which has been normalized to one.

Scalar field: In Fig. 2, we have plotted the behavior of massive scalar field \(\phi \) versus redshift \(z\) for different values of \(\phi _{0}\). We observed that \(\phi \) is positive and increasing function for all the three values of \(\phi _{0}\). We, also, observe that the scalar field increases as \(\phi _{0}\) increases. It can be observed that the scalar field shows increasing behavior and hence we can conclude that the corresponding kinetic energy decreases. The massive scalar field shows rapid increase from very low values and approaches maximum value. This behavior is quite similar to the behavior of exponential potential which correspond to cosmological scaling solutions obtained by Copeland et al. (2006) and interacting modified ghost SF models of DE constructed by Jawad (2015).

Fig. 2
figure 2

Plot of scalar field versus redshift \(z\) for \(M=1.5\), \(k=0.18\), \(\phi _{1}=10\), \(n=0.9\) and \(\beta _{0}=0.01\)

Full size image

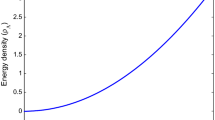
Energy density: Fig. 3 depicts the behavior of energy density of DE \(\rho _{\varLambda }\) versus redshift \(z\). It can be observed that \(\rho _{\varLambda }\) is positive and decreasing function. Also, \(\rho _{\varLambda }\) increases as the SF increases.

Fig. 3
figure 3

Plot of energy density \(\rho _{\varLambda }\) versus redshift \(z\) for \(M=1.5\), \(k=0.18\), \(\phi _{1}=10\), \(n=0.9\) and \(\beta _{0}=0.01\)

Full size image

EoS parameter: The EoS parameter of fluid relates its pressure \(p\) and energy density \(\rho \) by the relation, \(w=\frac{p}{ \rho }\). Different values of EoS parameter correspond to various epochs of the universe from early decelerating to present accelerating expansion phases. It includes stiff fluid, radiation and matter dominated (dust) for \(w =1\), \(w =\frac{1}{3}\) and \(w=0\) (decelerating phases) respectively. Also, it represents quintessence for \(-1< w<-1/3\), cosmological constant (vacuum) for \(w=-1\) and phantom for \(w<-1\). Figure 4 describes the behavior of EoS parameter of DE versus redshift for various values of \(\phi _{0}\). It is observed that for all the three values of \(\phi _{0}\) the model starts in quintessence region \(-1< w _{\varLambda }<-1/3\), crosses the phantom divided line \(w _{\varLambda }=-1\) at late times and approaches the aggressive phantom region \(w _{\varLambda } \ll -1\). Also, as scalar field increases the EoS parameter of our DE model approaches the quintessence region. The trajectories of EoS parameter of DE model coincide with the Planks collaboration (Ade et al. 2014) and WMAP nine years observational data (Hinshaw et al. 2013) which give the ranges for EoS parameter as

$$\begin{aligned}& -0.92\leq w _{\varLambda}\leq -1.26 \quad (\text{Planck} + \text{WP} + \text{Union~2.1}), \\& -0.89\leq w _{\varLambda}\leq -1.38 \quad (\text{Planck} + \text{WP} + \text{BAO}), \\& -0.983\leq w_{\varLambda}\leq -1.162 \quad (\text{WMAP} {+} \text{eCMB} {+} \text{BAO} {+} H_{0}). \end{aligned}$$

Skewness parameter: The physical significance of skewness parameters is that the amount of anisotropy in the DE fluid. Here the surviving skewness parameter \(\delta \) is depicted in Fig. 5 for various values of \(\phi _{0}\). We observed that the skewness parameter is positive in the initial epoch and attains a negative value at late times. We can conclude that the DE in our model is anisotropic throughout the evolution of the universe and hence it helps to study the anisotropies at small angular scales which play a key role in the formation of large scale structures of the universe.

Fig. 4
figure 4

Plot of EoS parameter versus redshift \(z\) for \(M=1.5\), \(k=0.18\), \(\phi _{1}=10\), \(n=0.9\) and \(\beta _{0}=0.01\)

Full size image
Fig. 5
figure 5

Plot of skewness parameter versus redshift \(z\) for \(M=1.5\), \(k=0.18\), \(\phi _{1}=10\), \(n=0.9\) and \(\beta _{0}=0.01\)

Full size image

Deceleration parameter: The nature of expansion of the model can be explained using the deceleration parameter (DP). For example, the model decelerates in the standard way for positive value of DP and the model expands with constant rate as DP vanishes. The model exhibits accelerated expansion for \(-1\leq q<0\), an exponential expansion for \(q=-1\) and super exponential expansion for \(q<-1\). Figure 6 describes the behavior of DP versus redshift \(z\) for various values of \(\phi _{0}\). We observe that DP remains less than −1 and hence we obtain a universe with exponential expansion. Also, it can be seen that the model approaches super exponential expansion for \(q<-1\). It can be seen that as EoS parameter of our model attains aggressive phantom region (\(w _{de}\ll -1\)) hence we get super exponential expansion. Also, as \(q<-1\) the model expands with super exponential expansion. The same phenomenon occurred in our model.

Fig. 6
figure 6

Plot of deceleration parameter versus redshift \(z\) for \(M=1.5\)

Full size image

Satefinders: In order to verify the viability of various DE models statefinder parameters \((r,s)\) are proposed. These represent well-known DE regions which are given as follows: \((r, s) = (1, 0), (1, 1)\) represent the \(\varLambda CDM\) and \(CDM\) limit, respectively. However, \(s>0\) and \(r<1\) shows the DE regions such as phantom and quintessence-like, \(s<0\) and \(r>1\) indicate the Chaplygin gas. In the present study, we develop \(r-s\) plane for \(\phi _{0}=0.5\) is shown in Fig. 7. It can be seen that our DE model corresponds to \(\varLambda CDM\) limit (\((r,s)=(1,0)\)) at late times which is in accordance with the recent observational data. Also, it can be observed that the \(r\)-\(s\) plane correspond to Chaplygin gas model.

Fig. 7
figure 7

Plot of \(r\) versus \(s\) for \(M=1.5\) and \(\phi _{0}=0.5\)

Full size image

6 Conclusion

In this work, we have constructed Kaluza-Klein DE model with massive scalar field within the framework of Lyra manifold. In order to obtain a deterministic solution of the field equations we have used various physically valid conditions. We have computed all the cosmological and kinematical parameters and discussed their physical significance in the light of the present cosmological scenario and observations. We summarize our results as follows:

Our Kaluza-Klein DE model with massive scalar field is non-singular and from a finite volume the model exhibits an exponential expansion leading to early inflation. The deceleration parameter also confirms that our model starts with exponential expansion (inflation) and attains a super exponential expansion at late times. The average anisotropy parameter is constant, the model is uniform throughout and homogeneous. Due to the exponential expansion of the model, all the physical quantities of the model are finite initially and approach to infinity at late times. The massive scalar field of our model is positive throughout the evolution of the universe and increases rapidly at present epoch. The behavior of massive scalar field in our DE model is quite similar to the behavior of exponential potential which correspond to cosmological scaling solutions obtained by Copeland et al. (2006) and interacting modified ghost SF models of DE constructed by Jawad (2015). Statefinders plane (r-s plane) analysis shows that the model finally approaches to \(\varLambda CDM\) limit which is in accordance with the recent observations and also our DE model corresponds to Chaplygin gas model. The energy density \(\rho _{\varLambda }\) of our model is always positive and decreasing function. It can be seen from the analysis of EoS parameter that the model starts in the quintessence region (\(-1< w _{\varLambda }<-1/3\)), crosses the phantom divided line and finally approaches to aggressive phantom region. We observed that the skewness parameter is positive in the initial epoch and attains a negative value at late times. We can conclude that the DE in our model is anisotropic throughout the evolution of the universe and hence it helps to study the anisotropies at small angular scales which are play a key role in the formation of large scale structures of the universe. In our model, it is observed that the massive scalar field influences all the physical parameters of the model at minimum scale. We hope and believe that the higher dimensional massive scalar field model in Lyra manifold will help to have a better insight into the understanding of DE which is responsible for cosmic acceleration.