1 Introduction

One of the outstanding developments in relativistic cosmology is the discovery of the accelerated expansion of the universe. It is believed that the reason for the accelerated expansion of the universe could be dark energy (DE), which is still a cosmological mystery. The concept of DE refers to a kind of exotic energy with negative pressure that has been proposed to explain the current accelerated expansion of the universe [1,2,3,4]. The thermodynamical studies reveal that the constituents of the DE may be massless particles (bosons and fermions) whose collective behaviors resemble with a kind of radiation fluid having negative pressure. The DE has been conventionally characterized by the equation of state (EoS) parameter \(\omega _{\Lambda }= \frac{p_{\Lambda }}{\rho _{\Lambda }}\), which is not necessarily a constant, \(p_{\Lambda }\) being the pressure and \(\rho _{\Lambda }\) is the energy density of the matter filling the space-time. The simplest candidate of DE is the cosmological constant \(\Lambda\) for which \(\omega _{\Lambda }=-1\). Different forms of dynamically changing DE with EoS parameter have been proposed so far such as \(\omega _{\Lambda } >-1\) for quintessence and as \(\omega _{\Lambda }<-1\) for phantom energy. The value \(\omega _{\Lambda } <-\frac{1}{3}\) is necessary for cosmic acceleration. Bamba et al. [5] have reviewed different DE isotropic cosmologies with early deceleration and late time acceleration.

Koivisto and Mota [6] have presented a cosmological model where the acceleration of the universe is driven by a fluid with an anisotropic EoS parameter by introducing skewness parameter to quantify the deviation of pressure from isotropy. Adhav et al. [7] have discussed the nature of anisotropic behavior of DE for a Bianchi type-\(\hbox {VI}_{0}\) space-time. Pradhan [8] has discussed accelerating DE models of Bianchi type-\(\hbox {VI}_{0}\) with an anisotropic fluid. Samanta [9] has investigated Bianchi type-III cosmological models within the framework of Lyra geometry with the assumptions on the anisotropy of the fluid, power-law and exponential volumetric expansion law. Many researchers have studied spatially homogeneous Bianchi type models with DE in general relativity within the framework of Lyra manifold in different physical contexts.

The limitations of general relativity in providing satisfactory explanation of the phases of the universe in its evolution have led researchers to adopt various hypothesis and study their implications in this context. These hypotheses include those assigning other geometric or physical fields with the universe. Such theories are expected to bring out a number of mathematical and physical aspects associated with them. As Einstein’s theory of general relativity is based on the geometrical description of gravitation, many researchers have generalized the idea of geometrizing the gravitation to include a geometrical description of electromagnetism. For the purpose of unification of gravitation, electromagnetic fields and some other fields, modifications to Riemannian geometry have been carried out. Lyra [10] has suggested one such modification to incorporate a gauge function into the structureless manifold giving rise to a displacement field. Halford [11] discussed Robertson–Walker models in Lyra geometry with a time-independent gauge function. Several researchers [12,13,14] have investigated cosmological models with time-dependent displacement vector field . Singh and Shri Ram [15] presented exact solutions of Einstein’s field equations in vacuum and in the presence of stiff matter in the normal gauge considering the time-dependent displacement for a Bianchi type-I metric. Shri Ram et al. [16] have obtained spatially homogeneous and anisotropic Bianchi type-V models filled with an imperfect fluid with bulk viscosity and heat conduction in Lyra geometry. Several researchers have investigated solutions of the field equations in general relativity and cosmology with time-independent and time-dependent displacement vector field in different physical contexts.

The study of interacting fields, one of the fields being the scalar field, is basically an attempt to look into yet unsolved problem of the unification of gravitational and quantum theories. In fact there are two types of scalar fields, namely zero-rest-mass scalar fields and massive scalar fields. The zero-rest-mass scalar fields represent long range interactions while massive scalar fields describe short range interaction. Considerable interest has been focused on a set of field equations representing scalar fields coupled with gravitational fields for the last few decades. Bergmann and Leipnik [17], Brahmachary [18] have investigated spherically symmetric zero-rest-mass scalar fields. Penney [19] and Gautreau [20] have extended the study to the axially symmetric fields and have found that the scalar fields obey flat space Laplace equations. Several researchers have studied various aspects of interacting fields in the framework of general relativity [21,22,23,24,25,26]. Mohanty and Pradhan [27] have discussed some non-static solutions of Einstein’s field equations in the presence of viscous fluid and attractive massive scalar fields. Singh and Shri Ram [28] have presented plane symmetric cosmological models with viscous fluid and massive scalar field. Singh [29] has discussed Bianchi type-V cosmologies in Lyra geometry in the presence of massive scalar field. Singh and Rani [30] have investigated Bianchi type-III cosmological models in Lyra geometry in the presence of massive scalar field. Subsequently, Reddy et al. [31] have discussed the dynamics of Bianchi type-II anisotropic DE cosmological model in the presence of zero-rest-mass scalar field. Aditya et al. [32] have investigated Kaluza–Klein DE model in Lyra geometry in the presence of massive scalar field. Deniel Raju et al. [33] have studied a spatially homogeneous Bianchi type-III DE cosmological model with massive scalar field.

Motivated from above studies, we present in this paper a spatially homogeneous Bianchi type-\(\hbox {VI}_{0}\) DE cosmological model with massive scalar field within the framework of Lyra geometry.

2 Metric and field equations

The diagonal form of the metric of spatially homogeneous and anisotropic Bianchi type-\(\hbox {VI}_{0}\) is taken of the form

$$\begin{aligned} \mathrm{d}s^{2}=\mathrm{d}t^{2}-A^{2}\mathrm{d}x^{2}-e^{-2mx} B^{2}\mathrm{d}y^{2}-e^{2mx} C^{2} \mathrm{d}z^{2} \end{aligned}$$
(1)

where A, B, C are functions of cosmic time t only and m is a constant parameter.

In general relativity the field equations in the normal gauge in Lyra manifold are given by

$$\begin{aligned} R_{ij}-\frac{1}{2}R g_{ij} +\frac{3}{2}\left( d_{i}d_{j}-\frac{1}{2}g_{ij}d_{k}d^{k}\right) =-T_{ij} \end{aligned}$$
(2)

where \(d_{i}\) is the displacement vector field of the Lyra manifold defined as

$$\begin{aligned} d_{i}=[\beta (t), 0, 0, 0]. \end{aligned}$$
(3)

Here we assume gravitational units so that \(8 \pi G=c=1\). The other symbols have their usual meaning. \(T_{ij}\) is energy-momentum tensor given by

$$\begin{aligned} T_{ij}= T_{ij}^{\text {(de)}}+T_{ij}^{\text {(s)}} \end{aligned}$$
(4)

where \(T_{ij}^{\text {(de)}}\) is the energy-momentum tensor of DE given by

$$\begin{aligned} T_{ij}^{\text {(de)}}=(\rho _{\Lambda }+p_{\Lambda }) u_{i}u_{j}-p_{\Lambda } g_{ij}, u^{i}u_{i}=1 \end{aligned}$$
(5)

which can also be written as

$$\begin{aligned} T_{ij}^{\text {(de)})}= \text { diag}[\rho _{\Lambda }, -p_{\Lambda }, -p_{\Lambda }, -p_{\Lambda }]. \end{aligned}$$
(6)

We assume anisotropic distribution of DE to ensure the present acceleration of the universe. Hence the energy-momentum tensor can be parameterized as

$$\begin{aligned} T_{ij}^{\text {(de)}}= & {} \text { diag} [1, -\omega _{x}, -\omega _{y}, -\omega _{z}] \rho _{\Lambda } \nonumber \\= & {} \text { diag} [ 1, -\omega _{\Lambda }, -(\omega _{\Lambda }+\gamma ), -(\omega _{{\Lambda }}+\delta )]\rho _{\Lambda } \end{aligned}$$
(7)

where \(\omega _{x}=\omega _{\Lambda }\), \(\omega _{y}=\omega _{\Lambda }+\gamma\) and \(\omega _{z}=\omega _{{\Lambda }}+\delta\) are the directional equation of state (EoS) parameters on x, y and z axes, respectively. Here \(\gamma\) and \(\delta\) are deviations from \(\omega _{\Lambda }\) on y and z, respectively.

The energy-momentum tensor \(T^{(s)}_{ij}\) for the massive scalar field is given by

$$\begin{aligned} T^{(s)}_{ij}= \phi _{, i} \phi _{, j}-\frac{1}{2} g_{ij} (\phi _{, k} \phi ^{, k}-M^2\phi ^2) \end{aligned}$$
(8)

where M is the mass of scalar field \(\phi\). The scalar function \(\phi\) satisfies the Klein–Gordon equation

$$\begin{aligned} g^{ij} \phi _{; ij}+ M^{2} \phi =0. \end{aligned}$$
(9)

Here a comma stands for ordinary derivative and semi-colon denotes covariant derivative.

Now, using comoving coordinates and Eqs. (3)–(9), the field equations (2) for the metric (1) can be written as

$$\begin{aligned}&\frac{{\ddot{B}}}{B}+ \frac{{\ddot{C}}}{C}+\frac{{\dot{B}}}{B}\frac{{\dot{C}}}{C}+\frac{m^{2}}{A^{2}}+\frac{3}{4} \beta ^{2}= -\omega _{\Lambda }\rho _{\Lambda }-\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+ \frac{{\ddot{C}}}{C}+\frac{{\dot{A}}}{A}\frac{{\dot{C}}}{C}-\frac{m^{2}}{A^{2}}+\frac{3}{4} \beta ^{2}= -(\omega _{\Lambda }+\gamma )\rho _{\Lambda }-\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(11)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+ \frac{{\ddot{B}}}{B}+\frac{{\dot{A}}{\dot{B}}}{AB}-\frac{m^{2}}{A^{2}}+\frac{3}{4} \beta ^{2}= -(\omega _{\Lambda }+\delta )\rho _{\Lambda }-\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{{\dot{A}}}{A}\frac{{\dot{B}}}{B}+ \frac{{\dot{A}}}{A}\frac{{\dot{C}}}{C}+ \frac{{\dot{B}}}{B}\frac{{\dot{C}}}{C}-\frac{m^{2}}{A^{2}}-\frac{3}{4} \beta ^{2}= \rho _{\Lambda }+\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{{\dot{B}}}{B}-\frac{{\dot{C}}}{C}=0, \end{aligned}$$
(14)
$$\begin{aligned}&\ddot{\phi }+{\dot{\phi }}\left( \frac{{\dot{A}}}{A}+\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}\right) +M^{2} \phi =0. \end{aligned}$$
(15)

The conservation law for energy momentum tensor gives

$$\begin{aligned} \left( \dot{\rho _{\Lambda }}+\frac{3}{2}\beta {\dot{\beta }}\right) +\left( \rho _{\Lambda }+p_{\Lambda }+\frac{3}{2}\beta ^2\right) \left( \frac{{\dot{A}}}{A}+\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}\right) =0. \end{aligned}$$
(16)

This equation can be split up into two equations

$$\begin{aligned}&{\dot{\beta }}+\left( \frac{{\dot{A}}}{A}+\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}\right) \beta =0, \end{aligned}$$
(17)
$$\begin{aligned}&\dot{\rho _{\Lambda }}+\left( \frac{{\dot{A}}}{A}+\frac{{\dot{B}}}{B}+\frac{{\dot{C}}}{C}\right) (\rho _{\Lambda }+p_{\Lambda }) =0. \end{aligned}$$
(18)

Here an overhead dot denotes derivative with respect to cosmic time t.

We now define some physical and kinematical parameters which are important in cosmological observations. The spatial volume V and average scale factor a are defined as

$$\begin{aligned} V=a^{3}=ABC. \end{aligned}$$
(19)

The anisotropy parameter \(A_{m}\) of the expansion is characterized by the directional Hubble parameters, and mean Hubble parameter is given as

$$\begin{aligned} A_{m}= \frac{1}{3}\sum _{i=1}^{3} \left( \frac{H_{i}-H}{H}\right) ^{2}. \end{aligned}$$
(20)

where \(H_{1}\), \(H_{2}\) and \(H_{3}\) are directional Hubble parameters in the direction of x, y and z-axes, respectively, and H is the mean Hubble parameter defined as

$$\begin{aligned} H_{1}=\frac{{\dot{A}}}{A},\; H_{2}= \frac{{\dot{B}}}{B} \; \text {and}\; H_{3}= \frac{{\dot{C}}}{C} \end{aligned}$$
(21)

and

$$\begin{aligned} H=\frac{1}{3} \left( H_{1}+H_{2}+H_{3}\right) \end{aligned}$$
(22)

The expansion scalar \(\theta\) and shear scalar \(\sigma ^2\) are defined as

$$\begin{aligned}&\theta =3H, \end{aligned}$$
(23)
$$\begin{aligned}&\sigma ^{2}=\frac{1}{2}\left( \sum _{i=1}^{3} H^2_{i}-3H^2\right) . \end{aligned}$$
(24)

An important observational quantity in cosmology is the deceleration parameter q defined as

$$\begin{aligned} q=\frac{-a\ddot{a}}{\dot{a}^2}=-1+\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{H}\right) . \end{aligned}$$
(25)

The sign of q indicates whether the model inflates or not. The positive sign of q corresponds to decelerating model, whereas the negative sign indicates inflation.

3 Exact solution of field equations and model

In this section, we obtain exact solutions of the field equations (10)–(18) and present the dark energy cosmological model in Lyra geometry.

On integration, Eq. (14) yields

$$\begin{aligned} B=kC \end{aligned}$$
(26)

where k is a constant of integration which can be taken as unity. Using \(B=C\), in the system of Eq. (10)–(18), we obtain

$$\begin{aligned}&2\frac{{\ddot{B}}}{B}+\frac{{\dot{B}}^{2}}{B^{2}}+\frac{m^{2}}{A^{2}}+\frac{3}{4} \beta ^{2}= -\omega _{\Lambda }\rho _{\Lambda }-\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(27)
$$\begin{aligned}&\frac{{\ddot{A}}}{A}+ \frac{{\ddot{B}}}{B}+\frac{{\dot{A}}}{A}\frac{{\dot{B}}}{B}-\frac{m^{2}}{A^{2}}+\frac{3}{4} \beta ^{2}= -(\omega _{\Lambda }+\delta )\rho _{\Lambda }-\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(28)
$$\begin{aligned}&2\frac{{\dot{A}}}{A}\frac{{\dot{B}}}{B}+ \frac{{\dot{B}}^{2}}{B^{2}}-\frac{m^{2}}{A^{2}}-\frac{3}{4} \beta ^{2}= \rho _{\Lambda }+\frac{{\dot{\phi }}^{2}}{2}+\frac{M^{2}\phi ^{2}}{2}, \end{aligned}$$
(29)
$$\begin{aligned}&\ddot{\phi }+{\dot{\phi }}\left( \frac{{\dot{A}}}{A}+\frac{{\dot{2B}}}{B}\right) +M^{2} \phi =0, \end{aligned}$$
(30)
$$\begin{aligned}&{\dot{\beta }}+\left( \frac{{\dot{A}}}{A}+\frac{{\dot{2B}}}{B}\right) \beta =0, \end{aligned}$$
(31)
$$\begin{aligned}&\dot{\rho _{\Lambda }}+\left( \frac{{\dot{A}}}{A}+\frac{2{\dot{B}}}{B}\right) (\rho _{\Lambda }+p_{\Lambda })=0 \end{aligned}$$
(32)

where we have taken \(\gamma =\delta\) in Eqs. (11) and (12) as these equations are identical.

Equations (27)–(31) are a set of five independent equations in seven unknowns A, B, \(\rho _{\Lambda }\), \(\omega _{\Lambda }\), \(\delta\), \(\beta\) and \(\phi\). Equation (32) is the consequence of field equations. Hence to obtain a deterministic solutions of these equations, we need two supplementary conditions.

We first assume that the shear scalar \(\sigma\) is proportional to the expansion scalar \(\theta\). According to Thorne [34], observations of velocity red-shift relation for extragalactic sources suggest that the Hubble expansion of the universe is isotropic today within 30% [35, 36]. More concisely, the red-shift studies place the limit \(\frac{\sigma }{H}\le 0.3\), the ratio of the shear to the Hubble parameter in the neighborhood of our galaxy today. Collins et al. [37] pointed out that for spatially homogeneous metric, the condition \(\frac{\sigma }{\theta } = constant\) has been verified by normal congruence to the homogeneous hypersurface. Also, it has been proposed by many other researchers [38, 39] and this condition leads to

$$\begin{aligned} A=B^{n} \end{aligned}$$
(33)

where \(n\ne 1\) is a positive constant.

To solve this complicated system of equations, we need one more supplementary constraint equation consisting of these parameters. To get the purpose solved, we assume the mathematical condition (Singh and Rani [30]):

$$\begin{aligned} (n+2)\frac{{\dot{B}}}{B}=-\frac{{\dot{\phi }}}{\phi } \end{aligned}$$
(34)

Equations (15) and (34) yield

$$\begin{aligned} \frac{\ddot{\phi }}{\phi }-\frac{{\dot{\phi }}^{2}}{\phi ^{2}}=-M^{2}. \end{aligned}$$
(35)

The general solution of Eq. (35) is given by

$$\begin{aligned} \phi =\exp {\left[ \phi _{0} t+\phi _{1}-\frac{M^{2}t^{2}}{2}\right] } \end{aligned}$$
(36)

where \(\phi _{0}\) and \(\phi _{1}\) are arbitrary constants. Using Eq. (36) in Eq. (34) and integrating, we obtain

$$\begin{aligned} B=\exp {\left[ \frac{(M^{2}t^{2}-2\phi _{0} t-2\phi _{1})}{2(n+2)}\right] }. \end{aligned}$$
(37)

Equations (33) and (37) together yield

$$\begin{aligned} A=\exp {\left[ \frac{n(M^{2}t^{2}-2\phi _{0} t-2\phi _{1})}{2(n+2)}\right] }. \end{aligned}$$
(38)

Now, using Eqs. (37) and (38) in Eq. (1), we can write the Bianchi type-\(\hbox {VI}_{0}\) model in the present case as

$$\begin{aligned}&\mathrm{d}s^{2}= \mathrm{d}t^{2}-\exp {\left[ \frac{n(M^{2}t^{2}-2\phi _{0} t-2\phi _{1})}{(n+2)}\right] } \mathrm{d}x^{2}\nonumber \\&\qquad -\exp {\left[ \frac{(M^{2}t^{2}-2\phi _{0} t-2\phi _{1})}{(n+2)}\right] }\nonumber \\&\quad \times \left( e^{-2mx}\mathrm{d}y^{2}+e^{2mx}\mathrm{d}z^{2}\right) \end{aligned}$$
(39)

with the massive scalar field given by Eq. (36).

4 Kinematical parameters of the model

In this section, we compute the values of the kinematical parameters of the model (37) which play a significant role in the discussion of the cosmological model of the universe.

The spatial volume in the model is given by

$$\begin{aligned} V=a^{3}=\exp {\left[ \frac{(M^{2}t^{2}-2\phi _{0} t-2\phi _{1})}{2}\right] }, \end{aligned}$$
(40)

The directional and average Hubble parameters in the model are given by

$$\begin{aligned} H_{1}=n\left( \frac{M^{2}t-\phi _{0}}{n+2}\right) , H_{2}=H_{3}=\left( \frac{M^{2}t-\phi _{0}}{n+2}\right) \end{aligned}$$
(41)

and

$$\begin{aligned} H=\frac{1}{3}(M^{2}t-\phi _{0}). \end{aligned}$$
(42)

The expansion scalar \(\theta\), shear scalar and anisotropy parameter associated with expansion in the model are obtained as

$$\begin{aligned}&\theta =M^{2}t-\phi _{0}, \end{aligned}$$
(43)
$$\begin{aligned}&\sigma =\sqrt{\frac{1}{3}}\left[ \frac{(n-1)}{(n+2)}(M^2t-\phi _{0})\right] , \end{aligned}$$
(44)
$$\begin{aligned}&A_{m}=\frac{2}{3}\left( \frac{n-1}{n+2}\right) ^{2}. \end{aligned}$$
(45)

The deceleration parameter of the model is obtained as

$$\begin{aligned} q=-1-\frac{3M^{2}}{(M^2t-\phi _{0})^{2}}. \end{aligned}$$
(46)

The jerk parameter j(t) of the model is given by

$$\begin{aligned} j(t)=q+2q^{2}-\frac{{\dot{q}}}{H}=1+\frac{9M^{2}}{(M^2t-\phi _{0})^{2}}. \end{aligned}$$
(47)

Using Eq. (40), the general solution of Eq. (31) is of the form

$$\begin{aligned} \beta = \frac{\beta _{0}}{V}=\beta _{0}\exp {\left[ \frac{2\phi _{0} t+ 2\phi _{1}-M^{2}t^{2}}{2}\right] }. \end{aligned}$$
(48)

where \(\beta _{0}\) is an arbitrary constant.

From Eqs. (27)–(29), the DE density \(\rho _{\Lambda }\), EoS parameter \(\omega _{\Lambda }\) and the skewness parameter \(\delta\) are calculated as

$$\begin{aligned}&\rho _{\Lambda }=\frac{(2n+1)(M^{2}t-\phi _{0})^{2}}{(n+2)^{2}}\nonumber \\&\quad -m^{2}\exp \left[ \frac{n(2\phi _{0}t+2\phi _{1}-M^{2}t^{2})}{n+2}\right] \nonumber \\&\quad -\left( \frac{2M^{2}+2(M^{2}t-\phi _{0})^{2}+3\beta _{0}^{2}}{4}\right) \nonumber \\&\quad \exp {(2\phi _{0}t+2\phi _{1}-M^{2} t^{2})}, \end{aligned}$$
(49)
Fig. 1
figure 1

Plot of energy density (\(\rho _{\Lambda }\)) versus cosmic time (t) for \(n = .05\), \(m = 12\), \(M = 15\), \(\phi _{0}=5.5\), \(\phi _{1}=.4\) and \(\beta _{0}=.006\) respectively

Full size image
$$\begin{aligned}&\omega _{\Lambda }=-\frac{1}{\rho _{\Lambda }}\left[ \frac{2(n+2)M^{2} +3 (M^{2}t-\phi _{0})^{2}}{(n+2)^{2}}\right. \nonumber \\&\left. \quad +m^{2}\exp {\left( \frac{n(2\phi _{0}t+2\phi _{1}-M^{2}t^{2})}{n+2}\right) }\right. \nonumber \\&\quad \left. -\left( \frac{2M^{2} -2 (M^{2}t-\phi _{0})^{2}-3\beta _{0}^{2}}{4}\right) \right. \nonumber \\&\left. \quad \exp {(2\phi _{0}t+2\phi _{1}-M^{2}t^{2})}\right] , \end{aligned}$$
(50)
$$\begin{aligned}&\delta =\frac{1}{\rho _{\Lambda }}\left[ \frac{(2-n-n^2)(M^{2}t-\phi _{0})^{2}}{(n+2)^{2}}+\frac{M^{2}(1-n)}{n+2}\right. \nonumber \\&\quad \left. +2m^{2}\exp {\left( \frac{n(2\phi _{0}t+2\phi _{1}-M^{2}t^{2})}{n+2}\right) }\right] . \end{aligned}$$
(51)

The energy density associated with the scalar field is given by

$$\begin{aligned}&\epsilon =\frac{1}{2}\left( {\dot{\phi }}^{2}+M^{2} \phi ^{2}\right) \nonumber \\&\quad =\frac{1}{2}\left[ (M^{2}t-\phi _{0})^{2}+M^{2}\right] \exp {(2\phi _{0} t+2\phi _{1}-M^{2}t^{2})}. \end{aligned}$$
(52)
Fig. 2
figure 2

Plot of EoS parameter versus cosmic time (t) for \(n = .05\), \(m = 12\), \(M = 15\), \(\phi _{0}=5.5\), \(\phi _{1}=.4\) and \(\beta _{0}=.006\) respectively

Full size image
Fig. 3
figure 3

Plot of skewness parameter versus cosmic time (t) for \(n = .05\), \(m = 12\), \(M = 15\), \(\phi _{0}=5.5\), \(\phi _{1}=.4\) and \(\beta _{0}=.006\) respectively

Full size image

5 Discussions

The above dynamical and physical parameters will help us to discuss their significance in the universe.

From Eq. (40), we observe that the spatial volume increases exponentially with cosmic time. This shows that the universe expands from a finite volume. Observations of average scale factor reveal that the model is non-singular since the exponential function never vanishes. We also observe that the physical parameters H, \(\theta\) and \(\sigma ^{2}\) all diverge when t approaches infinity and will have finite values at \(t=0\). The scalar expansion of the model is always positive for small values of \(\phi _{0}\). Since

$$\begin{aligned} \frac{\sigma }{\theta }=\mathrm{constant}. \end{aligned}$$
(53)

So our model is totally anisotropic and spatially homogeneous. The mean anisotropy parameter of expansion \(A_{m}\) being the measure of the deviation from isotropic expansion plays an important role in the decision of the model being isotropic or anisotropic. The universe expands isotropically when \(A_{m}=0\). Here \(A_{m}\) is independent of time and hence it is uniform throughout the evolution of the universe. We observe that the universe will approach to isotropy provided \(n=1\).

The deceleration parameter plays a very important role in the description of the nature of the cosmological models. From Eq. (46), we observe that \(q<-1\) for finite time and it attains the value \(q=-1\) for large time. Hence, the universe expands with super-exponential expansion for finite time and exhibits an exponential accelerated expansion at late time and thus the universe asymptotically achieves the de Sitter phase which expands forever with the dominance of DE. The jerk parameter j(t) is positive for all cosmic time and attains the constant value unity at late time. Hence, the accelerated expansion in the universe is smooth.

From Eq. (48), it is clear that the gauge function \(\beta\), being constant at \(t=0\), is a decreasing function of time and tends to zero as \(t \rightarrow \infty\). Therefore the concept of Lyra manifold does not remain for very large time.

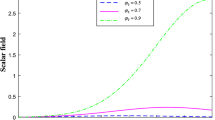
From Eq. (36), it is clear that the scalar field \(\phi\) increases with cosmic time and reaches a maximum value at the time \(t=\frac{\phi _{0}}{M^2}\) and then decreases to vanish at later point of time. From Eqs. (36) and (52) it can be observed that the energy density of scalar field \((\epsilon )\) attains the extremum value at a faster rate than the scalar field \(\phi\). For physically acceptable model, we have \(\epsilon >0\).

The energy density, EoS parameter and skewness parameter of DE are given in Eqs. (49)–(51). The behavior of energy density is shown in Fig. 1 with appropriate choice of constants. From Fig. 1 we observe that the energy density of DE is positive for all time t, which increases as time increases. Figure 2 shows the variation of equation of state parameter with cosmic time t. It may be observed that at \(t=0\), the model starts in the matter dominated region, varies in the phantom region (\(\omega _{\Lambda }<-1\)) and finally approaches to phantom limit \(\omega _{\Lambda }=-1\) (\(\Lambda CDM\) model). A graph of skewness parameter (\(\delta\)) is shown in Fig. 3 which shows that skewness parameter is negative at \(t=0\) and vanishes at late times, hence the DE isotropises for large time.

6 Conclusion

In modern cosmology, the investigations of dark energy models in modified Einstein’s theories of gravity are drawing attention of several cosmologists to explain the present scenario of accelerated expansion of the universe. In this paper, we have presented an exact solution of Einstein’s field equations in the presence of an anisotropic dark energy and a massive scalar field in the framework of Lyra manifold, which corresponds to a spatially homogeneous and anisotropic Bianchi type-\(\hbox {VI}_{0}\) dark energy model of the universe. We have evaluated various cosmological and kinematical parameters to study the physical features of the model in view of recent cosmological scenario and observations.

The anisotropic DE cosmological model with massive scalar field is non-singular which exhibits the super-exponential expansion for finite time \(q<-1\). Also it shows an early inflation with finite volume. At late time the universe exhibits an exponential expansion \((q=-1)\) and thus the universe asymptotically achieves de Sitter phase which expands forever due to the dominance of DE.

The physical quantities H, \(\theta\), \(\sigma ^2\) are increasing functions of time and tend to infinity for sufficiently large value of cosmic time.

The average anisotropy parameter associated with the expansion is constant and therefore the model is anisotropic. It deserves mention that it becomes isotropic and shear free for \(n=1\).

The energy density of DE is always positive and is increasing function of time. It can be seen from the analysis of EoS parameter that the model starts in the matter dominated region, varies in the phantom region (\(\omega _{\Lambda }<-1\)) and finally approaches to \(\Lambda CDM\) model. Skewness parameter tends to zero as t tends to infinity. Hence, the anisotropy of the DE vanishes at late times.

The gauge function \(\beta\) is positive and plays the same role as the cosmological constant. As volume of the universe increases, \(\beta\) decreases continuously and tends to zero as \(t\rightarrow \infty\). Hence, the concept of Lyra manifold is physically meaningful for finite time, but does not remain significant for very large time.

At the initial epochs the massive scalar field influences all the physical parameters of the model. At late times they are independent of scalar field and approach to constant values. Hence, the effect of scalar field gradually decreases during the course of evolution of the model.

The jerk parameter remains positive and finally approaches to unity, i.e. the present model approaches \(\Lambda CDM\) model at late times.

It is observed that all the physical and dynamical parameters behave in such a way that they are in good agreement with the recent experimental observation of modern cosmology.