1 Introduction

Complex astroplasmas, particularly in the intergalactic scales of space and time, have widely been attracting researchers for years. One of the main reasons behind it, as is clearly understood from the literature (Jeans 2009; Balsara 1996; Beznogov and Yakovlev 2013), is the associated collective wave-instability dynamics leading to local fragmentation and fillamentation processes of global self-gravitating interstellar clouds, which in turn, form self-gravitationally, condensed bounded sub-structures as galactic constituent units and elements. The involved mechanism intrinsically behind such gravitating dusty cloud matter reorganization is attributable to the Jeans instability (Jeans 2009). This instability is uniquely and solely responsible for re-distribution of momentum, energy and material transfer leading to normal self-gravitational condensation. It eventually renders large-scale self-gravitating cloud structures gravitationally unstable, via the developmental growth of mechanical waves of large wavelength, provided the cloud scale size exceeds the critical Jeans scale length as the basic instability criterion (Jeans 2009; Bliokh et al. 1995). In such dusty plasma environments, the dust grains get electrically charged via contact electrification. The dust-charge is normally and mostly negative due to high electronic mobility relative to that of ions under identical conditions. As a consequence, an overlapped gravito-electrostatic instability of hybrid type onsets co-spatial and co-temporal, if the dust-grain charge-to-mass ratio (Gisler et al. 1992) becomes, \(( Q_{d} / m_{d} ) \sim\sqrt{G}\), where \(G = 6.67 \times 10^{ - 11}~\mbox{m}^{3}\,\mbox{kg}^{-1}\,\mbox{s}^{-2}\) is the Newtonian gravitational coupling constant via which the self-gravitating plasma media interact. It can be added moreover that purely self-electrostatic instability for \(( Q_{d} / m_{d} ) > \sqrt{G}\) and purely self-gravitational instability for \(( Q_{d} / m_{d} ) < \sqrt{G}\) have natural existence in such complex plasma backdrops. In the presence of self-gravity effects in the cold cloud plasma system, the gravitational-to-electromagnetic force ratio in generic notations becomes, \(Gm_{d}^{2} / Q_{d}^{2} \approx O ( 1 ) \), which implicates the dust charge-to-mass ratio as, \(Q_{d} / m_{d} \approx \sqrt{G}\), in a perfect gravito-electro-magnetic equilibrium. Thus, for bounded structure to form, evolve and exist, the charge-to-mass ratio in the SI units is \(Q_{d} / m_{d} \approx10^{ - 5}\).

The importance of the complex grainy plasma dynamics and associated wave features are realizable even on the laboratory scale too, like in thermonuclear fusion reactors, tokamak, Q-machine, and so forth (Shukla and Mamun 2002). The charge of dust particulates, or dust grain-like impurity ions play vital roles in introducing as well as modifying diverse collective wave-instability phenomena. The astrophysical environments, embedded with dusty ingredients, have also been experimentally conceived via innumerable microgravity conditions (Shukla and Mamun 2002). An overall conclusion in the most of such experimentations is that gravity plays a drastic role in influencing both normal linear and non-linear kinetics of the plasma structures detected through the observations of diverse eigenmodes. However, understanding the composite evolution of gravito-electro-magnetic wave instability remains intriguingly an open challenge on both the spatiotemporal scales of laboratory as well as interstellar space (Spitzer 2004). It may further be noted that, since the charged grains are highly massive, unlike the other lighter charged constituents interacting via the Coulombic force field only, so the grains experience both electromagnetic and gravitational forces. Thus, the dust polarization force originates from the interaction of the thermal electron-ionic currents over the grain surface (Hamaguchi and Farouki 1994; Spitzer 2004) As a consequence, the Jeans instability in the presence of polarization force is drastically modified thereby creating a plethora of open challenges (Bliokh et al. 1995) Nevertheless, to the best of our knowledge, the gravitational fluctuation dynamics in astrophysical gravito-magneto-active non-thermal dusty fluids (Du 2006, 2007), with considerable collective cooperative correlation and dust-charge variation due to random thermal currents taken into account on the Jeans scales of space and time, is yet to be well formulated and understood in the domains previously remaining unexplored.

In this paper, we propose a new theoretical formalism, based on the generalized hydrodynamic conservation laws, to investigate the exotic aspects of gravito-electro-magnetic fluctuation dynamics on the relevant fluid scales of space and time. The model is devised in the presence of grain polarization force, fluid-viscoelasticity, and dust-charge fluctuations with the \(q\)-nonextensive distributions of tiny electrons and ions. A Fourier-based plane-wave analysis, at the backdrop that the plasma is unbounded and boundary effects are insignificant on the considered fluctuation dynamics, is constructed methodologically in a modified form to derive a linear generalized dispersion relation (cubic in degree) epitomizing the fluctuations. Finally, we strategically develop a constructive scheme for numerical analysis to illustrate and explore the quantitative flavor of the fluctuation spectra in the framework of realistic intergalactic parameter values, which are especially suitable for astrophysical, space and cosmic environments.

2 Governing equations

We consider a complex astrocloud composed of nonextensive electrons and ions, and fluctuating negatively charged identical dust grains embedded in a uniform magnetic field \(B (0, 0, B_{0} )\). The origin of interstellar magnetic field is still in debate (Spitzer 2004). It, however, is known that the magnetic field springs up because of the plasma currents arising due to convective circulation dynamics of the constituent charged species. The interstellar magnetic field is relatively weak and has a typical value \(B\sim10^{ - 6}~\mbox{G}\) (Spitzer 2004). In normal dust cloud, let us take \(m_{d} = 2 \times 10^{ - 12}~\mbox{gm}\), \(n_{d0} = 10^{-4}~\mbox{cm}^{-3}\), \(Q_{d} = 10^{3}e\), \(T = 1~\mbox{eV}\) and \(T_{d} = 0.01~\mbox{eV}\) (Spitzer 2004; Yaroshenko et al. 2007). In such situations, our estimation shows that the dust gyro radius, \(r_{g} = m_{d}v_{td} / Q_{d}B \approx3.5 \times10^{9}~\mbox{cm}\) with dust thermal speed \(v_{td} = \sqrt{T_{d} / m_{d}} \approx2.82 \times10^{ - 1}~\mbox{cm}\,\mbox{s}^{-1}\). Further, the Jeans length comes out as \(\lambda_{J} = C_{ss} / \omega_{J} = \sqrt{T / 4\pi Gm_{d}n_{d0}} \approx6 \times10^{11}~\mbox{cm}\). It implicates that \(r_{g} \ll \lambda _{J}\), thereby validating our magnetized plasma consideration. The heavy cold dust grains, unlike the light non-thermal electrons and ions, are strongly coupled through collective cooperative correlation effects via viscoelasticity (Frenkel 1946; Brevik 2016). The viscoelastic properties of self-gravitating and astrophysical media are justifiable under the condition that the astrofluid is strongly coupled with the correlation range on the coupling parameter, \(1 \ll \varGamma< \varGamma_{\mathrm{c}}\), \(\varGamma_{\mathrm{c}}\) is the coupling parameter value at which crystallization develops (Kaw and Sen 1998). It is found that self-gravitating media, which are the large-scale cosmic fluids, indeed obey this, and hence, exhibits viscoelastic behavior (Brevik 2016). The extended non-isothermal inhomogeneous cloud is analytically simplified by the Jeans homogenization assumption by treating it initially as “homogeneous” one. We also neglect the electrostatic fragmentation of the like charged massive dust-grains into smaller ones due to the modified Coulombic repulsive force field (Hamaguchi and Farouki 1994; Bliokh et al. 1995; Shukla and Mamun 2002). The assumed global quasi-neutrality enables us to analyze the low-frequency large-scale phenomena in divergence-free current configuration (Karmakar and Borah 2016). It is free from any contribution of displacement current sourced by space-charge fluctuation effects. External gravity influences due to other cosmic sources, dark matter and distant stellar structures are also ignored without loss of any generality. This is against the conventional viewpoint of treating astrophysical fluids in the neutral fluid framework due to the fact that the Debye-to-Jeans length ratio is asymptotically of zero-value (Chandrasekhar 1961; Gisler et al. 1992; Bliokh et al. 1995; Karmakar and Borah 2016).

Self-gravitating fluids and astrophysical plasma media, on a large scale, are nonextensive in nature (Jiulin 2006, 2007; Zheng and Du 2014). Therefore, the macroscopic state of such a nonextensive astroplasma with the generic symbols is described by the non-Maxwellian (\(q\)-nonextensive) electron and ion population distributions (Livadiotis and McComas 2013; Gong and Du 2012; Zheng and Du 2014) as

$$\begin{aligned} &n_{e} = n_{e0} \biggl[ 1 + ( 1 - q_{e} ) \frac{e\phi}{T _{e}} \biggr] ^{\frac{1}{1 - q_{e}}},\quad\mbox{and} \end{aligned}$$
(1)
$$\begin{aligned} &n_{i} = n_{i0} \biggl[ 1 - ( 1 - q_{i} ) \frac{e\phi}{T _{i}} \biggr] ^{ \frac{1}{1 - q_{i}}}. \end{aligned}$$
(2)

Now, the dynamics of the inertial dust fluid is described by the generalized hydrodynamic equations of continuity and momentum in closed conservative form, respectively, as

$$\begin{aligned} &\frac{\partial n_{d}}{\partial t} + \vec{\nabla}. ( n_{d} \vec{v}_{d} ) = 0,\quad\mbox{and} \end{aligned}$$
(3)
$$\begin{aligned} & \biggl[1 + \tau_{\mathrm{m}} \biggl(\frac{\partial}{\partial t} + \vec{\nabla}. \vec{v}_{d} \biggr) \biggr] \biggl[m_{d}n_{d} \frac{d\vec{v}_{d}}{dt} + m_{d}n_{d}\vec{\nabla}\psi \\ &\qquad {}+Q_{d}n_{d} \vec{\nabla} \phi- Q_{d}n_{d}R \biggl( \frac{n_{i}}{n_{i0}} \biggr)^{\frac{1}{2}} \vec{\nabla} \phi+ Q_{d}n_{d} ( \vec{v}_{d} \times \vec{B}) \biggr] \\ &\quad = \eta\vec{\nabla} ( \vec{\nabla}.\vec{v}_{d} ) + \biggl( \zeta+ \frac{\eta}{3} \biggr) \vec{\nabla} ( \vec{\nabla}.\vec{v}_{d}) . \end{aligned}$$
(4)

It is seen from Eq. (4) that the plasma (convective) flow dynamics generates electric current, which in turn, develops the magnetic field. The field, however, may not have any important role to play in the dust-charging process in usual cloud conditions. Finally, the astrofluid is closed by the coupling Poisson equations, which govern the electrostatic and gravitational potential distributions, set out respectively as

$$\begin{aligned} &\nabla^{2}\phi= 4\pi e ( n_{e} - n_{i} ) - 4 \pi Q_{d}n _{d},\quad\mbox{and} \end{aligned}$$
(5)
$$\begin{aligned} &\nabla^{2}\psi= 4\pi G m_{d} ( n_{d} - n_{d0} ) . \end{aligned}$$
(6)

The considered spherical grains are identical, i.e., with the same mass \(m _{d}\), radius \(r_{d}\) and charge \(Q_{d} = Z_{d}e\), where \(e\) is the unit electronic charge. The grains statistically acquire charges from the background plasma via the collective interaction processes of the plasma thermal currents and contact electrifications (Gong and Du 2012). Now, applying the definition of thermal currents and following the normal ansatz (Pandey et al. 1999; Gong and Du 2012), the electronic and ionic currents are methodologically derived after long integration and respectively expressed as

$$\begin{aligned} &I_{e} = - \sqrt{8\pi} r_{d}^{2}n_{e} ( r_{e} ) e B_{qe}\sqrt{\frac{T _{e}}{m_{e}}} \biggl[ 1 + ( 1 - q_{e} ) \frac{e\phi}{T _{e}} \biggr] ^{\frac{3 - 2q_{e}}{1 - q_{e}}} \end{aligned}$$
(7)

and

$$\begin{aligned} &I_{i} = \sqrt{8\pi} r_{d}^{2}n_{i} ( r_{i} ) e B_{qi}\sqrt{\frac{T _{i}}{m_{i}}} \biggl[ 1 - ( 3 - 2q_{i} ) \frac{e\phi}{T _{i}} \biggr] , \end{aligned}$$
(8)

where, the nonextensivity normalization constant, which typifies the associated probability conservation rule, is described as

$$ B_{qj} = \left \{ \textstyle\begin{array}{l} \frac{ ( 5 - 3q_{j} ) ( 3 - q_{j} ) \sqrt{1 - q _{j}}}{4 ( 2 - q_{j} ) ( 3 - 2q_{j} ) }.\frac{ \varGamma ( \frac{1}{1 - q_{j}} + \frac{1}{2} ) }{\varGamma ( \frac{1}{1 - q_{j}} ) }, q_{j} < 1 \\ \frac{ ( 5 - 3q_{j} ) \sqrt{q_{j} - 1}}{2 ( 2 - q_{j} ) ( 3 - 2q_{j} ) }.\frac{\varGamma ( \frac{1}{q_{j} - 1} ) }{\varGamma ( \frac{1}{q_{j} - 1} - \frac{1}{2} ) }, q_{j} > 1 \end{array}\displaystyle \right \} . $$
(9)

Finally, the fluctuating grain-charge is dictated by the electronic and ionic non-thermal currents entering the grain, subject to the grain surface potential relative to the local plasma background. The grain-charge evolutionary dynamics is statistically governed by the charging equation as

$$ \biggl( \frac{\partial}{\partial t} + \vec{v}_{d}.\vec{\nabla} \biggr) Q_{d} = I_{e} + I_{i}. $$
(10)

Here, \(n_{e0}\), \(n_{i0}\) and \(n_{d0}\) are the equilibrium values of the population densities \(n_{e}\), \(n_{i}\) and \(n_{d}\) of electrons (at \(T_{ e}\mbox{ eV}\)), ions (at \(T_{ i}\mbox{ eV}\)) and dust grains (at \(T_{ d}\mbox{ eV}\)), respectively. Here, \(n_{do}\) accounts for the Jeans swindle (Chandrasekhar 1961; Karmakar and Borah 2016). The symbols, \(\phi\) and \(\psi\), denote the self-consistent electrostatic and self-gravitational plasma potentials, respectively. Further, \(q_{j}\) (\(q_{j} < 1\)), with \(j=e\) for electrons and \(i\) for ions, denotes the nonextensive plasma parameters. The effect of polarization force on the dust grains moving with velocity \(v_{ \mathrm{d}}\) and interacting self-gravitationally via \(G\), in the customary scheme of notations, is described by \(R = ( 1 / 4 ) ( \vert Q_{d0} \vert e / \lambda_{D}T_{i} ) ( 1 - T _{i} / T_{e} ) \), where \(\lambda_{D} = \lambda_{Di} / \sqrt{1 + ( \lambda_{Di} / \lambda_{De} ) ^{2}}\) is the effective Debye screening length with \(\lambda_{De ( i ) } = \sqrt{T_{e ( i ) } / 4\pi e^{2}n_{e ( i ) }}\). Moreover, \(\tau_{\mathrm{m}}\) is the viscoelastic relaxation (memory) time; \(\eta\) and \(\zeta\) are shear and bulk viscosity coefficients (Frenkel 1946; Brevik 2016), respectively.

3 Linear stability analysis

We allow the hydrodynamic plasma model to undergo linear perturbation on the relevant physical variables about the respective homogeneous equilibrium values, after relaxing from any contribution of gravity-induced electrostatic polarization effects (Bally and Harrison 1978; Shukla and Mamun 2002), as follows

$$\begin{aligned} &n_{e} = n_{e0} + n_{e1},\qquad n_{i} = n_{i0} + n_{i1},\qquad n_{d} = n_{d0} + n_{d1}, \\ &\phi= \phi_{0} + \phi_{1},\qquad \psi= \psi_{0} + \psi_{1}, \qquad v_{d} = v_{d0} + v_{d1}, \\ &Q_{d} = Q_{d0} + Q_{d1}. \end{aligned}$$
(11)

Here, the term with subscript ‘0’ indicates the equilibrium and the subscript ‘1’ indicates the corresponding perturbed parts. The considered plasma is unbounded and boundary effects are negligible. We allow the perturbed quantities to vary in the form of plane-waves as \(e^{ - ( i\omega t - ik.r ) }\), where, \(\omega\) is the angular frequency and \(k = k_{x}x + k_{z}z\) is the angular wave number of the harmonic disturbance considered. The plane-wave approximation (Shukla and Mamun 2002; Karmakar and Borah 2016) may be justified due to the fact that the plasma system is unbounded, which is free from any kind of significant geometrical boundary effects. Thus, the corresponding perturbed parts resulting from Eqs. (1)–(2) with the help of expression (11) are respectively as

$$\begin{aligned} &n_{e1} = n_{e0}\frac{e\phi_{1}}{T_{e}},\quad\mbox{and} \end{aligned}$$
(12)
$$\begin{aligned} &n_{i1} = - n_{i0}\frac{e\phi_{1}}{T_{i}}. \end{aligned}$$
(13)

It is seen that the \(q\)-nonextensivity role is absent in Eqs. (12)–(13) for the lowest-order perturbation description, because they describe a hot plasma configuration (\(T \gg e\phi\)), introduced via the lowest-order binomial expansion of Eqs. (1)–(2). The perturbed dust density from Eq. (3) can likewise be expressed as

$$ n_{d1} = \biggl( \frac{k}{\omega} n_{d0} \biggr) v_{d1}. $$
(14)

Now, Eq. (4) gives the perturbed momentum transfer as

$$\begin{aligned} &(1 - i\omega\tau_{m}) \bigl[ - im_{d}n_{d0} \omega v_{d1} + im_{d}n_{d0}k\psi_{1} \\ &\qquad {}+ iQ_{d0}n_{d0} ( 1 - R ) k\phi _{1} + Q_{d0}n_{d0} \bigl\vert (\vec{v}_{d1} \times \vec{B}) \bigr\vert \bigr] \\ &\quad {} = - k^{2} \biggl( \frac{4\eta}{3} + \zeta \biggr) v_{d1}. \end{aligned}$$
(15)

From Eqs. (5)–(6), the perturbed electrostatic and self-gravitational potentials respectively are as

$$\begin{aligned} &\phi_{1} = \frac{4\pi}{k^{2}} \bigl[ e ( n_{i1} - n_{e1} ) + Q_{d0}n_{d1} + Q_{d1}n_{d0} \bigr] ,\quad\mbox{and} \end{aligned}$$
(16)
$$\begin{aligned} &\psi_{1} = - \frac{\omega_{J}^{2}}{k^{2}}\frac{n_{d1}}{n_{d0}}. \end{aligned}$$
(17)

Finally, using Eqs. (7), (8) and (9) in Eq. (10), the dust-charging equation becomes

$$\begin{aligned} Q_{d1} =& - \frac{i}{\omega} 4\sqrt{2\pi} r_{d}^{2} e^{2} \biggl[ B _{qe}\sqrt{\frac{T_{e}}{m_{e}}} \frac{n_{e0}}{T_{e}} ( 2 - q _{e} ) \\ &{}+ B_{qi}\sqrt{\frac{T_{i}}{m_{i}}} \frac{n_{i0}}{T_{i}} ( 2 - q_{i} ) \biggr] \phi_{1}. \end{aligned}$$
(18)

Now, Eq. (15), with the help of Eqs. (14) and (17), becomes

$$ n_{d1} = \frac{(1 - i\omega\tau_{m})Q_{d0}n_{d0}(1 - R)k^{2} / m_{d}}{(1 - i\omega\tau_{m}) ( \omega^{2} + \omega_{J}^{2} + i \omega\omega_{cd} ) + i ( \frac{4\eta}{3} + \zeta ) \frac{ \omega k^{2}}{m_{d}n_{d0}}}\phi_{1} , $$
(19)

where, \(\omega_{cd} = Q_{d0}B / m_{d}\) is the dust-cyclotron frequency. Using Eqs. (12)–(13) and (18) in Eq. (16), we obtain the generalized linear dispersion relation as

$$\begin{aligned} \omega =& \biggl( \frac{\lambda_{D}^{2}}{1 + k^{2}\lambda_{D}^{2}} \biggr) \\ &{}\times \biggl\{ \frac{ ( 1 - i\omega\tau_{m} ) \omega_{pd}^{2} \omega ( 1 - R ) k^{2}}{ ( 1 - i\omega\tau_{m} ) ( \omega^{2} + \omega_{J}^{2} + i\omega\omega_{cd} ) + i \omega\tau_{m}k^{2}V_{cd}^{2}} \\ &{}- iA \biggr\} , \end{aligned}$$
(20)

where, \(\omega_{pd} = \sqrt{4\pi Q_{d0}^{2}n_{d0} / m_{d}}\) is the dust-plasma radian oscillation frequency and \(\omega_{J} = ( 4 \pi G m_{d}n_{d0} ) ^{1 / 2}\) is the critical Jeans frequency. Further, \(V_{cd} = [( 4\eta/ 3 + \zeta )/m_{d}n _{d0}\tau_{m} ] ^{1 / 2}\) is the phase velocity of the viscoelastic relaxation mode. The non-thermal coupling factor of the electrons and ions with the identical grains appearing in Eq. (20) is defined as

$$\begin{aligned} A =& 16 \sqrt{2} \pi^{\frac{3}{2}}n_{d0} r_{d}^{2} e^{2} \biggl[ B_{qe}\sqrt{\frac{T _{e}}{m_{e}}} \frac{n_{e0}}{T_{e}} ( 2 - q_{e} ) \\ &{}+ B_{qi}\sqrt{\frac{T_{i}}{m_{i}}} \frac{n_{i0}}{T_{i}} ( 2 - q_{i} ) \biggr] . \end{aligned}$$
(21)

Subsequently, in the current fluid-limit approximation (Hamaguchi and Farouki 1994; Gong and Du 2012; Karmakar and Borah 2016), the low-frequency fluctuations \(( \omega\tau_{m} \ll 1 ) \) of our interest are described by the following cubic-degree dispersion relation

$$ \omega^{3} + a_{2}\omega^{2} + a_{1} \omega+ a_{0} = 0, $$
(22)

where, the various involved coefficients are defined as

$$\begin{aligned} a_{0} =& i \biggl( \frac{\lambda_{D}^{2}}{1 + k^{2}\lambda_{D}^{2}} \biggr) A \omega_{J}^{2}, \end{aligned}$$
(23)
$$\begin{aligned} a_{1} =& \biggl\{ \omega^{2}_{J} - \biggl( \frac{\lambda^{2}_{D}}{1 + k^{2}\lambda^{2}_{D}} \biggr)\omega^{2}_{pd}(1-R)k^{2} \\ &{}- \biggl(\frac{\lambda^{2}_{D}}{1 + k^{2}\lambda^{2}_{D}} \biggr)\omega_{cd}A \\ &{}+ \biggl( \frac{\lambda^{2}_{D}}{1 + k^{2}\lambda^{2}_{D}} \biggr)k^{2}V^{2}_{cd} \tau_{m}A \biggr\} , \quad \mbox{and} \end{aligned}$$
(24)
$$\begin{aligned} a_{2} =& i \biggl\{ \omega_{cd} + \tau_{m}k^{2}V_{cd}^{2} + \biggl( \frac{\lambda_{D}^{2}}{1 + k^{2}\lambda_{D}^{2}} \biggr) A \biggr\} . \end{aligned}$$
(25)

In order to analyze the complex gravito-electro-magnetic fluctuations, we normalize Eq. (22) with a standard astrophysical normalization procedure, with detailed typical quantifications as presented in the appendix, defined here as follows

$$\begin{aligned} &\left . \textstyle\begin{array}{l} \displaystyle \varOmega= \frac{\omega}{\omega_{J}}, K = \frac{kc_{ss}}{\omega_{J}}, \varOmega_{cd} = \frac{\omega_{cd}}{\omega_{J}}, \varOmega_{pd} = \frac{\omega _{pd}}{\omega_{J}}, \\ \displaystyle \varLambda_{D} = \frac{\lambda_{D}\omega_{J}}{c_{ss}}, \tau_{m}^{ *} = \tau _{m}\omega_{J}, M_{rx} = \frac{V_{cd}}{c_{ss}}\mbox{ and } P = A \biggl( \frac{\lambda_{D}^{2}}{\omega_{J}} \biggr). \end{array}\displaystyle \right \} \end{aligned}$$
(26)

As a result, the normalized form of Eq. (22) reads as

$$\begin{aligned} &\varOmega^{3} + i \biggl\{ \varOmega_{cd} + K^{2} \tau_{m}^{*}M_{rx}^{2} + \biggl( \frac{P}{1 + K^{2}\varLambda_{D}^{2}} \biggr) \biggr\} \varOmega^{2} \\ &\quad {}+ \Biggl\{ 1 - \biggl( \frac{\varLambda_{D}^{2}}{1 + K^{2}\varLambda_{D}^{2}} \biggr) \varOmega_{pd}^{2} ( 1 - R ) K^{2} \\ &\quad {}- \biggl( \frac{P}{1 + K^{2}\varLambda_{D}^{2}} \biggr) \varOmega_{cd} + \biggl( \frac{P}{1 + K^{2}\varLambda_{D}^{2}} \biggr) K^{2}\tau_{m}^{*}M _{rx}^{2} \Biggr\} \varOmega \\ &\quad {}+ i \biggl( \frac{P}{1 + K^{2}\varLambda_{D}^{2}} \biggr) = 0. \end{aligned}$$
(27)

The appearance of the imaginary unit ‘\(i\)’ in Eq. (27) is due to non-adiabatic dust-charge fluctuations on the Jeans scales of space and time. It dictates the evolution of the low-frequency fluctuations under the joint influence of viscoelasticity, polarization force, nonextensivity, dust-charge variation, and so forth. Out of all, the most interesting exotic goal of our investigation, the \(q\)-nonextensivity effects appear in Eq. (27) via the parameters \(A\) and \(P\) (Eqs. (21) & (26)). The inclusion of diversified complexities makes it extremely difficult to study the fluctuation dynamics analytically, via deriving mathematical conditions as usual tradition, despite rare possibilities for transforming Eq. (27) into a simpler form. Therefore, we directly proceed numerically in order to explore the fluctuation-underlying insights in exact form.

4 Results and discussions

A cubic polynomial dispersion relation (Eq. (27)) is constructed by the Fourier technique to investigate the low-frequency fluctuations in the complex astrofluid under the simultaneous action of all the possible factors of astrophysical significance. It is now integrated numerically by applying the well-known Cardan method (McKelvey 1984). The obtained results, based on the inverse-square law force (Shukla and Stenflo 2006) of the dust grains, as displayed in Figs. 1–5, are discussed as follows.

Fig. 1
figure 1

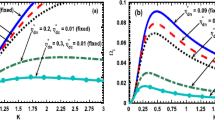
Profile of the normalized (a) real frequency of fluctuations and (b) growth rate with variation in the normalized wave number for different values of the normalized dust cyclotron frequency. Various lines correspond to case (1): \(\varOmega_{cd} = 0.0025\) (Line 1, blue), case (2): \(\varOmega_{cd} = 0.005\) (Line 2, red) and case (3): \(\varOmega_{cd} = 0.01\) (Line 3, green), respectively. Various input parameters kept fixed are \(\tau_{m}^{*} = 0.01\), \(Q_{d0} = 1.6 \times 10^{ - 16} \mathrm{C}\), \(R = 0.1\) and \(q_{e} = 0.1\). The other inputs used here are, \(n_{e0} = 8~\mbox{cm}^{-3}\), \(n_{i0} = 1~\mbox{cm}^{-3}\), \(n_{d0} = 10^{ - 1}~\mbox{cm}^{-3}\), \(m_{e} = 9.1 \times10^{ - 28}~\mbox{g}\), \(m_{i} = 1.67 \times10^{ - 24}~\mbox{g}\), \(m_{d} = 2 \times10^{ - 11}~\mbox{g}\), \(T_{e} = 1~\mbox{eV}\), \(T_{i} = 0.8~\mbox{eV}\), \(T_{d} = 0.01~\mbox{eV}\), \(B = 10^{ - 4}~\mbox{G}\), \(Q_{d} = 10^{3}~\mbox{e}\) and \(r_{d} = 1.28~\upmu\mbox{m}\)

Full size image

Figure 1 depicts the profile structures of the normalized (a) real frequency of fluctuations and (b) growth rate with variation in the normalized wave number for different values of the normalized dust cyclotron frequency (\(\varOmega_{cd}\)). Various lines correspond to case (1): \(\varOmega_{cd} = 0.0025\) (Line 1, blue), case (2): \(\varOmega_{cd} = 0.005\) (Line 2, red) and case (3): \(\varOmega_{cd} = 0.01\) (Line 3, green), respectively. Various input parameters kept fixed are \(\tau_{m}^{*} = 0.01\), \(R = 0.1\) and \(q_{e} = 0.1\). The other inputs used here are, \(n_{e0} = 2\mbox{--}45~\mbox{cm}^{-3}\), \(n_{i0} = 1\mbox{--}20~\mbox{cm}^{-3}\), \(n_{d0} = 10^{-3}\mbox{--}10^{-1}~\mbox{cm}^{-3}\), \(m_{e} = 9.1 \times10^{ - 28}~\mbox{g}\), \(m_{i} = 1.67 \times10^{-24}~\mbox{g}\), \(m_{d} = 2 \times10^{ - 12}~\mbox{g}\), \(T_{e} \approx T_{i} \approx1\mbox{--}10~\mbox{eV}\), \(T_{d} = 0.01~\mbox{eV}\), \(B = 10^{ - 6}~\mbox{G}\) and \(r_{d} = 1.28~\upmu\mbox{m}\) (Yaroshenko et al. 2007). Clearly, the fluctuations evolve as dispersive disturbance for \(K \le2.5\) (Fig. 1(a)), beyond which, they turn into quasi-dispersive form. It is found that the growth rate of the instability decreases towards the high-\(K\) region. It is also evident that, with increase in \(\varOmega_{cd}\), the growth rate decreases, and vice-versa. It means that the homogeneous magnetic field plays a stabilizing role on the fluctuation dynamics. The reason behind this is the dust gyro-kinetic effects associated with the fluctuating-charged grains in the pre-defined magnetized plasma background. It establishes dust-cyclotron resonance (low-frequency phenomena), which subsequently, acts as a damping agency to the fluctuation evolutionary process in the considered model.

Figure 2 displays the same as Fig. 1, but with the \(\tau_{m}^{ *}\)-variation. Various lines correspond to case (1): \(\tau _{m}^{ *} = 0.01\) (Line 1, blue), case (2): \(\tau_{m}^{ *} = 0.02\) (Line 2, red) and case (3): \(\tau_{m}^{ *} = 0.03\) (Line 3, green), respectively. It is seen that the growth rate remains almost unchanged in the extremely large-wavelength region (\(K \le1\)). But, toward the short-wavelength region (\(K > 1\)), the growth rate decreases with increase in \(\tau_{m}^{*}\). Thus, the viscoelasticity acts as a damping agency and thereby stabilizes the fluctuations.

Fig. 2
figure 2

Same as Fig. 1, but with the \(\tau_{m}^{ *}\)-variation. Various lines correspond to case (1): \(\tau_{m}^{ *} = 0.01\) (Line 1, blue), case (2): \(\tau_{m}^{ *} = 0.02\) (Line 2, red) and case (3): \(\tau_{m}^{ *} = 0.03\) (Line 3, green), respectively

Full size image

Figure 3 reflects the same as Fig. 1, but with the \(Q_{d0}\)-variation. Various lines correspond to case (1): \(Q_{d0} = 1.6 \times10^{ - 16}~\mbox{C}\) (Line 1, blue), case (2): \(Q_{d0} = 2.1 \times10^{ - 16}~\mbox{C}\) (Line 2, red) and case (3): \(Q_{d0} = 2.6 \times10^{ - 16}~\mbox{C}\) (Line 3, green), respectively. It is seen that the growth rate remains almost unaffected for \(K \le1\), as in Fig. 2. However, for \(K > 1\), it is observed that dust-charge variation plays a stabilizing role to the fluctuation dynamics. Thus, it can be inferred that the dust-charge fluctuations provide a damping source to the considered instability.

Fig. 3
figure 3

Same as Fig. 1, but with the \(Q_{d0}\)-variation. Various lines correspond to case (1): \(Q_{d0} = 1.6 \times10^{ - 16}~\mbox{C}\) (Line 1, blue), case (2): \(Q_{d0} = 2.1 \times10^{ - 16}~\mbox{C}\) (Line 2, red) and case (3): \(Q_{d0} = 2.6 \times10^{ - 16}~\mbox{C}\) (Line 3, green), respectively

Full size image

Figure 4 exhibits the same as Fig. 1, but with the polarization \(R\)-variation. Various lines correspond to case (1): \(R = 0.1\) (Line 1, blue), case (2): \(R = 0.2\) (Line 2, red) and case (3): \(R = 0.3\) (Line 3, green), respectively. It is seen that growth rate here evolves in a similar way, as in earlier Figs. 2–3. This is pertinent that, if the polarization force exceeds over the electrostatic one, a self-gravitational reorganization takes place. As a result, the gravitational collapse occurs relatively more rapidly.

Fig. 4
figure 4

Same as Fig. 1, but with the \(R\)-variation. Various lines correspond to case (1): \(R = 0.1\) (Line 1, blue), case (2): \(R = 0.2\) (Line 2, red) and case (3): \(R = 0.3\) (Line 3, green), respectively

Full size image

In Fig. 5, we depict the same as Fig. 1, but with the \(q_{e}\)-variation. Various lines correspond to case (1): \(q_{e} = 0.1\) (Line 1, blue), case (2): \(q_{e} = 0.5\) (Line 2, red) and case (3): \(q_{e} = 0.9\) (Line 3, green), respectively. It is evident that the growth rate augments with increase in \(q_{e}\). Thus, \(q_{e}\) acts as a destabilizing factor for the wave propagation. It is due to deviation from the thermalization, which introduces secular (thermal) instability. This, in turn, non-resonantly couples with the usual Jeans instability to yield such observed dynamical behaviors. The \(q_{i}\)-effects, however, due to similar pattern dynamics are not shown graphically. In a broader sense, destabilizing role of the \(q\)-factors (nonextensivity) is interestingly found. The reason behind this, as already mentioned above, is the non-resonant mode-mode coupling of the gravito-electro-magnetic fluctuations with the thermal instability triggered by the non-thermal dynamics of the electrons and ions. In contrast, moreover, the non-thermal electrons and ions cause the equilibrium dust-charge to fluctuate around the equilibrium value in our cold dust-cloud approximation. Thus, the damping nature of the wave behavior in our cold cloud model, incorporated via the \(q\)-factors, may also be attributable to the dust-charge variational dynamics on the astrophysical hydrodynamic scales of space and time.

Fig. 5
figure 5

Same as Fig. 1, but with the \(q_{e}\)-variation. Various lines correspond to case (1): \(q_{e} = 0.1\) (Line 1, blue), case (2): \(q_{e} = 0.5\) (Line 2, red) and case (3): \(q_{e} = 0.9\) (Line 3, green), respectively

Full size image

It is further seen that, in all the cases (Figs. 1–5), the mean value of the fluctuation phase speed comes out as \(\langle v_{p}\rangle \approx3\times 10^{-1}~\mbox{C}_{\mbox{ss}}\), where, \(\mbox{C}_{\mbox{ss}}=\sqrt{T / m_{d}}\) is the dust-acoustic phase velocity as defined before. This implies that the fluctuations propagate with velocities that are comparable with the plasma normal mode phase velocity.

5 Conclusions

A theoretical model analysis is methodologically carried out to see the gravito-electro-magnetic fluctuations dynamics supported in a realistic complex astrofluid on the astrophysical fluid scales of space and time. All the realistic effects of dynamical significance are considered concurrently in non-thermal equilibrium. The numerical scheme of illustrations developed here shows that the evolution of the fluctuations is drastically influenced by viscoelasticity, polarization force, non-extensivity and the equilibrium dust-charge fluctuations. If all the incorporated effects are switched off, earlier results by others (Shukla and Stenflo 2006) get qualitatively re-produced from the dispersion analysis (cf. Eq. (27)) without any loss of physical insights. The newly investigated results, although yet to be further concretized on the basis of non-local analyses after the Jeans swindle (Karmakar and Borah 2016; Chandrasekhar 1961) relaxation, can be significant to trigger the astroclouds to fragment into smaller local structures via redistribution of dynamical properties (energy, momentum, matter transfer, etc.) leading to regions for diverse cosmic and galactic unit formation.

In summary, we study the conjoint effects of dust-polarization force, dust-charge fluctuations, and viscoelasticity on the gravito-electro-magnetic instability in a nonextensive magnetized self-gravitating plasma in the framework of generalized hydrodynamic model. A standard Fourier-based plane-wave analysis is carried out to reduce the basic closed structure equations into a cubic dispersion relation involving plasma-dependent variable coefficients followed by numerical illustrations and portrayals. It is found that the magnetic field and linear viscoelasticity have stabilizing influences on the instability. Moreover, conversely, the polarization force and nonextensivity play the destabilizing roles on its dynamic evolution.

It is admitted that the analysis is based on the Coulombic interaction of the dust grains, which in reality, is of a Lennard-Zones-like shielding potential (Shukla and Stenflo 2006; Delzanno et al. 2004; Delzanno and Lapenta 2005). This indicates that our investigation needs further refinements with proper inclusion of the latter. The local nonextensivity effects lead to inhomogeneous non-thermal forces, which in turn, may support the global cloud as a new halting mechanism, at least in principle, against further dynamical collapsing. It is further recognized that, despite this and assumed homogeneous equilibrium, the large-scale magnetized plasma fluctuations and instabilities, as simply and methodically presented herein, can play an important role in the transport of dust grains leading to dust-coagulation (from nano-to-micron range), and also, in the formation mechanism of planets and stars. Thus, we believe that such results can promisingly be useful as analytic elements in understanding bounded large-scale cosmic structures with source mechanisms triggered through self-gravitational collapse dynamics leading to the establishment of galaxies and their clustering unit associations.