1 Introduction

The dwarf planet Haumea was discovered in the Kuiper Belt in 2005 (Brown et al. 2005) and is one of the largest objects beyond the Neptune. It revolves around the Sun with period 281.83 years and has the orbital resonance \(12:7\) with Neptune. The main surprise was the fact that for its impressive size (∼1000 km) Haumea has a very fast rotation. Indeed, rotation period of Haumea was less than four hours and equal to

$$ T = 3.915483113\mbox{ h}. $$
(1)

Among the currently known objects in Solar system, which large across 100 km, Haumea rotates faster than anyone (Ćuk et al. 2013; Lockwood et al. 2014). Therefore, it is desired to construct the equilibrium figure of Haumea.

According to the articles (Rabinowitz et al. 2006; Fraser and Brown 2009; Lacerda 2009), the light curve of this object has two unequal to each other maxima. Analyzing the light curve, the authors (Rabinowitz et al. 2006; Lykawka et al. 2012) concluded that Haumea has an elongated ellipsoidal shape. However, yet no direct evidence about orientation of rotation axis of Haumea, so it is convenient to assume that this axis is perpendicular to line of sight of the observer. Assuming that the Haumea has equilibrium form of the Jacobi ellipsoid, then its semiaxes are equal to (Rabinowitz et al. 2006)

$$ \begin{aligned} & a_{1} = 980\mbox{ km}, \\ & a_{2} = 759\mbox{ km}, \\ & a_{3} = 498\mbox{ km}, \\ & R = (a_{1}a_{2}a_{3})^{\frac{1}{3}} \approx 718.178\mbox{ km}, \end{aligned} $$
(2)

where \(R\) is the average radius of the planet.

Next, Haumea has two small satellites (Ragozzine and Brown 2009) that has allowed to determine its mass

$$ M = 4.006 \cdot 10^{24}\mbox{ g} $$
(3)

and average density

$$ \rho = 2.582 \mbox{ g}/\mbox{cm}^{3}. $$
(4)

Besides, studying the reflection spectrum showed that the surface of Haumea is covered with almost pure water crystal ice, with insignificant content of impurity of more difficult substances. It is important that the similar spectrums have also its satellites. This suggests that the satellites were formed of substance of the outer layer of Haumea.

About satellites of Haumea we know the following (Ragozzine and Brown 2009). The largest and most bright is the outer satellite Hi’iaka. It has the mass \(m_{1} = 1.79 \cdot 10^{19}\mbox{ kg}\) (\(0.00451M\)) and the diameter of about 310 km. The Hi’iaka’s orbit is almost circular (\(e = 0.0513\)) with the semi-major axis \(a_{1} = 49880\mbox{ km}\) and the orbital period \(T_{1} = 49.462\mbox{ d}\). The second satellite (Namaka) revolves around Haumea for \(T_{2} = 18.2783\mbox{ d}\). on highly elliptical orbit with \(e = 0.249\) and \(a_{2} = 25657\mbox{ km}\). Namaka has the small mass \(m_{2} = 1.79 \cdot 10^{18}\mbox{ kg}\) and the diameter of about 170 km. The size and mass of the satellites is calculated under the assumption that their albedo coincides with the albedo of Haumea. The orbit planes of the satellites are inclined to each other at an angle 13.2°. According to hypothesis of impact (Rabinowitz et al. 2006; Leinhardt et al. 2010), the satellites appeared as a result of collision of Haumea with another asteroid. The collision occurred in early history of the Solar system for billions of years ago and the Hi’iaka’s orbit gradually widened. The Namaka’s orbit highly disturbed by the orbital resonance \(8:3\) with more massive Hi’iaka. Both satellites are gradually removed from Haumea due to the tidal acceleration.

By the above remarks we turn to the formulas for the triaxial Jacobi ellipsoids (see Appel 1932; Chandrasekhar 1969):

$$ \begin{aligned} & \frac{\varOmega^{2}}{2\pi G\rho } = \frac{A_{1}a_{1}^{2} - A_{2}a_{2} ^{2}}{a_{1}^{2} - a_{2}^{2}}; \\ & a_{1}^{2}a_{2}^{2}\frac{A_{2} - A_{1}}{a_{1}^{2} - a_{2}^{2}} = A_{3}a_{3}^{2}, \end{aligned} $$
(5)

where

$$ \begin{aligned}[c] & I = a_{1}a_{2}a_{3}\int_{0}^{\infty } \frac{du}{\Delta ( a_{i},u ) }, \\ & A_{i} = a_{1}a_{2}a_{3}\int_{0}^{\infty } \frac{du}{(a_{i}^{2} + u) \Delta ( a_{i},u ) }, \\ & \Delta ( a_{i},u ) = \sqrt{(a_{1}^{2} + u)(a_{2}^{2} + u)(a_{3}^{2} + u)}. \end{aligned} $$
(6)

By using these equations and exact value of the rotation period (1), we can specify the shape of Haumea:

$$ \begin{aligned} &a_{1} = 978\mbox{ km}, \\ &a_{2} = 757.61\mbox{ km}, \\ &a_{3} = 496\mbox{ km}, \\ &R = (a_{1}a_{2}a_{3})^{\frac{1}{3}} = 716.29\mbox{ km}, \end{aligned} $$
(7)

and its average density

$$ \rho = 2.602 \mbox{ g}/\mbox{cm}^{3}. $$
(8)

Further, we use these values as basic parameters to calculate the refined model of Haumea.

In this paper we eliminate some gaps in research of 3D internal gravitational potentials of the inhomogeneous triaxial ellipsoidal model and also find its rotational and gravitational energy. We apply this model for studying the internal structure and near-equilibrium form of the dwarf planet Haumea. In Sect. 2 we carefully study its dynamic properties, and we achieve, that the gravitational potential on an external and an intermediate (between the core and the mantle) surfaces was square-law function from coordinates. In Sect. 3 we study the level surfaces in this model and develop necessary mathematical tools. In Sects. 4 and 5 the formulas are used for calculations of the refined Haumea model. We come to conclusion that the Haumea may not be in exact equilibrium, since the angular velocity of outer surface is slightly greater than the angular velocity of a core. This fact is very important for the considered process of secular evolution of the Haume’s model, which leads to separating the masses of ice and to formation of the satellites. In Sect. 6 we study the parameters of rotation of Haumea, which this planet had before separation from it two satellites Hi’iaka and Namaka. In Sect. 7 we present some additional arguments in favor of physical reality of the latent mechanism of stresses between a stone core and an ice shell. Other applications of this mechanism we consider in Sect. 8.

2 Statement of the problem and gravitational potential of inhomogeneous triaxial ellipsoidal model

We suppose that the figure of inhomogeneous planet consists of two subsystems: from the internal homogeneous ellipsoidal stone core with the density \(\rho_{\mathit{core}}\) and the surface \(S'\)

$$ \frac{x_{1}^{2}}{a_{1}^{\prime 2}} + \frac{x_{2}^{2}}{a_{2}^{\prime 2}} + \frac{x_{3}^{2}}{a_{3}^{\prime 2}} = 1, \quad a'_{1} > a'_{2} >a'_{3}, $$
(9)

on which is superimposed a layer of ice in the form of homogeneous ellipsoidal shell with the outer surface \(S\)

$$ \frac{x_{1}^{2}}{a_{1}^{2}} + \frac{x_{2}^{2}}{a_{2}^{2}} + \frac{x _{3}^{2}}{a_{3}^{2}} = 1 $$
(10)

with the semiaxes \(a_{1} > a_{2} > a_{3}\) and the density \(\rho_{\mathit{sh}}\). For stability of this figure it is necessary to accept \(\rho_{\mathit{core}} > \rho_{\mathit{sh}}\).

Consider the equilibrium equation of a liquid mass, rotating around the axis \(\mathit{Ox}_{3}\) with the angular velocity \(\varOmega \)

$$ \operatorname{grad} p = \rho \operatorname{grad} \varPhi , $$
(11)

where \(p ( \boldsymbol{x} ) \) is the pressure in liquid, and total potential \(\varPhi ( \boldsymbol{x} ) \) is equal to the sum of gravitational \(\varphi ( \boldsymbol{x} ) \) and centrifugal potentials

$$ \varPhi ( \boldsymbol{x} ) = \varphi ( \boldsymbol{x} ) + \frac{1}{2} \varOmega^{2} \bigl( x_{1}^{2} + x_{2}^{2} \bigr) . $$
(12)

According to (11), for equilibrium of a rotating configuration is necessary, that the surfaces of equal pressure \(p ( \boldsymbol{x} ) = \mathit{const}\) and density \(\rho ( \boldsymbol{x} ) = \mathit{const}\) coincided with the level surfaces

$$ \varPhi ( \boldsymbol{x} ) = \varphi ( \boldsymbol{x} ) + \frac{1}{2} \varOmega^{2} \bigl( x_{1}^{2} + x_{2}^{2} \bigr) = \mathit{const}. $$
(13)

Therefore, for equilibrium of the model you must require that the gravitational potential on outer \(S\) and inner \(S'\) surfaces of icy shell was a quadratic function of coordinates \(\boldsymbol{x}\). This condition imposes strong limitations on the model. First of all, the shell may not be a classic homeoid. This follows from the fact that the external potential of homogeneous ellipsoidal core in the points of icy layer

$$ \varphi ( \boldsymbol{x} ) = \pi G\rho_{\mathit{core}} \int_{\lambda}^{\infty } \frac{du}{\Delta ( a'_{i},u ) } \biggl( 1 - \frac{x_{i}^{2}}{a_{i}^{\prime 2} + u} \biggr) , $$
(14)

where \(\Delta ( a'_{i},u ) \) from (6), isn’t the square function from coordinates. Here the ellipsoidal coordinate \(\lambda ( \boldsymbol{x} ) \) is a positive root of the cubic equation

$$ \frac{x_{1}^{2}}{a_{1}^{\prime 2} + \lambda } + \frac{x_{2}^{2}}{a _{2}^{\prime 2} + \lambda } + \frac{x_{3}^{2}}{a_{3}^{\prime 2} + \lambda } = 1. $$
(15)

In accordance with general theory, the potential is quadratic function only in the case when the outer ellipsoidal shell is confocal with the elliptical core. In other words, the homogeneous outer layer in this model must be the focaloid. This requirement is not trivial and is associated with some specific gravitational properties of homogeneous and heterogeneous focaloids, which were studied in the classical works (Maclaurin and Laplace; Hamy (see Todhunter 1973); Pizzetti 1933), and nowadays more thoroughly in Kondratyev (1989, 2003, 2007). For existence of a focaloid the focal points of the all three elliptic cross-sections \(S'\) and \(S\) must match:

$$ a_{1}^{\prime 2} = a_{1}^{2} - \lambda ,\qquad a_{2}^{\prime 2} = a_{2}^{2} - \lambda ,\qquad a_{3}^{\prime 2} = a_{3}^{2} - \lambda , $$
(16)

where \(\lambda \) is the largest root of cubic equation (15).

Now find the potentials of our combined model. First, we consider the potential at the points \(x_{i}\) of the outer surface \(S\), which consists of two members:

$$ \varPhi (\boldsymbol{x}) = \varphi_{\mathit{sh}} ( \rho_{\mathit{sh}} ) + \varphi_{\mathit{core}} ( \rho_{\mathit{core}} ) . $$
(17)

Here \(\varphi_{\mathit{sh}} ( \rho_{\mathit{sh}} ) \) is contribution to the potential from the shell, which according to the modified theorem of attraction of focaloids (Kondratyev 2007, p. 146), will be equal to

$$ \varphi_{\mathit{sh}} ( \rho_{\mathit{sh}} ) = \biggl( 1 - \frac{a'_{1}a'_{2}a'_{3}}{a_{1}a_{2}a_{3}} \biggr) \varphi_{\mathit{core}} ( \rho_{\mathit{sh}} ) , $$
(18)

and \(\varphi_{\mathit{core}} ( \rho_{\mathit{sh}} ) \) is the internal potential of homogeneous ellipsoid with the surface \(S\) and the density \(\rho_{\mathit{sh}}\)

$$ \varphi_{\mathit{core}} ( \rho_{\mathit{sh}} ) = \pi G\rho_{\mathit{sh}} \bigl( I - A_{i}x_{i}^{2} \bigr) , $$
(19)

where the coefficients are defined in (6).

The second member in (17) represents the potential on external point from the ellipsoid with density \(\rho_{\mathit{core}}\). According to the classical Maclaurin–Laplace theorem, \(\varphi_{\mathit{core}} ( \rho_{\mathit{core}} ) \) can be expressed through the known potential \(\varphi_{\mathit{sh}} ( \rho_{\mathit{sh}} ) \):

$$ \varphi_{\mathit{core}} ( \rho_{\mathit{core}} ) = \frac{a'_{1}a'_{2}a'_{3}}{a _{1}a_{2}a_{3}} \frac{\rho_{\mathit{core}}}{\rho_{\mathit{sh}}}\varphi_{\mathit{sh}} ( \rho _{\mathit{sh}} ) . $$
(20)

As a result, the potential (17) on outer surface it is possible to write down in the form

$$ \tilde{\varPhi } = \pi G\rho_{m}\bigl(I - A_{i}x_{i}^{2} \bigr), $$
(21)

where we introduced the “average” density \(\rho_{m}\)

$$ \rho_{m} = \rho_{\mathit{sh}} + (\rho_{\mathit{core}} - \rho_{\mathit{sh}})\frac{a'_{1}a'_{2}a'_{3}}{a _{1}a_{2}a_{3}}. $$
(22)

Thus, introducing the average density (22) we achieve that the potential (21) on the outer surface \(S\) was indeed a quadratic function of coordinates.

Besides, the potential at surface \(S'\), which separates the stone core from the icy shell must also be a quadratic function of coordinates \(x_{i}\). This potential can also be represented as a sum of two terms (compare with (17))

$$ \tilde{\varPhi '}(\boldsymbol{x}) = \varphi '_{\mathit{sh}} ( \rho_{\mathit{sh}} ) + \varphi '_{\mathit{core}} ( \rho_{\mathit{core}} ) . $$
(23)

However, unlike (17), the first member \(\varphi '_{\mathit{sh}} ( \rho_{\mathit{sh}} ) \) in (23) presents now the potential of the shell on its inner surface. The second term in (23) \(\varphi '_{\mathit{core}} ( \rho_{\mathit{core}} ) \) presents the contribution from the core

$$ \varphi '_{\mathit{core}} ( \rho_{\mathit{core}} ) = \pi G \rho_{\mathit{core}} \bigl( I' - A'_{i}x_{i}^{2} \bigr) , $$
(24)

where

$$ \begin{aligned}[c] & A'_{i} = a'_{1}a'_{2}a'_{3}\int_{0}^{\infty } \frac{du}{(a_{i}^{ \prime 2} + u)\Delta ( a'_{i},u ) }, \\ & \Delta ( a'_{i},u ) = \sqrt{(a_{1}^{\prime 2} + u)(a_{2} ^{\prime 2} + u)(a_{3}^{\prime 2} + u)}. \end{aligned} $$
(25)

In turn, the shell’s potential \(\varphi '_{\mathit{sh}} ( \rho_{\mathit{sh}} ) \) we present now as a difference of the potentials of two ellipsoids with the same density \(\rho_{\mathit{sh}}\):

$$ \varphi '_{\mathit{sh}} ( \rho_{\mathit{sh}} ) = \pi G \rho_{\mathit{sh}} \bigl[ \bigl( I - A_{i}x_{i}^{2} \bigr) - \bigl( I' - A_{i}^{\prime } x_{i}^{2} \bigr) \bigr] . $$
(26)

Taking into account (24), the formula (23) gives

$$ \begin{aligned}[b] \tilde{\varPhi '} ( \boldsymbol{x} ) & = \pi G ( \rho_{\mathit{core}} - \rho_{\mathit{sh}} ) \bigl( I' - A_{i}^{\prime } x_{i}^{2} \bigr) \\ & \quad {}+ \pi G \rho_{\mathit{sh}} \bigl( I - A_{i}x_{i}^{2} \bigr) . \end{aligned} $$
(27)

To convert the coefficients \(A_{i}^{\prime }\) need to replace the variable of integration \(s = u - \lambda \). After transformation, we have

$$ A_{i}^{\prime } = \frac{a'_{1}a'_{2}a'_{3}}{a_{1}a_{2}a_{3}}A_{i} + \tilde{A}_{i}, $$
(28)

where \(A_{i}\) from (6), and \(\tilde{A}_{i}\) is

$$ \begin{aligned}[c] & \tilde{A}_{i} = a'_{1}a'_{2}a'_{3}\int_{ - \lambda }^{0} \frac{ds}{(a _{i}^{2} + s)\Delta ( a_{i},s ) }, \\ & \Delta ( a_{i},s ) = \sqrt{(a_{1}^{2} + s)(a_{2}^{2} + s)(a _{3}^{2} + s)}. \end{aligned} $$
(29)

After some additional transformations we receive the desired potential at core surface \(S'\)

$$ \tilde{\varPhi '} ( \boldsymbol{x} ) = \mathit{const} - \pi G \bigl[ \rho _{m}A_{i} + ( \rho_{\mathit{core}} - \rho_{\mathit{sh}} ) \tilde{A}_{i} \bigr] x _{i}^{2}. $$
(30)

Thus, the potential (30) on surface \(S'\) is also presented by a quadratic function of coordinates. This property of the potential is important for the theory of equilibrium figures (see also Pizzetti 1933; Martinez et al. 1990).

3 The equipotential surfaces inside the figure

The foregoing suggests that the equilibrium of the rotating configuration should require that the surfaces of equal density coincided with the level surfaces. Thus, for equilibrium in our model, it is necessary to require that the outer surface and the surface between the core and mantle were the level surfaces.

Taking into account Eqs. (10) and (21), the above requirement for the outer surface leads to the following proportionality condition

$$ A_{i}x_{i}^{2} - \frac{\varOmega^{2}}{2\pi G\rho_{m}} \propto \frac{x _{1}^{2}}{a_{1}^{2}} + \frac{x_{2}^{2}}{a_{2}^{2}} + \frac{x_{3}^{2}}{a _{3}^{2}}, $$
(31)

which implies, that there are two equations

$$ a_{1}^{2} \biggl( A_{1} - \frac{\varOmega^{2}}{2\pi G\rho_{m}} \biggr) = a _{2}^{2} \biggl( A_{2} - \frac{\varOmega^{2}}{2\pi G\rho_{m}} \biggr) = A _{3}a_{3}^{2}. $$
(32)

The first of them

$$ \frac{\varOmega^{2}}{2\pi G\rho_{m}} = \frac{A_{1}a_{1}^{2} - A_{2}a_{2} ^{2}}{a_{1}^{2} - a_{2}^{2}} $$
(33)

gives the normalized square of angular velocity as the function \(\frac{a_{2}}{a_{1}}\) and \(\frac{a_{3}}{a_{1}}\), and the second equation

$$ a_{1}^{2}a_{2}^{2}\frac{A_{2} - A_{1}}{a_{1}^{2} - a_{2}^{2}} = A_{3}a _{3}^{2} $$
(34)

implicitly links the relationship of semiaxes of the ellipsoid (10). Analyzing the case of outer surface we note, that our model differs from the classical Jacobi ellipsoid in that important point that the value \(\frac{\varOmega^{2}}{2\pi G\rho_{m}}\) from (33) is normalized to the average density \(\rho_{m}\) from (22).

Similarly, we conclude that for existence of level surface at the boundary \(S'\) must be met two equations

$$ \begin{aligned}[b] & a_{1}^{\prime 2} \biggl( A'_{1} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho _{m}}\tilde{A}_{1} - \frac{\varOmega^{\prime 2}}{2\pi G\rho_{m}} \biggr) \\ &\quad =a_{2}^{\prime 2} \biggl( A'_{2} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho _{m}}\tilde{A}_{2} - \frac{\varOmega^{\prime 2}}{2\pi G\rho_{m}} \biggr) \\ &\quad =a_{3}^{\prime 2} \biggl( A'_{3} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho _{m}}\tilde{A}_{3} \biggr) . \end{aligned} $$
(35)

From (35) follow the important relations

$$ \begin{aligned}[b] \frac{\varOmega^{\prime 2}}{2\pi G\rho_{m}} = \frac{A'_{1}a_{1}^{\prime 2} - A'_{2}a_{2}^{\prime 2} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho_{m}} ( \tilde{A}_{1}a_{1}^{ \prime 2} - \tilde{A}_{2}a_{2}^{\prime 2} ) }{a_{1}^{\prime 2} - a_{2}^{\prime 2} }, \end{aligned} $$
(36)
$$ \begin{aligned}[b] & a_{1}^{\prime 2}a_{2}^{\prime 2}\frac{A_{2} - A_{1} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho_{m}} ( \tilde{A}_{2} - \tilde{A}_{1} ) }{a _{1}^{2} - a_{2}^{2}} \\ &\quad = a_{3}^{\prime 2} \biggl( A_{3} + \frac{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}{\rho_{m}} \tilde{A}_{3} \biggr) , \end{aligned} $$
(37)

which define as the angular velocity \(\varOmega '\), and the shape of ellipsoidal core in Haumea. Note, that in contrast to (33) and (34), in the formulas (35)–(37) appear the additional coefficients \(\tilde{A}_{i}\) from (29). As check we will notice that in the case \(\rho_{\mathit{core}} = \rho_{\mathit{sh}}\) the new equations become equivalent to the Eqs. (33) and (34). It is also useful to notice that for inequalities \(a'_{1} > a'_{2} > a'_{3}\) we have

$$ \tilde{A}_{1} \le \tilde{A}_{2} \le \tilde{A}_{3}. $$
(38)

4 Calculations for Haumea model

Then we will apply our formulas to calculations for the Haumea model. First of all, for the external surface \(S\) from (10) we find from (7) the semiaxes \(a_{i}\) and the normalized coefficients \(A_{i}\):

$$ \begin{aligned} & a_{1} = 1.365369; \qquad A_{1} = 0.4318686; \\ & a_{2} = 1.057686; \qquad A_{2} = 0.598298; \\ & a_{3} = 0.692457; \qquad A_{3} = 0.969833. \end{aligned} $$
(39)

Then, the equilibrium angular velocity (33) is equal to

$$ \frac{\varOmega^{2}}{2\pi G\rho_{m}} = 0.182134. $$
(40)

To calculate angular velocity by the formula (36), we must first find a thickness of the shell. The thickness of the shell in this model may not be arbitrary, and for its calculation it is necessary to equate the densities (22) and (8). This gives another important equation

$$ \frac{a'_{1}a'_{2}a'_{3}}{a_{1}a_{2}a_{3}} = \frac{\rho_{m} - \rho _{\mathit{sh}}}{\rho_{\mathit{core}} - \rho_{\mathit{sh}}}. $$
(41)

Now it is necessary to set the real density of a stone and ice. The density of a stone is about \(\rho_{\mathit{core}} = 3 \mbox{ g}/\mbox{cm}^{3}\), and the density of an ice in the shell is \(\rho_{\mathit{sh}} = 1 \mbox{ g}/\mbox{cm}^{3}\). Taking into account (14), the Eq. (41) for unknown ellipsoidal coordinate \(\lambda \) becomes

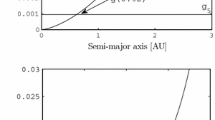
$$ \frac{\sqrt{ ( a_{1}^{2} - \lambda ) ( a_{2}^{2} - \lambda ) ( a_{3}^{2} - \lambda ) }}{a_{1}a_{2}a_{3}} = 0.801. $$
(42)

Numerical solution of the cubic equation (42) gives (Fig. 1)

$$ \lambda \equiv \frac{\lambda }{R^{2}} \approx 0.114. $$
(43)

The value \(\lambda \) from (43) determines the thickness of icy shell in this model.

Fig. 1
figure 1

Numerical solution of the cubic equation (42)

Full size image

Knowing \(\lambda \), by numerical integration we find the ratio of masses

$$ \frac{M_{\mathit{sh}}}{M_{\mathit{core}}} = \biggl( 1 - \frac{a'_{1}a'_{2}a'_{3}}{a_{1}a _{2}a_{3}} \biggr) \frac{\rho_{\mathit{sh}}}{\rho_{\mathit{core}}} = 0.0663. $$
(44)

Thus, the mass of ice shell in the model of Haumea is only 6.6 % on the mass of stone core. Our result for the mass of a shell considerably specifies the previous quality assessments (∼11 %). In favor of the relation (44) says that only in this case the calculated period of axial rotation of Haumea is consistent with the observed period (1) \(T = 3.915483113\mbox{ h}\). On the basis of (44), the mass of the icy shell is equal to

$$ M_{\mathit{sh}} = 2.49 \cdot 10^{23}\mbox{ g}. $$
(45)

By using \(\lambda \) from (43) and the formulas (16), (25) and (29), we find another characteristics of the core of Haumea

$$\begin{aligned} \textstyle\begin{array}[b]{@{}l@{\qquad}l@{\qquad}l} a'_{1} = 1.322964; & A'_{1} = 0.402696;& \tilde{A}_{1} = 0.056469; \\ a'_{2} = 1.002348; & A'_{2} = 0.575913;& \tilde{A}_{2} = 0.096262; \\ a'_{3} = 0.604563; & A'_{3} = 1.021391;& \tilde{A}_{3} = 0.243883. \end{array}\displaystyle \end{aligned}$$
(46)

Then, by the formula (36) we find the square of angular velocity on the core surface \(S'\)

$$ \frac{\varOmega ^{\prime 2}}{2\pi G\rho_{m}} = 0.1710101472. $$
(47)

Comparing the values of (40) and (47) we see that difference of squares of the angular velocities at the outer surface and at the boundary between a core and a shell

$$ \frac{\varOmega^{2} - \varOmega ^{\prime 2}}{2\pi G \rho_{m}} = 0.0111242667 > 0 $$
(48)

is positive. This means that two surfaces \(S\) and \(S'\) are not simultaneously level surfaces. In other words, we deal with the almost equilibrium model of Haumea. This fact plays a key role when studying evolution of the planet.

By using our formulas, we have made much calculations, and obtained the following results. Figure 2 shows the dependence \(\lambda \) from oblateness \(\varepsilon_{13}\) of an outer surface. We see that thickness of an ice layer has a maximum at \(\varepsilon_{13} = 0\) i.e. (for the Maclaurin spheroid). Along sequence of equilibrium models the thickness of the icy layer monotonically decreases and in limiting case of a needle the thickness is zero.

Fig. 2
figure 2

Dependence of the square of the normalized shell thickness \(\lambda \) from meridian oblateness \(\varepsilon_{13}\) of outer boundary of the model. The dashed line shows the coordinate \(\lambda \) for the Haumea’s model

Full size image

Figure 3 (top curve) shows dependence of \(\frac{\varOmega^{2}}{2\pi G\rho _{m}}\) from oblateness \({\varepsilon }_{13}\) of outer boundary of the model. The lower schedule shows the similar dependence for \(\frac{\varOmega ^{\prime2}}{2\pi G\rho_{m}}\), but at the surface between the core and the shell. Namely for these angular velocities both surfaces become the level surfaces. We will point to one important detail: on the presence on the lower curve of a local maximum:

$$ {\varepsilon }_{13} \approx 0.4292, \qquad \frac{\varOmega ^{\prime2}}{2 \pi G\rho_{m}} \approx 0.17653. $$
(49)

It is characteristic that the oblateness \({\varepsilon }_{13}\) from (49) is very close to the point of Haumea \({\varepsilon }_{13} \approx 0.4298\).

Fig. 3
figure 3

The relations \(\frac{\varOmega^{2}}{2\pi G\rho_{m}}\) (upper graph) and \(\frac{\varOmega ^{\prime 2}}{2\pi G\rho_{m}}\) (dots) as the functions of oblateness \(\varepsilon_{13}\)

Full size image

As we see, angular velocity in points of an external surface of an ice layer is always a little more, than in points of a surface of a stone core. Besides, the difference between these angular velocities decreases along the sequence (Fig. 4).

Fig. 4
figure 4

Dependence of the normalized difference of the squares angular velocities \(\frac{\varOmega^{2} - \varOmega ^{\prime 2}}{2\pi G\rho_{m}}\) from the oblateness \({\varepsilon }_{13}\) of the outer surface along sequence of inhomogeneous ellipsoidal equilibrium figures

Full size image

This distinction of angular velocities leads to launching the mechanism of relaxation inside Haumea.

5 Near-equilibrium mechanism of formation of satellites

Thus, the rotational angular velocity at an outer surface is always slightly more than the angular velocity of a core:

$$ \frac{\varOmega^{2} - \varOmega ^{\prime 2}}{2\pi G\rho_{m}} \approx 0.06 \frac{ \varOmega^{2}}{2\pi G\rho_{m}}. $$
(50)

In other words, the coating of the ellipsoidal stone core by a layer of ice leads to the fact that in the model appears very small deviation from equilibrium. Such deviation plays a key role in emergence of internal tension between the icy layer and the stone core.

Consider the process of accumulation of stresses in the ice layer in detail. First, we recall one important property of the Jacobi ellipsoids: if its angular momentum is fixed, the slower the ellipsoid rotates, the more it expands in the equatorial plane (Fig. 5).

Fig. 5
figure 5

Dependence of the normalized square of angular velocity from oblateness \({\varepsilon }_{13}\) along sequence of the Maclaurin spheroids (top curve, at the point \(K\) is the maximum), and along sequence of the Jacobi ellipsoids (lower curve, which starts at the point \(B\)). The dotted lines show two triaxial equilibrium figures of with big (a) and smaller (b) rotation

Full size image

Consider the angular momentum \(L_{J}\) for the Jacobi ellipsoid (Chandrasekhar 1969; Kondratyev 2003):

$$ \frac{L_{J}}{\sqrt{GM^{3}R}} = 0.1732 \cdot \varOmega_{J} \biggl( \frac{a _{1}^{2} + a_{2}^{2}}{R^{2}} \biggr) . $$
(51)

Differentiating (51), after transformations and some substitutions we will receive the ratio

$$ \frac{\Delta a'_{1}}{a'_{1}} \approx \frac{1}{2 ( \frac{a'_{1}}{R} ) ^{2}}\sqrt{\frac{\frac{\varOmega^{2} - \varOmega ^{\prime 2}}{2\pi G\rho_{m}}}{\frac{\varOmega^{2}}{2\pi G\rho_{m}}}}. $$
(52)

Thus, the difference of squares angular velocity (50) allows us to estimate the relative deformation \(\frac{\Delta a'_{1}}{a'_{1}}\) of a core. Substituting into (52) the found values, we find

$$ \frac{\Delta a_{1}}{a_{1}} \approx 0.1. $$
(53)

We see that the relaxation process (or process of alignment of the angular velocities on two surfaces) can lead to considerable (up to 10 %) lengthening the longest axis.

As a result, at changing the shape of a core appear the shear stresses in the icy mantle (Fig. 6).

Fig. 6
figure 6

The scheme of deformation of an ellipsoid (inner arrows) and influence of this deformation on stretching the icy shell (outer dark band)

Full size image

In stage of an elastic deformation the shear modulus for the ice is \(\mu \). Accumulation of these stresses will cause, in turn, the deformation of an icy shell.

Now it is important to emphasize that the difference between the angular velocities (50) on the surface and the intermediate boundary between the core and the mantle is only 6 % from \(\frac{\varOmega^{2}}{2\pi G\rho _{m}}\), so the relaxation processes inside the planet will proceed very slowly. Consider the sequence of stages of evolution. The ice is a more plastic than the stone, and on the first stage exactly the outer border of the planet comes to equilibrium. But at this stage the process of evolution does not stop, because the core’s surface is not yet equipotential (the core should spin slightly slower). Therefore, the second phase of evolution begins that leads to a small change of the core shape. The decrease of rotation of the figure will cause an increase of the equatorial section of a stone core (Fig. 5). Under these conditions, in the outer icy shell are accumulating the shear stresses. But the ice shell is deformed elastically as long as the stresses do not reach the tensile strength, then there is the restructuring the ice mantle. As found in (53), the relaxation changes of the major semiaxis in the core can reach the value \(\frac{\Delta a_{1}}{a_{1}} \approx 0.1\), therefore during the evolution, the above restructuring the mantle must takes place repeatedly.

The restructuring is repeated \(n\) times and, as the result, on the sharp ends of the rapidly spinning elongated ellipsoid occur accumulation of significant masses of ice. Then, there is almost equilibrium separation of mass of ice, as leads to formation of satellites. It is important that the model allows to estimate the relation of mass of the satellites to the mass of the shell (see (45)):

$$ \kappa = \frac{m_{1} + m_{2}}{M_{\mathit{sh}}} \approx 8~\%. $$
(54)

Thus, for formation of two satellites of the planet Haumea it has been spent only 8 % from the mass of a shell.

Further evolution of the satellites orbits happened under strong tidal influence of the planet. The external satellite Hi’iaka has greatest mass and its orbit under the tidal influence was gradually rounded and the considerably moved away from the planet on \(a_{1} = 49880\mbox{ km}\). In this process the part of the angular momentum of the planet was transferred towards the satellites, therefore the rotation of Xaymea was slowed down.

6 Rotation of Haumea before separating the satellites

To determine how fast the planet rotated before a separation from it of the satellites Hi’iaka and Namaka, we will perform some calculations. The angular momentum of a homogeneous ellipsoidal core is

$$ L_{\mathit{core}} = \frac{\varOmega }{5}M_{\mathit{core}} ( \rho_{\mathit{core}} ) \bigl( a _{1}^{\prime 2} + a_{2}^{\prime 2} \bigr) , $$
(55)

and the angular momentum of the planet’s shell is equal to difference

$$ \begin{aligned}[b] L_{\mathit{sh}} = \frac{\varOmega }{5} \bigl[ M_{\mathit{core}} ( \rho_{\mathit{sl}} ) \bigl( a_{1}^{2} + a_{2}^{2} \bigr) - M_{\mathit{core}} ( \rho_{\mathit{sh}} ) \bigl( a_{1}^{\prime 2} + a_{2}^{\prime 2} \bigr) \bigr] . \end{aligned} $$
(56)

Besides, the orbital angular moments of Haumea’s satellites are now equal to

$$ \begin{aligned} L_{1} = m_{1}\sqrt{G ( M + m_{1} ) a_{1}}; \\ L_{2} = m_{2}\sqrt{G ( M + m_{2} ) a_{2}}. \end{aligned} $$
(57)

Substituting the known parameters, we find

$$ \begin{aligned} &L_{\mathit{core}} = 4.665 \cdot 10^{36}\ \frac{\mbox{g} {\cdot} \mbox{cm}^{2}}{\mbox{sec}}; \\ &L_{\mathit{sh}} = 7.041 \cdot 10^{35}\ \frac{\mbox{g} {\cdot}\mbox{cm}^{2}}{\mbox{sec} }; \\ &L_{1} = 6.550 \cdot 10^{35}\ \frac{\mbox{g}{\cdot}\mbox{cm}^{2}}{\mbox{sec} }; \\ &L_{2} = 4.689 \cdot 10^{34}\ \frac{\mbox{g}{\cdot}\mbox{cm}^{2}}{\mbox{sec} }. \end{aligned} $$
(58)

Then, before separation of satellites, the total angular momentum of Haumea was equal

$$ L_{t} = 6.072 \cdot 10^{36}\ \frac{\mbox{g}{\cdot}\mbox{cm}^{2}}{\mbox{sec}}. $$
(59)

Thus, adding the satellites to the planet Haumea slightly increases its angular momentum:

$$ \frac{L_{t}}{L_{\mathit{core}} + L_{\mathit{sh}}} = 1.130723. $$
(60)

At present, the rotational energy of Xaumea is equal to

$$ E_{\mathit{rot}} = 1.197 \cdot 10^{33}\ \frac{\mbox{g} {\cdot} \mbox{cm}^{2}}{\mbox{sec}^{2}}, $$
(61)

and before separation of the satellites the energy was little more

$$ E_{\mathit{rot}} = 1.530 \cdot 10^{33}\ \frac{\mbox{g} {\cdot} \mbox{cm}^{2}}{\mbox{sec}^{2}}. $$
(62)

The ratio of the rotational energy to the gravitational one for Haumea is equal to

$$ t = \frac{E_{\mathit{rot}}}{\vert W \vert } \approx 0.1376. $$
(63)

The angular momentum (59) is used for calculation of the rotation period of Haumea before separation of its satellites. It turns out that this period was less on \(16^{m}\) and (compare with (1)) is equal to

$$ T \approx 3.64\mbox{ h}. $$
(64)

Our approach to the formation of satellites is consistent with the view that was proposed earlier in (Ortiz et al. 2012).

Another important characteristic is the normalized square of angular velocity. We see that instead of modern equilibrium value \(\frac{\varOmega ^{\prime 2}}{2\pi G\rho_{m}} = 0.17101\), in the era before separation of satellites, Xaumea had

$$ \frac{\varOmega ^{\prime2}}{2\pi G\rho_{m}} \approx 0.184. $$
(65)

It is interesting to note that this value is somewhat less than the maximum possible for the Jacobi ellipsoids

$$ \frac{\varOmega^{2}}{2\pi G\rho } \approx 0.187115. $$
(66)

This is surprising argument in favor of the fact that before separation of satellites the planet Haumea was also in near-equilibrium condition.

7 Physical reality of the latent mechanism of tensions between stone core and icy shell

To gain greater insight into the model, we note the following.

7.1

The existence of level surfaces directly follows from the equation of hydrostatic equilibrium (11) and is a fundamental property of any figure of relative equilibrium.

7.2

Analyzing the detailed properties of level surfaces in the triaxial equilibrium figures we come to a conclusion about the existence of stresses between the ellipsoidal stone core and the outer icy shell.

7.3

To compute the level surfaces, we need at first to find the gravitational potential of an inhomogeneous ellipsoid. The key to understanding these questions is related to finding the quadratic potential on two surfaces (at the outer surface and at the surface of a core). Introducing the average density \(\rho_{m}\) from (22), we try to obtain that the potential at outer surface of the model was indeed a quadratic function of the coordinates. To estimate the parameters of an ice shell, we equate the average density \(\rho_{m}\) and the observed density \(\rho = 2.602 \ \mbox{g}/\mbox{cm}^{3}\). This allows to get real values for the ice shell thickness \(h \approx 30\mbox{ km}\) and its mass \(M_{\mathit{sh}} = 2.5 \cdot 10^{23}\mbox{ g}\). The mass of the icy shell is only ∼6 % of mass of the planet Haumea, and this value specifies the previous estimate (∼11 %).

7.4

Another important conclusion is that inside the equilibrium heterogeneous ellipsoidal figure the level surfaces may not be strictly identical with the surfaces of equal density. Really, our model with \(\frac{\varOmega^{2}}{2\pi G\rho_{m}} = 0.182134\) has the outer level surface, whereas the surface of stone core is not level. That the border of a core was a level surface, its rotation must be reduced to the value \(\frac{\varOmega ^{\prime 2}}{2\pi G\rho_{m}} = 0.171010\). Although this difference is small \(\frac{\varOmega^{2} - \varOmega ^{\prime 2}}{\varOmega^{2}} \approx 0.06\), the one dynamically is still very important.

7.5

In the absence of coherence between two level surfaces, the inhomogeneous ellipsoidal model can only be in the near-equilibrium condition. The ice is more plastic than the stone, so that at beginning the evolution the outer surface of icy shell will be in hydrostatic equilibrium. However, the stone core is rotating slightly faster than necessary for its equilibrium, so that the core begins to slowly change its form. The decrease in rotation of the figure will cause an increase of the equatorial section of a stone core. Under these conditions, in the outer icy shell accumulate shear stresses. The situation here is that this restructuring will bring the planet to equilibrium, but at the same time will inevitably appear the tensile stresses in the crystalline ice shell. The relaxation process of alignment angular velocities can lead to a significant (up to 10 %) lengthening the longest axis. As a result, on the sharp ends of rapidly spinning elongated ellipsoid there is an accumulation of the significant masses of ice. Then, there is the near-equilibrium separation of the ice mass from the planet, which leads to the formation of its satellites.

7.6

We calculated, that adding the satellites slightly increases angular momentum of the planet and reduces its rotation period on \(16^{m}\) (\(T \approx 3.64\mbox{ h}\)). In addition, it was shown that before separation of satellites the Haumea was in near-equilibrium condition. Based on this, was designed a latent mechanism of separation of the satellites. With accumulation of the stresses, with sharp ends of rapidly rotating Haumea begin to separate the masses of ice, which leads to formation of the satellites. For formation of two satellites needed only 8 % of the shell’s mass. Our approach to the formation of satellites is consistent with the view that was proposed earlier in Ortiz et al. (2012).

Comparison with the available observations reveals good internal consistency of our model.

8 Other applications of the mechanism

Note that developed here the latent mechanism of action of stresses between the inner layers of equilibrium figure is not designed exclusively for Haumea. This mechanism could be extended also to other ice-covered planets or satellites.

It is important to emphasize that for axisymmetric spheroids with a small oblateness the effect of action of this mechanism will be reversed to the above. Indeed, for the Maclaurin spheroids (in Fig. 5 they are on a curve up to \(K\) point), the tensions in a ice shell will be directed from equator to poles. Therefore, accumulation of these stresses will lead to a rupture of the icy layer on equator. Such equatorial grooves are really observed, for example, on Charon’s surface (Cruikshank et al. 2015).

It is also well known that the flattening of the Earth a little more (this is effect of the second order of smallness) than this allows for the Earth the classical theory of equilibrium figures (Moritz and Hofmann 2005). Our method also can explain this fact as result of a full icing of the Earth in the remote past.

Of course, all these tasks are the topic of research for other articles.

9 Discussion

The dwarf planet Haumea is unique object. It is the only example, known in the nature, when the configuration left the sequence of flattened Maclaurin spheroids and settled on the sequence of triaxial ellipsoids.

The main result of this paper consists in constructing the near-equilibrium model of the dwarf planet Haumea and developing the latent mechanism of accumulation of the icy masses at the sharp ends of rapidly rotating planet. The model differs from the equilibrium classical Jacobi ellipsoid and represents a non-uniform equilibrium figure of deformable gravitating mass with additional superficial tension from the ice layer. By analyzing the properties of the level surfaces we come to a conclusion about existence of stresses between the stone core and the icy shell.

Using equilibrium conditions, we have received a cubic equation for the shell thickness \(h\), from which it follows \(h \approx 30\mbox{ km}\) and that the mass of the shell is only 6.6 % from mass of the stone core. Inside heterogeneous ellipsoidal figure of equilibrium the level surfaces can’t be strictly identical with the surfaces of equal density. Although difference \(\varOmega^{2} - \varOmega ^{\prime 2} \approx 0.06 \varOmega^{2}\) is very small, this dynamical fact is very important since activates a special relaxation mechanism that aligns this distinction.

In favor of this near-equilibrium mechanism says that the ice on Haumea is in the crystalline state (possibly due to radioactive heating). This circumstance is significant, because only in the crystalline ice can accumulate the shear stresses. The situation is that restructuring the core brings the planet to equilibrium, but at the same time will inevitably appear the tensile stresses in the crystalline ice shell. The relaxation may lead to a significant (up to 10 %) lengthening the equatorial body size.

As a result, on the sharp ends of rapidly spinning elongated ellipsoid there is an accumulation of the significant masses of ice. The relaxation processes inside the planet will proceed very slowly. Then, there is the near-equilibrium separation of the ice mass from the planet, which leads to the formation of its satellites. For formation of two satellites of the planet Haumea it has been spent only 8 % from the mass of a shell.

Before separation of satellites the planet Haumea was in near-equilibrium state, and its angular momentum was at 1.13 more, and the period of rotation was \(16^{m}\) shorter and made \(T \approx 3.64\mbox{ h}\).

The mechanism predicts that the orbits of satellites can not deviate much from the equatorial plane of Haumea. This is consistent with observations: really, the orbit of Namaka is almost in the equatorial plane, and the orbit of Hi’iaka deviates only on 13°.

The new mechanism can be useful also for studying the evolution of other ice-cover planets and satellites.