1 Introduction

Although standard four-dimensional (4D) General Relativity (GR) is believed to be the correct description of gravity at the classical level, its quantization faces many well-known problems. Therefore, three-dimensional (3D) gravity has gained much interest, since classically it is much simpler and thus one can investigate more efficiently its quantization. Amongst others, in 3D gravity one obtains the Banados-Teitelboim-Zanelli (BTZ) black hole (Banados et al. 1992), which is a solution to the Einstein equations with a negative cosmological constant. This black-hole solution presents interesting properties at both classical and quantum levels, and it shares several features of the Kerr black hole of 4D GR (Carlip 1995).

Furthermore, remarkable attention was addressed recently to topologically massive gravity, which is a generalization of 3D GR that amounts to augment the Einstein-Hilbert action by adding a Chern-Simons gravitational term, and thus the propagating degree of freedom is a massive graviton, which amongst others also admits BTZ black-hole as exact solutions (Deser et al. 1982a, 1982b). The renewed interest on topologically massive gravity relies on the possibility of constructing a chiral theory of gravity at a special point of the parameter-space, as it was suggested in Li et al. (2008). This idea has been extensively analyzed in the last years (Strominger 2008; Carlip et al. 2008, 2009; Carlip 2008; Giribet et al. 2008; Park 2008; Blagojevic and Cvetkovic 2009; Grumiller et al. 2008; Garbarz et al. 2009; Grumiller and Johansson 2008, 2009; Henneaux et al. 2009), leading to a fruitful discussion that ultimately led to a significantly better understanding of the model (Maloney et al. 2010). Moreover, another 3D massive gravity theory known as new massive gravity (Bergshoeff et al. 2009, 2010) (where the action is given by the Einstein-Hilbert term plus a specific combination of square-curvature terms which gives rise to field equations with a second order trace) have attracted considerable attention, this theory also admits interesting solutions, see for instance Clement (2009a, 2009b), Oliva et al. (2009). Furthermore, 3D gravity with torsion has been extensively studied in Mielke and Baekler (1991), Garcia et al. (2003), Blagojevic and Cvetkovic (2008a, 2008b), Blagojevic et al. (2009), Gonzalez and Vasquez (2011) and references therein.

On the other hand, hairy black holes are interesting solutions of Einstein’s Theory of Gravity and also of certain types of Modified Gravity Theories. The first attempts to couple a scalar field to gravity was done in an asymptotically flat spacetime. Then, hairy black hole solutions were found Bocharova et al. (1970), Bekenstein (1974, 1975) but these solutions were not examples of hairy black hole configurations violating the no-hair theorems because they were not physically acceptable as the scalar field was divergent on the horizon and stability analysis showed that they were unstable (Bronnikov and Kireyev 1978). To remedy this a regularization procedure has to be used to make the scalar field finite on the horizon. Hairy black hole solutions have been extensively studied over the years mainly in connection with the no-hair theorems. The recent developments in string theory and specially the application of the AdS/CFT principle to condense matter phenomena like superconductivity (for a review see Hartnoll 2009), triggered the interest of further study of the behavior of matter fields outside the black hole horizon (Gubser 2005, 2008). There are also very interesting recent developments in Observational Astronomy. High precision astronomical observations of the supermassive black holes may pave the way to experimentally test the no-hair conjecture (Sadeghian and Will 2011). Also, there are numerical investigations of single and binary black holes in the presence of scalar fields (Berti et al. 2013). The aforementioned is a small part on the relevance that has taken the study of hairy black holes currently in the field of physics, for more details see for instance Gonzalez et al. (2013, 2014) and references therein. Also, we refer the reader to references Martinez and Zanelli (1996), Henneaux et al. (2002), Zhao et al. (2014), Xu and Zou (2014), Cardenas et al. (2014) and references therein, where black holes solutions in three space-time dimensions with a scalar field (minimally and/or conformally) coupled to gravity have been investigated.

In the present work we are interested in investigating the existence of 3D hairy black holes solutions for theories based on torsion. In particular, the so-called “teleparallel equivalent of General Relativity” (TEGR) (Einstein 1928; Unzicker and Case 2005; Hayashi and Shirafuji 1979, 1982) is an equivalent formulation of gravity but instead of using the curvature defined via the Levi-Civita connection, it uses the Weitzenböck connection that has no curvature but only torsion. So, we consider a scalar field non-minimally coupled with the torsion scalar, with a self-interacting potential in TEGR, and we find three-dimensional asymptotically AdS, hairy black holes. It is worth mentioning, that this kind of theory (known as scalar-torsion theory), has been studied in the cosmological context, where the dark energy sector is attributed to the scalar field. It was shown that the minimal case is equivalent to standard quintessence. However, the nonminimal case has a richer structure, exhibiting quintessence-like or phantom-like behavior, or experiencing the phantom-divide crossing Geng et al. (2011, 2012), Gu et al. (2013), see also Horvat et al. (2014) for applications of this theory (with a complex scalar field) to boson stars.

It is also worth to mention that a natural extension of TEGR is the so called f(T) gravity, which is represented by a function of the scalar torsion T as Lagrangian density (Ferraro and Fiorini 2007, 2008; Bengochea and Ferraro 2009; Linder 2010a, 2010b). The f(T) theories picks up preferred referential frames which constitute the autoparallel curves of the given manifold. A genuine advantage of f(T) gravity compared with other deformed gravitational schemes is that the differential equations for the vielbein components are second order differential equations. However, the effects of the additional degrees of freedom that certainly exist in f(T) theories is a consequence of breaking the local Lorentz invariance that these theories exhibit. Despite this, it was found that on the flat FRW background with a scalar field, up to second order linear perturbations does not reveal any extra degree of freedom at all (Izumi and Ong 2012). As such, it is fair to say that the nature of these additional degrees of freedom remains unknown. Remarkably, it is possible to modify f(T) theory in order to make it manifestly Lorentz invariant. However, it will generically have different dynamics and will reduce to f(T) gravity in some local Lorentz frames (Li et al. 2011; Weinberg 1972; Arcos et al. 2010). Clearly, in extending this geometry sector, one of the goals is to solve the puzzle of dark energy and dark matter without asking for new material ingredients that have not yet been detected by experiments (Capozziello and Francaviglia 2008; Ghosh and Chattopadhyay 2013). For instance, a Born-Infeld f(T) gravity Lagrangian was used to address the physically inadmissible divergences occurring in the standard cosmological Big Bang model, rendering the spacetime geodesically complete and powering an inflationary stage without the introduction of an inflation field (Ferraro and Fiorini 2008). Also, it is believed that f(T) gravity could be a reliable approach to address the shortcomings of general relativity at high energy scales (Capozziello and De Laurentis 2011). Furthermore, both inflation and the dark energy dominated stage can be realized in Kaluza-Klein and Randall-Sundrum models, respectively (Bamba et al. 2013). In this way, f(T) gravity has gained attention and has been proven to exhibit interesting cosmological implications. On the other hand, the search for black hole solutions in f(T) gravity is not a trivial problem, and there are only few exact solutions, see for instance Capozziello et al. (2013), Atazadeh and Mousavi (2012), Wang (2011), Ferraro and Fiorini (2011a), Hamani Daouda et al. (2011, 2012), Iorio and Saridakis (2012), Gonzalez et al. (2012), Nashed (2013a, 2013b, 2014), Paliathanasis et al. (2014), Rodrigues et al. (2013). Remarkably, it is possible to construct other generalizations, as Teleparallel Equivalent of Gauss-Bonnet Gravity (Kofinas and Saridakis 2014a, 2014b), Kaluza-Klein theory for teleparallel gravity (Geng et al. 2014) and scalar-torsion gravity theories (Geng et al. 2011; Kofinas et al. 2015).

The paper is organized as follows. In Sect. 2 we give a brief review of three-dimensional Teleparallel Gravity. Then, in Sect. 3 we find asymptotically AdS black holes with scalar hair, and we conclude in Sect. 4 with final remarks.

2 3D teleparallel gravity

In 1928, Einstein proposed the idea of teleparallelism to unify gravity and electromagnetism into a unified field theory; this corresponds to an equivalent formulation of General Relativity (GR), nowadays known as Teleparallel Equivalent to General Relativity (TEGR) (Einstein 1928; Unzicker and Case 2005; Hayashi and Shirafuji 1979, 1982), where the Weitzenböck connection is used to define the covariant derivative (instead of the Levi-Civita connection which is used to define the covariant derivative in the context of GR). The first investigations on teleparallel 3D gravity were performed by Kawai almost twenty years ago (Kawai 1993, 1995a, 1995b). The Weitzenböck connection mentioned above has not null torsion. However, it is curvatureless, which implies that this formulation of gravity exhibits only torsion. The Lagrangian density T is constructed from the torsion tensor. To clarify, the torsion scalar T is the result of a very specific quadratic combination of irreducible representations of the torsion tensor under the Lorentz group SO(1,3) (Hehl et al. 1995). In this way, the torsion tensor in TEGR includes all the information concerning the gravitational field. The theory is called “Teleparallel Equivalent to General Relativity” since the field equations are exactly the same as those of GR for every geometry choice.

The Lagrangian of teleparallel 3D gravity corresponds to the more general quadratic Lagrangian for torsion, under the assumption of zero spin-connection. So, the action can be written as (Muench et al. 1998; Itin 2001)

$$ S=\frac{1}{2 \kappa}\int ( \rho_{0} \mathcal{L}_{0}+ \rho_{1} \mathcal{L}_{1}+ \rho_{2} \mathcal{L}_{2}+\rho_{3} \mathcal{L}_{3}+ \rho_{4} \mathcal{L}_{4} ), $$
(1)

where κ is the three-dimensional gravitational constant, ρ i  are parameters, and

$$ \begin{aligned} {}&\mathcal{L}_{0}= \frac{1}{4}e^{a} \wedge\star e_a,\qquad\mathcal{L}_{1}=de^{a} \wedge\star de_{a},\\ &\mathcal{L}_{2}= \bigl(de_{a} \wedge \star e^a\bigr) \wedge\star\bigl(de_b \wedge e^b\bigr),\\ &\mathcal{L}_{3}=\bigl(de^{a} \wedge e^{b}\bigr) \wedge\star(de_{a} \wedge e_{b}),\\ &\mathcal{L}_{4}= \bigl(de_{a} \wedge\star e^b\bigr) \wedge \star \bigl(de_b \wedge e^a\bigr), \end{aligned} $$
(2)

where e a denotes the vielbein, d is the exterior derivative, ⋆ denotes the Hodge dual operator and ∧ the wedge product. The coupling constant \(\rho_{0}=-\frac{8}{3} \varLambda\) represents the cosmological constant term. Moreover, since \(\mathcal{L}_{3}\) can be written completely in terms of \(\mathcal{L}_{1}\), in the following we set ρ 3=0 (Muench et al. 1998). Action (1) can be written in a more convenient form as

$$ S=\frac{1}{2\kappa} \int (T -2\varLambda )\star1, $$
(3)

where ⋆1=e 0∧e 1∧e 2, and the torsion scalar T is given by

$$\begin{aligned} T =& \star \bigl[\rho_{1}\bigl(de^{a} \wedge \star de_{a}\bigr)+\rho_{2}\bigl(de_{a} \wedge e^a\bigr) \wedge\star\bigl(de_b \wedge e^b \bigr) \\ &{}+\rho_{4}\bigl(de_{a} \wedge e^b\bigr) \wedge\star\bigl(de_b \wedge e^a\bigr) \bigr]. \end{aligned}$$
(4)

Expanding this expression in terms of its components, the torsion scalar yields

$$\begin{aligned} T =&\frac{1}{2} (\rho_{1}+\rho_{2}+ \rho_{4})T^{abc}T_{abc}+\rho _{2}T^{abc}T_{bca} \\ &{}- \rho_{4}T_{a}^{ac}T^{b}_{bc}, \end{aligned}$$
(5)

note that for TEGR ρ 1=0, \(\rho_{2}=-\frac{1}{2}\) and ρ 4=1. A variation of action (3) with respect to the vielbein provides the following field equations:

$$\begin{aligned} \delta\mathcal{L} =&\delta e^{a}\wedge \bigl\{ \bigl\{ \rho _{1} \bigl[2d\star de_{a}+i_{a} \bigl(de^{b}\wedge\star de_{b}\bigr) \\ &{}-2i_{a} \bigl(de^{b}\bigr)\wedge \star de_{b} \bigr] \\ &{} +\rho_{2} \bigl\{ -2e_{a}\wedge d\star\bigl(de^{b}\wedge e_{b}\bigr) +2de_{a}\wedge\star\bigl(de^{b}\wedge e_{b} \bigr) \\ &{}+i_{a} \bigl[de^{c}\wedge e_{c}\wedge \star \bigl(de^{b}\wedge e_{b}\bigr) \bigr] \\ &{} -2i_{a}\bigl(de^{b}\bigr)\wedge e_{b}\wedge\star \bigl(de^{c}\wedge e_{c}\bigr) \bigr\} \\ &{}+\rho_{4} \bigl\{ -2e_{b}\wedge d\star\bigl(e_{a}\wedge de^{b} \bigr)+2de_{b}\wedge\star \bigl(e_{a}\wedge de^{b} \bigr) \\ &{}+i_{a} \bigl[e_{c}\wedge de^{b}\wedge\star \bigl(de^{c}\wedge e_{b}\bigr) \bigr] \\ &{} -2i_{a}\bigl(de^{b}\bigr)\wedge e_{c}\wedge\star \bigl(de^{c}\wedge e_{b}\bigr) \bigr\} \bigr\} \\ &{} -2\varLambda\star e_a \bigr\} =0, \end{aligned}$$
(6)

where i a is the interior product and for generality’s sake we have kept the general coefficients ρ i , and we have used ϵ 012=+1. Through the following choice of the coefficients ρ 1=0, \(\rho_{2}=-\frac {1}{2}\) and ρ 4=1 Teleparallel Gravity coincides with the usual curvature-formulation of General Relativity and therefore the following BTZ metric is solution of TEGR

$$ ds^2=N^2dt^2-N^{-2}dr^2-r^2(d \varphi+N_{\varphi}dt)^2, $$
(7)

where the lapse N and shift N φ functions are given by,

$$ N^2= -8GM+\frac{r^2}{l^2}+\frac{16G^2J^2}{r^2},\qquad N_{\varphi}=-\frac{4GJ}{r^2}, $$
(8)

and the two constants of integration M and J are the usual conserved charges associated with the asymptotic invariance under time displacements (mass) and rotational invariance (angular momentum) respectively, given by flux integrals through a large circle at spacelike infinity, and Λ=−1/l 2 is the cosmological constant (Banados et al. 1992). Finally, note that the torsion scalar can be calculated, leading to the constant value

$$ T=-2\varLambda, $$
(9)

which is the cosmological constant as the sole source of torsion.

3 3D teleparallel hairy black holes

3.1 The model

In this section we will extend the above discussion considering a scalar field ϕ non-minimally coupled with the torsion scalar with a self-interacting potential V(ϕ), and then we will find hairy black hole solutions. So, the action can be written as

$$\begin{aligned} S=\int \biggl( \frac{1}{2 \kappa} T \star1 - \xi\phi^2 T \star1 + \frac{1}{2} d\phi\wedge\star d\phi-V(\phi)\star1 \biggr), \end{aligned}$$
(10)

where T is given by (4) and ξ is the non-minimal coupling parameter. Thus, the variation with respect to the vielbein leads to the following field equations:

$$\begin{aligned} \delta_{e^{a}} \mathcal{L} =&\delta e^{a}\wedge \biggl\{ \biggl(\frac{1}{2\kappa}-\xi\phi^2 \biggr) \bigl\{ \rho _{1} \bigl[2d\star de_{a}+i_{a} \bigl(de^{b}\wedge\star de_{b}\bigr) \\ &{}-2i_{a} \bigl(de^{b}\bigr)\wedge \star de_{b} \bigr] \\ &{} +\rho_{2} \bigl\{ -2e_{a}\wedge d\star \bigl(de^{b}\wedge e_{b}\bigr)+2de_{a}\wedge\star \bigl(de^{b}\wedge e_{b}\bigr) \\ &{}+i_{a} \bigl[de^{c}\wedge e_{c}\wedge \star\bigl(de^{b} \wedge e_{b}\bigr) \bigr] \\ &{} -2i_{a} \bigl(de^{b}\bigr)\wedge e_{b}\wedge\star \bigl(de^{c}\wedge e_{c}\bigr) \bigr\} \\ &{} +\rho_{4} \bigl\{ -2e_{b}\wedge d\star \bigl(e_{a}\wedge de^{b}\bigr)+2de_{b}\wedge\star \bigl(e_{a}\wedge de^{b}\bigr) \\ &{} +i_{a} \bigl[e_{c}\wedge de^{b}\wedge\star\bigl(de^{c} \wedge e_{b}\bigr) \bigr] \\ &{} -2i_{a}\bigl(de^{b}\bigr) \wedge e_{c}\wedge\star\bigl(de^{c}\wedge e_{b} \bigr) \bigr\} \bigr\} \\ &{} -4\xi \bigl[\rho_1\phi d\phi\wedge\star de_a+\rho_2 \phi d\phi\wedge e_a\wedge \star \bigl(de_b\wedge e^b\bigr) \\ &{}+\rho_4\phi d\phi \wedge e_b\wedge\star\bigl(de^b \wedge e_a \bigr) \bigr] \\ &{} - V(\phi) i_a(\star1)-\frac{1}{2}d \phi\wedge i_a(\star d\phi) \\ &{}-\frac{1}{2} i_a(d\phi) \wedge\star d\phi \biggr\} =0, \end{aligned}$$
(11)

and the variation with respect to the scalar field leads to the Klein-Gordon equation

$$ \delta_{\phi} \mathcal{L}=\delta\phi \biggl(-2\xi\phi T \star1-d\star d\phi- \frac{dV}{d\phi}\star1 \biggr)=0. $$
(12)

3.2 Circularly symmetric hairy solutions

Let us now investigate hairy black hole solutions of the theory. In order to analyze static solutions we consider the metric form as

$$ ds^{2}=A ( r ) ^{2}dt^{2}- \frac{1}{B ( r ) ^{2}} dr^{2}-r^{2}d\varphi^{2}, $$
(13)

which arises from the triad diagonal ansatz

$$ e^{0}=A ( r ) dt,\qquad e^{1}=\frac{1}{B ( r ) }dr, \qquad e^{2}=rd\varphi. $$
(14)

Then, inserting this vielbein in the field equations (11), (12) yields

$$\begin{aligned} &{-\frac{1}{r}{\biggl(\frac{1}{2\kappa}-\xi\phi(r)^2\biggr) \frac{dB^2}{dr}}+\frac {4}{r}\xi B(r)^2\phi(r) \frac{d\phi}{dr}} \\ &{\quad{}-\frac{1}{2}B(r)^2\biggl(\frac{d\phi }{dr} \biggr)^2-V(\phi)=0,} \end{aligned}$$
(15)
$$\begin{aligned} &{\frac{B(r)^2}{rA(r)^2}{\biggl(\frac{1}{2\kappa}-\xi\phi(r)^2\biggr) \frac{dA^2}{dr}}} \\ &{\quad{}-\frac{1}{2}B(r)^2\biggl(\frac{d\phi}{dr} \biggr)^2+V(\phi)=0,} \end{aligned}$$
(16)
$$\begin{aligned} &{2 \xi\phi(r) \frac{d\phi}{dr}\frac{B(r)^2}{A(r)^2}\frac {dA^2}{dr}- \frac{1}{2}B(r)^2\biggl(\frac{d\phi}{dr}\biggr)^2}\\ &{\quad{}+\frac{1}{2A(r)^4}\biggl(\frac{1}{2\kappa}-\xi\phi(r)^2 \biggr) \biggl(-A(r)^2\frac{dA^2}{dr}\frac{dB^2}{dr}}\\ &{\quad{}+B(r)^2 \biggl(\frac {dA^2}{dr}\biggr)^2-2A(r)^2 B(r)^2\frac{d^2A^2}{dr^2} \biggr)} \\ &{\quad{}-V(\phi)=0,} \end{aligned}$$
(17)
$$\begin{aligned} &{-\frac{2B(r)^2}{rA(r)^2}\xi\phi(r)\frac{dA^2}{dr}+\frac{1}{r}B(r)^2 \frac {d\phi}{dr}+\frac{1}{2}\frac{dB(r)^2}{dr}\frac{d\phi}{dr}} \\ &{\quad{}+ \frac {B(r)^2}{2A(r)^2}\frac{dA(r)^2}{dr}\frac{d\phi}{dr}+B(r)^2 \frac{d^2\phi }{dr^2}-\frac{dV}{d\phi}=0.} \end{aligned}$$
(18)

It is worth mentioning that, in the case of a minimally coupled scalar field, the above simple, diagonal relation between the metric and the vielbeins (14) is always allowed, due to in this case the theory is invariant under local Lorentz transformations of the vielbein. In contrast, in the extension of a non-minimally coupled scalar field with the torsion scalar, the theory is not local Lorentz invariant, therefore, one could have in general a more complicated relation connecting the vielbein with the metric, with the vielbeins being non-diagonal even for a diagonal metric (Sotiriou et al. 2011). However, for the three-dimensional solutions considered here, using a preferred diagonal frame is allowed, in the sense that this frame defines a global set of basis covering the whole tangent bundle, i.e., they parallelize the spacetime (Fiorini et al. 2014; Ferraro and Fiorini 2011b).

In the following, and in order to solve the above system of equations, we will consider two cases: first, we analyze the case A(r)=B(r), and then we analyze the more general case A(r)≠B(r).

3.2.1 A(r)=B(r)

In this case the field equations (15)–(18) simplify to

$$\begin{aligned} &{-\frac{1}{r}{\biggl(\frac{1}{2\kappa}-\xi\phi(r)^2\biggr) \frac{dA^2}{dr}}+\frac {4}{r}\xi A(r)^2\phi(r) \frac{d\phi}{dr}} \\ &{\quad{}-\frac{1}{2}A(r)^2\biggl(\frac{d\phi }{dr} \biggr)^2-V(\phi)=0,} \end{aligned}$$
(19)
$$\begin{aligned} &{\frac{1}{r}{\biggl(\frac{1}{2\kappa}-\xi\phi(r)^2\biggr) \frac{dA^2}{dr}}-\frac {1}{2}A(r)^2\biggl(\frac{d\phi}{dr} \biggr)^2+V(\phi)=0,} \end{aligned}$$
(20)
$$\begin{aligned} &{2\xi\phi(r) \frac{d\phi}{dr}\frac{dA^2}{dr}-\frac{1}{2}A(r)^2 \biggl(\frac {d\phi}{dr}\biggr)^2} \\ &{\quad{}-\biggl(\frac{1}{2\kappa}-\xi \phi(r)^2\biggr)\frac {d^2A^2}{dr^2}-V(\phi)=0,} \end{aligned}$$
(21)
$$\begin{aligned} &{-\frac{2}{r}\xi\phi(r)\frac{dA^2}{dr}+\frac{1}{r}A(r)^2 \frac{d\phi }{dr}+\frac{dA(r)^2}{dr}\frac{d\phi}{dr}} \\ &{\quad{}+A(r)^2 \frac{d^2\phi }{dr^2}-\frac{dV}{d\phi}=0.} \end{aligned}$$
(22)

Now, by adding Eqs. (19) and (20) we obtain

$$ A(r)^2\frac{d \phi}{dr} \biggl( \frac{4 \xi}{r} \phi- \frac{d \phi }{dr} \biggr)=0. $$
(23)

Therefore, the nontrivial solution for the scalar field is given by

$$ \phi(r)=Br^{4\xi}, $$
(24)

and by using this profile for the scalar field in the remaining equations, we obtain the solution

$$\begin{aligned} &{A(r)^2=Gr^{2}+H {}_{2}F_1 \biggl(1,-\frac{1}{4\xi}, 1-\frac{1}{4\xi}, 2\kappa B^2\xi r^{8\xi}\biggr),} \end{aligned}$$
(25)
$$\begin{aligned} &{V(\phi) = \frac{H}{\kappa} \biggl(\frac{\phi}{B} \biggr)^{-\frac {1}{2\xi}}+2G \biggl(-\frac{1}{2\kappa}+B^2\xi(1+4\xi) \biggl(\frac{\phi }{B} \biggr)^2 \biggr)} \\ &{\phantom{V(\phi)=}{} -2H \biggl(\frac{\phi}{B} \biggr)^{-\frac{1}{2\xi}} \biggl( \frac {1}{2\kappa}-B^2\xi(1+4\xi) \biggl(\frac{\phi}{B} \biggr)^2 \biggr)} \\ &{\phantom{V(\phi)=}{}\times{}_{2}F_1\biggl(1,- \frac{1}{4\xi}, 1-\frac{1}{4\xi}, 2\kappa\xi\phi^2\biggr),} \end{aligned}$$
(26)

where B, G, and H are integration constant and 2 F 1 is the Gauss hypergeometric function. In the limits ξ→0 or B→0 the theory reduces to TEGR, therefore, we must hope our solution reduces to the BTZ black hole, this is indeed the case, as we show below. For those limits we obtain:

$$\begin{aligned} &{\lim_{\xi\rightarrow0} {}_{2}F_1\biggl(1,- \frac{1}{4\xi}, 1-\frac {1}{4\xi}, 2\kappa B^2\xi r^{8\xi}\biggr)=1,} \end{aligned}$$
(27)
$$\begin{aligned} &{\lim_{B \rightarrow0} {}_{2}F_1\biggl(1,- \frac{1}{4\xi}, 1-\frac{1}{4\xi }, 2\kappa B^2\xi r^{8\xi}\biggr)=1,} \end{aligned}$$
(28)

therefore,

$$ \lim_{\xi\rightarrow0 \ \mathrm{or}\ B \rightarrow0} A(r)^2=Gr^{2}+H, $$
(29)

which is the non-rotating BTZ metric. In order to see the asymptotic behavior of A(r)2, we expand the hypergeometric function for large r and ξ<0:

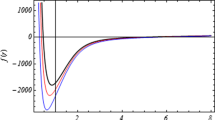
$$\begin{aligned} {}_{2}F_1\biggl(1,-\frac{1}{4\xi}, 1- \frac{1}{4\xi}, 2\kappa B^2\xi r^{8\xi }\biggr)\approx1- \frac{\kappa B^2 r^{8 \xi}}{2 ( 1-\frac{1}{4 \xi} )}+\cdots. \end{aligned}$$
(30)

This expansion shows that the hairy black hole is asymptotically AdS. On other hand, in the limit ϕ→0 the potential goes to a constant (the effective cosmological constant) \(V(\phi)\rightarrow -\frac{G}{\kappa}=\varLambda\). In Fig. 1 we plot the behavior of the metric function A(r)2 given by Eq. (25) for a choice of parameters H=−1, G=1, B=1, κ=1, and ξ=−0.25,−0.5,−1. The metric function A(r)2 changes sign for low values of r, signaling the presence of a horizon, while the scalar field is regular everywhere outside the event horizon (for ξ<0) and null at large distances. In Fig. 2 we show the behavior of the potential, and we observe that it tends asymptotically (ϕ→0) to a negative constant (the effective cosmological constant). We also plot the behavior of the Ricci scalar R(r), the principal quadratic invariant of the Ricci tensor R μν R μν (r), and the Kretschmann scalar R μνλτ R μνλτ (r) in Fig. 3 by using the Levi-Civita connection, and we observe that there is not a Riemann curvature singularity outside the horizon for ξ=−0.25,−0.5,−1. Also, we observe a Riemann curvature singularity at r=0 for ξ=−0.25 and the torsion scalar is singular at r=0 for ξ=−0.25, see Fig. 4.

Fig. 1
figure 1

The behavior of A(r)2, for H=−1, G=1, B=1, κ=1, and ξ=−0.25,−0.5,−1

Full size image
Fig. 2
figure 2

The Potencial V(ϕ), for H=−1, G=1, B=1, κ=1, and ξ=−0.25,−0.5,−1

Full size image
Fig. 3
figure 3

The behavior of R(r), R μν R μν (r) and R μνλτ R μνλτ (r) for H=−1, G=1, B=1, κ=1, and ξ=−0.25 (left figure), ξ=−0.5 (right figure), and ξ=−1 (bottom figure)

Full size image
Fig. 4
figure 4

The behavior of torsion scalar T as function of r for H=−1, G=1, B=1, κ=1, and ξ=−0.25,−0.5,−1

Full size image

3.2.2 A(r)≠B(r)

Now, by considering the following ansatz for the scalar field

$$ \phi(r)=Br^{\gamma}, $$
(31)

we find the following solution to the field equations

$$\begin{aligned} &{A(r)^2=Gr^{2}+H {}_{2}F_1\biggl(- \frac{1}{\gamma},\frac{\gamma}{4\xi}, 1-\frac {1}{\gamma}, 2\kappa B^2\xi r^{2\gamma}\biggr),} \end{aligned}$$
(32)
$$\begin{aligned} &{B(r)^2= \biggl( \frac{1}{2\kappa} - r^{2 \gamma} \xi B^2 \biggr)^{-2+\frac {\gamma}{2 \xi}} A(r)^2,} \end{aligned}$$
(33)
$$\begin{aligned} &{ V(\phi) = 2H \biggl( \frac{ \phi}{B} \biggr)^{-\frac{2}{ \gamma}} \biggl( \frac{1}{2\kappa}-\xi\phi^2 \biggr)^{-1+\frac{\gamma }{2 \xi}} \bigl( 1-2 \kappa\xi\phi^2 \bigr)^{-\frac{\gamma}{4 \xi}}}\\ &{\phantom{V(\phi)=}{} -\frac{G}{2} \biggl( \frac{1}{2\kappa}-\xi\phi^2 \biggr)^{-2+\frac {\gamma}{2 \xi}} \biggl( \frac{2}{\kappa}-\bigl(\gamma^2+4\xi \bigr) \phi^2 \biggr)} \\ &{\phantom{V(\phi)=}{} -\frac{H}{2} \biggl( \frac{ \phi}{B} \biggr)^{-\frac{2}{ \gamma}} \biggl( \frac{1}{2\kappa}-\xi\phi^2 \biggr)^{-2+\frac{\gamma}{2 \xi}} } \\ &{\phantom{V(\phi)=}{}\times\biggl( \frac{2}{\kappa}-\bigl(\gamma^2+4\xi \bigr) \phi^2 \biggr) } \\ &{\phantom{V(\phi)=}{}\times{}_{2}F_1\biggl(- \frac {1}{\gamma},\frac{\gamma}{4\xi}, 1-\frac{1}{\gamma}, 2\kappa\xi \phi^2\biggr),} \end{aligned}$$
(34)

where B, G and H are integration constants. This solution is asymptotically AdS and generalizes the previous one, because if we take γ=4ξ it reduces to the solution of the case A(r)=B(r). Furthermore, for γ=0 we recover the static BTZ black hole. On the other hand, in the limit ϕ→0 the potential tends to a constant \(V(\phi) \rightarrow-2G (2 \kappa )^{1-\frac{\gamma}{2 \xi}}=\varLambda\).

As in the previous case, we plot the behavior of the metric function B(r)2 given by (33), in Fig. 5 for a choice of parameters H=−1, G=1, B=1, κ=1, ξ=−0.25 and γ=−0.25,−1,−2. The metric function B(r)2 changes sign for low values of r, signaling the presence of a horizon, while for γ<0 the scalar field is regular everywhere outside the event horizon and null at large distances. In Fig. 6 we show the behavior of the potential, asymptotically (ϕ→0) it tends to a negative constant (the effective cosmological constant) as in the previous case. Also, we plot the behavior of R(r), R μν R μν (r), and R μνλτ R μνλτ (r) in Fig. 7 by using the Levi-Civita connection, and we observe that there is not a Riemann curvature singularity outside the horizon for γ=−0.25,−1,−2. Also, we observe a Riemann curvature singularity at r=0 and the torsion scalar is singular at r=0 for all the cases considered. Asymptotically, the torsion scalar goes to −2Λ since this spacetime is asymptotically AdS, see Fig. 8. Therefore, we have shown that there are three-dimensional black hole solutions with scalar hair in Teleparallel Gravity.

Fig. 5
figure 5

The behavior of B(r)2, for H=−1, G=1, B=1, κ=1, ξ=−0.25 and γ=−0.25,−1,−2

Full size image
Fig. 6
figure 6

The Potencial V(ϕ), for H=−1, G=1, B=1, κ=1, ξ=−0.25 and γ=−0.25,−1,−2

Full size image
Fig. 7
figure 7

The behavior of R(r), R μν R μν (r) and R μνλτ R μνλτ (r) for H=−1, G=1, B=1, κ=1, ξ=−0.25 and γ=−0.25 (left figure), γ=−1 (right figure), and γ=−2 (bottom figure)

Full size image
Fig. 8
figure 8

The behavior of torsion scalar T as function of r for H=−1, G=1, B=1, κ=1, ξ=−0.25 and γ=−0.25,−1,−2

Full size image

4 Final remarks

Motivated by the search of hairy black holes solutions in theories based on torsion, we have considered an extension of three-dimensional TEGR with a scalar field non-minimally coupled to the torsion scalar along with a self-interacting potential, and we have found three-dimensional asymptotically AdS black holes with scalar hair. These hairy black holes are characterized by a scalar field with a power-law behavior and by a self-interacting potential, which tends to an effective cosmological constant at spatial infinity. We have considered two cases A(r)=B(r) and A(r)≠B(r). In the first case the scalar field depends on the non-minimal coupling parameter ξ, and it is regular everywhere outside the event horizon and null at spatial infinity for ξ<0, while for ξ=0 we recover the non-rotating BTZ black hole. In the second case the scalar field depends on a parameter γ, and it is regular everywhere outside the event horizon and null at spatial infinity for γ<0, this solution generalizes the solution of the first case, which is recovered for γ=4ξ. Furthermore, for γ=0 we recover the non-rotating BTZ black hole. Moreover, the analysis of the Riemann curvature invariants and the torsion scalar shows that they are all regular outside the event horizon. In furthering our understanding, it would be interesting to study the thermodynamics of these hairy black hole solutions in order to study the phase transitions. Work in this direction is in progress.