1 Introduction

Few years ago Petr Hořava suggested new candidate of quantum field theory of gravity with dynamical critical exponent being equal to z=3 in the UV (Ultra-Violet). This theory is a non-relativistic power-counting renormalizable theory in four dimensions which admits the Lifshitz scale-invariance in time and space that reduces to Einstein’s general relativity at large scales (Hořava 2009a, 2009b). The Hořava theory has received a great deal of attention and since its formulation various properties and characteristics have been extensively analyzed, ranging from formal developments (Visser 2009), cosmology (Takahashi and Soda 2009), dark energy (Saridakis 2010), dark matter (Mukohyama 2009), and spherically symmetric or axial symmetric solutions (Cai et al. 2009).

In the paper of Lobo et al. (2010) the possibility of observationally testing Hořava gravity at the scale of the Solar System, by considering the classical tests of general relativity (perihelion precession of the planet Mercury, deflection of light by the Sun and the radar echo delay) for the Kehagias-Sfetsos (KS) asymptotically flat black hole solution of Hořava-Lifshitz gravity has been studied. The stability of the Einstein static universe by considering linear homogeneous perturbations in the context of an Infra-Red (IR) modification of Hořava gravity has been studied in Böhmer and Lobo (2010). Potentially observable properties of black holes in the deformed Hořava-Lifshitz gravity with Minkowski vacuum: the gravitational lensing and quasinormal modes have been studied in Konoplya (2009). Lü et al. (2009) derived the full set of equations of motion, and then obtained spherically symmetric solutions for UV completed theory of gravity proposed by Hořava. The particle motion in the space-time of a Kehagias-Sfetsos black hole which is a static spherically symmetric solution of a Hořava-Lifshitz gravity model has been studied in Enolskii et al. (2011).

Although a black hole is not visible, it may be observable nonetheless—since it may create a shadow if it is in front of a bright background. The apparent shape of an extremely rotating black hole has been first studied by Bardeen (1973), later a Schwarzschild black hole with an accretion disc has been visualized by Luminet (1979). Accretion discs around an extremely rotating black hole as viewed from different angles of latitude has been considered in detail in Quien et al. (1995). Supplementing these numerical approaches, the closed photon orbits in general Kerr-Newman space-times have been analytically studied in de Vries (2000), including the cases where the so-called cosmic censorship is violated. It is strongly believed that the observability of black hole shadows in the near future is very realistic. Recently, great interest emerged especially for the observability of the black hole in the center of our Milky Way, Sgr A* (Falcke et al. 2000). The shadow of Schwarzschild (Darwin 1959; Luminet 1979), Kerr-Taub-NUT (Abdujabbarov et al. 2013), and Reissner-Nordström (Eiroa et al. 2002), and other spherically symmetric black holes (Bozza 2002) have been intensively studied. Non-rotating braneworld black holes were studied as gravitational lenses (Frolov et al. 2003) as well. The shadow cast by a rotating braneworld black hole has been studied in Amarilla and Eiroa (2012) in the Randall-Sundrum scenario.

Kerr black hole gravitational lenses were considered by many authors see, for example, Bozza (2003), Bozza and Scarpetta (2007), Vázquez and Esteban (2004), Kraniotis (2011). Rotating black holes present apparent shapes or shadows with an optical deformation due to the spin (Bardeen 1973; Chandrasekhar 1992), instead of being circles as in the case of non-rotating ones. This topic has been reexamined by several authors in the last few years (Bozza and Scarpetta 2007; Hioki and Maeda 2009; Hioki and Miyamoto 2008; Zakharov et al. 2005), with the expectation that the direct observation of black holes will be possible in the near future (Zakharov et al. 2005). Therefore the study of the shadows could be useful for measuring the properties of astrophysical black holes. Optical properties of rotating braneworld black holes were studied by Schee and Stuchlik (2009). For more details about black hole gravitational lensing and a discussion of its observational prospects, see the recent review article (Bozza 2010) and the references therein.

Exploring the spacetimes discussed here, we have studied optical features of the black hole in Hořava-Lifshitz gravity. Following work of Pineault and Roeder (1977), we have used the Newman-Penrose formalism (Newman and Penrose 1962) adapted to the locally non-rotating frames (Bardeen et al. 1972) to obtain the rotation of the polarization vector of the light in the geometrical optics regime which is appropriate for high frequency electromagnetic waves. In this approach, the light propagates along null geodesics and its polarization vector is parallelly transported.

The paper is organized as follows: in Sect. 2, we review the basic aspects of the geometry and the geodesics of the Hořava-Lifshitz black hole. In Sect. 3, we obtain the shadows of black holes with different values of the black hole’s spin parameter a and parameters of Hořava-Lifshitz spacetime. In Sect. 4 the presented spacetimes were explored with application involving geometric optics, in particular, rotation of polarization vector of electromagnetic wave. Finally in Sect. 5 we discuss the results obtained.

Throughout the paper, we use a space-like signature (−,+,+,+) and a system of units in which G=1=c (However, for those expressions with an astrophysical application we have written the speed of light explicitly.). Greek indices are taken to run from 0 to 3 and Latin indices from 1 to 3; covariant derivatives are denoted with a semi-colon and partial derivatives with a comma.

2 Photon motion around rotating Hořava-Lifshitz black holes

2.1 Extreme rotating black hole

The four-dimensional metric of the spherical-symmetric spacetime written in the ADM formalism (Lobo et al. 2010) has the following form:

$$ ds^{2}=-N^{2}c^{2}dt^{2}+g_{ij} \bigl(dx^{i}+N^{i}dt\bigr) \bigl(dx^{j}+N^{j}dt \bigr), $$
(1)

where N is the lapse function and N i is the shift vector to be defined.

The Hořava-Lifshitz action describes a nonrelativistic renormalizable theory of gravitation and is given by (see for more details Hořava (2009a), Lobo et al. (2010), Harko et al. (2011), Böhmer and Lobo (2010), Konoplya (2009), Abdujabbarov et al. (2011))

$$\begin{aligned} S =& \int dtdx^3 \sqrt{-g} N \biggl[ \frac{2}{\kappa ^2}\bigl(K_{ij}K^{ij}-\lambda_g K^2\bigr) \\ &{}+\frac{ \kappa^2\mu}{2\nu_g^2}\epsilon^{ijk}R_{il} \nabla_j R^l_{k} -\frac{\kappa^2 \mu^2}{8}R_{ij}R^{ij}+ \frac{\kappa^2\mu^2}{8(3\lambda_g-1)} \\ &{}\times \biggl(\frac{4\lambda_g- 1}{4}R^2-\varLambda_WR+3 \varLambda_W^2 \biggr)-\frac{\kappa^2}{2\nu_g^4}C_{ij}C^{ij} \biggr] , \end{aligned}$$
(2)

where κ,λ g ,ν g ,μ, and Λ W are constant parameters, the Cotton tensor is defined as

$$ C^{ij}=\epsilon^{ikl}\nabla_k \biggl(R^{j}_{l}-\frac{1}{4} R\delta^j_l \biggr), $$
(3)

R ijkl is the three-dimensional curvature tensor, and the extrinsic curvature K ij is defined as

$$ K_{ij}=\frac{1}{2N}(\dot{g}_{ij}-\nabla_i N_j -\nabla_j N_i), $$
(4)

where dot denotes a derivative with respect to coordinate t.

Up to second derivative terms in the action (2), one can find the known topological rotating solutions given by Klemm et al. (1998) for equations of motion in the Hořava-Lifshitz gravity. Since we are considering matter coupled with the metric in a relativistic way, we can consider the metric in Boyer-Lindquist coordinates instead of its ADM form which is the solutions of Hořava-Lifshitz gravity. In the Einstein’s gravity this spacetime metric reads in Boyer-Lindquist type coordinates in the following form (see, e.g. Ghodsi and Hatefi 2010; Abdujabbarov et al. 2011):

$$\begin{aligned} ds^2 =& -\frac{\Delta_{\rm r}}{\varSigma^2 \rho^2} \bigl[dt-a \sin^2 \theta d\varphi \bigr]^2+\frac{\rho^2}{\Delta_{\rm r}} dr^2 \\ & {}+ \frac{\rho^2}{\Delta_{\rm \theta}}d\theta^2 + \frac{\Delta_{\rm \theta}\sin^2 \theta}{\varSigma^2 \rho^2} \bigl[adt- \bigl(r^2+a^2\bigr)d\varphi \bigr]^2 ,\ \ \end{aligned}$$
(5)

where the following notations

$$\begin{aligned} &{\Delta_{\rm r}= \bigl(r^2 + a^2\bigr) \biggl(1+\frac{r^2}{l^2} \biggr)-2Mr,} \\ &{\Delta_{\rm \theta} = 1-\frac{a^2}{l^2}\cos^2 \theta ,} \\ &{\rho^2= r^2+a^2\cos^2\theta,} \\ &{\varSigma=1-\frac{a^2}{l^2}, l^2=-2/\varLambda_W} \end{aligned}$$

are introduced, M is the total mass of the central BH, a is the specific angular momentum of the BH.

Note that metric (5) in ADM form can be written as (Klemm et al. 1998; Abdujabbarov et al. 2011):

$$\begin{aligned} ds^2 =& -\frac{\rho^2 \Delta_{\rm r} \Delta_{\rm \theta}}{\varSigma^2 \varXi^2} dt^2 + \frac{\rho^2}{\Delta_{\rm r}} dr^2 + \frac{\rho^2}{\Delta_{\rm \theta}}d\theta^2 \\ & {}+ \frac{\varXi^2 \sin^2 \theta}{\varSigma^2 \rho^2} [d\varphi -\varpi dt ]^2 ,\ \ \end{aligned}$$
(6)

where

$$\begin{aligned} &{ \varXi^2= \bigl(r^2 + a^2 \bigr)^2 \Delta_{\rm \theta} -a^2 \Delta_{\rm r} \sin^2\theta ,} \\ &{ \varpi=-\frac{a}{\varXi^2} \bigl[ -\bigl(r^2+a^2 \bigr)\Delta_{\rm \theta} +\Delta_{\rm r}\bigr] .} \end{aligned}$$

Consider a black hole placed between a source of light and an observer. Then the light reaches the observer after being deflected by the black hole’s gravitational field. But some part of the deflected light with small impact parameters can be emitted by the source falling into the black hole. This phenomena result a dark figure in the map of the space called the shadow. The boundary of this shadow defines the shape of a black hole (see e.g. Amarilla and Eiroa 2012). The study of the geodesic structure around black hole is very important to obtain the apparent shape. The Hamilton-Jacobi equation determines the geodesics for a given space-time geometry:

$$ \frac{\partial S}{\partial \lambda}=-\frac{1}{2}g^{\mu\nu} \frac{\partial S}{\partial x^{\mu}}\frac{\partial S}{\partial x^{\nu}}, $$
(7)

where λ is an affine parameter along the geodesics, g μν are the components of the metric tensor and S is the Jacobi action. If the problem is separable, the Jacobi action S can be written in the form

$$ S = \frac{1}{2}m^2 \lambda - \mathcal{E} t + \mathcal{L} \phi + S_{r}(r)+S_{\theta}(\theta), $$
(8)

where m is the mass of a test particle. The second term on the right hand side is related to the conservation of energy \(\mathcal{E}\), while the third term is related to the conservation of the angular momentum \(\mathcal{L}\) in the direction of the axis of symmetry. In the case of null geodesics, we have that m=0, and from the Hamilton-Jacobi equation, the following equations of motion are obtained:

$$\begin{aligned} \rho^2\frac{dt}{d\lambda} =& \frac{\varSigma^2(r^2+a^2)}{\Delta_{\rm r}} \bigl[ \bigl(r^2+a^2\bigr)\mathcal{E} -a \mathcal{L} \bigr] \\ &{} + \frac{\varSigma^2 a}{\Delta_{\rm \theta}}\biggl[\frac{\mathcal{L}}{\sin^2 \theta} -a \mathcal{E} \biggr] , \end{aligned}$$
(9)
$$\begin{aligned} \rho^2\frac{d\phi}{d\lambda} =&\frac{\varSigma^2 a}{\Delta_{\rm r}} \bigl[ \bigl(r^2+a^2\bigr)\mathcal{E} -a \mathcal{L} \bigr] \\ &+{} \frac{\varSigma^2}{\Delta_{\rm \theta}}\biggl[\frac{\mathcal{L}}{\sin^2 \theta} -a \mathcal{E} \biggr], \end{aligned}$$
(10)
$$\begin{aligned} \rho^2\frac{dr}{d\lambda} =&\sqrt{\mathcal{R}}, \end{aligned}$$
(11)
$$\begin{aligned} \rho^2\frac{d\theta}{d\lambda} =&\sqrt{\varTheta}, \end{aligned}$$
(12)

where the functions \(\mathcal{R}(r)\) and Θ(θ) are defined as

$$\begin{aligned} &{\mathcal{R}=\varSigma^2 \bigl[\bigl(r^2+a^2 \bigr)\mathcal{E} -a \mathcal{L} \bigr]^2-\Delta_{\rm r} \mathcal{K},} \end{aligned}$$
(13)
$$\begin{aligned} &{\varTheta =\Delta_{\rm \theta}\mathcal{K}-\frac{\varSigma^2}{\sin^2\theta} \bigl[a \mathcal{E} \sin^2\theta-\mathcal{L} \bigr]^{2} ,} \end{aligned}$$
(14)

with \(\mathcal{K} \) as constant of separation.

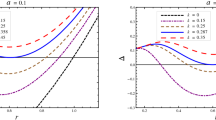
In Fig. 1 the radial dependence of effective potential of the massless particle’s radial motion is shown, where we introduce new dimensionless parameter δ=a 2/l 2≪1. From this dependence one can easily see that with the increase of δ parameter photon orbits come closer to the central object. Then the stability of photon orbits will increase with the increasing the parameter δ.

Fig. 1
figure 1

The radial dependence of the effective potential of radial motion of the massless particles for the different values of the δ parameter: solid line for δ=0.001, dashed line for δ=0.01, and dot-dashed line for δ=0.1

Full size image

Equations (9)–(12) determine the propagation of light in the Hořava-Lifshitz spacetime. The light rays are in general, characterized by two impact parameters which can be expressed in terms of the constants of motion \(\mathcal{E}\), \(\mathcal{L}\) and the Carter constant \(\mathcal{K}\). Combining these quantities we define as usual \(\xi=\mathcal{L}/\mathcal{E}\) and \(\eta=\mathcal{K}/\mathcal{E}^{2}\) which are the impact parameters for general orbits around the black hole. We use Eq. (11) to derive the orbits with constant r in order to obtain the boundary of the shadow of the black hole. These orbits satisfy the conditions \(\mathcal{R}(r)=0=d\mathcal{R}(r)/dr\) which are fulfilled by the values of the impact parameters that determine the contour of the shadow, namely

$$\begin{aligned} &{\xi(r)=\frac{(1-\delta)(a^2+r^2)r a -a(3r^2-a^2)}{a^2(1-r)-r\delta(a^2+2r^2)},} \end{aligned}$$
(15)
$$\begin{aligned} &{\eta(r)=\frac{4\varSigma^2 r^2[a^2(a^2+r^2-2r)+r^2\delta(a^2+r^2)]}{[a^2(1-r)-r\delta(a^2+2r^2)]^2}.} \end{aligned}$$
(16)

In above expressions we put M=1 for simplicity.

2.2 Rotating Kehagias-Sfetsos black hole

Now we will study massless particles motion in the vicinity of a black hole of mass M described by the Kehagias-Sfetsos asymptotically flat solution in Hořava-Lifshitz gravity. The metric describing the above mentioned black hole has the following form (Hyung et al. 2010):

$$\begin{aligned} &{ds^{2}=f(r)dt^{2}-\frac{dr^{2}}{f(r)}-r^{2}d \theta^{2}-r^{2}\sin^{2}\theta (d \phi-aNdt)^{2},} \end{aligned}$$
(17)

where metric functions f(r) and N are defined as

$$\begin{aligned} &{N=\frac{2M}{r^{3}},} \end{aligned}$$
(18)
$$\begin{aligned} &{f(r)=1-\frac{2M}{r}+\frac{2M^2}{\omega r^4},} \end{aligned}$$
(19)

here a and M were introduced and ω is so-called KS parameter.

Once more using the Hamilton-Jacobi equation (7) and the action in the form of (8) the following equations of motion can be obtained:

$$\begin{aligned} &{\frac{dt}{d\lambda}= \frac{1}{f} [\mathcal{E} -a N \mathcal{L} ],} \end{aligned}$$
(20)
$$\begin{aligned} &{r^2\frac{d\phi}{d\lambda}=\frac{a N r^2}{f} [\mathcal{E} -a N \mathcal{L} ] + \frac{1}{\sin^2\theta}\mathcal{L},} \end{aligned}$$
(21)
$$\begin{aligned} &{r^2\frac{dr}{d\lambda}=\sqrt{\mathcal{R'}},} \end{aligned}$$
(22)
$$\begin{aligned} &{r^2\frac{d\theta}{d\lambda}=\sqrt{\varTheta'},} \end{aligned}$$
(23)

where the functions \(\mathcal{R'}(r)\) and Θ′(θ) are defined by

$$\begin{aligned} \mathcal{R'} =& \frac{r^2}{f^2} [\mathcal{E} -a N \mathcal{L} ]^2- \frac{1}{f} \bigl[\mathcal{K}+\mathcal{L}^2 \bigr], \end{aligned}$$
(24)
$$\begin{aligned} \varTheta' =&\mathcal{K}-\cos^2\theta \frac{\mathcal{L}^2}{\sin^2\theta}, \end{aligned}$$
(25)

with \(\mathcal{K} \) as constant of separation.

In the Fig. 2 the radial dependence of the effective potential of radial photon motion is shown. From the figure it is seen that with decreasing the KS parameter the shape of effective potential is going to be shifted to the central object. This corresponds to increasing the event horizon of the KS black hole. Note that the case ωM 2→∞ corresponds to general relativity. Moreover, one may conclude from the Fig. 2 that with decreasing the KS parameter the circular photon orbits become unstable.

Fig. 2
figure 2

The radial dependence of the effective potential of radial motion of the massless particles for the different values of the KS parameter: solid line for ωM 2=2, dashed line for ωM 2=1.5, and dot-dashed line for ωM 2=1.1

Full size image

Equations (20)–(23) determine the propagation of light in the Hořava-Lifshitz spacetime. The impact parameters that determine the contour of the shadow, for the KS spacetime are given by

$$\begin{aligned} \xi'(r) =&\frac{3 \omega r^3 -\omega r^4 -6}{2 a \omega(2r-3)}, \end{aligned}$$
(26)
$$\begin{aligned} \eta'(r) =&4 a^{-2}(2r-3)^{-2} \omega^{-2} \bigl\{36 a^{2} \omega\bigl[\omega r^{4}-2\omega r^{3}+2\bigr] \\ &{}-\bigl[3\omega r^{3}-\omega r^{4}-6\bigr]^{2} \bigr\}. \end{aligned}$$
(27)

In above expressions we put M=1 for simplicity.

3 Shadow of Rotating Hořava-Lifshitz black hole

Using the celestial coordinates one can easily describe the shadow (see for example Vázquez and Esteban 2004):

$$ \alpha=\lim_{r_{0}\rightarrow \infty} \biggl( -r_{0}^{2} \sin\theta_{0}\frac{d\phi}{dr} \biggr), $$
(28)

and

$$ \beta=\lim_{r_{0}\rightarrow \infty}r_{0}^{2} \frac{d\theta}{dr}, $$
(29)

since here an observer far away from the black hole is considered at r 0→∞, θ 0 is the angular coordinate of the observer, i.e. the inclination angle between the rotation axis of the black hole and the line of sight of the observer. The geometry of the new introduced coordinates is shown in Fig. 3. The coordinates α and β are the apparent perpendicular distances of the image as seen from the axis of symmetry and from its projection on the equatorial plane, respectively.

Fig. 3
figure 3

The schematic geometry of the gravitational lens. An observer far away from the black hole can set up a reference coordinate system (x,y,z) with the black hole at the origin. The Boyer-Lidquist coordinates coincide with this system only at infinity. The tangent vector to an incoming light ray defines a straight line which intersects the α–β plane at the point (α i ,β i )

Full size image

Calculating dϕ/dr and dθ/dr from the metric given by expressions (5), (17) and taking the coordinate’s limit of a far away observer we obtain celestial coordinate’s functions of the constants of motion in the form

$$ \alpha=-\xi\varSigma^2\csc\theta_{0} , $$
(30)
$$ \beta=\pm \sqrt{\Delta_{\theta}\eta -\frac{\varSigma^2}{\sin ^{2}\theta_{0}} \bigl[a-\xi-a \cos ^{2}\theta_{0}\bigr]^2}, $$
(31)

and

$$ \alpha'=-\xi'\csc\theta_{0}, $$
(32)
$$ \beta'=\pm \sqrt{\eta' -\xi'^{2} \cot ^{2}\theta_{0} }, $$
(33)

where Eqs. (10), (11), (12) and (21), (22), (23) were used to calculate dθ/dr and dϕ/dr. These equations have implicitly the same form as one for the Kerr spacetime metric with the new ξ, ξ′ and η, η′ given by Eqs. (15), (16) and (26), (27) [a detailed calculation of the values of ξ and η and the expressions of the celestial coordinates α and β as a function of the constants of motion for Kerr geometry are given in Vázquez and Esteban (2004)].

In the case of rotating black hole one may introduce two observables which approximately characterize the apparent shape. First one should approximate the apparent shape by a circle passing through three points which are located at the top position, bottom and the most right end of the shadow as shown in Fig. 5, the radius R s of the shadow is defined by the radius of this circle. One can also define the distortion parameter δ s of the black hole shadow as δ s =D cs /R s . Two variables (R s and δ s ) can be interpreted as observables in astronomical observation (Hioki and Maeda 2009).

When the observer is situated in the equatorial plane of the black hole, the inclination angle is θ 0=π/2 and the gravitational effects on the shadow, which grow with θ 0, are larger. The inclination angle corresponding to the Galactic supermassive black hole is also expected to lie close to π/2. In this interesting case, we have simply

$$ \alpha=-\xi\varSigma^2, $$
(34)
$$ \beta=\pm \sqrt{\eta-\varSigma^2(a- \xi)^2} $$
(35)

and

$$ \alpha'=-\xi', $$
(36)
$$ \beta'=\pm \sqrt{\eta'}. $$
(37)

For the visualization of the shape of the black hole shadow one needs to plot β vs α and β′ vs α′. In Fig. 4, we show the contour of the shadows of black holes with rotation parameters a=0.7 (upper row, left), a=0.8 (upper row, right), a=0.9 (lower row, left), and a=0.99 (lower row, right), for several values of the δ parameter. From the Fig. 4, one can see that with increasing δ parameter, the shadow of the black hole decreases.

Fig. 4
figure 4

Silhouette of the shadow cast by a Hořava-Lifshitz black hole situated at the origin of coordinates with inclination angle θ=π/2, having a rotation parameter a and a δ parameter (we put M=1). (Upper row, left) a=0.7, δ=0 (solid line), δ=0.001 (dashed line), and δ=0.01 (dashed-dotted line). (Upper row, right) a=0.8, δ=0 (solid line), δ=0.001 (dashed line), and δ=0.01 (dashed-dotted line). (Lower row, left) a=0.9, δ=0 (solid line), δ=0.001 (dashed line), and δ=0.01 (dashed-dotted line). (Lower row, right) a=0.99, δ=0 (solid line), δ=0.001 (dashed line), and δ=0.01 (dashed-dotted line). The shadow corresponds to each curve and the region inside it

Full size image
Fig. 5
figure 5

The observables for the apparent shape of a rotating black hole are the radius R s and the distortion parameter δ s =D cs /R s . Here D cs is the difference between the left endpoints of the circle and of the shadow

Full size image

The observable R s can be calculated from the equation

$$ R_{s}=\frac{(\alpha _t -\alpha_r)^2 + \beta_t ^2}{2|\alpha _t -\alpha_r|}, $$

and the observable δ s is given by

$$ \delta _s=\frac{\tilde{\alpha}_p - \alpha_p}{R_{s}}, $$

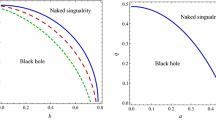
where \((\tilde{\alpha}_{p}, 0)\) and (α p ,0) are the points where the reference circle and the contour of the shadow cut the horizontal axis at the opposite side of (α r ,0), respectively. In Fig. 6, the observables R s and δ s as functions of the δ parameter are shown for the value of the rotation parameter of the black hole a=0.99.

Fig. 6
figure 6

Observables R s and δ s as functions of the δ parameter, corresponding to the shadow of a black hole situated at the origin of coordinates with inclination angle θ=π/2 and spin parameter a=0.99 (we put M=1)

Full size image

In Fig. 7, we show the contour of the shadows of black holes with rotation parameters a=0.4 (upper row, left), a=0.6 (upper row, right), a=0.8 (lower row, left), and a=0.99 (lower row, right), for several values of the KS parameter ω. From the Fig. 7, one can see that with increasing KS parameter(ω), the shadow of the black hole also increases.

Fig. 7
figure 7

Silhouette of the shadow cast by a Hořava-Lifshitz black hole situated at the origin of coordinates with inclination angle θ=π/2, having a rotation parameter a and a KS parameter ω (we put M=1). (Upper row, left) a=0.4, ω=1.1 (solid line), ω=1.14 (dashed line), and ω=1.18 (dashed-dotted line). (Upper row, right) a=0.6, ω=0.1 (solid line), ω=1.14 (dashed line), and ω=1.18 (dashed-dotted line). (Lower row, left) a=0.8, ω=1.1 (solid line), ω=1.14 (dashed line), and ω=1.18 (dashed-dotted line). (Lower row, right) a=0.99, ω=1.1 (solid line), ω=1.14 (dashed line), and ω=1.18 (dashed-dotted line). The shadow corresponds to each curve and the region inside it

Full size image

In Fig. 8, the observables R s and δ s as functions of the KS parameter ω are shown for the value of the spin parameter of the black hole a=0.99 .

Fig. 8
figure 8

Observables R s and δ s as functions of the KS parameter corresponding to the shadow of a black hole situated at the origin of coordinates with inclination angle θ=π/2 and spin parameter a=0.99 (we put M=1)

Full size image

4 Rotation of polarization vector around Hořava-Lifshitz black hole

In order to analyze possible effects of the parameters of Hořava-Lifshitz gravity in terms of measurable quantities we focus on geometrical optics of the light propagating around rotating Hořava-Lifshitz black hole. The approach employed here was presented by Pineault and Roeder (1977), Neves and Molina (2012) where the Newman-Penrose formalism was used to calculate optical quantities in the weak-field approximation with a≪M.

The equations which govern the tangent vector k μ (the wave vector) to the null congruence and the polarization vector f μ are

$$ k^{\mu}k_{\mu} = 0 , \qquad k^{\mu} {_{;\nu}k^{\nu}} = 0 $$
(38)

and

$$ k^{\mu} f_{\mu} = 0 , \qquad f^{\mu} {_{;\nu}k^{\nu}} = 0 $$
(39)

with the ; denoting covariant derivative in the k μ direction.

In the Newman-Penrose (1962) formalism a null tetrad is adopted, \(\{ e_{a\mu} \} = (m_{\mu},\bar{m}_{\mu},l_{\mu},k_{\mu} )\) with the vector m μ given by

$$ m^{\mu}=\frac{\sqrt{2}}{2}\bigl(a^{\mu}+ib^{\mu} \bigr) . $$
(40)

The vector m μ is particularly relevant to the approach developed here, as will be seen. An important feature of the formalism is that the k μ direction is preserved under null rotations as

$$ k'^{\mu}=Ak^{\mu} , $$
(41)
$$ m'^{\mu}=e^{-i\chi} \bigl(m^{\mu}+Bk^{\mu} \bigr) , $$
(42)
$$ l'^{\mu} = A^{-1} \bigl(l^{\mu}+B \bar{m}^{\mu}+\bar{B}m^{\mu}+B\bar{B}k^{\mu} \bigr) , $$
(43)

with A>0, B is complex and χ is real. The Newman-Penrose formalism provides 12 constants, the spin coefficients to the characterization of the spacetime. Some coefficients will be used to estimate the variation of the polarization vector in rotating Hořava-Lifshitz black hole background.

As shown in Newman and Penrose (1962) when k μ is tangent to the null congruence the spin coefficient τ≡−k μ ;ν k ν m μ is zero. Moreover considering that the null tetrad must parallelly propagate along the null congruence this assumption implies that other two spins coefficients vanish: ϵ=π=0. Then the plane spanned by k μ and a μ can be identified with the polarization plane which is parallelly propagated in the k μ direction. That is the polarization vector can be identified with the a μ vector of the Newman-Penrose formalism. From this one can built an orthonormal frame

$$ \bigl\{ \boldsymbol{e}_{a}^{(\mu)} \bigr\} = \bigl\{ r^{(\mu)},\bar{r}^{(\mu)},q^{(\mu)},p^{(\mu)} \bigr\}, $$
(44)

such that this tetrad corresponds to the one-forms σ (0)=e ν dt, σ (1)=e λ dr, σ (2)=e μ dθ, and σ (3)=(dϕ−Ωdt)e ψ of the locally non-rotating frame (LNRF). (The LNRF indices are indicated between parenthesis; Bardeen et al. 1972.) For the metric given by Eq. (6) the expressions for e ν, e λ, e μ and e ψ are presented in the Appendix Eq. (55). Therefore, if the source and the observer are at rest with respect to the LNRF they are dragged by rotation of the black hole. In Pineault and Roeder (1977) this construction was made, with the expression for the \(m_{+}^{(\mu)}\) vector (i.e., a μ)—the projection of m μ on the LNRF—given by

$$\begin{aligned} a_{+}^{(\mu)} = & \frac{1}{\sqrt{2}} \biggl(0,- \frac{k^{(2)}}{k^{(0)}},1-K \bigl(k^{(2)} \bigr)^{2},Kk^{(2)}k^{(3)} \biggr), \end{aligned}$$
(45)
$$\begin{aligned} b_{+}^{(\mu)} = & \frac{1}{\sqrt{2}} \biggl(0,- \frac{k^{(3)}}{k^{(0)}},-Kk^{(2)}k^{(3)},1-K \bigl(k^{(3)} \bigr)^{2} \biggr), \end{aligned}$$
(46)

where K=1/[k (0)(k (0)+k (1))] and k (μ) is the projection of k μ on the LNRF according to Eq. (54). A null rotation was performed

$$ m_{+}^{(\mu)}\rightarrow m^{(\mu)} = e^{-i\chi} m_{+}^{(\mu)} , $$
(47)

such that ϵ=0. With this choice and considering the ϵ coefficient as \(\epsilon\equiv Dm_{\mu}\bar{m}^{\mu}/2\) it is shown that

$$ D\chi=-2i\epsilon_{+} . $$
(48)

Expression (48) indicates how the χ angle varies in the k μ direction i.e. the congruence direction. This variation will be important to calculate the variation of polarization vector in that direction. For the spacetime metric (6) presented in the previous section we obtain

$$\begin{aligned} D\chi =& -2i\epsilon_{+} \\ =& { \bigl(\varGamma_{(\theta)(t)}^{(t)}k^{(t)}+ \varGamma_{(\theta)(r)}^{(r)}k^{(r)}+\varGamma_{(\theta)(\theta)}^{(r)}k^{(\theta)}+ \varGamma_{(\theta)(\phi)}^{(t)}k^{(\phi)} \bigr)} \\ &{} \times k^{(\phi)}\big/ \bigl({k^{(t)}+k^{(r)}}\bigr) - \bigl(\varGamma_{(\phi)(t)}^{(r)}k^{(t)} \\ & {}+ \varGamma_{ (\phi)(r)}^{(t)}k^{(r)}+\varGamma_{(\phi)(\theta)}^{(t)}k^{(\theta)}+ \varGamma_{(\phi)(\phi)}^{(r)}k^{(\phi)} \bigr) \\ &{}\times k^{(\theta)}\big/ \bigl({k^{(t)}+k^{(r)}}\bigr) + \varGamma_{(\phi)(\phi)}^{(\theta)}k^{(\phi)}+ \varGamma_{(\phi)(t)}^{(\theta)}k^{(t)} , \end{aligned}$$
(49)

where the values of \(\varGamma_{(\nu)(\gamma)}^{(\mu)}\) and k (μ) were projected on the LNRF presented in the Appendix. Using the results presented in Eqs. (54) and (56), Dχ is given in first order in a by

$$ D\chi = -D\chi( \cos\theta) + 3M \frac{r^{2}a \sin\theta}{\varXi^2}\frac{d\theta}{d\mu} + \mathcal{O}\bigl(a^2\bigr) . $$
(50)

The expression in Eq. (50) is associated with the variation between a (μ) and \(a_{+}^{(\mu)}\) according to the null rotation indicated in Eq. (47).

The total variation of polarization vector taking into account Eq. (50) and the spacetime dragging is given by

$$ \Delta \sigma=\Delta\chi+\Delta\phi . $$
(51)

The second term in right side of Eq. (51) is due to the spacetime dragging. The first term is obtained with the integration of Dχ in Eq. (50) with respect to the ψ coordinate (see Pineault and Roeder 1977), which plays the role of the azimuthal angle in the orbital plane of the null congruence. Moreover a new angle was defined: α is the angle of the orbital plane with respect to the equatorial plane. That is sinα=cosθsinψ and Eq. (50) is reduced to

$$ D\chi=-D\chi( \cos\theta) + D \chi' + \mathcal{O} \bigl(a^2\bigr) , $$
(52)

where

$$ D\chi'=-3M \frac{ r^{2}a \sin \alpha}{\varXi^2}\frac{d(\sin \psi)}{d\mu} . $$
(53)

Here, we have found the dependence of polarization vector from δ parameter in equatorial plane (θ=π/2). In the Fig. 9 the radial dependence of the polarization vector is shown for the different values of δ parameter. From the dependence one can easily see that presence of the δ parameter due to Hořava-Lifshitz modification increases the polarization angle. This dependence may help to get constraints on δ parameter from observational data related to the geometrical optics features of compact objects.

Fig. 9
figure 9

The radial dependence of the polarization vector for the different values of the δ parameter: solid line for δ=0, dashed line for δ=0.05, and dot-dashed line for δ=0.1

Full size image

5 Conclusion

We have studied the radial dependence of effective potential of the massless particles radial motion around Hořava-Lifshitz black hole and obtained that with increase of δ parameter photon orbits come closer to the central object. The stability of photon orbits will increase with the increasing the parameter δ.

We have shown that with decreasing the KS parameter the shape of the effective potential is going to shift to the central object. This corresponds to the decrease of the event horizon of the KS black hole. Other important conclusion is that with decreasing the KS parameter the circular photon orbits become unstable. We have analyzed how the shadow of the black hole is distorted by the presence of the δ and ω parameters. The shape of the shadow of the black hole was affected by the δ parameter that is with increasing δ parameter the radius of the shadow and distortion parameter decrease. The influence of black hole spin parameter a is opposite that is with the increase of black hole spin a the distortion parameter is increasing. Therefore the effect of parameter δ compensates the influence of the parameter a. The shape of the shadow of the black hole is also affected by the KS parameter that is with increasing KS parameter the radius of the shadow and distortion parameter also increase.

Since black hole’s shadows give the region where one can never observe any light from the gravitational source, one should look for a part of the shape of realistic light source (Hioki and Maeda 2009). In the near future if the instrumental astronomy would give more accurate measurements, at least, on part of the black hole’s shape one can find constraints on δ and KS parameter in Hořava-Lifshitz space-time. The recent measurements of the Gravitational Lens Systems (Narasimha 2007) may give alternate constraints on the numerical values of the δ parameter in Hořava-Lifshitz model. Astrophysical quantities related to the observable properties of the polarization vector can be obtained from the spacetime metric and observations have provided important information about the δ parameter. In order to get the estimation for the value of δ parameter one should compare the observational results with obtained theoretical results on polarization angle. For the nuclei of spiral galactic systems B0218+357 and PKS1830-211 the polarization angle has been found as \(913 \pm 31~\mathrm{rad\,m}^{-2}\) and \(1480 \pm 83~\mathrm{rad\,m}^{-2}\), respectively (Subrahmanyan et al. 1990 and Patnaik et al. 1993), from the observed correlation of the Faraday rotation measurements. Since the effect of the additional δ parameter is within the error of the observation we may put D χ (δ≠0)/D χ (δ=0)=1+ϵ, where ϵ is the relative error of the observation. Putting the value of ϵ from the observations (Subrahmanyan et al. 1990 and Patnaik et al. 1993) into the above condition one can easily make an estimation on upper limit for the δ parameter as δ≤2.1⋅10−3.