1 Introduction

A number of difficult problems in cosmology have been put forward by the discovery of the accelerated expansion of the universe (Riess et al. 1998; Perlmutter et al. 1999). This cosmic acceleration can be explained via the introduction of a so-called dark energy (for a recent review, see Bamba et al. 2012a, 2012b; Li et al. 2011). It follows from recent observational results that dark energy currently accounts for about 73 % of the total mass/energy of the universe (Kowalski 2008). It may have rather strange properties, as a negative pressure and/or a negative entropy, the fact that it is undetectable in the early universe, etc. It is not excluded, however, that General Relativity (GR) and the ensuing vacuum fluctuations (as those leading, e.g., to the Casimir effect) could lead to an explanation of the issue, see e.g. Elizalde (2006, 2012), Cognola et al. (2005), Elizalde et al. (1994). One should also stress the following important connection: with the help of an ideal fluid GR can actually be rewritten, in an equivalent way, as some modified gravity (for a recent review, see Nojiri and Odintsov 2011).

For dark energy with density ρ D and pressure p D , the equation of state (EoS) parameter w D ,

$$ w_{D}=p_{D}/\rho_{D}<0 $$
(1)

is known to be negative and also, that astrophysical observations favor the standard ΛCDM cosmology. Dark energy as just a cosmological constant (w D =−1) is the simplest and maybe most preferred model from the theoretical point of view, too. In this model over 70 % of the current energy budget is dark energy (Einstein’s cosmological constant Λ), in perfect accordance with the data coming from observations, as reported above.

At present, several independent observational procedures provide strong evidence in favor of the ΛCDM model, in particular SNIa apparent magnitude measurements as a function of the redshift, cosmic microwave background (CMB) anisotropies, baryon acoustic oscillation (BAO) peak length scale measurements, Hubble parameter determinations etc., but the error bars associated with all these types of data are still too large to allow for a significant observational discrimination between the ΛCDM model and other existing, theoretically very well founded alternatives to it.

When w<−1 (phantom dark energy) (Caldwell 2002; Caldwell et al. 2003) we are dealing with the most interesting and less understood theoretical case. A simultaneous violation of all four energy conditions occurs in this case and the involved field is unstable, although it could perhaps be made stable in classical cosmology (Carroll et al. 2003). For a universe filled with phantom energy there are many possible new scenarios for the end of such universe, among which the most typical cases are those of a Big Rip singularity (Caldwell 2002; Caldwell et al. 2003; Frampton and Takahashi 2003; Starobinsky 2000; McInnes 2002; Nojiri and Odintsov 2003, 2011; Faraoni 2002; Gonzalez-Diaz 2004; Elizalde et al. 2004; Singh et al. 2003; Nesseris and Perivolaropoulos 2004; Stefancic 2004, 2011) and of a sudden future singularity (Shtanov and Sahni 2002; Barrow 2004; Nojiri and Odintsov 2004a, 2004b; Cotsakis and Klaoudatou 2005; Fernandez-Jambrina and Lazkoz 2004; Barrow and Tsagas 2005; Stefancic 2005; Tretyakov et al. 2006; Sami et al. 2006; Yurov et al. 2008; Barrow and Lip 2009). However, a final evolution without singularities is also possible: if the parameter w asymptotically tends to −1, and the energy density increases with time or remains constant, no finite-time future singularity will be ever formed (Sahni and Shtanov 2003; Frampton et al. 2011, 2012a, 2012b; Astashenok et al. 2012a, 2012b, 2012c; Brevik et al. 2011; Frampton and Ludwick 2011; Nojiri et al. 2011; Ito et al. 2011; Makarenko et al. 2012; Saitou and Nojiri 2012) or if the universe starts to decelerate in far future. In any case, if the energy density grows up to some value, the disintegration of any bound structure will eventually occur, in a way quite similar to that in the case of the Big Rip singularity, but this may only happen very far in the future evolution.

For the dark energy pressure one can choose the general expression

$$ p=g(\rho), $$
(2)

with g a function of the energy density.

In this paper a number of dark energy models on the brane will be considered (for general introduction to brane-world cosmology, see Maartens and Koyama 2010). The theoretical predictions of these models will be compared with the various types of existing independent data observations, including the luminosity distance modulus vs redshift for SNe Ia, the data accumulated on the evolution of the Hubble parameter H(z), the latest baryon acoustic oscillation (BAO) results, and matter density perturbation data. In Sect. 2 a brief overview of the EoS fluid formalism will be presented. A comparison of dark energy in Friedmann-Robertson-Walker (FRW) cosmology and on the brane is carried out. The main constraints coming from the observational survey data will be analyzed in Sect. 3. In the following two sections, Sects. 4 and 5, we will study the simplest ΛCDM model on the brane and will show that a careful joint analysis of the various observational data allows to estimate, in a clear fashion, any possible deviation of our cosmological model from the standard FRW cosmology. Due to the increasing interest in teleparallel theories (F(T) models), we deal with them in Sect. 6 where we find explicit formulas of the so-called state-finder parameters in teleparallel theories, which could be useful to test the models proposed in those theories, in particular to test Loop Quantum Cosmology and Brane Cosmology. Finally, Sect. 7 is devoted to conclusions.

2 Comparison of dark energy in FRW cosmology and on the brane

We start with a brief description of dark energy models in the frame of the FRW cosmology. The cosmological equations corresponding to a spatially flat universe, endowed with a metric

$$ ds^{2}=-dt^{2}+a^{2}(t) \bigl(dx^{2}+dy^{2}+dz^{2} \bigr), $$
(3)

are the following

$$ \biggl(\frac{\dot{a}}{a} \biggr)^2 = \frac{\rho}{3} , \qquad\dot{\rho} = -3 \biggl(\frac{\dot{a}}{a} \biggr) (\rho+ p) $$
(4)

with ρ and p, respectively, the total energy-density and pressure, while a is the scale factor, the dot means time derivative, and were natural system units are being used, with 8πG=c=1.

For dark energy, the EoS can be rewritten, for convenience, in the form

$$ p_{D}=-\rho_{D}-f(\rho_{D}), $$
(5)

being f(ρ D ) a function of the energy-density. We observe that f(ρ D )>0 corresponds to w<−1, and f(ρ)<0 to w>−1. The future evolution of the universe depends on the EoS for dark energy chosen. Let us here describe two main possible cases.

  1. (i)

    Evolution without future singularities. This case includes a so-called “Little Rip” (these models are described in detail in Frampton et al. 2011, 2012a, 2012b). The dark energy density grows with time so slowly that a Big Rip cannot occur in finite time. For the realization of this scenario, one needs that the asymptotic behavior of the function \(g(\rho_{D})\sim\rho_{D}^{\beta}\), as β≤1/2. But, eventually, a dissolution of all bound structures will also happen in the future.

    One should note that, for some specific equations of state with branch points, a de(phantomization) process can occur Wei et al. (2012). Therefore, after the acceleration phase, a slowdown of the future universe might be possible. In other words, the universe maybe decelerating in the future.

    Interesting alternatives to the ΛCDM model are models in which the dark energy density asymptotically tends to a constant value (an “effective cosmological constant” Astashenok et al. 2012a, 2012b). One should remark that if the value of this “effective cosmological constant” is sufficiently large (for example, if Λ eff ∼1 in Planck units) a possibility of disappearance of the bound structures due to the enormous acceleration of the universe still remains.

  2. (ii)

    Evolution with finite-time singularities. If \(g(\rho_{D})\sim\rho_{D}^{\beta}\), with β>1/2, the dark energy density grows so rapidly that the universe ends its existence in a singularity of the Big Rip type or in a type III singularity, according to the classification in Nojiri et al. (2005). The key difference between these singularities is that the energy density in the second case grows so rapidly with time that the scale factor does never reach the infinite value. These scenarios can be realized only in the case of having a phantom energy. Another interesting case occurs if f(ρ D )→±∞ at ρ D =ρ Df , i.e., the dark energy pressure becomes infinite at finite energy density. The second derivative of the scale factor diverges, while the first derivative remains finite.

As an alternative to the FRW cosmology let us consider the simplest brane model in which spacetime is homogeneous and isotropic along three spatial dimensions, being our 4-dimensional universe an infinitesimally thin wall, with constant spatial curvature, embedded in a 5-dimensional spacetime (Sahni and Shtanov 2008; Langlois 2003). In the Gaussian normal coordinate system, for the brane which is located at y=0, one gets

$$ ds^{2}=-n^{2}dt^{2}+a^{2}(t,y) \gamma_{ij}dx^{i}dx^{j}+dy^{2}, $$
(6)

where γ ij is the maximally 3-dimensional metric. Let t be the proper time on the brane (y=0), then n(t,0)=1. Therefore, one gets the FRW metric on the brane

$$ ds^{2}_{|y=0}=-dt^{2}+a^{2}(t,0) \gamma_{ij}dx^{i}dx^{j}. $$
(7)

The 5-dimensional Einstein equations have the form

$$ R_{AB}-\frac{1}{2}g_{AB}R=\chi^{2}T_{AB}+ \varLambda g_{AB}, $$
(8)

where Λ is the bulk cosmological constant, χ 2=8πG (5)/c 4, G (5) is the gravitational constant in 5-dimensional spacetime. The next step is to write the total energy momentum tensor T AB on the brane as

$$ T^{A}_{B}=S^{A}_{B}\delta(y), $$
(9)

with \(S^{A}_{B}=\mbox{diag}(-\rho_{b},p_{b},p_{b},p_{b},0)\), where ρ b and p b are the total brane energy density and pressure, respectively.

One can now calculate the components of the 5-dimensional Einstein tensor which solve Einstein’s equations. One of the crucial issues here is to use appropriate junction conditions near y=0. These reduce to the following two relations:

$$ \frac{dn}{ndy}_{|y=0+}=\frac{\chi^{2}}{3}\rho_{b}+ \frac{\chi ^{2}}{2}p_{b},\qquad\frac{da}{ady}_{|y=0+}=- \frac{\chi^{2}}{6}\rho_{b}. $$
(10)

After some calculations, one obtains the following result

$$ H^{2}=\chi^{4}\frac{\rho_{b}^{2}}{36}+\frac{\varLambda}{6}- \frac{k}{a^{2}}+\frac{C}{a^{4}}. $$
(11)

This expression is valid on the brane only. Here \(H=\dot {a}(t,0)/a(t,0)\) and C is an arbitrary integration constant. The energy conservation equation is correct, too,

$$ \dot{\rho_{b}}+3\frac{\dot{a}}{a}(\rho_{b}+p_{b})=0. $$
(12)

Now, let ρ b =ρ+λ, where λ is the brane tension. For a fine-tuned brane with Λ=λ 2 χ 4/6, we have the following equation (for k=0)

$$ \frac{\dot{a}^{2}}{a^{2}}=\frac{\lambda\chi ^{4}}{6}\frac{\rho}{3} \biggl(1+ \frac{\rho}{2\lambda} \biggr)+\frac{C}{a^{4}}. $$
(13)

In what follows we will consider a single brane model which mimics GR at present but differs from it at late times. We set 8πG=σχ 4/6. For simplicity, we set C=0 (the term with C is usually called “dark radiation”). In fact, setting C≠0 does not lead to additional solutions on a radically new basis, in the framework of our approach. Equation (13) can be simplified to

$$ \frac{\dot{a}^{2}}{a^{2}}=\frac{\rho}{3} \biggl (1+\frac{\rho }{2\lambda} \biggr). $$
(14)

One can see that Eq. (14), for ρ≪|λ|, differs insignificantly from the FRW equation. The brane model with a positive tension has been discussed in Copeland et al. (2001), Sahni et al. (2002), Sami and Sahni (2004) in the context of the unification of early- and late-time acceleration eras. The braneworld model with a negative tension and a time-like extra dimension can be regarded as being dual to the Randall-Sundrum model (Shtanov and Sahni 2003; Randall and Sundrum 1999; Copeland et al. 2005). Note that, for this model, the Big Bang singularity is absent. And this fact does not depend upon whether or not matter violates the energy conditions (Ashtekar et al. 2006). This same scenario has also been used to construct cyclic models for the universe Kanekar et al. (2001).

One can assume that in our epoch the ρ/2λ≪1 and so there is no significant difference between the brane model and FRW cosmology. But the universe evolution in the future, for brane cosmology, can in fact differ from such convenient cosmology, due to the non-linear dependence of the expansion rate on the energy density.

The equation-of-state formalism for dark energy models on the brane was considered in Astashenok et al. (2012c). Here we briefly describe this approach. One gets the following link between time and dark energy density, assuming that ρ D ≫ρ m :

$$ t(\rho_{D})-t_{0}=\frac{1}{\sqrt{3}}\int _{\rho_{D0}}^{\rho _{D}}\frac{d\rho}{\rho^{1/2} (1+\frac{\rho}{2\lambda} )^{1/2}f(\rho)}. $$
(15)

For the present time, t 0, we can set t 0=0. For the scale factor as a function of the dark energy density, we have the same relation as in the FRW cosmology, namely

$$ a=a_{0}\exp\biggl(\frac{1}{3}\int _{\rho_{D0}}^{\rho_{D}}\frac {d\rho}{g(\rho)} \biggr). $$
(16)

In the case of a positive tension, the following possibilities can be realized:

  1. 1.

    If the integral (15) converges while (16) diverges, we have a Big Rip. It is interesting to note that the Big Rip on a brane considered in Yurov et al. (2006) occurs faster than in the FRW cosmology.

    For the simplest EoS with constant state parameter w 0=−1−α 2, the function g(ρ D )=α 2 ρ D . If ρ D ≫λ, then the dark energy density grows with time substantially faster than in ordinary cosmology (λ→∞).

  2. 2.

    If the integrals (15) and (16) diverge when ρ D →∞, then a Little Rip occurs. The acceleration of the universe increases with time definitely faster than in the FRW universe, owing to the brane tension (see the corresponding time equation for the case (1)).

  3. 3.

    Asymptotic de Sitter expansion is realized if g→0 for ρ D →ρ Df , and the integral (15) diverges.

  4. 4.

    There is a type III singularity if both integrals converge when ρ D →∞.

  5. 5.

    If g(ρ D )→∞ for ρ D →ρ Df , the universe ends its existence in a sudden future singularity.

The case of negative tension allows for the following interesting possibilities:

  1. 1.

    Asymptotic de Sitter expansion, if g(ρ D )→0 for ρ D →ρ Df .

  2. 2.

    An asymptotic breakdown (i.e. the rate of expansion of universe tends to 0) will occur if g(ρ D )→0 for ρ D →2λ.

  3. 3.

    A sudden future singularity, if f(ρ D )→∞ when ρ D →ρ Df .

One should note that dark energy with an EoS such that f(ρ)∼ρ γ, with γ≤2, leads to a Big Rip on the brane while, in the case of the conventional FRW universe, such dark energy leads to a Little Rip only.

3 Observational data

The parameters of the cosmological models can be determined from a strict comparison of their predictions with accurate observational data. We here consider the data coming from SNe observations, the evolution of the Hubble parameter, baryon acoustic oscillation, and the evolution of matter perturbations.

3.1 SNe observations

The modulus μ vs redshift z=a 0/a−1 relation to type Ia supernovae from the Supernova Cosmology Project (Amanullah et al. 2010) is, as well known,

$$ \mu(z)=\mu_{0}+5\lg D_{L}(z). $$
(17)

The relation for the luminosity distance D L (z) as a function of the redshift, in the FRW cosmology (FC), is

$$ \begin{array}{l} D^{FC}_{L}=\displaystyle\frac{c}{H_{0}}(1+z)\int_{0}^{z}h^{-1}(z)dz,\\[12pt] h(z)= \bigl[\varOmega_{m0}(1+z)^{3}+ \varOmega_{D0}F(z) \bigr]^{1/2}. \end{array} $$
(18)

Here, Ω m0 is the total fraction of matter density, Ω D0 the fraction of dark energy energy density, and H 0 is the current Hubble parameter. The constant value μ 0 depends on the chosen Hubble parameter:

$$\mu_{0}=42.384-5\log h,\quad h=H_{0}/100\ \mbox{km/s/Mpc} $$

The function F(z)=ρ D (z)/ρ D0 can be determined from the continuity equation

$$ \dot{\rho}_{D}-3\frac{\dot{a}}{a}g(\rho_{D})=0, $$
(19)

which can be rewritten as

$$ \int_{\rho_{D0}}^{\rho_{D}(z)}\frac{dy}{g(y)}=-3\ln(1+z). $$
(20)

For simplicity, we neglect the contribution of radiation.

For cosmology on the brane (BC), Eq. (18) can be rewritten as

$$ D^{BC}_{L}=\frac{c(1+z)}{H_{0}}\int _{0}^{z} h^{-1}(z) \bigl(1+\delta h^{2}(z)\bigr)^{-1/2}(1+\delta)^{1/2}d z, $$
(21)

where the convenient parameter δ=ρ 0/2λ has been introduced. For the analysis of the SNe data one needs to calculate the parameter χ 2, which is defined by

$$ \chi^{2}_{SN}=\sum_{i} \frac{(\mu_{obs}(z_{i})-\mu _{th}(z_{i}))^{2}}{\sigma^{2}_{i}}, $$
(22)

where σ i is the corresponding 1σ error. The parameter μ 0 is independent of the data points and, therefore, one needs to perform a uniform marginalization over μ 0. But the minimization with respect to μ 0 can be made simply by expanding the \(\chi^{2}_{SN}\) with respect to μ 0, as

$$ \chi^{2}_{SN}=A-2\mu_{0}B+ \mu_{0}^{2}C, $$
(23)

where

The expression (23) has a minimum for μ 0=B/C at

$$\bar{\chi}_{SN}^{2}=A-B^{2}/C. $$

One can minimize \(\bar{\chi}_{SN}^{2}\) instead of \({\chi}_{SN}^{2}\). Following Nesseris and Perivolaropoulos (2005), one determines the 68.3 % confidence level (C.L.) by \(\Delta\chi^{2}=\chi^{2}-\chi^{2}_{\min}<1.0\) for the one-parametric or 2.3 for two-parametric model. Similarly, the 95.4 % confidence level is determined by \(\Delta\chi^{2}=\chi ^{2}-\chi^{2}_{\min}<4.0\) or 6.17 for the one- and two-parametric models, correspondingly.

3.2 Hubble parameter

The evolution of the Hubble parameter with time in the past is now well observed. The Hubble parameter depends on the differential age of the universe as a function of the redshift, in the form

$$dt=-\frac{1}{H}\frac{dz}{1+z}. $$

Therefore, a determination of dz/dt directly measures H(z). These measurements are possible due to data we have on the absolute age for passively evolving galaxies, determined from fitting stellar population models. We use the 11 datapoints for H(z) from Stern et al. (2010) for constraining the model parameters. These data are listed in Table 1. The theoretical dependence of the Hubble parameter in the brane model is

$$ H(z)=H_{0}h(z) \bigl(1+\delta h^{2}(z)\bigr)^{1/2}(1+ \delta)^{-1/2}. $$
(24)
Table 1 Hubble parameter versus redshift data from Stern et al. (2010)
Full size table

The parameter \(\chi^{2}_{H}\) is

$$ \chi^{2}_{H}=\sum_{i} \frac {(H_{obs}(z_{i})-H_{th}(z_{i}))^{2}}{\sigma^{2}_{i}}. $$
(25)

One needs to perform a uniform marginalization over the parameter H 0. Again, one can expand

The parameter \(\chi^{2}_{H}\) has a minimum at the point \(H_{0}^{2}=B_{1}/C_{1}\),

$$\bar{\chi}_{H}^{2}=A_{1}-B_{1}^{2}/C_{1}. $$

As in the case of the SNe data, one can minimize \(\bar{\chi}_{H}^{2}\) instead of \({\chi}_{H}^{2}\).

3.3 BAO data

To constrain cosmological parameters using BAO data we follow the procedure described in Blake et al. (2011). We use the measurements of the acoustic parameter A(z) from Blake et al. (2011), where the theoretically-predicted A th (z) is given by the relation

$$ A_{th}(z)=\frac{D_{V}(z)H_{0}\sqrt{\varOmega_{m0}}}{z}, $$
(26)

where D V (z) is a distance parameter defined as

$$ D_{V}(z)= \biggl\{(1+z)^{2}d_{A}^{2}(z) \frac{cz}{H(z)} \biggr\}^{1/3}. $$
(27)

Here, d A (z) is the angular diameter distance

$$ \begin{array}{l} d_{A}(z)=\displaystyle\frac{y(z)}{H_{0}(1+z)},\quad y(z)=\int_{0}^{z} \frac {dz}{E(z)},\\[12pt] E(z)=H(z)/H_{0}. \end{array} $$
(28)

Using Eqs. (26)–(28) we have

$$ A_{th}(z)=\sqrt{\varOmega_{m0}} \biggl(\frac{y^{2}(z)}{z^{2}E(z)} \biggr). $$
(29)

Using the WiggleZ A obs (z) data from Table 3 of Blake et al. (2011), we compute \(\chi^{2}_{A}\) as

$$ \chi^{2}_{A}=\Delta\mathbf{A}^{T}(C_{A})^{-1} \Delta\mathbf{A}. $$
(30)

Here, ΔA is a vector consisting of differences, ΔA i =A th (z i )−A obs (z i ) and \(C^{-1}_{A}\) is the inverse of the 3×3 covariance matrix given in Table 3 of Blake et al. (2011).

3.4 Matter density perturbations

As it was shown in Christopherson (2010) one can neglect the density perturbations of dark energy. In this case the dark matter perturbations effectively decouple from DE perturbations. The equation that determines the evolution of the density contrast δ in a flat background filled by matter with density ρ m is

$$ \ddot{\delta}_{m}+2H\dot{\delta}_{m}= \frac{1}{2}\rho_{m}\delta_{m}. $$
(31)

It is convenient to introduce the growth rate function of the perturbations f=dlnδ m /dlna. Using the FRW equations, one can get the following equation for f

$$ \frac{df}{d\ln a}+f^{2}+ \biggl(\frac{\dot{H}}{H^{2}}+2 \biggr)f- \frac{3}{2}\varOmega_{m}(1+\rho/2\lambda)^{-1}=0, $$
(32)

where Ω m is the matter fraction of the total energy-density Ω m =Ω m0(1+z)3/(Ω m0(1+z)3+Ω D0 F(z)). Finally, using the relation

$$\frac{d}{d\ln a}=-(1+z)\frac{d}{dz} $$

and taking into account that

$$\frac{\ddot{a}}{a}-\frac{\dot{a}^{2}}{a^{2}}=-\frac{\rho +p}{2}(1+\rho/\lambda), $$

we get

$$-(1+z)\frac{df}{dz}+f^{2}+ \biggl(2-\frac{3\Delta}{2}\varOmega _{m}+\frac{3\Delta}{2}\frac{g(\rho_{D})}{\rho} \biggr)f- $$
$$ -\frac{3}{2}\varOmega_{m}(1+\rho/2 \lambda)^{-1}=0, $$
(33)

where Ω D =ρ D /ρ and we have introduced the parameter Δ=(1+ρ/λ)(1+ρ/2λ)−1.

For a dark fluid with given EoS, one can find the DE density as a function of the redshift z. Then, Eq. (33) can be solved numerically. The observational data for the growth factor f obs at various redshifts are given in Table 2.

Table 2 The available data growth factor f obs at various redshifts from the change of power spectrum Ly-α forest data in SDSS
Full size table

4 ΛCDM model on the brane

First, we consider the simple cosmological model on the brane with vacuum energy ρ D =Λ=const. This model coincides in fact, in the future, with the FRLW cosmology with a redefined cosmological constant. The asymptotic behavior of the scale factor is

$$a(t)\sim a_{0}\exp\bigl(({\varLambda_{eff}/3})^{1/2}t \bigr),\quad t\rightarrow\infty, $$
$$ \quad\varLambda_{eff}=\varLambda(1+\varLambda/2\lambda). $$
(34)

One can consider the ΛCDM model on the brane as a one-parametric one, at fixed values of δ. The results of the calculations corresponding to this case are given in Table 3 (we have also included in our consideration the case δ=0, i.e. the FRW cosmology, for comparison). The BAO data favor smaller values of Ω D0 than the H(z) and SNe data. The optimal value of Ω Λ is closer to the one coming from the SNe data analysis only. One easily sees that the addition of the observational data for the matter density perturbations does not change the best-fit value of Ω Λ from the SNe+H+BAO analysis. One can also conclude that the best consistent description of all observational data is realized in the frame of the FRW cosmology (δ=0 or λ→∞). The minimal value of the total χ 2 is 562.39. As δ grows, the corresponding χ 2 increases.

Table 3 The best fitting value for Ω Λ within 1σ and 2σ errors for various δ from observational data analysis for ΛCDM model on brane. In the last column the minimal value of \(\chi^{2}_{\min}= \bar{\chi}^{2}_{SN}+\bar{\chi}^{2}_{H}+\chi^{2}_{A}+\chi^{2}_{f}\) is given
Full size table

For δ>0 we have the following picture. The analysis of data sets separately does not yield a significant constraint on the maximal value of δ. The parameter χ 2 for SNe, BAO and matter density perturbation data grows very slowly with increasing δ. For instance, for δ=0, \(\bar{\chi}^{2}_{SN,\mathrm{min}}=553.18\), while for δ=0.1 the minimal value of \(\chi^{2}_{SN}\) is 553.34. The data on the evolution of the Hubble parameter are more sensitive to increasing δ: for δ=0.1 we found that \(\bar{\chi}^{2}_{H,\mathrm{min}}=8.12\), in comparison with \(\chi ^{2}_{H,\mathrm{min}}=7.62\) in the FRW model. But one can see that at δ≈0.05 the 1σ intervals of the possible values of Ω Λ for SNe and BAO data do not intersect. The 2σ intervals for Ω Λ from these data sets do not have common points for δ≈0.10. Therefore, one can estimate the maximal value of δ from the joint analysis of all observational data sets.

For this, we consider the ΛCDM model on the brane as a two-parametric one, with free parameters δ and Ω Λ . One can see that, although the areas corresponding to the 1σ and 2σ contours from the SNe, BAO and H(z) data analysis are sufficiently large (see Fig. 1) these contours intersect in a quite narrow region of the parameter space. The joint data analysis allows us to define the 1σ and 2σ contours in the Ω Λ −δ parameter space (Fig. 2). Therefore, we can estimate the upper limit of the parameter δ at which the ΛCDM model is relevant to the observational data.

Fig. 1
figure 1

The 68.3 % (upper panel) and 95.4 % (down panel) confidence level contours in the Ω Λ −δ parameter space from the analysis of SNe (solid), H(z) (bold solid) and BAO (dotted) data, respectively

Full size image
Fig. 2
figure 2

The 68.3 % (solid) and 95.4 % (dotted) confidence level contours in the Ω Λ −δ parameter space from the SNe+H(z)+BAO+matter density perturbation data analysis. The best-fit parameters for the observational data are Ω Λ =0.712, δ=0 with χ 2=562.39

Full size image

5 Other dark energy models on the brane

Let us now consider the following model with a quite simple EoS,

$$ g(\rho_{D})=\alpha^{2}\rho_{D0} \biggl( \frac{\rho_{D}}{\rho _{D0}} \biggr)^{\beta}, $$
(35)

where α and β are dimensionless constants. If β=1, we have an ordinary phantom energy model with constant EoS parameter w=−1−α 2. From Eqs. (15) and (16) one can see that, for various values of β, the model (35) describes three types of future universe evolution:

  1. (a)

    Little Rip, if β≤0,

  2. (b)

    Big Rip, for 0<β≤1, and

  3. (c)

    a type III singularity, if β>1.

One note that in the FRW cosmology the Little Rip occurs for β≤1/2. Simple calculations allow to define the function F(z):

$$ F(z)=\left \{ \begin{array}{l@{\quad}l} \{1-3\alpha^{2}(1-\beta)\ln(1+z) \} ^{\frac{1}{1-\beta}},& \beta\neq1,\\[6pt] (1+z)^{-3\alpha^{2}},& \beta=1. \end{array} \right . $$
(36)

We consider the case β=0 (Little Rip) and β=1.

The analysis of observational data for the Little Rip model leads to the same conclusions as in a case of the ΛCDM model: with a decreasing of the brane tension, the common area of the confidence level contours for SNe, H(z), and BAO data in the α 2−Ω D0 parameter space decreases, i.e. the agreement with observational data becomes worse. In Fig. 3 the 1σ confidence level contours from the data set analysis are shown. The results for the joint observational data analysis are depicted in Fig. 4. One can see that for larger values of δ the description of the observational data is better for larger α 2.

Fig. 3
figure 3

The 68.3 % confidence level contours in the Ω Λ −α 2 parameter space from the analysis of SNe (solid), H(z) (bold solid), and BAO (dotted) data for the FRW cosmology (A), δ=0.05 (B) and δ=0.10 (C) in the case of the Little Rip model with β=0. We see that, for each of the data sets, the best-fit parameters correspond to the ΛCDM model (α 2=0)

Full size image
Fig. 4
figure 4

The 68.3 % (solid) and 95.4 % (dotted) confidence level contours in the Ω Λ −α 2 parameter space from the analysis of SNe+H(z)+BAO+matter density perturbation data for the FRW cosmology (A), δ=0.05 (B) and δ=0.10 (C) in the case of the Little Rip model with β=0. The best-fit parameters are (α 2=0.03, Ω D0=0.713) with χ 2=562.20 for the FRW cosmology, (α 2=0.08, Ω D0=0.714) with χ 2=563.73 for δ=0.05 and (α 2=0.10, Ω D0=0.722) with χ 2=566.78 for δ=0.10

Full size image

Similar results can be derived for the simplest phantom model with constant EoS parameter w 0. The best-fit parameters for the FRW cosmology are (w 0=−1.01, Ω D0=0.713) with χ 2=562.16 (recall, for comparison, that in the ΛCDM model we have the slightly larger value of \(\chi^{2}_{\min}=562.38\)). In Fig. 5 the results of the joint analysis are depicted. For δ>0 the observational data analysis speaks evidently in favor of w 0<−1.

Fig. 5
figure 5

The 68.3 % (solid) and 95.4 % (dotted) confidence level contours in the Ω Λ −w 0 parameter space from the analysis of SNe+H(z)+BAO+matter density perturbation data for δ=0.05 in the case of the simplest phantom model. The best-fit parameters are (w 0=−1.08, Ω D0=0.718) with χ 2=563.84

Full size image

6 State-finder parameters in teleparallel theories

In this section we will compute the so-called state-finder parameters in universes described by teleparallel models which maybe considered as one example of Loop Quantum Cosmology. The first of these parameters is the effective ω parameter and the second one the deceleration parameter, and both are well-known in the literature. The other two, due to increase in the accuracy of cosmological data, were introduced in Sahni et al. (2003) (see also Bamba et al. 2012b) in order to advance beyond the effective ω and deceleration parameters. They are defined as follows:

  1. 1.

    The effective ω parameter is

    (37)
  2. 2.

    the deceleration parameter

    (38)
  3. 3.

    the jerk parameter

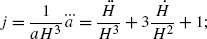    (39)
  4. 4.

    and the snark parameter

    (40)

We consider again a universe filled by a perfect fluid with EoS p=g(ρ)≡−ρ−f(ρ). Teleparallel theories in flat FRW cosmology are defined via a Lagrangian of the form \({\mathcal{L}}_{T}=VF(T)-V\rho\) (see Hehl et al. 1976; Hayashi and Shirafuji 1979; Bamba et al. 2013 for a review of the topic), where V is the volume of the spatial part and T=−6H 2 is the so-called scalar torsion (Bengochea and Ferraro 2009; Bamba et al. 2012b).

From this Lagrangian we can see that the conjugate momentum of V is then given by \(p_{V}=\frac{\partial{\mathcal{L}}}{\partial\dot{V}}= -4HF'(T)\), and thus the Hamiltonian is

(41)

It is well-known that in general relativity the Hamiltonian is constrained to be zero. This constrain leads to the modified Friedmann equation

(42)

which is a curve on the plane (H,ρ).

Conversely, given a curve of the form ρ=G(T) for some function G, it could be obtained from the modified Friedmann equation by choosing Bamba et al. (2013)

(43)

The modified Raychaudhuri equation is obtained from the modified Friedmann equation by taking its derivative with respect to time and using the conservation equation \(\dot{\rho} = 3Hf(\rho) \), giving rise to the equation \(\dot{H}=-\frac{f(\rho)}{4G'(T)}\). Then, the dynamics of the universe is given by the modified Raychaudhuri equation and the conservation equation, i.e. by the system

(44)

provided the universe moves along the curve ρ=G(T).

To compute the state-finder parameters, one has to use the modified Friedmann, Raychauduri and conservation equations, to get

(45)

These formulas mean that the parameters are functions of H. Then, since H 0 (the current value of the Hubble parameter) is well-known, one can test all the F(T) models with current observations without actually solving them. In particular, as we will see, one can test loop quantum cosmology or brane cosmology in the Randall-Sundrum scenario, i.e., brane cosmology described in Sect. 2. In fact, H 0 could be calculated from measurement of the luminosity distance D L (z) via the well-known formula (Sahni et al. 2003)

(46)

being z the redshift, or as we have already explained in Sect. 3.2.

A remark is important: the formulas (45) could be expressed in function of ρ via the relation T=G −1(ρ). This will be relevant when we deal with loop quantum cosmology and brane cosmology. The formulas read

(47)

We start calculating the parameters for the simplest but one of the most interesting EoS, namely when the dependence between pressure and energy density is linear, i.e., when

$$p=\omega\rho\quad \Longleftrightarrow\quad f(\rho)=-(1+\omega)\rho. $$

In that case, one has

$$ \begin{array}{l} \omega_{eff}(T)=-1+(1+\omega)\displaystyle\frac{G}{TG'},\\[12pt] q_{dec}(T)=- \biggl(-\displaystyle\frac{3}{2}(1+\omega)\frac{G}{TG'}+1 \biggr),\\[12pt] j(T)=-\displaystyle\frac{9}{2}(1+\omega)\frac{G}{T(G')^3} \bigl (-\omega \bigl(G'\bigr)^2 +(1+\omega)GG'' \bigr)+1,\\[12pt] s(T)=\displaystyle\frac{(1+\omega)G[-\omega G' +(1+\omega )GG'']}{(G')^2[-(1+\omega)G+TG']}. \end{array} $$
(48)

As an application, we study FRW cosmology with an small cosmological constant Λ. In this case \(G(T)=-\frac{T}{2}-\varLambda\), and from (48) a simple calculation yields

(49)

We should remark that, when ω>−1, at late times ρ→0 and thus T→−2Λ. Obviously one has ω eff (T)→−1, q dec (T)→−1, j(T)→1 and s(T)→0. On the other hand, when ω<−1 at late times one has a Big Rip singularity.

Another interesting model in FRW cosmology has recently been introduced in de Haro and Amoros (2013) in order to deal with non-singular universes. One considers once again the curve \(\rho=G(T)=-\frac{T}{2}-\varLambda\), but with a non-linear EoS

$$ p(\rho)=-\frac{\rho^2}{\rho_i} \Leftrightarrow f(\rho )=-\rho\biggl(1- \frac{\rho}{\rho_i} \biggr), $$
(50)

where ρ i is a constant satisfying Λ≪ρ i .

This model has two de Sitter solutions \(H_{f}=\sqrt{\frac{\varLambda }{3}}\) and \(H_{i}=\sqrt{\frac{\varLambda+\rho_{i}}{3}}\), and shows a universe evolving from an early inflationary phase (de Sitter phase H i ) to a late time accelerated expansion (de Sitter phase H f ) passing trough a matter dominated phase which allows the formation of structures. It could be also understood as an universe which a huge cosmological constant ρ i at early times, that evolves, at late times, to a small cosmological constant Λ leading the current cosmological acceleration.

In this case, for the current (small) value of T , using (47), (50) and G −1(ρ)=−2(ρ+Λ) one gets

$$ \begin{array}{l} \omega_{eff}(\rho)=-1-\displaystyle\frac{\rho(\rho_i-\rho)}{\rho_i(\rho +\varLambda)}\\[12pt] q_{dec}( \rho)=-1-\displaystyle\frac{3\rho(\rho_i-\rho)}{2\rho_i(\rho+\varLambda )},\\[12pt] j(\rho)=1-\displaystyle\frac{9\rho^2(\rho_i-\rho)}{\rho_i^2(\rho +\varLambda )},\qquad s(\rho)=-2\displaystyle\frac{\rho^2(\rho_i-\rho)}{\rho_i(\rho^2+\rho _i\varLambda)}. \end{array} $$
(51)

6.1 Loop quantum cosmology and brane cosmology with a small cosmological constant Λ

In loop quantum cosmology which reminds brane one the effective Friedmann equation depicts the following ellipse (see for example Bamba et al. 2013)

(52)

in the plane (H,ρ). Where ρ c is the so-called critical density, that satisfies Λ≪ρ c . In this case this curve can be written in two pieces ρ m =G −(T) and ρ m =G +(T), where

(53)

Since nowadays H 0 and ρ 0 have small values, we need to choose G(T)≡G −(T) and then, using the formula (43), one gets

(54)

what shows that the effective formulation of LQC is a teleparallel theory.

To compare with FRW cosmology, since nowadays T is small compared with ρ c , we can expand G(T) up to second order in T, to get

(55)

and inserting this expression into (45), one obtains the first order correction to the FRW cosmology. Moreover, in order to obtain exact formulas one has to use Eq. (47), because in that case G −1(ρ) has a very simple, quadratic expression:

$$G^{-1}(\rho)=-2({\rho+\varLambda}) \biggl(1-\frac{\rho+\varLambda }{\rho_c} \biggr). $$

A straightforward calculation gives

(56)

On the other hand, as we have already seen in Sect. 2, in brane cosmology in the Randall-Sundrum scenario the modified Friedmann equation depicts the following hyperbola

(57)

on the plane (H,ρ).

Finally, by comparing this equation with (52) it follows that, in order to obtain the corresponding formulas in brane cosmology, we just need to make the change ρ c →−2λ. Moreover, with this replacement one can apply the general formulas (56) to any EoS, in particular to the model studied is Sect. 4.

A very important remark is here in order. As a result of the above replacement it follows that the dynamics resulting for both theories, LQC and BC, are very different, because their corresponding Freedmann equations depict two completely different curves. In particular, Rip singularities, as we have seen in Sect. 5, are allowed in BC because the hyperbola is an unbounded curve. But, since in LQC the Friedmann equation depicts a bounded curve (an ellipse), Rip singularities cannot appear in this case. For example, for the EoS p(ρ)=ωρ, the universe is non-singular (see de Haro and Amoros 2013 for a detailed explanation). In fact, for ω>−1 (resp. for ω<−1) it moves in an anti-clockwise (resp. clockwise) way from the anti de Sitter solution \(H=-\sqrt{\frac{\varLambda}{3}}\sqrt{1-\frac{\varLambda}{\rho_{c}}}\) (resp. from the de Sitter solution \(H=\sqrt{\frac{\varLambda}{3}}\sqrt{1-\frac{\varLambda}{\rho _{c}}}\)) to the de Sitter one \(H=\sqrt{\frac{\varLambda}{3}}\sqrt{1-\frac{\varLambda}{\rho _{c}}}\) (resp. to the anti de Sitter one \(H=-\sqrt{\frac{\varLambda}{3}}\sqrt{1-\frac{\varLambda}{\rho_{c}}}\)).

In the early universe the parameter ρ c is very large ρ c ≫ρ 0. In principle, the parameter ρ c can vary with time or, in other words, we can consider LQC with the parameter ρ c in some cosmological epoch. For illustration we can estimate the possible value ρ/ρ c at the present epoch (at redshifts 0<z<1.75). As the LQC equations formally coincide with the cosmological equations on the brane in the RS scenario, one can confront the simplest loop quantum cosmology model (ρ=ρ m ) with observational data, in the same manner as it was done in Sect. 4. The analysis shows (see Fig. 6) that the best fit for the SNe+H(z)+BAO data is achieved for γ=(ρ 0+Λ)/ρ c ≈0.03. Maybe this result can be considered as an argument in favor of loop quantum cosmology.

Fig. 6
figure 6

The 68.3 % (solid) and 95.4 % (dotted) confidence level contours in the Ω Λ −γ parameter space from the SNe+H(z)+BAO data analysis in the case when ρ=ρ m . The best-fit parameters for the observational data are Ω Λ =0.712, ρ/ρ c =0.03 with χ 2=560.58 (to compare with \(\chi^{2}_{\min}=561.31\) for the ΛCDM model)

Full size image

7 Conclusion

We have confronted in this paper several DE models on the brane with combined data coming from different and independent cosmological surveys. The analysis here performed shows that the fitting of these observational data is actually better for the FRW cosmology in the frame of the chosen model for dark energy. Also, owing to the fact that the LQC equations formally coincide with the cosmological equations on the brane in the RS scenario, we could additionally confront the simplest (but very important) loop quantum cosmology model (ρ=ρ m ) with observational data, in the same manner as it was done with the brane models. The analysis we carried out showed (Fig. 6) that the best fit for SNe+H(z)+BAO data is achieved for γ=(ρ 0+Λ)/ρ c ≈0.03, what could be actually viewed as an argument in favor of loop quantum cosmology.

Taking everything into account, the observational cosmological results do not exclude, in principle, that the real cosmology could in fact differ from that of the FRW model. A window is still open to discrepancy. The importance of joint analysis of the various observational independent data sources has been clearly manifested, in the discussions of the several tables and plots. Taking into account together the SNe apparent magnitude measurements, Hubble parameter evolution data, and BAO and matter density perturbation data we are able to get a quite rigid constraint on the allowed value for the brane tension in the frames of the different brane models considered here.